Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.179 Medellín maio/jun. 2013
APLICACIÓN EXTENDIDA DE UNA TÉCNICA DE IMPEDANCIA DE SECUENCIA A LA LOCALIZACIÓN DE FALLAS EN SISTEMAS DE DISTRIBUCIÓN
EXTENDED APPLICATION OF A SEQUENCE IMPEDANCE BASED FAULT LOCATION TECHNIQUE APPLIED TO POWER DISTRIBUTION SYSTEMS
ANDRÉS BEDOYA-CADENA
M.Sc., Investigador ICE3, Universidad Tecnológica de Pereira. Colombia. afbedoya@utp.edu.co
JUAN MORA-FLÓREZ
Ph.D., Profesor asociado, Universidad Tecnológica de Pereira. Colombia, jjmora@utp.edu.co.
SANDRA PÉREZ-LONDOÑO
M.Sc., Profesora titular, Universidad Tecnológica de Pereira. Colombia, saperez@utp.edu.co.
Recibido para revisar Mayo 12 de 2012, aceptado Abril 26 de 2013, versión final Mayo 2 de 2013
RESUMEN: En este artículo se presenta la definición y aplicación extendida de una técnica de localización de fallas para sistemas de distribución, que se fundamenta en la estimación de la distancia a la falla a partir de la interconexión de las redes de secuencia equivalentes, en condición de falla. La técnica de localización propuesta utiliza medidas de tensión y corriente adquiridas en la cabecera del circuito y considera el hecho que la carga es variable, por medio de un factor proporcional a las medidas de corriente adquiridas en la subestación. Se presenta el análisis asociado a tres tipos de fallas paralelas, monofásicas, bifásicas y trifásicas balanceadas. La técnica de localización se valida en el sistema de prueba IEEE de 34 nodos de tensión nominal de 24,9kV, que incluye ramales monofásicos y trifásicos, para todos los tipos de fallas, en dos escenarios de carga y considerando resistencias de falla entre 0W y 40W. De acuerdo con las pruebas, se presentan errores en la estimación de la distancia a la falla inferiores a 2,5%.
PALABRAS CLAVE: Calidad de energía, localización de fallas, técnicas basadas en la impedancia, radial equivalente, redes de secuencia y sistemas de distribución
ABSTRACT: This paper presents the definition and the extended application of a fault location technique for power distribution systems based on the well defined equivalent sequence networks. The proposed location technique uses single end measurements of voltage and current and considers variable load, through a proportional factor applied to the measured currents. The analysis is presented for three types of shunt faults, single phase to ground faults, phase to phase faults and three phase faults. The localization technique is tested on the 34 bus IEEE test feeder of 24.9kV; it includes three-phase and single phase laterals, for all types of faults in two different load scenarios and considering fault resistances between 0W and 40W. The estimation errors obtained in fault distance lower than 2.5%.
KEYWORDS: Power quality, fault location, impedance based techniques, equivalent feeder, sequence networks and power distribution systems.
1. INTRODUCCIÓN
Como es ampliamente reconocido, las fallas causan interrupciones en el suministro de energía eléctrica y afectan directamente los índices de continuidad [1]. Con relación a la continuidad, en Colombia se definió el Índice de Referencia Agrupado de la Discontinuidad (IRAD), que relaciona la cantidad promedio de energía no suministrada, durante el período utilizado como referencia, y el Índice Trimestral Agrupado de la Discontinuidad (ITAD) que relaciona la cantidad promedio de energía no suministrada durante el trimestre de evaluación, según la resolución CREG 097 de 2008 [2].
Los localizadores de falla ayudan a mejorar los índices de continuidad por tres aspectos. El primero de ellos se asocia con el incremento de la velocidad en el proceso de restauración del sistema después de la ocurrencia de una falla. Otro aspecto, hace referencia a que si se realiza la ubicación adecuada de una falla, es posible mejorar las operaciones de reconfiguración del sistema con el objetivo de reducir el área afectada. El último aspecto, se enfoca en la localización de fallas de naturaleza transitoria para mejorar las tareas de mantenimiento y prevención de futuras fallas [3].
En sistemas de transmisión los métodos de localización de fallas propuestos funcionan adecuadamente. Sin embargo, estos algoritmos no son aplicables de forma extendida en los sistemas de distribución debido a características propias, como tener un único punto de medida de tensión y corriente, la presencia de ramales monofásicos, la presencia de cargas variables, la topología radial y las secciones de línea no homogéneas.
La temática de localización de fallas en sistemas de distribución se ha tratado primordialmente a partir de dos metodologías. Las metodologías de localización que calculan una distancia en función de la impedancia vista desde la subestación, denominadas técnicas basadas en el modelo eléctrico de la red, como las presentadas en [4 - 8]. Otro tipo de metodologías son las técnicas de explotación computacional, que consisten en el aprendizaje y clasificación de información a partir de grandes bases de datos y son conocidas como métodos de clasificación basados en el conocimiento, como las analizadas en [3, 9, 10].
En este artículo se presenta una técnica alternativa para la localización de fallas en sistemas de distribución que se basa en la estimación de la impedancia de secuencia y utiliza las medidas del fundamental de tensión y corriente adquiridas en la subestación. Algunas metodologías como [5] y [6], desprecian el efecto de la carga en el análisis, factor que es de suma importancia para determinar adecuadamente la sección bajo falla; otras como [7] si lo consideran pero limitan la descripción del análisis a una sección de línea simplificada, lo cual no permite su aplicación extensiva.
La técnica que se propone en este artículo tiene como aporte principal, la utilización de un circuito equivalente generalizado, que considera las características propias de cualquier sistema de distribución real. Además, combina el uso de los equivalentes de secuencia con el análisis de componentes de fase, para determinar la distancia a la falla. La técnica propuesta emplea los equivalentes de secuencia para simplificar el análisis circuital de cada sección de línea; los componentes de fase se utilizan para actualizar los fasores de tensiones y corrientes en cada tramo de línea. Finalmente, otro aporte consiste realizar el análisis de la carga y su incertidumbre en cada sección del circuito.
Como contenido, en la segunda sección se presenta el desarrollo matemático asociado a la técnica de localización de fallas propuesta. En la sección tres se describe el algoritmo implementado para la aplicación de la metodología al problema extendido de localización. En la sección cuatro se describen las pruebas y los buenos resultados obtenidos al aplicar la técnica de localización de fallas en un sistema de prueba. Finalmente, en la sección cinco se presentan las conclusiones más importantes de la investigación realizada.
2. TÉCNICA PROPUESTA PARA LA LOCALIZACIÓN DE FALLAS
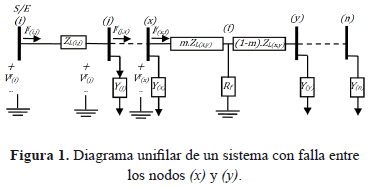
La metodología de localización de fallas es definida a partir del circuito de la figura 1, que muestra una sección de línea entre los nodos (x) y (y) de un alimentador de distribución bajo falla.
Donde,
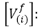 Tensiones de fase en condición de falla, medidas en la subestación (nodo (i)).
Tensiones de fase en condición de falla, medidas en la subestación (nodo (i)).
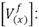 Tensiones de fase, calculadas en el nodo (x) en condición de falla.
Tensiones de fase, calculadas en el nodo (x) en condición de falla.
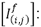 Corrientes de fase en condición de falla, medidas en la subestación.
Corrientes de fase en condición de falla, medidas en la subestación.
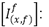 Corrientes de fase, calculadas entre el nodo (x) y (f) en condición de falla.
Corrientes de fase, calculadas entre el nodo (x) y (f) en condición de falla.
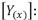 Matriz admitancia de carga en el nodo (x).
Matriz admitancia de carga en el nodo (x).
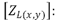 Matriz impedancia de fase en W, de la sección de línea entre los nodos (x) y (y).
Matriz impedancia de fase en W, de la sección de línea entre los nodos (x) y (y).
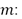 Distancia a la falla por unidad de longitud.
Distancia a la falla por unidad de longitud.
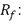 Resistencia de falla.
Resistencia de falla.
2.1. Análisis para fallas monofásicas a tierra
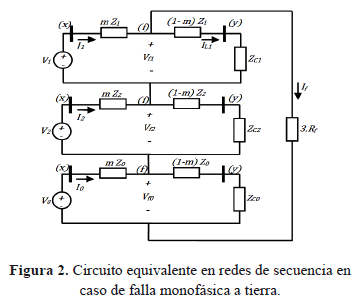
En caso de una falla monofásica a tierra, en la sección de línea entre los nodos (x) y (y) del alimentador mostrado en la figura 1, los circuitos equivalentes en redes de secuencia se conectan en serie, como se presenta en la figura 2. Se conocen las tensiones de secuencia positiva (V1), negativa (V2) y cero (V0) en el nodo (x), las corrientes de secuencia positiva (I1), negativa (I2) y cero (I0) que fluyen desde el nodo (x) al punto de falla (f) y las impedancia de secuencia positiva (Z1), negativa (Z2) y cero (Z0) de la sección de línea entre los nodos (x) y (y).
La figura 2, muestra tres impedancias (Zc1, Zc2 y Zc0) que permiten considerar la carga que alimenta el circuito en condición falla, las cuales por ahora se asumen conocidas. En la sección 3.4 se presenta la forma de calcular la impedancia de carga de secuencia positiva (Zc1), que se requiere para el análisis circuital que a continuación se realiza.
Del circuito de la figura 2, se obtienen las ecuaciones (1), (2), (3) y (4).

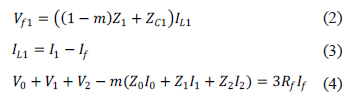
De las ecuaciones (1), (2), y (3) se obtiene la ecuación (5).

Reemplazando la ecuación (5) en (4) y realizando las operaciones respectivas se obtiene la ecuación (6).
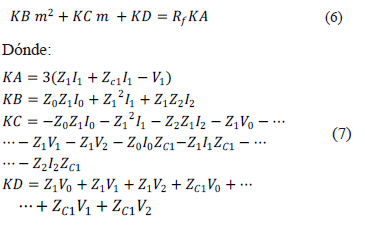
La ecuación (6) es un polinomio de segundo orden con constantes complejas con dos incógnitas (Rf y m). Para resolver este polinomio, se separa en parte real y parte imaginaria a la expresión (6), y se obtienen dos ecuaciones con dos incógnitas, tal como lo muestra la ecuación (8) en donde los subíndices r e i hacen referencia a la parte real e imaginaria de cada constante.
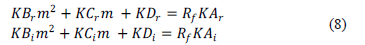
De la parte real se despeja la resistencia de falla (Rf) y se remplaza en la parte imaginaria obteniendo la expresión (9), que al ser resuelta permite obtener la distancia a la falla (m).
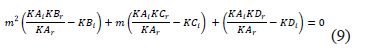
2.2. Análisis para fallas bifásicas
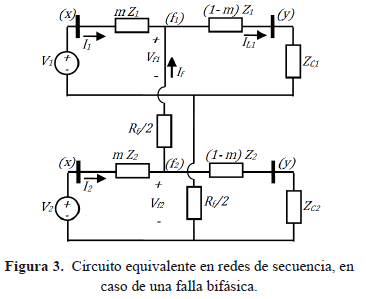
Para una falla bifásica, en la sección de línea entre los nodos (x) y (y), del circuito presentado en la figura 1, las redes de secuencia se conectan en paralelo, y se obtiene el circuito de la figura 3.
Del circuito de la figura 3, se obtienen las ecuaciones (10), (11), (12) y (13).
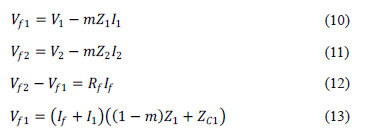
Igualando las ecuaciones (10) y (13) se obtiene la ecuación (14) y de las ecuaciones (11) y (12) se obtiene (15).
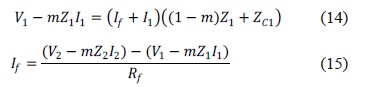
Reemplazando la ecuación (15) en (14) y realizando las operaciones respectivas se obtiene (16).
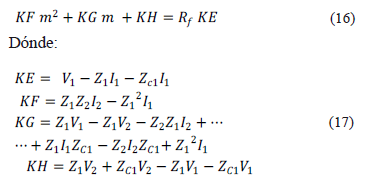
La ecuación (16) corresponde a una ecuación cuadrática compleja, que se puede resolver separando (16) en parte real y parte imaginaria, obteniendo dos ecuaciones muy similares a las presentadas en (8) con dos incógnitas (Rf y m).
2.3. Análisis para fallas trifásicas
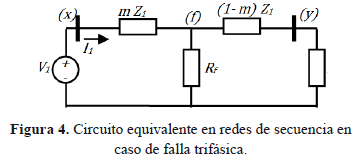
Para la falla trifásica, las redes de secuencia se consideran de forma independiente. Por lo tanto se realiza el análisis únicamente con el circuito de secuencia positiva, que se presenta en la figura 4.
Del circuito de la figura 4, se obtiene (18).
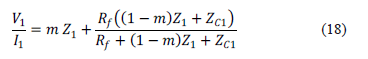
Realizando las operaciones indicadas en (18), es posible llegar a la ecuación (19).
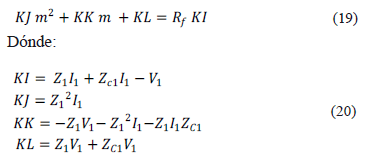
La ecuación (19) es a una ecuación cuadrática compleja, que se resuelve separando su parte real e imaginaria y obteniendo dos ecuaciones muy similares a las presentadas en (8), con dos incógnitas (Rf y m).
3. ALGORITMO PROPUESTO PARA LA APLICACIÓN EXTENDIDA DE LA TÉCNICA DE LOCALIZACIÓN DE FALLAS.
El algoritmo propuesto para la localización de fallas requiere como información inicial los fasores de tensión y corriente, de prefalla y falla, adquiridos en la cabecera del circuito y los radiales equivalentes del sistema de distribución que se pretende analizar. Estos radiales equivalentes son descritos en la sección 3.1.
Como paso inicial, se selecciona uno de los radiales equivalentes del sistema de distribución, luego a partir de las medidas de corriente se determina el tipo de falla, tal como se describe en la sección 3.2. A continuación se transforman las medidas de tensión y corriente, de falla y prefalla, en redes de secuencia y se obtienen los parámetros de secuencia (Z1, Z2 y Z3) del segmento de línea, tal como se describe en la sección 3.3.
El paso siguiente es calcular la impedancia de carga de secuencia positiva asociada al tramo de línea a examinar, tal como se describe en la sección 3.4.
De acuerdo al tipo de falla se calculan las constantes (KA,KB,KC,KD) ó (KE,KF,KG,KH) ó (KI,KJ,KK,KL) descritas en las secciones 2.1, 2.2 y 2.3. Luego se resuelve la ecuación cuadrática asociada a cada grupo de constantes para obtener la distancia a la falla m.
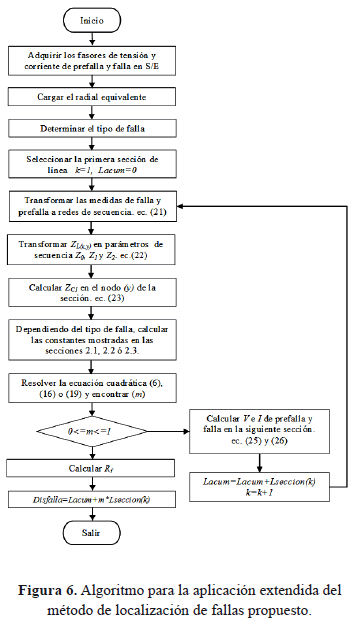
El valor de m corresponde a la distancia a la falla por unidad de longitud; si su valor estimado se encuentra en un intervalo entre 0 y 1, se asume que se encontró la sección bajo falla y la distancia a la falla estimada corresponde al producto de m y la longitud total de la primera sección de línea. De lo contrario, se calculan tensiones y corrientes en la siguiente sección de línea como se muestra en la sección 3.5, y se repite el procedimiento hasta que se verifique que m tenga un valor entre 0 y 1. El diagrama de flujo del algoritmo se presenta en la figura 5.
3.1. Definición de radiales equivalentes
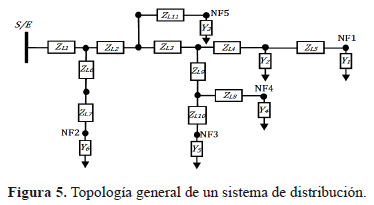
Los sistemas de distribución reales son de topología radial y bastante ramificados, con diferentes tipos de conductor, longitud y configuración tal como se muestra en la figura 6.
En [11] los autores proponen una metodología de reducción de sistemas de distribución ramificados a radiales equivalentes para la aplicación extendida del método propuesto en la sección 2.
Los radiales equivalentes son una simplificación del sistema de distribución original y son múltiples alimentadores radiales conformados sólo por líneas y cargas que representan una parte del sistema de distribución original.
En la figura 6, ZLK es la matriz de impedancia del tramo k del circuito, que depende del calibre, de la disposición y de la longitud de los conductores de cada sección. La matriz admitancia asociada a cada carga del sistema es YK.
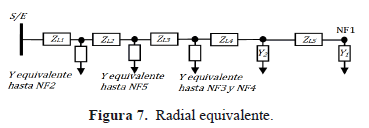
Un sistema de distribución posee tantos radiales equivalentes como nodos finales tenga. Para el sistema presentado en la Figura 6, se tienen 5 radiales equivalentes y uno de éstos corresponde al presentado en la Figura 7.
3.2. Determinación de la ocurrencia y del tipo de falla
Para determinar la ocurrencia de una falla y determinar su tipo se definen dos corrientes de umbral, una asociada a las fallas de fase y otra asociada a las fallas que involucran contacto con tierra. Estas corrientes de umbral generalmente se definen de acuerdo con la carga máxima que alimente el circuito a analizar.
Como se conocen las medidas de corriente en la subestación en cada una de las fases, en el instante que ocurra una falla se realiza una comparación sucesiva con las corrientes de umbral, de tal forma que si la corriente de alguna de las fases es mayor que la corriente de umbral, se asume que ocurrió una falla. Además usando el algoritmo descrito en [12] es posible determinar el tipo de falla.
3.3. Transformación de tensiones y corrientes en componentes simétricas e impedancia de secuencia de líneas
De forma general, los equivalentes de componentes simétricas [13], se obtienen al transformar un sistema de n fasores desbalanceados, en n-1 sistemas balanceados de n fasores con secuencia de fase diferente y un sistema de n fasores idénticos. Para transformar las medidas de tensión y de corriente de un sistema de tres fases a redes de secuencia se utilizan las expresiones presentadas en (21).
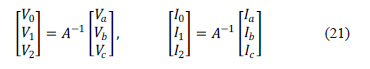
Es importante tener en cuenta que dependiendo del tipo de falla se toma como referencia una fase diferente, y por lo tanto la matriz de transformación de parámetros de fase a parámetros de secuencia cambia. La tabla 1 muestra la matriz a emplear para cada tipo de falla.
Para obtener la impedancia de secuencia de cada tramo de línea se utiliza la expresión (22), en donde 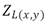 corresponde a la matriz que representa la impedancia del segmento de línea entre los nodos (x), (y).
corresponde a la matriz que representa la impedancia del segmento de línea entre los nodos (x), (y).
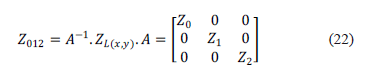
3.4. Cálculo de la impedancia de carga en cada sección de línea
La impedancia de carga de secuencia positiva (ZC1) se calcula por medio de (23), que relaciona la tensión de prefalla de secuencia positiva 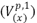 estimada en el nodo (x) con la corriente de secuencia positiva
estimada en el nodo (x) con la corriente de secuencia positiva 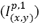 que fluye desde el nodo (x) al nodo (y) en condición de prefalla, y a esta relación se le sustrae la impedancia de secuencia positiva (Z1) de la sección de línea entre los nodos (x) y (y) (figura 9).
que fluye desde el nodo (x) al nodo (y) en condición de prefalla, y a esta relación se le sustrae la impedancia de secuencia positiva (Z1) de la sección de línea entre los nodos (x) y (y) (figura 9).

3.5. Actualización de medidas en cada sección y variación de la carga
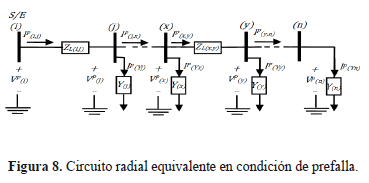
Normalmente, las únicas medidas disponibles del sistema de distribución, se encuentran asociadas a la subestación. Por lo tanto, para calcular las tensiones y corrientes en condición de prefalla y falla en los demás nodos del radial equivalente, se realiza un barrido iterativo sección por sección tal como se muestra en la figura 8.
Debido a que el modelo de carga es de admitancia constante y en un sistema real la carga es variable, se considera la variación en la carga mediante un factor de corriente complejo por fase, el cual se calcula como se muestra en (24). Este factor de compensación se utiliza para actualizar la corriente en la sección de línea entre los nodos (i) y (j), tal como lo muestra la expresión (27).
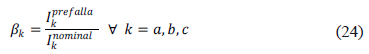
Para calcular las tensiones y las corrientes en el nodo (j) del circuito de la figura 8, a partir de las medidas de tensión y corrientes adquiridas en la subestación (nodo (i)), se emplea (21) y (22), respectivamente.
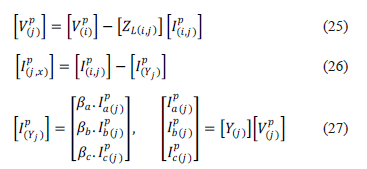
Donde,
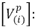 Tensiones de fase en condición de prefalla, medidas en la subestación (nodo (i)).
Tensiones de fase en condición de prefalla, medidas en la subestación (nodo (i)).
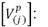 Tensiones de fase, calculadas en el nodo (j) en condición de prefalla.
Tensiones de fase, calculadas en el nodo (j) en condición de prefalla.
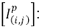 Corrientes de fase en condición de prefalla, medidas en la subestación.
Corrientes de fase en condición de prefalla, medidas en la subestación.
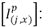 \sCorrientes de fase, calculadas entre el nodo (j) y (x) en condición de prefalla.
\sCorrientes de fase, calculadas entre el nodo (j) y (x) en condición de prefalla.
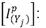 Corrientes de fase, requeridas por la admitancia de carga Yj en condición de prefalla.
Corrientes de fase, requeridas por la admitancia de carga Yj en condición de prefalla.
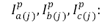 Corrientes de fase calculadas en el nodo (j) en condición de prefalla.
Corrientes de fase calculadas en el nodo (j) en condición de prefalla.
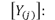 Matriz admitancia de carga en el nodo (j).
Matriz admitancia de carga en el nodo (j).
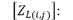 Matriz impedancia de fase, de la sección de línea entre los nodos (i) y (j).
Matriz impedancia de fase, de la sección de línea entre los nodos (i) y (j).
Las ecuaciones (25), (26) y (27) se utilizan para calcular las tensiones y corrientes de prefalla en todas las secciones de línea del radial equivalente del sistema de distribución. Adicionalmente, se emplean para calcular las tensiones y corrientes de falla a partir de las medidas adquiridas en las subestación, ya que el modelo del sistema de distribución en condición de falla (figura. 1), es equivalente al de la condición de prefalla para todos los tramos antes de la sección de línea bajo falla.
4. PRUEBAS Y ANÁLISIS DE RESULTADOS
4.1. Sistema de distribución utilizado en las pruebas del localizador
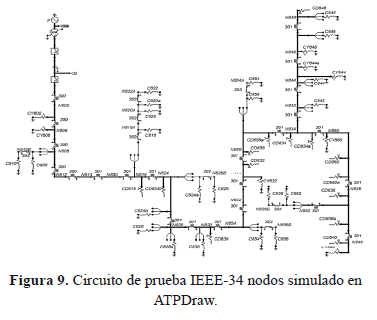
Como sistema de prueba para validar el algoritmo de localización de fallas se emplea el IEEE de 34 nodos de la figura 9 el cual se simula en ATP [14]. Los datos del sistema se obtienen del "test feeders" del "Distribution system subcommittee" del "Institute Electrical and Electronics Enginieers" [15]. Este alimentador de distribución está ubicado en el estado de Arizona (Estados Unidos) y opera a una tensión de 24,9 kV. Entre sus principales características están la presencia de radiales monofásicos y trifásicos, múltiples calibres de conductor y la presencia de cargas desbalanceadas con conexiones en delta y estrella.
4.2. Descripción de las pruebas y resultados
Con el sistema descrito en la sección anterior, se realizan pruebas extensivas al localizador de fallas que consisten en simular fallas monofásicas, bifásicas y trifásicas con resistencias en un rango de 0 a 40W en pasos de 8W, en todos los nodos del radial de mayor longitud del circuito.
El radial de mayor longitud comprende los nodos que van desde la subestación nodo (N800), hasta el nodo final (N848) y tiene una longitud de 57,75 km. Los registros de falla se obtienen para la condición de carga nominal y en un escenario con variación aleatoria de carga entre un 20% y un 150% de la carga nominal, utilizando ATP y una herramienta de simulación automática de eventos desarrollada en Matlab® [16].
Para analizar el comportamiento del método de localización de fallas propuesto, se emplea como indicador el error, calculado por medio de (28).

Los resultados se presentan en curvas de desempeño, cuyo eje vertical corresponde al error y su eje horizontal a la distancia real entre la subestación y cada nodo analizado del radial.
4.3. Validación de la metodología a condición nominal de carga
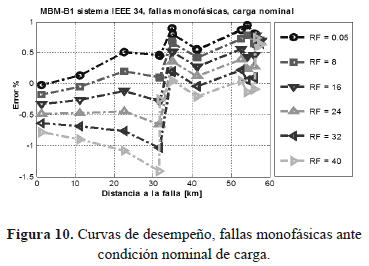
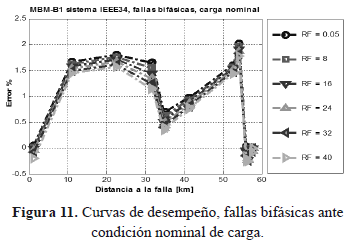
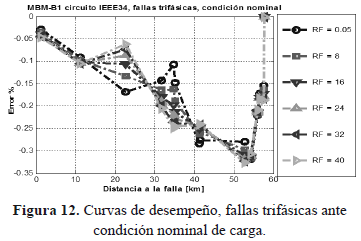
Las figuras 10, 11 y 12 muestran el desempeño del localizador en condición nominal de carga, ante fallas monofásicas, bifásicas y trifásicas respectivamente.
La figura 10, muestra una subestimación generalizada de la distancia calculada para las fallas monofásicas con resistencia de 0,05 W y una sobreestimación generalizada para fallas con resistencia de 40W. Para las demás resistencias de falla analizadas se observa una sobreestimación de la distancia en las primeras cuatro secciones de línea y de ahí en adelante se observa un comportamiento de subestimación. El desempeño del método de localización propuesto, evidenciado por los errores obtenidos, se encuentra en un rango entre -1,5% y 1%, lo que demuestra un buen comportamiento ante fallas de este tipo, que son las más frecuentes en sistemas de distribución.
El desempeño ante fallas de tipo bifásicas se encuentra en un rango entre -0,4% y 2%, y en general se observa un comportamiento de sobreestimación. Adicionalmente, para este tipo de fallas, la variación en la resistencia no muestra un impacto considerable en el desempeño del localizador propuesto.
4.4. Validación de la metodología a condición aleatoria de carga
En un sistema de distribución real, la carga no es constante y depende fundamentalmente de las características de utilización impuestas por los usuarios del sistema. Por otra parte en el ATP, los modelos de carga con que se cuenta actualmente son de admitancia constante y sus valores se pueden calcular a partir de la potencia promedio, proveniente de estudios preliminares que estiman el consumo de energía eléctrica. Para considerar esta situación y con el objeto de validar el método de localización propuesto, se realiza una modificación aleatoria de las impedancias de carga por fase y por componente real e imaginaria. Normalmente, la carga del circuito se incrementa hasta un 50% y puede disminuir hasta por lo menos un 80% de la condición promedio de carga, por lo tanto se considera adecuado para la validación del método, realizar una variación aleatoria en un rango entre el 20% y el 150% de la condición nominal.
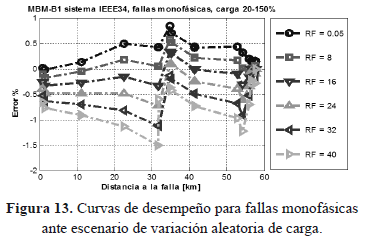
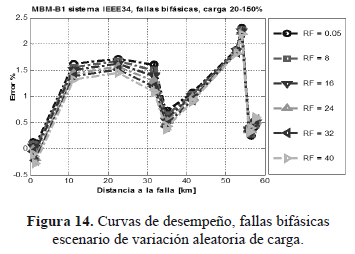
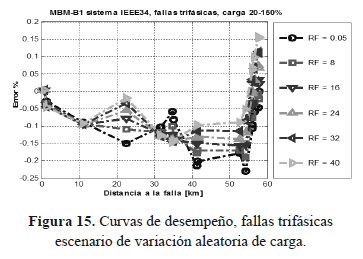
Las figuras 13, 14 y 15 muestran el desempeño del localizador en un escenario de variación aleatoria de carga entre el 20 y el 150% de la condición nominal, ante fallas monofásicas, bifásicas y trifásicas respectivamente.
La figura 13, muestra que los errores absolutos obtenidos para fallas monofásicas ante condición aleatoria de carga, oscilan entre -1,5% y 0,9% y su comportamiento es muy similar al obtenido en condición nominal de carga (figura 10).
En comparación con la condición nominal, el desempeño ante fallas bifásicas no muestra grandes diferencias, aunque el rango de error se incrementa un poco y está entre -0,4% y 2,3%.
De acuerdo con la figura 15, se observa que la metodología ante fallas trifásicas y en un escenario de variación aleatoria de carga, presenta un comportamiento de sobreestimación de la distancia de falla muy similar al obtenido en condición nominal de carga. La principal diferencia consiste en que para los últimos tramos de línea su comportamiento pasa a ser de subestimación y que el rango de errores cambia un poco y está en entre -0,23% y 0,16%.
Considerar la variación en la carga involucrando el factor 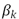 descrito en la sección (3.5), conlleva a que el desempeño del localizador ante una modificación aleatoria de la carga, que corresponde a una situación real en un sistema de distribución, tienda a ser muy similar al obtenido en condición nominal de carga, tal como lo muestran las figuras 13, 14 y 15.
descrito en la sección (3.5), conlleva a que el desempeño del localizador ante una modificación aleatoria de la carga, que corresponde a una situación real en un sistema de distribución, tienda a ser muy similar al obtenido en condición nominal de carga, tal como lo muestran las figuras 13, 14 y 15.
4.5. Principales fuentes de incertidumbre
El método requiere de una buena estimación de los fasores de prefalla y falla de las tensiones y corrientes, y una base de datos que represente correctamente el sistema de distribución.
Como casi siempre se tienen medidas adecuadas, el efecto más importante en el desempeño está asociado a la incertidumbre en la longitud de las líneas y principalmente en el valor de la carga. Sin embargo, la técnica propuesta considera la incertidumbre en la carga mediante el factor de compensación 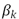 descrito en la sección 3.5.
descrito en la sección 3.5.
5. CONCLUSIONES
Según los resultados obtenidos, se valida el supuesto asociado a que la metodología de localización propuesta es solución satisfactoria y práctica al problema de localización de fallas. Ante fallas monofásicas, bifásicas y trifásicas, los errores en la estimación de la distancia no superan ±2,5%, para un rango de resistencias de falla entre 0 y 40W, y considerando los escenarios de variación aleatoria de carga propuestos. A partir de lo anterior y adicionalmente teniendo en cuenta que la técnica de localización de fallas requiere solamente de las medidas de tensión y corriente en prefalla y falla, y de los parámetros del circuito a analizar, se puede afirmar que la metodología propuesta es lo suficientemente robusta y puede ser implementada fácilmente y de manera extendida en los sistemas reales.
Finalmente, la técnica propuesta ayuda a mantener los índices de continuidad en sistemas de distribución de energía eléctrica, donde el problema de localización de fallas no es una tarea fácil de realizar.
AGRADECIMIENTOS
Este trabajo fue desarrollado en el grupo de investigación ICE3 y apoyado por la Universidad Tecnológica de Pereira por medio de la Vicerrectoría de Investigaciones, Innovación y Extensión y por el programa de Jóvenes investigadores e innovadores "Virginia Gutiérrez de Pineda" de Colciencias.
REFERENCIAS
[1] IEEE Std 37.114. IEEE Guide for Determining Fault Location on AC Transmission and Distribution Lines, Power System Relaying Committee 2004. [ Links ]
[2] CREG Comisión Reguladora de Energía y Gas, Resolución 097 de 2008, Ministerio de Minas y Energía de Colombia 2008. [ Links ]
[3] Mora, J., Morales, G. and Perez, S., Learning Based Strategy for Reducing the Multiple Estimation Problem of Fault Zone Location in Radial Power Systems. IET Generation, Transmission & Distribution. Vol. 3, Issue 4, pp. 346-356, 2009. [ Links ]
[4] Mora, J, Carrillo, G. Meléndez, J., Comparison of Impedance Based Fault Location Methods for Power Distribution Systems. Electric Power Systems Research, pp. 657-666. Vol. 28. 2008. [ Links ]
[5] Warrington, A. and Van, C., Protective relays. Their theory and practice, Vol I, Chapman and Hall Ltd. London, 1968. [ Links ]
[6] Girgis, A., Fallon, C., Lubkeman, D., A Fault Location Technique for Rural Distribution Feeders, IEEE Transactions on Industry Applications, Vol. 29, pp. 1170-1175, November 1993. [ Links ]
[7] Novosel, D., Hart, D. and Myllymaki, J., System For Locating Faults and Estimating Fault Resistance in Distribution Networks With Tapped Loads, No. USpatent 5, pp. 839,093. 1998, [ Links ]
[8] Morales, G., Mora, J. and Vargas, H., Elimination of Multiple Estimation for Fault Location in Radial Power Systems by Using Fundamental Single-End Measurements. IEEE Transactions on Power Delivery, Vol. 24, 1382 - 1389, 2009. [ Links ]
[9] Purushothama, G. and Narendranath, A., ANN Applications in Fault Locators. International Journal of Electrical Power and Energy Systems, pp. 491-506. 2001. [ Links ]
[10] Mora, J., Carrillo, G. and Barrera, V., Fault Location in Power Distribution Using a Learning Algorithm for Multivariable Data Analysis. IEEE Transaction On Power Delivery, Vol. 22, No. 3, 2007. [ Links ]
[11] Bedoya, A., Mora, J. and Pérez, S., Estrategia de reducción para la aplicación generalizada de localizadores de fallas en sistemas de distribución de energía eléctrica. Revista EIA, Volumen 17, pp. 21-37, 2011. [ Links ]
[12] Das, R., Determining the locations of Faults in distribution systems. [PhD Thesis] Saskatoon, Canada, University of Saskatchewan, 1998. [ Links ]
[13] Anderson, P., Analysis of Faulted Power Systems. Wiley-IEEE Press. 1995. [ Links ]
[14] Alternative Transient Program: ATP/EMTP, Bonneville Power Administration, Available: http://www.emtp.org/. [Citado 30 de abril 2013] [ Links ].
[15] IEEE Distribution System Analysis Subcommittee. Radial Test Feeders. Available http://www.ewh.ieee.org/soc/pes/dsacom/testfeeders/index.html. [Citado 30 de abril de 2013] [ Links ].
[16] Pérez, L., Pérez, S. and Mora, J., Diseño de una herramienta eficiente de simulación automática de fallas en sistemas eléctricos de potencia. Revista Dyna, Año 77, Nro. 164, pp. 178188, ISSN 00127353. Medellín, 2010. [ Links ]