Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.180 Medellín jul./ago. 2013
AN INTERPOLATING CURVE SUBDIVISION SCHEME BASED ON DISCRETE FIRST DERIVATIVE
UN ESQUEMA DE SUBDIVISIÓN INTERPOLANTE BASADO EN LA PRIMERA DERIVADA DISCRETA
ALBEIRO ESPINOSA BEDOYA
M.Sc., Universidad Nacional de Colombia - Sede Medellín, Colombia, aespinos@unal.edu.co
GERMÁN SÁNCHEZ TORRES
Ph.D. Universidad del Magdalena - Santa Marta, Colombia, gsanchez@unimagdalena.edu.co
JOHN WILLIAN BRANCH BEDOYA
Ph.D., Universidad Nacional de Colombia - Sede Medellín, Colombia, jwbranch@unal.edu.co
Received for review January 29th, 2013, Accepted March 26th, 2013, final version June, 15th, 2013
ABSTRACT: This paper develops a new scheme of four points for interpolating curve subdivision based on the discrete first derivative (DFDS), which reduces the apparition of undesirable oscillations that can be formed on the limit curve when the control points do not follow a uniform parameterization. We used a set of 3000 curves whose control points were randomly generated. Smooth curves were obtained after seven steps of subdivision using five schemes DFDS, Four-Point (4P), New four-point (N4P), Tight four-point (T4P) and the geometrically controlled scheme (GC4P). The tortuosity property was evaluated on every smooth curve. An analysis for the frequency distributions of this property using the Kruskal-Wallis test reveals that DFDS scheme has the lowest values in a close range.
KEYWORDS: Curve subdivision, curve interpolation, four-point subdivision scheme.
RESUMEN: En este artículo se desarrolla un nuevo esquema de cuatro puntos para la subdivisión interpolante de curvas basado en la primera derivada discreta (DFDS), el cual, reduce la formación de oscilaciones indeseables que pueden surgir en la curva límite cuando los puntos de control no obedecen a una parametrización uniforme. Se empleó un conjunto de 3000 curvas cuyos puntos de control fueron generados aleatoriamente. Curvas suaves fueron obtenidas tras siete pasos de subdivisión empleando los esquemas DFDS, Cuatro-puntos (4P), Nuevo de cuatro-puntos (N4P), Cuatro-puntos ajustado (T4P) y el Esquema interpolante geométricamente controlado (GC4P). Sobre cada curva suave se evaluó la propiedad de tortuosidad. Un análisis de las distribuciones de frecuencia obtenidas para esta propiedad, empleando la prueba de Kruskal-Wallis, revela que el esquema DFDS posee los menores valores de tortuosidad en un rango más estrecho.
PALABRAS CLAVE: Subdivisión de curvas, interpolación de curvas, esquema de subdivisión de cuatro puntos.
1. INTRODUCTION
Curves are a powerful tool used in engineering to interpolate or approximate a set of points, with the aim to provide pleasant shapes [1]. Splines, NURBS and Subdivision are the most common techniques.
Subdivision has become a popular technique in computer graphics to create smooth curves and surfaces. Currently, it is the industry standard for character animation. It dates back to the work of Chaikin [2], where the corners of a control polygon are iteratively trimmed until a smooth curve is obtained in the limit. This an approximating scheme with 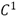 continuity.
continuity.
Four point schemes for interpolating curve subdivision have two fundamental challenges: first, obtain 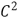 continuity on the whole curve, and the second is to prevent the apparition of undesirable oscillations. Several schemes have been proposed to date from Dubuc's work [3], which are characterized by having at most
continuity on the whole curve, and the second is to prevent the apparition of undesirable oscillations. Several schemes have been proposed to date from Dubuc's work [3], which are characterized by having at most 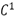 continuity interpolating the given points. Recent techniques have achieved curves with
continuity interpolating the given points. Recent techniques have achieved curves with 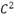 continuity, but do not interpolate the original data properly.
continuity, but do not interpolate the original data properly.
This paper focuses on the undesirable oscillations which may appear in the limit curve after an interpolating subdivision process. This problem has received little attention. Recently Hernandez et al. [4] proposed a new interpolatory subdivision scheme based on incenter subdivision which avoids undesirable oscillations.
2. PREVIOUS WORKS
For interpolating subdivisions it is common to use geometrical local schemes, such as four-point or six-point schemes. Earlier works such as Dubuc's [3] and Deslauriers and Dubuc's [5] propose four-point interpolating schemes, which insert a new point by fitting a cubic polynomial to neighboring points over uniformly spaced parameter values. The idea behind this scheme is that if the original control points fall on a defined polynomial, then the next level's control points must also lie on the same polynomial. This four-point scheme is exact for cubic polynomials. Equations 1 and 2 describe the new control points as a function of the old control points.
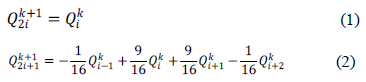
One generalization is presented by Dyn et al. in [6], who uses a four-point based scheme with a tension parameter 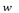 ; the limit curve presents
; the limit curve presents 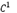 continuity when
continuity when 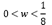 . Hechler et al. [7] showed that the
. Hechler et al. [7] showed that the 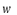 tension parameter generates limit curves, if and only if,
tension parameter generates limit curves, if and only if, 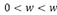 , where
, where 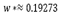 . One improvement is presented by Nira Dyn et al. in [8], where one new four-point scheme is developed with the tension parameter
. One improvement is presented by Nira Dyn et al. in [8], where one new four-point scheme is developed with the tension parameter 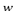 , where the limit curve presents
, where the limit curve presents 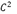 continuity, and the resulting curve is near to be interpolating.
continuity, and the resulting curve is near to be interpolating.
The characteristic of previous works has been that the tension parameter is always constant. Marinov et al. [9] presents a new scheme with a variable tension parameter, which is locally adapted according to the geometry of the control polygon. Beccari et al. [10] proposes a subdivision scheme which provides 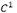 continuity with a single tension parameter that can be either arbitrarily increased or appropriately chosen. In the same way Floater [11] derives an algorithm for expressing the n - th order divided differences of the scheme at level
continuity with a single tension parameter that can be either arbitrarily increased or appropriately chosen. In the same way Floater [11] derives an algorithm for expressing the n - th order divided differences of the scheme at level 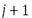 as an affine combination of n - th order divided differences at level j. This algorithm could be a useful tool for analyzing the smoothness of the scheme, especially when the grid points are irregularly spaced.
as an affine combination of n - th order divided differences at level j. This algorithm could be a useful tool for analyzing the smoothness of the scheme, especially when the grid points are irregularly spaced.
In Dubuc's work [3], uniform parameter values were assumed. Nira Dyn et al. [12] replaced those values by chordal and centripetal values since parameterization is updated at each refinement level. Related to this, Floater [13] derived an approximation property of four-point interpolating curve subdivision, based on local cubic polynomial fitting.
A step of subdivision can be considered as a sequence of simple, highly local stages. Dodgson et al. [14] proposes to create families of schemes by manipulating the stages of a subdivision step. Applications in the field of finite elements or construction of functions are provided by Zhijie [15] and Floater [16].
There are some works on four-point subdivision for binary and ternary schemes. This is shown in Siddiqui [17-18] and Hassan et al., Hed, Beccari et al. and Ko et al. [19-22].
3. CURVE SUBDIVISION
A Subdivision is an iterative process to get a smooth curve or surface from a coarse mesh. A simple definition is given by Augsdorfer: "Given a sequence of vertices, subdivision is a process by which, in each refinement step, new vertices are inserted as linear combinations of old vertices. Repeating the process leads eventually to a smooth limit curve" [14].
A Subdivision can be interpolating or approximating, depending on whether the limit curve passes through the control points. The spirit of subdivision was presented by Chaikin in [2].
3.1. Four-point interpolatory subdivision
It is an interpolating scheme presented by Nira Dyn et al. in [6] which inserts a new vertex 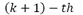 in every subdivision step, given a tension parameter
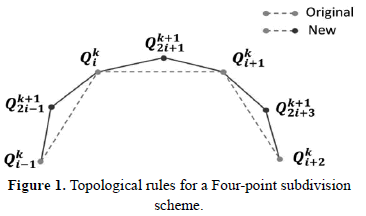
in every subdivision step, given a tension parameter 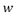 without deleting old vertexes. The topological rules are simple; for each edge on a control polygon, a new vertex preserving old vertexes is inserted, as shown in Figure 1.
without deleting old vertexes. The topological rules are simple; for each edge on a control polygon, a new vertex preserving old vertexes is inserted, as shown in Figure 1.
Let the control points be specified by 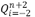 where
where 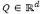 . The geometrical rules are specified by Equations 3 and 4.
. The geometrical rules are specified by Equations 3 and 4.
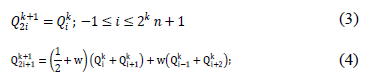
This scheme produces a 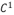 continuity curve.
continuity curve.
3.2. New four-point subdivision
In search for a subdivision with 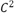 continuity, Nira Dyn et al. presents in [8] several schemes close to be interpolating. In this paper, only those subdivision schemes with four-points will be referenced. One of these is the new four-point subdivision scheme, which is based on data interpolation by a cubic polynomial (Eq. 5) evaluated on
continuity, Nira Dyn et al. presents in [8] several schemes close to be interpolating. In this paper, only those subdivision schemes with four-points will be referenced. One of these is the new four-point subdivision scheme, which is based on data interpolation by a cubic polynomial (Eq. 5) evaluated on 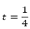 and
and 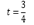 .
.
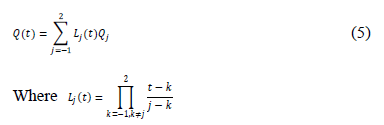
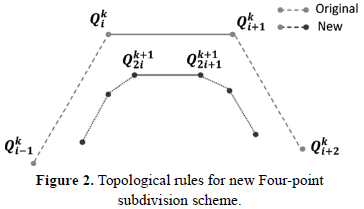
Topological rules express that for every edge, two new vertexes are created, and the old ones do not exist anymore in the next subdivision step. This is shown in Figure 2.
The Geometrical rules are expressed by:
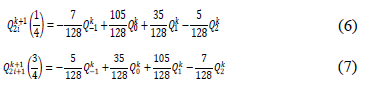
3.3 Tight four-point subdivision
Nira Dyn et al. [8] considering the new four-point subdivision as a perturbation of Chaikin's scheme introduces a tension parameter 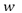 , producing an extended scheme. For
, producing an extended scheme. For 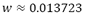 this new scheme is named tight four-point subdivision, which is
this new scheme is named tight four-point subdivision, which is 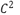 continuous. The topological rules are the same of the New Four-Point Subdivision. The Geometrical rules are expressed by Equation 8 and 9.
continuous. The topological rules are the same of the New Four-Point Subdivision. The Geometrical rules are expressed by Equation 8 and 9.
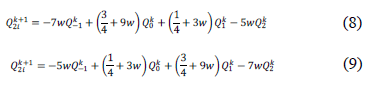
3.4 Geometrically controlled four point interpolatory scheme
Marinov et al. [9] proposes several four-point subdivision schemes based on the classical four-point scheme using Equation 10 and 11, with variable tension parameters 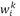 defined on Eq. 12, which is adjusted according to the geometry of the control polygon.
defined on Eq. 12, which is adjusted according to the geometry of the control polygon.
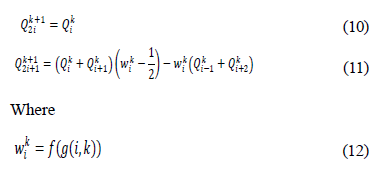
Experimentally, Marinov found that the four-point scheme produces visually pleasing curves when the insertion rule includes equidistant edges. The proposed functions are:
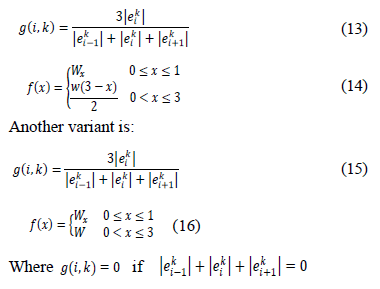
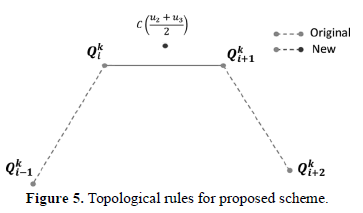
4. DFDS SCHEME
A cubic Spline 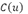 is a parametric curve from a control point set
is a parametric curve from a control point set 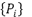 with
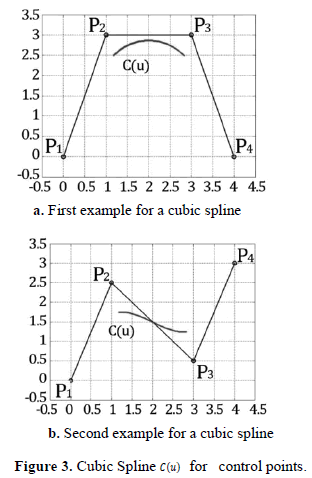
with 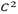 continuity, described by Eq. 17. A good description of how this formula is obtained is shown in [23]. Figure 3 shows a typical Spline.
continuity, described by Eq. 17. A good description of how this formula is obtained is shown in [23]. Figure 3 shows a typical Spline.
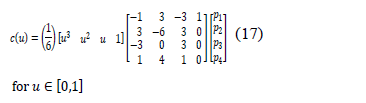
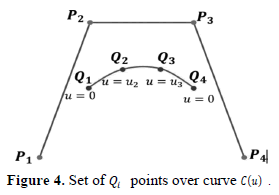
This Spline definition is approximate. For an interpolating definition it is necessary to redefine the Eq. 17, in terms of a point set 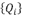 where
where 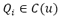 . One selection for
. One selection for 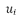 is shown in Figure 4.
is shown in Figure 4.
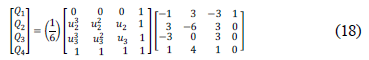
Equation 17 can be expressed in a simple way in terms of Eq. 18 as:
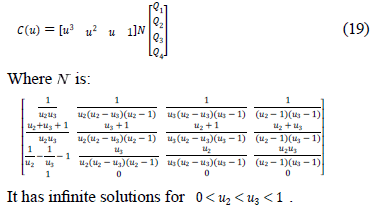
In order to developing our method, a smooth interpolating curve  is assumed so that:
is assumed so that:
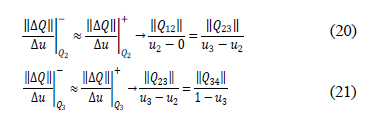
Solving Equations 20 and 21 simultaneously:
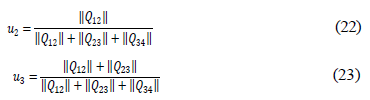
The and values are obtained. The new point is shown in Figure 5.
5. TORTUOSITY
Tortuosity is an intrinsic curve property of having twists and turns.
A formal definition of tortuosity was not found in the literature reviewed, but several criteria have been applied to measure it, such as presented by Kalitzeos et al. [24], which are resumed in Table 1.
The main applications of this property are found in porous media and ophthalmology, as can be viewed in Bullit et al. and Dougherty et al. [24-26]. In the attempt to measure this property, several metrics have been developed. The Table 1 describes the most important.
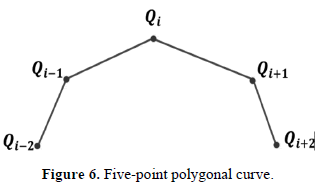
The most recent tortuosity indexes are based on the curvature, which has shown to be more robust in the calculation of this property. This work presents a discrete form considering the existence of a distance 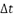 uniformly spaced between data points of the polygon, which is consistent with the concept of subdivision. Equation 24 presents the continuous version of the curvature definition.
uniformly spaced between data points of the polygon, which is consistent with the concept of subdivision. Equation 24 presents the continuous version of the curvature definition.

For the discrete case of curvature, Figure 6 shows a neighboring scheme of the point to be evaluated.
Equations 25, 26 and 27 present an approximation to the first derivative at points 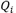 ,
, 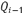 and
and 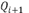 respectively.
respectively.
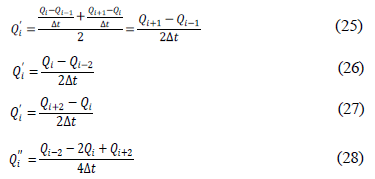
Using these results and the same concept, it is possible to calculate the value of 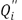 , which is expressed in Eq. 28.
, which is expressed in Eq. 28.
Taking these results into Equation 24 and simplifying leads to the expression presented in Equation 30.
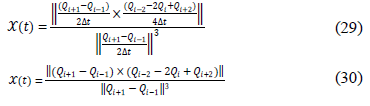
6. RESULTS
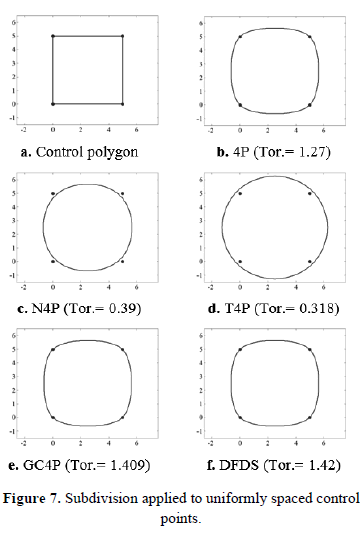
In this section, we compare the proposed subdivision scheme (DFDS) with the classical Four-point subdivision scheme (4P), New four-point subdivision scheme (N4P), the Tight four-point subdivision scheme (T4P) and the Geometrically controlled subdivision scheme (GC4P), which were described in section 2. Figure 7a, shows the control points for the first example. Figures 7-b to 7.f show the resulting curves after seven subdivision steps.
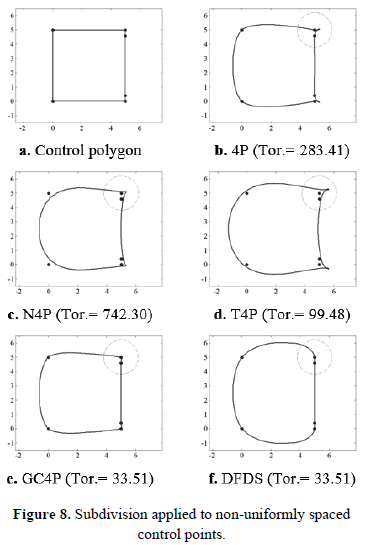
Figure 8a shows the control points for the second example. Figures 8-b to 8.f show the resulting curves after seven subdivision steps.
It can be seen that in the presence of non-homogeneously spaced control points unwanted oscillations can be present, as shown by Figures 8b, 8c and 8d.
A set of 3000 curves was randomly generated, each one had nine control points. The curves were interpolated one by one with each one of the interpolation methods. In all cases there were seven subdivision steps. The discrete curvature was evaluated at all points of each curve, taking the measure of tortuosity as its maximum value.
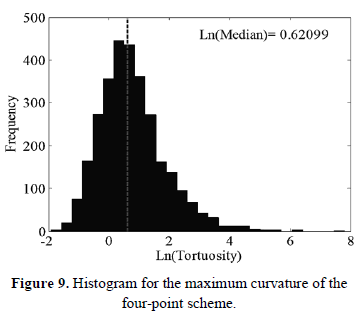
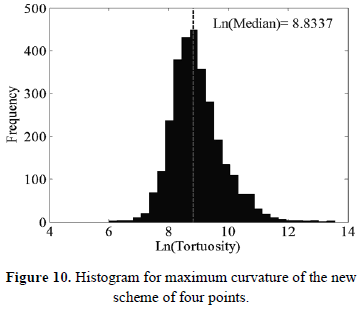
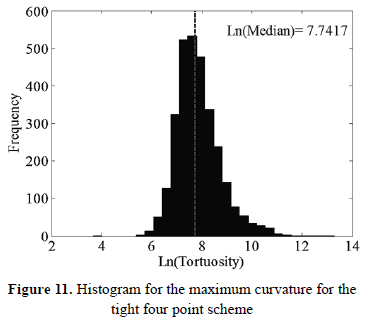
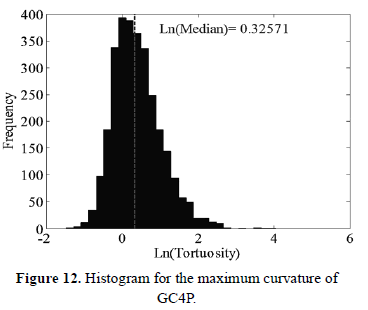
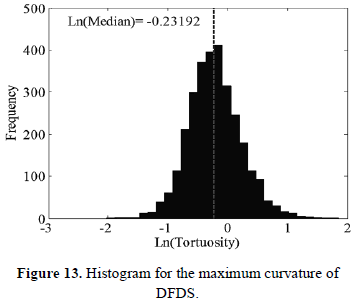
Figures 9 to 13 show a histogram for each evaluated subdivision method, the median is plotted over each histogram. A normality analysis reveals that none of the distributions are normal, the analysis was performed using a non-parametrical test, Kruskal-Wallis.
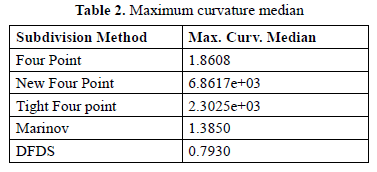
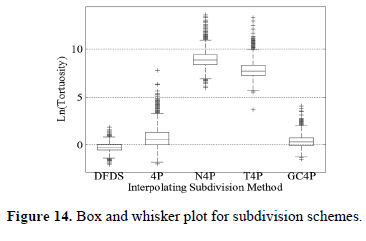
A comparative analysis using a box and whisker plot between these distributions is shown in Figure 14, which reveals that DFDS has a lower tortuosity median that the other subdivision methods. Values of medians are shown in Table 2, where DFDS has a lower value.
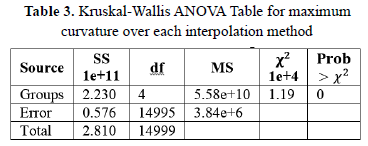
A Kruskal-Wallis analysis shows that the tortuosity data using DFDS, 4-P, New 4-P, Tight 4-P and GC Subdivision come from populations with different medians. Since the P value of the F test is less than 0.05, we can conclude that the new scheme has a lower tortuosity median than the others methods, as shown in Table 3.
6. CONCLUSION AND FUTURE WORK
This work presents DFDS, a new four-point based interpolating curve subdivision scheme. The most important advantage is the low tendency to produce artifacts, as evidenced by the ANOVA analysis, where it is compared with the other methods. Another advantage is the absence of weights or tension parameters for interpolation. The shape of the limit curve is only a function of the neighboring geometry. It is expected to have 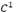 continuity because it is based on the first derivative.
continuity because it is based on the first derivative.
Future work is directed to extend the new scheme to surfaces, reverse curve subdivision and reverse surface subdivision.
REFERENCES
[1] Rojas, J. I., Fernandez-Sora, A., Serrano-Tierz, A., and Hernandez-Diaz, D. A., Historical Review: from Engineering Graphics to Engineering Design., Dyna, 78, pp. 17-26, 2011. [ Links ]
[2] Chaikin, G. M., An Algorithm for High-Speed Curve Generation. Computer Graphics and Image Processing, 3, pp. 346 - 349, 1974. [ Links ]
[3] Dubuc, S. Interpolation through an Iterative Scheme, Journal of Mathematical Analysis and Applications, 114, pp. 185 - 204, 1986. [ Links ]
[4] Mederos, V. H., Sarlabous, J. E., and Ivrissimtzis, I., Generalization of the Incenter Subdivision Scheme. Graphical Models, 75, pp. 79 - 89, 2013. [ Links ]
[5] Deslauriers G. and Dubuc S., Symmetric Iterative Interpolation Processes, Constructive Approximation, 5, pp. 49-68, 1989. [ Links ]
[6] Dyn N., Levin D., and Gregory, J. A., A 4-Point Interpolatory Subdivision Scheme for Curve Design, Computer Aided Geometric Design, 4, pp. 257-268, 1987. [ Links ]
[7] Hechler, J., Mobner, B., and Reif, U., C1 Continuity of the Generalized Four-Point Scheme, Linear Algebra and its Applications, 430, pp. 3019-3029, 2009. [ Links ]
[8] Dyn, N., Floater, M.S., and Hormann K., A C2 Four-Point Subdivision Scheme with Fourth Order Accuracy and its Extensions, Analysis, 1, pp. 1-12, 2005. [ Links ]
[9] Marinov, M., Dyn, N., and Levin, D., Geometrically Controlled 4-Point Interpolatory Schemes, In Advances in Multiresolution for Geometric Modelling, pp. 301-315, 2005. [ Links ]
[10] Beccari, C., Casciola, G., and Romani, L., A Non-Stationary Uniform Tension Controlled Interpolating 4-Point Scheme Reproducing Conics, Computer Aided Geometric Design, 24, pp. 1 - 9, 2007. [ Links ]
[11] Floater, M. S., An Algorithm for Divided Differences of Dubuc-Deslauriers Subdivision, 2011. [ Links ]
[12] Dyn, N., Floater, M. S., and Hormann, K., Four-Point Curve Subdivision based on Iterated Chordal and Centripetal Parameterizations., Computer Aided Geometric Design, 26, pp. 279-286, 2009. [ Links ]
[13] Floater, M. S., The Approximation Order of Four-Point Interpolatory Curve Subdivision., Journal of Computational and Applied Mathematics, 236, pp. 476-481, 2011. [ Links ]
[14] Augsdorfer, U.H., Dodgson, N.A., and Sabin, M.A., Variations on the Four-Point Subdivision Scheme, Computer Aided Geometric Design, 27, pp. 78 - 95, 2010. [ Links ]
[15] Zhijie, C., Modified Four-Point Scheme and its Application, Computer Aided Geometric Design, 15, pp. 251 - 260, 1998. [ Links ]
[16] Floater, M.S., Notes on 4-Point Interpolatory Subdivision, 2009. [ Links ]
[17] Siddiqi, S. S. and Rehan, K., Curve Subdivision Schemes for Geometric Modeling, International Journal of Computer Mathematics, 88, pp. 851-863, 2011. [ Links ]
[18] Siddiqi, S. S. and Rehan, K. Improved Binary Four Point Subdivision Scheme and New Corner Cutting Scheme, Computers and Mathematics with Applications, 59, pp. 2647 - 2657, 2010. [ Links ]
[19] Hassan, M. F, Ivrissimitzis, I. P., Dodgson, N. A., and Sabin, M. A., An Interpolating 4-Point C2 Ternary Stationary Subdivision Scheme, Computer Aided Geometric Design, 19, pp. 1 - 18, 2002. [ Links ]
[20] Hed, Y., A New Interpolating Subdivision based on Approximating Subdivision Scheme, Journal of Information and Computational Science, 7, pp. 631-636, 2010. [ Links ]
[21] Beccari, C.,Casciola,G. and Romani, L., An Interpolating 4-Point C2 Ternary Non-Stationary Subdivision Scheme with Tension Control, Computer Aided Geometric Design, 24, pp. 210 - 219, 2007. [ Links ]
[22] Ko, K. P., Lee, B. G., and Yoon, G. J., A Ternary 4-Point Approximating Subdivision Scheme, Applied Mathematics and Computation, 190, pp. 1563 - 1573, 2007. [ Links ]
[23] Salomon, D., Curves and Surfaces for Computer Graphics, Springer-Verlag, New York Inc, 2006. [ Links ]
[24] Kalitzeos, A., Lip, G.Y.H., and Heitmar, R., Retinal Vessel Tortuosity Measures and their Applications, Experimental Eye Research, 106, pp. 40-46, 2013. [ Links ]
[25] Bullitt, E., Gerig, G., Pizer, S.M., Lin, W., and Aylward, S.R., Measuring Tortuosity of the Intracerebral Vasculature from MRA Images, Medical Imaging, IEEE Transactions, 22, pp. 1163 -1171, 2003. [ Links ]
[26] Dougherty, G., Johnson, M.J., and Wiers, M.D., Measurement of Retinal Vascular Tortuosity and its Application to Retinal Pathologies, Medical and Biological Engineering and Computing, 48, pp. 87-95, 2010. [ Links ]