Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.180 Medellín jul./ago. 2013
ROUTE OPTIMIZATION OF URBAN PUBLIC TRANSPORTATION
OPTIMIZACIÓN DE RUTAS DE TRANSPORTE PÚBLICO URBANO
PATRICIA JARAMILLO-ÁLVAREZ
Ph. D., Professor, Universidad Nacional de Colombia, Sede Medellín, gpjarami@unal.edu.co
CARLOS A. GONZÁLEZ-CALDERÓN
M.S., Professor, Universidad de Antioquia, Medellín, Colombia, gonzalez@udea.edu.co
GUILLERMO GONZÁLEZ-CALDERÓN
M.S., Professor, Universidad Nacional de Colombia, Sede Medellín, ggonzal@unal.edu.co
Received for review September 07th, 2012, accepted April 22th, 2013, final version July, 12th, 2013
ABSTRACT: In this paper we show the optimization process of urban public transportation routes based on operations research techniques. This is shown in the outline of the development and importance of public transportation planning, its stages, its design and models. We present the design of networks of bus routes showing the overview and background of suitable optimization models for the public transportation system. We developed an optimization model minimizing transfers and we discuss the results according to the proposed theory. The article ends with the main conclusions and recommendations found in the study to improve the route optimization of urban public transportation.
KEYWORDS: Urban transportation planning, route optimization, transit.
RESUMEN: Este artículo muestra el proceso de optimización de rutas de transporte público urbano basado en las técnicas de investigación de operaciones. Éste muestra en el contorno del desarrollo e importancia de la planificación del transporte público colectivo, sus etapas, diseño y modelos. Se presenta el diseño de redes de rutas de buses donde se muestran las generalidades y antecedentes de los modelos de optimización aptos para el sistema de transporte público colectivo. Se desarrolla un modelo de optimización minimizando transbordos y se discuten sus resultados de acuerdo a la teoría planteada. El artículo finaliza con las principales conclusiones y recomendaciones encontradas en el estudio para mejorar la optimización de rutas del transporte público urbano.
PALABRAS CLAVE: Planeación de transporte urbano, optimización de rutas, transporte público.
1. PLANNING OF URBAN PUBLIC TRANSPORTATION
Urban transportation, particularly the phenomena of congestion and pollution, are among the major problems of society [1]. In this sense, empirical evidence has shown, repeatedly, that the construction of new infrastructure or expansion of existing roads is not the best alternative solution. There must be an adequately planning of the system - providing incentives to use public transportation - to mitigate the adverse effects associated with the operation of the system. Transit should also be planned to optimize its performance for the benefit of users and the city. With the growth of cities, the need for people for transport increases, and not all of these journeys may be in private transport due to congestion that is generated. Therefore, the government must provide a transit system well distributed and organized to meet the demand efficiently. All this must be planned with a holistic view of the problem in order to get the best use of economic resources, the best functionality for commuters, preserve the environment and make energy savings [2]. To justify the need for a transit route is necessary to determine the current and future demand of the system and its coverage, i.e., analyze both the current and necessary supply to provide an efficient, comfortable, safe, and economical service. Thus, the demand study constitutes basic information for proper planning of transportation [3]. Predicting future flows of the system to different situations is important and requires, in some degree, to know human behavior, characteristics of land use, economy and others, being necessary to do an analysis of socio-demographic information, of the plans of land use and development, as well as action plans in the region, and all that which affects or is affected by the transportation system being analyzed. When planning transport it is also intended to infer changes in transport demand, due to modifications to the current system. To determine the current demand for transport there are several methods that can corroborate each other, some of the most commonly used are origin-destination studies that can be done with surveys, traffic counts, and traffic studies [3].
The planning of transit systems can be for short-term (operational planning) or for medium to long term (strategic planning). Usually the design of bus routes, frequencies and scheduling of vehicles are short-term problems. This operational planning consists of several sequential steps [2]: 1. Study of the demand that travels from the different origins to different destinations in the city, 2. Modal split, 3. Design of the lines or routes, 4. Frequency determination of the number of passengers for each line, 5. Determining schedules, 6. Vehicle scheduling, and 7. Scheduling of drivers. The first three steps are usually performed by the regulators, i.e. the municipality. The last four steps are generally executed by the service operators. To solve and optimize these stages, it has been used operations research. It integrates a large number of mathematical tools, including optimization and simulation, who allow addressing rationally some of the complex problems of transit planning to support decision making. The global solution to the problem depends on the solution of each of the stages of the process [4].
2. STAGES IN THE PLANNING OF THE OPERATION OF COLLECTIVE URBAN TRANSPORTATION
It is essential to study urban transportation as a component of the city and as a function of it [2]. This should ensure that accessibility for people to different activities effectively meets through adequate mobility (in terms of time and monetary cost), so there must be adequate physical-spatial connectivity that makes it possible, neutralizing the negative effect of the distance [5]. To materialize these functions, transportation must be supported by at least two main physical instances: first, a road system that ensures connectivity between different areas or zones of the city, and secondly, a transportation system that using road infrastructure, allows the movement of people between their origins and destinations. Due to the high dimensional complexity, planning of collective public transportation can be broken down into 2 major phases, and each is subdivided into several stages. The two phases are:
Strategic planning phase of the transportation system: it is based on the socioeconomic classification of people, the regional distribution of households and firms, and road infrastructure. At this stage we estimate the number of trips that are generated from different origins to different destinations, which is synthesized in a matrix commonly called "origin-destination (OD) matrix." This phase could be considered descriptive: the analyst attempts to describe the possible behavior of people, hence the most useful tools are simulation and forecasting [2]. For more information about transportation planning refer to Ortuzar and Willumsen [6]
Planning phase of the system operation of the collective public transportation. This step might be considered normative, because it attempts to establish the best way to operate the system, so that the most useful tool may be optimization [2]. In general, this phase could be divided into the following stages: Study of the demand that travels from the different origins to different destinations in the city: it depends on the configuration of the city, on the projection of the population and their socioeconomic characteristics, etc. The modal split is the estimated number of trips to be made by the mode of transport in evaluation, distributed in time: it depends on the projection of the population, on its socioeconomic characteristics, on the characteristics of the modes, etc. For the design of the lines or routes, the number of lines of transport (bus, subway or other mass transit vehicles) is set as well as the layout of its routes. The frequency determination of the number of passes for each line is based on demand studies and distance or travel time defined by the routes. In determining schedules, for each line, the departure times from the station of origin and arrival at destination stations are determined as well as the synchronization of shipments between routes that share or transfer crossing points. In the vehicle scheduling, the fleet assignment is given based on vehicles available for traveling. Finally, in the scheduling of drivers, available staff and resources are assigned for scheduled trips per line. Readers interested in more detail of the operational and strategic transport planning stage, can refer to Sheffi [7], McNally [8], Ortuzar and Willumsen [6], and Jaramillo and Lotero [2].
3. NETWORK DESIGN OF BUS ROUTES
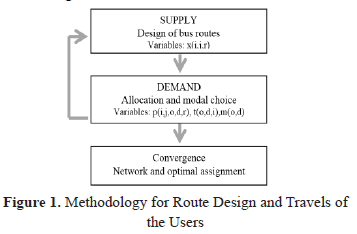
The design model of public transportation routes identifies the best options for bus routes that travel over a territory, considering that it should serve the maximum possible demand. People must travel from origins to destinations, and have to choose their travel from the bus routes that are offered in competition to other modes of transportation (e.g. car, motorbike) [2]. It also needs to consider the route design to protect the interests of the operators for the bus system to be economically viable. Specifically, the model must choose R bus routes on a network of nodes and potential segments defined a priori. It must consider maximizing coverage, minimizing both transfers and cost of trips made by travelers, but in turn, minimizing operating costs of the bus system. The model characterizes the behavior of the system user on two choices: the first, regarding the choice of route if using the bus system, and second, regarding their choice of transportation mode in which the user will travel eventually. The choice of route is defined as an allocation model, which follows the principles of Wardrop [9] that characterize the equilibrium reached in the system. As for the choice of transportation mode, it is required to have a comparison of the costs that users would assume if they opt for the bus system, and the costs of private options (distance, price, or travel time) which are exogenous parameters to the model.
The model can then be considered as the integration of two sub-models: the first is the design of routes offered by the operator and the second represents the decisions of the end-user of the system (assignment and mode choice). They are modeled simultaneously as a feedback system because the objectives of the operators do not coincide with those of the end-users of the system. Therefore a subsystem must influence the other one and vice versa. The first sub-model represents the decisions of the supply (the operators): bus routes and stations. Their objectives are to minimize operating costs and maximize revenues, which can be assessed indirectly by covering the demand which opts for the bus system. The second submodel represents demand decisions, choice of bus routes considering minimum transfers and costs (distance, time or rate) of travel. If the first sub-model is optimized without considering the second one, the solution would be a local optimum and a global suboptimum, the same for the second sub-model. Therefore they must be integrated into a single model. It would be more complete if it simultaneously makes decisions about the frequency of release of the buses. However, this purpose becomes very complex when solving the model, since it is characterized as NP-hard (nondeterministic polynomial problem) even for models representing territories of small areas, so it is not considered in the current model. Other conditions that influence the choices of the users of the system such as comfort and security are also not considered due to the difficulty in acquiring and treating reliable data, and the computational effort that would be added. Travel demand is highly variable at different times of the day; however, the model represents decisions for a single period, considering a critical time, for example, the peak hours of the morning when demand is usually higher.
3.1. Background
Wardrop [9] proposed two principles for the assignment of trips to a transportation network representing the behavior of users when deciding on the route by opting to travel from an origin Oi to a destination Dj. The first principle states that each traveler chooses the path that offers minimum cost (User equilibrium). Wardrop's second principle states that in steady state, the average travel time of the global system is minimal, considering that the travel behavior is cooperative (System optimum). Based on these principles, Beckmann, et al. [10] made the first equilibrium model of transportation networks.
Bruno, et al. [11] incorporated data from OD arrays to this model. Laporte, et al. [12] and Hamacher, et al. [13] address the problem of stations location on a given route. García and Marín [14, 15] studied the problem of network design using bi-level programming considering multimodal assignment in public and private modes. Marín [16] continued the above study without considering previous rail lines. Laporte, et al. [17] proposed the static model of network design of public transportation. Then, Marín and Jaramillo [18] proposed the capacity expansion of these systems using an accelerated Benders decomposition algorithm. Guihaire and Hao [19] present a comprehensive review of design and route scheduling proposing a classification of 69 methodological approaches that have to do with the design of routes, frequency and scheduling. Fan and Machemehl [20] formulated an entire multi-objective mixed model for the design of public transportation routes using Tabu Search. Using this method, Martínez Cuart [21] analyzes from a related point of view the design of public transportation networks and the complementarity of different hierarchy services by introducing the hierarchical structure of traditional modes of urban transportation (bus, tram or LRT, and metro). The author proposes a model and an algorithm to create its own network. Using Tabu Search, Yan, et al. [22] show that the objective functions could converge to the Pareto optimal set and be equally distributed along the Pareto curve with the help of the optimization algorithm proposed by them. Blum and Edsel [23] propose to optimize the design problem of public transportation networks for a reference transit network using a selective solution of Pool Pruning agent. Curtin and Biba [24] use a new method of maximizing the Arc-Node type service to determine optimal routes of public transportation. Finally, Yu, et al. [25] develop a model to design a transit network considering the density of demand in relation to direct demands, transfers, and the length of the routes.
3.2. Model
The proposed model is an extension of the models of Marín [16] and Marín and Jaramillo [18] for the design of lines. It is added the objective of minimizing the number of transfers, as a traveler may prefer a longer route with fewer transfers than a shorter path with many transfers. Then we require adding new decision variables and constraints to the original formulation. It increases computational complexity to solve the problem. In contrast, we aim to eliminate variables associated with the stations. For instance, Marín [16] identified stations counting an additional cost of building and defined the optimal locations of the initial and final stations of lines. The model assumes that the scheduler provides a priori location of the initial and final stations of the bus lines.
In Figure 1 we show the schema for the model considering the decision variables.
3.2.1 Model considerations
- In the model, the territory is represented by a network of N nodes
 Among nodes are defined arcs ij that are potential segments of bus routes.
Among nodes are defined arcs ij that are potential segments of bus routes. - The model suggests the design of R routes on the network, which initial and final stations are determined beforehand by the scheduler.
- The model is stationary, i.e., considers only a critical period and the demand is deterministic. This is represented by an OD matrix. Travelers have the option to choose between two modes: the bus system and an alternative. Their choice will depend on the comparison of the costs of traveling in both modes. The costs of the alternative mode are exogenous to the model.
- The nodes o and d belong to the network N. There are dummy arcs od, one for each demand od, which can choose that arc in the event that, given the solution of bus routes, is not feasible to travel through them, or because traveling in the bus system will represent large costs.
- The model does not consider costs of walking to stations or waiting times, because it does not include the frequency design. Future work will incorporate these variables.
- Besides the network definition, we require some additional data: lengths of the potential segments ij, lij; initial stations e(r) and terminal stations f(r) of the r routes; demand od: refers to the number of passengers Dod traveling from node o to destination d; the cost to be assumed by the user in case of choosing the alternative mode Caltod; and the data of traffic conditions through the arcs ij, as average vehicle speed vij and other parameters that will be presented in detail later.
3.2.2. Sets
The sets of the model are:
- i: network nodes (represented as j,k,o,d)
- ij: segments that directly connect nodes i and j
- od: segments that directly connect nodes o and d and represent an alternative system.
- r: routes to design
- o: origin nodes of the demand od
- d: destination nodes of the demand od
- od: travelers going from node o to node d
3.2.3. Decision Variables

3.3. Objective Functions
In this section we present the objective functions for supply, demand and transfers of collective public transportation
3.3.1. Supply
Maximize the demand to be served by the bus service

Minimize operating costs. As usually there is no enough information for its evaluation, it is possible to use the length of the designed routes as an indirect evaluator, as shown in Eq. (2):

3.3.2. Demand
Minimize the cost of travel: The costs assumed by users of the global system (all modes) are:
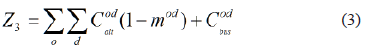
Where Cbus is the function of the total costs of the assignment of users to the bus system. This is a function of travel time of all travelers through the different segments ij, which depends on the traffic, i.e., on the number of travelers who pass through them. It is considered an all-or-nothing assignment. Although this paradigm is far from reality, is an approximate and practical approach to the problem because the corresponding function is linear. The objective function is given by Eq. (4):
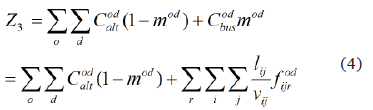
3.3.3. Minimize transfers
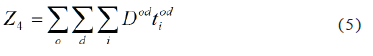
3.4. Constraints
The constraints are divided into three sections: the first is directly related to the design of routes, the second with the allocation of demand on these routes, and the last one with the link between those two sub-problems. The constraints of the design of routes are:
Initial Station: For each route r, must be assigned a segment originating from the initial station e(r), as shown in Eq. (6):
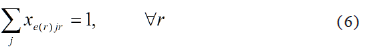
Final Station: For each route r, must be assigned a segment destined for the terminal station f(r), as shown in Eq. (7):
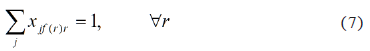
For each route and the different nodes to the origin and terminal station, there must be balance: if a segment of route r arrives at node i, a segment must also leave from it. The corresponding constraint is defined by:
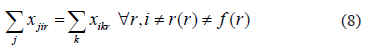
If desired, in the design of routes that assign segments from e(r) to f(r) and then be returned along the same path, the following constraints can be incorporated. This is defined by:
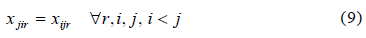
The former submodel corresponds to the standard problem which is called the problem of minimum-cost path, whose solution often presents the problem of the presence of loops. To ensure that no cycles will occur, we integrate the following constraint given by Eq. (10):
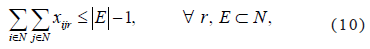
Where E is a subset of the network N, with more than 2 nodes. This constraint adds further complexity to the resolution of the problem so it is usually incorporated only if the optimal solution has a cycle, in which case it is advisable to only incorporate the constraint that points to the solution of that particular cycle. The constraints on the allocation of the demand to routes are given by Eq. (11) to (17). From the trip origin o of each demand od, the entire demand should be allocated as follows:
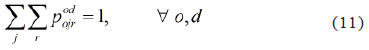
Toward the final destination trip d of each demand od, the entire demand should be allocated as follows:
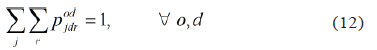
In the other nodes i, different from the trip origin or destination of each demand od, balance must be met: if a traveler arrives at that node, he must continue his journey to another node, as shown in Eq. (13).
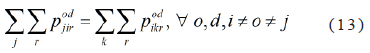
Modal disaggregation of demand: this constraint represents the behavior of the traveler, which is often complex because it depends on objective and subjective evaluations of the decision maker on the system. For computational simplicity, in this model we consider that the demand od opt for the bus system if the cost (time) of its course is cheaper than an alternative way Codalt, which is considered an exogenous parameter to the model. Thus the constraint can be stated as follows:
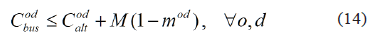
Where M is a constant with high value compared to the other terms of the problem. The constraint is explained as follows: if mod=1, then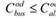 , and if mod=0, the constraint becomes trivial. The demand w(o,d), makes a transfer at the station i (different from its origin o and its destination d), if when arriving to that station on the line l does not continue its journey on it. The constraint associated is:
, and if mod=0, the constraint becomes trivial. The demand w(o,d), makes a transfer at the station i (different from its origin o and its destination d), if when arriving to that station on the line l does not continue its journey on it. The constraint associated is:
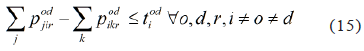
If demand od travels through a segment ji of the route r and does not travel through any segment ik of the same route, it means that it descended on the station i (without being this its destination). In that case, the constraint is 1≤ tiod, and therefore tiod =1 is mandatory, given its binary condition. If demand od travels through a segment ji of the route r and it also travels through the segment ik of the same route, it means that it didn't descend at the station i and continued its journey on the same route. In that case the constraint is 0≤ tiod, so tiod could take any value between 0 and 1. If demand od does not travel through a segment ji of the route r, but it does travel through the segment ik of the same route, it means that it did transfer but it will not count as such because it was counted when descended from another route. In this case the constraint is -1≤ tiod, so tiod could take any value between 0 and 1. If demand od does not travel through a segment ji of the route r nor travels through segment ik of the same route, it means that its journey does not pass through the station i. In this case the constraint 0≤ tiod, so tiod could take any value between 0 and 1. In all cases in which the variable can take any value between 0 and 1, it takes the value 0 because it is more convenient for the objective function to minimize transfers.
For each demand od the number of transfers should not exceed trmax, which can be represented indirectly by restricting the number of routes of the travel of each demand od.
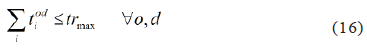
The location-allocation constraints stipulate that passengers may only use segments assigned to one of the routes:
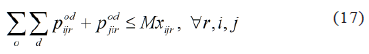
3.5. Multi-objective Solution
In general, the model is mixed integer programming. Because it contains large amounts of binary variables, it is difficult to solve. Then it is necessary to use powerful solvers, decomposition techniques or metaheuristics techniques such as Genetic Algorithms, Tabu Search, Ant Colony, etc. In this paper we used the software GAMS 22.7 and its solver CPLEX.
The problem considers multiple conflicting objectives so it does not have a global optimal solution, but it has a set of Pareto-optimal solutions. They are defined as the set of solutions that meet the condition that no other feasible solution surpasses them in all objectives. Then, it is required to face the problem by a multi-objective optimization method. There are many of these methods and they all try to solve the problem from different points of view. Interested readers in multi-objective optimization methods can refer to Smith, et al. [26]. In our case, we will apply the method of weightings [27] for being the most recognized and applied, due to its low computational effort.
3.6. Example
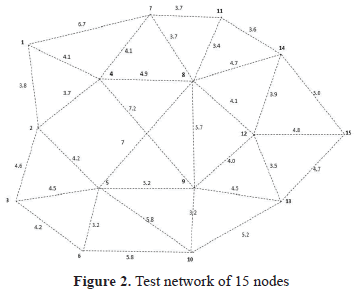
To test the model we used a network that represents a region with 15 nodes corresponding to possible stops and strategic interconnections. We want to design 4 bus routes knowing the demand matrix of potential travels D for a peak period of demand. Each arc has a length lij. In Figure 2 we show the corresponding network.
The matrix of demands of travels D is exogenous to the model and is as follows:
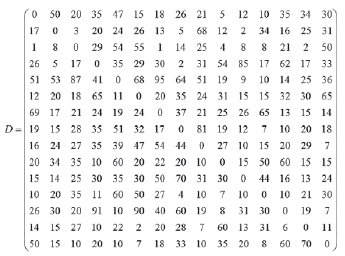
In order to satisfy all possible demand from the bus network we consider Calt= M (a very high value) for all demands, such that the demand Dod only uses the alternate mode if it is not possible for it to access any of the designed routes.
The multi-objective optimization method of weighting factors integrates into a single objective function, the weighted sum of all objective functions of the problem. Those weights correspond to the relative importance that the decision maker gives to each one and all must sum 1. Each objective function must be normalized by a factor that let the functions to be dimensionless because they are all represented in different units (passengers, costs, etc.). The normalizing factor must be such that the values of the normalized objective function takes values between 0 to 1. In addition, the objective functions to be minimized must be multiplied previously by -1 because they are included in a global objective function to be maximized, as shown in Eqs. (18) to (22):
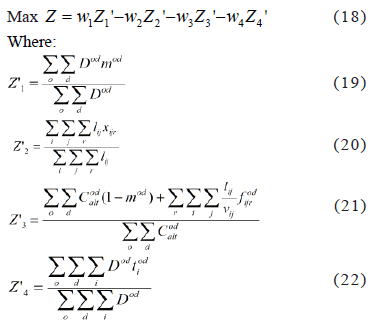
The relative importance weights used are w1=0.25, w2=0.25, w3=0.25 and w4=0.25, in order to neutralize its influence on the model analysis. For simplicity, costs are considered in units of distance, so that vij=1. The maximum number of transfers is trmax=2. We consider all the constraints defined for the model, except for the constraints that prevent loops, which may be included in the solution only if loops are detected, incorporating them to break them. In the example it was not necessary to incorporate any of them.
Results
The defined routes are as follows:
Route 1:
2-3-5-8-9-12-14 (it returns along the same route), length: 29.70 km
Route 2:
2-4-7-8-9-10-13-15 (it returns along the same route), length: 30.30 km
Route 3:
3-5-6-10-13-15(it returns along the same route), length: 23.40 km
Route 4:
3-5-8-11(It returns along the same route), length: 14.90 km
The values for the objective functions are:
Total length of routes: 98.30 km
Length of paths: 2376.30 km
Satisfied demand: 77%
Total transfers: 52.00
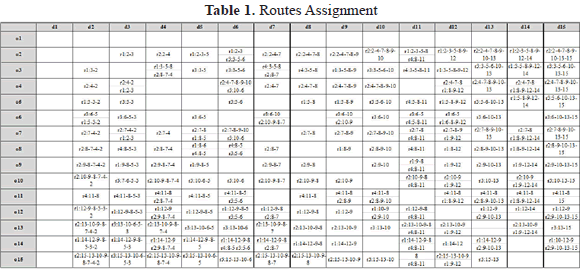
The results of the allocation of routes are presented in Table 1. The results were consistent with the assumptions of the model. This is an academic exercise because it does not incorporate aspects that could be relevant in a real application. Where appropriate, the planner can introduce new constraints to the problem, information about fees, maximum cost limits that users are willing to assume, etc.
4. CONCLUSIONS AND FUTURE WORK
The proposed model advances over those found in the literature as it includes additional features such as minimizing transfers. Previous models did not included this aspect, so they gave inconsistent solutions with the usual wishes of the decision-makers, who may prefer more expensive trips in time or length but do less transfers.
Regarding the solution of the model we suggest the application of meta-heuristic techniques as Genetic Algorithms. This would allow better management of non-linear functions, including binary variables and application to large networks. We also propose the incorporation of non-linear functions of congestion and modal choice, such as logit models, as well as other functions which represent the decision maker's behavior, including latent variables and characteristics of the bounded rationality of the decision-maker. It is also advisable to include stochasticity in some variables, demand, travel times, etc. in order to obtain more robust models.
REFERENCES
[1] Noland, R. and Lem, L. A Review of the Evidence for Induced Travel and Changes in Transportation and Environmental Policy in the US and the UK, Transportation Research Part D: Transport and Environment, vol.7, pp. 1-26, 2002. [ Links ]
[2] Jaramillo, P. and Lotero, L., Modelos de optimización de la operación del transporte público colectivo, 150 años Facultad de Ingeniería ed. Bogotá: Universidad Nacional de Colombia, 150 años Facultad de Ingeniería, 2011. [ Links ]
[3] Posada, J. and González, C., "Metodología para estudio de demanda de transporte público de pasajeros en zonas rurales, Revista Facultad de Ingeniería Universidad de Antioquia, pp. 106-118, 2010. [ Links ]
[4] Ceder, A. and Wilson, N., Bus Network Design, Transportation Research Part B: Methodological, vol. 20, pp. 331-344, 1986. [ Links ]
[5] Gonzalez, C. and Sarmiento, I., Modelación de la distribución de viajes en el Valle de Aburrá utilizando el modelo gravitatorio, DYNA, pp. 199-208, 2009. [ Links ]
[6] Ortuzar, J. and Willumsen, L., Modelling Transport, Third Edition ed. Chichester: John Wiley and Sons, 2001. [ Links ]
[7] Sheffi, Y., Urban Transportation Networks: Equilibrium Analysis with Mathematical Programming Methods: Prentice-Hall Englewood Cliffs, NJ, 1985. [ Links ]
[8] McNally, M., The Four-Step Model, Handbook of transport modelling, vol. 1, pp. 35-41, 2000. [ Links ]
[9] Wardrop, J., Some Theoretical Aspects of Road Traffic Research, in Road Engineering Division Meeting, 1952, pp. 325-362. [ Links ]
[10] Beckmann, M., McGuire, C. and Winsten, C., Studies in the economics of transportation: Published for the Cowles Commission for Research in Economics by Yale University Press, 1956. [ Links ]
[11] Bruno, G., Ghiani, G. and Improta, G., A Multi-Modal Approach to the Location of a Rapid Transit Line, European Journal of Operational Research, vol. 104, pp. 321-332, 1998. [ Links ]
[12] Laporte, G., Mesa, J. and Ortega, F., Locating Stations on Rapid Transit Lines, Computers & Operations Research, vol. 29, pp. 741-759, 2002. [ Links ]
[13] Hamacher, H., Liebers, A., Schöbel, A., Wagner, D. and Wagner, F., Locating New Stops in a Railway Network, Electronic notes in theoretical computer science, vol. 50, pp. 13-23, 2001. [ Links ]
[14] García, R. and Marín, A., Urban Multimodal Interchange Design Methodology, Mathematical methods on optimization in transportation Systems, pp. 49-79, 2001. [ Links ]
[15] García, R. and Marín, A., Parking Capacity and Pricing in Parkin Ride Trips: A Continuous Equilibrium Network Design Problem, Annals of Operations Research, vol. 116, pp. 153-178, 2002. [ Links ]
[16] Marín, A., Urban Rapid Transit Network Design, in International Conference on Industrial Engineering and Systems Management Marrakech., 2005, pp. 16-19. [ Links ]
[17] Laporte, G., Marín, A., Mesa, J. and Ortega, F., An Integrated Mthodology for the Rapid Transit Network Design Problem, Algorithmic Methods for Railway Optimization, pp. 187-199, 2007. [ Links ]
[18] Marín, A. and Jaramillo, P., Urban Rapid Transit Network Capacity Expansion, European Journal of Operational Research, vol. 191, pp. 45-60, 2008. [ Links ]
[19] Guihaire, V. and Hao, J., Transit Network Design and Scheduling: A Global Review, Transportation Research Part A: Policy and Practice, vol. 42, pp. 1251-1273, 2008. [ Links ]
[20] Fan, W. and Machemehl, R., A Tabu Search based Heuristic Method for the Transit Route Network Design Problem, Computer-aided Systems in Public Transport, pp. 387-408, 2008. [ Links ]
[21] Martínez, F., Modelo de diseño de redes de servicios interurbanos BRT complementarios a la oferta de transporte público en áreas urbanas, 2010. [ Links ]
[22] Yan, J., Li, J. and Shao, G., Urban Transit Route Network Design Optimization, Computer Measurement & Control, vol. 18, 2010. [ Links ]
[23] Blum, J. and Edsell, S. Selective Solution Pool Pruning in Multi-agent Optimization Systems for the Transit Route Network Design Problem, 2011, pp. 710-715. [ Links ]
[24] Curtin, K. and Biba, S., The Transit Route Arc-node Service Maximization Problem, European Journal of Operational Research, vol. 208, pp. 46-56, 2011. [ Links ]
[25] Yu, B., Yang, Z., Jin, P., Wu, S. and Yao, B., Transit Route Network Design-maximizing Direct and Transfer Demand Density, Transportation Research Part C: Emerging Technologies, vol. 22, pp. 58-75, 2012. [ Links ]
[26] Smith, R., Dyner, I., Mesa, O., Jaramillo, P., Poveda, G. and Valencia, D., Decisiones con multiples objetivos e incertidumbre. Medellin: Facultad de Minas, Universidad Nacional de Colombia, 2000. [ Links ]
[27] Zadeh, L., Optimality and Non-scalar-valued Performance Criteria, Automatic Control, IEEE Transactions on, vol. 8, pp. 59-60, 1963. [ Links ]