Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.180 Medellín July/Aug. 2013
NUMERICAL CALCULATION OF THE RECIRCULATION FACTOR IN FLAMELESS FURNACES
CÁLCULO NUMÉRICO DEL FACTOR DE RECIRCULACIÓN EN HORNOS DE COMBUSTIÓN SIN LLAMA
CAMILO LEZCANO
Grupo de Ciencia y Tecnología del Gas y Uso Racional de la Energía, Master en ingeniería, Universidad de Antioquía, camilolez@gmail.com
ANDRÉS AMELL
Grupo de Ciencia y Tecnología del Gas y Uso Racional de la Energía, docente investigador, Universidad de Antioquia, anamell@udea.edu.co
FRANCISCO CADAVID
Grupo de Ciencia y Tecnología del Gas y Uso Racional de la Energía, docente investigador, Universidad de Antioquia, fcadavid@udea.edu.co
Received for review December 6th, 2011, accepted March 15th, 2013, final version March, 21th, 2013
ABSTRACT: This paper performs calculations of the recirculation factor in simulations of a flameless combustion furnace with different percentages of oxygen in air (from 21% to 100% O2). Results are compared with Magnussen's recirculation theory and show that when there are chemical reactions, the recirculation results are overpredicted. An alternative correlation to Magnussen's theory is proposed, useful in calculating the recirculation factor in flameless furnaces. Also, calculation of the recirculation factor obtained through numerical simulation for different configurations of confined jets taken from literature which do not involve chemical reactions, when compared with the recirculation confined jet theories of Craya-Curtet, Thring-Newby and Magnussen show that as recirculation increases, all the theories overpredict the recirculation factor.
KEYWORDS: recirculation factor, flameless combustion, numerical simulation, Magnussen's recirculation theory.
RESUMEN: En este trabajo es realizado el cálculo del factor de recirculación en simulaciones de un horno de combustión sin llama con diferentes porcentajes de oxígeno en el comburente (de 21% a 100% de O2).Los resultados se comparan con la teoría de recirculación de Magnussen, teniéndose que cuando hay reacciones químicas los resultados de recirculación son sobrepredecidos por esta teoría, entonces en lugar de usar la teoría de Magnussen, se propone usar una correlación obtenida por medio de simulaciones, para calcular el factor de recirculación en hornos de combustión sin llama. También se presentan los resultados obtenidos del cálculo del factor de recirculación por medio de simulación numérica para diferentes configuraciones de jets confinados tomadas de la literatura, las cuales no involucran reacciones químicas, cuyos resultados son comparados con teorías de recirculación de jets confinados de Craya-Curtet, Thring-Newby y Magnussen, obteniéndose que a medida que la recirculación es mayor, los resultados numéricos se van alejando de estas teorías.
PALABRAS CLAVE: factor de recirculación, combustión sin llama, simulación numérica, teoría de recirculación de Magnussen.
1. INTRODUCTION
For the purpose of reducing polluting emissions, several combustion techniques have been developed and put into practical use during recent years. One of those consists of carrying out combustion with an oxygen concentration below atmospheric levels, so that the combustion process is characterized by: slower chemical reaction rates, uniform temperature distribution, bigger reaction zones and a not visible flame [1]. However, when oxygen concentration is quite low, the mixture could be outside of the flammability limits, and therefore combustion does not take place. For that reason the oxidizer should be preheated up to a certain value, because the flammability limits expand as temperature increases [2]. This type of combustion, where the oxidizer-fuel mixture should be preheated before the reaction takes place due to the lower oxygen concentration, is called flameless combustion, because of the special characteristic of a non-visible reaction zone.
In flameless combustion dilution of oxygen plays a very important role. An oxygen concentration of around 5% in molar fraction is mandatory to prevent flame formation [3]. 5% is very low when compared with conventional combustion which is carried out with 21% (mol) oxygen. A method to reach the appropriate oxygen concentration is using internal recirculation, where air and fuel jets in a confined space entrain combustion products from surroundings. In order to quantify the recirculation that exists in a confined system Wunning and Wunning [4] defined a parameter known as the recirculation factor (Kv), which is the ratio between the gas mass flow entrained by all jets  , and the sum of air
, and the sum of air  and fuel mass flows
and fuel mass flows 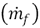 in the discharge.
in the discharge.

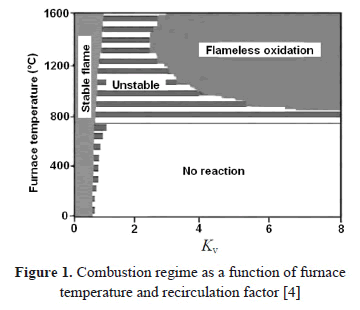
Depending on the recirculation factor, as Figure 1 shows, different combustion regimes take place. To obtain the flameless combustion regime it is necessary to have a recirculation factor higher than 3 and a furnace wall temperature over the autoignition temperature.
Given the importance of the recirculation factor to obtain the flameless combustion phenomenon, it is necessary to establish methods to determine this parameter. As Equation (1) shows, the main difficulty to determine the recirculation factor is in the calculation of the mass of recirculated gases. So in order to overcome this problem, some researchers, have developed analytical theories, methods or equations that predict or estimate the mass flow of recycled gases [5-7]. The results obtained by those researchers are applicable mainly for coflow jets of constant density, and the mass of recirculated gases is given in terms of similarity parameters. The expressions for the calculation of the recirculated gases that are derived from these works are shown in Equations (2), (3) and (4), which correspond respectively to the expressions given by Thring and Newby [5], Craya-Curtet [6] and Magnussen [7].
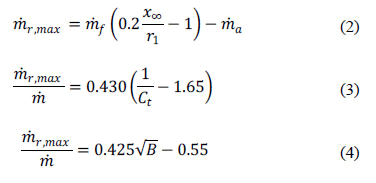
where 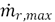 is the maximum recirculated flow,
is the maximum recirculated flow, 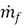 is the flow of the central jet,
is the flow of the central jet, 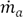 is the coflow mass flow,
is the coflow mass flow, 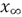 is the distance from discharge to the point where the jet hits the walls,
is the distance from discharge to the point where the jet hits the walls, 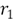 is nozzle radius,
is nozzle radius, 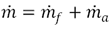 ,
, 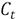 is known as the Craya-Curtet number [8], and B is Magnussen's similarity parameter given by the equation (5).
is known as the Craya-Curtet number [8], and B is Magnussen's similarity parameter given by the equation (5).

where 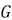 corresponds to the coflow momentum subtracted from the jet momentum,
corresponds to the coflow momentum subtracted from the jet momentum, 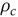 and
and 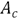 are the density and the cross sectional area in the section of maximum recirculation, respectively.
are the density and the cross sectional area in the section of maximum recirculation, respectively.
Due to the difficulty to obtain an analytical expression that estimates the amount of recirculated gases when chemical reactions exist or when the configuration of the furnace is complex (as it is in a flameless combustion furnace), it is important to define a methodology that allows calculation of the quantity of recycled gases from a numerical simulation.
Numerically Cavigiolo et al. [9] used a general purpose computational fluid dynamics (CFD) code to calculate the recirculation factor of several configurations of flameless combustion burners, although they did not clarify the way how this calculation was carried out. Mi et al. [10] calculated the mass of recirculated gases and determined the counter-flow mass in different sections from the jet discharge, which is a similar approach to the one we propose in this study.
An important characteristic of a jet discharging into a confined area is that the mass flux in the axial direction remains constant, which is given by Equation (6).
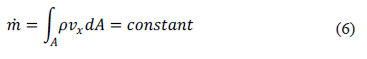
The fact that mass flux is constant allows the use of negative speeds to calculate the mass of recirculated gases in different transversal planes and establish a profile of recycled gases that increases progressively until reaching a maximum at the center of the vortex and then diminishes until zero (Figure 2a). The use of more transversal planes to calculate the recirculated gases improves the resolution of the profile (Figure 2b), and simplify the identification of the maximum value, which is used to calculate the recirculation factor (Kv).
2. NUMERICAL METHODOLOGY TO CALCULATE THE RECIRCULATED MASS FLOW
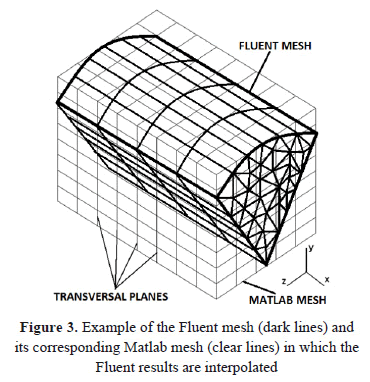
Given the difficulties that the Fluent software poses to obtain transversal cell areas, which are necessary for equation (6), the velocity and density fields were exported from Fluent with a custom-designed code developed in Matlab 7.7.0, which generates a uniform rectangular (2D) or box shaped (3D) mesh (Figure 3), over which Fluent results are interpolated by Delanuay triangulation [11]. In Figure 3 the dark lines correspond to a tetrahedral Fluent mesh and the clear lines are the mesh made in Matlab based on the Fluent mesh. The results exported from Fluent consisted of a file with x, y and z coordinates, velocity and density in each node of the Fluent mesh. These values were used in Matlab, where an orthogonal mesh was constructed. This new mesh was a box that had the same dimensions of the Fluent mesh. For each vertex of the Matlab mesh an interpolated value of velocity and density from the Fluent results was obtained. For the results in Matlab to be as close as possible to the Fluent results, the Matlab mesh had to be finer than the Fluent mesh.
From the interpolated values in the Matlab mesh, the recirculated mass flow was calculated by Equation (6), which was used in each transversal plane, but only including velocities in the x-negative direction, density and cross sectional area of each node. The node area was calculated easily because the mesh in Matlab is orthogonal, and the neighbors of the node are well known. In this way, the maximum recirculated flow was obtained and, therefore, the recirculation factor.
One advantage of this methodology for the calculation of the recirculated mass flow is that it does not depend on the type of mesh, as it will work with hexahedral or tetrahedral meshes.
3. GEOMETRICAL CHARACTERISTICS AND NUMERICAL MODEL
Although the main aim in this paper is to calculate the recirculation factor in simulations of a flameless furnace, different simulations of non-reactive coflow jets were carried out in 2D and 3D as support of this work. These simulations were generated using experimental data from literature [12-13].
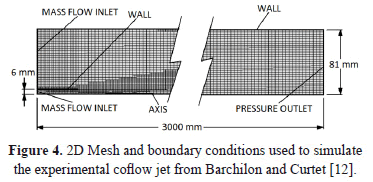
Figure 4 shows the 2D mesh, dimension and boundary conditions used to simulate Barchilon and Curtet's experiments [12]. This configuration was meshed with 2D-axisymmetric quadrilateral cells and the 3D configuration was meshed with hexahedral cells. To reduce the computation time and the memory requirements, only one-eighth of the 3D geometry was simulated. At walls, a non-slip condition was used, so there is friction between fluid and walls.
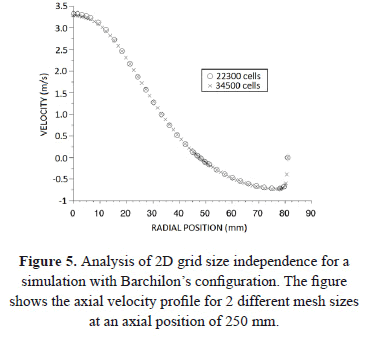
Grid independence in these simulations was guaranteed by increasing the number of cells and comparing the resulting axial profiles of the different grids, as shown in Figure 5 for the 2D case. For Barchilon's 2D simulations grid size independence was obtained with around 22,300 cells and for 3D simulations the grid size independence was obtained with around 143,800 cells, but the graph of size independence is not shown for the 3D case because is similar to the result shown in Figure 5. Is important to note that grid independence is only done in one simulation for each of the 2D and 3D cases, and is assumed that all other simulations with the same geometrical configuration are grid independent with the same amount of cells
Figure 6 shows the 2D mesh and geometrical configuration used to simulate the Cohen de Lara and Curtet [13] experimental facility. In this geometrical configuration, grid size independence was guaranteed with 18,000 cells following the same procedure described above.
Figure 7 shows an overview of the furnace modeled in this study. The fuel is injected through a central nozzle, which is surrounded by another four peripheral nozzles that extract the combustion products and inject the combustion air, for more details see references [14, 15]. Figure 7 also shows the mesh and boundary conditions used to simulate the flameless furnace. The pressure of the ejection nozzles was adjusted so that the mass flow passing through those nozzles was close to 75% of the total mass flow of air and fuel entering the furnace. At the walls, a non-slip condition was used.
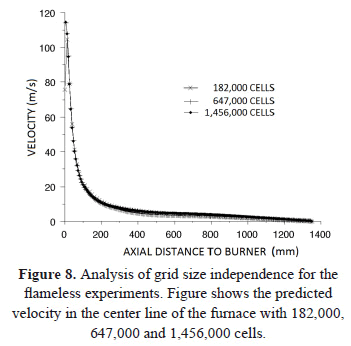
Figure 8 shows the velocity profiles in the furnace center line, for a simulation with an oxidant of 21% O2 (air), changing the number of cells, from 182,000 to 1,456,000. It was found that 182,000 cells are satisfactory, and any increase beyond this size would lead to an insignificant change in the resulting solution. This analysis was done only for this simulation and it was assumed that all other flameless simulations with different oxidant conditions, will have mesh independence with the same number of cells, i.e. 182,000.
To carry out all the non-reactive confined coflow jet simulations in 2D and 3D, and to simulate the flameless furnace, the software Gambit 2.2.3 and Fluent 6.2.16 were used for creating the meshes and performing the simulation process respectively. The governing equations are the Favre-averaged Navier-Stokes equations (for more detail refer to [16]). In all non-reactive coflow jet simulations the realizable  model was used to simulate turbulence, because this model works better for jet discharges and recirculation zones compared with other
model was used to simulate turbulence, because this model works better for jet discharges and recirculation zones compared with other 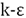 models [17]. To couple the speed and pressure field, the SIMPLE algorithm was used to enforce mass conservation. Finally to discretize all the conservation equations the upwind second order scheme was used.
models [17]. To couple the speed and pressure field, the SIMPLE algorithm was used to enforce mass conservation. Finally to discretize all the conservation equations the upwind second order scheme was used.
In flameless furnace simulations the standard 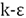 model was used for turbulence, because the realizable
model was used for turbulence, because the realizable 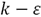 model did not guarantee convergence, since when velocity and temperature in a line was observed, these parameters kept oscillating. To model combustion the finite rate/eddy dissipation with a modification in its constants, proposed by [18], was used. Radiation was modeled by the discrete ordinate model; a 2-step methane irreversible reactional mechanism [19] represented chemical reactions, and the discretization of the conservation equations by a second order upwind scheme.
model did not guarantee convergence, since when velocity and temperature in a line was observed, these parameters kept oscillating. To model combustion the finite rate/eddy dissipation with a modification in its constants, proposed by [18], was used. Radiation was modeled by the discrete ordinate model; a 2-step methane irreversible reactional mechanism [19] represented chemical reactions, and the discretization of the conservation equations by a second order upwind scheme.
To determine if a simulation has converged, three different criterions were used: (1) verification that residuals are asymptotic; (2) energy balance (the difference between energy at inputs and at outputs), was less than 5% of burner power; (3) the average temperature and velocity in a line located in the reaction zone did not change with new iterations.
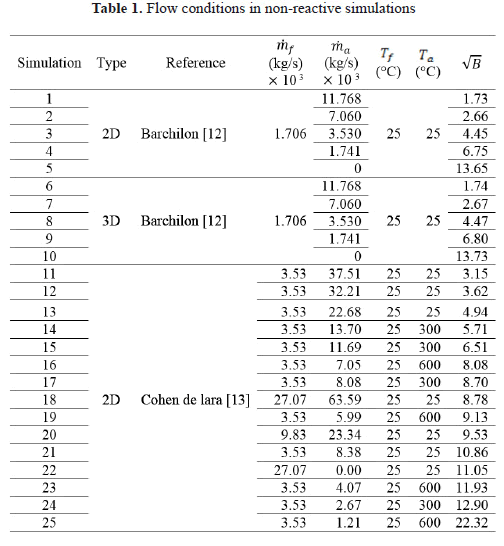
Table 1 shows inlet conditions of the mass flows of the jet  and coflow
and coflow 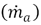 for the non-reactive simulations whose values are multiplied by 103. Also the temperature of the jet
for the non-reactive simulations whose values are multiplied by 103. Also the temperature of the jet 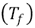 , the coflow
, the coflow 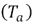 and the square root of Magnussen's parameter are shown.
and the square root of Magnussen's parameter are shown.
4. RESULTS AND DISCUSSION
4.1. Non-reactive coflow jet
Figure 9 shows the streamlines of a representative simulation, in this case simulation 21 in Table 1. The recirculation zone, the point of flow separation and the reattachment point can be clearly observed. Figure 10 shows the graph obtained with the Matlab code applied to the simulation 21, where the maximum value of the curve of recirculated gases is used to calculate 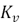 .
.
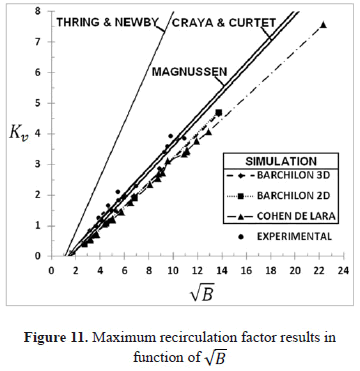
Figure 11 compares the results of the recirculation factor obtained from the simulations and the Matlab code with those of empirical correlations as a function of 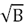 . The results of the simulations number 1 to 5 (2D simulations) and 6 to 10 (3D simulations), lie along the same line, which suggests that the interpolation process does not alter the data. It is also observed that all non-reactive results have a lineal trend, and these are below the theoretical estimates derived from the empirical correlations of Craya-Curtet and the Magnussen curve. It is important to note that experimental data fits to the theoretical estimates, but those data are not completely reliable because the velocities were measured with a pitot tube and in the recirculation zone the velocity is too low to be properly measured by a pitot tube. Furthermore, as
. The results of the simulations number 1 to 5 (2D simulations) and 6 to 10 (3D simulations), lie along the same line, which suggests that the interpolation process does not alter the data. It is also observed that all non-reactive results have a lineal trend, and these are below the theoretical estimates derived from the empirical correlations of Craya-Curtet and the Magnussen curve. It is important to note that experimental data fits to the theoretical estimates, but those data are not completely reliable because the velocities were measured with a pitot tube and in the recirculation zone the velocity is too low to be properly measured by a pitot tube. Furthermore, as 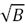 increases, the simulation results are farther from the theoretical lines.
increases, the simulation results are farther from the theoretical lines.
4.2. Flameless furnace
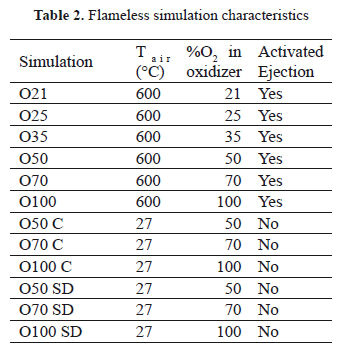
Table 2 summarizes the most important conditions of the 20 kW flameless furnace. simulations labelled with "C" imply that the oxidizer was at room temperature as they do not include ejection because the furnace regeneration system was not activated. Simulations labelled with "SD" used an air nozzle diameter 4 times smaller than in the other simulations. This was in order to increase discharge velocity to compensate the reduction in mass flow, due to the increase in the O2 percentage in the oxidizer.
To calculate the recirculation in these simulations the procedure was similar to that used for the non-reactive case, except in cases with ejection, because the ejected gas mass flow 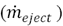 has to be subtracted from the recirculated gas mass flow (equation (7)).
has to be subtracted from the recirculated gas mass flow (equation (7)).

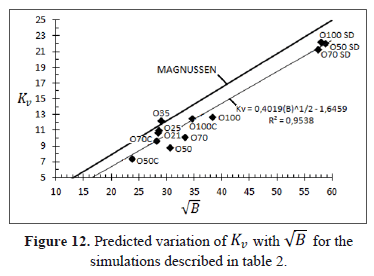
Figure 12 shows the result of the recirculation factor, as a function of  , calculated for these simulations.
, calculated for these simulations. 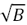 was calculated with equation (5) because this parameter does not change when the flow is reactive. Most predictions are below the theoretical Magnussen's curve, as was the case for the non-reactive simulations. Furthermore, the lineal trend is not as good as that observed in Figure 11. Nevertheless, the lineal tendency is good enough to obtain a correlation factor (R2) of 0.9538.
was calculated with equation (5) because this parameter does not change when the flow is reactive. Most predictions are below the theoretical Magnussen's curve, as was the case for the non-reactive simulations. Furthermore, the lineal trend is not as good as that observed in Figure 11. Nevertheless, the lineal tendency is good enough to obtain a correlation factor (R2) of 0.9538.
Instead of the Magnussen's recirculation theory, or other theories derivated from single non-reactive coflow jets to calculate the recirculation factor, we recommend the use of equation (8), which is obtained for a multiple jet flameless furnace.

5. CONCLUSIONS
The equation 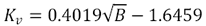 should be used instead of the Magnussen's theory to predict the recirculation factor in multiple-jet flameless furnaces, because the coflow jet theories tend to overpredict the recirculation as
should be used instead of the Magnussen's theory to predict the recirculation factor in multiple-jet flameless furnaces, because the coflow jet theories tend to overpredict the recirculation as  increases.
increases.
The methodology used to numerically calculate the recirculation factor gives results that fit well with the experimental and theoretical results of non-reactive coflow jets.
The realizable k-e model generally predicts the recirculation factor well with non-reactive flows, but there are some convergence problems when implemented in flameless combustion furnaces.
ACKNOWLEDGEMENTS
We gratefully acknowledge the financial support provided by Colciencias to develop the project "Desarrollo y evaluación de un quemador de combustión sin llama a gas natural usando aire enriquecido con oxígeno, under contract Nº 355-2008", also for their financial support of Camilo Lezcano with the "Jovenes Investigadores" program, to Carlos Arrieta for his great support and to the University of Antioquia for the financial support through the "Sostenibilidad" program for A1 and A groups, year 2013/2014.
REFERENCES
[1] Blasiak, W., Narayanan, K. and Yang, W., Evaluation New Combustion Technologies for CO2 and NOx Reduction in Steel Industries, in Twelfth International Conference on Modelling, Monitoring and Magnagement of Air Pollution. 2004. Rhodes, Greece. [ Links ]
[2] Katsuki, M. and Hasegawa, T., The science and technology of combustion in highly preheated air, Proc. Comb. Inst., 27 (2), pp. 3135-3146, 1998. [ Links ]
[3] Mancini, M., Weber, R. and Orsino, S., On mathematical modelling of flameless combustion. Combustion and Flame, 150, pp. 54-59, 2007. [ Links ]
[4] Wünning, J.A. and Wünning, J.G., Flameless oxidation to reduce thermal NOx-formation, Progress in Energy and Combustion Science, 23 (1), pp. 81-94, 1997. [ Links ]
[5] Thring, M.W. and Newby, M.P., Combustion Lenght of Enclosed Turbulent Jet Flames, in Proc. Comb. Inst., 1953, Pittsburgh. [ Links ]
[6] Curtet, R., Confined jets and recirculation phenomena with cold air, Combustion and Flame, 2 (4), pp. 383-411, 1958. [ Links ]
[7] Magnussen, B.F., Prediction of Characteristics of Enclosed Turbulent Jet Flames, Proc. Comb. Inst., 14 (1), pp. 553-565, 1973. [ Links ]
[8] Becker, H.A., Hottel, H.C. and Williams, G.C., Mixing and flow in ducted turbulent jets, Proc. Comb. Inst., 9 (1), pp. 7-20, 1963. [ Links ]
[9] Cavigiolo, A., Galbiati, M.A., Effuggi, A., Gelosa, D. and Rota, R., Mild combustion in a laboratory-scale apparatus, Combust. Sci. and Tech., 175, pp. 1347-1367, 2003. [ Links ]
[10] Mi, J., Li, P. and Zheng, C., Numerical Simulation of Flameless Premixed Combustion with an Annular Nozzle in a Recuperative Furnace, Chinese Journal of Chemical Engineering, 18(1), pp. 10-17, 2010. [ Links ]
[11] De Berg, M., Cheong, O, van KREVELD M., and Overmars, M., Computational Geometry: Algorithms and Applications, Berlin, Springer-Verlag, third edition, 2008. [ Links ]
[12] Barchilon, M. and Curtet, R., Structure detaillee D'un jet en presence de recirculation, 5eJournée D'études sur les flammes, 21 Noviembre 1963. [ Links ]
[13] Cohen de Lara G. and Curtet, R., Étude de la recirculationdans des modeles schématiques de fours a flammes de diffusion, 3eJournée d'études sur les flammes, Vendredi 28 Février 1958. [ Links ]
[14] Colorado, A.F., Herrera, B.A. and Amell, A.A., Performance of a flameless combustion furnace using biogas and natural gas, Bioresourse technology, 101 (7), pp. 2443-2449, 2010. [ Links ]
[15] Copete, H., Amell, A.A. and Cadavid, F., Simulación numérica de una cámara de combustión de alta velocidad con dos configuraciones de inyección de combustible, Dyna, 156, pp. 109-120, 2008 [ Links ]
[16] Poinsot, T. and Veynante, D., Theoretical and numerical combustion, Philadelphia, Edwards, second edition, 2005. [ Links ]
[17] Shih, T.H., Liou, W.W., Shabbir, A., Yang, Z. and Zhu, J., A new k-e eddy-viscosity model for high Reynolds number turbulent flows - Model development and validation, Computers fluids, 24 (3), pp. 227-238, 1995. [ Links ]
[18] Lupant, D., Pesenti, B. and Lybaert, P., Assessment of combustion models of a self-regenerative flameless oxidation burner. Mons (Belgic), Faculté Polytechnique de Mons, pp. 1-7, 2004. [ Links ]
[19] Westbrook, C. and Dryer, F., Simplified reaction mechanisms for the oxidation of hydrocarbon fuels in flames, Combustion Science and Technology, 27 (1-2), pp. 31-43. 1981. [ Links ]