Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.182 Medellín nov./dez. 2013
MR-DTI RICIAN DENOISING
ELIMINACIÓN DE RUIDO RICIAN EN MR-DTI
ADRIAN MARTIN
M.Sc. Departamento de Matemática Aplicada, Universidad Rey Juan Carlos, Madrid, España, adrian.martin@urjc.es
JUAN F. GARAMENDI
Ph.D. INRIA-VisAGeS Research Team, Rennes, France, juan-francisco.garamendi_bragado@inria.fr
EMANUELE SCHIAVI
Ph.D., Departamento de Matemática Aplicada, Universidad Rey Juan Carlos, Madrid, España, emanuele.schiavi@urjc.es
Received for review March 23th, 2012, accepted May 15th, 2013, final version July, 21th, 2013
ABSTRACT: In this work we tackle the problem of Magnetic Resonance Images (MRI) Rician denoising to enhance Diffusion Tensor Image (DTI) reconstruction. In a variational framework based on the Total Variation operator, the model of the Rician noise leads to the resolution of a highly nonlinear equation associated to the energy minimization problem. An iterative algorithm is proposed and validated on synthetic images. Finally the application to real Diffusion Weighted Images (DWI) is considered.
KEYWORDS: MRI, DWI, DTI, Rician noise, Variational
RESUMEN: En este trabajo se trata el problema de eliminación de ruido Rician en imagen de Resonancia Magnética para la mejora de la reconstrucción de las imágenes de DifusiónTensorial. El modelado del ruido Rician es enfocado desde un marco variacional basado en el operador de Variación Total, convirtiéndolo en un problema de minimización de energía que conduce a la resolución de ecuaciones severamente no lineales. La solución propuesta es un algoritmo iterativo validado con imágenes sintéticas, que finalmente es probado en imágenes ponderadas en difusión reales.
PALABRAS CLAVE: Resonancia Magnética, DWI, DTI. ruido Rician, variacional
1. INTRODUCTION
MRI denoising is a fundamental step in medical image processing that leads to the assumption that MR magnitude images are corrupted by Rician noise (which is a signal dependent noise) (see [1] and [2]). The bias with respect to the typical Gaussian noise assumption is particularly severe when low Signal-to-Noise Ratio (SNR) images are used. In this paper we present a denoising model for MR Rician noise contaminated images, recently presented in [3]. In a variational framework it combines the Total Variation operator with a data fitting term, which was previously suggested in [4] for DWI Rician denoising. When the resulting energy functional is considered for minimization, the variational approach leads to the resolution of a nonlinear degenerate elliptic Partial Differential Equation (PDE) which is the associated Euler Lagrange equation for optimization. This has a number of theoretical problems when the Total Variation (TV) operator is considered as a prior, because the associated energy functional is not differentiable at the origin (i.e.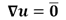 ) and approximating problems must be considered. We also embed the PDE in the general iterative regularization procedure presented in [5] which allows to recover high contrast images. The model is then validated using synthetic brain images and finally we apply this framework on a set of real DW brain Images.
) and approximating problems must be considered. We also embed the PDE in the general iterative regularization procedure presented in [5] which allows to recover high contrast images. The model is then validated using synthetic brain images and finally we apply this framework on a set of real DW brain Images.
The denoising step is crucial for a good Diffusion Tensor reconstruction, which allows the study of white matter tissues in the brain. Rician denoising is also essential when anatomical MRI studies are done to characterize differences between healthy and diseased subjects [6].
This paper is organized as follows: in sections 2 and 3 we characterize Rician noise and the equations which define the denoising process. These equations are then embedded in an iterative regularization procedure and solved numerically, in section 4. In section 5 we use synthetic images for model validation and finally in section 6 we show the results for real images validating the proposed model.
2. THE RICIAN DISTRIBUTION OF NOISE IN MRI
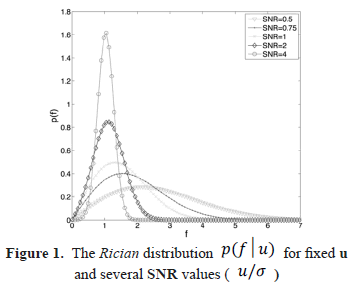
In MRI the original complex signal is measured in the frequency domain (called K-space). It is assumed that the noise in each channel (real and imaginary) follows a Gaussian distribution with zero mean and identical variance 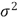 Using the Inverse Fourier Transform the real and imaginary images are obtained from K-space data. Due to the fact that the Fourier Transform is a linear and orthogonal map, it preserves the characteristics of the noise and this noise can be assumed to be uncorrelated in each voxel. Nevertheless the final image typically used for subsequent analysis is the magnitude image, obtained by calculating the modulus from the real and imaginary images voxel by voxel. This nonlinear mapping transforms the Gaussian noise distribution into a Rician distribution [1]:
Using the Inverse Fourier Transform the real and imaginary images are obtained from K-space data. Due to the fact that the Fourier Transform is a linear and orthogonal map, it preserves the characteristics of the noise and this noise can be assumed to be uncorrelated in each voxel. Nevertheless the final image typically used for subsequent analysis is the magnitude image, obtained by calculating the modulus from the real and imaginary images voxel by voxel. This nonlinear mapping transforms the Gaussian noise distribution into a Rician distribution [1]:
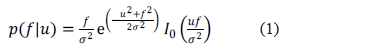
where  denotes the (ideal) uncorrupted image intensity,
denotes the (ideal) uncorrupted image intensity,  the noisy data,
the noisy data,  is the variance of the original Gaussian noise and
is the variance of the original Gaussian noise and 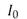 is the modified zeroth-order Bessel function of the first kind.
is the modified zeroth-order Bessel function of the first kind.
In Figure 1 the behavior of the Rician probability density function is shown for different values of the SNR (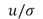 ). It can be seen how the distribution is far from being Gaussian especially for small SNR values. When the original signal is zero (
). It can be seen how the distribution is far from being Gaussian especially for small SNR values. When the original signal is zero (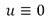 ) a special case of the Rician distribution (1) has to be considered:
) a special case of the Rician distribution (1) has to be considered:
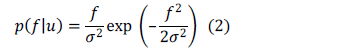
which is called the Rayleigh distribution. The mean and the variance of this distribution can be calculated analytically. This allows the parameter 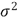 in (1) and (2) to be estimated (see [2] for more details).
in (1) and (2) to be estimated (see [2] for more details).
3. MODEL EQUATIONS
Following [3], the problem of Rician denoising can be modeled as follows: Given 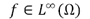 , representing the noisy image, find
, representing the noisy image, find 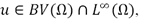 the denoised image, minimizing the energy:
the denoised image, minimizing the energy:
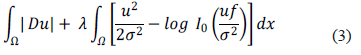
where 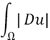 is the Total Variation of the function
is the Total Variation of the function 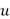 and
and 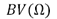 is the space of functions with bounded variation; furthermore
is the space of functions with bounded variation; furthermore 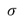 is the standard deviation of the Rician noise of the data and
is the standard deviation of the Rician noise of the data and 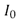 is as before, the modified zeroth-order Bessel function of the first kind. The scale parameter
is as before, the modified zeroth-order Bessel function of the first kind. The scale parameter 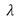 tunes the model by weighting the likelihood term derived from the Rician p.d.f. (1).
tunes the model by weighting the likelihood term derived from the Rician p.d.f. (1).
This functional minimization can be accomplished by calculating the Euler-Lagrange equation of functional (2). Due to the fact that the Total Variation is not differentiable at the origin, a regularization of the resulting diffusion term 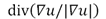 in the form of
in the form of 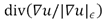 ,
, 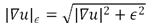 and
and 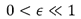 is implemented to avoid degeneration of the equation where
is implemented to avoid degeneration of the equation where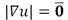 . Using this approximation it is possible to give a (weak) meaning to the following formulation: Given
. Using this approximation it is possible to give a (weak) meaning to the following formulation: Given 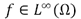 find
find 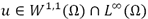 solving:
solving:
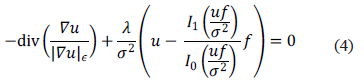
where 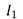 is the modified first-order Bessel function of the first kind.
is the modified first-order Bessel function of the first kind.
4. ITERATIVE REGULARIZATION AND NUMERICAL RESOLUTION
In this work we apply the iterative regularization method for total variation-based denoising, proposed in [3], to the recovering of MRI images corrupted by Rician noise. It is well known that this iterative regularization process allows the original contrast present in the image [3,5] to be preserved. The general iterative procedure is as follows: Let 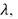
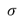 be positive real parameters and set
be positive real parameters and set 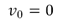 .
.
1) Given 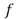 and
and 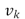 compute
compute 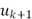 as the minimum of the energy:
as the minimum of the energy:
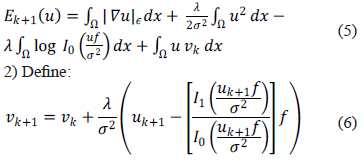
The procedure stops when the high frequencies introduced are clearly a product of the noise. So at each iteration we have to minimize the energy (5) solving the associated Euler-Lagrange equations; for notational simplicity we introduce the nonlinear function
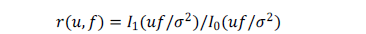
and the analogous of equation (4) reads:
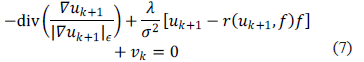
These are nonlinear elliptic problems that we solve with a gradient descent scheme until the solution stabilizes to a solution of the elliptic problem. Using forward finite difference for the temporal derivative and a semi-implicit iterative scheme we deduce the (explicit) equation: 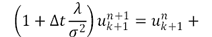
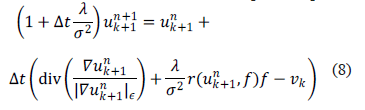
where the spatial discretization for the TV-term is performed following [7] .
5. MODEL VALIDATION ON SYNTHETIC BRAIN IMAGES
In order to assess the performance of the proposed algorithm we tested it with synthetic brain images obtained from the BrainWeb Simulated Brain Database (http://www.bic.mni.mcgill.ca/brainweb) at the Montreal Neurological Institute. The original phantoms were contaminated artificially with Rician noise, the known amount and distribution of it providing a gold standard for our study. In this case we used the value 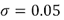 and
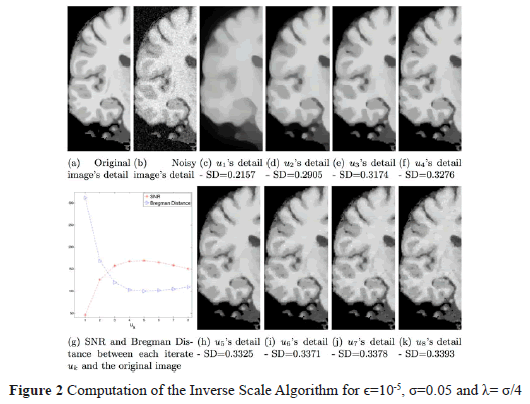
and 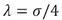 that assures that the result in the first iteration is a low frequency image and subsequent iterations recover details. In Figure 2 we present the sequence of images
that assures that the result in the first iteration is a low frequency image and subsequent iterations recover details. In Figure 2 we present the sequence of images 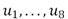 .
.
These images show the evolution of the inverse scaling procedure presented in (4), starting with a structural cartoon image and subsequently adding details (and noise) eventually approximating the original noisy data. Two metrics were considered to determine the best iteration in the inverse scaling procedure. The first is the Signal-to-Noise-Ratio (SNR) between the possible solution 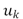 and the original (clean) image
and the original (clean) image 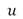 . It is defined as
. It is defined as
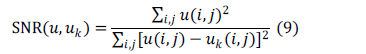
The second metric is the Bregman Distance [5] between 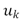 and
and 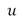 . It can be seen in Figure 2(g), how the maximum SNR value and the minimum value for the Bregman Distance are obtained at
. It can be seen in Figure 2(g), how the maximum SNR value and the minimum value for the Bregman Distance are obtained at 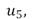 as shown in Figure 2(h).
as shown in Figure 2(h).
These results as well as visual inspection confirm that the images: 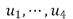 are over-smoothed versions of with few details while the subsequent images,
are over-smoothed versions of with few details while the subsequent images, 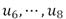 , become noisier. We also notice that, as we stated, the contrast of the image sequence measured as the standard deviation (SD) of the pixel intensity is monotonically increasing, so providing a high contrast image suitable for tissue classification.
, become noisier. We also notice that, as we stated, the contrast of the image sequence measured as the standard deviation (SD) of the pixel intensity is monotonically increasing, so providing a high contrast image suitable for tissue classification.
6. DIFFUSION TENSOR IMAGES APPLICATION
DTI is becoming one of the most popular methods for the analysis of the white matter (WM) structure of the brain, where some alterations can be found in early stages of some degenerative diseases. A complete review of this technique can be found in [8].
This technique measures the Brownian motion (random motion) of the water molecules in the brain. This motion is assumed to be isotropic when it is not restricted by surrounding structures, but the WM regions contain densely packed fiber bundles that cause an anisotropic diffusion of the water molecules along the perpendicular directions to the fiber bundles. At each voxel of a DTI the water diffusion is represented by a symmetric 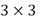 tensor. The information of the preferred directions of the motion and the relevance of these directions is represented by the eigenvectors and the eigenvalues of the tensor. The information contained in a DTI is encoded by different scalar measurements; one of them is the Fractional Anistropy (FA) of the tissue, which is defined as
tensor. The information of the preferred directions of the motion and the relevance of these directions is represented by the eigenvectors and the eigenvalues of the tensor. The information contained in a DTI is encoded by different scalar measurements; one of them is the Fractional Anistropy (FA) of the tissue, which is defined as
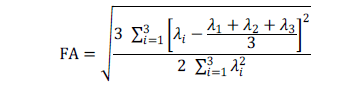
with 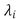 being the eigenvalues of the tensor. The FA values vary from 0 (when the motion in the voxel is completely isotropic) to 1 (totally anisotropic). For the reconstruction of the DTI a set of DWI has to be acquired, scanning the tissue in different directions of space. At least six DWI volumes are needed in order to be able to calculate the DTI but in clinical practice more than 15 DWI volumes are usually acquired. More DWI data imply better DTI reconstruction but longer scanning time. As a result of this bias (image quality vs. scanning time) the noise in the images is high. This shows the importance of the denoising step previous to the DTI reconstruction.
being the eigenvalues of the tensor. The FA values vary from 0 (when the motion in the voxel is completely isotropic) to 1 (totally anisotropic). For the reconstruction of the DTI a set of DWI has to be acquired, scanning the tissue in different directions of space. At least six DWI volumes are needed in order to be able to calculate the DTI but in clinical practice more than 15 DWI volumes are usually acquired. More DWI data imply better DTI reconstruction but longer scanning time. As a result of this bias (image quality vs. scanning time) the noise in the images is high. This shows the importance of the denoising step previous to the DTI reconstruction.
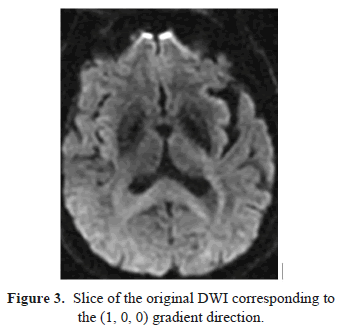
For this preliminary study we have used a DW-MR brain volume provided by Fundación CIEN-Fundación Reina Sofía which was acquired with a 3 Tesla General Electric scanner equipped with an 8-channel coil. The DW images have been obtained with a single-shot spin-eco EPI sequence (FOV=24cm, TR=9100, TE=88.9, slice thickness=3mm, spacing=0.3, matrix size=128x128, NEX=2). The DW-MRI data consists of a volume obtained with b=0/mm2 and 15 volumes with b=1000s/mm2 corresponding with the gradient directions specified in [9]. These DW-MR images, which represent diffusion measurements along multiple directions, are denoised with the proposed method previous to the Diffusion Tensorial Image reconstruction, which was done with the 3d Slicer tools (freely available at http://www.slicer.org). These data were acquired from a patient who suffers from a progressive supranuclear palsy (PSP), a degenerative disease which impairs movements and balance, so the scanner time must be as short as possible. In Figure 3 we show a slice of the original DWI data corresponding to the (1, 0, 0) gradient direction where the effect of noise is clearly visible. The complete DW-MRI data volume is denoised using the proposed method where the Rician noise magnitude (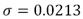 ) has been estimated following [2], while the
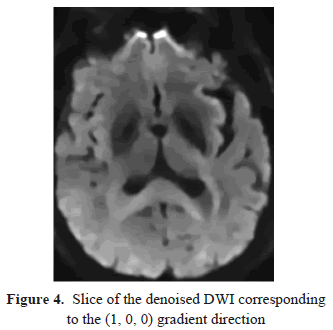
) has been estimated following [2], while the 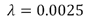 value used has been assessed empirically as well as the selection of the fifth iteration of the Inverse Scaling procedure. A slice from the associated denoised volume is shown in Figure 4. It can be observed that the noise has been removed but the details and the edges have been fully preserved.
value used has been assessed empirically as well as the selection of the fifth iteration of the Inverse Scaling procedure. A slice from the associated denoised volume is shown in Figure 4. It can be observed that the noise has been removed but the details and the edges have been fully preserved.
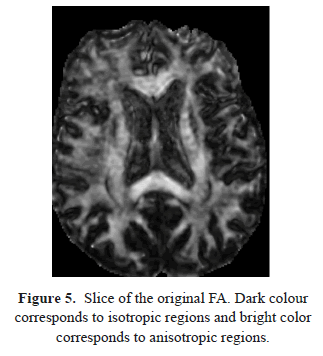
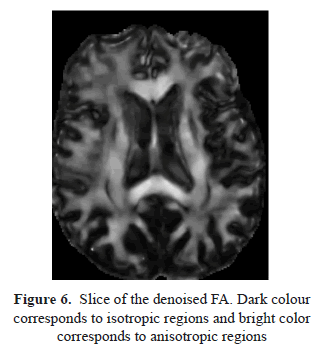
The effect of this denoising process over the reconstructed tensor can be observed comparing the Fractional Anisotropy images (Figures 5 and 6), where the structures and details are enhanced when the DWI data have been preprocessed. The denoising step is even more important when directional information (such as the main eigenvector of the tensor) is required (Figures 7 and 8). The noise on the original DWI data causes artificial inhomogeneities in the eigenvectors field. The directional information provided by the eigenvectors field is crucial for subsequent postprocessing such as tractography, an emergent technique in recent neurological studies [10].
7. CONCLUSIONS
In this paper we deal with the problem of accurate Rician denoising in DT-MRI. The proposed model successfully incorporates a Rician likelihood term which is regularized in a variational framework by means of the Total Variation operator. Staircasing artifacts in the solution are avoided through the inverse scaling procedure. The results obtained in real images are promising and open the way to the method's use in clinical practice.
Further work should include advanced numerical techniques to avoid the approximation of the total variation operator.
8. ACKNOWLEDGEMENTS
This work was supported by project TEC2012-39095-C03-02 of the Spanish Ministry of Science.
9. REFERENCES
[1] Gudbjartsson, H. and Patz, S., The rician distribution of noisy MRI data, Magnetic Resonance in Medicine 34 (6), pp. 910-914, 1995. [ Links ]
[2] Sijbers, J. et al., Estimation of the noise in magnitude MR images, Magnetic Resonance Imaging 1 (16) pp. 87-90, 1998. [ Links ]
[3] Martín, A. et al., Iterated Rician Denoising, Proceedings of IPCV'11, Las Vegas, Nevada, USA, pp. 959-963, 2011 [ Links ]
[4] Basu, S. et al., Rician noise removal in Difusion Tensor MRI, Medical Image Computing and Computer-Assisted Intervention 9 (Pt 1) pp. 117-125, 2006. [ Links ]
[5] Osher, S. et al., An iterative regularization method for Total Variation-based image restoration, Multiscale Modeling & Simulation 4 (2) 460-489, 2005. [ Links ]
[6] Rueda, A. et al., Saliency-Based Characterization Of Group Differences For Magnetic Resonance Disease Classification. Dyna 178, pp. 21-28, 2013. [ Links ]
[7] Nikolova, M., Algorithms for finding global minimizers of image segmentation and denoising models, SIAM Journal of Applied Mathematics 66 (5) pp. 1632-1648, 2006. [ Links ]
[8] Le Bihan, D. et al., Diffusion Tensor Imaging: Concepts and Applications, Journal of Magnetic Resonance Imaging 13 pp. 534-546, 2001. [ Links ]
[9] Jones, S. et al., Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magnetic Resonance in Medicine 42 (3), pp. 515-525, 1999. [ Links ]
[10] Ciccarelli, O. et al., Diffusion-based tractography in neurological disorders: concepts, applications, and future developments. The Lancet Neurology 7(8), pp. 715-727, 2008. [ Links ]