Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.182 Medellín nov./dez. 2013
ON-LINE DYNAMIC SECURITY ASSESSMENT OF A MICRO-GRID USING FUZZY LOGIC AND DISTRIBUTED PROCESSING
EVALUACIÓN DE LA SEGURIDAD DINÁMICA EN LÍNEA DE UNA MICRO-RED USANDO LÓGICA DIFUSA Y PROCESAMIENTO DISTRIBUIDO
GUSTAVO SCHWEICKARDT
PhD., CONICET, Universidad Tecnológica Nacional, Argentina. gustavoschweickardt@conicet.gov.ar
JUAN MANUEL GIMENEZ ALVAREZ
PhD., CONICET, Facultad de Ingeniería, Universidad Nacional de San Juan, Argentina, jgimenez@unsj.edu.ar
Received for review August 4th, 2012, accepted May 16th, 2013, final version June, 11th, 2013
ABSTRACT: Dynamic security assessment (DSA) is defined as the ability of a power system to withstand sudden contingencies and to survive the transient and to reach an acceptable steady-state condition. During system operation, the on-line assessment of the dynamic security level is essential in order to take adequate countermeasures aimed to restore the system, if necessary, to a more secure operating condition. Due to both the great complexity of latest power systems and the large number of components, the on-line DSA leads to excessive computational complexity which makes it not fully operational, particularly with the inclusion of complex emerging grid-tied AC micro grids. To overcome this problem, a new approach of on-line DSA of micro grids is presented in this paper. The proposal employs distributed processing and artificial intelligence (AI) techniques in order to reduce the computing times; thus allowing its execution on-line.
KEYWORDS: Artificial intelligence techniques, on-line dynamic security assessment (DSA), distributed processing, fuzzy dynamic security index (FDSI), fuzzy inference system (FIS), grid-interactive AC micro grid.
RESUMEN: La evaluación de la seguridad dinámica en línea se define como la habilidad de un sistema de potencia a soportar contingencias repentinas y sobrevivir el transitorio y llegar a un nuevo estado estacionario aceptable. Durante la operación del sistema la evaluación del nivel de seguridad dinámica es esencial para tomar medidas de control preventivas con el objetivo de llevar al sistema, en caso de que sea necesario, a un estado de operación más seguro. Debido a la gran complejidad de los sistemas de potencia y al gran número de componentes, la evaluación de la seguridad es computacionalmente compleja lo que la hace poco útil. Esto es más complejo cuando se desea evaluar la seguridad dinámica considerando las nuevas micro redes. Para afrontar este problema, se presenta un nuevo enfoque de evaluación de la seguridad dinámica en línea de micro redes. La propuesta emplea procesamiento distribuido y técnicas de inteligencia artificial para reducir los tiempos de cálculo lo que permite su ejecución en línea con la operación del sistema.
PALABRAS CLAVE: Técnicas de inteligencia artificial, evaluación de la seguridad dinámica en línea, procesamiento distribuido, índice de seguridad dinámica fuzzy, sistema de inferencia fuzzy, micro redes interactivas.
1. INTRODUTION
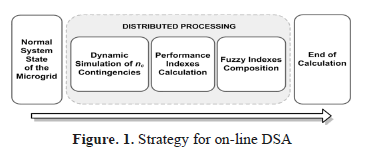
Due to the intensive use of modern electricity networks, security has become one of the most important issues in power system operation. In order to take the control actions needed to improve the power system operation security it is essential to assess both the static and the dynamic security level [1]. On one hand, static security assessment (SSA) is performed by analyzing all relevant static constraints of post-fault (post-contingency) steady-state variables. Since this procedure does not require excessive computational efforts, and thus computing times, to meet its goal, an on-line SSA analysis is capable of being implemented effectively and efficiently [2]. On the other hand, dynamic security assessment (DSA) analyzes the transient dynamics developed in the post-contingency period. A key element of DSA is the assessment of stability; the ability of an electrical power system, for a given operating condition, to regain a state of operating equilibrium after being subjected to a disturbance, with most system variables bounded so that system integrity is preserved. Due to both, the great complexity of latest power systems and the large number of components, the DSA leads to excessive computational complexity. The time needed for obtaining the DSA results is by far longer than that required for taking the above-mentioned pre-contingency control actions, when they are needed. Furthermore, these conditions have been made worse in modern power systems because of the increased complexity recently introduced with the development of emerging grid-interactive AC microgrids (MGs) [3] [4]. In such integrated energy systems, the grid-interactive AC microgrid is a novel network structure that allows better use of distributed energy resources (DERs) to be obtained, by operating a cluster of loads, distributed generation (DG) and distributed energy storage (DES), as a single controllable system with predictable generation and demand that provides both power and heat to its local area by using advanced equipment and control methods [5]. This small grid, which usually operates connected to the main power network but can be autonomously isolated (islanded) during an unacceptable power quality condition, is a new concept developed to cope with the integration of renewable energy sources (RESs) [6]. In this way, the DSA turns into a crucial requirement to be met by modern grid-tied AC microgrids. The power system dynamic security assessment can be carried out by using two main methods, approximate methods and numerical integration methods, referred to as full time domain simulations (TDS) [7]. The approximate methods include techniques such as sensitivity methods for assessing the voltage security and direct methods for assessing the transient stability such as Lyapunov like methods, equal-area criterion-based methods, etc. Alternatively, full simulation methods include power flow solutions of PV curves, that is, voltage curves in terms of the active power, used to define the collapse point of the steady-state voltages, time-domain full simulations for transient security and analysis of eigenvalues for assessing the small signal stability. Although approximate methods offer some computational advantages, full simulation methods provide the most accurate DSA. Another advantage of full simulation methods is that they make it possible to have both knowledge of the post-contingency state of each system variable and to use various models of system components depending on the degree of detail required. When an approximate method is used, some assumptions are made which must be verified in order to confirm the applicability when the system conditions change. This verification is not needed when full simulation methods are used [8]. However, a big drawback of full simulation methods, which is currently a major challenge, is the computing time and computational effort required [8], [9]. This difficulty becomes higher when more detailed models are used and even more when there is an increase in the size of the microgrid, such as the case of a large cluster of grid-interactive microgrids with many RES-based DG systems composing a bulk power system. Therefore, in order to exploit the advantages of such indirect procedures, the computing time must be reduced, both in dynamic simulations and in the analysis of the results. This paper presents a new approach of DSA of grid-interactive AC microgrids which reduces the computing times of indirect methods so that it makes their use on-line possible. This is achieved through the application of both, distributed processing of dynamic simulations and artificial intelligence (AI) techniques for the analysis of the results obtained from the full simulations. Figure. 1 summarizes the proposed strategy for the on-line DSA of microgrids.
The AI techniques are implemented through a cascading three-stage fuzzy inference system (FIS) to compose a fuzzy dynamic security index. This index is in turn calculated on the basis of seven performance indexes, which are obtained by quantification of the transient behavior of the system considering pre-contingency conditions, during it and the post-contingency ones.
2. GENERAL CONSIDERATIONS
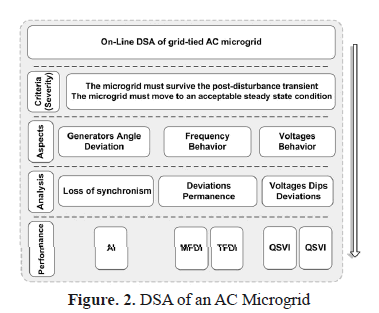
The strategy for on-line implementation of DSA of an AC Microgrid is split up in three major stages, as summarized in Fig. 1. First, beginning from a normal system state of the microgrid, the dynamic simulation of the system must be executed for each one of the "nc" critical contingencies considered. Second, taking into account the transient behavior of the microgrid, several performance indexes are calculated. These indexes are the angle index AI, the maximum frequency deviation index MFDI, the total frequency deviation index TFDI, the dynamic voltage index DVI, the quasi-stationary voltage index QSVI, the power flow index PFI, and the load shedding index LSI. Third, in this stage the composition of all indexes is made by using a cascading three-stage FIS. Full simulations, calculation indexes and composition indexes are implemented using distributed processing. The general considerations for the on-line implementation of the DSA of a grid-connected AC microgrid are described in Figure. 2. Any microgrid has to meet two major sets of criteria: (1) the MG must survive the post-disturbance transient, and (2) it must move into an acceptable steady-state condition. The basic aspects taken into consideration in the developed strategy are the following: generator angle deviation, microgrid frequency behavior and bus voltages performance. In order to get them, the loss of synchronism of generators, the frequency deviation from nominal value, the permanence of the frequency deviation, transient voltages dips and voltages deviation is evaluated. From a dynamic point of view, a microgrid is said to be secure if it can withstand all probable contingencies without violating any of the system constraints and can move into a new stable steady-state condition. The most significant fact is that the transition from the initial state to the post-disturbance final state must not cause other outages that can lead the MG to a total blackout. The criterion to define the performance indexes is based on two major aspects related to the post-disturbance state: (a) an unacceptable performance is related to large variations of system parameters, particularly voltages and frequency, and (b) the resultant post-disturbance system trajectory must converge to an acceptable steady-state condition. Unexpected generator outages or power line outages modify the normal operation values of the microgrid, such as machines angles, frequency and bus voltages. In some cases, this can even lead to a change of these system variables out of their range of admissible values. In addition, the power flows through the lines are affected by contingencies. In the most severe cases, this would cause the loss of lines and/or loss of generators due to protective relay tripping, especially for the case of emerging smart microgrids. Another effect is the potential loss of load due to the operation of the automatic load shedding scheme. In order to quantify the magnitude in which the mentioned variables of the system are affected by contingencies, seven performance indexes are proposed.
3. PERFORMANCE INDEX
1) Angle Index (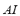 ): Generators usually have protection to avoid asynchronous operation. The protection is generally based on a relay that monitors the impedance observed in the transformer high-voltage bars. Typically this protection is adjusted in such a way that the load angle of the generator (
): Generators usually have protection to avoid asynchronous operation. The protection is generally based on a relay that monitors the impedance observed in the transformer high-voltage bars. Typically this protection is adjusted in such a way that the load angle of the generator (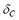 ) does not exceed 120° [10]; otherwise, the relay acts causing the generator to separate from the MG. The maximum slip of the load angle offers a suitable security margin since, in case this is not exceeded, the generator may regain its synchronism. The
) does not exceed 120° [10]; otherwise, the relay acts causing the generator to separate from the MG. The maximum slip of the load angle offers a suitable security margin since, in case this is not exceeded, the generator may regain its synchronism. The 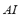 is defined by (1):
is defined by (1):
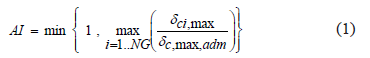
where 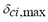 is the maximum deviation of the generator load angle
is the maximum deviation of the generator load angle 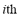 during the entire simulation time,
during the entire simulation time, 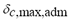 is the maximum admissible load angle given by the protection relay and
is the maximum admissible load angle given by the protection relay and 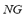 is the number of generators operating in the microgrid.
is the number of generators operating in the microgrid.
2) Maximum Frequency Deviation Index (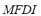 ): The maximum frequency deviation from its rated value is a clear representative of the dynamic effect produced by the contingency analyzed on the microgrid. The higher the maximum frequency deviation the bigger the disturbing effect produced by the contingency. Therefore, an index is proposed that is calculated as the maximum frequency deviation
): The maximum frequency deviation from its rated value is a clear representative of the dynamic effect produced by the contingency analyzed on the microgrid. The higher the maximum frequency deviation the bigger the disturbing effect produced by the contingency. Therefore, an index is proposed that is calculated as the maximum frequency deviation 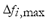 relative to the maximum admissible frequency deviation
relative to the maximum admissible frequency deviation 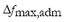 . This index ranges from 0 for the case in which no frequency deviation is produced to 1 for the case in which frequency reaches its maximum admissible value, thus indicating the system collapse. The
. This index ranges from 0 for the case in which no frequency deviation is produced to 1 for the case in which frequency reaches its maximum admissible value, thus indicating the system collapse. The 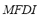 is defined by (2):
is defined by (2):
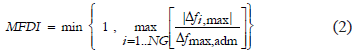
where 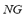 is the number of generators operating on the MG. The maximum admissible value is related to the under- and over-frequency protection of generators. These protections are set about
is the number of generators operating on the MG. The maximum admissible value is related to the under- and over-frequency protection of generators. These protections are set about 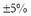 of rated frequency. These protections are fundamental to avoid the negative aspects on the auxiliary services and on the generating units related to the increase or decrease of the MG frequency beyond its rated value [11].
of rated frequency. These protections are fundamental to avoid the negative aspects on the auxiliary services and on the generating units related to the increase or decrease of the MG frequency beyond its rated value [11].
3) Total Frequency Deviation Index (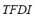 ): This index stands for the time during which the frequency remained out of its rated value. It is calculated as the quotient between the absolute area of frequency deviation and the maximum admissible area. The range of variation of this index is from 0 for the case in which no variation of frequency occurs at any time, to 1 for the case in which frequency remained at its maximum admissible value for all the simulation time. The
): This index stands for the time during which the frequency remained out of its rated value. It is calculated as the quotient between the absolute area of frequency deviation and the maximum admissible area. The range of variation of this index is from 0 for the case in which no variation of frequency occurs at any time, to 1 for the case in which frequency remained at its maximum admissible value for all the simulation time. The 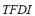 is defined by (3):
is defined by (3):
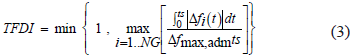
here 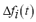 is the temporal frequency deviation,
is the temporal frequency deviation, 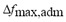 is the maximum admissible frequency deviation,
is the maximum admissible frequency deviation, 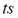 is the simulation time, and
is the simulation time, and  is the number of generators operating on the microgrid.
is the number of generators operating on the microgrid.
4) Dynamic Voltage Index (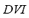 ): A requirement that must be met for voltage transients is that at no point on the network, except during application of the fault in the case of short circuit analysis, should the voltage level remain below certain limit [12]. The dynamic voltage index is related to the requirement mentioned above. The
): A requirement that must be met for voltage transients is that at no point on the network, except during application of the fault in the case of short circuit analysis, should the voltage level remain below certain limit [12]. The dynamic voltage index is related to the requirement mentioned above. The 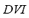 is defined by (4):
is defined by (4):
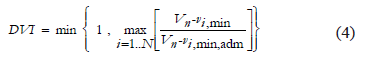
where 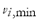 is the minimum instantaneous voltage at bus
is the minimum instantaneous voltage at bus 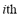 during the transient,
during the transient, 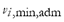 is the minimum admissible voltage value (0.7 p.u. in this work),
is the minimum admissible voltage value (0.7 p.u. in this work), 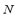 the number of buses of the system, and
the number of buses of the system, and 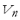 the rated voltage.
the rated voltage.
5) Quasi-Stationary Voltage Index (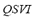 ): This index takes into account the recovery and control of the bus voltage at the end of the transient period following the contingency. The index is calculated as the quotient between the voltage deviation at the end of the transient period
): This index takes into account the recovery and control of the bus voltage at the end of the transient period following the contingency. The index is calculated as the quotient between the voltage deviation at the end of the transient period 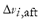 (post-contingency voltage deviation at bus
(post-contingency voltage deviation at bus 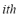 ) and the maximum voltage deviation limit
) and the maximum voltage deviation limit 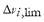 . The
. The 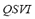 is defined by (5):
is defined by (5):
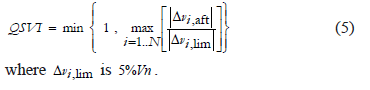
6) Power Flow Index (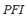 ): This index takes into account the fact that the power flow after the contingency should not exceed the maximum acceptable value, since an excess of power flow through the lines in the post-contingency steady-state can activate line protections, thus damaging the microgrid security. The power flow through the transmission lines can be limited due to thermal limits, voltage drop limits, or other stability limits. The
): This index takes into account the fact that the power flow after the contingency should not exceed the maximum acceptable value, since an excess of power flow through the lines in the post-contingency steady-state can activate line protections, thus damaging the microgrid security. The power flow through the transmission lines can be limited due to thermal limits, voltage drop limits, or other stability limits. The 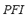 is defined by (6):
is defined by (6):
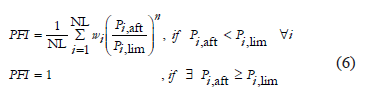
where 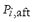 is the power flow through the line
is the power flow through the line 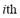 at the end of the transient period following the contingency;
at the end of the transient period following the contingency; 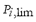 is the power flow limit taking into account the strictest restriction (thermal limit, voltage limit or stability limit),
is the power flow limit taking into account the strictest restriction (thermal limit, voltage limit or stability limit), 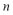 is the norm, which is used to reduce the contribution to the PFI index of lines that have not reached their limits; at the same time, this norm is used to amplify the contribution of lines that have exceeded their limits [13]. In this work the norm is taken to be equal to 1,
is the norm, which is used to reduce the contribution to the PFI index of lines that have not reached their limits; at the same time, this norm is used to amplify the contribution of lines that have exceeded their limits [13]. In this work the norm is taken to be equal to 1, 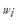 is a weight factor, that is, a real non-negative number, which stands for the relative importance of the lines in the system. In this work, the weight factor is taken to be equal to 1 for all lines (i.e. all lines have equal importance). Finally,
is a weight factor, that is, a real non-negative number, which stands for the relative importance of the lines in the system. In this work, the weight factor is taken to be equal to 1 for all lines (i.e. all lines have equal importance). Finally, 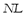 represents the number of power lines on the microgrid. The
represents the number of power lines on the microgrid. The 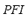 is related to line protections. The value 1 represents that at least in one line of the microgrid the power flow reaches its maximum limit. This situation trips the circuit breakers associated with this line, causing its outage.
is related to line protections. The value 1 represents that at least in one line of the microgrid the power flow reaches its maximum limit. This situation trips the circuit breakers associated with this line, causing its outage.
7) Load Shedding Index (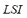 ): When an unexpected generator outage occurs, or a generation area is lost due to an unexpected line outage, in order to compensate the unbalance between the generated power and the load demand, in some extreme cases it is necessary to disconnect load so that the microgrid integrity may be kept. The amount of load disconnected depends on the magnitude of the unbalance and on the used automatic load shedding scheme. A load shedding index is proposed. This is calculated as the quotient between the total disconnected load
): When an unexpected generator outage occurs, or a generation area is lost due to an unexpected line outage, in order to compensate the unbalance between the generated power and the load demand, in some extreme cases it is necessary to disconnect load so that the microgrid integrity may be kept. The amount of load disconnected depends on the magnitude of the unbalance and on the used automatic load shedding scheme. A load shedding index is proposed. This is calculated as the quotient between the total disconnected load 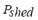 and the total demand of the microgrid
and the total demand of the microgrid 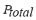 previous to the contingency. The
previous to the contingency. The 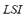 is defined by (7):
is defined by (7):

4. FUZZY INDEXES COMPOSITION
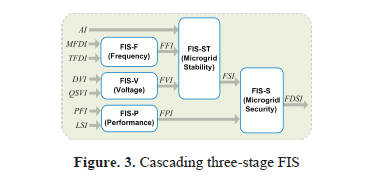
The seven performance indexes previously described are capable of capturing both the dynamic state and the quasi-stationary state of the microgrid immediately following a contingency. From experience in SSA, it is well known that some indexes work better than others for particular power systems and that combination of indexes usually works better than a single index [14, 15, 16]. The statement to the problem is the following: given the seven calculated performance indexes, it is necessary to compose their effects, in order to develop a single index of dynamic security. This index must exhibit the effect that each individual contingency causes to the power system variables, and in addition must indicate the distance to the security limit taking into consideration the specific criterion of evaluation defined in this work. All performance indexes that take part in the composition are continuous. The composition of several phenomena has already been made in SSA. Nevertheless, there is neither a clear methodology nor a mathematical model to make such composition. On the other hand, the composition requires the combination of several different effects, so, the use of averages or weighed sums would not be adequate. The occurrence of a contingency modifies the normal operation values of the power system, such as machines angles, frequency, bus voltages, and power flow. It is known that calculated variable using models of system components are simply reasonable approximations of the actual values, and therefore there is an uncertainty associated with these calculated values. Taking into account these characteristics of the problem, continuous variables and the lack of a mathematical model, it is appropriate to use a FIS for the index composition [17]. A scheme of this FIS is shown in Figure. 3.
The FIS provides a robust mathematical framework for modeling the uncertainty associated with models of components used and for computing with both linguistic terms and numerical values [18]. In this paper a three-stage FIS is used to compose a fuzzy dynamic security index 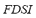 .
.
1) Fuzzy Frequency Index (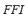 ): The consequence of an particular contingency on the microgrid frequency is represented through the fuzzy frequency index
): The consequence of an particular contingency on the microgrid frequency is represented through the fuzzy frequency index 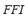 , which results from the composition of the maximum frequency deviation index
, which results from the composition of the maximum frequency deviation index 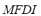 and the total frequency deviation index
and the total frequency deviation index 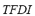 by means of the FIS-F. The universe of discourse of the input variables and of the output for the FIS-F has been partitioned into three linguistic values: LOW, MEDIUM and HIGH. These variables are equally distributed along the interval [0, 1]. Triangular fuzzy sets have been chosen to model each linguistic value, because they are naturally associated to the intuitive meaning of "approximately equal to LOW, or MEDIUM, or HIGH". Each rule has two antecedents (
by means of the FIS-F. The universe of discourse of the input variables and of the output for the FIS-F has been partitioned into three linguistic values: LOW, MEDIUM and HIGH. These variables are equally distributed along the interval [0, 1]. Triangular fuzzy sets have been chosen to model each linguistic value, because they are naturally associated to the intuitive meaning of "approximately equal to LOW, or MEDIUM, or HIGH". Each rule has two antecedents (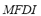 and
and 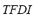 ) and one consequent (
) and one consequent (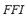 ). The closer the
). The closer the 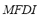 or the
or the 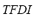 is to one, the greater its influence on the
is to one, the greater its influence on the 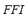 . The closer the
. The closer the 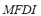 and the
and the 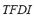 is to zero, the smaller its influence on the
is to zero, the smaller its influence on the 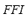 .
.
2) Fuzzy Voltage Index (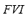 ): The consequence of the particular contingency on the bus voltages is represented through the fuzzy voltage index
): The consequence of the particular contingency on the bus voltages is represented through the fuzzy voltage index 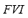 , which results from the composition of the dynamic voltage index
, which results from the composition of the dynamic voltage index 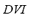 and the quasi-stationary voltage index
and the quasi-stationary voltage index 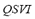 by means of the FIS-V. The way in which the composition is carried out is identical to the one of the frequency index, thus, it is not repeated here.
by means of the FIS-V. The way in which the composition is carried out is identical to the one of the frequency index, thus, it is not repeated here.
3) Fuzzy Performance Index (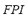 ): The effects of the specific contingency on the power flow index
): The effects of the specific contingency on the power flow index 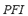 and on the load shedding index
and on the load shedding index 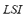 are composed by means of the FIS-P in order to obtain the fuzzy performance index
are composed by means of the FIS-P in order to obtain the fuzzy performance index 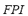 . The universe of discourse of the input variables for the FIS-P has been partitioned into three linguistic values: LOW, MEDIUM and HIGH. The set of terms and membership function for the
. The universe of discourse of the input variables for the FIS-P has been partitioned into three linguistic values: LOW, MEDIUM and HIGH. The set of terms and membership function for the 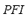 and for the
and for the 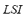 are comparable to the inputs variables of the FIS-F. The output of the FIS-P has been partitioned into five linguistic values: LOW, MEDIUM-LOW, MEDIUM, MEDIUM-HIGH and HIGH. These variables are equally distributed along the interval [0, 1]. Each rule has two antecedents (
are comparable to the inputs variables of the FIS-F. The output of the FIS-P has been partitioned into five linguistic values: LOW, MEDIUM-LOW, MEDIUM, MEDIUM-HIGH and HIGH. These variables are equally distributed along the interval [0, 1]. Each rule has two antecedents (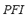 and
and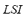 ) and one consequent (
) and one consequent (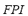 ).
).
4) Fuzzy Stability Index (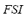 ): The fuzzy frequency index
): The fuzzy frequency index 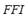 and the fuzzy voltage index
and the fuzzy voltage index 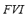 are composed with the angle index
are composed with the angle index 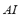 on the FIS-ST in order to obtain the fuzzy stability index
on the FIS-ST in order to obtain the fuzzy stability index 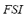 . The universe of discourse of the input variables and of the output variable has been partitioned into three linguistic values: LOW, MEDIUM and HIGH. These variables are equally distributed along the interval [0, 1]. The set of terms and membership function for the
. The universe of discourse of the input variables and of the output variable has been partitioned into three linguistic values: LOW, MEDIUM and HIGH. These variables are equally distributed along the interval [0, 1]. The set of terms and membership function for the 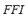 ,
, 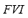 ,
, 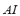 , and for the
, and for the 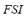 are comparable to the one for the FIS-F. Each rule has three antecedents (
are comparable to the one for the FIS-F. Each rule has three antecedents (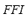 ,
,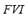 , and
, and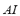 ) and one consequent (
) and one consequent (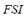 ).
).
5) Fuzzy Dynamic Security Index (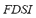 ): The fuzzy stability index
): The fuzzy stability index 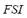 and the fuzzy performance index
and the fuzzy performance index 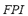 are composed in the FIS-S in order to obtain the fuzzy dynamic security index
are composed in the FIS-S in order to obtain the fuzzy dynamic security index 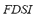 . The universe of discourse of the input variables and of the output variable has been partitioned into three linguistic values: LOW, MEDIUM and HIGH. These variables are equally distributed along the interval [0, 1]. Triangular fuzzy sets have been chosen for modeling each linguistic value. The
. The universe of discourse of the input variables and of the output variable has been partitioned into three linguistic values: LOW, MEDIUM and HIGH. These variables are equally distributed along the interval [0, 1]. Triangular fuzzy sets have been chosen for modeling each linguistic value. The 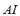 , the
, the 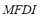 , the
, the 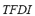 , the
, the 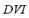 , and the
, and the 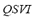 are calculated considering the maximum and/or minimum admissible values of three parameters of the microgrid: angles of generating machines, system frequency and bus voltages. The FIS-ST has been designed so that when any of mentioned parameters reaches its maximum and/or minimum value, the output will be equal to one. On the other hand, only when all inputs are equal to zero, the output of the FIS-ST will be equal to zero. The
are calculated considering the maximum and/or minimum admissible values of three parameters of the microgrid: angles of generating machines, system frequency and bus voltages. The FIS-ST has been designed so that when any of mentioned parameters reaches its maximum and/or minimum value, the output will be equal to one. On the other hand, only when all inputs are equal to zero, the output of the FIS-ST will be equal to zero. The 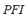 is calculated taking into consideration power flows on the lines in relation to their maximum values. This index represents an "average" of the effect of the considered contingency over power flows.
is calculated taking into consideration power flows on the lines in relation to their maximum values. This index represents an "average" of the effect of the considered contingency over power flows. 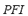 jointly with
jointly with 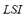 compose the
compose the 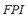 , which represents a "combined performance" of the effect caused by the contingency over the power flows and on the amount of load disconnected. These previous explanations are made in order to understand the strategy of composition of the
, which represents a "combined performance" of the effect caused by the contingency over the power flows and on the amount of load disconnected. These previous explanations are made in order to understand the strategy of composition of the 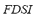 . The
. The 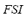 is the index that mainly defines the value of the
is the index that mainly defines the value of the 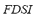 . The
. The 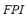 will contribute with a small proportion to the
will contribute with a small proportion to the 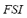 ; this amount will increase in the case that
; this amount will increase in the case that 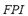 is high, and will not modify the
is high, and will not modify the 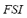 in the case that
in the case that 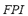 is small. Each rule has two antecedents (
is small. Each rule has two antecedents (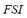 and
and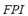 ) and one consequent (
) and one consequent (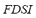 ). For the previously described FIS, in order to obtain numeric values from the fuzzy sets derived as a result of the inference, the Fuzzy Mean method is used for defuzzyfication [19].
). For the previously described FIS, in order to obtain numeric values from the fuzzy sets derived as a result of the inference, the Fuzzy Mean method is used for defuzzyfication [19].
5. DISTRIBUTED PROCESSING
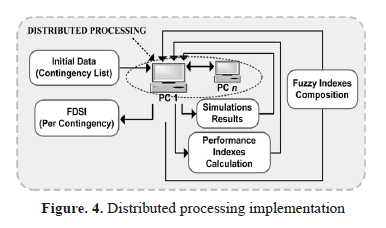
The implementation of the block which must perform the full time-domain simulations of the microgrid for each one of the critical contingencies (CC) is carried out using a software that allows representing the microgrid short-term dynamic behavior. This software must include all the models necessary to characterize the behavior of the various electrical components of the electrical microgrid, e.g. generators, loads, and the network itself. In this work, the Power System Simulator for Engineering (PSS/E) software package from Siemens Power T&D, Inc. is employed for this aim. It is an integrated, interactive program for simulating, analyzing, and optimizing power system performance and provides probabilistic and dynamic modeling features. For each determined CC, a time-domain simulation must be executed. Each simulation is independent of the remaining ones, so that each one can be run in a different thread. This task is performed in PSS/E by creating user defined input batch files (IDV file) as response files that control a single simulation in a batch mode. These files allow the user of PSS/E to automate the execution of a sequence of activities. The structure of computation of the TDS for each considered critical contingency is shown in Figure. 4.
A system consisting of a 1GB/s network of n personal computers (PCs) performing individual functions and linked with a main computer (PC1) through a hub used for composing more complex tasks is employed as the proposed distributed computing. Such PCs can differ in their individual characteristics but all share the same communication protocol TCP/IP. By using remote method invocation (RMI) of Java [20], a tool is developed to implement distributed applications, including a main program and auxiliary ones. It schedules the execution of multiple PSS/E simulations on all available computers. This tool is optimized for parametric simulations, where the same basic simulation is executed many times with different input parameters, as required for performing on-line DSA. By distributing execution over multiple computers, the results are obtained faster or more simulations can be performed in the same time period. The main program runs in PC1, and the auxiliary ones run in the other PCs (up to n personal computers). The goal of the main program is to control the initialization of the distributed process and to transfer to the other PCs the input files to perform the full TDSs for each CC. The input files notify which contingency must be evaluated, among with other data necessary for the simulation. The auxiliary programs execute the simulation program when its corresponding input files are received. Upon finishing the simulation for each critical contingency specified, the simulation programs generate the respective output files and they send back to the main program the files containing the results obtained for the subsequent analysis, the performance indexes calculation and the fuzzy indexes composition.
6. APPLICATION EXAMPLE
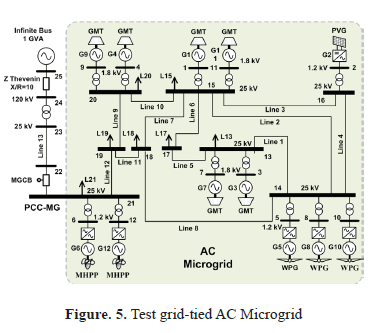
The test power system used to validate the proposed on-line DSA methodology of the microgrid is depicted in Figure. 12 as a single-line diagram. This electric power network implements a bulk power system providing a small AC microgrid, which includes a variety of distributed energy resource (DER) units (DG based on fossil and renewable fuels) and different types of loads. The microgrid is moderately meshed and implements a dynamically-modeled multiple generator-type DG linked to a utility system represented by a classical single machine-infinite bus type (SMIB) system. A microgrid central breaker (MGCB) is employed for the interconnection of the microgrid (bus 21) to the bulk power network. This basic 25-bus network operates at 120 kV/50 Hz on the bulk system side and at 25 kV on the microgrid side, and implements a 1 GVA short circuit power level infinite bus through a Thevenin equivalent circuit. The six DGs based on fossil fuels are composed of dispatchable units powered by typical gas microturbines (GMTs). The six DGs based on renewable fuel are made up of two 1.5 MW run-of-the-river (ROR) variable speed micro hydro power plants (MHPPs), a wind farm [20] consisting of a three rows with three turbines per row of 1 MW variable speed wind power generators (WPGs) grid-tied via full-scale power converters and a 3.6 MW photovoltaic generator (PVG) compound of an array with 18 000 polycrystalline modules (200 Wp each at standard test conditions).
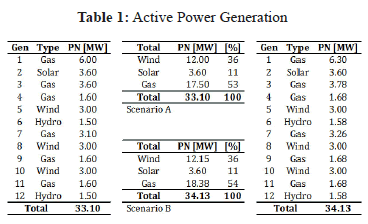
In order to verify the effectiveness of the proposed DSA strategy, two scenarios are proposed (scenarios A and B), for which the inference of the dynamic security level is carried out. The first scenario, i.e. the scenario A, corresponds to the base case study and the scenario B represents the case with a demand increase of 5 % in relation to the scenario A. The idea is to prove the efficiency of the tool by comparing the results of the scenario A with those results obtained from other scenarios where the microgrid total load has been increased. The additional load on scenario B has been uniformly distributed on load buses with respect to the base case. The first case study (scenario A) considers the worst case study with the AC microgrid operating isolated from the bulk power system (island conditions), i.e. the MGCB is open at all times. Under these circumstances, since all RES-based DG units are not dispatchable and are considered operating at rated nominal power, the set of gas microturbine units themselves must supply all the power required by the microgrid loads. In these conditions, the spinning reserve of all GMT units is sufficiently large for supporting the MG frequency and thus avoiding the activation of the automatic load shedding scheme. In this island operation in steady state, the MG frequency is at its rated value (1 p.u. of 50 Hz) and the voltages for all buses are within the admissible limits, although not all of them are at 1 p.u. (base voltage of 25 kV). Table 1 shows the active power generation in steady state of all microgrid DG units for both studied scenarios. As can be observed, approximately 53 % of the demand is provided by GMT dispatchable units (17.5 MW) and about 47 % (15.6 MW) via uncontrolled renewable energy sources (11% or 3.6 MW of PV solar, 27 % or 9 MW of wind and 9 % or 3 MW of hydro).
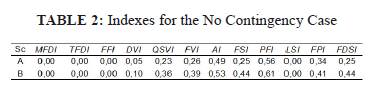
As derived from Table 1, since the scenario B considers the island operation of the AC microgrid with a demand increase of 5 %, only the gas microturbine units increase their power in order to balance the load demand change. In these conditions, as in the previous case study, the spinning reserve of all GMT units is suitably large to support the MG frequency and thus also avoiding the activation of the automatic load shedding scheme. The demand change is shared equally (in percentage of active load) between the GMT generators, even though the generators vary in size. The results obtained from all simulated cases and the composed fuzzy indexes for on-line DSA of the microgrid are analyzed in the following scenarios A and B with different specific contingencies. Contingencies that are evaluated include: (1) the unexpected trip of the entire wind farm, i.e. the 9 wind power generators (9 MW). (2) the sudden trip of the PV solar generator. Performance indexes and fuzzy indexes for the no contingency case on both scenarios (A and B) are shown in Table 2. As can be noted, a growth in all partial indexes occurs for the scenario B with respect to A. This is a consequence of the increase in the load demand, which enforces greater deviations of load bus voltages, and increases the generators angles and larger power flows on the lines. All these changes are reflected through the value of the fuzzy dynamic security index (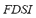 ). Only indexes related to frequency and load shedding remain zero due to the absence of contingency, and the fact that the spinning reserve of all dispatchable units is enough to support and control the MG frequency at 1 p.u.; this also avoiding the shedding of load. The increase of the
). Only indexes related to frequency and load shedding remain zero due to the absence of contingency, and the fact that the spinning reserve of all dispatchable units is enough to support and control the MG frequency at 1 p.u.; this also avoiding the shedding of load. The increase of the 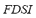 in scenario B (with load increase) is also reflected in the case of generators tripping. The microgrid has a non-linear behavior, so that the increase of the
in scenario B (with load increase) is also reflected in the case of generators tripping. The microgrid has a non-linear behavior, so that the increase of the 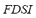 is also non-linear.
is also non-linear.
Table 3 shows the performance indexes and fuzzy indexes for the case with contingency 1, i.e. with a sudden trip of the entire 9 MW wind farm, on both scenarios (A and B).
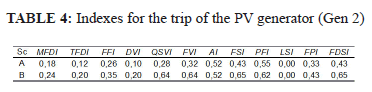
In this case, the tripping of 9 WPGs on both scenarios (A and B) increases drastically the dynamic security indices, making them reach the maximum values (equal to 1). This is due to several reasons: first, the amount of power that is discontinued in the microgrid is about 27 % of total demand in both scenarios. The load disconnected by the load shedding scheme is not enough to support the MG frequency, so that the frequency excursions falls outside the acceptable region, determined by the minimum admissible value; this causing the system to collapse. A massive voltage collapse is also developed in the microgrid. In addition, the restriction on the distribution system power lines limits the capability to transmit power, thus decreasing the available generation reserve provide by all GMT generators. From this, the necessity of having available enough short-term generation reserve emerges, in order to preserve adequate security levels. This reserve must be properly activated by means of the primary frequency control (PFC) in order to keep the system frequency above the admissible minimum level during the transient subsequent to a contingency. Otherwise, serious problems could occur that would lead to MG collapse. Table 4 shows the performance indexes and fuzzy indexes for the case with contingency 2, i.e. with a sudden trip of the 3.6 MW photovoltaic solar generator (no. 2), in both scenarios (A and B). Considering the case of tripping the 3.6 MW photovoltaic solar generator (gen. 2) in both scenarios (A and B), it produces no major problems, as can be seen from Table 4. This solar generator provides to the grid only 11 % of demanded load, a value that can be handled by the automatic load shedding scheme. Therefore, the activation of several frequency steps for implementing a rather higher than 3.6 MW of load rejection is required in order to recover the system frequency to its scheduled value. Under these circumstances, the required demand cannot be fully satisfied bringing technical and economic consequences that are related to costs of deficits. This issue can be resolved by starting a new GMT generator to meet the requirements of balance between supply and demand, until the PVG is operating again.
7. CONCLUSIONS
The penetration of these DG units based on RESs into microgrids is growing rapidly (especially wind and solar energies), reaching a high percentage of the installed generating capacity. However, the fluctuating and intermittent nature of this renewable generation causes variations of power flow that can significantly affect the operation of the electrical grid. This situation can lead to severe problems that dramatically jeopardize the microgrid security, such as system frequency oscillations, and/or violations of power lines capability margin, among others. To overcome these problems, distributed energy storage (DES) systems based on emerging technologies arise as a potential alternative in order to balance any instantaneous mismatch between generation and load in the microgrid. With proper controllers, these advanced DESs are capable of supplying the microgrid with both active and reactive power simultaneously and very fast, and thus are able to provide the required security level. The analysis of results obtained using the proposed FIS jointly with the distributed processing implementation allows accelerating the DSA strategy, so that it can be implemented on-line. In contrast to some indexes that are calculated in an off-line way considering typical states of the microgrid, and then, in an on-line stage they can estimate its value interpolating between two pre-calculated values; the 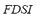 is calculated in an on-line stage for the current state of the system. As a result, the
is calculated in an on-line stage for the current state of the system. As a result, the 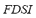 can reflect the non-linear characteristic of the microgrid, which can be hidden as a result of the interpolation. The cascading FIS allows not only to speed up the process of security assessment, but also to compose the effect of various dissimilar state variables. It is important to remark that the seven calculated performance indexes are based on full time-domain simulations, not using approximate methods or accelerated time-domain simulators. Moreover, the tool for on-line inference of DSA is easy to use and to understand. At the same time, it allows system operators to modify the rule base of each FIS, on the basis of their experience.
can reflect the non-linear characteristic of the microgrid, which can be hidden as a result of the interpolation. The cascading FIS allows not only to speed up the process of security assessment, but also to compose the effect of various dissimilar state variables. It is important to remark that the seven calculated performance indexes are based on full time-domain simulations, not using approximate methods or accelerated time-domain simulators. Moreover, the tool for on-line inference of DSA is easy to use and to understand. At the same time, it allows system operators to modify the rule base of each FIS, on the basis of their experience.
REFERENCES
[1] Kundur, P. et al., Definition and classification of Power system stability, IEEE/CIGRE Joint Task Force on Stability Terms and Definitions, IEEE Trans. Power Systems, vol. 19(3), pp. 1387-1401, August 2004. [ Links ]
[2] Tomsovic, K., Project Leader. Integrated security analysis, Final Report. Power Systems Engineering Research Center PSERC Publication 03-06. May 2003. Washington State University. 2003. [ Links ]
[3] Guerrero, J. M. et al., Distributed generation: toward a new energy paradigm, IEEE Industrial Electronics Magazine, vol. 4(1), pp. 52-64, March 2010. [ Links ]
[4] Hatziargyriou, N. et al., Microgrids, IEEE Power & Energy Magazine, vol. 5(4), pp.78-94, July-Aug. 2007. [ Links ]
[5] Kroposki, B. et al., Making microgrids work, IEEE Power & Energy Magazine, vol. 6(3), pp. 40-53, May/June 2008. [ Links ]
[6] Rahman, S., Going green: the growth of renewable energy, IEEE Power & Energy Magazine, pp. 16-18, Nov./Dec. 2003. [ Links ]
[7] Zhang, Y. et al.; SIME: A hybrid approach to fast transient stability assessment and contingency selection," Electrical Power and Energy System. vol. 19, (9). pp. 195-208, 1997. [ Links ]
[8] Morison, K.,Wang, L. and Kundur, P., Power system security assessment, IEEE Power and Energy Magazine, vol. 2(5), pp.30-39, September-October 2004. [ Links ]
[9] Meyer, B., New Trends and Requirements for Dynamic Security Assessment, CIGRE Task Force 38.02.13 Report, Paris, 1997. [ Links ]
[10] Kundur, P., Power system stability and control, United State of America: McGraw-Hill, Inc, , P. 924, ch. 13. 1994. [ Links ]
[11] Ungrand, H., Winkler, W. and Wiszniewski, A., Protection Techniques in Electrical Energy Systems, Marcel Dekker, Inc, 1995. [ Links ]
[12] Yusheng, et al., Quantitative assessments for transient voltage security, IEEE Trans. Power Systems, vol. 15(3), pp.1077-1083, Aug. 2000. [ Links ]
[13] Wasley, R. G. and Daneshdoost. M., Identifications and Ranking of Critical Contingencies in Dependent Variable Space, IEEE Trans. Power Apparatus and Systems, vol. PAS-102, no. 4, pp. 881, April 1983. [ Links ]
[14] Brandwajn, V. et al., Severity indices for contingency screening in dynamic security assessment, Power Systems, IEEE Transactions on. Volume 12(3), Aug, pp. 1136-1142, 1997. [ Links ]
[15] Fu, C. and Bose, A., Contingency ranking based on severity indices in dynamic security analysis, Power Systems, IEEE Transactions on. Volume 14 (3), Aug. pp. 980-985, 1999. [ Links ]
[16] Cox, E.; Fuzzy Fundamentals, Spectrum, IEEE Volume 29, (10), Oct, pp. 58-61. 1992. [ Links ]
[17] Mendel, J. M., Uncertain Rule-Based Fuzzy Logic Systems. Introduction and New Directions. Englewood Cliffs, NJ: Prentice-Hall, 2001. [ Links ]
[18] Tsoukalas, L. H. and Uhring, R. E., Fuzzy and neural approach in engineering. 1st ed., John Wiley and Sons, Inc., 1987. [ Links ]
[19] http://java.sun.com/products/jdk/rmi/ [ Links ]
[20] Gimenez, J. M., Schweickardt, G., Gomez, J. C., An overview of wind energy, taking into consideration several important issues, including an analysis of regulatory requirements for the connection of wind generation into the power system, Revista DYNA, Vol. 79, Tomo 1, pp. 108-117, Abril de 2012. [ Links ]