Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.182 Medellín Nov./Dec. 2013
NON-UNIFORM HEATING COMPENSATION FOR SEQUENCES OF THERMAL IMAGES USING MEDIAN FILTERING
COMPENSACIÓN DEL CALENTAMIENTO NO UNIFORME EN SECUENCIAS DE IMÁGENES TÉRMICAS MEDIANTE FILTRADO DE MEDIANA
ANDRÉS DAVID RESTREPO GIRÓN
M.Sc., Universidad Santiago de Cali, Campus Pampalinda, Cali, Valle, Colombia, adareg378@gmail.com
HUMBERTO LOAIZA CORREA
Ph.D.,Universidad del Valle, Ciudad Universitaria Meléndez, Cali, Valle, Colombia, humberto.loaiza@correounivalle.edu.co
Received for review February 5th, 2012, accepted December 14th, 2012, final version January, 21th, 2013
ABSTRACT: Herein, we introduce a new thermal contrast enhancement procedure for infrared images, acquired from a non-destructive evaluation of composite slabs through active infrared thermography experiments. This technique can compensate for the vignetting effect, as well as the non-uniform heating produced by the thermal excitation scheme. The proposed technique does not depend on any heat propagation model but almost exclusively on experimental data, because it is based on an unsharp mask operation using a median filter. The preliminary results show that real and apparent non-uniform heating is effectively compensated with this method, resulting in better images of possible internal defects than other classic methods like Differential Absolute Contrast (DAC), and therefore increasing the probability of more efficient detection and characterization procedures; specifically, the non-uniformity effect on the original sequence could be reduced by about 74%, according to a non-uniformity parameter defined in this work, as well.
KEYWORDS: infrared thermography, active infrared thermography, thermal contrast, non-uniform heating, vignetting, unsharp masking, median filter.
RESUMEN: Se expone un nuevo procesamiento para el mejoramiento del contraste térmico en una secuencia de imágenes infrarrojas adquiridas a partir de un procedimiento de Termografía IR activa sobre placas de material compuesto, capaz de compensar el efecto óptico de vignetting y el calentamiento no uniforme producido por el esquema de excitación de la muestra. La técnica propuesta no depende de ningún modelo de propagación de calor sino casi exclusivamente de los datos experimentales, al basarse en una operación de énfasis usando un filtro de mediana. Los resultados preliminares muestran que el calentamiento no uniforme se compensa efectivamente con este procedimiento, permitiendo obtener imágenes más contrastadas de los defectos posibles al interior del material en comparación con otras técnicas como el Contraste Absoluto Diferencial (CAD), aumentando así la probabilidad de una detección y caracterización más eficaces; específicamente, el efecto de no uniformidad de fondo de la secuencia térmica original puede ser reducido en un 74%, de acuerdo con un parámetro de no-uniformidad propuesto también en este trabajo.
PALABRAS CLAVE: termografía infrarroja, termografía infrarroja activa, contraste térmico, calentamiento no uniforme, vignetting, filtros de énfasis, filtro mediana.
1. INTRODUCCIÓN
Infrared Thermography (IT) is defined as a technique that allows detecting and estimating characteristics or phenomena present under the surface of a body, through sensing the infrared radiation from the body, and determining the temperature distribution on its surface. In this sense, thermography can be used under two schemes: passive thermography, which works with system's natural heat radiation, generated by its own operation or by interaction with other heat sources and fluxes [1]; and active thermography in which heating the material or system under study is required to create differences in temperature, which otherwise, would not be present or be imperceptible under natural conditions, [2] [3] [4].
The fundamental requirement for an active thermography experiment providing useful information is the existence of thermal contrast (dT), or temperature difference between objects of interest (usually the defects sought) and the immediate surroundings. This phenomenon takes place provided that these features have different thermal properties from the base material; therefore a thermal reflection occurs at the change of propagation medium [5].
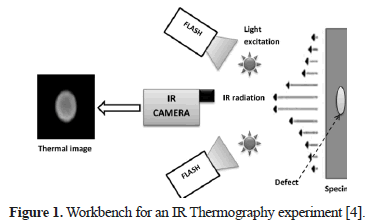
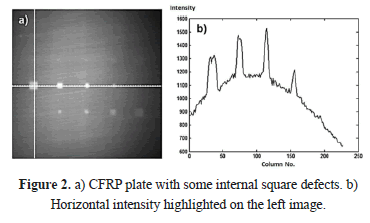
The most common active IT technique is called Pulsed Thermography (PT) [6] in which the heating of the specimen is generated by a heat pulse (using lamps or high intensity flashes) whose width, in direct relation to the thermal conductivity of material, can be set from several milliseconds to a few seconds, making it a relatively fast method (Figure 1). The relevant information focuses on the cooling curves of the object studied, given that thermal contrast will be present in the region where a defect (change of medium) occurs under the surface; although, many researchers see a weakness in the contrast decay with time when using PT, a suitable pre-processing of pulsed thermograms can give this method strong advantages over phase or lock-in methods [7]. Figure 2a shows an example of a thermogram or thermal image extracted from a sequence of images obtained via Cincinnati Electronics InSb camera from a Carbon Fiber Reinforced Plastic (CFRP), in which there are several artificial square flaws of different sizes and depths.
If you look, for example, at the intensity profile along the horizontal white line in Figure 2a, you get the trace of Figure 2b. Note the clear presence of four peaks corresponding to defects whose intensity contrasts with the lower intensity of background; however, it is quite remarkable that the background thermal profile fits a concave curve. This behavior is basically due to two phenomena: the first, known as vignetting, that makes the captured image darker as it progresses towards its periphery, because of the distortion introduced by the camera lens, the own camera thermal radiation, and the conditions of the scene; and the second, known as non-uniform heating, caused by the natural dispersion of light from the lamps that heat the material in the PT, making the focal point where the lamps illuminate, more irradiated (and brighter) than its surroundings [5].
The direct consequence of the presence of uneven heating in the thermal images acquired from an active IT experiment is the reduction in intensity contrast in these images, and this contrast is proportional to the thermal contrast needed to detect and subsequently characterize any defective areas. Thus, the compensation of the uneven heating phenomenon improves the thermal contrast and the subsequent image analysis. This article presents a proposal for compensation of uneven heating, for which section 2 provides an overview of the most important techniques to improve the thermal contrast, following the description of the proposed methodology based on the filtering of images in section 3, to end the paper with the discussion of results and conclusions.
2. BACKGROUNDS OF THERMAL CONTRAST ENHANCEMENT
The original technique to improve thermal contrast is absolute thermal contrast Ca (AC) [8] which is the difference between the temperature 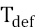 at any point on the surface (recorded on a thermogram) and the temperature
at any point on the surface (recorded on a thermogram) and the temperature 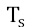 of a healthy reference region (without flaws) throughout all of the recorded thermogram sequence (Equation 1). However, the temporal evolution of heat propagation is a common aspect in most of the contrast enhancement techniques taken into account, which influences all of them to a greater or lesser extent by uneven heating, which is primarily a spatial phenomenon.
of a healthy reference region (without flaws) throughout all of the recorded thermogram sequence (Equation 1). However, the temporal evolution of heat propagation is a common aspect in most of the contrast enhancement techniques taken into account, which influences all of them to a greater or lesser extent by uneven heating, which is primarily a spatial phenomenon.
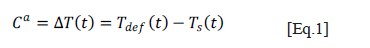
This kind of contrast enhancement does not change the profile shape with respect to Figure 2b; it only subtracts an offset for all pixels of a thermogram, which depends on the reference region and the thermogram itself.
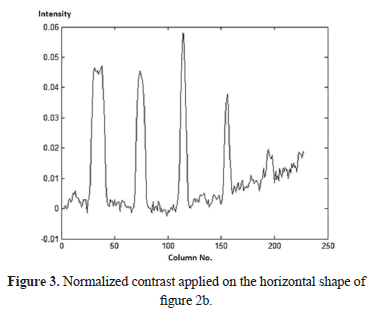
Other techniques are: relative thermal contrast Cr (RC), normalized contrast Cn (NC - whose result is shown in Figure 3) and standard contrast Cs (SC) [5], which are refinements to the definition of Equation 1 to reduce sensitivity to uneven heating, but they still need a priori selection of a healthy region. In an attempt to avoid this requirement, differential absolute contrast (DAC) emerged [9] based on the adiabatic one-dimensional model of heat transfer on the surface of a semi-infinite plate of flawless solid material heated by a thermal impulse.
The DAC method consists of using this model to predict the values of the surface temperature the material would exhibit if it had no defects, to subtract them from the actual values taken with the infrared camera; so, considerable differences would be present in those defective regions. Then, instead of choosing a healthy area of the material, the thermogram at time t' is chosen, when the thermal front reaches the surface (reference thermogram). This thermogram is located between the time t0 of the heat pulse transmission, and time t1 of the appearance of the first defect, resulting in Equation 2 for the DAC technique:
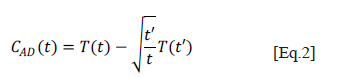
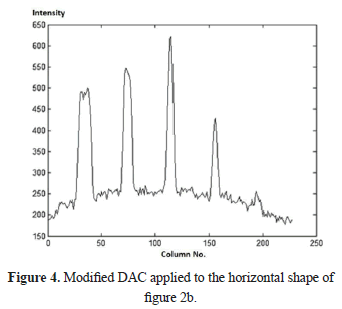
An important refinement of DAC arises with the modified DAC method (m-DAC) [9], which takes into account the reflection of the thermal front at the non-irradiated side of the plate under inspection, as well as the effect of using a squared or exponential heat pulse, wide enough to hinder the approximation to an impulse d(t), when working with materials of poor thermal conductivity. Taking these aspects into account, the m-DAC method leads to Equation 3 (in the continuous frequency domain), where L is the thickness of the slab, a is the thermal diffusivity of the material, and s is the Laplace complex variable. Nevertheless, when m-DAC is applied to thin plates and heat excitation approaches d(t), the results obtained are equal to the classic DAC for the first thermograms only. The Figure 4 shows the resulting profile from the application of m-DAC.
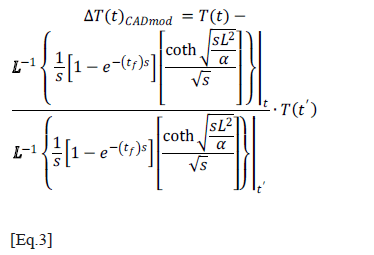
Another interesting technique exists, called adaptive filtering, which is applied to 3D inspection of frescos [10]. This procedure takes into account the thermal spread in the three spatial dimensions [3] [11] to keep lateral conduction of heat from generating false alarms, which may occur with classical techniques based on a one-dimensional model. In this case, the proposed contrast is based on the difference between the real normalized contrast and the simulated normalized contrast by means of the 3D model of heat propagation as shown in Equation 4. In this equation, e groups the optical properties of the material, Fij(t) and jij are respectively the real and the calculated intensity of pixel i,j of the thermogram corresponding to the time t, t' is the time for a thermogram just after the thermal excitation and before receiving any internal defect (reference image), and time t0 is the time for a thermogram captured before the heat pulse application, known as cold image. This technique works better when thermal parameters and geometry of the studied material are known with sufficient accuracy for computer simulation (a non-common case).
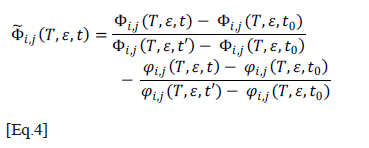
3. DETAILS OF THE THERMAL CONTRAST METHOD PROPOSED
In general, the idea behind the proposed method is to try to identify and automatically remove the background of the picture from any defects that contrast with it. The background of thermograms consists of the sound surface of the slab tested, and so, it contains the information about non-uniform heating. Because this information corresponds to a low spatial frequency, a selective low-pass filtering could isolate the background warming, with the advantage of that filtering is based only on the information intensity of the pixels, not on the definition of intrinsic parameters of the material.
A fairly common type of filter to remove impulse noise or spurious details in an image, while preserving almost intact the low spatial frequency information, is the median filter [12] [13] [14]. Precisely, the more avowed feature is the less blurring effect it generates, because of two reasons: the non-attenuating intensity difference across edges and the non-shifting of borders unlike linear mask filtering [13]. In addition to the minimum blurring, the median operation allows even an outstanding and unwanted region or detail, of certain area in pixels, can be eliminated [12]. Actually, this work is based on using the median filter in order to extract the background heating profile, for which it is necessary to assume that defects are the main details to be removed from the original image.
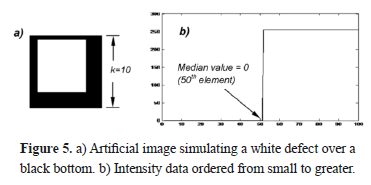
Figure 5 shows a simple binary artificial image to represent the idea behind using the median filter to retrieve background information: given that the median value is set from the central position of the sorted data, it can be inferred theoretically that the maximum area in pixels of a defective region AM (formed by one or more pixels close to each other) framed within a squared kernel of side k pixels, to reject such a region, would be given by Equation 5:

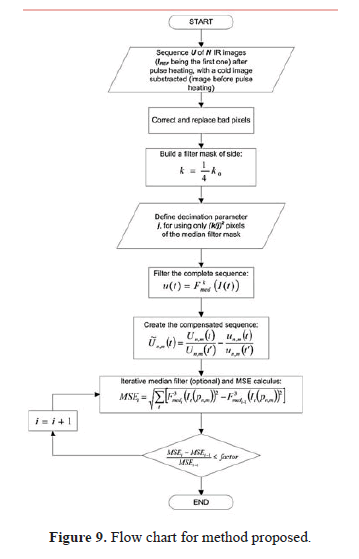
Clearly, the kernel required for such an operation could become considerably large according to the expected size of the defects; for that reason, a strategy is also proposed to reduce the execution time that a large median filter mask would usually require. In the next paragraphs the steps of the proposed contrast enhancement methodology, called Background Thermal Compensation by Filtering (BTCF), are presented:
- Initially, the images acquired just after the excitation of heat reaches the surface of the material, are extracted from a thermographic sequence, and then one of the cold pictures (not included in the analyzed sequence because it appears before the pulse heat) is subtracted from them to reduce the noise patterns of the IR camera. Also, if camera has manufacturing defective pixels, these should be previously corrected [15].
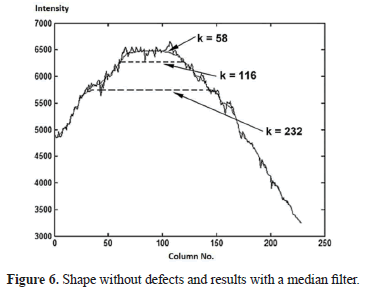
- As a primary requirement, the mask for the median filter must cover an area large enough to filter the non-uniform heating profile, eliminating the abrupt contrasts caused by possible defects. However, a considerable size can distort the actual background profile (Figure 6) and demand an exaggerated runtime. For the sequences used in this work, it was found that a value suitable for the lateral dimension k of the filter mask is ¼ of the smallest side of the image, named k0; nevertheless, smaller fractions of k0 can be used.

Thereby, the maximum area of defects that can be discarded by median filtering would theoretically be:

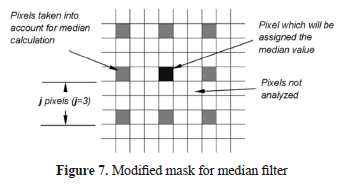
- To decrease the filtering runtime, while retaining the size of the region processed during the median value calculation, a strategy was chosen taking into account only some pixels inside the region. Each pixel is considered separately from its neighbors analyzed by a number of pixels j in the four cardinal directions, as shown in Figure 7.
Then, applying this strategy, the calculation of the filtering value for the central pixel in the mask of side k, demands the same execution time as the application of the typical median filter with a mask of
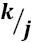 pixels side; thereby, j plays a role of decimate factor. With such a mask, and an odd number of pixels on its sides, each side needs to be expanded to
pixels side; thereby, j plays a role of decimate factor. With such a mask, and an odd number of pixels on its sides, each side needs to be expanded to 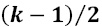 pixels, retaining the value of pixels from the edge of original image area before applying the filter.
pixels, retaining the value of pixels from the edge of original image area before applying the filter. - Once the median filter is applied on each image of the resulting sequence after step 1 (Figure 8a), the evolution with time of the non-uniform heating,
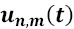 , is obtained (Figure 8b). So, the compensated sequence (Figure 8c) is generated by subtracting the normalized non-uniform heating sequence, from a normalized version of the initial sequence, similar to the way that an unsharp masking technique gives an edge image [16]. In Equation 8, Un,m(t) and un,m(t) are equivalent to the intensities of pixel pn,m in the thermogram corresponding to instant t for the experimental and filtered sequences, respectively, and t' is the time for the reference thermogram. Although absolute subtraction can be performed, normalization brings better results.
, is obtained (Figure 8b). So, the compensated sequence (Figure 8c) is generated by subtracting the normalized non-uniform heating sequence, from a normalized version of the initial sequence, similar to the way that an unsharp masking technique gives an edge image [16]. In Equation 8, Un,m(t) and un,m(t) are equivalent to the intensities of pixel pn,m in the thermogram corresponding to instant t for the experimental and filtered sequences, respectively, and t' is the time for the reference thermogram. Although absolute subtraction can be performed, normalization brings better results. 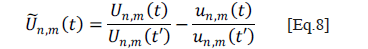
- As an optional processing step, it is possible to apply an iterative filtering [17] on the final sequence to improve the SNR of the compensated images. If
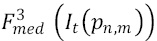 denotes the value of a pixel n,m filtered with a 3x3 median filter and belonging to the image of instant t, then the iterative filtering stops (according to a user-definable factor) in the iteration i if the following is satisfied:
denotes the value of a pixel n,m filtered with a 3x3 median filter and belonging to the image of instant t, then the iterative filtering stops (according to a user-definable factor) in the iteration i if the following is satisfied:
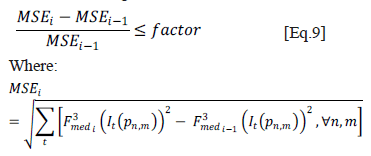
As can be seen, the mean squared error calculation is based on the differences among the filtered values of all the pixels of the entire sequence in any iteration and those calculated in the previous iteration. The flow diagram in Figure 9 summarizes the entire proposed procedure.
4. DISCUSSION OF RESULTS
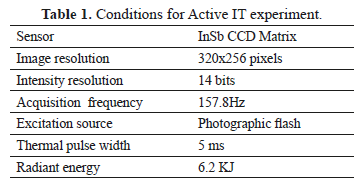
The thermal sequence used in tests was acquired from an active IT experiment under the conditions shown in Table 1.
Since the objective of this contrast enhancement technique is to compensate the effect of uneven heating, a quantitative criterion to evaluate this non-uniformity was defined, as expressed by Equation 10.
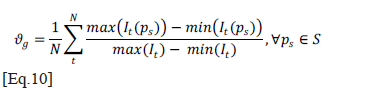
Where: It is the image corresponding to instant t, S is a subset of pixels belonging to the sound area of the material, N is the total number of thermograms, and ϑg is the named global relative background non-uniformity value. In practice, 36 pixels (ps) were extracted forming a symmetric grid, which extends lengthwise and crosswise over sound areas of each image.
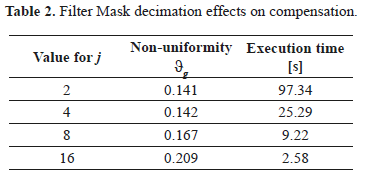
Equation 10 seeks at first, to calculate the difference between the maximum and minimum points on the background heating curve, only using the information given by the previous 36 pixels; later, this difference is normalized with respect to the dynamic range of the image (taking all pixels). Because the background heating curvature is different for each thermogram (decreasing with time), all of differences calculated with Equation 10 are added, resulting in a unique value. Using this criteria, Table 2 shows the effect of different decimate factors j over the performance of the compensation technique proposed, and execution time in MATLAB, running on a PC with 2.93GHz CORE 2 DUO processor and 4GB of RAM. As a comparison, the non-uniformity value ϑg of the original thermal sequence, with no bad pixels, is 0.55.
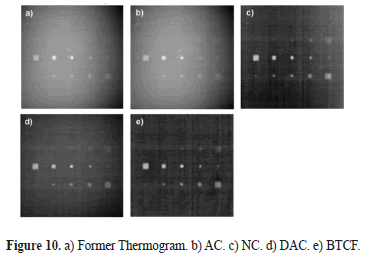
Figure 10 reveals the thermal contrast obtained after applying the methods AC, NC, DAC, and BTCF on the same thermogram from a sequence of 132 thermograms of 226 x 228 pixels each one. The BTCF technique was applied with k=57, j=4 and without iterative filtering at the end.
It may be noted that results of the last three contrasts considered are similar, but the proposed technique virtually eliminates non-uniform behavior from the background intensity, which is related to both uneven heating and vignetting effect. In Figure 10e, in spite of showing a more uniform background, in some regions the image is a little less dark than images 10c and 10d, because the medium and high frequency intensity variations (especially noise) are distributed above and below the new filtered background of each thermogram, intensity of which tends to zero after compensation; as the minimum gray intensity is zero, the backgrounds are a little lighter on average, although much more uniform.
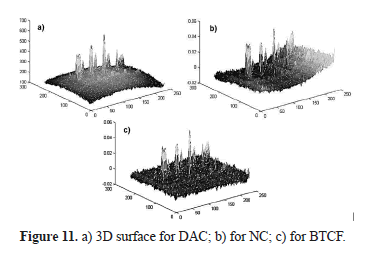
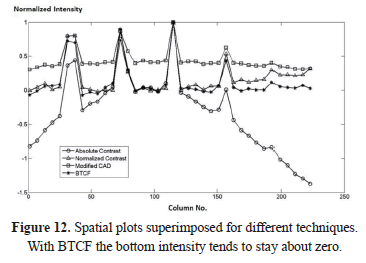
The previous result is more noticeable in Figure 11 where 3D surfaces are obtained by taking the intensity of the pixels as a third dimension. Meanwhile, Figure 12 compares the spatial profiles (peak amplitude normalized to 1) extracted from contrast thermograms of Figure 10 by taking the pixels of row 116 (the same as in Figure 2); here, the best performance in contrast enhancement is also appreciable.
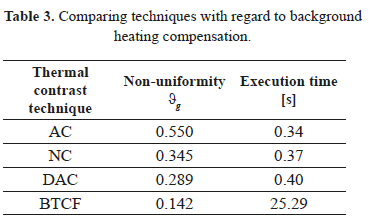
Furthermore, Table 3 compares the performance of the four techniques used, based on the non-uniformity values for resulting sequences after application of each, and their execution times in MATLAB (without considering iterative post-filtering for BTCF contrast). The best compensation reached by BTCF algorithm is evident. Although its time of execution is greater than the others, this time may be reduced by adjusting the decimate factor j for filtering mask size.
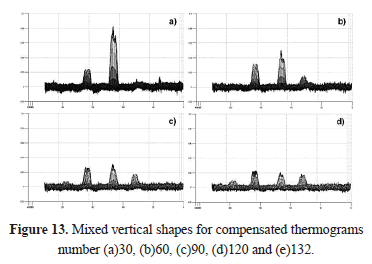
To demonstrate the consistent performance of the proposed compensation technique, the vertical mixed profiles for thermograms 30, 60, 90 and 120 are shown in figure 13. It is clear that SNR gets worse with time because the heat propagates in such a way that all points inside the material tend to reach a thermal balance; however, the level of noise in the images is preserved throughout the sequence. In the same way, it is noticeable that the mean level of sound points (background of contrast images) remains close to zero; so, the great advantage of the proposed method is that it virtually preserves a flat background for all regions of the image (Figures 10, 11 and 12) and for all thermograms (Figure 13).
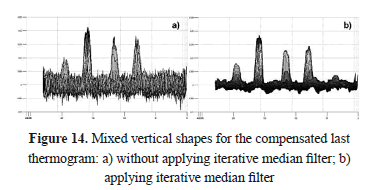
Finally, Figure 14 compares an expanded version of Figure 13d with the same profiles after passing through iterative median filtering: the noise level decreases significantly, and SNR improves.
5. CONCLUSIONS
An algorithm to improve thermal contrast from an active IR thermography procedure on composite plates was developed, which is able to compensate adequately for the vignetting effect (optical effect) and non-uniform background heating without relying on any model of heat propagation and based only on experimental data acquired. The main idea of this method lies in that the physical effects mentioned correspond to variations in intensity of low spatial frequency, and so a median filter can be used to extract the background heating profile from each thermogram of the sequence, assuming that any defects are higher frequency details; later, those profiles are subtracted from the original images to obtain the information generated by the heterogeneity of the material and possible internal defects of such. Thus, the non-uniformity effect on the original sequence could be reduced by about 74%, under conditions described in former paragraphs.
The algorithm proposed requires as parameters, the size k of median filter mask, and the decimation factor j of the same. Respecting dimensions, the size of mask must be chosen according to the size of possible defects and the shape of background heating profile. Thereby, the kernel area in pixels should be greater than twice the area of the largest expected defective region; at the same time, the kernel should not be too large to distort the very low frequency profile and increase the filtering runtime too much. After an experimental study, a mask size equal or less than to ¼ of the shorter side of images was found to be suitable for a minimal distortion of the background heating profile, whilst sufficiently large to eliminate defective details visualized.
With regard to execution time, the decimation of the median filter mask has a positive effect in decreasing execution time of the algorithm proposed, without substantially changing the heating profile information needed to enhance the thermal contrast. This technique consists of discarding some pixels in the mask to perform the filtering, but preserving the effective area of filtering.
Also, it is interesting to note that the noise level and its mean around zero tend to be preserved for all thermograms with the technique proposed. The iterative median filter at the end of the five procedures tested improves SNR of the final images; however, this is most noticeable in the proposed technique because the background intensity values are distributed around zero.
As future work, the enhanced intensity data obtained from this contrast method will be used as input to a detection and characterization stage of internal flaws, to carry out a comparative analysis that allows establishing quantitatively the impact of BTCF contrast on detection and characterization goals, although it is presumable that the more contrast enhancement, the more success in finding defects and estimating their features.
ACNOWLEDGMENTS
The authors thank COLCIENCIAS for the scholarship granted to advance doctoral studies, through its National PhD Program, to engineer Hernán Darío Benítez, PhD., and the laboratory of the Research Group in Multipolar Infrared Vision (MIVIM) from University Laval in Quebec, for infrared thermal image files and for their advice; also, to the PhD Program in Engineering and Postgraduate Program in Electrical and Electronic Engineering (PPIEE) at Universidad del Valle.
REFERENCIAS
[1] Lorenzo, H. et al., Ten Years of applying Geomatics to Construction Engineering in Spain: a Review. DYNA, year 79, special edition, pp. 129-146, October 2012. [ Links ]
[2] Maldague, X., Theory and Practice of Infrared Technology for Non Destructive Testing. Wiley-Interscience - New York, USA, 2001. [ Links ]
[3] Maldague, X., (technical editor). Infrared and Thermal Testing. Nondestructive Testing Handbook, Vol. 3, 3° edition, American Society for Non Destructive Testing, USA, 2001. CD-ROM. ISBN 1-57117-081-5. [ Links ]
[4] The NDT Validation Centre. Available at: http://www.ndt-validation.com/technologies/pr_17.jsp?menu_pos=50 [Cited on May 2009] [ Links ].
[5] Benítez, H., Ibarra-Castanedo, C., Bendada, A., Maldague, X., Loaiza, H. and Caicedo, E., Defect Characterization in Infrared Nondestructive Testing with Learning Machines. NDT&E, Vol. 42, issue 7, pp. 630-643, October 2009. [ Links ]
[6] Snell J.R. and Spring, R., Infrared Thermography Advances. Featured Articles - NDT Database & Journal, October 2007. Available at: http://marinecompositesnde.com/images/Snell,_2007.pdf [Cited on October 2007] [ Links ].
[7] Balageas, D., Defense and Illustration of Time Resolved Pulsed Thermography for NDE. Thermosense: Thermal Infrared Applications XXXIII, Florida, USA. Proc. of SPIE Vol. 8013, 80130V. May, 2011. [ Links ]
[8] Ibarra-Castanedo, C., Gonzàlez D., Klein, M., Pilla, M., Vallerand, S. and Maldague, X., Infrared Image Processing and Data Analysis. Infrared Physics and Technology, Vol. 46, issue 1-2, pp. 75-83, December 2004. [ Links ]
[9] Benítez, H., Ibarra-Castanedo, C., Bendada, A., Maldague, X., Loaiza, H. and Caicedo, E., Procesamiento de Imágenes Infrarrojas para la Detección de Defectos en Materiales. Tecnura journal, Facultad Tecnológica, Universidad Distrital FJC, year 10(20), pp. 41-50, 1º semester, 2007. [ Links ]
[10] Grinzato, E., Bison, P., Marinettti, S. and Vavilov, V., Thermal NDE enhanced by 3D Numerical Modeling applied to Works of Art. CNR-ITEF Corso Stati Uniti, Italy - Tomsk Polytechnic University, Russia. 2000. Available at: http://www.ndt.net/article/wcndt00/papers/idn909/idn909.htm [Cited on December 2008] [ Links ].
[11] Darabi, A. and Maldague, X. Neural Networks based Defect Detection and Depth Estimation in TNDE. NDT&E International, Vol. 35, issue 3, pp. 165-175, April 2002. [ Links ]
[12] González, R. and Woods, R., Digital Image Processing. 2nd edition, Prentice Hall, 2002. [ Links ]
[13] Russ, J., The Image Processing Handbook. 3rd edition, CRC Press, Springer, IEEE Press. USA, 1998. [ Links ]
[14] Young, I., Gerbrands, J. and Van Vliet, L., Fundamentals of Image Processing. Delft University of Technology. The Netherlands, 1998. [ Links ]
[15] Restrepo, A. and Loaiza, H., A new algorithm for detecting and correcting bad pixels in infrared images. Ingeniería e Investigacion journal, Facultad de Ingeniería, Universidad Nacional de Colombia. Vol. 30 (2), pp. 197-207, August 2010. [ Links ]
[16] Fisher, R., Perkins, S., Walker, A. and Wolfart, E., Image Processing Learning Resources. Unsharp Filter. Available at: http://homepages.inf.ed.ac.uk/rbf/HIPR2/unsharp.htm [ Links ]
[17] Restrepo, A. y Loaiza, H., Filtrado 3D Espacio-Temporal Iterativo para la Atenuación de Ruido en Secuencias de Imágenes Térmicas para END. Ingenium journal, Facultad de Ingeniería, Universidad santiago de Cali. No.13, September 2012. [ Links ]