Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.182 Medellín nov./dez. 2013
STOCHASTIC FRACTURED ROCK FACIES FOR GROUNDWATER FLOW MODELING
REPRESENTACIÓN ESTOCÁSTICA DE FACIES DE ROCAS FRACTURADAS PARA LA MODELACIÓN DEL FLUJO DE AGUAS SUBTERRÁNEAS
DANIELA BLESSENT
Ph.D., Profesora, Programa de Ingeniería Ambiental, Universidad de Medellín, Medellín, Colombia, Dblessent@edu.com.co
Received for review July 8th, 2012, accepted July 12th, 2013, final version July, 29th, 2013
ABSTRACT: This paper presents simulation results of groundwater flow in fractured rocks. A stochastic approach is employed to build the conceptual model, a stochastic Equivalent Porous Medium fractured rock facies model, for the low-permeability bedrock found at Olkiluoto (Finland), which is the site chosen for the case-study. The volume of rock investigated is located around a cluster of boreholes and it covers an area of 160000 square meters. Field measurements during hydraulic interference tests are used to calibrate the groundwater flow model. Multiple stochastic facies realizations are considered to evaluate the impact of distribution and number of facies on simulated hydraulic heads and flow rates. This study quantifies the variability of numerical results, which is important for uncertainty analysis of hydrogeologic systems. Moreover, it shows that the stochastic facies conceptual model is a suitable alternative to discrete fracture network conceptual models.
KEYWORDS: Groundwater, numerical simulations, fractured rocks, stochastic model.
RESUMEN: Este artículo presenta los resultados de una simulación de flujo de agua subterránea en rocas fracturadas. Se emplea un enfoque estocástico (modelo estocástico equivalente en medio poroso fracturado) para construir el modelo conceptual y para usar este último en la roca de baja permeabilidad encontrada en el sitio elegido como caso de estudio (Olkiluoto, Finlandia). La roca que se investiga se encuentra localizada alrededor de un grupo de pozos de sondeo y cubre un área de algunas hectáreas. Las mediciones de campo de pruebas de interferencia hidráulica se utilizan para calibrar el modelo de flujo de agua subterránea. Múltiples combinaciones de facies estocásticos se consideran para evaluar el impacto de la distribución y del número de facies en las cargas hidráulicas y en los caudales. Este estudio cuantifica la variabilidad de los resultados numéricos, lo cual es importante para el análisis de la incertidumbre en los sistemas hidrogeológicos. Por otra parte, este estudio muestra que el modelo conceptual de facies estocásticos es una alternativa adecuada a los modelos conceptuales de redes de fracturas discretas.
PALABRAS CLAVE: Agua subterránea, simulaciones numéricas, rocas fracturadas, modelo estocástico.
1. INTRODUCTION
Low-permeability rock formations can be investigated for a wide range of applications. They can be crossed by discontinuities, such as joints, fractures, faults, which govern their overall behavior. Exploitation of groundwater, mineral, petroleum and geothermal resources is the main reason for characterizing and modeling rock formations. Moreover, geotechnical and mine engineering issues, as well as construction of deep geological repositories for nuclear waste are other examples of applications which require rock investigations and modeling. To build a numerical model for groundwater flow analysis, a conceptual model to represent fractured rocks is required. However, applying a suitable conceptual model is challenging because the distribution of discontinuities in the rock mass is often complex and unknown.
As mentioned by Neumann [7], suitable conceptual models are Discrete Fracture Network (DFN) with permeable or impermeable matrix blocks [3], nonuniform continuum [1], or hybrid models of a nonuniform continuum containing a relatively small number of discrete dominant features [6]. For all conceptual models, the description can be deterministic or stochastic. Equivalent porous medium (EPM) models can be used as an alternative by developing relationships between discrete fracture properties and equivalent porous media properties. An alternate and promising approach to represent heterogeneous porous media relies on transition probability and Markov chain geostatistics to create a three-dimensional model of categorical facies [5]. Application of this approach allows capturing hydraulic properties variability, which is always found in fractured rocks, without using the more complex DFN approach [2,8]. Geostatistics is an important tool to provide spatial distribution of hydrogeological data [10].
Stochastic Equivalent Porous Medium fractured rock facies is the conceptual model chosen to represent background fractures in the crystalline bedrock at Olkiluoto Island (Finland), which is the case-study considered here. The development of this conceptual model, the procedure applied to calibrate the groundwater flow model, and the parameter uncertainty analysis were described by Blessent et al. [2]. The impact of using multiple realizations of fractured rock facies to model groundwater flow is discussed in this paper. The results presented here show the importance of appropriate mesh resolution, conditioned boreholes, and facies category definition.
2. SITE DESCRIPTION
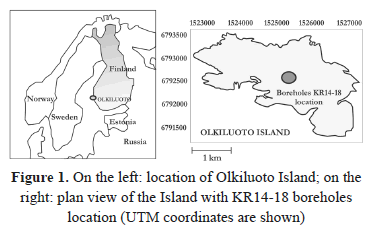
Olkiluoto is a flat island located on the Baltic Sea coast in southwestern Finland (Fig. 1). An underground research laboratory is being built to verify the suitability of the bedrock to host a deep geological repository for Finnish spent nuclear fuel [9]. Site characterization activities, such as geophysical surveys, borehole logging, pumping tests, and water sampling, have been conducted for over twenty years.
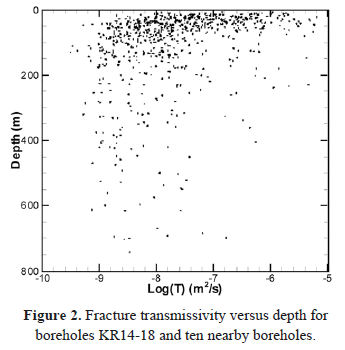
Major fracture zones identified in the bedrock are defined as having a transmissivity greater than 1 x 10-8 [m2/s] and a spatial extent of several hundred meters (the same zone crosses several boreholes). In contrast, background fractures have lower transmissivity and limited extent (a fracture cannot be traced from one borehole to another). Background fractures decrease with depth and their transmissity follows the same trend, although it is less evident (Fig. 2).
Shallow (45 m) and deep (100-500 m) boreholes, indicated by the acronym KR and KRB, respectively, have been drilled at Olkiluoto. Hydraulic cross hole interference tests conducted in open boreholes KR14-18 and KRB15-18 (Fig. 1) are simulated here. The average distance between these boreholes is 45 m. These hydraulic tests are described by Rouhiainen and Pöllänen [11]. Boreholes are open since there are no packers separating distinct borehole sections. A unique aspect of these tests is the combined measurement of flow rates and drawdowns. Flow rates are measured using the Posiva Flow Log (PFL) probe where water conductive fractures intersect boreholes. The probe consists of an electronic tube, a flow sensor and a flow guide, which are fitted with a set of rubber discs against borehole walls. More details are given by Rouhiainen and Pöllänen [11].
3. GROUNDWATER MODELING
3.1. Numerical code
HydroGeoSphere [12] is the 3D numerical simulator for subsurface flow used in this study. The Control Volume Finite Element numerical method is used to discretize the governing equations. The global matrix assembled from the nodal discretized equations for the 3D porous rock matrix elements, the 2D fracture elements and the 1D borehole elements is solved by a preconditioned iterative solver. Fracture elements correspond to the faces of 3D finite elements and borehole elements correspond to 3D finite element edges.
3.2 Fractured rock facies model
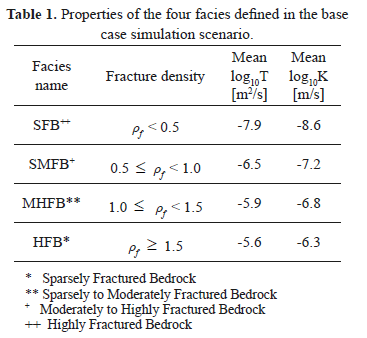
The Transition PRObability Geostatistical Software, TPROGS [4], is employed to generate fractured rock facies distributions in the area surrounding KR14-KR18 boreholes. Facies are obtained from background fracture density: the transmissive fractures per 5 m of borehole interval are computed and then facies are arbitrarily defined (Table 1).
Transmissive fractures are those characterized by a flow rate measured with the PFL tool. The transmissivity T [L2/T] of a given borehole interval is the sum of the transmissivities of individual fractures identified in that interval. The hydraulic conductivity K [L/T] is the ratio between the interval transmissivity and its length [2].
T-PROGS computes transition probabilities of facies and Markov chains are then fitted to the observed facies transition probabilities, as explained by Blessent et al. [2]. Sparsely Fractured Bedrock (SFB) is the most abundant facies in the bedrock (around 70 % of the rock belongs to this facies). Once the 3D transition probability model is built, the module TSIM of T-PROGS is used to generate conditional facies simulations. Simulations are conditioned at borehole locations, where the simulated facies correspond to the observed facies.
3.3 Simulation setup
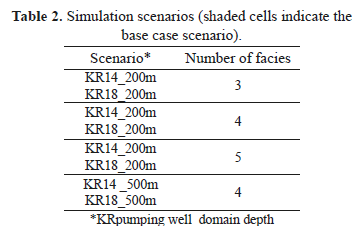
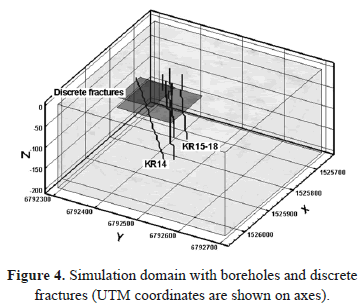
A regular block-based mesh is used to discretize the simulation domain. Blocks have the same length of 5 cm along the x, y, and z direction. This element length is chosen as trade-off between a reasonable computing time and an appropriate representation of background fractures. The simulation domain has dimensions of 400 x 400 x 200 m in the base case scenario. The simulation domain with its facies distribution is presented in Fig. 3. Some modifications to the vertical extent of the domain are considered, as shown in Table 2, where all simulation scenarios are listed.
Boreholes are discretized using block edges, as mentioned in Section 3.1. Since some boreholes have an inclined axis, especially KR14, they are represented by a stairway profile (Fig. 4). Two discrete fractures, representing the joints that were identified by Vaittinen et al. [13], are added to the model because the hydraulic response observed during the interference test cannot be adequately represented by fractured rock facies only [2]. These two fractures are represented by parallel horizontal planes intersecting the boreholes at depths of 60 and 35 m (Fig. 4).
Steady-state regime is considered. Steady-state flow is assumed because the crystalline rock has low storage capacity and drawdown stabilized quickly after the start of the test. No-flow boundary conditions are set to the bottom and top of the domain. A specified hydraulic head equal to the mean long-term water table elevation is attributed to the lateral boundary. Uniform pumping rates of 25 l/min and 7 l/min are attributed to boreholes KR14 and KR18, respectively.
3.4 Simulation scenarios
Besides the four facies basic case scenario, three and five facies scenarios are tested to better analyze how the stochastic facies distribution impacts numerical results (Table 2).
Another modification made to the base case scenario is the variation of the vertical extent of the simulation domain. Domain depth is varied from 200 m to 500 m, since boreholes KR14 and KR15 have a length of 500 m. The 200 m vertical extent is chosen for the base case scenario because it was supposed that groundwater flow was compartmentalized between the topographic surface and that depth (200 m), where a major fracture zone crosses the domain of interest [2]. In fact, PFL flow rates were all measured in the first 200 m, since background fracture density decreases with depth, as mentioned in Section 2. However, with a 200 m deep domain, axes of boreholes KR14 and KR15 were truncated. Hydraulic interference tests are thus here simulated with a deeper domain to include the whole borehole axes.
For each scenario, twenty equally probable stochastic facies realizations are computed with T-PROGS. This number of realizations is judged to be suitable to analyze variability and trends in simulated hydraulic heads and flow rates.
4. RESULTS
The four facies base case scenario was calibrated with an automatic procedure that includes the computation of uncertainty associated to facies hydraulic conductivity [2]. Other scenarios, with three and five facies, are calibrated by trial and error, since the objective is to investigate the influence of facies distribution and not to analyze parameter uncertainty.
An anisotropic hydraulic conductivity is attributed to the least permeable fractured rock facies, while other facies are considered isotropic. Calibrated hydraulic conductivity values are listed in Table 3.
Variance is calculated for simulated flow rates and hydraulic heads. Variance at conditioned boreholes is compared to variance at observation points located around KR boreholes, at different distances and directions.
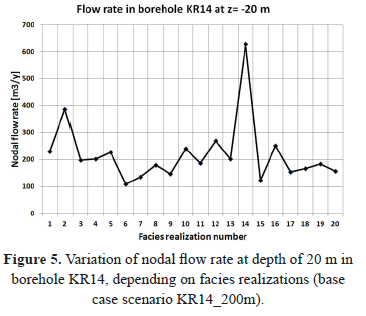
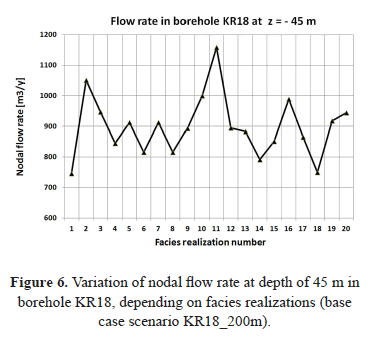
For the base case scenario, with four facies and 200 m depth, flow rates in boreholes KR14 and KR18 are shown in Fig. 5 and Fig. 6, respectively. Flow rates are observed at depths of 20 m and 45 m in borehole KR14 and KR18, respectively. These depths are chosen arbitrarily to illustrate some results. Any node along borehole axes can be chosen and similar curves can be traced. Fig. 5 and Fig. 6 show that for the twenty equally probable facies realizations, flow rates show a limited variation around the average value, which is about 200 [m3/y] and 900 [m3/y], for boreholes KR14 and KR18, respectively. Although a peak above 600 [m3/y] for realization 14 is observed in Fig. 5, the order of magnitude of simulated flow rates does not change: a few hundreds of cubic meters per year are simulated, no matter the facies realization.
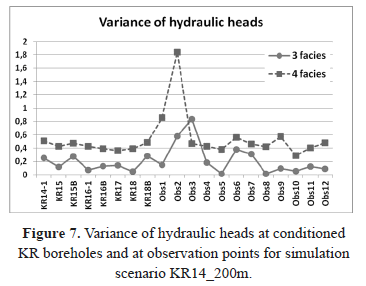
For the scenarios with three and four facies and 200 m depth, variance of simulated hydraulic heads is shown in Fig. 7. Values at KR boreholes, where facies are conditioned, and at twelve observation points located around the KR boreholes, where facies vary depending on the realization, are illustrated in the same graph.
The goal is to show the effect of conditioning facies at KR boreholes, where variance is expected to be smaller than at locations where facies are not conditioned. In general, the variance is quite similar. Neverthless, as expected, the largest variance is observed at observation points obs1, obs2, and obs3, which are located close to pumping boreholes, where a large variation of hydraulic heads is observed because of the drawdown cone caused by pumping.
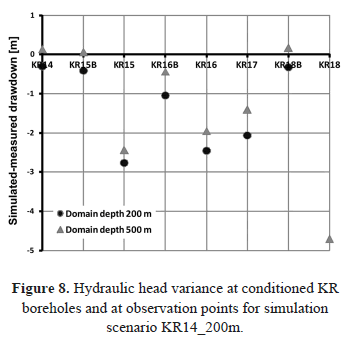
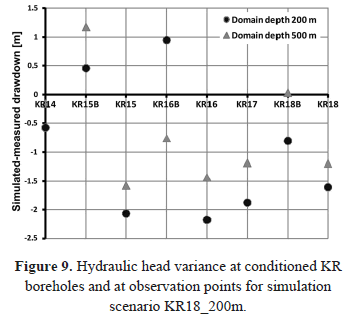
Simulation results obtained with a domain 500 m deep are showed in Fig. 8 and Fig. 9, together with the same results obtained for the base case scenario, where the domain is 200 m deep. The difference between the simulated and the measured drawdown, which should be zero for a perfect match between numerical model results and observed hydraulic responses, is illustrated. Although few flow rates were measured with the PFL probe along boreholes below 200 m, better results are obtained considering a domain of 500 m and the whole borehole axes. In fact, as shown in Fig. 8 and 9, the simulated drawdown is generally closer to the measured one when the simulation domain is 500 m deep. The only exception is shallow borehole KR15B.
5. DISCUSSION AND CONCLUSION
Subsurface flow models are powerful tools to help understanding groundwater movement and solute contamination, which are important topics to be considered for various engineering applications, such as exploitation of groundwater, mineral, petroleum and geothermal resources, slope stability, and waste disposal. However, a numerical model needs to be calibrated with field data and needs to be numerically robust to be used to make predictions and to help decision makers.
Stochastic fractured rock models are an alternative to equivalent porous medium (EPM), dual permeability (DP) and discrete fracture network (DFN) models. Their main advantage is that they allow the natural heterogeneity of many geological environments to be represented in a relatively simple way, without the need to define discrete fractures or a dual continuum. However, hydraulic and physical material properties must be estimated for each facies, making the model more complex than a classic EPM model.
Facies definition plays an essential role when the Stochastic Equivalent Porous Medium fractured rock facies conceptual model is used. The borehole interval length for computing fractures is the first modeler’s choice. This length influences the mesh resolution of the numerical model and the characterization of the fractured rock. A larger interval allows a coarser mesh to be built, thus reducing computing time, but it can overestimate rock hydraulic conductivity. On the other hand, if the interval is too small, fracture density will probably be zero in too many intervals and facies variability will not be properly captured. It is thus recommended to carefully analyze available fracture data to select a suitable borehole interval length that is a trade-off between the resolution required by simulation purposes and the necessity to capture fractured rock heterogeneity.
Facies distribution is generated on a block-based mesh, where each facies is associated to a (x,y,z) location, as a nodal property. In contrast, material properties are usually attributed to mesh elements for numerical simulation purposes, like in this study. Moreover, since boreholes are usually represented by mesh element edges, the user should carefully transfer facies information to preserve the generated distribution, especially at conditioned boreholes. It is therefore important to conceive a suitable way to transfer the generated stochastic facies distribution to the numerical code used for simulation purposes. To simplify this task, the same mesh type and resolution are recommended in T-PROGS and in the associated numerical model. Upscaling may be performed, if needed, as a successive modeling step. No matter what simulation tools that are used, it is important to know how facies generated during conditional simulations are assigned to the elements of the mesh used for numerical simulations.
Fractured rock facies are here conditioned around pumping wells KR14 and KR18, within a radial distance of 5 m from their axis. However, the water removed by pumping comes from a rock volume that largely exceeds this 5 m radial distance, where facies are conditioned. Therefore, facies distribution has a large impact near pumping wells, where hydraulic heads show great variation (Fig. 7). In contrast, for moderate hydraulic head variations (far from pumping wells), the difference between conditioned (KR and KRB boreholes) and not conditioned boreholes (observation points) is less evident.
If facies, and thus hydraulic rock properties, change, some variability in simulation results is expected. The quantification of this variability should be investigated by executing multiple equally probable facies realizations. A suitable number of realizations should be chosen to analyze their impact on simulated hydraulic heads and flow rates. This analysis is important when analyzing the uncertainty associated to hydrogeological systems along with model predictions. It is recommended to test alternative models with different number or definition of facies to find the most appropriate representation of the fractured porous rock investigated.
6. ACKNOWLEDGEMENTS
This project was made possible with funding obtained from the DRI (Direction de la Recherche and Innovation) of the École Polytechnique de Montréal. Field data come from the Task 7 project of the Äspö Task Force that the author participated in and that was financed by the Canadian NWMO. The work conducted by undergraduate student Abderrahmane Menjra during his internship at the Department of Civil, Geological and Mining engineering was greatly appreciated. Steven F. Carle kindly provided the TPROGS code.
REFERENCES
[1] Ando, K., Kostner, A. and Neuman, S.P., Stochastic continuum modeling of flow and transport in a crystalline rock mass: Fanay-Augères, France, revisited. Hydrogeology Journal, 11(5), pp. 521-535, 2003. [ Links ]
[2] Blessent, D., Therrien, R. and Lemieux, J.M., Inverse modeling of hydraulic tests in fractured crystalline rock based on a transition probability geostatistical approach. Water Resour. Res., 2011. [ Links ]
[3] Bogdanov, I. I., Mourzenko, V.V., Thovert, J.-F. and Adler, P.M., Pressure drawdown well tests in fractured porous media. Water Resour. Res., 39(1), P. 1021, 2003. [ Links ]
[4] Carle, S.F., T-PROGS: Transition Probability Geostatistical Software, Version 2.1. Hydrologic Sciences Graduate Group: University of California, Davis, P. 84, 1999. [ Links ]
[5] Carle, S.F. and Fogg, G.E., Modeling spatial variability with one and multidimensional continuous-lag Markov chains. Mathematical Geology, 29(7), pp. 891-918, 1997. [ Links ]
[6] Lee, S.H., Lough, M.F. and Jensen, C.L., Hierarchical modeling of flow in naturally fractured formations with multiple length scales. Water Resour. Res., 37(3), pp. 443-455, 2001. [ Links ]
[7] Neuman, S.P., Trends, prospects and challenges in quantifying flow and transport through fractured rocks. Hydrogeology Journal, 13(1), pp. 124-147. 2005, [ Links ]
[8] Park, Y.J., Sudicky, E.A., McLaren, R.G. and Sykes, J.F., Analysis of hydraulic and tracer response tests within moderately fractured rock based on a transition probability geostatistical approach. Water Resources Research, 40(12), 2004. [ Links ]
[9] Posiva, O., Olkiluoto Site Description 2008. 2009, Posiva Oy: Finland. [ Links ]
[10] Rivera, O.M., Betancur Vargas, T., and Londoño Ciro, L., Geostatistics techniques in bajo Cauca Antioqueño hydrogeology. Dyna, Año 74, Nro. 152, pp. 137-149. 2007. ISSN 0012-7353. [ Links ]
[11] Rouhiainen, P. and Pöllänen, J., Hydraulic crosshole interference test at the Olkiluoto site in Eurajoki, boreholes KR14-KR18 and KR15B- KR18B. Olkiluoto, Finland. P. 238, 2003. [ Links ]
[12] Therrien, R., Sudicky, E.A., McLaren, R.G. and Panday, S.M., HydroGeoSpehre - A three-dimensional numerical model describing fully-integrated subsurface and surface flow and solute transport. Université Laval and University of Waterloo, Canada, P. 483, 2010. [ Links ]
[13] Vaittinen, T., Ahokas, H., Heikkinen, E., Hellä, P., Nummela, J., Saksa, P., Tammisto, E. Paulamäki, S. Pananen, M., Front, K. and Kärki, A,. Bedrock model of the Olkiluoto site, version 2003/1., Posiva Oy: Finland. 2003 [ Links ]