Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.182 Medellín nov./dez. 2013
ADVANTAGES AND THERMODYNAMIC LIMITATIONS OF THE EXPERIMENTAL SORPTION ISOSTERIC METHOD
VENTAJAS Y LIMITACIONES TERMODINÁMICAS DEL MÉTODO EXPERIMENTAL ISOSTÉRICO DE SORCIÓN
FARID B. CORTÉS
Ph.D., Sistemas Energéticos, Universidad Nacional de Colombia sede Medellín, fbcortes@unal.edu.co
BENJAMÍN ROJANO
Ph.D., Alimentos, Universidad Nacional de Colombia sede Medellín, brojano@unal.edu.co
FARID CHEJNE JANNA
Ph.D., Ingeniería, Universidad Nacional de Colombia sede Medellín, fchejne@unal.edu.co
Received for review January 31th, 2013, accepted June 6th, 2013, final version July, 17th, 2013
ABSTRACT: A review of advantages and thermodynamic limitations present in the sorption isosteric method (SIM) showed that SIM does not guarantee a constant adsorbed amount. Isosteres computed considering ideal gas behavior show that in SIM the mass of gas in the system dead volume increases as equilibrium pressure increases due to desorbed materials. SIM is useful and effective in obtaining highly accurate thermodynamic data for sorption of gases by microporous and nanoporous materials at low temperatures and pressures. At high temperatures and pressures desorption is not negligible, therefore SIM can not be applied. The errors in the calculation of the isosteric heat using SIM can be reduced using traditional experimental procedures such as adsorption isobars and isotherms to generate isosteres at high temperatures and pressures. Alternatively, corrections by pressure and temperature or an experiment that, after each temperature increase, allows gas dosage to compensate for the amount of mass desorbed would guarantee a constant adsorbed amount and, therefore, isosteric behavior by direct measurements.
KEYWORDS: sorption, isosteric method, isosteres, isotherms, isobars.
RESUMEN: Una revisión de las ventajas y las limitaciones termodinámicas presentes en el método experimental sorción isostérica (SIM) muestra que el SIM no garantiza una cantidad adsorbida constante. Las isósteras calculadas que consideran comportamiento de gas ideal muestran que en el SIM la masa de gas en el volumen muerto del sistema al incrementar la presión de equilibrio debido a los materiales desorbidos. El SIM es útil y efectivo para obtener datos termodinámicos de alta precisión para la sorción de gases en materiales micro y nanoporosos a bajas presiones y temperaturas. Por el contrario, cuando la presión y la temperatura son altas la desorción no es despreciable, por lo tanto el SIM no es aplicable. Los errores en los cálculos del calor isostérico usando SIM pueden ser reducidos usando procedimientos experimentales tradicionales como las isobaras e isotermas de adsorción para generar las isósteras a altas presiones y temperaturas. Como alternativa, correcciones por presión y temperatura, o un experimento que, después de cada incremento de temperatura permita a la dosis de gas compensar la masa desorbida, garantizaría una cantidad adsorbida constante y, por consiguiente, un comportamiento isostérico mediante medidas directas.
PALABRAS CLAVE: Sorción, método isostérico, isósteras, isotermas, isóbaras.
1. INTRODUCTION
The sorption phenomena is considered one of the most frequents and relevant processes in nature. It allows selective capture of different species, pollutant emission control, adsorption refrigeration using solar energy and storage of hydrogen, methane and other substances.
The sorption capacity of a porous material depends on, among other factors, internal surface area, pore size distribution, total volume, pressure and temperature. The traditional literature [1] identifies three ways for the characterization of the total surface area of a solid: isotherms, isobars and isosteres depending on whether measurements are conducted at constant temperature, pressure or adsorbed volume these methods yield isotherms, isobars and isosteres respectively. While isotherms are constructed by plotting adsorbed volume vs. pressure, in isobars plots of adsorbed volume against temperature are used. Isosteres are constructed by plotting equilibrium pressure vs. temperature. Adsorption isotherms are the most frequently used way for surface area characterization [2-4].
Adsorption isotherms have been used for the characterization of adsorptive pairs, despite the fact that numerous experimental points are required to construct one isotherm. Gravimetric and manometric methods are used to determine the amount of mass adsorbed while constructing an isotherm [5]. For water vapour, both methods are cumbersome because of the difficulty of maintaining the system at temperatures above the saturation temperature and uncertainties in weight measurements due to buoyancy. An alternative to the isothermal method is the sorption isosteric method (SIM) that has been used [6-10] to determine the solid/gas thermodynamic equilibrium and thermodynamic properties for some pairs, including water vapor. SIM is based on a simple and low-cost experimental device that allows thermodynamic data for gas sorption on porous materials to be obtained. After adsorbent regeneration at vacuum and high temperature, the system was prepared to the desired temperature and the sorbent is injected until equilibrium is reached. Later the temperature is increased by 2 to 5 K and the new equilibrium pressure is measured, at constant adsorbed mass. This procedure is repeated for different adsorbed volumes until saturation [6-10].
Different authors [6-10] have used SIM to characterize adsorption by porous materials. The first to report the use of SIM were Meinert et al., as quoted by Bülow et al. [7]. Meinert et al. measured the adsorption properties of single gas on zeolite (n-alkanes on FAU). The group lead by Bülow [7] extended the single gas adsorbent theory to gas mixture adsorption on microporous solids using SIM. The most important characteristics in SIM as recommended by Bülow et al. [7-10] are:
- Minimum dead volume: minimum void volume and large sorbent volume, ca. (5-15 g)
- Minimum gas-phase volume (Vg) to sorption-phase volume (Vs) ratio, Vg / Vs < 5
- Low pressure at equilibrium (0.0133- 13.337 kPa)
- Small increments of temperature, ca. (2-5 K)
- Constant adsorbed mass over a wide range of temperature and pressure
Studies reported in the literature show that it is difficult for SIM to guarantee a constant adsorbed mass during the measurement of isosteres [2,7,11]. This method is particularly sensitive to errors in the measurement of equilibrium pressures, mainly in the region of low surface coverage (Henry region) [2]. This is the reason why the isosteric enthalpies calculated by SIM are often sometimes unreliable [2]. For instance, Anashin et al. [11] measured isosteres for the hydrogen/carbon fiber pair for temperatures varying between 10 and 35 K. Experiments were carried out in a prototype LHC LSS vacuum chamber where there was a constant flow of hydrogen for one hour until equilibrium between gaseous and adsorbed phases was obtained at a constant temperature. The temperature was then decreased to a fixed value until new equilibrium conditions were obtained.
The values of temperature and equilibrium pressure were plotted vs. fed mass as opposed to the traditional isosteric method in which pressure and temperature are plotted vs. adsorbed mass.
Anashin et al. [11] showed that the gas-phase mass increased as temperature increased, which implies that the adsorbed mass decreased and the isosteric condition was not maintained.
This paper reviews the performance of SIM to compute the isosteric heat. Our goal is to show the physical constrains required to obtain a truly isosteric behavior during SIM. Our analysis shows that SIM does not guarantee a constant adsorbed amount because mass desorption at each equilibrium point increases the gaseous phase mass and, therefore, the system pressure. Mass desorption causes errors that are significant for high pressures and temperatures in the region of low surface coverage. The paper proposes an alternative to SIM for the construction of adsorption isosteres as well as a method that reduces the error incurred when SIM is used to compute the isosteric heat.
2. THEORETICAL CONSIDERATIONS REGARDING THE CONSTRUCTION OF ISOSTERES
SIM is carried out in a closed system in which the adsorbed amount (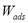 ) at each equilibrium point can be computed according to [7]:
) at each equilibrium point can be computed according to [7]:
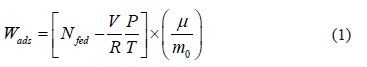
where 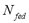 is the dosed amount,
is the dosed amount, 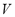 is the dead volume,
is the dead volume, 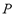 and
and 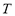 are the system pressure and temperature at equilibrium,
are the system pressure and temperature at equilibrium, 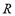 is the universal gas constant,
is the universal gas constant, 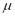 is the molecular weight and
is the molecular weight and 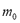 is the mass of adsorbent present in the adsorber. The second term of the right hand side is the gas phase mass according to the ideal gas law. Eq. (1) can be used to calculate the mass that was adsorbed during the construction of isotherms, isobars and isosteres.
is the mass of adsorbent present in the adsorber. The second term of the right hand side is the gas phase mass according to the ideal gas law. Eq. (1) can be used to calculate the mass that was adsorbed during the construction of isotherms, isobars and isosteres.
Because 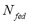 and
and 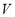 are constant in a closed system, an isosteric conditions (
are constant in a closed system, an isosteric conditions (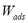 = constant) applied to Eq. (1) demands that at each equilibrium point i:
= constant) applied to Eq. (1) demands that at each equilibrium point i:
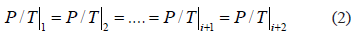
Eq. (2) implies that for a closed system the adsorbed mass as well as the mass in the gaseous phase must remain constant, independent of changes in the system temperature [10]. However, in SIM, as temperature increases, equilibrium favors desorption and pressure increases due to an increase in gas-phase mass. This means that SIM does not guarantee a constant adsorbed mass because there is mass desorption at each equilibrium point. Desorption increases the mass in the gaseous phase and the system pressure departs from the pressure required to guarantee constant adsorbed mass (Eq. (2)) and generates errors in the measurement of the isosteric heat.
The isosteric heat is the energy released during adsorption and can be computed from the Gibbs isotherm that reduces to a constant adsorbed mass function called isostere, which is given as:
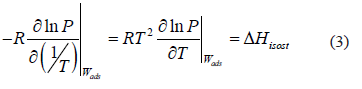
The isosteric heat 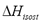 is a constant in Eq. (3) and is independent of changes in temperature and pressure. It is calculated from the slope of a straight line of
is a constant in Eq. (3) and is independent of changes in temperature and pressure. It is calculated from the slope of a straight line of 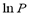 vs. 1/T.
vs. 1/T. 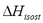 can also be obtained as a function of pressure and temperature using the Clapeyron and Dubinin - Astakhov equations. The last one is commonly used for adsorption equilibrium in microporous materials such as activated carbon and zeolites. The Dubinin and Astakhov's [9] adsorption isotherm can be represented by:
can also be obtained as a function of pressure and temperature using the Clapeyron and Dubinin - Astakhov equations. The last one is commonly used for adsorption equilibrium in microporous materials such as activated carbon and zeolites. The Dubinin and Astakhov's [9] adsorption isotherm can be represented by:
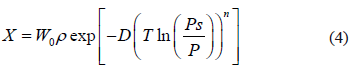
where 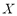 is the adsorbed mass per unit of adsorbent mass,
is the adsorbed mass per unit of adsorbent mass, 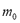 the maximum adsorption capacity (volume of adsorbate/mass of adsorbent),
the maximum adsorption capacity (volume of adsorbate/mass of adsorbent), 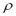 the specific mass of adsorbate in the condensed phase,
the specific mass of adsorbate in the condensed phase, 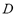 the coefficient of affinity,
the coefficient of affinity, 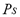 the saturation pressure and
the saturation pressure and 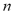 a characteristic parameter of the adsorbent-adsorbate pair.
a characteristic parameter of the adsorbent-adsorbate pair.
Differentiation of Eq. (4) with respect to temperature and rearrangement yields:
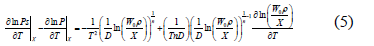
Multiplying each term of the differential equation (5) by (RT2) yields an expression for the isosteric heat:
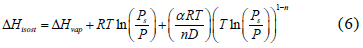
where 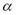 is the coefficient of thermal expansion of the liquid adsorbate, which can be obtained from [13]:
is the coefficient of thermal expansion of the liquid adsorbate, which can be obtained from [13]:
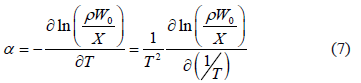
To compute the isosteric heat from Eq. (6) one could use experimental data, such as that by Bülow et al. [7], and using a single linear regression procedure to obtain the parametric values 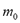 ,
, 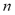 and
and 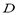 in Eq. (4) and (6). This approach was used in the remaining part of this paper to compute
in Eq. (4) and (6). This approach was used in the remaining part of this paper to compute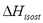 .
.
3. DEVIATION OF SIM
This section describes how SIM experiments deviate from ideal behavior and compares experimental results obtained with SIM to results obtained with alternative techniques, such as volumetric apparatus and TGA, which guarantee a constant adsorbed mass.
3.1. DEVIATION OF SIM FROM IDEAL BEHAVIOR
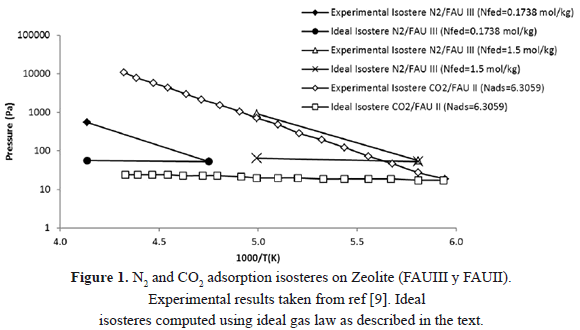
Figure 1 compares experimental and theoretical N2 and CO2 adsorption isosteres on two different zeolites. The experimental data were obtained from [9]. The ideal lines were calculated considering ideal gas behavior, as described in the previous section. This is, the calculation assumes that the adsorbed amount and gas-phase mass are constant and that the only changes in pressure are due to variations in temperature as predicted by the ideal gas law. As expected there is a great difference between the theoretical and experimental line for same amounts fed to the system. The higher pressure for the SIM experiments compared to those predicted by ideal gas law occurs because of accumulation of gas released from the adsorbed phase.
Bülow et al. [9] obtained experimental isosteres of nitrogen adsorption on zeolite (FAU III) using SIM. They found that the adsorbed mass decreased by 1% due to an increase in temperature that caused desorption.
The gas desorbed is negligible when is compared to the total mass in the condensed phase. However, that is not the case when the desorbed mass is compared to the gas-phase mass. For the isostere reported by Bülow et al. [6], where the dosed molar mass per adsorbent mass was 0.174 mol/kg (the most extreme case), initially 0.174 mol/kg was adsorbed, and the remaining 0.0002 mol/kg was in the gaseous phase resulting in an initial equilibrium pressure of 51.74 Pa. Knowledge of pressure, temperature and initial gas-phase mass allows calculation of the dead volume as 0.00675 m3.
At the highest temperature of their experiments, Bülow et al. [9] report that 0.0017 mol/kg desorbed and 0.1719 mol/kg remained in the adsorbed phase. This implies that the mass of the gaseous phase increased to 0.0019 mol/kg. For this condition of mass of material in the gaseous phase, system dead volume and temperature, the ideal gas law predicts an equilibrium pressure of 555.94 Pa. This value agrees with that measured by Bülow et al. [9] which suggests that the equilibrium pressure is a result of the desorbed mass and not of the condition of constant adsorbed mass that SIM demands.
If the condition of constant adsorbed mass is satisfied, i.e. for a negligible desorbed mass, the ideal gas law suggests that the system pressure would be 59.61 Pa (see Figure 1 for N2 and 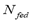 = 0.1738 mol/kg). This value is almost 10 times smaller than the experimental value. This confirms that SIM does not guarantee a constant adsorbed mass because the processes of adsorption and desorption are related to the transfer of materials between adsorbed and gaseous phases caused by an increase in temperature that raises pressure and generates errors in the calculation of the isosteric heat.
= 0.1738 mol/kg). This value is almost 10 times smaller than the experimental value. This confirms that SIM does not guarantee a constant adsorbed mass because the processes of adsorption and desorption are related to the transfer of materials between adsorbed and gaseous phases caused by an increase in temperature that raises pressure and generates errors in the calculation of the isosteric heat.
3.2. Deviation of sim from real behavior
3.2.1. High pressure
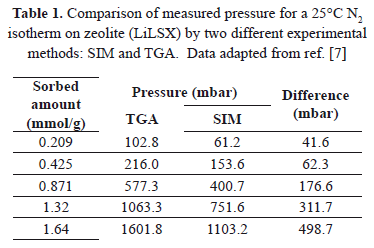
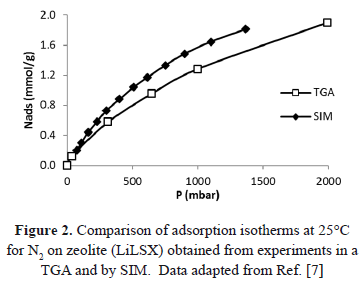
Table1 and Figure 2 compare the pressure for adsorption isotherms at 25°C obtained by Bülow et al. [7] by two different experimental methods:SIM and the thermogravimetric analyzer (TGA). TGA guarantees a constant adsorbed mass, whereas, as discussed before, SIM does not. The comparison shows that the absolute difference between equilibrium pressures determined by SIM and TGA, increases as the adsorbed amount increases. The higher pressures obtained from SIM occur, as explained above, because of the inability of SIM to guarantee real isosteric behavior.
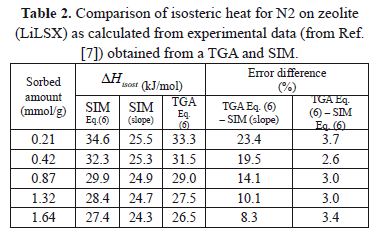
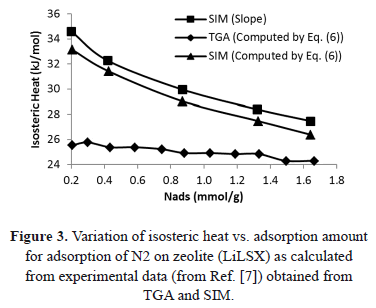
Table 2 and Figure 3 show a comparison of the isosteric heat for nitrogen on zeolite LilSX using data from Bülow et al. [7] obtained from a TGA and SIM. For TGA, 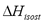 was computed by Eq. (6). For SIM, two different calculation procedures were carried out. The approach used by Bülow et al. [7] for calculating
was computed by Eq. (6). For SIM, two different calculation procedures were carried out. The approach used by Bülow et al. [7] for calculating 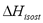 , i.e. the "slope" method using the Clapeyron diagram and Eq. (6). Table 2 shows that the difference (%) between
, i.e. the "slope" method using the Clapeyron diagram and Eq. (6). Table 2 shows that the difference (%) between 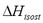 calculated using the experimental data obtained by TGA (Eq. (6)) and SIM (slope) varies from 8.3 to 23.4%, being the highest value for the lowest sorbed amount (0.21 mmol/g), this is, in the region of low surface coverage. If the isosteric heat is calculated from the SIM experimental data and Eq. (6), the difference decreases to a maximum of 3.7% compared to 23.4% obtained using the Clapeyron diagram. The lower differences between
calculated using the experimental data obtained by TGA (Eq. (6)) and SIM (slope) varies from 8.3 to 23.4%, being the highest value for the lowest sorbed amount (0.21 mmol/g), this is, in the region of low surface coverage. If the isosteric heat is calculated from the SIM experimental data and Eq. (6), the difference decreases to a maximum of 3.7% compared to 23.4% obtained using the Clapeyron diagram. The lower differences between 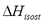 computed with TGA and SIM data when Eq. 6 is used occur because this has implicit corrections for pressure and temperature that compensate for the error associated with the non-isosteric behavior that occurs in SIM.
computed with TGA and SIM data when Eq. 6 is used occur because this has implicit corrections for pressure and temperature that compensate for the error associated with the non-isosteric behavior that occurs in SIM.
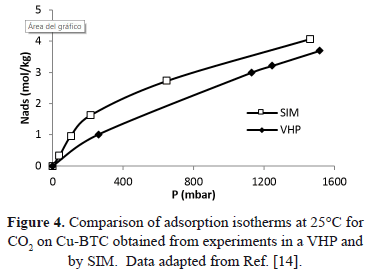
Similarly, Figure 4 compares the pressure reported for adsorption isotherms at 298K obtained by Wang et al. [14] by two different experimental methods: SIM and a volumetric high-pressure analyzer (VHP).
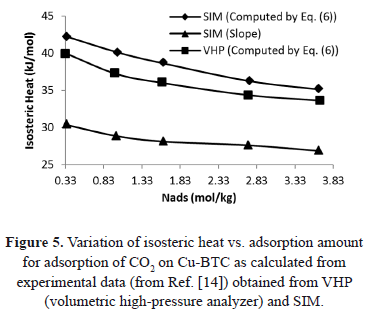
Figure 5 shows a comparison of the isosteric heat for carbon dioxide on Cu-BTC (Cu- Benzene-1,3,5-tricarboxylate) using data from Wang et al. [14] obtained from a VHP and SIM. Figure 5 shows that the difference between 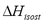 calculated with the experimental data obtained by VHP and Eq. (6) and that obtained by SIM (slope) varies from 20.6% to 24.3%, being the highest for the lowest sorbed amount (0.33 mol/kg). If the isosteric heat is calculated from the SIM experimental data and Eq. (6), the difference decreases to a maximum of 7.8%.
calculated with the experimental data obtained by VHP and Eq. (6) and that obtained by SIM (slope) varies from 20.6% to 24.3%, being the highest for the lowest sorbed amount (0.33 mol/kg). If the isosteric heat is calculated from the SIM experimental data and Eq. (6), the difference decreases to a maximum of 7.8%.
The reduction in the difference is because of implicit pressure and temperature corrections associated to Eq. (6), as already explained.
3.2.2. Low pressure
SIM performance at low pressures (or low temperatures) minimized desorbed mass and therefore the calculated error due to the isosteric heat also become lower. To revise this expectation, we reviewed experimental data [15] obtained for methane adsorbed on silicalite-1 and for a dead volume of 1.8 cm3/g, a pressure of 100 torr, and a loading of 2.3 mol/kg gives an isosteric heat of 21.55 kJ/mol. The difference (%) between this value and that calculated from the slope of the isostere and Eq. (3) (19.82 kJ/mol) is close to 10%. This value is lower than those reported in the previous section for high pressure. However, the difference of 10% at low pressure in the determination of heats of sorption by SIM is still important and becomes more significant when, as pressure increases, the isostere bends.
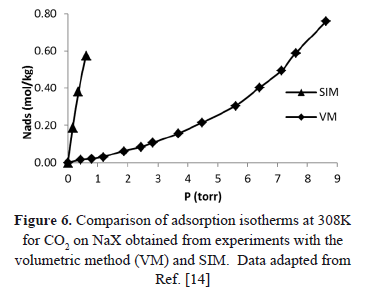
Additional evidence of the difference between SIM and other methods that guarantee constant volume can be obtained from Figure 6 that compares the pressure reported for isotherms at 308 K by Shen et al. [15] by two different experimental methods: a conventional volumetric apparatus (VM) and SIM. Figure 6 shows that the isotherms obtained from both methods are significantly different.
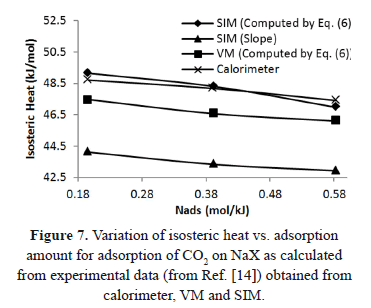
Figure 7 compares the isosteric heat for CO2 adsorption on NaX as computed using Eq. (6) and the "slope" method from the experimental data of Shen et al. [15]. These data were obtained with a calorimeter, VM and SIM. Although, the values of 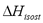 in Figure 7 are similar, the difference between SIM (slope) and calorimeter is close to 10%. When the data from SIM are analyzed using Eq. (6), this difference decreases to a maximum of 1%. This result agrees with that obtained for low pressure and shows that Eq. (6) is a useful tool to correct errors in the heat of adsorption caused by mass desorption during SIM.
in Figure 7 are similar, the difference between SIM (slope) and calorimeter is close to 10%. When the data from SIM are analyzed using Eq. (6), this difference decreases to a maximum of 1%. This result agrees with that obtained for low pressure and shows that Eq. (6) is a useful tool to correct errors in the heat of adsorption caused by mass desorption during SIM.
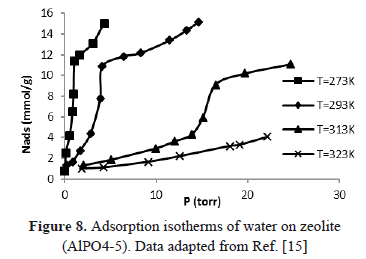
The errors in the calculation of the isosteric heat can be avoided using traditional experimental procedures such as adsorption isobars and isotherms to generate isosteres at high temperatures and pressures. In addition, the errors in the calculation of the isosteric heat using experimental data taken from SIM can be reduced doing pressure and temperature corrections according to Eq. (6). Alternatively, an experiment that, after each increase in temperature, allows input of gas into the system to compensate for the amount of mass desorbed would guarantee a constant adsorbed amount and, therefore, isosteric behavior by direct measurements. To illustrate this, Figure 8 shows for typical isotherms how, for a constant adsorbed volume, the equilibrium pressure increases as temperature increases [16]. In this way, for an adsorbed mass of 2 mmol/g, the equilibrium pressure for the adsorption isotherm at 273 K is less than for the isotherm at 313 K. This is because, for the isotherm at 313 K, the mass in the gaseous phase increases because of the addition of adsorbate and the increase in temperature.
Applying Eq. (1) to the isotherm at 273 K (1) and 313 K (2) in Figure 8 yields:

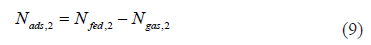
Isosteric conditions require that:
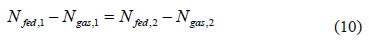
Eq. (10) implies that for a constant fed volume at 273 and 313 K an identical gas-phase mass for both isotherms is required, therefore:

Under this condition, a hypothetical isostere can be obtained that is identical to that obtained by Eq. (2) for a closed system. The analysis above illustrates how an experiment in an open system can be performed to obtain real isosteres. Basically, once the temperature is increased, and therefore there is some mass desorption, an amount of gas is allowed into the system causing an increase in pressure and restoring a constant adsorbed mass.
4. RESULTS AND DISCUSSION
The sorption isosteric method (SIM) based on direct measurements at apparent constant sorbed mass does not guarantee isosteric behavior because mass desorption increases the system pressure. Mass desorption occurs as a response to an increase in temperature and emulates the behavior of isosteres obtained from adsorption isotherm and isobares. At high pressures and temperatures, desorption is not negligible and a plot of pressure vs. inverse temperature is not lineal causing errors in the evaluation of isosteric heat, particularly in the region of low coverage. For isosteres construction, the indirect process of obtaining them from a set of adsorption isotherms or isobars is recommended. Alternatively, adsorption isosteres can be constructed by direct measurement as long as the adsorbed amount is maintained constant by gas dosage for each equilibrium point. The errors in the calculation of the isosteric heat using experimental data taken from SIM can be reduced doing pressure and temperature corrections using Eq. (6).
ACKNOWLEDGEMENTS
The authors thank Professor Alejandro Molina, National University of Colombia, and Francis Meunier, CNAM, Paris, for his fruitful collaboration as well as COLCIENCIAS for logistical and financial support.
REFERENCES
[1] Lowell, S., Shields, J.E., Thomas, M.A. and Thommes, M. Powder Surface Area and Porosity, Springer, Netherlands, 347, 1984. [ Links ]
[2] Rouquerol, F., Rouquerol, J. and Sing, K. Adsorption by Powders and Porous Solids: Principles, Methodology and Applications, Academic Press, London, 467, 1999. [ Links ]
[3] Ciro, H., Osorio, J.A. and Cortes, E.A., Determination of the isosteric heat to platain pulp (musa paradisiaca) by sorption isotherms, Dyna, 156, pp. 127-134, 2008. [ Links ]
[4] Chen, C., Obtaining the isosteric sorption heat directly by sorption isotherm equations, J. Food Eng., 74(2), pp. 178-185, 2006. [ Links ]
[5] Franco, C.A., Giraldo, J., Ruiz, M.A., Rojano, B.A. and Cortes, F.B., Kinetic and thermodynamic equilibrium of asphaltenes sorption onto formation rock: evaluation of the wash in the adsorptive properties, Dyna, 176, pp. 81-89, 2012. [ Links ]
[6] Yang, Y. and Rees, L.V.C., Adsorption of normal hexane in silicalite-1: an isosteric approach, Micropor. Mater. 12, 117, 1997. [ Links ]
[7] Bülow, M., Shen, D. and Jale, S., Measurement of sorption equilibria under isosteric conditions: The principles, advantages and limitations, Appl. Surf. Sci., 196, pp. 157-172, 2002. [ Links ]
[8] Shen, D. and Bülow, M., Isosteric study of sorption thermodynamics of single gases and multi-component mixtures on microporous materials, Micropor. Mesopor. Mat., 22, pp. 237-249, 1998. [ Links ]
[9] Bülow, M. and Shen, D., Fundamentals of Adsorption-6, Paris, Elsevier, 87, 1998. [ Links ]
[10] Sharonov, V.E., Veselovskaya, J.V. and Aristov, Y.I., Ammonia sorption on composites 'CaCl2 in inorganic host matrix': isosteric chart and its performance, Int. Jour. of Low Carbon Technol. 1,pp. 191-200, 2006. [ Links ]
[11] Anashin, V.V., Dostovalov, R.V. and Krasnov, A.A., The vacuum studies for LHC beam screen with carbon fiber cryosorber, In: APAC, Gyeongju, P. 329, 2004. [ Links ]
[12] Dubinin, M.M. and Astakhov, V.A., Development of the concept of volume filling of micropores in the adsorption of gases and vapors by microporous adsorbents, Washington, DC, American Chemical Society, 1971. [ Links ]
[13] Leite, A.P.F. and Daguenet. M., Performance of a new solid adsorption ice maker with solar energy regeneration, Energy Conver. Manag., 41, pp. 1625-1647, 2000. [ Links ]
[14] Wang, Q. M., Et al. Metallo-organic molecular sieve for gas separation and purification, Micropor. Mesopor. Mat. 55, pp.217-230, 2002. [ Links ]
[15] Shen, D., Bülow, M., Siperstein, F., Engelhard, M. and Myers, A.L., "Comparison of experimental techniques for measuring isosteric heat of adsorption, Adsorp. 6, pp. 275-286, 2000. [ Links ]
[16] Izmailova, S.G., Vasiljeva, E.A., Karetina, I.V., Feoktistova, N.N. and Khvoshchev, S.S., Adsorption of Methanol, Ammonia and Water on the Zeolite-Like Aluminophosphates AlPO4-5, AlPO4-17, and AlPO4-18, Journ. Colloid Interf. Sci., 179, pp. 374-379, 1996. [ Links ]