Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.182 Medellín nov./dez. 2013
COMPARISON BETWEEN RESONANT-COLUMN AND BENDER ELEMENT TESTS ON THREE TYPES OF SOILS
COMPARACIÓN ENTRE ENSAYOS DE COLUMNA RESONANTE Y BENDER ELEMENT EN TRES TIPOS DE SUELO
JAVIER FERNANDO CAMACHO-TAUTA
PhD, Associate Professor, Universidad Militar Nueva Granada, Colombia. javier.camacho@unimilitar.edu.co
OSCAR JAVER REYES-ORTIZ
PhD, Full Profesor, Universidad Militar Nueva Granada, Colombia. oscar.reyes@unimilitar.edu.co
JUAN DAVID JIMÉNEZ ÁLVAREZ
Civil Eng., Universidad Militar Nueva Granada, Colombia. u1100849@unimilitar.edu.co
Received for review July 10th, 2012, accepted May 16th, 2013, final version May, 28th, 2013
ABSTRACT: The bender element (BE) test is used in laboratory to obtain the shear wave velocity of soils. Different execution and interpretation techniques have been proposed. However, there is not a specialized technique with an adequate level of accuracy and reproducibility to be adopted as a standard. Several factors affect the reliability of this method, mainly because of complex phenomena of wave propagation in the small volume of the specimen. Three type of soils were tested by Resonant-Column (RC) and two BE test methods (BETD and BEFD). Results suggest that in non-plastic soils the stiffness tends to be underestimated compared with the stiffness obtained by the RC test. The BETD method could be affected by the soil plasticity. The frequency domain method (BEFD) had less agreement with respect to the RC test.
KEYWORDS: Bender element, resonant-column test, shear modulus, shear-wave velocity
RESUMEN: El ensayo bender element es utilizado en laboratorio para obtener la velocidad de la onda cortante de suelos. Con base en este equipo, se han propuesto diferentes técnicas de ejecución e interpretación. Sin embargo, aún no existe una técnica especializada con la suficiente precisión y reproducibilidad para que pueda ser adoptada como ensayo normalizado. Diferentes factores afectan la confiabilidad de este método, principalmente debido a la complejidad del fenómeno de propagación de ondas en un volumen tan pequeño. Se ensayaron tres tipos de suelo mediante el ensayo de columna resonante (RC) y dos tipos de ensayo BE (BETD y BEFD). Los resultados sugieren que en suelos no plásticos la rigidez es tiende a ser subestimada en comparación con la rigidez obtenida mediante el ensayo RC. El ensayo BETD puede estar afectado por la plasticidad del suelo. El ensayo en el dominio de la frecuencia (BEFD) resultó menos concordante con el ensayo RC.
PALABRAS CLAVE: Columna resonante, bender element, módulo cortante, velocidad de onda cortante
1. INTRODUCTION
Shirley and Hampton [1] and Shirley [2] introduced the use of bender elements (BE) to generate and measure shear waves in soils. A BE system relies on the piezoelectric property, which allows the generation and detection of small shear waves travelling in a soil specimen. Electronic devices connected to piezoelectric transducers allow generation, acquisition and storing of input and output signals. Data analysis techniques are used to compute the soil properties from the acquired data. A detailed description of the bender elements and their application is presented in Dyvik and Madshus [3].
The degree of perturbation associated with the vibratory movement of the particles is small enough to avoid permanent deformation of the material. Therefore, it is assumed that the material behaves under an elastic range, but with a level of vibration sufficiently large to be detected by the sensor. Using the analysis of transmitted and received movements of the sensors; it is possible to compute the shear-wave velocity Vs by (1), where tt is the time of propagation of the signal and LTT is the distance between sensors.

Usually, the BE system is installed in a geotechnical device capable of controlling stresses while measuring deformations, or vice versa. Ferreira [4] synthesized the increasing use of BE in equipment such as: oedometers [5, 6], direct shear devices [5], triaxial cells [7-9], cyclic triaxial devices [10, 11], stress-path cells [12, 13], resonant-columns, centrifuges [14, 15], hollow cylinders [16], calibration chambers [17, 18], true triaxials and cubical cells [19, 20].
The correct selection of the arrival time is more complex than it seems initially. In fact, Shirley [2] suggested evaluating the travel time between two easily recognizable features of the input and output signals because the distortion of the received signal does not permit the exact determination of the starting point of the response. Dyvik and Madshus [3] did not include details about the travel time selection method that they adopted; they only indicated that the arrival time corresponds to the time difference between the rise of the square wave and the first significant jump in the received signal.
Many studies were made considering this issue and a number of testing and interpretation methods have been proposed. All methods deal with "appropriate" criteria to select the arrival time. The initial classification of such methods appears in Arulnathan et al. [21]. Viana da Fonseca et al. [22] updated this classification including more recently developed methods, and presenting a combined framework taking advantage of both time and frequency domain interpretations. These last authors found that there is no specialized technique with an adequate level of accuracy and reproducibility to be adopted as a standard.
Different factors affect the reliability of this testing method [23]: quality of manufacturing and installation of BE; coupling and alignment of BE into the specimen [24]; near-field effect [8, 21, 25-27], geometric and boundary effects [21, 28, 29]. Due to these factors, the waveform that is effectively induced to the soil is different to the signal generated by the electronic device and the perturbation changes during the travel. Four characteristics summarize the differences between input and output signals: magnitude, time delay, polarity and shape [24].
There is evidence, that grain size distribution of the soil could affect the coupling with BE, due to the decrease of the effective contact area [30]. Yang and Gu [31] studied the effect of the grain size in the shear stiffness at small strain by testing three types of glass beads of different mean sizes (0.195mm, 0.920mm and 1.750mm). They observed that BE measurements in fine grain materials are consistently higher than RC measurements.
In this paper, three soils specimens were studied: a sand specimen reconstituted by dry compaction and further saturation; a kaolinite specimen reconstituted in a laboratory by vertical consolidation from kaolinite mud; and an undisturbed specimen of low plasticity clay. These specimens were tested by Resonant-Column (RC) and two kind of BE methods (BETD and BEFD) in order to obtain information about the possible influence of the soil in the differences between these types of tests.
2. ESTIMATION OF THE TRAVEL TIME IN BE TESTING
The interpretation methods of BE tests can be grouped in two main categories: time domain and frequency domain [22]. This section explains the two methods used in this work.
2.1. Time Domain Analysis (BETD)
Time domain analysis is made with the input and/or output waveforms plotted along the axis of time. Two points of these plots are selected following a given criterion, where their time difference is defined as the travel time (tt), between the transmitter and the receiver of the wave under analysis.
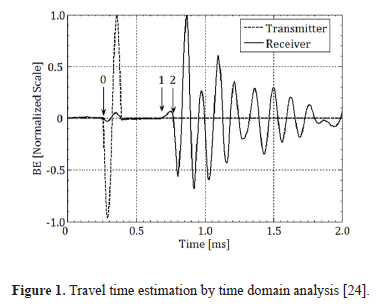
The travel time is the time that a wave requires to travel across a specific path, usually, the direct distance between the two sensors from where waveforms were recorded. Following the method used on in-situ geophysical measurements, the first direct arrival in the output signal (point 1 in Figure 1) was the method initially adopted [1-3].
Viggiani and Atkinson [32], suggested the point of first inversion (point 2 in Figure 1) of the received signal because it exhibits more consistency. But, the first inversion can not always be clearly identified as shown by Brignoli et al. [8], who analyzed three examples concluding: a) the arrival of shear waves should be estimated according to the general shape of the received signal; b) the signal may or may not include the presence of the near-field effect and therefore the analysis should be made carefully. Arulnathan et al. [21] recommended the use of various methods to improve the reliability of the data [22, 33].
Based on these suggestions, as well as the experience of the authors, the first inversion point is the method used in this work.
2.1. Frequency domain analysis (BEFD)
The frequency domain analysis requires transformation of the signals as a function of frequency. The operation can be executed using wave analysis tools available in commercial software.
Assuming the propagation of plane wavefronts, Kaarsberg [34] observed that using continuous sine signals at constant frequency (f) it is possible to establish the elastic-wave velocity, by using the mathematical relationship:

Nevertheless, the wavelength l cannot be measured directly. To address this issue, it is possible to take advantage of the variation in the phase lag between input and output signals as the frequency of the input signal increases. Defining N as the number of wavelengths occurring in the travel distance Ltt, the shear wave velocity can be expressed as:

From (2), l varies only if the frequency changes. N can be related to the phase angle (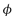 ) through:
) through: 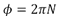 and the shear wave velocity therefore can be expressed in a differential form as:
and the shear wave velocity therefore can be expressed in a differential form as:

A graph of phase angle as a function of frequency is the phase of a cross-spectrum between two signals. The tangent of the phase spectrum is 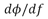 . The frequency domain method is a logical progression of the method proposed by Kaarsberg [35]. The method uses the sine sweep signal as the input signal. The sine sweep is a sinusoidal signal in which the frequency varies linearly with time from an initial frequency to a final frequency.
. The frequency domain method is a logical progression of the method proposed by Kaarsberg [35]. The method uses the sine sweep signal as the input signal. The sine sweep is a sinusoidal signal in which the frequency varies linearly with time from an initial frequency to a final frequency.
The sine sweep function applied by the transmitter produces the wave train that travels through the soil to the receiver. The response of the system is recorded and the transfer function H(f) between input x(t) and output y(t) signals is computed as:

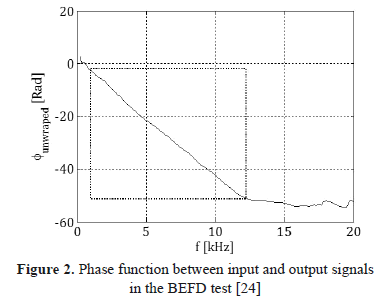
Where  is the Fourier transform operator, * is the complex conjugate function and the bar over the functions should be interpreted as average of multiple tests. The phase of the transfer function is illustrated in Figure 2. The square highlights the area where there is an approximately constant slope, which allows computing Vs from (4).
is the Fourier transform operator, * is the complex conjugate function and the bar over the functions should be interpreted as average of multiple tests. The phase of the transfer function is illustrated in Figure 2. The square highlights the area where there is an approximately constant slope, which allows computing Vs from (4).
The frequency domain method in BE testing was introduced by Greening and Nash [35]. The method has been used by Santos, Camacho-Tauta, Viana da Fonseca, Ferreira and their co-workers [36-40]. From these experiences, some degree of subjectivity persists in the travel time estimation whereas it is not possible to adopt a unique criterion to define a better travel time value [22].
A framework combining time-domain and frequency-domain methods was proposed by Viana da Fonseca et al. [22] in which two steps are followed. Primarily, sine-wave pulses at various frequencies are applied and the first direct arrival method is used to determine the travel time. Secondly, a continuous sine sweep is applied, followed by an interpretation method based on different frequency ranges [35-37].
3. EXPERIMENTAL PROCEDURE
3.1. Equipment
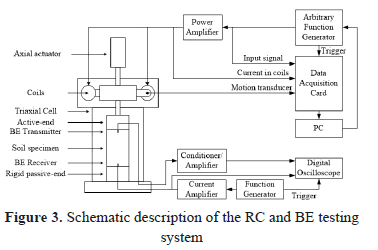
A resonant-column device (Drnevich model) was equipped with a set of bender elements [19] both in the top cap and in the base pedestal. The input signal is generated by a function generator (RIGOL, DG1022). A current amplifier stabilizes the signal and sends it to the BE transmitter. The output signal of the BE receiver is amplified and both input and output signals are collected by a digital oscilloscope (Tektronics, 3S2012B). Figure 3 shows a schematic view of the system.
The connections of the bender-element were given special attention to assure that the cables do not interfere in the movement of the active-end. Nevertheless, a new calibration was performed because variations in the mass and inertia of the top cap due to the introduction of bender elements should produce small changes in the apparatus calibration constants. The method proposed by Tatsuoka and Silver [41] was used to evaluate the apparatus calibration constant.
3.2. Resonant-Column Test (RC)
The resonant-column (RC) test is the most common laboratory testing method used for measuring the small-strain properties of soils. A cylindrical soil specimen is subjected to harmonic loading. The amplitude and frequency of the load are controlled and a motion transducer measures the resulting vibration level. By shifting gradually the frequency of the input force, the resonant frequency is found. The resonant frequency is the particular frequency in which the vibration level is a maximum for the load level imposed on the system. With the resonant frequency value, it is possible to back-calculate the shear wave velocity of the soil. The RC method is described in detail by the ASTM method D4015 [42], being the only standardized dynamic laboratory test to obtain the soil stiffness at small-strain levels. For this reason, the RC test was used in this work to compare with the BE test.
3.3. Bender Element Test
Two techniques for testing and analysis of BE were used in this paper. The first one is applied in the time domain (BETD), based on the first inversion in the output signal when the transmitter is excited with a single sine pulse. The second one is done in the frequency domain with a sine sweep excitation (BEFD), where the travel time is estimated from the slope of the unwrapped phase function (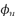 ).
).
3.4. Materials
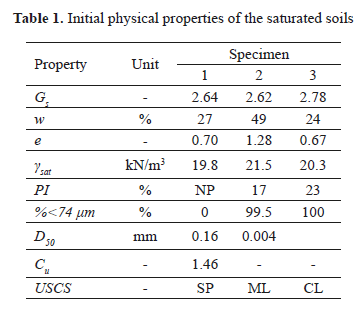
Three soil specimens were prepared and tested by means of the RC, BETD and BEFD test methods. As mentioned previously, specimen 1 is a sand sample reconstituted by dry compaction and further saturation; specimen 2 is a kaolinite sample reconstituted in laboratory by vertical consolidation of 50kPa from kaolinite mud; and specimen 3 is an undisturbed sample of low plasticity clay. Table 1 shows the initial physical properties of the three saturated specimens including: specific gravity of solids (Gs), water content (w), void ratio (e), saturated unit weight (gsat), Plasticity index (PI), fine content (%<74µm) and uniformity coefficient (Cu).
3.4.1. Specimen 1
The specimen of sand was prepared by the dry deposition method [43]. According to the specimen dimensions and the required void ratio, the soil mass was separated and divided into 5 equal portions. A vacuum pump was use to force the membrane to stick to the mold, taking on the cylindrical shape of it.
The soil was carefully poured into the interior of the membrane using a funnel. Each layer was lightly compacted and capped with a piston. The final height of each layer was verified with a caliper in order to guarantee the previously defined void ratio. Once the top cap and soil were in full contact, the membrane was accommodated to cover the top cap and two o-rings. Then 20 kPa of vacuum was applied inside the specimen and the mold was removed. The chamber was placed in position and filled with water. Finally, the vacuum was gradually replaced by lateral pressure and vertical load according to the required isotropic stress condition.
3.4.2. Specimen 2
The liquid and plastic limits of the commercial kaolinite were first determined. The material was disintegrated by the use of a hammer, passed through a sieve and lumps disintegrated again until total reduction of the material to a powder. The powder was mixed with water in proportions to obtain a water content equivalent to 1.5 times the liquid limit of the clay. The mixture was poured into a cylindrical mold, which rests on a bed of sand covered by filter paper. The set was placed in a water tank and the soil was gradually loaded.
After the consolidation process, the specimen was extruded and cut. The specimen was weighed and its dimensions measured before its installation in the equipment. Filter papers were used to avoid solid migration into the porous stones. The latex membrane was placed by means of the membrane expansion tube and the top cap was carefully positioned on the specimen. Once full contact was obtained between the top cap and the specimen, the membrane was fixed to the top cap by means of two o-rings. Finally, the triaxial chamber was installed, filled with water and pressurized up to 20 kPa. Vertical load was adjusted in order to impose the isotropic stress state.
3.4.3. Specimen 3
The soil sample of low plasticity clay was obtained by tube sampling. The sample was extruded from the tube by means of a hydraulic jack and placed in a hand lathe and was cut with a steel wire. The ends of the sample were cut orthogonally to the axis. The weight and dimensions were taken and the specimen was put on the base cap, which was covered by a filter paper. The latex membrane was placed surrounding the specimen and the top end carefully located on the specimen. The o-rings were placed at the end caps to seal the membrane. Finally, the triaxial chamber was used and filled with water. Lateral pressure and vertical load were adjusted to provide the desired stress state.
4. RESULTS AND DISCUSSION
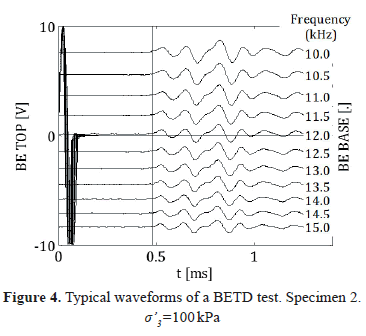
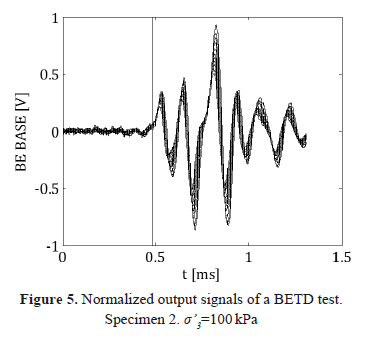
Typical waveforms of the BETD test are presented in Figure 4. The test is carried out using sine pulses at different frequencies. The arrival time is estimated by a superposition of the normalized outputs as shown in Figure 5. This representation simplifies the selection of the most probable arrival time. The arrival is approximately constant for the frequencies tested. The same technique was used for the three specimens and effective confinements of 100, 200 and 400 kPa.
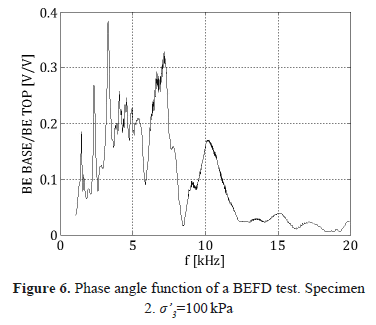
Figure 6 represents the magnitude of the transfer function of the BE system obtained by the BEFD method. This graph allows the frequencies where the output-to-input ratio is higher to be identified. The amplitude of this ratio decreases as the frequencies moves away from 10 kHz.
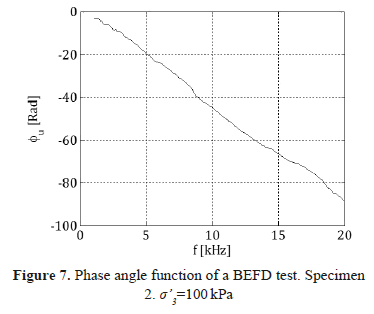
Figure 7 shows the phase function of the BEFD test; the slope of this figure is proportional to the travel time and can be computed using different frequency ranges [22]. The slope of the range between 1-15 kHz is nearly constant in accordance with the results of the BETD tests presented in Figure 5, in which the arrival time is constant for the frequency bandwidth tested. This procedure was repeated for isotropic effective confinements of 100, 200 and 400 kPa, on the three specimens.
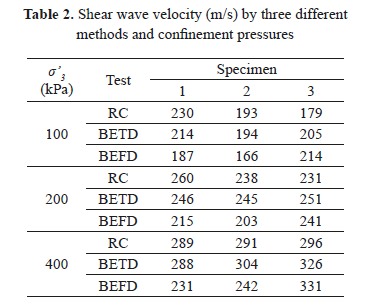
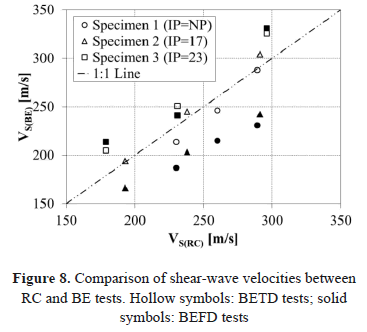
Table 2 resumes the shear wave velocities obtained by RC, BETD and BEFD methods for three different confinement pressures, s'3. Figure 8 shows a graphic comparison of the shear-wave velocities obtained by BETD and BEFD against RC. BEFD tests (marked with solid symbols) exhibit lower velocities than BETD and RC tests. The exception to this trend, occurs only in the specimen 3, in which BEFD and BETD tests produce similar results, but higher than RC tests.
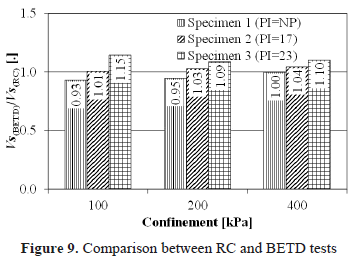
Figure 9 shows the ratio between the shear wave velocity from the BETD test and the shear wave velocity from the RC test, in order to compare with the reference method. This ratio varies between 0.93 and 1.15. According to this figure, the shear-wave velocity was generally underestimated in the case of the specimen 1 (non-plastic soil). In contrast, results of specimen 3 overestimate the reference value. In the middle, results from specimen 2 were approximately adjusted to the value measured by the RC method. This finding is in concordance with a previous study [30], which suggest better coupling between BE and soil particles in the case of fine-grained soils.
The effect of the confinement is not conclusive: for the specimen 1 (non-plastic) and the specimen 2, the ratio increases as the confinement increases. Nevertheless, in specimen 3 the effect is contrary. This trend could be due to the increase of intergranular contacts caused by the confinement, which could be more efficient in sands than in fine-grained soils.
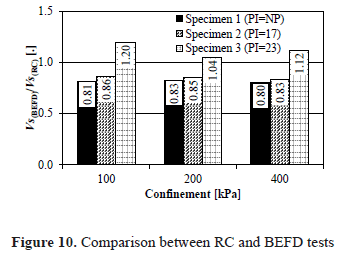
The results of the BEFD tests were compared against the RC results as illustrated in Figure 10. In this case, shear-wave velocities from the BEFD test were lower than the actual value in specimens 1 and 2. In specimen 3 the ratio was greater than unity for all confinements.
The differences between velocities obtained by the two methods make it evident the lower consistency of the BEFD method in comparison with the RC method. There is no conclusive trend either with the variation of confinement, or the with soil type.
5. CONCLUSIONS
BETD provides an approximate value of the shear wave velocity. This test however, requires careful execution and interpretation, the frequency of the input signal must be selected taking into account the need to avoid undesirable effects like near-field or signal contamination by compressional waves.
According to the BETD tests presented in this paper, the accuracy of the BETD method is affected by the plasticity of the soil: in non-plastic soils the stiffness tends to be underestimated. The amount of tests is not completely conclusive in this issue. A more extensive parametric study could clarify this trend.
Based on the results presented in this paper, the BEFD method was less reliable than the BETD method when they are compared against the RC test. Complex phenomena, like dispersion and multiple reflections on the boundaries in the small volume of the specimen could have a more undesirable effect in BEFD tests than in BETD tests.
ACKNOWLEDGEMENTS
This paper is a result of the Research Projects PIC ING-906 and ING-953 funded by Universidad Militar Nueva Granada. The authors acknowledge this financial support.
REFERENCES
[1] Shirley, D. J., and Hampton L. D. Shear-wave measurement in laboratory sediments, J Acoust Soc Am, 63, pp. 607-13, 1978. [ Links ]
[2] Shirley, D. J., An improved shear wave transducer, J Acoust Soc Am, 63, pp. 1643-45, 1978. [ Links ]
[3] Dyvik, R. and Madshus, C., Lab measurements of Gmax using bender elements, Proc, ASCE Annual Convention on Advances in the Art of Testing Soils under Cyclic Conditions, Detroit, Michigan, pp. 186-96, 1985. [ Links ]
[4] Ferreira, C., The use of seismic wave velocities in the measurement of stiffness of a residual soil [PhD Thesis], Porto: University of Porto, 2008. [ Links ]
[5] Dyvik, R. and Olsen, T. S., Gmax measured in oedometer and DSS tests using bender elements, Proceedings of the Twelfth International Conference on Soil Mechanics and Foundation Engineering, Rio de Janeiro, 1, pp. 39-42, 1985. [ Links ]
[6] Zeng, X. and Ni, B., Stress-induced anisotropic Gmax of sands and its measurement, Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 125, pp. 741-49, 1999. [ Links ]
[7] Bates, C. R., Dynamic soil property measurements during triaxial testing, Géotechnique 39, pp. 721-26, 1989. [ Links ]
[8] Brignoli, E. G., Gotti M. and Stokoe, K. H. I., Measurement of shear waves in laboratory specimens by means of piezoelectric transducers, Geotechnical Testing Journal, ASTM, 19, pp. 384-97, 1996. [ Links ]
[9] Jovicic, V. and Coop, M. R., The measurement of stiffness anisotropy in clays with bender element tests in the triaxial apparatus, Geotechnical Testing Journal, ASTM, 21, pp. 3-10, 1998. [ Links ]
[10] Sahaphol, T. and Miura, S., Shear moduli of volcanic soils, Soil Dynamics and Earthquake Engineering, 25, pp. 157-65, 2005. [ Links ]
[11] Wichtmann, T. and Triantafyllidis, T., Influence of a cyclic and dynamic loading history on dynamic properties of dry sand, part II: cyclic axial preloading, Soil Dynamics and Earthquake Engineering, 24, pp. 789-803, 2004. [ Links ]
[12] Kuwano, R., Connolly T. M. and Jardine, R. J., Anisotropic stiffness measurements in a stress-path triaxial cell, Geotechnical Testing Journal, ASTM, 23, 141-57, 1999. [ Links ]
[13] Kuwano, R. and Jardine, R. J., Stiffness measurements in a stress-path cell, In: Pre-failure deformation behaviour of geomaterials, ICE (Jardine, R. J. and et al, eds.). London Thomas Telford Ltd, pp. 391-94, 1998. [ Links ]
[14] Ismail, M. and Hourani Y., An innovative facility to measure shear-wave velocity in centrifuge and 1-g models, Proceedings of Deformation Characteristics of Geomaterials, Lyon, pp. 21-29, 2003. [ Links ]
[15] Fu, L., Application of piezoelectric sensors in soil property determination [PhD Thesis], Case Western Reserve University, 2004. [ Links ]
[16] Chaudhary, S. K., Kuwano J. and Hayano, Y., Measurement of quasi-elastic stiffness parameters of dense Toyoura sand in hollow cylinder apparatus and triaxial apparatus with bender elements, Geotechnical Testing Journal, ASTM, 27, pp. 23-35, 2004. [ Links ]
[17] Bellotti, R., Jamiolkowski M., Lo Presti D. C. F. and O'neill, D. A., Anisotropy of small strain stiffness in Ticino sand, Géotechnique 46, pp. 115-31, 1996. [ Links ]
[18] Brignoli, E. G. M., Fretti C., Jamiolkowski M., Pedroni, S. and Stokoe Ii, K. H., Stiffness of gravelly soils to small strains, Proceedings of the 14th International Conference on Soil Mechanics and Foundation Engineering, Hamburg, 1, pp. 37-40, 1997. [ Links ]
[19] Ismail, M., Sharma, S. S. and Fahey, M., A small true triaxial apparatus with wave velocity measurement, Geotechnical Testing Journal, ASTM, 28, pp. 113-22, 2005. [ Links ]
[20] Wang, Y., Yang, W. M. and Lo, K. F., Damping-ratio measurements by the spectral-ratio method, Canadian Geotechnical Journal, 43, pp. 1180-94, 2006. [ Links ]
[21] Arulnathan, R., Boulanger, R. W. and Riemer, M. F. Analysis of bender element tests, Geotechnical Testing Journal, ASTM, 21, pp. 120-31, 1998. [ Links ]
[22] Viana Da Fonseca, A., Ferreira C. and Fahey, M., A framework interpreting bender element tests, combining time-domain and frequency-domain methods, Geotechnical Testing Journal, ASTM, 32, pp. 1-17, 2009. [ Links ]
[23] Camacho-Tauta, J., Jiménez, J. D. and Reyes-Ortiz, O. J., A Procedure to Calibrate and Perform Bender Element Test, Revista Dyna, 79, pp. 10-18, 2012. [ Links ]
[24] Camacho-Tauta, J., Evaluation of the small-strain stiffness of soil by non-conventional dynamic testing methods [PhD Thesis], Lisbon: Technical University of Lisbon, 2011. [ Links ]
[25] Sanchez-Salinero, I., Roesset, J. M. and Stokoe, K. H., I. Analytical studies of body wave propagation and attenuation [Report GR 86-15], Austin: University of Texas, 1986. [ Links ]
[26] Arroyo, M., Muir Wood D. and Greening P. D. Source near-field effects and pulse tests in soils samples, Géotechnique, 53, 337-45, 2003. [ Links ]
[27] Lee, J.-S. and Santamarina, J. C., Bender elements: performance and signal interpretation, Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 131, 1063-70, 2005. [ Links ]
[28] Rio, J., Greening P. and Medina, L., Influence of sample geometry on shear wave propagation using bender elements, Deformation Characteristics of Geomaterials, Lyon, 963-67, 2003. [ Links ]
[29] Arroyo, M., Muir Wood D., Greening P. D., Medina L. and Rio J. Effects of sample size on bender-based axial G0 measurements, Géotechnique, 56, pp. 39-52, 2006. [ Links ]
[30] Wicaksono, R. I., Tsutsumi, Y., Sato, T., Koseki, J. and Kuwano, R., Stiffness measurements by cyclic loading, triggger accelerometer, and bender element on sand & gravel, Deformational Characteristics of Geomaterials, Atlanta, GA, 2, pp. 733-39, 2008. [ Links ]
[31] Yang, J. and Gu, X. Q., Shear stiffness of granular material at small strains: does it depend on grain size?, Géotechnique, 63, 165-79, 2013. [ Links ]
[32] Viggiani, G. and Atkinson, J. H., Interpretation of bender element tests, Géotechnique, 45, 149-54, 1995. [ Links ]
[33] Jovicic, V., Coop, M. R. and Simic, M., Objetive criteria for determining Gmax from bender element tests, Géotechnique, 46, pp. 357-62, 1996. [ Links ]
[34] Kaarsberg, E. A., Elasic-wave velocity measurements in rocks and other materials by phase-delay methods, Geophysics, 40, 955-60, 1975. [ Links ]
[35] Greening, P. D. and Nash, D. F.T. Frequency domain determination of G0 using bender elements, Geotechnical Testing Journal, ASTM, 27, pp. 1-7, 2004. [ Links ]
[36] Santos, J. A., Camacho-Tauta, J., Parodi, M., Viana Da Fonseca, A. and Ferreira, C., Use of random vibrations to measure stiffness of soils, Experimental Vibration Analysis for Civil Engineering Structures (EVACES'07), Porto, 1169-78, 2007. [ Links ]
[37] Camacho-Tauta, J., Santos J. A., Ferreira, C. and Viana, Da., Fonseca A. Moving windows algorithm to reduce uncertainties in bender element testing, XI Portuguese National Congress of Geotechnics, Coimbra, 1, 149-56, 2008. [ Links ]
[38] Greening, P. D., Nash D. F. T., Benahmed N., Ferreira C. and Viana Da Fonseca A. Comparison of shear wave velocity measurements in different materials using time and frequency domain, Proceedings of the 3rd International Symposium on Deformation Characteristics of Geomaterials, IS-Lyon '03, Lyon, France, 1, 2003. [ Links ]
[39] Ferreira, C., Bender element test measurements using time and frequency domain techniques, Proceedings of the Workshop on current practices of the use of bender element technique, Lyon, France, 2003. [ Links ]
[40] Ferreira, C., Viana, Da., Fonseca, A. and Santos. J. A., Comparison of simultaneous bender element test and resonant column tests on Porto residual soils, In: Soil Stress-Strain Behavior: Measurement, Modeling and Analysis A Collection of Papers of the Geotechnical Symposium in Rome, March pp. 16-17, 2006 (Ling, H. I., Callisto L., Leshchinsky D. and Koseki J., eds.).Springer, 523-36, 2006. [ Links ]
[41] Tatsuoka, F. and Silver, L., New method for the calibration of the Inertia of resonant column devices, Geotechnical Testing Journal, ASTM, 3, pp. 30-34, 1980. [ Links ]
[42] ASTM International. Standard test methods for modulus and damping of soils by the resonant-column method (D 4015-92), In: Annual Book of ASTM Standards (West Conshohocken 2002. [ Links ]
[43] Ishihara, K., Soil behaviour in earthquake geotechnics, Oxford Science Publications, 1996. [ Links ] ;