Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.182 Medellín nov./dez. 2013
EFFECTS OF USING REDUCTS IN THE PERFORMANCE OF THE IRBASIR ALGORITHM
EFECTO DEL USO DE REDUCTOS EN EL DESEMPEÑO DEL ALGORITMO IRBASIR
YUMILKA B. FERNÁNDEZ
MSc. Profesora Asistente, Universidad de Camagüey, Cuba, yumilka.fernandez@reduc.edu.cu
RAFAEL BELLO
PhD. Profesor Titular, Universidad Central "Marta Abreu" de Las Villas, Cuba, rbellop@uclv.edu.cu
YAIMA FILIBERTO
PhD. Profesora Asistente, Universidad de Camagüey, Cuba, yaima.filiberto@reduc.edu.cu
MABEL FRIAS
Ing. Profesora Asistente, Universidad de Camagüey, Cuba, mabel.frias@reduc.edu.cu
YAILE CABALLERO
PhD. Profesora Titular, Universidad de Camagüey, Cuba, yaile.caballero@reduc.edu.cu
Received for review October 9th, 2012, accepted February 5th, 2013, final version February 20th, 2013
ABSTRACT: Feature selection is a preprocessing technique with the objective of finding a subset of attributes that improve the classifier performance. In this paper, a new algorithm (IRBASIRRED) is presented for the generation of learning rules that uses feature selection to obtain the knowledge model. Also a new method (REDUCTSIM) is presented for the reduct's calculation using the optimization technique, Particle Swarm Optimization (PSO). The proposed algorithm was tested on data sets from the UCI Repository and compared with the algorithms: C4.5, LEM2, MODLEM, EXPLORE and IRBASIR. The results obtained showed that IRBASIRRED is a method that generates classification rules using subsets of attributes, obtaining better results than the algorithm where all attributes are used.
KEYWORDS: Feature selection, classification rules, Particle Swarm Optimization
RESUMEN: La selección de atributos es una técnica de preprocesado cuyo objetivo es buscar un subconjunto de atributos que mejore el rendimiento del clasificador. Basándonos en este concepto en este trabajo se presenta un nuevo algoritmo para la generación de reglas de aprendizaje que utiliza la selección de atributos para obtener el modelo de conocimiento (IRBASIRRED). Se presenta también un nuevo método (REDUCTSIM) para el cálculo de reductos utilizando la técnica de optimización PSO (Particle Swarm Optimization). El algoritmo propuesto fue probado en conjuntos de datos de la UCI Repository y se comparo con los algoritmos C4.5, MODLEM, EXPLORE e IRBASIR. Los resultados obtenidos demuestran que IRBASIRRED es un método que genera reglas de clasificación utilizando subconjuntos de atributos reducidos, obteniendo mejores resultados que con el algoritmo donde se utilizaban todos los atributos.
PALABRAS CLAVE: Selección de atributos, reglas de clasificación, Optimización
1. INTRODUCTION
In the process of solving classification problems it appears that the most important thing is to have the maximum possible information. This way, it seems that it would be better to use more characteristics. However, in practice, this is not always that the case [1]. The yield of real learning algorithms can deteriorate in the case of the abundance of information. Many characteristics can be totally irrelevant for the problem. Also, several characteristics can provide the same information, so all but one are redundant. Therefore, the problem can be solved without enhancing information, with no negative impacts, and even to improving the results in diverse aspects. Hence it would be advantageous to carry out a selection of features before proceeding to the classification process.
It is a fact that the behavior of classifiers improve when the redundant attributes are eliminated [2]. In the selection of attributes the minimum subset of attributes is chosen that satisfy two conditions: the rate of successes does not decrease significantly and the distribution of the resulting class is as similar as possible to the distribution of the original class with all the attributes. In general, the application of feature selection helps in all phases of the process of data mining for knowledge discovery. The algorithms of feature selection choose a minimum subset of characteristics that satisfies an evaluation approach. Ideally, the methods for feature selection look for the subsets of attributes trying to find the best among the 2m (m: total number of attributes) subset candidates according to an evaluation function. When the algorithms of feature selection are applied before the classification, the interest goes to those attributes that classify the unknown data better up to that moment. If the algorithm provides a subset of attributes, this subset is used to generate the pattern of knowledge that will classify the new data.
In [3], authors state that the use of selection methods of characteristics in the development of classifiers, can contribute with advantages such as efficiency (in time and/or in space) for most learning algorithms, because this depends on the number of characteristics used.
In [4], authors carried out a revision of several algorithms of attribute reduction and strategies of reduction selection, demonstrating that training with classification systems obtains better results.
Indeed, the quality of the discovered knowledge does not depend only on the learning algorithm used, but also on the quality of the data. Often the existence of irrelevant attributes affects the precision of the learning algorithm in a remarkable way.
Therefore, the selection of characteristics can help to obtain better results in an algorithm by indicating the characteristics on which to concentrate; it can achieve the reduction of costs of acquisition of data and the improvement in the interpretability of the results, when based on a smaller number of characteristics.
An example of an algorithm for feature selection is C4.5 [5]. It builds a decision tree with the training data and it is a quick, robust and easy classification algorithm, therefore it is among the most popular machine learning methods. In each node of the tree, C4.5 chooses an attribute of the data that more efficiently divides the group of samples in subsets. Their approach is to use the gain of information (entropy difference) in the selection of an attribute to divide the data. The attribute with the biggest gain of normalized information is chosen as the decision parameter. The algorithm C4.5 successively divides the data in smaller lists.
On the other hand, rough sets have proven to be effective for data analysis; hence, machine learning is one of the areas where they have aroused great interest. The Rough Set Theory (RST) was introduced by Z. Pawlak in 1982 [6]. The rough set philosophy is based on approximating any concept for example a hard subset of the domain, such as a class in a supervised classification problem, by means of a pair of exact sets, called lower approximation and upper approximation of the concept. With this theory is possible to deal with both quantitative and qualitative data, particularly useful for dealing with uncertainty caused by inconsistencies in the information. Different algorithms have been developed for the discovery of classification rules (decision rules) based on rough sets. Among the best known are LEM2 (Learning from Examples Module v2), this algorithm is part of the data mining system LERS (Learning from Examples based on Rough Sets) [79], and two algorithms based on LEM2, MODLEM [1012]; and MLEM2 [13], which tries to find a minimum set of rules that allow the classification (which means that the examples of the training set are covered by the minimum number of non redundant rules). LEM2 algorithm, similar to ID3, only considers elementary conditions including equality operators (attribute = value); therefore, in the case of continuous domain features it requires a preprocessing phase in which these domains are discretized. MLEM2 and MODLEM algorithms are able to consider continuous domain attributes because they performed simultaneously discretization and induction and generate the P part of the rules as conjunctions with a more general syntax. The MODLEM algorithm seeks coverage on approximations of the classes of minimal sets of decision rules. In [11], authors present a comparative study on numerical data between LEM2 and MODLEM. The results showed that MODLEM achieved results with an accuracy comparable to that achieved by the best variant of LEM2, by considering several alternatives of discretization for LEM2. The results presented in [14] showed that MODLEM achieves a similar performance to the algorithm C4.5. Other studies on the discovery of decision rules using rough sets are presented in [10], [12] and [1519]. The EXPLORE algorithm is another learning method for discovering rules extending those based on the approach of rough sets. EXPLORE is able to generate rules which are general, simple, accurate and relevant. The EXPLORE algorithm, first presented in [20], is a procedure that extracts all decision rules that satisfy certain requirements. The algorithm can handle inconsistent examples either by using rough set theory to define approximations of decision classes, or by determining the appropriate threshold for confidence of induced rules to be used in prepruning [21].
2. MODIFICATION OF THE IRBASIR ALGORITHM USING Reducts.
The IRBASIR algorithm [22] is a method for discovering classification rules for decision systems with mixed data, i.e., the domain of condition features could be discrete or continuous.
This algorithm does not require discretizing continuous domains, neither as a prelearning step nor during the learning process; the conditional part of the rule is not expressed as a conjunction of elementary conditions. The algorithm is based on the use of a relation of similarity that allows constructing similarity classes of objects, the construction of relations of similarity is based on the extended Rough Set Theory. This algorithm finds a set of rules following a sequential covering strategy, which builds similarity classes of objects in the decision system.
The algorithm includes a main module with three steps and two procedures for the construction of the rules.
In this section a modification of the IRBASIR algorithm is presented, which is denominated IRBASIRRED, in which the generated rules include only the features that belong to reducts in their conditional part. The method for building the reduct is based on the metaheuristic Particle Swarm Optimization [23] and the quality of the similarity measure proposed by Filiberto, Y. et al. [2426]; this method is called REDUCTSIM (construction of reducts based on the quality of the similarity measure).
3. THE QUALITY OF THE SIMILARITY MEASURE
The quality of the similarity measure was presented in [2426].
Let be the decision system DS=(U, A∪{d}), where the domains of features in A∪{d} are discrete or continuous; and a similarity measure consisting of three major parts:
- Local similarity measures used to compare the values of single features (called the comparison functions of the feature, an example is expression (5)).
- Feature weights representing the relative importance of each attribute.
- A global similarity measure responsible for the computation of a final similarity value based on the local similarities and feature weights (called the similarity function, an example is expression (3)).
In order to compute the set of weights associated with features in A, the similarity relations R1 and R2 defined on U are introduced in the following form:
For all objects x and y in U:
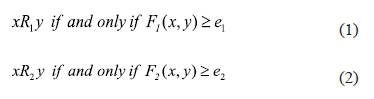
Where F1 and F2 are similarity functions to compare objects in U, F1 includes features in A and F2 computes the similarity degree between two objects according to the value of the decision feature d; e1 and e2 are thresholds.
The comparison functions can be defined by expressions (3) and (4):

A classic comparison function is defined by expression (5):
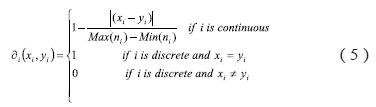
In order to find the similarity relations R1 and R2 the sets N1and N2 can be defined for all x in U by expressions (6) and (7), N1 and N2 of x is the neighbourhood of x according to the relations R1 and R2 respectively:
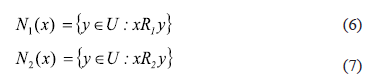
Then, the problem is to find the functions F1 and F2 such that N1(x) =N2(x), where the equal symbol (=) denotes the greatest similarity between N1(x) and N2(x) given the thresholds e1 and e2, and the comparison function ∂i() for each feature.
In order to build these functions the measure defined by expression (8) is proposed:
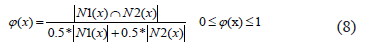
Using expression (8) the quality of similarity of a continuous decision system DS=(U, A+{d}) is defined by expression (9):
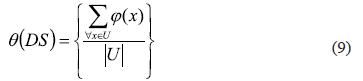
This measure q(DS) represents the degree in which the similarity among objects using de features in A is the same as the similarity according to the decision feature d.
Then, the problem of finding the set of weights W={w1, w2,…,wn}, where n is the number of features in the set A, is to maximize the expression (9):

The metaheuristic PSO is used to solve this optimization problem and hence the feature selection problems [27, 28]. The particles are vectors W=(w1, w2,…,wn). At the end of the search, the best particle is used to assign the weights to the features. The method REDUCTSIM uses these weights to build a reduct.
4. REDUCTSIM METHOD
The following steps were performed to determine the relevant features:
Step 1: The continuous features of the decision systems were discretized using the method Discretize of the System WEKA [29].
Step 2: The quality measure of the classification of the discretized decision system (DSd) was calculated, this value is called g(DSd).
Step 3: PSO was applied for both the measure quality of similarity [26] and for the calculation of weights W={w1, w2,…,wn} in the original decision systems DS.
Step 4: The features were ordered from bigger to smaller according to the value of the calculated weights.
Step 5: The features of smaller weights were removed and the measure quality of the classification in the discretized decision system was calculated, this value is denoted as g(DSd*). If the value g(DSd*) is equal or very close to g(DSd), continue removing features while this condition is true.
Step 6: The resulting features set is used as a reduct.
The algorithms of reduction of attributes QUICKREDUCT [30] and AFSBRSA (Algorithm for feature selection based on Rough Set and Ant Colony Optimization) [31] are used for the same purpose. The algorithm QUICKREDUCT calculates a minimum set without generating all the possible subsets. It begins starting from an empty set and then in each iteration it adds a feature that has the maximum increment in the grade of dependence, until the maximum value is obtained for the set of data. However, this does not guarantee to find the minimum set of features. In many cases, the algorithm QUICKREDUCT cannot find a set of features that satisfies the strict definition of reduct, and the subset of features found can contain irrelevant features. The quality of the classification can diminish when a classifier is designed using the subset of features containing irrelevant features.
On the other hand, the algorithm AFSBRSACO is a hybrid algorithm, where the Rough Set Theory (RST) is used to define the importance of the features by means of the lower and upper approximations. ACO (Ants Colony Optimization) is used to implement the search method; generating subsets of features that use a filter approach based on forward selection. In the case of this algorithm the ants leave the CORE or nucleus, the pheromone is also associated to the paths denoting the possibility to go from node j to node i.
5. IRBASIRRED
In IRBASIRRED the generated rules only include the resulting features of the REDUCTSIM method in their condition part. This modification is carried out in the GenRulSim Procedure(k, Cs, C; Rul) of the IRBASIR algorithm. This procedure builds a decision rule, which it returns in Rul, starting from the input parameters k (denotes a decision class), Cs (similarity class of the processed object) and C (subset of Cs, only containing the class objects).
Step1: Build a p vector with n reference components (one for each condition feature) for the set of objects in C. pi ← f(VRi), where VRi is the set of values of the i feature in the objects in C and f it is an aggregation operator.
Step2: Generate the rule starting from the reference vector p.
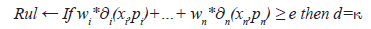
Where the weight wi is taken from the function (3); e is the threshold used in the similarity relations (1); pi is the value of the feature i in the reference vector p.
It is in this step where the modification is carried out in the following way (we take a very simple example for a better understanding):
Let the weights w1=0.5, w2=0.45, w3=0.05, and the subset {w1, w2} is a reduct.
- The weight of the features which are not included in the reduct, are set to 0, in this case:
- w1=0.5, w2=0.45, w3=0.0
- The feature weights that they are in the reduct, are normalized, so that their sum is equal to 1:
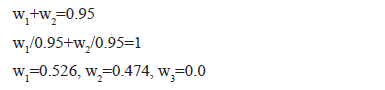
- Apply
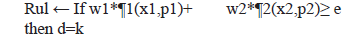
Step3: Calculate the rule coverage.
6. EXPERIMENTAL RESULTS
For the validation of the new method proposed to select features, the results obtained by REDUCTSIM were compared with the algorithms QUICKREDUCT and AFSBRSA.
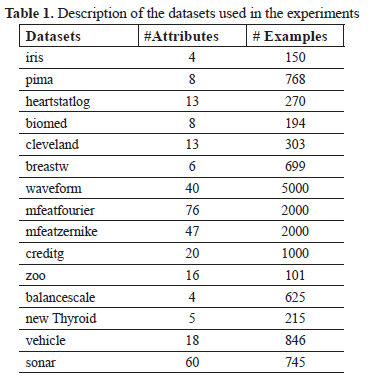
To evaluate the precision of the algorithm IRBASIRRED, 15 datasets of the UCI repository for machine learning [32] were used where most of conditional attributes have a continuous domain and the decision feature is discrete. For the validation of the results the K Fold Cross - Validation method [33] is used.
The description of these datasets appears in Table 1.
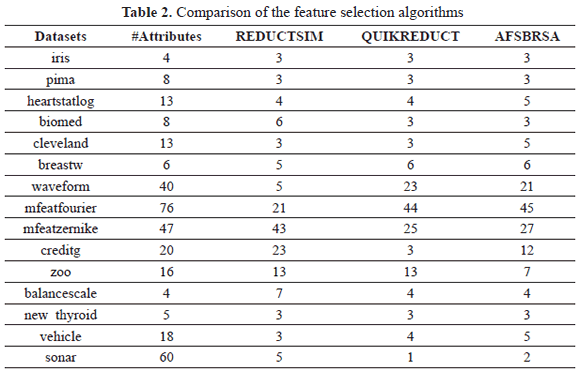
Experiment 1: Compare the results of the feature selection algorithms taking into account the quantity of selected features. The results are showed in Table 2.
The quantity of features selected by the method REDUCTSIM in most of the cases is equal to or lower than the other methods.
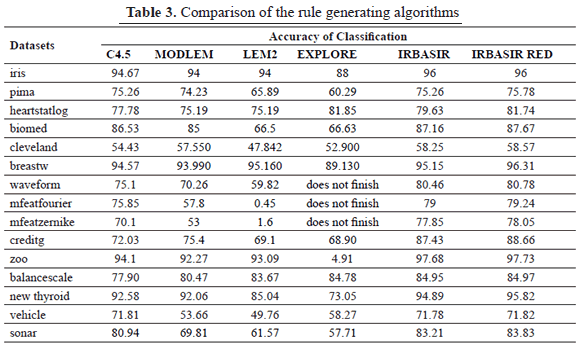
Experiment 2: Compare the results of the performance of C45, LEM2, MODLEM, EXPLORE, IRBASIR and IRBASIRRED for each of the datasets; a kfold with k=10 were carried out.
In the case of C4.5 the feature selection process is implicit in the method, IRBASIR, LEM2, MODLEM and EXPLORE consider all the features.. IRBASIRRED, is the IRBASIR algorithm but it uses only the features selected by REDUCTSIM.
In Table 3 the results of the comparison are shown among the classifiers.
The precision of the obtained classification using the rules induced by the algorithm IRBASIRRED was superior to those generated by the algorithms C45, LEM2, MODLEM, EXPLORE and IRBASIR.
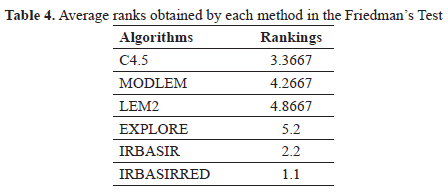
In order to compare the results a multiple comparison test is used to find the best algorithm. In Table 4 it can be observed that the best ranking is obtained by the proposal presented: IRBASIRRED.
An Iman-Davenport test is carried out (employing an Fdistribution with 5 and 70 degrees of freedom) in order to find statistical differences among the algorithms C45, LEM2, MODLEM, EXPLORE, IRBASIR and IRBASIRRED, obtaining a pvalue similar to zero. In this way, in Table 5 the results of the Holm procedure for comparing the proposal to the remaining ones are shown. The algorithms are ordered with respect to the obtained zvalue.
Thus, by using the normal distribution, the corresponding pvalue associated with each comparison can be obtained and this can be compared with the associated a/i in the same row of the table to show whether the associated hypothesis of equal behavior is rejected in favor of the best ranking algorithm; as can be observed, the test rejects all cases. This result indicates that the performance of IRBASIRRED is statistically superior to every compared method.
7. CONCLUSIONS
In this article a new method for feature selection denominated REDUCTSIM is presented, satisfactory results in most of the cases with regard to the quantity of selected features were obtained with this method. A modification to the IRBASIR algorithm is developed, called IRBASIRRED for the generation of classification rules which uses only the relevant features instead of all features of the data set; when compared with other known algorithms to discover rules (C4.5 LEM2, EXPLORE and MODLEM), experimental results show that the IRBASIRRED algorithm obtains the best performance.
REFERENCES
[1] Kohavi, R. and Frasca, B., Useful Feature Subsets and Rough Set Reducts. in Third International Workshop on Rough Sets and Soft Computing. 1994. [ Links ]
[2] Ruiz, R., et al. Analysis of feature rankings for classification. in In Advances in Intelligent Data Analysis VI (IDA 2005). 2005: Springer Verlag. [ Links ]
[3] Araúzo, A., Un sistema inteligente para selección de características en clasificación., in Departamento de Ciencias de la Computación e Inteligencia Artificial. 2006, Universidad de Granada: Granada, España. [ Links ]
[4] Hu, Q., Li Xiaodong, Daren, Yu., Analysis on Classification Performance of Rough Set Based Reducts. 2005. [ Links ]
[5] Quinlan, J.R., C4.5: Programs for machine learning, ed. M. Kaufmann, San Mateo, California. 1993. [ Links ]
[6] Pawlak, Z., Rough Sets. International journal of Computer and Information Sciences, 11 pp. 341356. 1982. [ Links ]
[7] GrzymalaBusse, J.W., LERS A system for learning from examples based on rough sets. Intelligent Decision Support, Handbook of Applications and Advances of the Rough Sets Theory, pp. 318. 1992. [ Links ]
[8] GrzymalaBusse, J.W., The rule induction systems LERS Q: a version for personal computers. in In Proceedings of the International Workshop on Rough Sets and Knowledge Discovery. 1993. [ Links ]
[9] GrzymalaBusse, J.W., A new version of the rule induction system LERS. Fundamenta Informaticae, 31, pp. 2739, 1997. [ Links ]
[10] Stefanowski, J., The rough set based rule induction technique for classification problems. in In Proceedings of 6th European Conference on Intelligent Techniques and Soft Computing EUFIT 98. Aachen, 1998. [ Links ]
[11] GrzymalaBusse, J.W. and Stefanowski, J., Three discretization methods for rule induction. International Journal of Intelligent Systems, 16, pp. 2938. 2001. [ Links ]
[12] Stefanowski, J., On combined classiffers, rule induction and rough sets. Transactions on Rough Sets VI Springer LNCS, 4374, pp. 329350, 2007. [ Links ]
[13] GrzymalaBusse, J.W., MLEM2: A new algorithm for rule induction from imperfect data. in Proceedings of the 9th International Conference on Information Processing and Management of Uncertainty in KnowledgeBased Systems, IPMU, Annecy, France, 2002. [ Links ]
[14] Stefanowski, J. and Nowaczyk, S., On using rule induction in multiple classiffiers with a combiner aggregation strategy. in In Proc. of the 5th Int. Conference on Intelligent Systems Design and Applications ISDA 2005, IEEE Press. 2005. [ Links ]
[15] Skowron, A., Boolean reasoning for decision rules generation. In: Komorowski. Methodologies for Intelligent Systems. Lectures Notes in Artificial Intelligence Springer,. 689, pp. 295305, 1993. [ Links ]
[16] Stefanowski, J. and Vanderpooten, D., A general twostage approach to inducing rules from examples. Rough sets, Fuzzy sets and Knowledge Discovery Springer, 1994, pp. 317325. [ Links ]
[17] GrzymalaBusse, J.W. and Zou, X., Classification strategies using certain and possible rules. Rough sets and current trends in Computing, Lectures Notes in Artificial Intelligence Springer, 1424, pp. 3744, 1998. [ Links ]
[18] Kryszkiewicz, M., Rough sets approach to rules generation from incomplete information systems. The Encyclopedia of Computer Sciences and Technology, 44, pp. 319346. 2001. [ Links ]
[19] Leung, Y. et al. Knowledge acquisition in incomplete information systems: A rough set approach. European Journal of Operational Research, 129, pp. 164180, 2006. [ Links ]
[20] Mienko, R, Stefanowski, J. et al., Discoveryoriented induction of decision rules. Cahier du Lamsade, 141, 1996. [ Links ]
[21] Stefanowski, J. and Wilk, S., Extending RuleBased Classifiers to Improve Recognition of Imbalanced Classes. Advances in Data Management SCI, 223, pp. 131154, 2009. [ Links ]
[22] Filiberto, Y., Bello, R. and Caballero, Y., Algoritmo para el aprendizaje de reglas de clasificación basado en la teoría de los conjuntos aproximados extendida. DYNA año 78, 169, pp. 6270. 2011. [ Links ]
[23] Kennedy, J. and Eberhart, R.C. Particle swarm optimization. in In Proceedings of the 1995 IEEE International Conference on Neural Networks. Piscataway, New Jersey: IEEE Service Center, 1995. [ Links ]
[24] Filiberto, Y. et al. Una medida de la Teoría de los Conjuntos Aproximados para sistemas de decisión con rasgos de dominio continuo. Revista de Ingeniería de la Universidad de Antioquia Science Citation Index Expanded (SCIE) del ISI, 2(60) pp. 153164. 2011. [ Links ]
[25] Filiberto, Y. et al. A method to built similarity relations into extended Rough set theory. in Proceedings of the 10th International Conference on Intelligent Systems Design and Applications (ISDA2010). 2010b. Cairo, Egipto. [ Links ]
[26] Filiberto, Y. et al., Using PSO and RST to Predict the Resistant Capacity of Connections in Composite Structures. In International Workshop on Nature Inspired Cooperative Strategies for Optimization (NICSO 2010) Springer, pp. 359370, 2010. [ Links ]
[27] Fan, H. and Zhong,Y., A Rough Set Approach to Feature Selection Based on Wasp Swarm Optimization. Journal of Computational Information Systems, 8(3): pp. 1037-1045, 2012. [ Links ]
[28] Liu, Y. et al., An Improved Particle Swarm Optimization for Feature Selection. Journal of Bionic Engineering, 8, 2011. [ Links ]
[29] Witten, I. and Frank, E., eds. Data Mining. Practical Machine Learning Tools and Techniques. Second Edition ed. Department of Computer Science. University of Waikato. 2005. [ Links ]
[30] Jensen, R. and Qiang, S., Finding rough sets reducts with Ant colony optimization. in UK Workshop on Computational Intelligence. UK, 2003. [ Links ]
[31] Ming, H., Feature Selection Based on Ant Colony Optimization and Rough Set Theory. in International Symposium on Computer Science and Computational Technology. 2008. [ Links ]
[32] Alcalá, J. et al. KEEL DataMining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. Journal of MultipleValued Logic and Soft Computing, 2010. [ Links ]
[33] Demsar, J., Statistical comparisons of classifiers over multiple data sets. Journal of Machine Learning Research, (7), pp. 130, 2006. [ Links ]