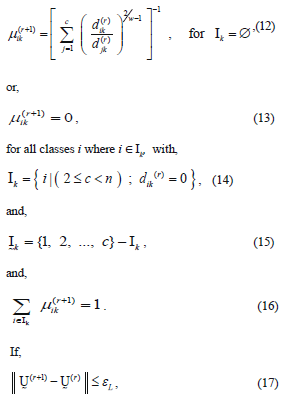Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.183 Medellín jan./fev. 2014
https://doi.org/10.15446/dyna.v81n183.36838
http://dx.doi.org/10.15446/dyna.v81n183.36838
COMPUTER-AIDED DIAGNOSIS OF BRAIN TUMORS USING IMAGE ENHANCEMENT AND FUZZY LOGIC
DIAGNÓSTICO ASISTIDO POR COMPUTADORA DE TUMORES CEREBRALES UTILIZANDO MEJORA DE LA IMAGEN Y LÓGICA DIFUSA
JEAN MARIE VIANNEY-KINANI
M.Sc., Instituto Politécnico Nacional de México,jeanmariekinani@yahoo.com.mx
ALBERTO J. ROSALES-SILVA
Ph.D., Instituto Politécnico Nacional de México, arosaless@ipn.mx
FRANCISCO J. GALLEGOS-FUNES
Ph.D., Instituto Politécnico Nacional de México, fgallegosf@ipn.mx
ALFONSO ARELLANO
Specialist in Neurosurgery, Instituto de Neurología y Neurocirugía de México, alfonso_arellano@yahoo.com
Received for review January 21th, 2013, accepted August 12th, 2013, final version September, 10th, 2013
ABSTRACT: A robust medical image processing system depends upon a variety of aspects, including a proper image enhancement, and an optimal segmentation. An algorithm was proposed in this paper to facilitate the implementation of these two steps. First a Magnetic Resonance (MR) image is enhanced via spatial domain filtering and its contrast is improved, next, the image is segmented using fuzzy C-mean clustering, then the region of interest which might be the tumor or edema, is detected and delineated. The key advantage of this image processing pipeline is the simultaneous use of features computed from the intensity properties of the image in a cascading pattern which makes the computation self-contained. Performance evaluation of the proposed algorithm was carried out on brain images from different MRI's and the algorithm proved to be successful, comparing it with other dedicated applications.
Key words: MRI, Region of interest, Segmentation, Clustering.
RESUMEN: Un sistema de procesamiento de imágenes médicas robusto depende de una variedad de aspectos, incluyendo una mejora apropiada de la imagen, y una segmentación óptima. En este artículo se propone un algoritmo para facilitar la implementación de estos dos pasos. En primer lugar, una imagen de resonancia magnética (RM) se mejora vía filtrado en el dominio espacial y también se mejora su contraste, luego, la imagen se segmenta utilizando el agrupamiento difuso "fuzzy C-means" (FCM), posteriormente, la región de interés, que puede ser el tumor o edema, se detecta y delinea. La ventaja clave de esta canalización de procesamiento de imagen es el uso simultáneo de características calculadas a partir de las propiedades de intensidad de la imagen en un patrón en cascada que hace que el cálculo sea auto-contenido. La evaluación del rendimiento del algoritmo propuesto se llevó a cabo en imágenes cerebrales de diferentes sistemas de resonancia magnética, el algoritmo desarrollado probó ser exitoso en comparación a otras aplicaciones relacionadas.
Palabras clave: IRM (Imagen de Resonancia Magnética), Región de interés, Segmentación, Algoritmo de agrupamiento.
1. INTRODUCTION
For every person diagnosed with brain tumor, their life expectancy decreases by 22 years on average. Due to their location, i.e., at the center of thought, physical function and emotion, brain tumors are difficult to diagnose and treat, and as a result, their death toll both in adults and children is highly disturbing. In many case, brain tumors, like any other type of cancer are a result of uncontrolled growth of brain cells, which may spread across the brain if not taken care of. For this reason, timely diagnosis and steady monitoring are imperative. As part of oncologic imaging, computer-aided diagnosis of these unhealthy tissues is not only of high interest in serial treatment monitoring of disease burden (i.e.,the impact this health problem may have in terms of financial cost, mortality, morbidity etc), but is also getting popular in many image guided surgical approaches. Using T1 weighted MR images which are obtained after administration of a contrast agent (gadolinium), our proposed algorithm, focuses on identifying brain structures, i.e., white matter, gray matter, cerebral spinal fluid, and then, it detects any abnormal region that always stands out due to its intensity spectrum; and with limited user interaction, the algorithm uses predefined parameters quantifying this region of interest (ROI) intensity to delineate it with higher precision thus facilitating subsequent treatment processes. Most of medical imaging modalities obtain images of gray scale intensities, including MRI's. It turns out that these images have noise, artifacts, poor resolution and contrast due to instrument and reconstruction algorithm limitations or even patient movement; this makes auto diagnosis a challenging task, and the algorithm's advantages and disadvantages may vary depending on the properties of the image under examination. Due to the image deterioration factors mentioned above, it's hard to develop a standard approach capable of working with all MR brain images [1]. For this reason, tradeoffs have always been present in computer-aided diagnosis systems. However, comparing our fuzzy clustering-based method to other methods like classifier, region growing, neural networks, deformable model-based systems, a big advantage of our approach is recognized especially when it comes to dealing with the adverse factors mentioned [2].
2. METHODOLOGY
2.1 Preprocessing
Medical images are often deteriorated by noise due to various sources of interference and other phenomena that affect the measurement processes in imaging and data acquisition systems. The nature of the physiological system under investigation may also diminish the contrast and the visibility of details [3]. Thus, pre-processing helps in generating enhanced versions of the original image that demonstrate certain features in manner that is better in some sense as compared to their appearance in the original image. Depending on the nature and quality of the original image, different methods are used to enhance the visibility of the image, among them, filtering, histogram equalization, intensity scaling, compensation for nonlinear characteristics, etc. In the methodology proposed, spatial filtering and histogram equalization were adopted because they turned out to be effective in dealing with most of the problems that show up in the post-acquisition phase, and this is the right way to tackle the issue since other types of artifacts are best taken care of during the acquisition process [4].
2.1.1. Filtering
In the proposed algorithm, filtering was carried out in the spatial domain using a Laplacian Filter. The Laplacian operator is an example of a second order method of enhancement. The Laplacian proved to be good at finding the fine detail in an MRI image in a much better way compared to other spatial filters like the median, Gaussian, gradient or fuzzy filters, because it sharpens the image in a manner that portrays the heterogeneity of the image components in a much clearer view, and this is thanks to the fact that it is a second derivative operator that works successfully on heterogeneous images like MR images [5]. This filter is implemented by applying a Laplacian to an image f(x, y) as follows:
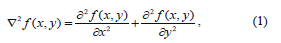
Commonly used digital approximations of the second derivative are:
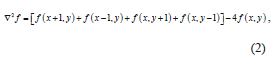
After this transformation we obtain a sharper image with a higher degree of heterogeneity better suited for further processing.
2.1.2. Histogram equalization
Another way to improve the quality of MR images was through the enhancement of their contrast. This is a very important aspect for subsequent processing phases, because it produces images that have the same contrast, hence ensuring a consistent response from the detection algorithm. This adjustment was carried out using histogram equalization technique, because it is fully automatic, can cover the entire gray scale which means there is no loss of information, and is based on information that can be extracted directly from the given image without the need for further parameter specification.
Suppose the intensity levels are continuous quantities normalized to the range [0, 1] and let 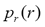 denote the probability density function (PDF) of the intensity levels in a given MRI image, where the subscript is used for differentiating between the PDFs of the input and output images[5]. Suppose that we perform the following transformation on the input levels to obtain output (processed) intensity levels s,
denote the probability density function (PDF) of the intensity levels in a given MRI image, where the subscript is used for differentiating between the PDFs of the input and output images[5]. Suppose that we perform the following transformation on the input levels to obtain output (processed) intensity levels s,
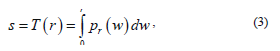
where w is a dummy variable of integration and r is in the range [0, L-1], we define L being the gray scale intensity levels, with r=0 representing black and r=L-1 representing white. It can be shown that the PDF of the output levels is uniform, that is,

In other words, the preceding transformation generates an image whose intensity levels are equally likely, and in addition covers the entire range [0, 1]. The net result of this intensity-level equalization process is an image with increased dynamic range, which will tend to have a higher contrast, and when applied to the MR image, the sharpness increases and our detection stage will be more efficient since we will be dealing with images whose contrast has increased.
2.2. Segmentation
The principal goal of the segmentation process is to partition an image into regions (also called classes or subsets) that are homogeneous with respect to one or more characteristics or features [3]. In medical imaging, the segmentation step is important for feature extraction, image measurement and display, classification of image pixels into anatomical regions or pathological regions such as cancer (tumor in our case), tissue deformities, among others. There are a number of methods used for this classification task, and each of them maybe selected depending on the application and the type of image to be dealt with. In our case, the most preferable was fuzzy classification due to reasons that will become clear in the next sections.
2.2.1. Fuzzy C-mean Clustering
One of the well-established concepts in image segmentation is pixel classification. This concept assumes that the pixels in each subclass (tissue) have nearly constant intensities, which is true for anatomical structures with similar physiological properties [3]. This applies to structures like White Matter (WM), Gray Matter (GM), or the Cerebral Spinal Fluid (CSF) that are found in the brain. This is also true for the unhealthy tissues like tumors because the cells that make up these tissues present similar physiological properties, thus uniformly responding to the BO field and the Radio-frequency system of the MRI. And for this reason, they always stand out in the classification process, since their intensity spectrum differs from the rest of other tissues; in this regard, any tissues in the MR image whose intensity spectrum differs from the WM, GM and CSF spectra and is spatially found in one of these tissues' locations will always be treated as a region of interest that catches the doctor's attention. This explains why our diagnosis methodology seeks to sort out all the tissues that show up in the MR brain image using an adaptive classification method, that is, a method that is capable of estimating the centroid and bounds of each tissue in an adaptive fashion. It was proved that the right tool for this identification process would be fuzzy classification as a clustering technique since it classifies pixels in their respective clusters [6] bearing in mind the variability of gray value along with pixel statistical uncertainty due to the randomness [7].
We can now define a family of fuzzy partition matrices Mfc, for the classification involving c classes (clusters) and n data points (pixels):
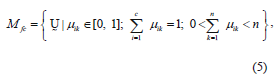
where 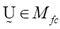 is a fuzzy c-partition,
is a fuzzy c-partition, 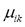 is the membership value that the k-th pixel has in the i-th cluster, with i= 1, 2,…,c, and k = 1, 2,…,n; c being the number of clusters, and n the number of pixels, and
is the membership value that the k-th pixel has in the i-th cluster, with i= 1, 2,…,c, and k = 1, 2,…,n; c being the number of clusters, and n the number of pixels, and 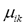 must have the following restrictions:
must have the following restrictions:
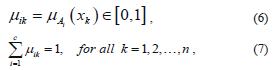
with A being a family of fuzzy sets, and x, the data sample. It follows from the overlapping character of the classes and the infinite number of membership values possible for describing class membership that the cardinality of Mfc is also infinity, that is, 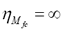 [8].
[8].
To describe a method to determine the fuzzy c-partition matrix 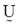 for grouping a collection of n data sets (i.e., n pixels that quantify the corresponding intensities of our MR image) into c classes (i.e., c brain tissues including our ROI), we define an energy function Jm for a fuzzy c-partition [8],
for grouping a collection of n data sets (i.e., n pixels that quantify the corresponding intensities of our MR image) into c classes (i.e., c brain tissues including our ROI), we define an energy function Jm for a fuzzy c-partition [8],
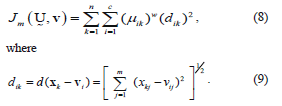
with dik representing the Euclidean distance between the i-th cluster center and the k-th pixel (data point in m space or k-th pixel's intensity); and the parameter 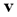 is a vector of cluster centers. Another parameter introduced in (8) is w, called a weighting parameter whose value has a range
is a vector of cluster centers. Another parameter introduced in (8) is w, called a weighting parameter whose value has a range 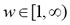 . This parameter controls the amount of fuzziness in the classification process.
. This parameter controls the amount of fuzziness in the classification process.
Furthermore, in (9) appears 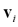 which is the i-th cluster center, and is described by m features (m coordinates) that can be arranged in vector form, that is,
which is the i-th cluster center, and is described by m features (m coordinates) that can be arranged in vector form, that is,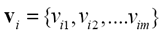 .
.
Each of the cluster centers mentioned above can be calculated in the following manner:
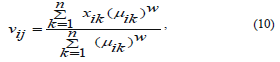
where j is a variable on the feature space, that is, j = 1, 2, . . .,m. and i, k define the cluster and pixel number respectively.
It should be pointed out that the function Jm can have a large number of values, the smallest one associated with the best clustering or in our case, the best detection. Because of the large number of possible values (now infinite due to the infinite cardinality of fuzzy sets) we seek to find the best possible, or optimum, solution without resorting to an exhaustive, or expensive, search.
The optimum fuzzy c-partition will be the smallest of the partitions described in (8), that is,
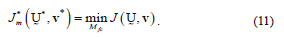
As with many optimization processes, the solution to (11) cannot be guaranteed to be a global optimum because of its fuzziness in nature. What we seek is the best solution available within a prespecified level of accuracy. To get to this, an iterative optimization algorithm proved to be the best option [8].The steps of this algorithm are as follows:
- Fix c (2 ≤ c < n) and select a value for parameter w depending on the degree of fuzziness of the images to be processed (w>1). Initialize the partition matrix,
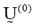 . Each step in this algorithm will be labeled r, where r = 0, 1, 2, .…It should be noted that c was chosen to be equal to 4, referring to Cerebral Spinal fluid, White matter, Gray matter and region of interest, i.e. tumor/edema.
. Each step in this algorithm will be labeled r, where r = 0, 1, 2, .…It should be noted that c was chosen to be equal to 4, referring to Cerebral Spinal fluid, White matter, Gray matter and region of interest, i.e. tumor/edema. - Calculate the c centers
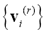 for each step.
for each step. - Update the partition matrix for the r-th step,
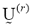 , as follows:
, as follows:
then stop, otherwise set r=r+1 and return to step 2.
The parameters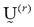 and
and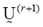 represent the partition matrix for the rth and the (r+1)th steps respectively, as it was mentioned in step 1 and 3 of the algorithm. And the parameter
represent the partition matrix for the rth and the (r+1)th steps respectively, as it was mentioned in step 1 and 3 of the algorithm. And the parameter 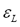 represents a prescribed level of accuracy that is used to determine whether the solution is good enough to stop the algorithm. This comparison of a matrix norm || of two successive fuzzy partitions to a prescribed level of accuracy, eL, is due to the restrictions of (11).
represents a prescribed level of accuracy that is used to determine whether the solution is good enough to stop the algorithm. This comparison of a matrix norm || of two successive fuzzy partitions to a prescribed level of accuracy, eL, is due to the restrictions of (11).
In step 3, there is a considerable amount of logic involved in (12)-(16). Equation (12) is straightforward enough, except when the variable djk is zero. Since this variable is in the denominator of a fraction, the operation is undefined mathematically, and computer calculations are abruptly halted. So the parameters Ik and 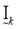 comprise a bookkeeping system to handle situations when some of the distance measures, dij, are zero, or extremely small in a computational sense. If a zero value is detected, (13) sets the membership for that partition value to be zero. Equations (14) and (15) describe the bookkeeping parameters Ik and
comprise a bookkeeping system to handle situations when some of the distance measures, dij, are zero, or extremely small in a computational sense. If a zero value is detected, (13) sets the membership for that partition value to be zero. Equations (14) and (15) describe the bookkeeping parameters Ik and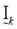 , respectively, for each of the classes. Equation (16) simply says that all the nonzero partition elements in each column of the fuzzy classification partition,
, respectively, for each of the classes. Equation (16) simply says that all the nonzero partition elements in each column of the fuzzy classification partition, 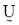 sum to unity [9], [10].
sum to unity [9], [10].
2.2.2. Level set methods
Level set methods (LSM) seek to define the active contours of ROI through the evolution of a numerical level set equation, which is actually a Hamilton-Jacobi equation [11], [12]:
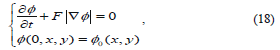
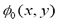 where F represents comprehensive forces, including internal forces from the interface geometry like mean curvature, contour length, area and external forces from image gradient.
where F represents comprehensive forces, including internal forces from the interface geometry like mean curvature, contour length, area and external forces from image gradient. 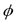 is the level set function and,
is the level set function and, 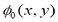 is the initial contour. A complete level set equation can actually be written as:
is the initial contour. A complete level set equation can actually be written as:
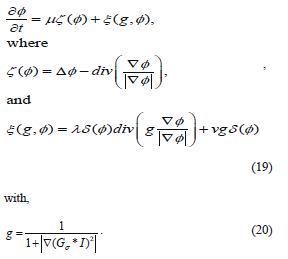
Equation (19) is an edge indication function that regularizes F in order to stop level set evolution near the optimal solution [13]. The constants m, l and n control the individual contribution of the terms above and they are tuned using trial by error method, and they vary from case to case. In our experiment these values varied from (0.01 to 0.3), (0.1 to 7), (-2 to 2) respectively.
Basically, the terms x(g,f) attracts the level set function towards the variation boundary, and x(f) forces the function to approach the genuine signed distance function automatically. And the Dirac function is computed as follows [14]:
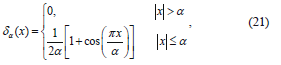
where a is a constant regulating the Dirac function and is tuned using trial by error method . The interface defined as T(t) can be determined by tracking the values of level set function according to the conditions,

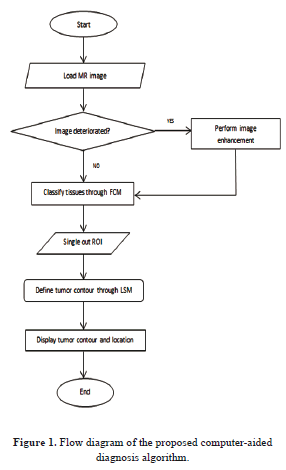
The steps of the proposed algorithm are shown in figure 1 below.
3. EXPERIMENTAL RESULTS AND ANALYSIS
The experiments were carried out on MR brain images baring different resolutions varying between 1.5 to 4mm/pixel. The algorithm was implemented using MATLAB R2007b (Mathworks), on the Windows 7 operating system, and 3.00 GHz dual processor; its execution time was about 15 seconds which is quite acceptable. Another overwhelming advantage was the precision to track even the most negligible intensity change, which implies that our algorithm could carry out a quicker and more reliable diagnosis than a general clinician, especially in case of poor quality MR images because human eye is unable to trace these changes so easily.
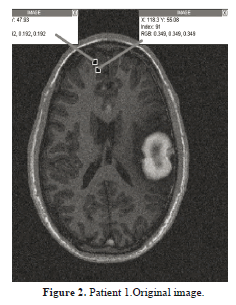
As mentioned, the original image is preprocessed using the methods mentioned in Section 2, and then brain structures are categorized into white matter, gray matter, cerebral spinal fluid and the unhealthy tissue. Then, this tissue is selected and the algorithm works to define its contour. To carry out a much more reliable segmentation, it is necessary to find the region that has minimum energy, i.e., the region where the intensity shift is not that sharp. An example was taken and displayed in figure 2 where a gray matter region measuring 52 levels of intensity (index) is weighed against a white matter region in its vicinity measuring 91 levels of intensity. Taking into account the whole image's intensity spectrum, this intensity difference is not that big, and this is confirmed by the negligible difference of lightness of the two regions. Our fuzzy c-mean clustering should be able to segment this neighborhood into 2 different regions, so as to identify the expansion of the region of interest.
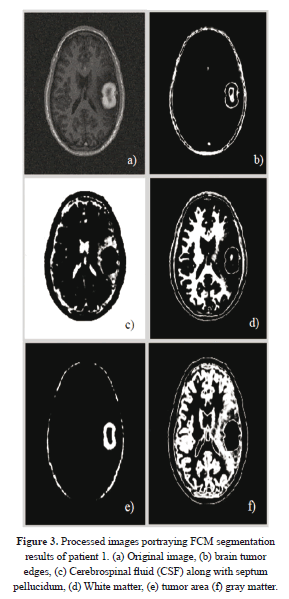
As far as the tissues classification is concerned, one can see that in Figure 3, the fuzzy c-mean clustering routine takes in an MRI image (a) which was cleaned according to Section 2.1, processes it, using the classification scheme described in 2.2.1, then it outputs five different clusters (b)-(f) that correspond to five different types of regions, including the ROI. It is obvious that this fuzzy clustering phase is capable of detecting even very tiny shifts in intensity levels as portrayed on figure 2; this undoubtedly demonstrates the sensitivity of the system. This is followed by a ROI boundary definition that shows exactly the expansion of this region relative to the entire original image.
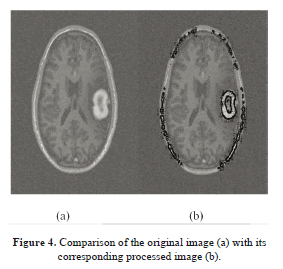
Figure 4 illustrates the final results (in green) of active contouring as described in equation (21). These results were obtained after 110 iterations. One can see that the image (b) portrays the contour of the tumor relative to the other tissues, and this delineation is obtained from the results of Figure 3(b) previously obtained from FCM segmentation.
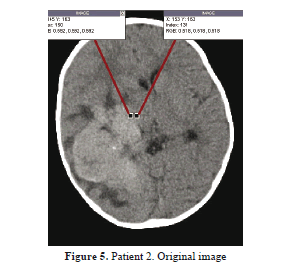
Figure 5 illustrates the intensity distribution of a different patient's MR image, with very tiny intensity shift along the tumor edge. However, the FCM should detect this transition with accuracy.
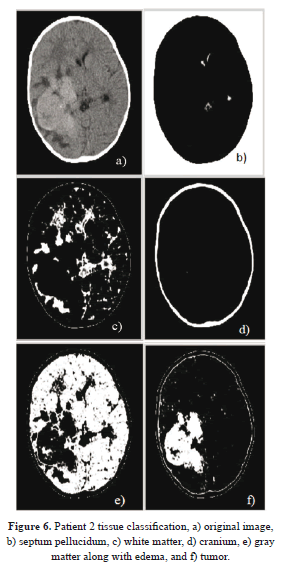
In figure 6, patient 2 who is in critical condition is diagnosed, as one can see his septum pellucidum was shifted upward (b) due to the expansion of edema that appears in (e). (c) Shows white matter tissues which were reduced because of the edema that spread over. Then (d) carries the cranium contour, whereas (e) portrays the gray matter intertwined with the edema. And (f) illustrates the tumor region. These results were obtained after FCM processing of figure 6(a) and, the specialist chooses his image of interest so that the level set method may give a final result of detection.
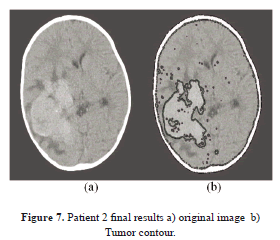
Figure 7 demonstrates two images, one being the input image, and the other one being the final processed image, where the tumor region is well outlined in spite of a cluttered neighborhood, and one can see clearly the high sensitivity of the system by comparing the two images. The tumor intensity spectrum is not that sharp, yet the algorithm can still trace its boundaries with high sensitivity.
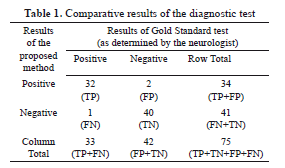
Talking about the sensitivity, a quantitative evaluation of the performance and reliability of our system was carried out by numerically computing both the sensitivity and specificity using 75 images. Table 1, shows the results of the proposed method as compared to the neurologist's findings. The sensitivity of the system quantifies its ability to correctly identify subjects with the disease condition. In other words, it is the proportion of true positives (TP) that are correctly identified by the system, given by:
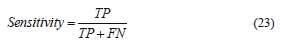
where FN represents the false negatives, and (TP+FN) represents the total number of subjects with the condition. On the other hand, the specificity is the ability of a system to correctly identify subjects without the condition. In other words, it is the proportion of true negatives (TN) that are correctly identified by the system:
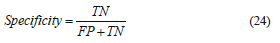
where FP represents the false positives, and (FP+TN) represents total number of subjects without the condition. Based on the results presented in Table 1, the sensitivity and specificity of the system is 32/(32+1)=0.97 and 40/(2+40)=0.95 respectively.
Finally, another statistic that was used to measure the reliability of our system is the accuracy, which is the proportion of true results, either true positive or true negative, in a population. It measures the degree of veracity of a diagnostic test on a condition, and is given by:
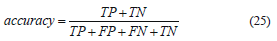
with (TP+FP+FN+TN) representing total number of subjects in study. Therefore the accuracy is (32+40)/(32+2+1+40)=0.96 in other words, 96% accurate.
4. CONCLUSION
The work mainly focused on the development of an algorithm that could promptly and accurately diagnose brain tumors even in their early stage of growth using both statistical and fuzzy methods. This was not an easy task due to the poor quality of some of the MR images; however, our preprocessing phase alleviated this issue significantly, thus facilitating the implementation of subsequent processing. A fuzzy c-mean clustering was implemented to classify different brain structures thereby allowing the detection of unhealthy tissues whose intensity span differed from the healthy ones i.e. white matter, gray matter, and cerebral spinal fluid. This method proved to be quite successful in the 75 cases studied; because it could accurately (96% of accuracy) process these images irrespective of their resolution. Using the controlling parameters generated by this clustering phase, a level set method could delineate these unhealthy regions, outlining their shape, position and expansion. This contour definition is normally the hardest task in manual segmentation due to changes in intensity as well as manual variations, (i.e., the manual segmentation's low degree of repeatability which is always present, even with the most meticulous surgeons). It is worth mentioning that an error of 4% i.e., (100-96% of accuracy) was due to artifacts generated by the brain tissues' heterogeneity, as it was proved by two false positives generated during the experiment.
5. ACKNOWLEDGEMENT
We would like to thank the Instituto Politécnico Nacional de México (National Polytechnic Institute of Mexico) for promoting our research, and the National Institute of Neurology and Neurosurgery of Mexico for providing us with medical guidance along with MR images, undoubtedly the support from these two institutions was vital in the accomplishment of this work.
REFERENCES
[1] Strickland, N. R., Image Processing Techniques for Tumor Detection. New York, Marcel Dekker, 2002. [ Links ] [2] Bezdek, J. C., Hall, L. O. and Clarke, L. P., Review of MR Image Segmentation Techniques Using Pattern Recognition. Baltimore, Medical Physics, 1993. [ Links ] [3] Bankman, N. I., Handbook of Medical Image Processing and Analysis. Burlington, Academic Press, 2009. [ Links ] [4] Liang, Z., Principles of Magnetic Resonance Imaging; A Signal Processing Perspective. Bellingham, IEEE press, 2000. [ Links ] [5] Gonzalez, C. R., Digital Image Processing. Upper Saddle River, Pearson, 2008. [ Links ] [6] Bezdek, J. C., Pattern Recognition with Fuzzy Objective Function Algorithms. New York, Plenum Press, 1981. [ Links ] [7] Tamalika, C. and Ajoy, K., Fuzzy Image Processing and Applications with MATLAB. Boca Raton, CRC Press, 2010. [ Links ] [8] Bezdek, J., Keller, J., Pal, N. and Krishnapuram, R., Fuzzy Models and Algorithms for Pattern Recognition and Image Processing. New York, Springer, 1999. [ Links ] [9] Krishnapuram, R., Generation of Membership Functions via Possibilistic Clustering. Columbia, IEEE, 1994. [ Links ] [10] Krishnapuram, R. and Keller, J. K., The Possibilistic C-Means Algorithm: Insights and Recommendations. Columbia, IEEE, 1996. [ Links ] [11] Xu, C. and Prince, J. L., Snakes, Shapes and Gradient Vector Flow, IEEE Transaction on Image Processing 7. Baltimore, IEEE, 1998. [ Links ] [12] http://www.cs.ubc.ca/~mitchell/ToolboxLS. [ Links ] [13] Osher, S. and Fedkiw, R., Level Set Methods and Dynamic Implicit Surfaces. New York, Springer-Verlag, 2009. [ Links ] [14] Li, C., Xu, C. and Andgui, C., Fox Level Set Evolution without Re-initialization, A New Variational Formulation in Proceedings of the 2005 IEEE Computer Vision and Pattern Recognition. Baltimore, IEEE, 2005. [ Links ]