http://dx.doi.org/10.15446/dyna.v81n184.39069

Influence of the normal stresses to direction of shear flow in the rheology of concentrated kaolin suspensions

Influencia de los esfuerzos normales a la dirección de flujo cizallante en la reología de suspensiones concentradas de caolín

 

Néstor Ricardo Rojas-Reyes ^a & Moisés Oswaldo Bustamante-Rúa ^b

^a Dr. Facultad de Minas. Universidad Nacional de Colombia sede Medellín. nrrojasr@unal.edu.co
^b Dr. Facultad de Minas. Universidad Nacional de Colombia sede Medellín. mobustam@unal.edu.co

 

Received: July 29^th, 2013. Received in revised form: October 7^th, 2013. Accepted: November 5^th, 2013.

 

---

Abstract
Due to the multiple applications that kaolin has, including the ceramic industry where it is used as a slurry with high solid concentrations, its rheological behavior is quite important in mixing, agitation and pumping stages. After characterizing the kaolin by applying XRD, XRF, SEM and particle size methods, a rheological evaluation was performed in a rotational rheometer which consisted of measuring the primary normal stress difference N1 by a method that delivered good reproducibility results. With N1 data it was obtained a kind of viscosity known as dilatant viscosity which was found only for those suspensions with a volumetric concentration higher than 0.13. This dilatant viscosity depends on the shear rate and the CV, and it was modeled with the power law structure having good coefficients of determination. Finally it was found that the dilatant viscosity with a CV= 0.2 is almost five times the value of the shear viscosity, thus demonstrating that for a better understanding of the deformation stage must be taken into account the normal stresses in shear flow happening in the kaolin concentrated suspension.

Keywords: Kaolin concentrated suspensions, rheology, normal stress difference.

Resumen
Debido a las múltiples aplicaciones que tiene el caolín, entre ellas en la industria cerámica, donde se utiliza como suspensión con altas concentraciones de sólido, su comportamiento reológico es de suma importancia en etapas de mezclado, agitación y bombeo. Luego de caracterizar el caolín por DRX, FRX, SEM y tamaño de partícula, se le realizó una evaluación reológica en un reómetro rotacional, consistente en la medición de primera diferencia de esfuerzos normales N1, mediante un método que entregó buenos resultados de reproducibilidad. Con los datos de N1 se obtuvo un tipo de viscosidad denominada viscosidad dilatante, la cual se encontró sólo para suspensiones con concentración volumétrica de sólido, Cv, mayor a 0,13. Esta viscosidad dilatante depende de la tasa de cizalladura y de la Cv, y se modeló con la estructura de ley de potencia con buenos coeficientes de determinación. Por último se encontró que la viscosidad dilatante a Cv = 0,20 es casi 5 veces el valor de la viscosidad cizallante, demostrando con esto que para una mejor comprensión del escenario de deformación se deben tener en cuenta los esfuerzos normales en flujo cizallante que experimenta una suspensión concentrada de caolín.

Palabras Clave: Suspensiones concentradas de caolín, reología, diferencia de esfuerzos normales.

---

 

1. Introducción

El caolín es una roca masiva con un porcentaje variable de minerales de arcilla, de composición igual o próxima a la del mineral caolinita (2SiO₂•Al₂O₃•2H₂O), el cual está constituido por capas sucesivas de octaedros de alúmina y tetraedros de sílice, que se alternan para forman partículas laminares con forma pseudo-hexagonal [1]. Las arcillas caoliníferas son valoradas comercialmente debido al uso directo en la industria, mientras que los caolines son procesados previamente para incrementar las propiedades deseadas que residen en las partículas individuales [2]. El caolín posee múltiples aplicaciones industriales; las más conocidas son: como recubrimiento y relleno para papel, imprenta, lubricación, adhesión, industria cerámica, pinturas, plásticos, refractarios, cementos, muy importante en la industria de cosméticos y farmacéutica, construcción, en cauchos y hules, química y forraje [2, 3]. Esta variedad de usos deriva de sus propiedades fisicoquímicas, entre las que destacan: blancura, inerte ante reactivos químicos, atoxicidad, poder de recubrimiento, resistencia mecánica después de calcinación y elevada refractariedad [4]. El caolín es utilizado generalmente disperso en agua para determinadas aplicaciones industriales, como es el caso de recubrimiento de papel y relleno de plásticos, sin embargo, la formulación de algunos productos de la industria cerámica demanda suspensiones de altas concentraciones en sólidos, llegando incluso hasta un contenido sólidos de 60 % en peso (20% en volumen) [5].

El comportamiento reológico de las suspensiones de caolín depende de diferentes parámetros tales como las propiedades físicas y químicas del solvente, nivel de pH, fracción volumétrica de sólidos, distribución y tamaño de partícula, propiedades superficiales de las partículas, entre otros [6, 7]. Las suspensiones cerámicas con alta fracción volumétrica generalmente muestran un comportamiento no newtoniano caracterizado por una viscosidad cizallo-dependiente [8, 9].

Con respecto a la medición de la diferencia de esfuerzos normales DEN (como aparecerá de aquí en adelante), en estado estacionario, Brady y Vicic (1995) [10], quienes utilizaron suspensiones de partículas esféricas brownianas mono-tamaño en líquido newtoniano, determinaron que los esfuerzos en suspensiones concentradas divergen de la teoría debido a un alto empaquetamiento de las partículas y que también se deben tener en cuenta efectos termodinámicos e hidrodinámicos para predecir el comportamiento reológico de éstas suspensiones. Zarraga et al., (2001) [11], determinaron que la magnitud de la primera y segunda DEN se incrementa con la fracción volumétrica de sólidos, en suspensiones viscoelásticas de esferas no coloidales mono-dispersas, en un fluido puramente elástico. Mall-Gleissle et al., (2002) [12], con suspensiones de esferas de vidrio mono-tamaño sumergidas en fluido viscoelástico, encontraron, a diferencia de las demás investigaciones, que para éstas dispersiones la primera DEN disminuye con el contenido de sólidos. Boyer et al., (2010) [13], reportaron medidas de la DEN en suspensiones con esferas de poliestireno micrométrico mono-tamaño en fluido newtoniano, pero trabajaron con un reómetro de rodillo y un perfilómetro óptico para medir la deflexión superficial negativa o positiva, y de esta forma la DEN. En dicho trabajo ellos determinaron que la DEN se incrementa con el aumento en la concentración de sólidos y que éste comportamiento es tiempo-dependiente debido a la migración de las partículas. Garland et al., (2013) [14] quienes utilizaron suspensiones concentradas de esferas micrométricas de poliestireno con distribución de tamaño en un fluido polimérico, obtuvieron esfuerzos normales radiales mediante la medición de la presión en la pared de un sistema cilíndrico Taylor-Couette, determinando que el esfuerzo normal radial de la fase partícula no muestra dependencia con respecto al tamaño de partícula y se incrementa linealmente con la tasa de cizalladura y cuadráticamente con la concentración volumétrica de sólidos.

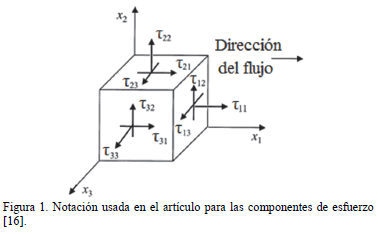
La distribución de esfuerzos en un líquido visco-elástico durante su flujo cizallante puede ser escrita formalmente definiendo el esfuerzo de cizalla t₂₁ y la primera DEN N1 y segunda DEN N2 (todas con unidades de Pa) como:

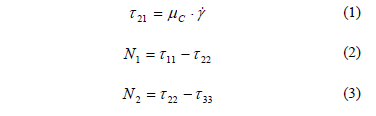
donde los subíndices 1, 2 y 3 denota la dirección de flujo, dirección normal al flujo y dirección de vorticidad, respectivamente [15 - 17], como se observa en la Figura 1. m_c es la viscosidad cizallante y g es la tasa de cizalladura, con unidades de Pa·s y s ^{- 1}, respectivamente. Se debe tener en cuenta que valores negativos de N1 (Ecuación 2) aparecen cuando los esfuerzos en dirección normal al flujo son mayores que los esfuerzos normales en dirección paralela al flujo, pero los reómetros registran este valor como positivo. Aunque el valor de N1 y N2 para fluidos newtonianos es cero, para líquidos poliméricos o fluidos viscoelásticos, N1 es positiva y N2 es negativa y/o mucho más pequeña que N1 [18 - 20]. Un ejemplo de respuesta visible a un valor N1 positivo, aparece cuando un fluido o suspensión "asciende" por una varilla que está girando dentro de él, fenómeno que se conoce como efecto Weissenberg [15, 16].

Hasta el momento generalmente la medición de la DEN ha sido asociada sólo a suspensiones con fluidos poliméricos [21, 22], y aparece debido a la anisotropía de los esfuerzos cizallantes y normales que se presentan en este tipo de suspensiones [11] y no se encuentra relacionada al comportamiento pseudoplástico o cizallo-adelgazante de suspensiones cerámicas comunes [8, 23 - 25]. El objetivo del presente estudio es determinar la importancia de los esfuerzos en dirección normal al flujo cizallante a partir de la medición de la primera DEN N1 (como aparecerá de aquí en adelante), encontrada en suspensiones concentradas de caolín.

 

2. Materiales y metodología

2.1. Material y equipo
La materia prima con la cual se trabajó en el proyecto es un caolín proveniente del departamento de Antioquia - Colombia. Este caolín se comercializa para diferentes empresas cerámicas y cementeras de la región. El valor promedio de la densidad del caolín es 2,46 g/cm³ y para su venta se asegura que el 80% de los tamaños de partícula sean menores de 44 micrones. La caracterización del caolín consistió en un análisis por DRX, FRX, tamaño de partícula y SEM. El análisis por DRX se llevó a cabo en un equipo Panalytical Xpert-Pro con una lámpara de cobre de longitud de onda 1,548 Å, con 2q de cero hasta 60° y una velocidad de barrido de 2°/min, utilizando el método de polvo de Debye Scherrer, y se comparó con una muestra de caolín estándar, este último adquirido a la empresa Motamineral - Minerais Industriais, S.A. (Brasil). El equipo utilizado para el análisis por FRX fue un Bruker S1 Turbo SD. La distribución de tamaño de partícula (DTP) se determinó en un analizador por difracción láser Mastersizer 2000, de la casa Malvern (UK), y el análisis por SEM fue realizado en un equipo JEOL JSM-6490LV. Las medidas reológicas se llevaron a cabo en un reómetro rotacional Bohlin Instruments C-VOR 200 (Malvern Instruments), en la celda Peltier a temperatura controlada (25 °C ±0,01), con la geometría cono-plato de 4° y 40 mm de diámetro, fabricada en titanio bajo norma, con una separación entre platos de 150 micras, la cual es predeterminada por la geometría. Las suspensiones se fabricaron a diferente concentración volumétrica de sólidos Cv, pesando la cantidad de sólido calculada en seco, mezclando con agua desionizada y microfiltrada, a pH natural de 4,5, agitándola por un tiempo mínimo de 5 minutos antes de realizar cada medición reológica y con tres repeticiones para cada medición.

2.2. Método para medición de la DEN
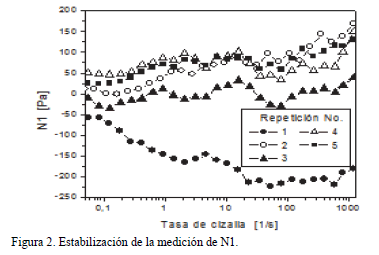
Valores de la DEN aparecen en el estado de equilibrio, el cual se obtuvo al repetir la aplicación de la cizalla sobre la muestra 3 veces, encontrándose que los valores de la tercera medida poseen buena reproducibilidad entre diferentes pruebas, como se observará en la sección de resultados. La respuesta particular de la suspensión en estudio es atribuida a la existencia de una estructura anisotrópica cizallo-inducida debido precisamente a la aparición de esfuerzos normales [13, 26]. Con base en que las investigaciones que se encontraron en la literatura siempre trabajan con partículas esféricas [11, 12, 27], se supone que el mayor tiempo que tarda la suspensión de caolín en reportar valores de N1 con poca variación, es decir, estabilización de la medida con la aplicación de la cizalla por lo menos 3 veces, se relaciona con la morfología laminar que presentan las partículas de caolín, pues éstas van a tardar más tiempo en migrar y organizase (comparadas con partículas esféricas) hasta lograr una medición de esfuerzos normales con una variación de los datos relativamente pequeña, como se observa en la Figura 2. Todos los valores reportados en el presente trabajo provienen de la tercera medida reométrica de las suspensiones de caolín.

2.3. Definición de viscosidad dilatante m_D
La N1 positiva puede ser medida a partir de la fuerza normal F, que trata de separar el cono del plato inferior cuando la suspensión se está ensayando [28]. Para la geometría cono-plato la proporcionalidad de la N1 a la fuerza axial o empuje F ejercido, donde R es el radio de la geometría [11, 12], se define como:

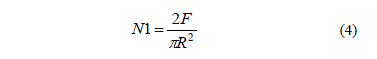
Las relaciones que utilizan el valor de N1, generalmente al trabajar con materiales viscoelásticos, tales como el coeficiente de esfuerzo normal Y₁ [16], la viscosidad de esfuerzo normal m_n(f) [27] y el esfuerzo normal adimensional x_n[11], son relaciones que no entregaron gráficos aptos para análisis con los valores de N1 obtenidos para las suspensiones de caolín; por esta razón se buscó una nueva relación para evaluar los efectos de las propiedades de la suspensión de caolín sobre la N1. Así como la viscosidad cizallante se define como la razón del esfuerzo cizallante sobre la tasa de cizalladura (Ecuación 1), la viscosidad dilatante se define en la presente investigación, como la razón de la primera diferencia de esfuerzos normales (N1) sobre la tasa de cizalladura:

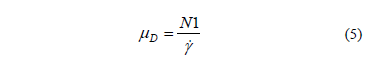
donde m_D también posee unidades Pa·s.

2.4. Ecuación para la modelación de m_D
Al graficar en escala log-log el esfuerzo de cizalla y la tasa de cizalladura de tal forma que aparece un comportamiento lineal en gran parte de la tasa de cizalladura elegida para el análisis, aparece una relación funcional empírica conocida como la ley de potencia, la cual fue propuesta originalmente por de Waele en 1923 y por Oswald en 1925 [29, 30], y se encuentra frecuentemente como:

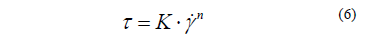
donde K es una medida de la "consistencia" del fluido, altos valores de K significan viscosidad alta del fluido; n es el "índice de potencia", entre más alejado de 1 indica un comportamiento más alejado del newtoniano. La viscosidad cizallante de un fluido que obedezca la ley de potencia puede ser expresada en términos de K y n como:

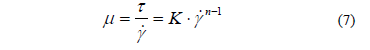
Esta ecuación puede modelar entre otros: polímeros de cadenas largas, suspensiones con polímeros, con cementos y con arcillas. Una interpretación de este comportamiento es que, con el incremento en la tasa de cizalladura, las moléculas o las estructuras de la suspensión son progresivamente alineadas [31].

 

3. Resultados y discusión

3.1. Caracterización del material
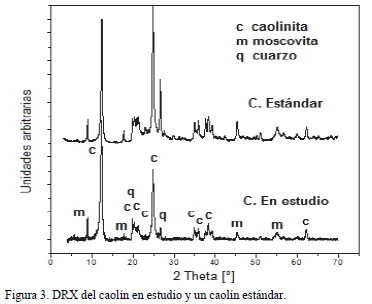
La Figura 3 muestra el análisis por DRX del caolín y una muestra estándar de caolín, donde se reporta que para el material en estudio la fase mineralógica principal es la caolinita con presencia del 89 %, y las fases secundarias son la moscovita con 8 % y el cuarzo con 3 %. Con respecto al caolín estándar, el análisis reportó un 99% de pureza.

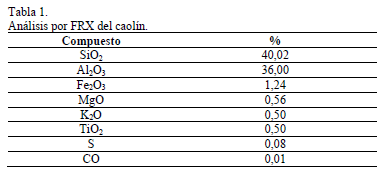
Los resultados del análisis por FRX se observan en la Tabla 1, donde se encuentra que los valores están acordes con los análisis reportados para diferentes tipos arcillas caoliníticas de acuerdo con Murray (2007) [32], Torres y Mejía (2007) [33] y Yuan y Murray (1997) [9].

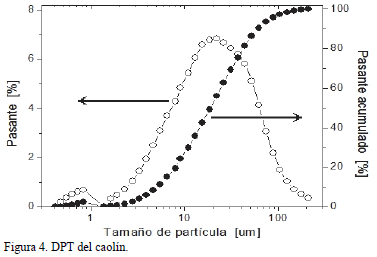
La distribución de tamaño de partícula (DTP) entrega valores para los percetiles d10, d50 y d90 de 2,67 ± 0,08 mm, 16,79 ± 0,19 mm y 60,91 ± 0,36 mm, respectivamente, como se puede observar en la Figura 4.

Las micrografías por SEM se presentan en la Figura 5, donde se observa en general una geometría de partículas completamente heterogénea (Figura 5a); y al detallar una de ellas se observa que está formada por varias láminas en forma de "libro" (Figura 5b), las cuales en contacto con el agua se separan y fluyen de forma tal que la superficie basal se organiza en dirección paralela al flujo [34].

3.2. Caracterización reológica
Dentro del procesamiento normal de un material cerámico, las suspensiones de caolín están sometidas a una serie de etapas tales como mezclado, agitación y bombeo, por lo que a menudo es importante analizar adecuadamente las propiedades reológicas del sistema en valores muy dispares de velocidad de cizalla [24]. Por esta razón se seleccionó un barrido de la tasa de cizalladura desde 0,01 hasta 1200 s ^{- 1} en un tiempo de 300 s.

3.2.1. Reproducibilidad del método
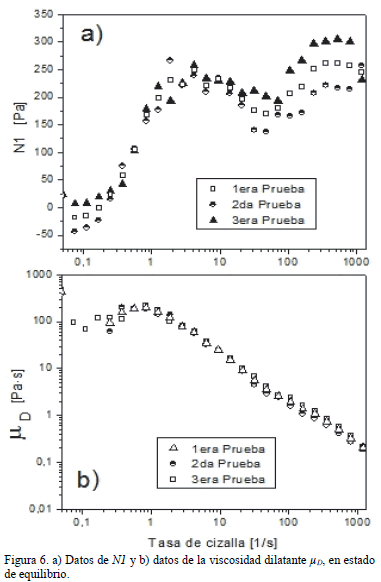
Cabe recordar que la N1 la reporta el reómetro positiva cuando los esfuerzos normales son mayores que los esfuerzos cizallantes, lo cual se obtuvo para suspensiones de caolín concentradas. La Figura 6 muestra un ejemplo de los datos obtenidos para una suspensión de caolín a una concentración volumétrica Cv = 0,16. En dicha figura se observa la conveniencia de graficar la viscosidad dilatante m_D en lugar de graficar la N1, con respecto a la reproducibilidad de datos y posterior análisis. También se observa la dependencia lineal de la viscosidad dilatante con respecto a la tasa de cizalladura.

3.2.2. Efecto de la concentración volumétrica de sólidos Cv
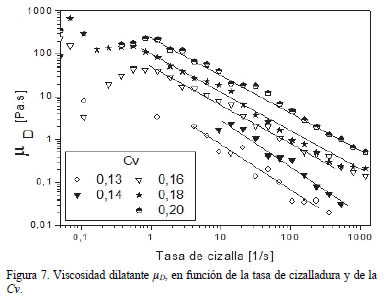
En la Figura 7 se grafica la viscosidad dilatante en función de la tasa de cizalladura y de la Cv, con datos de viscosidad dilatante a valores de Cv mayores a 0,13.

Los datos presentados en la Figura 7 se pueden modelar sobre la parte lineal que se observa a tasas de cizalladura superiores a 1 s ^{- 1}, con lo cual se plantea que a bajas velocidades de deformación existen micro-estructuras de partículas desordenadas y por lo tanto, una DEN nula; pero a medida que aumenta la tasa de cizalladura, las partículas de caolín se van organizando de forma direccionada y van fluyendo en la dirección de la cizalla. La estructura del modelo, basado en las ecuaciones 6 y 7, es la siguiente:

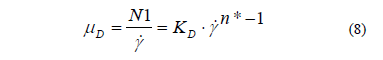
donde K_D es una función con unidades de Pa, y n* es una medida del grado de comportamiento de la viscosidad dilatante.

Los modelos reológicos de viscosidad dilatante con la estructura de ley de potencia obtenidos para las curvas de suspensiones de caolín con Cv > 0,13 se reportan en la Tabla 2, donde también se observa el coeficiente de determinación para cada una, con lo cual se puede determinar que existe una buena correlación entre los datos y el modelo. También se observa que existe una relación proporcional entre el valor de K_D y la concentración de sólidos, así que una generalización de las ecuaciones de la Tabla 2 en función de la Cv para K_D es la siguiente:

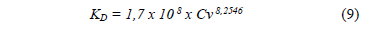
Y en relación a n*, también se puede obtener la siguiente relación:

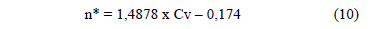
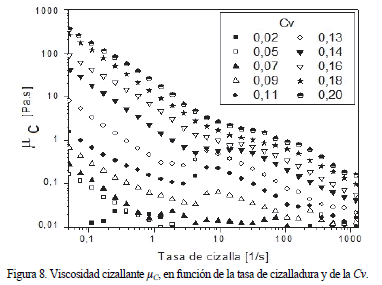
Con respecto a la viscosidad cizallante, la Figura 8 entrega las curvas de flujo donde se observa un comportamiento cizallo-adelgazante, el cual es típico de suspensiones arcillosas, con un aumento en el esfuerzo de cizalla a medida que crece la concentración de sólidos en la suspensión.

En la Figura 9 se observa que la aparición de la DEN coincide también con el reporte de valores relativamente altos de viscosidad cizallante. Entonces se puede determinar que a concentraciones altas de suspensiones de caolín, aunque el flujo del material vaya en sentido de la cizalla, se generan interacciones entre las partículas que crean desplazamientos de las mismas en dirección normal a la cizalla, y se observa además que dichas interacciones se van haciendo más significativas y evidentes a medida que aumenta la cantidad de partículas en suspensión.

La cuantificación de la influencia de dichas interacciones en función de la Cv en la Figura 9, se obtuvo a una tasa de cizalladura constante de 100 s ^{- 1}. Allí se observa que a bajas concentraciones de sólido existe un dominio de la fase continua que controla el comportamiento de la suspensión, de tal forma que las partículas de caolín se organizan en dirección del flujo cizallante, con ausencia de valores de DEN.

Para dispersiones con altas concentraciones de sólido (Cv > 0,13), los altos valores de viscosidad cizallante y dilatante no solamente son debidos al gasto energético necesario para trasladar las partículas en suspensión, sino además, a que la mayor proporción de estos esfuerzos es debida a la DEN que se encuentra en el sistema agua - caolín.

La Figura 10 muestra la razón de la viscosidad dilatante sobre la viscosidad cizallante, y además la ecuación que representa este comportamiento en función de la Cv y su buena correlación lineal. Los valores de viscosidad dilatante y cizallante para suspensiones de caolín con Cv = 0,13 son muy semejantes: 0,06 y 0,07 Pa·s, respectivamente; pero a concentraciones altas, como Cv = 0,20, los valores de viscosidad dilatante y cizallante son bastante disímiles: 4,39 y 0,9 Pa·s, respectivamente. Es decir, la viscosidad debida a esfuerzos normales es 488 % mayor que la viscosidad debida a esfuerzos cizallantes, datos nunca antes reportados, por lo menos en la literatura consultada por el autor.

Debido a que la viscosidad dilatante posee casi 5 veces el valor de la viscosidad cizallante, este fenómeno debería ser visible, lo cual se observa en la Figura 11, cuando una suspensión de caolín con Cv = 0,20 es expulsada por una jeringa. En dicha figura se muestra el cambio de volumen que aparece exactamente cuando la suspensión abandona la punta de la jeringa, lo cual es característico de algunos fluidos no newtonianos.

 

4. Conclusiones

Las conclusiones más relevantes del presente trabajo son las siguientes:

Se determinó un nuevo método para medir la primera diferencia de esfuerzos normales (N1) en suspensiones concentradas de caolín, los cuales aparecen debido a la existencia de interacciones entre las partículas de caolín que crean desplazamientos de las mismas en dirección normal a la cizalla.

A medida que crece el número de partículas colisionantes, aumentan los desplazamientos en dirección normal al flujo, por esta razón el valor de la N1, y por lo tanto de la viscosidad dilatante, es dependiente de la Cv.

Los valores de viscosidad dilatante se pueden modelar sobre la parte lineal a tasas de cizalladura superiores a 1 s ^{- 1}, para cada Cv estudiado con una estructura de ley de potencia, e incluso se puede obtener una generalización de estas ecuaciones en función de la Cv para los parámetros K_D y n*.

Existe una relación a la octava potencia entre el valor de K_D y la Cv para la suspensión de caolín en cuestión

El estudio reológico de este tipo de suspensiones se puede realizar mediante una nueva medida reométrica: la viscosidad dilatante, la cual es función de la tasa de cizalladura, lo cual se puede explicar debido a que las partículas se ordenan para su flujo, no sólo bajo la influencia del esfuerzo cizallante sino también en función de las interacciones en dirección normal entre las partículas, lo cual es coherente con la aparición de los esfuerzos normales.

En esta investigación se encuentra que para una mejor comprensión del escenario de deformación de una suspensión de caolín, la consideración de los esfuerzos normales, además de los clásicos de cizalladura, es imprescindible, pues el valor de la viscosidad dilatante es alrededor de 5 veces mayor que el valor de la viscosidad cizallante para suspensiones con Cv = 0,20.

 

Agradecimientos

Los autores expresan sus agradec]imientos a COLCIENCIAS por la financiación del proyecto con código 1118-479-22017 y a la Universidad Nacional de Colombia sede Medellín.

 

Referencias

[1] Greenwood, R., Lapcikova, B., Surýnek, M., Walters, K. and Lapcik, L., The zeta potential of kaolin suspensions measured by electrophoresis and electroacoustics. Chem. Pap. 61(2), pp. 83-92, 2007.         [ Links ]

[2] Bartolomé, J., El Caolín: composición, estructura, génesis y aplicaciones. Boletín de la Sociedad Española de Cerámica y Vidrio. 36 (1), pp. 7-19, 1997.         [ Links ]

[3] Teh, E., Leong, Y., Lui, Y., Fourie, A. and Fahey, M., Differences in the rheology and surface chemistry of kaolin clay slurries: The source of the variations. Chem. Eng. Sci. 64, pp. 3817-3825, 2009.         [ Links ]

[4] Murray, H., Traditional and new applications for kaolin, smectite and palygorskite: a general review. Applied Clay Science. 17, pp. 207-221, 2000.         [ Links ]

[5] Monzo, M., Martínez, A. y Enrique, J., Estudio de las propiedades reológicas de pastas cerámicas para atomización. Bol. Soc. Esp. Ceram. Vidr. Vol. 18 (4). pp. 239-241, 1979.         [ Links ]

[6] Horri, B., Ranganathan, P., Selomulya, C. and Wang, H., A new empirical viscosity model for ceramic suspensions. Chemical Engineering Science 66, pp. 2798-2806, 2011.         [ Links ]

[7] Johnson, S., Russell, A. and Scales, P., Volume fraction effects in shear rheology and electroacoustic studies of concentrated alumina and kaolin suspensions. Colloids Surf. A 141, pp. 119-130, 1998.         [ Links ]

[8] Nuntiya, A. and Prasanphan, S., The rheological behavior of kaolin suspensions. Chiang Mai J. Sci. 33(3), pp. 271 - 281, 2006.         [ Links ]

[9] Yuan, J. and Murray, H., The importance of cristal mosphology on the viscosity of concentrated suspensions of kaolins. Appl. Clay Sci. 12, pp. 209-219, 1997.         [ Links ]

[10] Brady, J. and Vicic, M., Normal stresses in colloidal dispersions. J. Rheol. 39(3), pp. 545-566, 1995.         [ Links ]

[11] Zarraga, I., Hill, D. and Leighton, D., Normal stresses and free surface deformation in concentrated suspensions of non-colloidal spheres in a viscoelastic fluid. J. Rheol. 45(5), pp. 1065-1084, 2001.         [ Links ]

[12] Mall-Gleissle, S., Gleissle, W., Mckinley, G., and Buggisch, H., The normal stress behavior of suspensions with viscoelastic matrix fluids. Rheol. Acta 41, pp. 61-76, 2002.         [ Links ]

[13] Boyer, F., Pouliquen, O. and Guazzelli, É., Dense suspensions in rotating flows: normal stresses and particle migration. Under consideration for publication in J. Fluid Mech. pp. 1-18, 2010.         [ Links ]

[14] Garland, S., Gauthier, G., Martin, J. and Morris, J., Normal stress measurements in sheared non-Brownian suspensions. J. Rheol. 57(1), pp. 71-88, 2013.         [ Links ]

[15] Morris, J., A review of microstructure in concentrated suspensions and its implications for rheology and bulk flow. Rheol Acta 48, pp. 909-923, 2009.         [ Links ]

[16] Macosko, C., Rheology. Principes, Measurements and Applications. Advances in Interfacial Engineering Series . Wiley-VCH. New York, 68-77, pp. 135-142, 1994.         [ Links ]

[17] Barnes, H., Hutton, J. and Walters, K., An Introduction to Rheology. Rheology Series, 3. Elsevier Science Publishers B.V. The Netherlands, pp. 55-66, 1989.         [ Links ]

[18] Chhabra, R. and Richardson, J., Non-Newtonian Flow and Applied Rheology. Engineering Applications. Second Edition. Elsevier. pp. 34-38, 2008.         [ Links ]

[19] Larson, R., The Structure and Rheology of Complex Fluids. Oxford University Press, Inc. New York, Oxford, 11, pp. 164-166, 1999.         [ Links ]

[20] Bird, B. and Wiest, J., Constitutive Equations for Polymeric Liquids. Annu. Rev. Fluid Mech. 27, pp. 169-93, 1995.         [ Links ]

[21] Malkin, A., Non-Newtonian viscosity in steady-state shear flows. Review. Journal of Non-Newtonian Fluid Mechanics. 192, pp. 48-65, 2013.         [ Links ]

[22] Barnes, H., A review of the rheology of filled viscoelastic systems. Rheology Reviews. pp.1-36, 2003.         [ Links ]

[23] Amorós, J., Beltrán, V., Sanz, V. y Jarque, J., Electrokinetic and rheological properties of highly concentrated kaolin dispersions: Influence of particle volume fraction and dispersant concentration. Appl. Clay Sci. 49, pp. 33-43, 2010.         [ Links ]

[24] Moreno, R., Reología de suspensiones cerámicas. Biblioteca de Ciencias 17. Consejo Superior de Investigaciones Científicas. Madrid, pp. 39-49, 2005.         [ Links ]

[25] Linares, J., Huertas, F., y Barahona, E., Reología de suspensiones de minerales de arcilla. Ciencia y Técnica. Noviembre - diciembre, pp. 635-643, 1969.         [ Links ]

[26] Kolli, V., Pollauf, E. and Francis, M., Transcient normal stress response in a concentrated suspension of spherical particles. J. Rheol. 46(1), pp. 321-334, 2002.         [ Links ]

[27] Morris, J. and Boulay, F., Curvilinear flows of noncolloidal suspensions: The role of normal stresses. J. Rheol. 43(5), pp. 1213-1237, 1999.         [ Links ]

[28] Tadros, T., Rheology of dispersions. principles and applications. Wiley-VCH Verlag Gmbh & Co. KGaA. Weinheim. Chapter 5, 2010.         [ Links ]

[29] Mezger, T., The Rheology Handbook. For users of rotational and oscillatory rheometers. 2nd revised edition Coatings Compendia, 33-35, 53-58, 2006.         [ Links ]

[30] Tanner, R., Engineering Rheology. Oxford Universiy Press. Second Edition. Oxford Engineering Science Series. USA, Chapter 1, 2000.         [ Links ]

[31] Quemada, D., Rheological modelling of complex fluids. I. The concept of effective volume fraction. The European Physical Journal. Applied Physics. 1, pp. 119-127, 1998.         [ Links ]

[32] Murray, H., Applied clay mineralogy. Occurrences, processing and application of kaolins, bentonites, palygorskite-sepiolite and common clays. Developments in clay science, 2. First edition, Elsevier. 87, 2007.         [ Links ]

[33] Torres, J. y Mejía, R., Influencia de la composición mineralógica de los caolines sobre el desempeño de morteros adicionados con MK. Dyna, Año 74(153), pp. 61-67, 2007.         [ Links ]

[34] Bergaya, F., Theng, B and Lagaly, G., "Handbook of Clay Science". Developments in Clay Science, Vol 1. Colloid Clay Science. Elsevier Ltd. Chapter 5, 2006.         [ Links ]