http://dx.doi.org/10.15446/dyna.v81n184.37303

Proactive local search based on FDC

Búsqueda local proactiva basada en FDC

 

Mailyn Moreno-Espino ^a & Alejandro Rosete-Suárez ^b

^a MSc. Instituto Politécnico "José Antonio Echeverría" (CUJAE), La Habana, Cuba, my@ceis.cujae.edu.cu
^b Dr., Instituto Politécnico "José Antonio Echeverría" (CUJAE), La Habana, Cuba, rosete@ceis.cujae.edu.cu

 

Received: February 28^th, 2013. Received in revised form: October 17^th, 2013. Accepted: November 27^th, 2013.

 

---

Abstract
This paper introduces a proactive version of Hill Climbing (or Local Search). It is based on the identification of the best neighborhood through the repeated application of mutations and the evaluation of theses neighborhood by using FDC (Fitness Distance Correlation). The best neighborhood is used during a time window, and then the analysis is repeated. An experimental study was conducted in 28 functions on binary strings. The proposed algorithm achieves good performance compared to other metaheuristics (Evolutionary Algorithms, Great Deluge Algorithm, Threshold Accepting, and RRT).

Keywords: Metaheuristics, Agents, Proactive Behavior, Variable Neighborhood Search, FDC.

Resumen
En este trabajo se presenta ECE-MP-FDC, una variante proactiva del algoritmo de búsqueda Escalador de Colinas (o Búsqueda Local). El algoritmo identifica la mejor estructura de vecindad a través de la aplicación repetida del operador de mutación, y evalúa la conveniencia de cada una usando la métrica FDC (Fitness Distance Correlation). La mejor estructura de vecindad se usa durante una ventana de tiempo, luego de la cual se repite el análisis. Se presenta un estudio experimental en 28 funciones sobre cadenas binarias de 100 bits con distintos grados de dificultad. La variante proactiva del Escalador de Colinas basada en FDC logra resultados similares o mejores que otras metaheurísticas (Algoritmos Evolutivos, Algoritmo del Gran Diluvio, Aceptación por Umbral, RRT).

Palabras Clave: Metaheurísticas, Agentes, Proactividad, Búsqueda con Vecindad Variable, FDC.

---

 

1. Introducción

Las metaheurísticas [1] son métodos de optimización muy populares, debido su flexibilidad para resolver problemas complejos, con muchas aplicaciones exitosas en distintas ramas de la ciencia y la ingeniería; como el diseño de estructuras y motores, la minería de datos y la planificación de tareas [2, 3] . Algunas metaheurísticas conocidas son los Escaladores de Colinas (Búsqueda Local), los Algoritmos Genéticos y el Recocido Simulado, etc. [1, 4] .

Es un problema abierto saber cuándo conviene usar cada metaheurística. Incluso, el Teorema No Free Lunch (NFL) establece que todas las metaheurísticas se comportan igual en promedio [5] , y si una metaheurística es mejor que otra para unos problemas, debe esperarse que existan otros donde ocurra lo contrario. Para tratar de comprender cómo funcionan las metaheurísticas se han definido varias métricas para caracterizar los problemas [6] , siendo FDC (Fitness Distance Correlation) [7] una de las más conocidas.

Este trabajo presenta ECE-MP-FDC, una variante proactiva de la Búsqueda Local inspirada en el paradigma de los agentes inteligentes [8] , que evalúa diferentes variantes de vecindad utilizando FDC para guiar mejor la búsqueda.

El trabajo comienza (sección 2) con los conceptos fundamentales de las metaheurísticas y los agentes, relevantes para esta propuesta. La sección 3 introduce el algoritmo ECE-MP-FDC. La sección 4 muestra un estudio experimental en 28 funciones sobre cadenas binarias de 100 bits que muestra que ECE-MP-FDC tiene un comportamiento similar o superior que muchas otras metaheurísticas en estos problemas.

 

2. Metaheurísticas y agentes

2.1. Metaheurísticas
Las metaheurísticas son bien conocidas como métodos aproximados de optimización de funciones en dominios o espacios de soluciones grandes, que no garantizan encontrar el óptimo, pero que usualmente obtienen soluciones buenas en un tiempo razonable [1] . En los años recientes han surgido muchas nuevas variantes y combinaciones de metaheurísticas [1, 4] .

La característica esencial de las metaheurísticas es no restringir el problema a tratar. Solo necesitan que se defina una forma de evaluar las soluciones, y unos operadores para construir una solución inicial y para transformar unas soluciones en otras nuevas.

Hay dos grandes ramas en que pueden dividirse las metaheurísticas: las P-Metaheurísticas (basadas en una población de soluciones) y las S-Metaheurísticas (basadas en un punto o una sola solución) [1] . Todas las S-Metaheurísticas se basan en mantener una solución como referencia, a partir de la cual se generan nuevas soluciones aplicando un cambio (operador de mutación [1] ). Al final, se devuelve la mejor solución encontrada durante la ejecución completa de la metaheurística. Las S-Metaheurísticas incluyen a la búsqueda local [1] , el recocido simulado, la búsqueda con vecindad variable (VNS: Variable Neighborhood Search), etc [1, 4] . Todas se derivan de la Búsqueda Local según Talbi ( [1] , p. 24).

La Búsqueda Local cambia su referencia sólo cuando se genera una nueva solución que no sea peor que la referencia. Su deficiencia fundamental es que queda atrapada en un óptimo local si la referencia es mejor que las soluciones vecinas (generables por mutación). Para resolver esto, otras S-Metaheurísticas aceptan soluciones peores que la referencia. Algunos ejemplos son: aceptar soluciones con una diferencia respeto a la referencia que no exceda cierto umbral (aceptación por umbral), aceptar soluciones con una diferencia respeto a la mejor encontrada que no exceda cierto umbral (RRT), aceptar soluciones que estén por encima de cierto parámetro (algoritmo del gran diluvio) [1] .

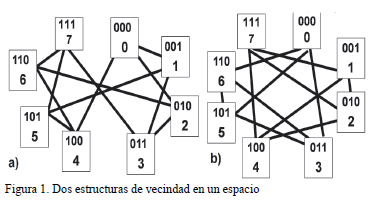
Es importante comentar que la existencia de óptimos locales para la Búsqueda Local depende de las vecindades que definan los operadores [7] . La figura 1 muestra dos estructuras de vecindad (paisajes o "landscapes" [1, 7] ) diferentes en el mismo espacio de búsqueda (cadenas 3 bits).

La figura 1a) muestra la estructura de vecindad definida por el operador de cambiar un bit, mientras que la figura 1b) muestra la estructura usando el operador de cambiar dos bits. En la figura 1b) la solución 110 con valor 6 es un óptimo local, pero no lo es en la figura 1a).

Una alternativa diferente a la aceptación de soluciones peores para poder salir de óptimos locales, es modificar la estructura del espacio de búsqueda cambiando las vecindades, como lo hacen los algoritmos de VNS [1] . En estas metaheurísticas, se proveen varios operadores de vecindad, y se establece un plan para usarlas.

2.2. Cambios en las vecindades
Variando los operadores se cambian las vecindades y así el algoritmo puede salir de un óptimo local (según una vecindad) usando otra.

Con suficientes operadores, se logran buenos resultados, ya que es difícil que una solución sea la mejor en muchas estructuras de vecindades, sin ser el óptimo global.

Una variante equivalente a VNS, es la de cambiar la representación de las soluciones. Como el cambio de representación cambia las soluciones que son vecinas, el efecto es similar. Los algoritmos de Búsqueda Mórfica [9] y los Escaladores de Colinas Dinámicos [10] son ejemplos de esto. En todos los casos, la persona que ejecuta la metaheurística define un plan de cómo variar las vecindades.

2.3. Métricas de comportamiento
Desde hace muchos años, hay investigadores tratando de encontrar métricas que sirvan para entender y predecir el comportamiento de las metaheurísticas (por ejemplo [6, 7, 11] .

A la luz del Teorema NFL [5] esto es aún más importante, porque para cada metaheurística parece existir un grupo de problemas en los cuales funciona bien. De todas las métricas, la más conocida es FDC, que mide la correlación entre la distancia al óptimo de cada solución (D) y su evaluación (fitness, F). La definición de FDC según [7] se muestra en (1), donde CFD es la covarianza de F y D, mientras que SF y SD son las desviaciones estándares de F y D.

Para obtener esta métrica en un problema, se deben evaluar todas las soluciones y calcular para cada una de ellas la distancia respecto al óptimo. Cuando la correlación es cercana a -1, significa que las soluciones cercanas al óptimo, tiene mayor evaluación. Es importante notar que la métrica FDC se usa para entender la dificultad de un problema del cual se conoce el espacio de búsqueda y el óptimo. No se conoce que se haya intentado usar FDC para seleccionar una estructura de vecindad que sea más conveniente.

2.4. El paradigma de agentes
Los agentes inteligentes constituyen un paradigma que ha crecido mucho en los últimos años, considerándose como un salto evolutivo en la programación y la ingeniería de software [8] .

Un agente es un programa que está en un entorno, del cual recibe información y sobre el que puede actuar. El paradigma de agentes promueve el desarrollo de software con características novedosas como la autonomía, la proactividad y la habilidad social.

De estas características, la proactividad es una de las menos desarrolladas. Un agente es proactivo cuando actúa persiguiendo objetivos o metas, sin esperar una orden. Para lograrlo, el programa debe tener metas, y planes que les doten de la capacidad para acercase al logro de las metas.

Se han desarrollado varios modelos de metaheurísticas basados en el paradigma de agentes, por ejemplo [12-16] .

La propiedad de los agentes más estudiada es la habilidad social para intercambiar información y orientar la búsqueda.

No se han encontrado trabajos en que se le asigne a la metaheurística una meta a alcanzar y se le dote de planes para que sea proactiva. Particularmente, la decisión proactiva de cuál estructura de vecindad debe explorarse no se ha modelado desde la visión de agentes.

Debe aclararse que en los trabajos sobre el ajuste dinámico de parámetros en metaheurísticas (por ejemplo [17] ) no se han definido explícitamente las metas, ni se ha visto la evolución como un ambiente a ser observado, sobre el que las metaheurísticas actúan a través de sus parámetros, para lograr las metas. También se han usado metaheurísticas para optimizar un sistema de agentes (como en [18] , lo cual es un interés recíproco al de este trabajo.

 

3. Búsqueda proactiva con FDC

3.1. Estructura de vecindad
Entendiendo la vecindad de una solución como el conjunto de soluciones que se pueden obtener a partir de ella aplicando un operador, se puede entender como estructura de vecindad un grafo donde cada nodo es una solución y cada arco entre ellas implica la existencia de un operador que permite transitar de una a otra [7, 11] . La figura 1 mostró como la estructura de la vecindad define los óptimos locales. En consecuencia, también cambia el comportamiento de la Búsqueda Local.

Particularmente, en la figura 1 se vio el cambio en la estructura de la vecindad cuando en lugar de aplicar el operador una vez, se asumen como vecinas a aquellas relacionadas por la aplicación repetida del operador (en ese caso dos veces).

Esto puede extrapolarse a un número mayor, siendo las soluciones vecinas si están separadas por la aplicación del operador definido N veces.

Es importante aclarar que la aplicación repetida del operador solo implica un cambio en la estructura de la vecindad y no mayor cantidad de evaluaciones de la función objetivo. La aplicación repetida del operador, produce vecindades nuevas, sin necesidad de obligar al usuario a definir diferentes operadores.

No es simple ajustar el valor de N por el usuario. Más aún, este parámetro no es una meta en sí mismo, sino que es un recurso del que se puede dotar a la metaheurística para explorar el espacio de búsqueda de una manera más eficiente. Esta exploración más eficiente sí puede ser una meta a pasar a la metaheurística. Para lograr satisfacerla, la metaheurística dispone de recursos (parámetros, historia de soluciones generadas, etc) para intentar lograrlas.

La historia de la evolución es un ambiente en que la metaheurística actúa, y en el que trata de lograr encontrar la solución con el mejor valor posible en el tiempo del que dispone. En base a eso, puede ajustar proactivamente la forma de explorar para hacer la búsqueda más eficiente.

La historia de la evolución brinda información sobre las soluciones anteriormente generadas. Como las nuevas soluciones se obtienen por modificaciones (mutaciones) esto brinda información sobre la estructura de las vecindades. Con estas soluciones puede tenerse una idea aproximada sobre cómo es la zona más cercana del espacio de búsqueda. Esta información, puede servir para estimar lo que sucederá en un futuro cercano.

3.2. Evaluación de vecindades con FDC
El ambiente (historia) puede servir para analizar cuál estructura de vecindad es más conveniente, y la métrica FDC es un buen estimador de la dificultad de esta para un escalador de colinas.

La definición original de FDC exige un conocimiento total del espacio de búsqueda lo cual no es posible siempre. Sin embargo, puede obtenerse una aproximación de FDC usando una muestra del espacio de búsqueda, y se puede tomar la mejor solución de esa muestra como un pseudo-óptimo a los efectos del cálculo de FDC.

En el caso del escalador de colinas, cada nueva solución es generada a partir de la mejor solución (o de la más reciente de ellas si hay varias mejores). De esta manera, con un análisis retrospectivo de las últimas soluciones generadas, se puede obtener una serie de valores de distancia al pseudo-óptimo según el orden en que fueron generadas. Como también se cuenta con el valor de evaluación de estas soluciones se puede calcular el valor de FDC.

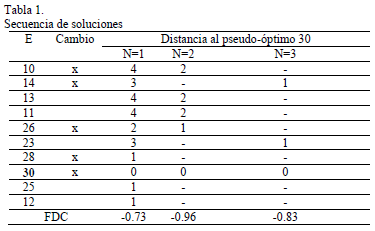
La Tabla 1 muestra un ejemplo de una secuencia de soluciones generadas por un escalador de colinas. La columna E muestra la evaluación obtenida por cada solución. Como el valor más alto es 30 se usa como pseudo-óptimo para el cálculo de FDC. La columna Cambio muestra una "x" cuando el escalador de colinas modificó la referencia. Así, las soluciones generadas sin cambio de referencia están a distancia 1 de ella.

La columna N=1 muestra la distancia en cantidad de veces que hay que aplicar el operador que se esté usando entre cada solución y el pseudo-óptimo. La soluciones 25 y 12 fueron generadas a partir de 30, y están a distancia 1. La solución 28 también está a distancia 1 de 30 porque 30 se generó a partir de 28. Transitivamente, como 28 se generó a partir de 26, entonces 26 está a distancia 1 de 28, y a distancia 2 de 30. De igual modo, 14 está a distancia 1 de 26, a 2 de 28 y a 3 de 30. Como 10, 13 y 11 están a distancia 1 de 14, están a distancia 4 de 30. Con estos 10 pares de datos se puede calcular el valor de FDC (fila FDC).

Con esta misma muestra, se puede calcular FDC para el operador doble (columna N=2, aplicación dos veces del operador básico). Las soluciones que están a una distancia par del óptimo en la columna N=1 pueden alcanzar el óptimo en la mitad de los pasos. Las que están a distancia impar no pueden llegar al óptimo, y no se sabe la distancia para ellos (indicado con "-" en la Tabla 1). Con esta serie de 5 pares de datos se puede calcular igualmente el valor de FDC para la estructura de vecindad con N=2. De manera análoga puede obtenerse para N=3.

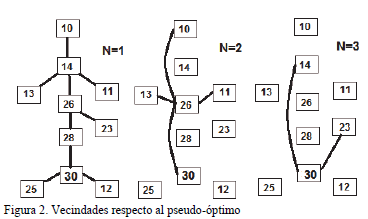
Estas estructuras de vecindad para distintos valores de N se muestran en la figura 2. Según N crece aparecen menos datos para estimar FDC para la estructura de vecindad definida para ese N. Por ejemplo, como no hay ningún valor de 5 en la columna N=1, no es posible estimarlo. La Tabla 1 mostró un ejemplo de soluciones generadas en una ventana de tiempo TW pequeña (TW=10 soluciones), lo cual hace imposible estimar FDC para N=5 o más. Si la ventana de tiempo fuera mayor, entonces sí podría hacerse.

3.3. Selección proactiva de la vecindad
Analizando los valores de FDC en la Tabla 1 y considerando que el Escalador de Colinas funciona bien cuando FDC está cerca de -1, puede verse que N=2 es el que proporciona una estructura de vecindad más favorable con FDC_N=2 = - 0.96. En base a esto, durante una próxima ventana de tiempo, la soluciones deberían generarse aplicando dos veces el operador básico de mutación (N=2), y por tanto explotando la estructura de vecindad que parece más conveniente. En cada paso se escoge el valor de N que implica un mejor FDC.

Esta decisión muestra cómo puede delegarse en la metaheurística la meta de explorar la vecindad de una manera más eficiente, para lo cual cuenta con los resultados de las últimas soluciones generadas que funcionan como un ambiente que puede ser analizado y utilizado proactivamente para lograr mejores resultados.

Es importante también analizar lo que ocurre cuando se generan soluciones con N=2. Siguiendo un razonamiento similar al que se hizo en la sección anterior respecto a la Tabla 1, ahora se pueden estimar los valores de FDC para N=2, y sus múltiplos. Por ejemplo, después de una ventana de tiempo usando N=2, se tiene un nuevo pseudo-óptimo. Luego, las soluciones que sirvieron para generar ese pseudo-óptimo y las que se generaron directamente a partir de él estarían a distancia 1 con N=2. Con esos valores a distancia 1 usando N=2 se puede recalcular FDC_N=2. El análisis que se hizo para distancia 2 en la Tabla 1 ahora se estaría refiriendo a N=4, y así sucesivamente.

Al pasar una ventana de tiempo, se puede recalcular FDC para diferentes valores de N, aunque no es posible hacerlo para todos en cada ventana de tiempo. Para mantener disponibles el máximo de estructuras de vecindades en cada momento, se mantiene una lista global de valores de FDC para cada N. Cuando pasa una ventana de tiempo TW, los nuevos valores de FDC calculados actualizan los anteriores, promediando el valor anterior y el nuevo calculado, y con esto se actualiza la lista de valores de FDC. Luego de esta actualización, se utiliza como operador de vecindad la aplicación de N repeticiones del operador de mutación básico.

3.4. Idea general del algoritmo
El algoritmo ECE-MP-FDC (Escalador de Colinas, con Mutación Proactiva basado en FDC) se describe a continuación.

Algoritmo ECE-MP-FDC

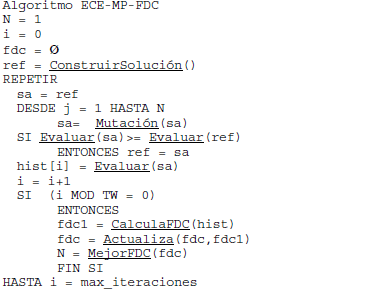
En el pseudocódigo anterior, los métodos Evaluar, ConstruirSolución y Mutación son métodos dependientes del problema que se encargan de evaluar, construir una solución inicial y de realizarle un cambio, respectivamente. El método CalculaFDC devuelve un conjunto de valores de FDC para distintos valores de N considerando solo las últimas TW soluciones generadas. Por su parte, Actualiza promedia los valores de FDC de dos conjuntos de estos valores. MejorFDC devuelve el valor de N correspondiente con el valor de FDC más cercano a -1. Todos estos métodos operan según la descripción dada en las secciones anteriores. El operador "mod" obtiene el resto de la división. En este caso se usa para saber si ha pasado la ventana de tiempo TW y hay que calcular los valores de FDC para actualizar proactivamente N.

La variable "hist" almacena la lista de soluciones generadas. La variable i controla la cantidad de soluciones generadas, y max_iteraciones es un parámetro que detiene la búsqueda, con una interpretación similar a las demás metaheurísticas [1] . La variable "ref" almacena la mejor solución generada hasta ese momento, mientras que "sa" contiene la solución generada en cada iteración. La variable N, es la que permite modificar la estructura de vecindad explorada en cada ventana de tiempo TW.

El paso de mayor complejidad computacional es el método CalculaFDC con complejidad Q(TW), para cada valor de N, ya que al calcularse FDC según (1), se recorren los elementos de la ventana para calcular la covarianza y las desviaciones.

 

4. Resultados experimentales

4.1. Funciones de bloques
Debido a la gran cantidad de problemas posibles, es necesario acotar siempre el marco experimental a un grupo de problemas que permita validar el interés de la propuesta. En este trabajo, se presentan los resultados para 28 funciones basadas en bloques sobre cadenas binaras, que han sido ampliamente estudiadas [7, 12, 19, 20] .

En las funciones basadas en bloques, se toman un grupo de bits consecutivos (bloque), se cuenta la cantidad de "1" presentes en el bloque, y a esta cantidad se le aplican distintas funciones base con distintos grados de dificultad, sumando luego el valor obtenido para cada bloque.

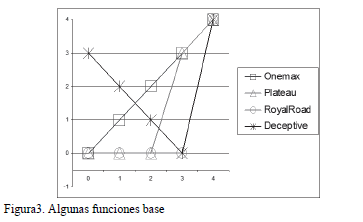
En la figura 3 se muestran algunos ejemplos de funciones base (de tamaño 4) que dada la cantidad de bits correctos (con valor 1) devuelven distintos valores. Es usual trabajar con problemas definidos sobre cadenas binarias de 100 bits, con 25 bloques de longitud 4 cada uno, y con un solo óptimo ubicado en la solución donde todos los bits son iguales a 1, con evaluación de 100. El espacio de soluciones es grande (2¹⁰⁰= 1,27 * 10³⁰) y al haber un solo óptimo global conocido (los 100 bits en 1) se puede estudiar el comportamiento de los algoritmos.

Las funciones base más usadas aparecen en la figura 3. Onemax, Plateau y Royal Road tienen un nivel de dificultad creciente, mientras Deceptive es difícil ya que las soluciones más cercanas en bits al óptimo tienen un peor valor de la función objetivo, y esto lleva al escalador de colinas a la solución con ningún bit en 1 que está muy lejana del óptimo global. Estas funciones base tienen algunos aspectos en común como es que solo recibe el máximo valor de 4 el bloque 1111 con los 4 bits correctos, mientras que para el resto de las cantidades posibles de bits correctos (0, 1, 2, o 3) la función vale 0, 1, 2 o 3.

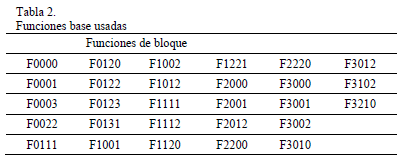
Como hay 4 valores posibles para cada una de las 4 cantidades posibles de bits correctos existen 256=44 funciones base con estas características. Con estas características se generaron 24 funciones aleatoriamente, dentro de las 256 posibles, que junto con las 4 de la figura 3 conforman el marco experimental de 28 funciones de la Tabla 2. Cada función Fwxyz es la función base que asigna el valor "w" cuando hay 0 bits correctos, "x" cuando hay 1 , "y" cuando hay 2, y "z" cuando hay 3 bits correctos. F0123, F0003, F0000 y F3210 se corresponden, respectivamente, con las funciones Onemax, Plateau, Royalroad y Deceptive.

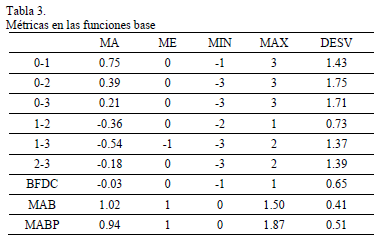
La Tabla 3 resume la dificultad de las 28 funciones, mostrando la media aritmética (MA), la mediana (ME), el mínimo (MIN), el máximo (MAX) y la desviación estándar (DESV) de varias métricas medidas en cada función base.

La métrica BFDC calcula el valor de la correlación entre la distancia en bits respecto al óptimo del bloque (1111) y la evaluación que recibe. MAB mide el promedio de los valores asignados por la función a cada cantidad de bits correctos. MABP es similar a MAB excepto en que es un promedio ponderado, teniendo en cuenta la cantidad de cadenas de 4 bits que tienen 0, 1, 2 o 3 bits iguales a 1111, que son 1, 4, 6 y 4 respectivamente. Las columnas 0-1, 0-2, 0-3, 1-2, 1-3 y 2-3, muestran la diferencia entre los valores asignados por la función a las cadenas con esas cantidades de bits. Por ejemplo, en F3210 (Deceptive) la diferencia entre el valor que le da la función a las soluciones con 1 bit correcto (2) respecto al valor para 3 bits correctos (0) es 2= 2-0.

La Tabla 3 muestra que las funciones escogidas tienen una variedad representativa, con distintos grados de dificultad. Por ejemplo, BFDC para F3210 (Deceptive) vale 1 y debe ser más difícil que F0123 (Onemax) en que BFDC vale -1.

4.2. Metaheurísticas a comparar
En los experimentos se compara el algoritmo propuesto con cuatro S-Metaheurísticas [1] (RRT, aceptación por umbral, algoritmo del gran diluvio y un escalador de colinas), y cuatro P-Metaheurísticas [1] (algoritmos evolutivos).

En todas se construye una solución inicial asignando a cada uno de los 100 bits de la cadena un valor binario aleatorio de 0 o 1.

Como operador de mutación se utiliza el cambio de un bit, escogido aleatoriamente entre los 100 posibles. En los Algoritmos Genéticos (AG) y las Estrategias Evolutivas (EE) se usó el reemplazo generacional [1] , seleccionando la nueva generación entre los M mejores entre las P nuevas soluciones (hijos) y las M anteriores (padres). En los AG se usa el cruzamiento uniforme [1] .

Los otros parámetros de cada una de las metaheurísticas y el identificador usado para nombrar a cada una aparecen en la Tabla 4.

Estos parámetros fueron fijados partiendo de las recomendaciones usuales [1, 17] y ajustados luego, usándose los parámetros que mejores resultados dieron.

En ECE-MP-FDC se usará una ventana de tiempo TW=200. Se experimentó previamente con valores de TW de 50, 100, 200 y 300. El valor de 200 fue el que obtuvo mayor promedio, aunque las diferencias no fueron significativas según la prueba de Kruskal-Wallis en cada función con 30 repeticiones, ni en la prueba de Friedman con los promedios en cada función. Se comienza usando el operador de mutación básico, es decir N=1 (cambiar un bit).

4.3. Resultados
Como el grupo de 28 funciones base no había sido cubierto en trabajos previos, se realizaron todos los experimentos. En cada uno de los 28 problemas, las metaheurísticas se ejecutaron 30 veces hasta alcanzar 10000 evaluaciones. Se registró la mejor solución encontrada en cada una de las ejecuciones, y luego se calculó la media aritmética por cada función y metaheurística.

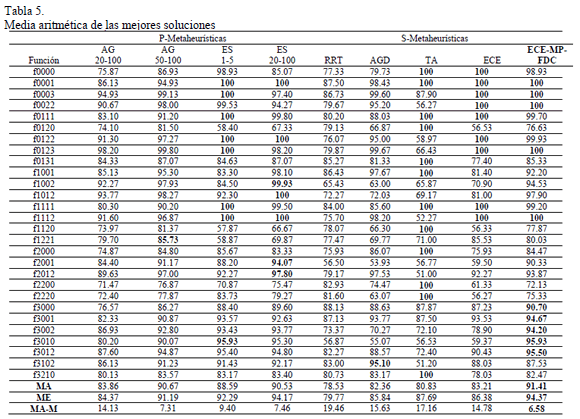
La Tabla 5 muestra estos resultados. Se incluyen las filas correspondientes a la media aritmética (MA) y mediana (ME), entre todas las funciones. La última fila MA-M muestra la media aritmética de la diferencia de los resultados respecto a la metaheurística que mejor se comporta en cada función.

La Tabla 6 muestra el resultado de la cantidad de veces que ECE-MP-FDC es inferior, igual o superior que cada una de las demás metaheurísticas realizando la prueba no pareada de Wilcoxon entre las 30 repeticiones respectivas. La columna "Total" acumula estos valores y permite tener una visión global de ECE-MP-FDC respecto a las demás metaheurísticas.

La última fila (WP-MA) muestra el resultado de la prueba de Wilcoxon pareada entre las medias mostradas en la Tabla 5, indicado si ECE-MP-FDC es inferior, igual o superior que cada una de las demás metaheurísticas en la prueba pareada de las medias. La importancia de usar la prueba de Wilcoxon ha sido defendida en [21] . Se trabajó con nivel de significación de 0.05.

4.4. Discusión
A partir de los resultados, puede observarse que ECE-MP-FDC se comporta bien en general, teniendo un resultado global similar o mejor que las P-Metaheurísticas, y superando generalmente a las otras S-Metaheurísticas.

En la Tabla 5 se ve que ECE-MP-FDC tiene el mayor valor de media aritmética (MA) y mediana (ME); y tiene, como promedio, una menor distancia al algoritmo mejor en cada caso (MA-M).

En la prueba pareada sobre los 28 promedios mostrada en la fila WP-MA de la Tabla 6 se puede ver que el algoritmo propuesto supera a 4 de las metaheurísticas con las que se compara, mientras que queda igual con las demás, y ninguna la supera en el comportamiento global.

También se puede ver que en la comparación directa de ECE-MP-FDC contra las demás metaheurísticas (tres primeras filas de la Tabla 6) usando la prueba de Wilcoxon en cada función, el algoritmo propuesto siempre es más veces superior que inferior, excepto con EE-20-100 con la que queda empatada. Esto muestra un resultado general competitivo, al menos en este tipo de funciones de bloques.

Para entender las características de los problemas que hacen más aconsejable el uso de uno u otra metaheurística se hizo un análisis de las características de las funciones donde cada metaheurística obtiene buenos resultados (primer o segundo lugar).

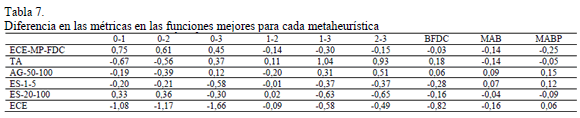
La Tabla 7 se muestra la diferencia entre la media aritmética de las métricas en las 28 funciones comparada con esa misma métrica medida en las funciones donde cada metaheurística trabaja bien. Se observan algunas características de las funciones que parecen favorecer a cada metaheurística.

Puede verse que BFDC influye menos en ECE-MP-FDC y en AG-50-100 que en las demás. Este resultado puede entenderse como que estos algoritmos son menos sensibles a esta medida debido a su forma de trabajo. Se puede ver que TA funciona mejor en funciones con BFDC más alto, mientras que ECE se beneficia de valores bajos de FDC, como era esperado.

ECE-MP-FDC se comporta mejor en funciones con altos valores de 0-1, 0-2 y 0-3, mientras que con TA pasa lo contrario. Para la métricas 1-3 y 2-3 ocurre lo contrario, favoreciendo a TA y en menor medida a AG y afectando a ECE-MP-FDC.

 

5. CONCLUSIONES

En este trabajo se presentó ECE-MP-FDC, una variante proactiva del Escalador de Colinas que revisa varias estructuras de vecindad y usa aquella donde la métrica FDC es más conveniente por su cercanía a -1.

ECE-MP-FDC se ha comparado con varias metaheurísticas en un grupo amplio de 28 funciones sobre cadenas de 100 bits, obteniendo buenos resultados.

También se han identificado algunas métricas que caracterizan a las funciones donde cada metaheurística tiene mejores resultados.

En el futuro se pretende estudiar este mismo enfoque con otras métricas y otras metaheurísticas.

 

Referencias

[1] Talbi, E.G., Metaheuristics: From Design to Implementation, John Wiley & Sons, 2009.         [ Links ]

[2] Doerner, K.F., Gendreau, M., Greistorfer, P., Gutjahr, W.J., Hartl, R.F., et al., Metaheuristics: Progress in Complex Systems Optimization, Springer Science+Business Media, 2007.         [ Links ]

[3] Moreno, J., Rivera, J.C., Ceballos, Y.F. Agrupamiento homogéneo de elementos con múltiples atributos mediante algoritmos genéticos, Dyna, 78 (165), pp. 246-254, 2010.         [ Links ]

[4] Blum, C., Roli, A. Metaheuristics in Combinatorial Optimization: Overview and Conceptual Comparison, ACM Computing Surveys, 35, pp. 268-308, 2003.         [ Links ]

[5] Wolpert, D., Macready, W. No Free Lunch Theorems for Optimization, IEEE Transactions on Evolutionary Computation, 1, pp. 67-82, 1996.         [ Links ]

[6] Naudts, B., Kallel, L. A Comparison of Predictive Measures of Problem Difficulty in Evolutionary Algorithms, IEEE Transactions on Evolutionary Computation, 4, pp. 1-15, 2000.         [ Links ]

[7] Jones, T., Forrest, S. Fitness distance correlation as a measure of problem difficulty for genetic algorithms. Memoria 6th International Conference on Genetic Algorithms. Pittsburgh, USA, pp. 184-192, julio 1995.         [ Links ]

[8] Wooldridge, M., An Introduction to MultiAgent Systems, John Wiley & Sons, 2009.         [ Links ]

[9] Kingdon, J., Dekker, L. Morphic Search Strategies. Memoria First IEEE International Conference on Evolutionary Computation. Nagoya, Japan, pp. 837-841, 1996.         [ Links ]

[10] Yuret, D., Maza, M.d.l. Dynamic Hill Climbing: Overcoming the limitations of optimization techniques. Memoria Second Turkish Symposium on Artificial Intelligence and Neural Networks. pp. 208-212, 1993.         [ Links ]

[11] Tomassini, M., Vanneschi, L., Collard, P., Clergue, M. A Study of Fitness Distance Correlation as a Difficulty Measure in Genetic Programming, Evolutionary Computation, 13, pp. 213-239, 2005.         [ Links ]

[12] González, J., Cruz, C., Amo, I.d., Pelta, D. An adaptive multiagent strategy for solving combinatorial dynamic optimization problems. Memoria Nature Inspired Cooperative Strategies for Optimization. Cluj-Napoca, Romania, pp. 41-55, Octubre 2012.         [ Links ]

[13] Aydin, M. Coordinating metaheuristic agents with swarm intelligence, Journal of Intelligent Manufacturing, 23, pp. 991-999, 2012.         [ Links ]

[14] Lepagnot, J., Nakib, A., Oulhadj, H., Siarry, P. A New multiagent Algorithm for Dynamic Continuous optimization, International Journal of Applied Metaheuristic Computing, 1, pp. 16-38, 2010.         [ Links ]

[15] Malek, R. Collaboration of Metaheuristics Algorithms through a Multi-Agent System, En: Holonic and Multi-Agent Systems for Manufacturing: 4th International Conference on Industrial Applications of Holonic and Multi-Agent Systems (Eds. V. Marik, T. Strasser, and A. Zoitl), Lecture Notes in Artificial Intelligence, Proc. Vol. 5696, Springer, pp. 72-81, 2009.         [ Links ]

[16] Li, B., Yu, H., Shen, Z., Miao, C. Evolutionary Organizational Search. Memoria 8th Int. Conf. on Autonomous Agents and Multiagent Systems. Budapest, Hungary, pp. 1329-1330, mayo 2009.         [ Links ]

[17] Birattari, M., Tuning Metaheuristics: A Machine Learning Perspective, Springer, 2009.         [ Links ]

[18] Gómez-Sanz, J., Botía, J., Serrano, E., Pavón, J. Testing and Debugging of MAS Interactions with INGENIAS, En: Agent-Oriented Software Engineering IX (Eds. M. Luck and J. Gomez-Sanz), Lecture Notes in Computer Science, Proc. Vol. 5386, Springer Berlin Heidelberg, pp. 199-212, 2009.         [ Links ]

[19] Wang, H., Wang, D., Yang, S. A memetic algorithm with adaptive hill climbing strategy for dynamic optimization problems, Soft Computing- A Fusion of Foundations, Methodologies and Applications, 13, pp. 763-780, 2009.         [ Links ]

[20] Cruz, C., González, J.R., Pelta, D.A. Optimization in dynamic environments: a survey on problems, methods and measures, Soft Computing, 15, pp. 1427-1448, 2011.         [ Links ]

[21] García, S., Molina, D., Lozano, M., Herrera, F. A study on the use of non-parametric tests for analyzing the evolutionary algorithms' behaviour: a case study, Journal of Heuristics, 15, pp. 617-644, 2009.         [ Links ]