Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.185 Medellín maio/jun. 2014
https://doi.org/10.15446/dyna.v81n185.34867
http://dx.doi.org/10.15446/dyna.v81n185.34867
Static and dynamic task mapping onto network on chip multiprocessors
Mapeo estático y dinámico de tareas en sistemas multiprocesador, basados en redes en circuito integrado
Freddy Bolaños-Martínez a, José Edison Aedo b & Fredy Rivera-Vélez b
a Facultad de Minas, Universidad Nacional de Colombia, Colombia. fbolanosm@unal.edu.co
b Facultad de Ingeniería, Universidad de Antioquia, Colombia. {farivera, joseaedo}@udea.edu.co
Received: November 16th, 2012. Received in revised form: April 2th, 2014. Accepted: April 10th, 2014.
Abstract
Due to its scalability and flexibility, Network-on-Chip (NoC) is a growing and promising communication paradigm for Multiprocessor System-on-Chip (MPSoC) design. As the manufacturing process scales down to the deep submicron domain and the complexity of the system increases, fault-tolerant design strategies are gaining increased relevance. This paper exhibits the use of a Population-Based Incremental Learning (PBIL) algorithm aimed at finding the best mapping solutions at design time, as well as to finding the optimal remapping solution, in presence of single-node failures on the NoC. The optimization objectives in both cases are the application completion time and the network's peak bandwidth. A deterministic XY routing algorithm was used in order to simulate the traffic conditions in the network which has a 2D mesh topology. Obtained results are promising. The proposed algorithm exhibits a better performance, when compared with other reported approaches, as the problem size increases.
Keywords: Task mapping, Multiprocessor System-on-Chip (MPSoC), Networks on Chip (NoC), Population-based Incremental Learning (PBIL).
Resumen
Las redes en circuito integrado (NoC) representan un importante paradigma de uso creciente para los sistemas multiprocesador en circuito integrado (MPSoC), debido a su flexibilidad y escalabilidad. Las estrategias de tolerancia a fallos han venido adquiriendo importancia, a medida que los procesos de manufactura incursionan en dimensiones por debajo del micrómetro y la complejidad de los diseños aumenta. Este artículo describe un algoritmo de aprendizaje incremental basado en población (PBIL), orientado a optimizar el proceso de mapeo en tiempo de diseño, así como a encontrar soluciones de mapeo óptimas en tiempo de ejecución, para hacer frente a fallos de único nodo en la red. En ambos casos, los objetivos de optimización corresponden al tiempo de ejecución de las aplicaciones y al ancho de banda pico que aparece en la red. Las simulaciones se basaron en un algoritmo de ruteo XY determinístico, operando sobre una topología de malla 2D para la NoC. Los resultados obtenidos son prometedores. El algoritmo propuesto exhibe un desempeño superior a otras técnicas reportadas cuando el tamaño del problema aumenta.
Palabras clave: Mapeo de tareas, Sistemas integrados multiprocesador (MPSoC), Redes en circuito integrado (NoC), Aprendizaje incremental basado en población (PBIL).
1. Introduction
MPSoC systems are a feasible alternative for implementing a complexity-growing and variable set of applications. NoC-based MPSoCs have appeared as a way to easily scale the size of the system, and to deal with application performance requirements, application variability and constraints, such as real time [1]. In such systems, it is necessary to establish an optimal way to map the executable tasks of an application onto the available resources for its implementation. Static mapping is performed at design time, before executing the application.
In [2], an Integer Linear Programming (ILP) approach is proposed for static mapping aimed to optimize energy in a NoC-based MPSoC. The algorithm considers both the processing and communication energy as optimization objectives. A simulated annealing heuristic is added to the optimization process, which suffers from large execution times. Similarly, reference [3] reports a custom algorithm for static mapping of tasks on a NoC platform. The algorithm optimizes the computation and communication energy, with a slight degradation of system's performance.
The work reported in [4] proposes a technique for mapping tasks onto a set of heterogeneous Processing Elements (PEs) operating at multiple voltage levels in a NoC platform. Such work is based on a Mixed Integer Linear Programming (MILP) formulation for the static mapping problem, and it aims to optimize the overall energy consumption of the system, under performance constraints. The only objective considered for optimization is energy, and there are some complex problems (for instance, those related with low voltage setups) for which a feasible solution may not be found.
On the other hand, Dynamic mapping is also often referred to as remapping and is used in two defined contexts. First, the workload of the system may change due to several reasons [5], so a remapping procedure may adjust the system to the new workload and traffic conditions according to the figures of merit to be optimized. In second place, as a consequence of current systems complexity, there is a growing set of malfunctions and failures that cannot be detected or avoided by using current design methodologies [6]. Fault tolerance may be achieved by using dynamic mapping, which distributes the current workload of the system and avoids the use of faulty resources.
Some of the reported dynamic mapping approaches are restricted to homogeneous networks [5, 7, 8], meaning that all the processing elements are identical. Some other reported works are limited to the mapping of single tasks onto each processor of the system [9]. In [10], a multi task dynamic mapping approach is proposed for heterogeneous networks, i.e., processing elements in the system are of different kinds. The mapping algorithm uses heuristics aimed at reducing the traffic overhead, by means of assessing the adjacent available resources and measuring of the proximity of the communicating tasks.
The work reported in [11], presents a set of simple heuristics for dynamic mapping in NoC-based MPSoCs. Due to its simplicity, these algorithms may run very fast and deal with changing conditions in the network's workload. However, link occupation is the only objective being considered in the optimization process. Besides, the mapping algorithms described are not designed for achieving optimal solutions, as derived from the reported results.
A multitask dynamic mapping approach is proposed in [12]. The work is aimed at providing fault tolerance in a heterogeneous network. The optimization algorithm is based on ILP, and performs a multiobjective space search, in order to minimize both the execution time and the communication cost. The main issue with ILP is that optimization becomes highly complex as the problem's size increases. The work reported in [13] proposes an algorithm for mapping and scheduling in MpSoC systems. The algorithm is able to map executable applications both to bus-based and to NoC-based architectures. The exploration of the solution space is performed by means of a simulated annealing algorithm, which starts from a given solution (usually a random solution), and improves it gradually until reaching an optimal. Working with a single solution, instead of a population of solutions, may carry problems related to local-optimal solutions, as stated in [14].
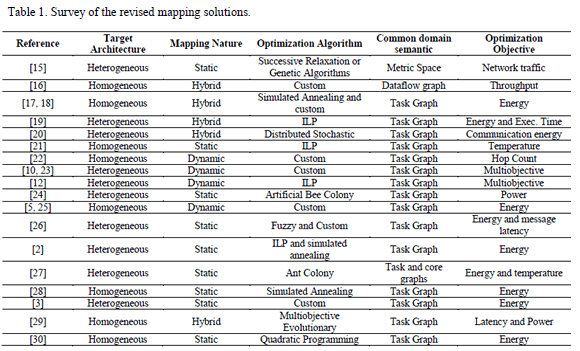
Table 1 summarizes most of the relevant related works concerning mapping of tasks into NoC-based systems. The mapping may be either static, dynamic, or hybrid, meaning that part of the mapping labor is performed in design time, and the remaining work takes place in runtime.
The common domain semantics refers to an intermediate representation, which combines features of both the high level specification of the application, and figures of merit related to the implementation platform [31]. As depicted in Table 1, task graphs are the most common approach as intermediate representation. Particularly, annotated task graphs (ATGs) allow the tasks structure (represented as dependences in the graph) and the figures of merit to optimize (supplied in the form of annotations) to be represented.
Some formal optimization methods, such as ILP, appear often in Table 1. Heuristics are also very common approaches for performing the optimization of the mapping problem. Such optimization may be devoted to a single objective, such as throughput, energy, traffic, temperature, and so on. Some of the mapping strategies are devoted to several objectives at once, i.e., they are multiobjective.
This paper describes an approach for static and dynamic mapping based on a PBIL optimization algorithm. The dynamic approach is aimed at providing fault tolerance in a single-node failure scenario. A heterogeneous NoC, based on a 2D mesh interconnection network, is used as a case study. Two objectives were taken into account for the optimization process: Completion time of the application, and peak bandwidth of the interconnection resources within the network. Bandwidth is related to the implementation costs of the system, since interconnection resources must be appraised at design time and placed into the system chip. For the sake of assessing the second objective, an XY routing algorithm was used in simulations. The remainder of this paper is organized as follows. Section 2 describes the static and dynamic mapping problems, as well as the experimental setup used to test the proposed approach. Section 3 describes the PBIL optimization algorithm and the customizations performed on it in order to deal with the dynamic and static mapping problems. Section 4 shows the simulation results. Concluding remarks and future work appear in Section 5.
2. Static And Dynamic Mapping
As mentioned before, static mapping is performed at design time and is aimed at choosing the optimal combination of available resources in a NoC, in order to implement an application, composed of a set of executable tasks. An annotated task graph (ATG) is often used as a middle-level representation of the application which is going to be implemented.
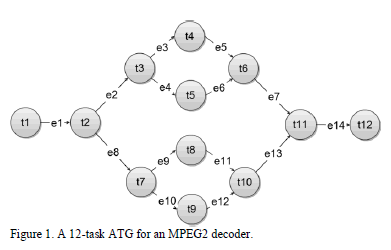
Fig. 1 shows a 12-task ATG for an MPEG-2 decoder [32]. In such graph, vertices are associated with executable tasks (labeled from t1 to t12), and edges represent data
dependences among the tasks of the system (labeled from e1 to e14). Annotations provide information about figures of merit such as performance, power, bandwidth, and some others. Such annotations allow exploring several implementation choices in the optimization process, and were omitted in Fig. 1 for space reasons.
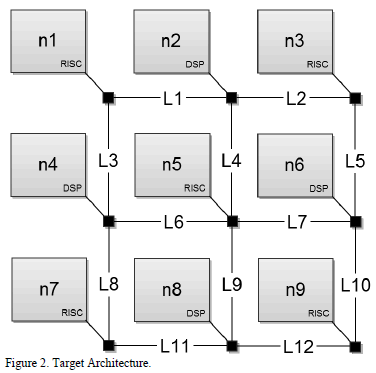
A 3 x 3 2D mesh was used as the target architecture. Fig. 2 shows such a mesh, composed of RISC and DSP processors. In such figure, there are nine nodes or tile spaces (labeled from n1 to n9) representing the processing elements, and twelve communication links between the different nodes (labeled from L1 to L12).
A deterministic XY routing algorithm was used to simulate the traffic conditions in the network. The PBIL optimization was performed for two conflicting objectives: First, the completion time of the application, which is equal to the maximum time stamp associated with the execution of tasks in the whole system. The second optimization objective was the peak bandwidth of the target NoC. This figure of merit may be calculated as the maximum value of bandwidth requirements for the links in the network, once the mapping has been performed.
Given the input task graph and the target architecture, the static mapping problem may be defined as finding the best task distribution, for the sake of optimizing both completion time and peak bandwidth in the system implementation.
On the other hand, dynamic mapping must deal with a subset of the system tasks and resources . Since dynamic mapping must deal only with exceptional situations, such as node failures or changing traffic conditions, the primer mapping solution (which was performed at design time) is still valid for most of the executable tasks on the system. Only a subset of the system tasks must be mapped at runtime to some other executable resources. Let's suppose that one of the nodes in Fig. 2 suffers a failure whilst the system is executing a given application. In order to provide some degree of fault tolerance, tasks that were running in a faulty node, may be redistributed to the remaining ones. In the proposed approach, dynamic mapping is performed to accomplish this aim. The main difference with respect to the static approach is that dynamic mapping must be performed at runtime. Besides, the number of tasks and resources that must be taken into account in the dynamic approach will be lower than that for static scenarios.
3. PBIL–Based Task Mapping
PBIL algorithms are stochastic search methods, which obtain directional information from the best solutions previously found in the solution space. Such algorithms have been used in design automation for embedded systems with promising results [33, 34]. PBIL techniques are a special case of a larger group of optimization approaches based on population. The main feature of the PBIL-based algorithms is an array of probabilities, which converge progressively to an optimal solution. The values in such an array must be updated iteratively. In the final stages of the optimization process, some entries of the PBIL array have greater probabilities, pointing to an optimal solution of the problem at hand.
Let's suppose a mapping problem (it may be either static or dynamic) with a set of N tasks and M available resources. The PBIL probability matrix for such a problem may take the form of the array shown in Fig. 3. In this figure, P(i,j) represents the probability of task j to be implemented on the resource i. Fig. 4 shows a basic version of the adaptive PBIL algorithm, which is intended to update the probabilities of the PBIL array iteratively, until an optimal solution becomes more probable than the remaining ones.
This algorithm starts with the PBIL probability array, namely P, with dimensions M x N, as shown in Fig. 3. All the probabilities in the array are initialized to 1/M, which is the value that ensures maximum population diversity, in such a way that all potential solutions to the mapping problem are being considered at the beginning of the optimization process.
The routine Create_Population generates a new population (namely Pop), starting from probabilities in the PBIL array. Rows (resources) in the array with the highest
values of probability are meant to appear more frequently in the population's individuals. The Evaluate_Population routine assesses the population's individuals just created. Fitness values allow choosing the best solution for the mapping problem. The Choose_Best routine is used to accomplish this goal. The learning rate or LR is a way to control the convergence speed of the PBIL algorithm. Higher values of LR will lead to fast convergences, although the quality of the solutions might not be satisfactory. If LR is reduced, quality will improve at the expenses of longer convergence time. In our adaptive approach, the LR
parameter must be adjusted in order to allow both exploration and exploitation of the PBIL search space. The entropy (E) of the probability array is calculated and used as an estimation of the population's diversity. In Fig. 4, the routine Learning_Rule represents the way in which the LR parameter is tuned as a function of the P array's entropy. Once the LR parameter is calculated, the P array must be updated in order to adjust the probabilities, according to the best solutions found in the population. Function Update_Array performs this.
The value of the E parameter in Fig. 4 is calculated as the systemic entropy of the PBIL array, just as is done in information theory. Equation (1) depicts the calculations performed inside the Entropy routine, for the entropy calculation.
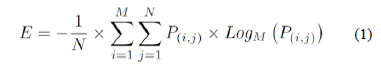
According to Equation (1), entropy values range from 0 to 1. E = 1 means that there is maximum population's diversity (this only happens when all values on the PBIL matrix are equal to 1/M). When E = 0, it means that the PBIL matrix points to a unique and completely defined solution. Entropy decreases as the probability array tends to concentrate on single entries of each column of the P array (i.e., when an optimal solution becomes more probable). For the sake of speeding up the convergence of the PBIL algorithm, the termination condition in Fig. 4 is a comparison between the Entropy value and a given tolerance. By using this strategy, it is not necessary to wait until the Entropy value becomes equal to zero, which may be very restrictive and time consuming.
The way in which the LR parameter is changed as a function of entropy is often referred to as the learning rule. Equation (2) describes a sigmoid learning rule, which was used inside the Learning_Rule routine. In the equation, LRMIN and LRMAX are the minimum and maximum values, respectively, for the learning rule parameter (LR), whilst D is an empirical value which usually ranges from 4 to 6. The idea is to keep the LR parameter low at the beginning of the algorithm, when there is a high population's diversity and the values of E are close to one. When entropy's value decreases, i.e., when the population approaches to a given optimal, LR parameter is increased to speed up the convergence process.
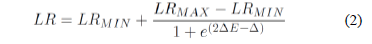
For each task of the mapping problem or, equivalently, for each column in the PBIL array, the function Update_Array must increase the probability of the choice which resulted in the best solution. Since each single column in the PBIL matrix represents a conjoint probability event, the probabilities sum along a column must be equal to one. Therefore, when a given probability in the array is increased, the remaining ones in that column must be decreased accordingly. Equation (3) shows the probability's updating formulae, which are based on the Hebbian learning rule [35]. In Equation (3), it is supposed that for a given attribute j, the best solution obtained is the choice k. Suffixes Old and New in Equation (3) are meant to denote the old and new versions of each probability, respectively.
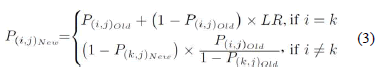
The PBIL approach described so far may be easily adapted to perform dynamic mapping. In the event of a single node failure, the number of columns in the probability array in Fig. 3 (N) would be equal to the number of tasks that the faulty node was executing. The number of rows may be kept the same. Then, all the probabilities associated with the faulty node (a single row in the array) must be set to zero. In such a case, the initialization stage of the array in Fig. 4, must set all the probabilities to (M - 1) -1.
The situation is not so different in the event of failures involving several nodes at once. The rows associated with the faulty resources must be equal to zero and the initialization stage, at the beginning of the optimization process, must take into account only the available resources for task implementation. In an improved version of the PBIL algorithm, the probability array must take the exact dimensions according with the specific dynamic mapping problem: N must be equal to the number of tasks to be remapped and M must be equal to the amount of available resources. This is the approach adopted for the remaining of this paper.
4. Experimental Results
The PBIL optimization algorithms, both for static and dynamic mapping, were written and tested in Matlab (R2011a), for an MPEG-2 decoder like the one represented in Fig. 1, with 12, 24 and 36 tasks. The NoC target architecture was that shown in Fig. 2. The traffic conditions in the network were simulated using a deterministic XY algorithm. The profiling information (annotations of the taskgraph) regarding execution time and bandwidth was extracted from [36].
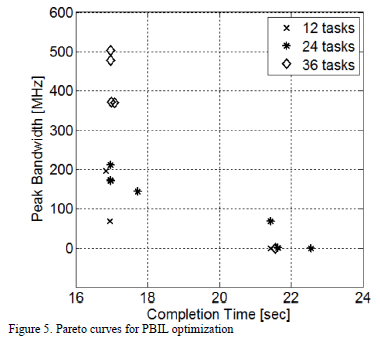
The routine Evaluate Population in Fig. 4, as described in previous section, assesses each solution in the population and gives it a fitness value. A weight vector was used to deal with the multiobjective issue in the optimization process. Each entry of the vector is associated with a given objective of the problem (such as completion time, energy consumption or bandwidth). The relative value of each entry with respect to the remaining ones, represent the probability of its associated objective to be optimized at each PBIL algorithm's iteration. By changing the relative values of the weight vector, it is possible to construct a Pareto curve, as shown in Fig. 5. Pareto curves show several trade-offs among the objectives to be optimized, because they define the set of solutions in which a given objective cannot be improved, without degrading some other objective.
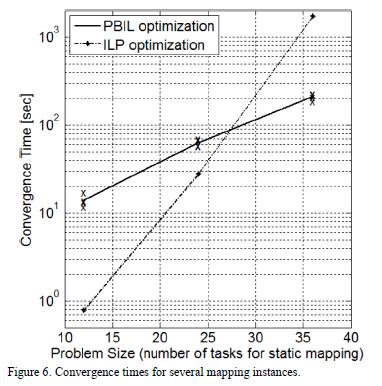
In order to profile our PBIL approach, static mapping may be considered as the worst-case scenario (i.e., the one which takes more convergence time). In static mapping, all tasks must be mapped, and all the resources are available for potential implementations. Alternatively, dynamic mapping must deal with a subset of the system's tasks and a subset of the available resources. Convergence times for several
instances of the PBIL static mapping optimization are shown in Fig. 6. In this figure, the continuous line represents a quadratic fit performed on the data. Data from an ILP optimization [12], performed over the same static mapping problem, was included in the figure for comparison purposes.
As shown in Fig. 6, the ILP approach exhibits a better performance than PBIL for small problems. However, if the number of tasks increases, optimization using the ILP algorithm becomes prohibitive. As reported in [12], the mean ILP convergence time for a 36-tasks optimization is around 1700 seconds. PBIL convergence time is around one order of magnitude lower than this value.
The PBIL algorithm for dynamic mapping starts from a previous mapping schema, obtained from the static optimization. The reference to the faulty node is also
necessary, for identifying the system tasks that must be remapped. By using such information, it is possible to define the dimensions of the PBIL probability array, and the optimization algorithm may take the form depicted in Fig. 4. For dynamic mapping, only single node failure scenarios were considered in the simulations. However, multiple-node failures may be easily considered with the proposed methodology: If a failure event affects two nodes simultaneously, two rows of the matrix in Fig. 3 must be set to zero. The remaining values of such a matrix should be set to 1/(M - 2). The PBIL algorithm may then perform the optimization process as described before. In a more general fashion, if a failure affects an amount of F nodes, the matrix in Fig. 3 must be initialized in such a way that F rows, in correspondence with the faulty resources, must be set to zero. The remaining values of the matrix must be set to 1/(M - F), for the sake of guaranteeing maximum population diversity.
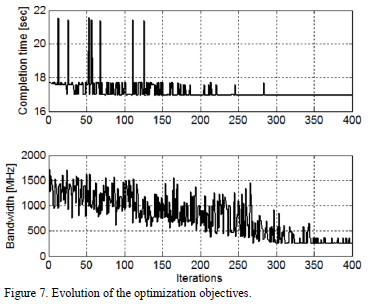
Fig. 7 depicts the evolution of the two optimization objectives (Completion Time and Bandwidth) as a function of the number of algorithm iterations. In this case, the size of the problem, or equivalently, the number of tasks to be mapped was equal to 36 and the weight vector was tuned to provide 60 % of probability to the Completion Time objective to be optimized, whilst the Bandwidth had a probability of 40 %.
5. Conclusions
A multiobjective PBIL optimization approach has been described and tested for static and dynamic mapping of tasks to an MPSoC based on NoC. The objectives considered in the optimization process were the completion time of the executable application and peak bandwidth. For our simulations, a 2D mesh architecture and a deterministic routing schema were adopted. The PBIL optimization algorithm seems to have a better performance than some other reported approaches, such as ILP, when the problem size increases. This is a major advantage, since the size of MPSoC systems has been increasing as well as the complexity of the applications involved.
Acknowledgements
The authors would like to thank ARTICA, COLCIENCIAS, the Communications Ministry of Colombia, the National University of Colombia and the University of Antioquia, for their support in the development this work.
References
[1] Marculescu R., Ogras U. Y., Peh L. S., Jerger N. E., Hoskote Y. Outstanding research problems in NoC design: system, microarchitecture, and circuit perspectives. Trans. Comp.-Aided Des. Integ. Cir. Sys., vol. 28, no. 1, pp. 3–21, Jan. 2009. [ Links ]
[2] Huang J., Buckl C., Raabe A., Knoll A. Energy-aware task allocation for network-on-chip based heterogeneous multiprocessor systems. In Parallel, Distributed and Network-Based Processing (PDP), 2011 19th Euromicro International Conference on, pp. 447 –454, Feb. 2011. [ Links ]
[3] Rajaei R., Hessabi S., Vahdat B. V. An energy-aware methodology for mapping and scheduling of concurrent applications in MPSOC architectures. In Electrical Engineering (ICEE), 2011 19th Iranian Conference on, pp. 1 –6, May 2011. [ Links ]
[4] Ghosh P., Sen A., Hall A. Energy efficient application mapping to noc processing elements operating at multiple voltage levels. In Networks-on-Chip, 2009. NoCS 2009. 3rd ACM/IEEE International Symposium on, pp. 80 –85, May 2009. [ Links ]
[5] Mandelli M., Ost L., Carara E., Guindani G. , Gouvea T., Medeiros G., Moraes F. Energy-aware dynamic task mapping for NoC-based MPSoCs. In Circuits and Systems (ISCAS), 2011 IEEE International Symposium on, pp. 1676 –1679, May 2011. [ Links ]
[6] Marculescu R. Networks-on-chip: The quest for on-chip fault-tolerant communication. In VLSI, 2003 Proceedings of the IEEE Computer Society Annual Symposium on, pp. 8 – 12, Feb. 2003. [ Links ]
[7] Schranzhofer A., Chen J. J., Santinelli L., Thiele L. Dynamic and adaptive allocation of applications on mpsoc platforms. In Design Automation Conference (ASP-DAC), 2010 15th Asia and South Pacific, pp. 885 –890, Jan. 2010. [ Links ]
[8] Wildermann S., Ziermann T., Teich J. Run time mapping of adaptive applications onto homogeneous noc-based reconfigurable architectures. In Field-Programmable Technology 2009. FPT 2009. International Conference on, pp. 514 –517, Dec. 2009. [ Links ]
[9] Carvalho E. de S., Calazans N., Moraes F. Dynamic task mapping for MPSoCs. Design Test of Computers, IEEE, vol. 27, no. 5, pp. 26 –35, Oct. 2010. [ Links ]
[10] Singh A. K., Srikanthan T., Kumar A., Jigang W. Communication aware heuristics for run-time task mapping on NoC-based MPSoC platforms. J. Syst. Archit., vol. 56, no. 7, pp. 242–255, Jul. 2010. [ Links ]
[11] Carvalho E., Calazans N., Moraes F. Heuristics for dynamic task mapping in NoC-based heterogeneous MPSoCs. In Proceedings of the 18th IEEE/IFIP International Workshop on Rapid System Prototyping, ser. RSP '07. Washington, DC, USA: IEEE Computer Society, pp. 34–40, 2007. [ Links ]
[12] Derin O., Kabakci D., Fiorin L. Online task remapping strategies for fault-tolerant network-on-chip multiprocessors. In Networks on Chip (NoCS), 2011 Fifth IEEE/ACM International Symposium on, pp. 129 –136, May 2011. [ Links ]
[13] Tafesse B., Raina A., Suseela J. , Muthukumar V. Efficient scheduling algorithms for MPSoC systems. In Information Technology: New Generations (ITNG), 2011 Eighth International Conference on, pp. 683 –688, April 2011. [ Links ]
[14] Russell S. J., Norvig P. Artificial Intelligence: A Modern Approach. 2nd ed. Pearson Education, 2003. [ Links ]
[15] Jang W., Pan D. Z. A3Map: Architecture-aware analytic mapping for Networks-on-Chip. ACM Trans. Des. Autom. Electron. Syst., vol. 17, pp. 26:1–26:22, July 2012. [ Links ]
[16] Singh A. K., Kumar A., Srikanthan T. A hybrid strategy for mapping multiple throughput-constrained applications on MPSoCs. In Proceedings of the 14th international conference on Compilers, architectures and synthesis for embedded systems, CASES '11, (New York, NY, USA), pp. 175–184, ACM, 2011. [ Links ]
[17] Antunes E., Soares M., Aguiar A., Filho S. J., Sartori M., Hessel F., Marcon C. A. M. Partitioning and dynamic mapping evaluation for energy consumption minimization on noc-based MPSoC. In ISQED (K. A. Bowman, K. V. Gadepally, P. Chatterjee, M. M. Budnik, and L. Immaneni, eds.), pp. 451–457, IEEE, 2012. [ Links ]
[18] Antunes E., Aguiar A., Johann F. S., Sartori M. , Hessel F., Marcon C. Partitioning and mapping on NoC-based MPSoC: an energy consumption saving approach. In Proceedings of the 4th International Workshop on Network on Chip Architectures, NoCArc '11, (New York, NY, USA), pp. 51–56, ACM, 2011. [ Links ]
[19] He O., Dong S., Jang W., Bian J., Pan D. Z. UNISM: Unified scheduling and mapping for general Networks on Chip. IEEE Trans. VLSI Syst., vol. 20, no. 8, pp. 1496–1509, 2012. [ Links ]
[20] Hosseinabady M., Nunez-Yanez J. L. Run-time stochastic task mapping on a large scale Network-on-Chip with dynamically reconfigurable tiles. IET Computers and Digital Techniques, vol. 6, no. 1, pp. 1–11, 2012. [ Links ]
[21] Hamedani P. K., Hessabi S., Sarbazi-Azad H., Jerger N. D. E. Exploration of temperature constraints for thermal aware mapping of 3D Networks on Chip. In PDP (R. Stotzka, M. Schiffers, and Y. Cotronis, eds.), pp. 499–506, IEEE, 2012. [ Links ]
[22] Wang C., Yu L., Liu L., Chen T. Packet triggered prediction based task migration for Network-on-Chip. In Proceedings of the 2012 20th Euromicro International Conference on Parallel, Distributed and Network-based Processing, PDP '12, (Washington, DC, USA), pp. 491–498, IEEE Computer Society, 2012. [ Links ]
[23] Kaushik S., Singh A. K., Jigang W., Srikanthan T. Run-time computation and communication aware mapping heuristic for NoC based heterogeneous MPSoC platforms. In Proceedings of the 2011 Fourth International Symposium on Parallel Architectures, Algorithms and Programming, PAAP '11, (Washington, DC, USA), pp. 203–207, IEEE Computer Society, 2011. [ Links ]
[24] Zhe L., Xiang L. NoC mapping based on chaos artificial bee colony optimization. In Computational Problem-Solving (ICCP), 2011 International Conference on, pp. 518 –521, oct. 2011. [ Links ]
[25] Mandelli M., Amory A., Ost L., Moraes F. G. Multi-task dynamic mapping onto NoC-based MPSoCs. In Proceedings of the 24th symposium on Integrated circuits and systems design, SBCCI '11, (New York, NY, USA), pp. 191–196, ACM, 2011. [ Links ]
[26] Habibi A., Arjomand M., Sarbazi-Azad H. Multicast-aware mapping algorithm for on-chip networks. In Proceedings of the 2011 19th International Euromicro Conference on Parallel, Distributed and Network-Based Processing, PDP '11, (Washington, DC, USA), pp. 455–462, IEEE Computer Society, 2011. [ Links ]
[27] Liu Y., Ruan Y., Lai Z., Jing W. Energy and thermal aware mapping for mesh-based NoC architectures using multi-objective ant colony algorithm. In Computer Research and Development (ICCRD), 2011 3rd International Conference on, vol. 3, pp. 407 –411, march 2011. [ Links ]
[28] Zhong L., Sheng J., Jing M., Yu Z., Zeng X. , Zhou D. An optimized mapping algorithm based on simulated annealing for regular NoC architecture. In ASIC (ASICON), 2011 IEEE 9th International Conference on, pp. 389 –392, oct. 2011. [ Links ]
[29] Sepulveda J., Strum M., Chau W. J., Gogniat G. A multiobjective approach for multi-application NoC mapping. In Circuits and Systems (LASCAS), 2011 IEEE Second Latin American Symposium on, pp. 1 –4, feb. 2011. [ Links ]
[30] Sheng J., Zhong L., Jing M., Yu Z. , Zeng X. A method of quadratic programming for mapping on NoC architecture. In ASIC (ASICON), 2011 IEEE 9th International Conference on, pp. 200 –203, Oct. 2011. [ Links ]
[31] Sangiovanni-Vincentelli A. Is a unified methodology for system-level design possible? IEEE Des. Test, vol. 25, pp. 346–357, July 2008. [ Links ]
[32] Bonatti P. A., Lutz C., Murano A., Vardi M. ISO IEC 13818-2 MPEG2. Information Technology - Generic Coding of Moving Pictures and Associated Audio Information: Video," in ICALP 2006. LNCS, pp. 540–551, Springer, 2006. [ Links ]
[33] Fan L. J., Li B., Zhuang Z. Q., Fu Z. Q. An approach for dynamic Hardware/Software partitioning based on DPBIL. In Proceedings of the Third International Conference on Natural Computation. Volume 05, ser. ICNC '07. Washington, DC, USA: IEEE Computer Society, 2007. [ Links ]
[34] Bolanos F., Aedo J., Rivera F. System-level partitioning for embedded systems design using Population-based Incremental Learning. In CDES, H. R. Arabnia and A. M. G. Solo, Eds. CSREA Press, pp. 74–80, 2010. [ Links ]
[35] White R. H. Competitive hebbian learning: Algorithm and demonstrations. Neural Networks, vol. 5, no. 2, pp. 261 – 275, 1992. [ Links ]
[36] Thiele L., Bacivarov I., Haid W., Huang K. Mapping applications to tiled multiprocessor embedded systems. In Proceedings of the Seventh International Conference on Application of Concurrency to System Design, ser. ACSD '07. Washington, DC, USA: IEEE Computer Society, pp. 29–40, 2007. [ Links ]