Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.185 Medellín maio/jun. 2014
https://doi.org/10.15446/dyna.v81n185.36038
http://dx.doi.org/10.15446/dyna.v81n185.36038
Dynamic stability of slender columns with semi-rigid connections under periodic axial load: theory
Estabilidad dinámica de columnas esbeltas con conexiones semirrígidas bajo carga axial periódica: teoría
Oliver Giraldo-Londoño a & J. Darío Aristizábal-Ochoa b
a Structural Researcher, M.S. Ohio University, USA ogirald86@gmail.com.
b 125-Year Generation Professor, Ph.D. School of Mines, National University. Medellin, Colombia jdaristi@unal.edu.co
Received: December 15th, de 2012. Received in revised form: September 26th, 2013. Accepted: October 22th, 2013
Abstract
The dynamic stability of an elastic prismatic slender column with semirigid connections at both ends of identical stiffness and with sidesway between the two ends totally inhibited, subject to parametric axial loads including the combined effects of rotary inertia and external damping is investigated in a classical manner. Closed-form expressions that can be used to predict the dynamic instability regions of slender columns are developed by making use of Floquet's theory. The proposed solution is capable of capturing the phenomena of stability of columns under periodic axial loads using a single column element. The proposed method and corresponding equations can be used to investigate the effects of damping, rotary inertia and semirigid connections on the stability analysis of slender columns under periodically varying axial loads. The effects produced by shear deformations along the span of the column as well as those produced by the axial inertia, the coupling between longitudinal and transverse deflections and the curvature are not taken into account. Sensitivity studies are presented in a companion paper that show the effects of rotary inertia, damping and semirigid connections on the dynamic stability of columns under parametric axial loads.
Keywords: Buckling; Columns; Dynamic Analysis; Damping; Semi-Rigid Connections; Parametric Loading; Periodic Loading; Stability.
Resumen
La estabilidad dinámica de una columna elástica prismática esbelta con conexiones semirrígidas en ambos extremos de rigidez idéntica y con desplazamiento lateral entre los dos extremos totalmente inhibido sujetos a cargas axiales paramétricos incluyendo los efectos combinados de inercia rotacional y amortiguación externas se investiga de una manera clásica. Expresiones cerradas que se pueden utilizar para predecir las regiones de inestabilidad dinámica de columnas esbeltas son desarrolladas haciendo uso de la teoría de Floquet. La solución propuesta es capaz de capturar el fenómeno de estabilidad en columnas sometidas a cargas axiales periódicas utilizando un solo elemento de columna. El método propuesto y las ecuaciones correspondientes se pueden utilizar para investigar los efectos del amortiguamiento, la inercia rotacional de la columna, y las conexiones semirrígidas en el análisis de estabilidad de columnas esbeltas sometidas a cargas axiales periódicas. Los efectos producidos por las deformaciones por cizallamiento a lo largo de la columna, así como los producidos por la inercia axial, el acoplamiento entre las deflexiones longitudinales y transversales y la curvatura no se tienen en cuenta. Estudios de sensibilidad que muestran los efectos de la inercia rotacional, el amortiguamiento y las conexiones semi-rígidas en la estabilidad dinámica de columnas sometidas a cargas axiales paramétricas son presentados en una publicación adjunta.
Palabras clave: pandeo, columnas, análisis dinámico amortiguado, conexiones semirígidas, cargas paramétricas, cargas periódicas, estabilidad.
1 Introduction
The stability analysis of columns and frames under time varying parametric axial loads are of great importance in civil, mechanical, and aerospace engineering. This subject generally termed "Dynamic Stability" has been investigated by numerous structural researchers since Koning and Taub [1] studied the stability of a simply supported elastic imperfect column subjected to a sudden applied axial load of known duration. Dynamic Stability encompasses many classes of problems and many different phenomena for the same configuration subjected to the same dynamic loads. Therefore, it is not surprising that several uses and interpretations of the term exist. Simitses and Hodges [2] on page 329 of their textbook state that: "The class of problems falling in the category of parametric excitation, or parametric resonance, includes the best defined, conceived, and understood problems of dynamic stability". The problem of parametric excitation is best defined in terms of an example. Consider an Euler column, which is loaded at one end by a periodic axial force. The other end is immovable. It can be shown that, for certain relationships between the exciting frequency and the column natural frequency of transverse vibration, transverse vibrations occur with rapidly increasing amplitudes. This is called parametric resonance and the system is said to be dynamically unstable. Moreover the loading is called "parametric excitation". Bolotin [3] is an excellent reference on Dynamic Stability. Because of space limitation a brief bibliography of some studies made in the last forty years is presented next.
Wirsching and Yao [4] developed a relationship for the stability condition of a pin-ended column with initial curvature excited by physical white noise. Iwatsubo et al. [5] studied the instabilities of a cantilever column subject to an axial periodic load (Euler-type problem) and to a tangential periodic load (Beck-type problem). Ahmadi and Glockner [6] studied the stability of a viscous-elastic column subject to deterministic axial load with sinusoidal time variation as well as stationary and non-stationary random variations. Simitses [7] presented the concept of dynamic stability for suddenly-loaded elastic structural configurations along the related criteria and estimates of critical conditions. Sridharan and Benito [8] studied experimentally the interaction of local and overall buckling in thin-walled columns and the effect of suddenly applied compression dynamic end loads. Shigematsu et al. [9] studied the dynamic stability of initially imperfect columns and plates under time-dependent axial compression in elastic and elastic-plastic regions using matrix functions.
Sophianopoulos and Kounadis [10] studied the dynamic stability of imperfect frames under joint displacements. Wong and Yang [11] studied the inelastic response of structures with strain-hardening and strain-softening properties as well as with elastic-plastic properties subjected to dynamic loadings using the force analogy method. Svensson [12] studied theoretically and experimentally the stability of a dynamic system with periodic coefficients including the effects of both internal damping and damping at the boundaries.
Yabuki et al. [13] studied the inelastic dynamic stability of steel columns subject to a steady axial force and an alternating dynamic axial force including the effects of support conditions and the frequency of the axial force. Kumar and Mohammed [14] studied the dynamic stability of columns and frames subjected to axial periodic loads using the FEM and Newmark method for the integration of the equations of motion. Dohnal et al. [15] studied the behavior of a uniform cantilever column under a time-periodic axial force using the FEM. Mailybaev and Seyranian [16] studied the classical problem of stabilization of a statically unstable elastic column (simply supported and clamped–hinged ends) by axial harmonic vibration.
The main objective of this paper is to present an analytical method and closed form equations that determine the dynamic stability of an elastic 2D prismatic column with semirigid end connections of identical stiffness and with sidesway between the two ends totally inhibited subject to parametric axial load described by a Fourier series. The proposed model and corresponding equations which are straightforward and relatively simple to apply can be used to investigate the effects of damping, rotary inertia and semirigid connections on the stability of slender columns under periodically varying axial loads using a single column element. The closed-form equations make use of Floquet's theory to predict the dynamic instability regions of slender columns. Nonlinear effects like those produced by the axial inertia, the coupling between longitudinal and transverse deflections, and the curvature are not taken into account. Sensitivity studies are included in a companion paper [17] that shows the effects of rotary inertia, damping and semirigid connections on the dynamic stability of prismatic columns under parametric axial loads.
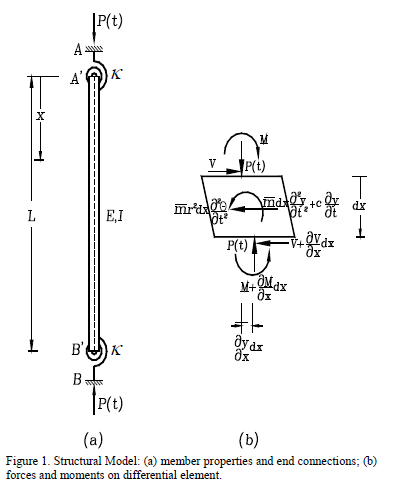
2 Structural model
Consider the 2D prismatic column elastically connected at both ends A and B as shown in Fig. 1a. The element AB consists of the column itself A'B' connected by elastic springs AA' and BB' both with identical flexural stiffness k (whose dimension is force-distance/radian) at ends A' and B', respectively. It is assumed that the column A'B': (1) is prismatic with cross sectional area A, principal moment of inertia I (about the axis of bending), and span L; (2) is made of a linear elastic, homogeneous and isotropic material with elastic modulus E; (3) its initial centroidal axis is a perfect straight line; (4) is subjected to a varying end axial load defined by a Fourier series
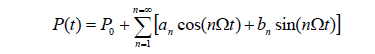
as shown by Fig. 1a; and (5) bending deformations and strains are small so that the principle of superposition can be applied.
The ratio 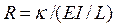 will be denoted as the stiffness index of the flexural connections. The stiffness index varies from zero for perfectly pinned connections to infinity for fully restrained connections (i.e., perfectly clamped). For convenience the term
will be denoted as the stiffness index of the flexural connections. The stiffness index varies from zero for perfectly pinned connections to infinity for fully restrained connections (i.e., perfectly clamped). For convenience the term 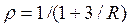 denoted as the fixity factor is used in the proposed equations.
denoted as the fixity factor is used in the proposed equations.
2.1. Dynamic Analysis
The lateral deflection of the column is derived by applying dynamic equilibrium on the differential element (Fig. 1b) and compatibility conditions at the ends of the member. The transverse and rotational dynamic equilibrium equations are:
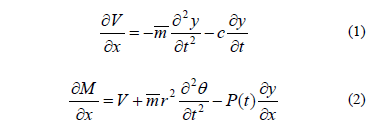
Using the governing bending equation for Euler-Bernoulli columns 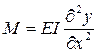 and substituting Eq. (1) into Eq. (2), the governing fourth-order differential equation of a prismatic column becomes:
and substituting Eq. (1) into Eq. (2), the governing fourth-order differential equation of a prismatic column becomes:
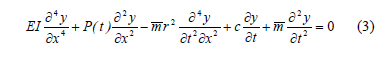
Equation (3) must meet the following four boundary conditions:
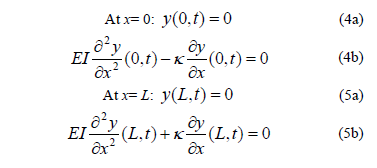
The solution of Eq. (3) can be written in the following form:
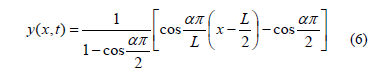
Where the constant a must satisfy the following condition:
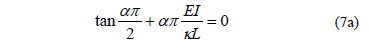
In terms of the fixity factor r Eq. (7a) becomes:
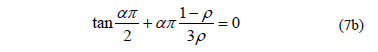
Equation (6) coupled with the condition given by Eq. (7b) satisfies the four boundary conditions expressed by Eqs (4a-b) and (5a-b) listed above. Substituting Eq. (6) into (3) the following ordinary differential equation in f(t) is obtained:
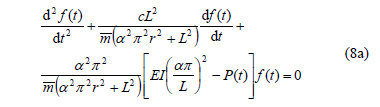
To facilitate the analysis of columns subjected to varying axial forces, the following six dimensionless parameters are introduced:
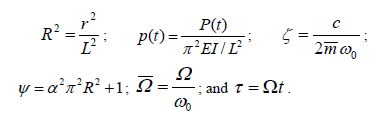
Where: 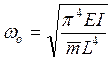 = the natural frequency of lateral vibration of a simply supported beam without axial load.
= the natural frequency of lateral vibration of a simply supported beam without axial load.
Then Eq. (8a) is reduced to
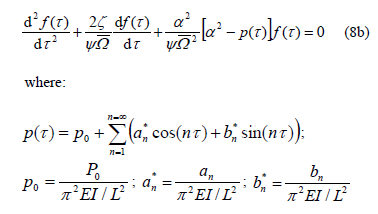
2.2. Proposed Equations for Instability Borders
The proposed equations are based on Floquet's theory. The derivation is presented in Appendix I for easy reference.
As can be seen the character of the solutions for Eq. (8b) depends on the values of its harmonically varying coefficients leading to stable or unstable conditions. From Floquet's theory it can be concluded that on the border between stable and unstable conditions the solutions for Eq. (8b) becomes periodic with period 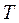 or
or  with
with 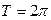 .
.
The proposed equations shown below are capable to capture the phenomena of parametric resonance of slender columns with semi rigid connections, considering the effects of damping and rotary inertia:
a) Solution with period 2T
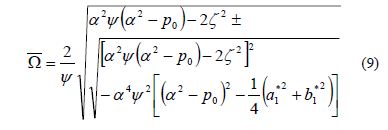
b) Solution with period T
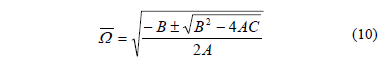
where A, B and C are calculated as indicated below.
When
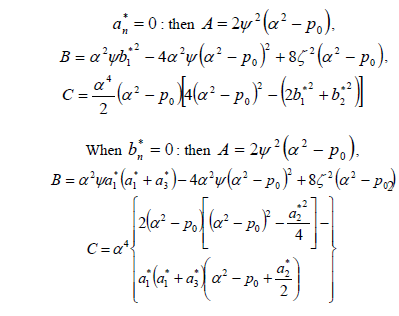
When both 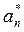 and
and 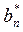 are different from zero, Eq. (10) is not applicable and the solution shall be obtained by solving Eq. (23b).
are different from zero, Eq. (10) is not applicable and the solution shall be obtained by solving Eq. (23b).
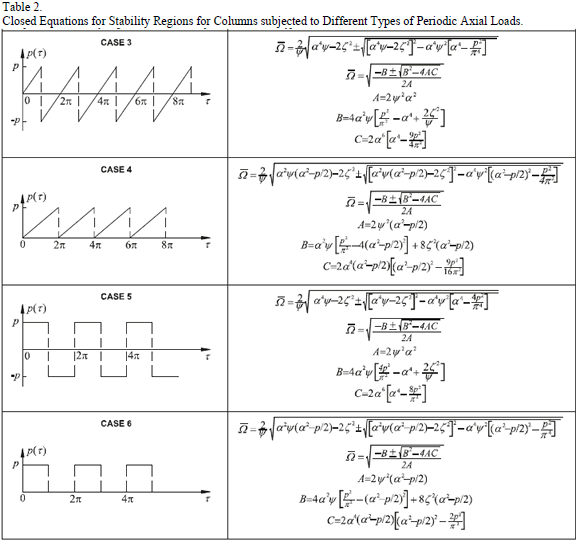
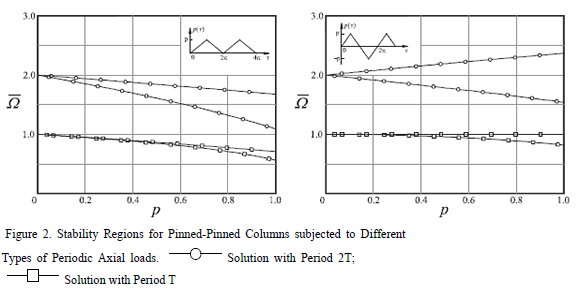
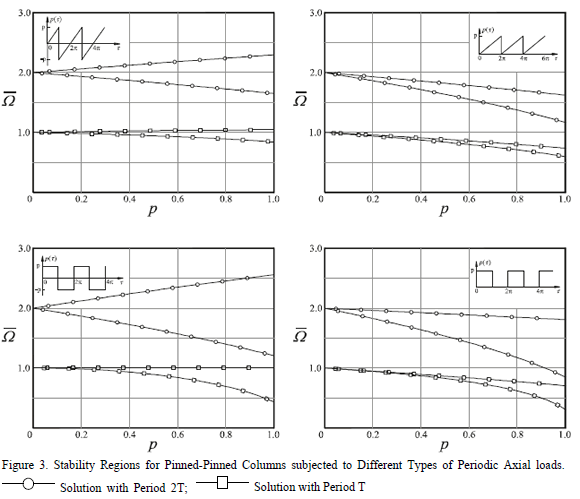
Table 1 lists closed expressions for different classic types of periodic axial loads. These expressions can be used to investigate the effects of damping, rotary inertia and semirigid connections on the stability of slender columns subject to periodic axial loads in a systematic manner. For periodic loadings that are not listed in Table 1, simply use Eqs. (9) and (10) with the appropriate values of 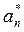 and
and 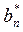 . shows graphically the two first regions of instability for all types of loading described in Table 1 by considering
. shows graphically the two first regions of instability for all types of loading described in Table 1 by considering 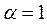 (i.e. pinned-pinned columns) and the corresponding values for
(i.e. pinned-pinned columns) and the corresponding values for 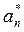 and
and 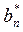 in Eqs. (9) and (10).
in Eqs. (9) and (10).
3. Step-by-step procedure
The following steps are proposed to evaluate the dynamic stability for columns subjected to periodic axial loads:
1. Enter the numerical values of the properties of the column: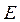 ,
, 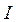 ,
, 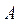 ,
, 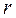 ,
, 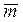 ,
, 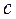 , and
, and 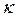 .
.
2. With the value of the flexural stiffness of the connection 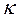 (or the fixity factor
(or the fixity factor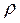 ), the value of the dimensionless parameter
), the value of the dimensionless parameter 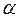 is calculated from Eq. (7a) or (7b) using numerical methods (i.e., Newton-Raphson or secant method). The values of
is calculated from Eq. (7a) or (7b) using numerical methods (i.e., Newton-Raphson or secant method). The values of 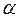 must be between 1 and 2 for hinged and clamped in both ends, respectively, to obtain a coherent solution to Eq. (6).
must be between 1 and 2 for hinged and clamped in both ends, respectively, to obtain a coherent solution to Eq. (6).
3. Calculate the natural frequency of lateral vibration for a simple supported beam without axial load:
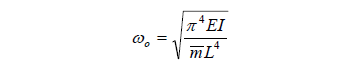
1. Determine the following dimensionless parameters:
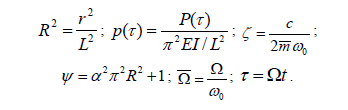
2. To determine the borders between regions of stability and instability Equations (9) and (10) must be used. Notice that the varying axial load can be defined by the Fourier series
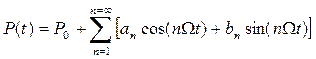 with the terms P0,
with the terms P0, 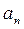 and
and 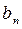 expressed by
expressed by
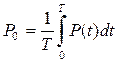 ;
; 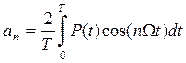 ; and
; and 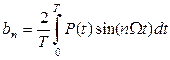 . Where:
. Where: 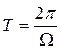 . (with
. (with 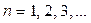 ). The values of these parameters determine the stability borders. Since the determination of the zeros of Eq. (16b) can become cumbersome when both
). The values of these parameters determine the stability borders. Since the determination of the zeros of Eq. (16b) can become cumbersome when both 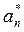 and
and 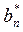 are different from zero, a numerical method similar to that used for solving Eq. (7a) or (7b) can be used.
are different from zero, a numerical method similar to that used for solving Eq. (7a) or (7b) can be used.
3. In order to estimate which regions at both sides of the borders, obtained from step (5), are of stability or instability is necessary to evaluate trial points located at both sides of the borders, and evaluate the behavior of 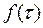 by applying a numerical method for solving the ordinary differential equations. The Runge-Kutta method is suggested in this case since it is simple, efficient and accurate. To describe how to solve Eq. (8b) using the Runge-Kutta method, the system of ordinary differential equations defined by Eq. (16) is rewritten as follows:
by applying a numerical method for solving the ordinary differential equations. The Runge-Kutta method is suggested in this case since it is simple, efficient and accurate. To describe how to solve Eq. (8b) using the Runge-Kutta method, the system of ordinary differential equations defined by Eq. (16) is rewritten as follows:
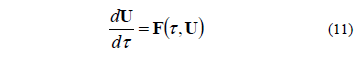
The method is given by:
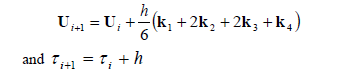
Where: 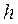 = time step size.
= time step size.
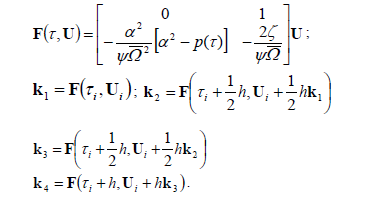
Once the points corresponding to parametric resonance and those that give stable solutions are known, the regions of stability and instability can be established, respectively.
3. Summary and conclusions
Closed-form expressions that can be used to predict the dynamic instability regions of slender Euler-Bernoulli columns are developed using Floquet's theory. The proposed method is straightforward and the corresponding equations are relatively easy to use. The proposed closed-form equations enable the analyst to explicitly evaluate the effects of damping, semirigid connections, and rotary inertia on the nonlinear elastic response and lateral stability of slender prismatic columns with sidesway inhibited, subject to static and dynamic axial loads. The proposed equations are not available in the technical literature.
The developing of simple closed-form expressions capable to predict the dynamic instability regions of slender columns with semi-rigid connections including the effects of external damping and rotary inertia under all types of periodic axial loads is a significant advance when compared with other complex numerical procedures that require high computing times to reach a good enough precision.
Acknowledgments
The authors wish to thank the Department of Civil Engineeering of the School of Mines of the National University of Colombia at Medellín and to COLCIENCIAS for their financial support.
Appendix: Derivation of instability regions
The equations for the borders between stable and unstable conditions for slender columns under parametric excitation proposed herein are based on Floquet's theory as some other researchers such as Svensson [12] and Kumar and Mohammed [14]. A brief description of Floquet's theory is given next.
Rewriting Eq. (8b) as a system of two first-order differential equations the following expression is obtained:
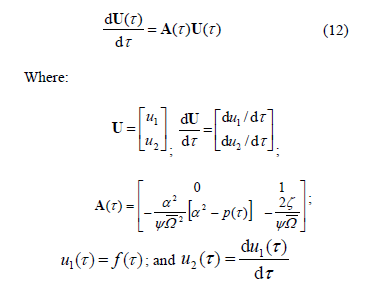
Since 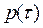 is periodic, it is clear that matrix
is periodic, it is clear that matrix 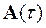 is periodic. The periodicity of matrix
is periodic. The periodicity of matrix 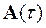 can be used to obtain the solution of Eq. (8b) by making use of the Floquet's theory. The character of the solutions for Eq. (8b) depends on the values of the harmonically varying coefficients.
can be used to obtain the solution of Eq. (8b) by making use of the Floquet's theory. The character of the solutions for Eq. (8b) depends on the values of the harmonically varying coefficients.
As shown by Timoshenko and Gere [18] depending on the magnitude and frequency of the periodic axial load, stable or unstable conditions can be reached. From Floquet's theory it is concluded that the borders between stable and unstable conditions the solutions for Eq. (8b) become periodic with period 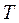 or
or 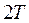 with
with 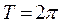 .
.
The solution with period 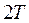 is considered first and can be expressed in the form of series expansion as follows:
is considered first and can be expressed in the form of series expansion as follows:
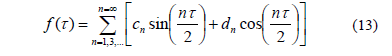
Substituting Eq. (13) into (8b) and grouping the terms appropriately, an expression of the following form is generated:
To satisfy Eq. (18) all terms 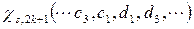 and
and 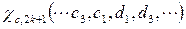 must be equal to zero. Then a homogenous system of linear equations expressed in terms of
must be equal to zero. Then a homogenous system of linear equations expressed in terms of 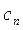 and
and 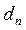 is produced which by making the determinant of its matrix equal to zero then the non-trivial solutions can be obtained as follow:
is produced which by making the determinant of its matrix equal to zero then the non-trivial solutions can be obtained as follow:
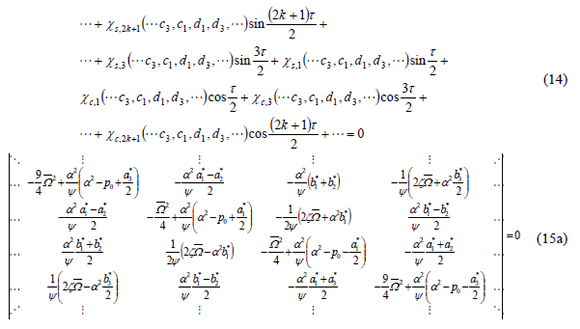
The solution with period 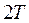 indicated by Eq. (13) is only applicable to the odd number of regions as described by Kumar and Mohammed [14]. Since closed expressions for the regions of instability are of interest, it is necessary to consider a finite part of the determinant shown in Eq. (19a). A sufficiently close approximation for the infinite eigenvalue problem is obtained by taking n= 1 inEq. (17) according to Svensson [12]. Now using this approximation Eq. (15a) is reduced to:
indicated by Eq. (13) is only applicable to the odd number of regions as described by Kumar and Mohammed [14]. Since closed expressions for the regions of instability are of interest, it is necessary to consider a finite part of the determinant shown in Eq. (19a). A sufficiently close approximation for the infinite eigenvalue problem is obtained by taking n= 1 inEq. (17) according to Svensson [12]. Now using this approximation Eq. (15a) is reduced to:
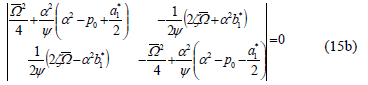
Eq. (15b) gives rise to a fourth-order algebraic equation of the form 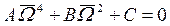 from which the following value of
from which the following value of 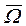 can be obtained:
can be obtained:
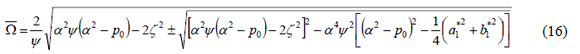
In a similar fashion the solution with period T can be determined taking the solution in the form of series expansion:
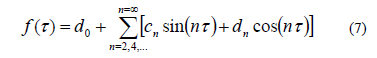
Following the same procedure used for the solution with period 2T, substituting Eq. (17) into (8b) and grouping the terms appropriately, an expression of the following form is generated:
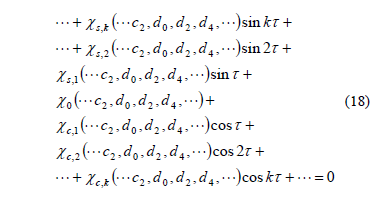
From the solution described in Eq. (17), only the even number of regions can be found according to Kumar and Mohammed [14]. As previously stated, closed formulas for the regions of instability are of interest, so it is necessary to consider a finite part of the determinant shown in Eq. (19a). In a similar way, a sufficiently close approximation for the infinite eigenvalue problem is obtained by taking n= 1 in Eq. (17). By using this approximation Eq. (19b) can be obtained. Unlike the previous case, the determinant expressed by Eq. (19b) does not produce a fourth-order algebraic equation of the form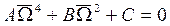 . To find an expression in this form it is necessary that either one
. To find an expression in this form it is necessary that either one 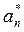 or
or 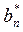 be equal to zero. If this condition is satisfied, closed expressions for the regions of instability can be found and written as
be equal to zero. If this condition is satisfied, closed expressions for the regions of instability can be found and written as

where A, B and C are calculated as listed below.
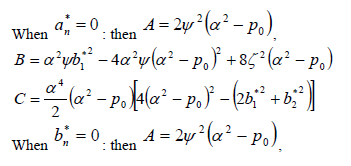
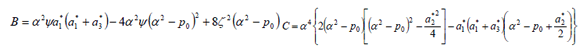
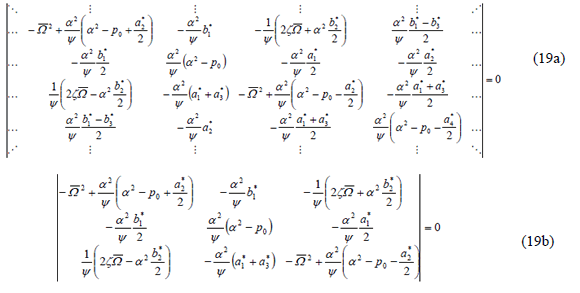
When both 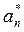 and
and 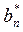 are different from zero, Eq. (20) is not applicable and the solution shall be obtained by solving Eq. (19b).
are different from zero, Eq. (20) is not applicable and the solution shall be obtained by solving Eq. (19b).
References
[1] C. Koning, C. and Taub, T., Impact buckling of thin bars in the elastic range hinged at both ends, Luftfahrtforschung, 10(2), pp. 55-64, 1933, (translated as NACA TM 748 in 1934). [ Links ]
[2] Simitses, G. J. and Hodges, D. H., Fundamentals of Structural Stability, ELSEVIER Inc, Chapter 12, pp. 329-332, 2006. [ Links ]
[3] Bolotin, V. V., The Dynamic Stability of Elastic Systems, Holden-Day San Franscisco. 1964. [ Links ]
[4] Wirsching, P. H. and Yao, T. P., Random Behavior of Columns," J. of the Engineering Mechanics Division, 97 (3), pp. 605-618, 1971. [ Links ]
[5] Iwatsubo, T., Sugiyama, Y. and Ishihara, K., Stability and Non-Stationary Vibration of Columns under Periodic Loads, J. of Sound and Vibration, 23 (2), pp. 245-257, 1972. [ Links ]
[6] Ahmadi, G. and Glockner, P. G., Dynamic Stability of Kelvin-Viscoelastic Column, J. of Engineering Mechanics, 109 (4), pp. 990-999, 1983. [ Links ]
[7] Simitses, G. J., Suddenly-Loaded Structural Configurations, J. of Engineering Mechanics, 110 (9), pp. 1320-1334, 1984. [ Links ]
[8] Sridharan, S. and Benito, R., (1984). Columns: Static and Dynamic Interactive Buckling, J. of Engineering Mechanics, 110 (1), pp. 49-65, 1984. [ Links ]
[9] Shigematsu, T., Hara, T. and Ohga, M., Dynamic Stability Analysis by Matrix Function, J. of Engineering Mechanics, 113 (7), pp. 1085-1100, 1987. [ Links ]
[10] Sophianopoulos, D. S. and Kounadis, A. N., Dynamic Stability of Imperfect Frames Under Joint Displacements, J. of Engineering Mechanics, 120 (8), pp. 1661-1674, 1994. [ Links ]
[11] Wong, K. K. F. and Yang, R., Inelastic Dynamic Response of Structures Using Force Analogy Method," J. of Engineering Mechanics, 125 (10), pp. 1190-1199, 1999. [ Links ]
[12] Svensson, I., Dynamic Instability regions in a Damped System, J. of Sound and Vibration, 244 (5), pp. 779-793, 2001. [ Links ]
[13] Yabuki, T., Yasunori, A., Fumishige, A. F. and Lu, W., Nonlinear Effect on Instability of Steel Columns under Dynamic Axial Loads, J. of Structural Engineering, 131 (12), pp. 1832-1840, 2005. [ Links ]
[14] Kumar, T. H. and Mohammed, A., Finite element analysis of dynamic stability of skeletal structures under periodic loading, J. of Zhejiang University SCIENCE A, 8 (2), pp. 245-256. 2007. [ Links ]
[15] Dohnal, F., Ecker, H. and Springer, H., Enhanced damping of a cantilever beam by axial parametric excitation, Arch Appl. Mech, 78, 935–947, 2008. [ Links ]
[16] Mailybaev, A. A. and Seyranian, A. P., Stabilization of statically unstable columns by axial vibration of arbitrary frequency, J. of Sound and Vibration, 328 (1-2), pp. 203–212, 2009. [ Links ]
[17] Giraldo-Londoño, O. and Aristizabal-Ochoa, J. D., Dynamic stability of slender columns with semi-rigid connections under periodic axial load: verification and examples, Revista DYNA, submitted for possible publication. [ Links ]
[18] Timoshenko S. P. and Gere, J. M., Theory of Elastic Stability, 2nd Ed., McGraw-Hill Book Inc., New York, N.Y, 1961 [ Links ]
Oliver Giraldo-Londoño: received the BS in Civil Engineering in 2010 from Universidad Nacional de Colombia, Sede Medellin, and the MS in Structural Engineering in 2014 from Ohio University at Athens, OH, USA. From 2006-2009, he worked as undergraduate teacher assistant for the department of mathematics at Universidad Nacional de Colombia, Sede Medellin. From 2010-present, he has been working in the Structural Stability Research Group (GES) at Universidad Nacional de Colombia, Sede Medellin, under the advice of Dr. J. Dario Aristizabal-Ochoa. From 2011-2012, he worked as instructor of statics of structures and numerical methods at Universidad de Antioquia. From 2012-present, he has been working as graduate assistant at Ohio University at Athens, OH, USA. He was awarded the Emilio Robledo award (Colombian Society of Engineers, 2009) and the Young Researcher award (COLCIENCIAS, 2010-2011). Also, he was COLFUTURO scholar (2012-2014). His research interests include analysis and design of steel and concrete structures, non-linear mechanics, finite element modeling, bridge engineering, earthquake engineering, and structural dynamics.
J. Dario Aristizabal-Ochoa: received the Bachelor degree. in Civil Engineering in 1970 from the National University of Colombia. Medellin, Colombia, the MS and PhD degrees in Structural Engineering in 1973 and 1976, respectively from the University of Illinois at Champaign –Urbana, USA. From 1977 to 1978, he worked for the Portland Cement Association, Skokie, Illinois, USA as Structural Researcher. From 1978-1981 he worked as Marketing Manager of Seismic Applications for MTS Systems at Eden Prairie, Minnessota, USA. From 1981-1995 as Professor for the Universities of Vanderbilt at Nashville, Tennessee and for the California State University at Fullerton California, USA. Currently, he is full Professor and director of the Structural Stability Research Group at the National University of Colombia at Medellin. He was awarded the "Engineering Foundation" grant in 1982 by the American Institute of Civil Engineers (ASCE), the Raymond Reese Structural award by the American Concrete Institute (ACI) in 1984, and NSF research grant in 1988. Currently, he is a Full Professor in Civil Engineering, School of Mines, and National University of Colombia at Medellin. He is an active editorial member and reviewer of several international Journals (ICE, ASCE, ACI, PCI, ELSEVIER). His research interests include: steel, reinforced concrete structures, structural dynamics and stability, composite materials, analysis and design of bridges, nonlinear analysis, seismic design, soil-structural interaction. His research work is referenced by numerous textbooks and construction codes (ACI, AISC, ASSHTO) and technical papers.