Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.185 Medellín maio/jun. 2014
https://doi.org/10.15446/dyna.v81n185.36469
http://dx.doi.org/10.15446/dyna.v81n185.36469
Straight-Line Conventional Transient Pressure Analysis for Horizontal Wells with Isolated Zones
Análisis Convencional de Pruebas de Presión en Pozos Horizontales con Zonas Aisladas
Freddy Humberto Escobar a, Alba Rolanda Meneses b & Liliana Marcela Losada c
a Facultad de Ingeniería.,Universidad Surcolombiana/CENIGAA, Colombia, fescobar@usco.edu.co
b Facultad de Ingeniería, Universidad Surcolombiana/CENIGAA, Colombia, albita_meneses@hotmail.com
c Facultad de Ingeniería, Universidad Surcolombiana/CENIGAA, lilianalosada@outlook.com
Received: January 22th, 2013. Received in revised form: January 23th, 2014. Accepted: January 30th, 2014
Abstract
It is common in the oil industry to complete horizontal wells selectively. Even, this selection is performed naturally since reservoir heterogeneity may cause segmented well performance. Segmentation may be partially open to flux due to high skin factor or low permeability bands. They can be treated as a nonuniform skin distribution. A few models have been introduced to capture these special details. Existing interpretation methodologies use non-linear regression analysis and the TDS technique; but, there is an absence of equations for the conventional technique. In this study, the conventional methodology is developed for the analysis of pressure transient tests in horizontal wells with isolated zones so directional permeabilities and skin factors can be obtained. The developed expressions were tested successfully with several examples reported in the literature and compared to results from other sources.
Key Words: Horizontal well, isolation zones, partial completion, flow regimes.
Resumen
Es común en la industria petrolera completar los pozos en forma selectiva. Incluso, dicha selección se efectúa de forma natural ya que la heterogeneidad del yacimiento podría causar comportamiento segmentado del pozo. La segmentación podría estar parcialmente abierto al flujo en virtud a la alto factor de daño bajas vetas de permeabilidad. Ellas pueden tratarse como una distribución no uniforme del factor de daño. Algunos pocos modelos se han introducido para capturar estos detalles especiales. Las metodologías de interpretación existentes usan análisis de regresión no lineal y la técnica TDS; pero, se adolece de ecuaciones para el método convencional. En este estudio se desarrolla la metodología convencional para la interpretación de pruebas de presión en pozos horizontales con zonas aisladas de modo que se puedan estimar las permeabilidades y los factores de daño. Las expresiones desarrolladas se probaron satisfactoriamente con varios problemas encontrados en la literatura y se compararon con los resultados procedentes de otras fuentes.
Palabras clave: Pozo horizontal, zonas aisladas, completamiento parcial, regímenes de flujo.
1. Introduction
Selective completion is a current operation performed on horizontal wells. Reservoir heterogeneity may also cause segmentation due to low permeability bands [1]. As indicated by [1], [2] and [3] the existence of an intermediate late radial or pseudorradial flow regime is the most important feature of the transient-pressure response of segmented horizontal wells. They found that the semilog slope of the late radial flow regime is affected by the number of equal-length segments.
Horizontal wells with isolated areas can be a practical solution for such problems presented in different formations such as gas/water coning, sand production and asphalt production; however, it has a great impact in the skin factor. Currently, the characterization of locations is important since it is a valuable tool which allows for the determination of the best exploitation scenario.
Recently, [4] introduced a new model for the type of geometry here discussed. They made a detailed discussion of the importance and impact of selective horizontal well completion. Also, they formulated the TDS methodology, initially introduced by [5] for horizontal wells, for interpretation of well pressure tests in segmented horizontal wells. In this study, the solution proposed by [4] is used to develop equations to be used in the conventional straight-line methodology and successfully applied to field examples provided by [4] and [6]. The results of the estimated permeabilities in the x and z directions and skin factors were compared with those from [4] using the TDS technique. Escobar et al. [7] have indicated the importance of the traditional-conventional analysis even in transient-rate tests interpretation.
So far, the only available methodology for well test interpretation in the systems under consideration was the one presented by [4] following the philosophy of the TDS technique [8]. However, the importance of its application is based upon some examples recently reported in the literature. For instance, [9] presented some examples for the use of zonal isolations in horizontal well completions in a hydraulic fracturing treatment which was conducted with five packer isolation systems so that five isolated zones were created. On the other hand, [10] introduced some field examples for well testing procedures in multi-zone openhole completion wells in which casing annulus packers, instead of cement, were used to provide the isolations.
2 Formulation
2.1. Mathematical Model
The model developed by [1] corresponds to the dimensionless pressure governing equation based upon the following assumptions: (1) homogeneous reservoir, with constant and uniform thickness with closed top and bottom boundaries. (2) Anisotropic system but with constant porosity and permeability in each direction, (3) negligible frictional and gravitational effects, and (4) the well extends in the midpoint of the formation height.
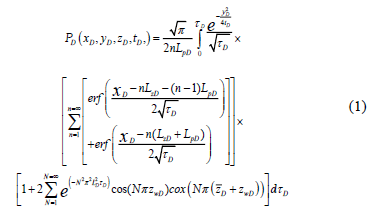
In which the dimensionless parameters are as follows:
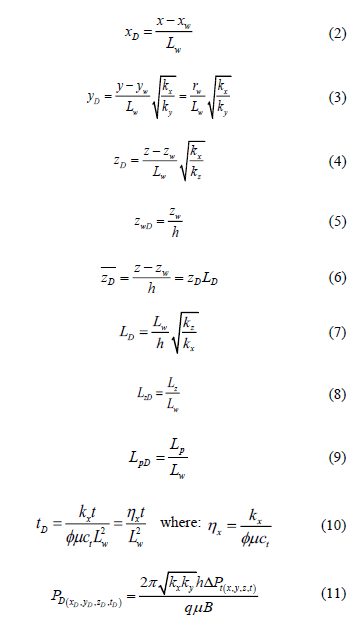
2.2. General equation of horizontal wells with isolated zones
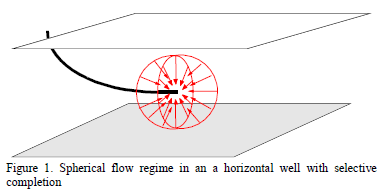
Flow regimes in horizontal wells depend upon several issues mainly related to geometry. When the ratio of the wellbore length to the reservoir thickness, LD, is less than 5 the well acts a single source/sink, then, early spherical flow develops. As example of such case is sketched in Fig. 1. If 5 < LD < 20 then, vertical early-radial flow takes places, however, if LD becomes larger than 20 then early-radial flow cannot be seen since the formation thickness results too thin compared to the wellbore length and the top and bottom of the formation are quickly reached.
As stated before, radial flow regime develops in short horizontal wells (LD=20) with or without isolated zones. The governing expression presented by [4] is given by:
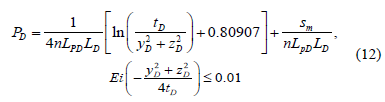
When Z=0, Equation 12 becomes:
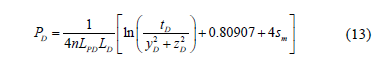
Replacing the dimensionless quantities in Equation (13), dividing by the natural log of 10 and solving for the well-flowing pressure, it yields:
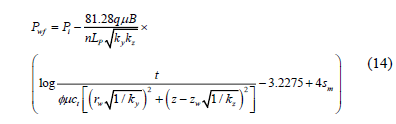
The slope, mER, from a semilog plot of pressure versus time allows for the estimation of (kykz)0.5,
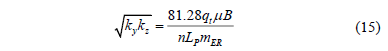
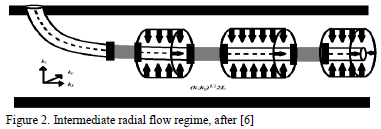
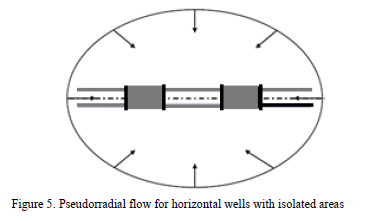
The sketch of Fig. 2 shows the development of an intermediate radial flow when a horizontal well possesses isolated zones indicating that 5 < LD < 20. The governing dimensionless pressure derivative equation for such flow regime is:
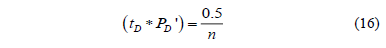
Since the semilog slope is natural log of 10 times higher than the pressure derivative value, Equation (16) allows one to find an expression to find the horizontal permeability, (kxky)0.5 from the semilog slope, mER, once the dimensionless pressure derivative is placed in oilfield units;
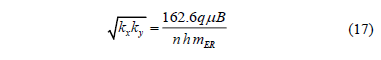
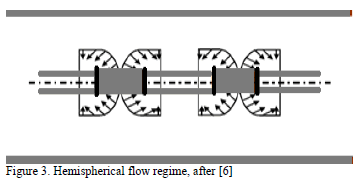
As described by Fig. 3, the pseudo-spherical (or two hemispherical) flow develops when the length of the
perforated area is so short compared to the formation thickness forcing the well to act as a single source/sink. The dimensionless pressure derivative governing equation presented by [4] is;
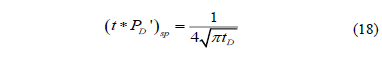
Integration of the Equation (18) leads us to obtain the dimensionless pressure for such flow regime:
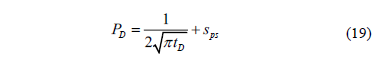
Replacing the dimensionless terms, we obtain:
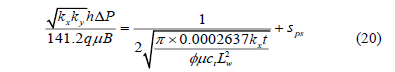
The slope of a Cartesian plot of pressure versus the inverse square root of time, mps, allows one to calculate (kx)0.5, knowing mps of a Cartesian graph.
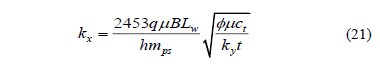
Needless to say that the pseudo-spherical skin factor can be obtained from the intercept of such a plot.
In long horizontal wells (LD>20), the early radial flow regime is hardly seen while early linear flow is dominant in the proximities to the well. The governing dimensionless pressure derivative equation for this linear flow is given by [4],
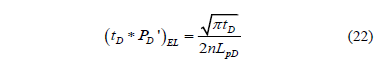
Integration of Equation 22 leads to the dimensionless pressure governing equation;
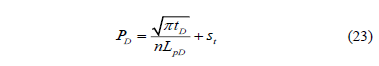
After replacing the dimensionless quantities, we obtain:
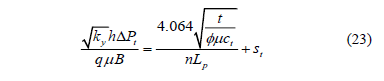
Equation (23) suggests that a plot of pressure versus the square root of time provides a straight line whose slope mEL can be used to estimate the square root of ky,
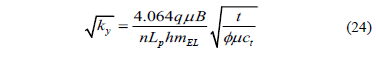
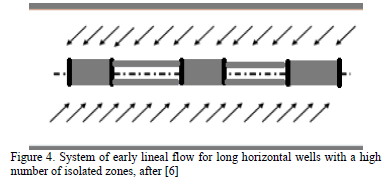
Fig. 4 shows that once early-radial flow vanishes, the well acts as a hydraulic fracture, then linear flow develops. A long horizontal well (LD>20) with a high number of isolated zones also exhibits an early linear flow regime which is effective to the whole wellbore. The dimensionless pressure derivative governing equation was presented by [4] as follows:
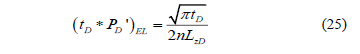
After integration of Equation 25, we obtain:
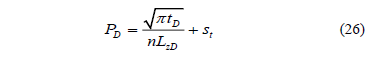
Once the dimensionless terms are replaced the expression for the dimensionless pressure is presented:
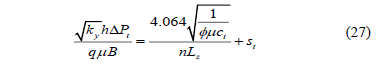
A plot of pressure versus the square root of time should a straight line which slope, mEL, allows the estimation of ky0.5,
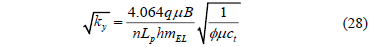
At later time, the pseudorradial or late radial flow regime develops in the horizontal plane without any influence of the vertical permeability. See Fig. 5. The dimensionless pressure governing equation was also introduced by [4] as follows:
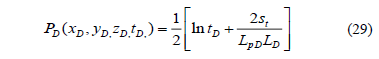
In oilfield units;
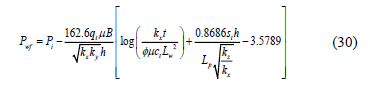
This flow regime corresponds to the radial flow regime observed in vertical wells. The dimensionless pressure derivative equation is:
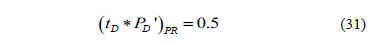
Equation (31) is useful to calculate the horizontal permeability (kxky)0.5 if the semilog slope of a plot of pressure versus time, mPR, is estimated during this flow regime, as:
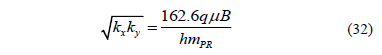
Such later flow regimes as late linear and pseudosteady state are similar to conventional horizontal wells.
Different expressions to estimate the skin factors are provided in Appendix A.
3. Examples
Example 1 was taken from [4]. Examples 2 and 3 were taken from [6]. In both cases the examples were worked by the TDS technique.
3.1. Example 1
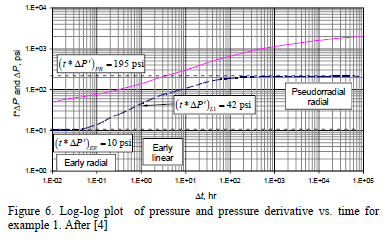
Fig. 6 presents pressure and pressure derivative data for a pressure drawdown test run in a horizontal well having two equal-length isolated zones, each of 400 ft. Other known reservoir and well data are:
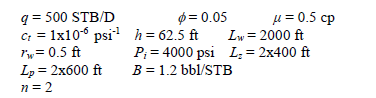
Estimate formation permeability in all directions using the conventional technique.
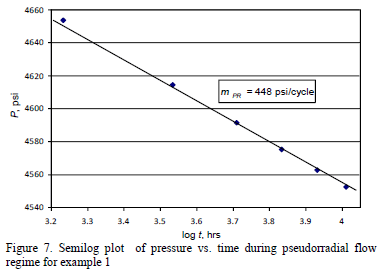
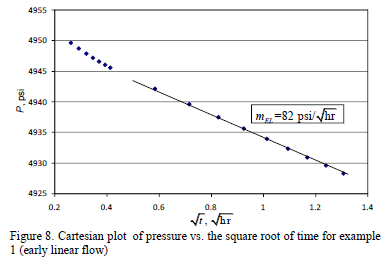
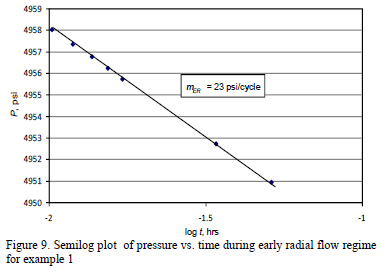
Solution. Three flow regimes are clearly seen in Fig. 6: early radial, early linear and pseudorradial. A semilog slope mPR of 448 psi/cycle is found from Fig. 7 during the late radial flow regime. Equation 32 allows estimating a horizontal permeability, (kxky)0.5 of 0.87 md. The Cartesian plot of pressure versus the square root of time given in Fig. 8 provides a slope, mEL, of 82 psi/hr0.5. Using Equation 24 a value of ky of 1.57 md is found. Knowing (kxky)0.5 and ky, a value of kx of 0.49 md is readily obtained. From Fig. 9, a semilog slope, mER, of 23 psi/cycle during the early radial flow regime is used to calculate a value of (kykz)0.5 of 0.88 md using Equation 17. From this, a value of 0.49 for kz is then found.
3.2. Example 2
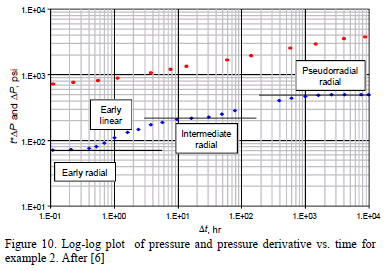
The pressure and pressure derivative data for a drawdown test of a horizontal well are given in Fig. 10. Other relevant data are given as follows:
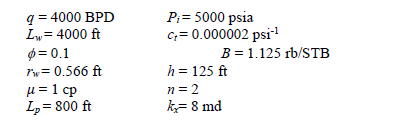
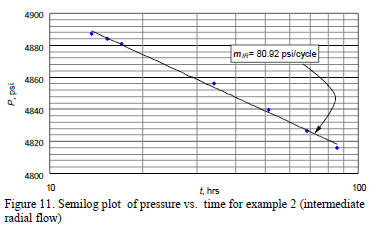
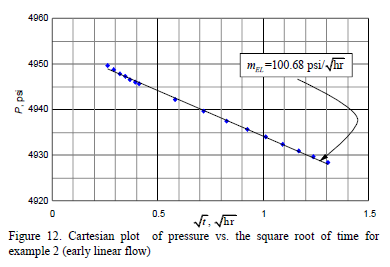
Solution. Early radial, early linear, intermediate radial and pseudorradial flow regimes are clearly seen in the pressure derivative curve of Fig. 10. A slope, mIR, of 80.92 psi/cycle is obtained from the semilog plot given in Fig. 11 which allows to estimate a (kykz)0.5 value of 2.82 md using Equation 15. Then, using a slope of 100.68 psi/hr0.5 read from Fig. 12, a y-direction permeability of 4.12 md is obtained by means of Equation 24. kz is readily found from (kykz)0.5 and ky to be 1.94 md.
3.3. Example 3
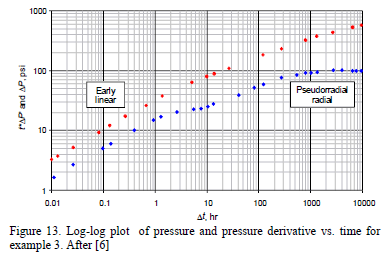
Figure 13 contains the pressure and pressure derivative data form a drawdown test of a horizontal well presented by [6].
Reservoir, fluid and well parameters are given below:
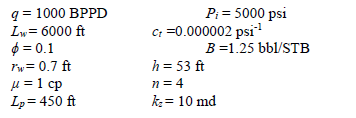
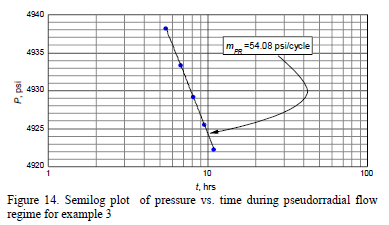
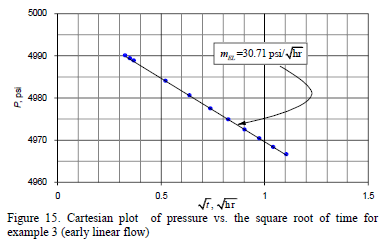
Solution. From the pressure and pressure derivative log-log plot of Fig. 13 the early linear and pseudorradial flow regimes are clearly observed. The semilog slope during the pseudorradial flow regime, Figure 14, mPR = 54.08 psi/cycle, leads to the estimation of a horizontal permeability value (kxky)0.5 of 17.73 md. A Cartesian slope during linear flow, mEL = 30.71 psi/hr0.5, obtained from Fig. 15 is used to estimate a ky = 15.04 md from Equation 24. kx is then estimated to be 20.9 md.
4. Comments on the Result
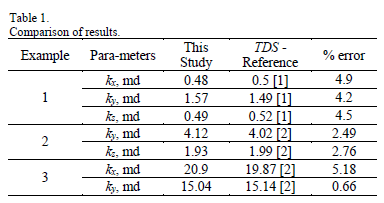
Table 1 presents the results obtained from this work and compared to the values reported by [1] and [2]. Notice that the deviation errors of the results obtained in this work are acceptable indicating that the equations developed work well.
5. CONCLUSION
The straight-line conventional method for pressure-transient analysis was complemented with new equations for horizontal wells with isolated zones. The equations were successfully applied to examples reported in the literature and provided similar results to the TDS technique.

Apendix A. Skin factor Equations
The mechanical skin factor from Equation 14 is:
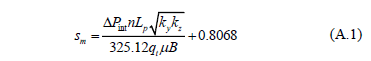
The pseudo-spherical skin factor from Equation 20 is:
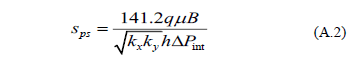
The total skin factor from Equation 23 is:
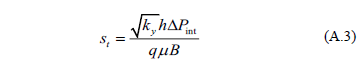
The total skin factor from Equation 30 is:
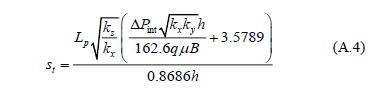
References
[1] Kamal, M.M., Buhidma, I.M., Smith, S.A., and Jones, W.R., Pressure Transient Analysis for a Well with Multiple Horizontal Sections. Paper SPE 26444, SPE Annual Technical Conference and Exhibition, Houston, 3-6 October. 1993 [ Links ]
[2] Ozkan, E., Analysis of Horizontal Well-Responses: Contemporary vs. Conventional. SPEREE 4 (4). pp. 260-269, 2001. [ Links ]
[3] Yildiz, T. And Oskan, E., Transient Pressure Behavior of Selectively Completed Horizontal Wells. Paper SPE 28388, SPE Annual Technical Conference and Exhibition, New Orleans, USA, pp. 25-28 Sep., 1994. [ Links ]
[4] Al Rbeawi, S. And D. Tiab, D., Effect of the Number and Length of Zonal Isolations on Pressure Behavior of Horizontal Wells. Paper SPE 142177, SPE production and operations Symposium held in Oklahoma City, Oklahoma, USA, pp. 27-29 March. 2011. [ Links ]
[5] Engler, T. W. And Tiab, D., Analysis of Pressure and Pressure Derivatives without Type-Curve Matching. 6- Horizontal Well Tests in Anisotropic Reservoirs. Journal of Petroleum Science and Engineering, 15, pp. 153-168, 1996. [ Links ]
[6] Al Rbeawi, S., Interpretation of Pressure Transient Tests of Horizontal Wells With Multiple Hydraulic Fractures and Zonal Isolations. [PhD Thesis]. Norman, OK: The University of Oklahoma, 2012. [ Links ]
[7] Escobar, F.H., Rojas, M.M. and Cantillo, J.H., Straight-Line Conventional Transient Rate Analysis for Long Homogeneous and Heterogeneous Reservoirs. Dyna. year 79, (172), pp. 153-163, 2012 [ Links ]
[8] Tiab, D., 1995, Analysis of Pressure and Pressure Derivative without Type-Curve Matching: 1- Skin and Wellbore Storage". Journal of Petroleum Science and Engineering, Vol 12, pp. 171-181. 1995. [ Links ]
[9] Maddox, B., Wahrton, M., Hinkie, R., Farabee, M. and Ely, J., Cementless Multi-Zone Horizontal Completion Yields Three-Fold Increase". Paper IADC/SPE 112774 presented at the IADC/SPE Drilling Conference in Orlando, FL. March, pp. 4-6, 2008. [ Links ]
[10] Brooks, R.T. and Scott, S., Improvement and Testing Multi-Zone Open-Hole Carbonate Formations. Paper SPE 119426 presented at the Middle East Oil and Gas Conference. Bahrain. March, pp. 15-18, 2009. [ Links ]
Freddy Humberto Escobar, received a BSc degree from Universidad de America in 1989, both the MSc received in 1995 and the PhD in 2002 were obtained from the University of Oklahoma. All his degrees are in Petroleum Engineering. Dr. Escobar joined Universidad Surcolombiana in 1996 and is the director of the Research Group on Transient Well Testing and the president of Cenigaa (Research Center for Sciences and geo-agro-environmental resources).
Alba Rolanda Meneses, received her BSc in Petroleum Engineering from Universidad Surcolombiana in 2013. She has recently joined Schlumberger Limited as a field engineer.
Liliana Marcela Losada, received her BSc in Petroleum Engineering from Universidad Surcolombiana in 2013.