http://dx.doi.org/10.15446/dyna.v81n185.37598

Thermodynamic analysis of R134a in an Organic Rankine Cycle for power generation from low temperature sources

Análisis termodinámico del R134a en un Ciclo Rankine Orgánico para la generación de energía a partir de fuentes de baja temperatura

 

Fredy Vélez ^a, Farid Chejne ^b & Ana Quijano ^c

 

^a CARTIF Centro Tecnológico, España. frevel@cartif.es
^b Universidad Nacional de Colombia, sede Medellín, Colombia. fchejne@unal.edu.co
^c CARTIF Centro Tecnológico, España. anaqui@cartif.es

 

Received: March 26^th, 2013. Received in revised form: December 23^th, 2013. Accepted: January 14^th, 2014

---

Abstract
This paper reports the main results of a thermodynamic study realized on the use of a low temperature heat source (150°C as maximum) for power generation through a subcritical Rankine power cycle with R134a as working fluid. The procedure for analyzing the behavior of the proposed cycle consisted of modifying the input pressure, temperature and/or discharge pressure of the turbine with working fluid at conditions of both saturation and overheating. Results show that the efficiency of the cycle for this fluid is a weak function of temperature, i.e., overheating the inlet fluid to the turbine does not cause a significant change in the efficiency. However, when the pressure ratio in the turbine increases, it is much more efficient, and also, as the input temperature to the turbine rises, the efficiency increases more sharply. Furthermore, the effect of adding an internal heat exchanger to the cycle was analyzed, giving as a result a maximum efficiency of 11% and 14% for the basic cycle and with an internal heat exchanger, respectively.

Keywords: Energy efficiency; organic Rankine cycle; power generation; waste heat; renewable energy.

Resumen
Este trabajo presenta los principales resultados del estudio termodinámico realizado sobre el uso de una fuente de calor de baja temperatura (150°C como máximo) para la generación de energía a través de un ciclo Rankine subcrítico con R134a como fluido de trabajo. El procedimiento para analizar el comportamiento del ciclo propuesto consistió en modificar la presión y temperatura de entrada y/o descarga de la turbina, con el fluido de trabajo en condiciones tanto de saturación, como sobrecalentamiento. Como resultado, se puede indicar que la eficiencia del ciclo con este fluido es una débil función de la temperatura, es decir, sobrecalentar el fluido a la entrada de la turbina no causa un cambio significativo en la eficiencia. Sin embargo, cuando la relación de presión en la turbina aumenta, la eficiencia incrementa, y también, conforme la temperatura de entrada a la turbina aumenta, la eficiencia aumenta pronunciadamente. Además, se analizó el efecto de adicionar un intercambiador interno de calor que aumentó los valores de eficiencia obtenidos, dando como resultado, una eficiencia máxima del 11% y 14% para el ciclo básico y con el intercambiador interno de calor, respectivamente.

Palabras clave: Eficiencia energética; ciclo Rankine Orgánico; generación de energía; calor residual; energías renovables.

---

 

1. Introduction

The use of fossil fuels (e.g., oil and coal) as an energy source has many negative environmental impacts, such as the release of pollutants and resource depletion. A high consumption rate of fossil-fuels will result in an increase in environmental pollution during the next century, due to the emission of CO₂ and other gases that cause global warming through what is known as the greenhouse effect [1]. In order to reduce CO₂ emissions and oil dependency, each country in the world is responsible for improving the quality of its energy sources [1]. One of these improvements is the use of waste heat or low temperature sources (such as some renewables) [2], being the organic Rankine cycle "ORC" a promising technology for their conversion into power [2-5]. The ORC principle of operation is equal to the conventional Rankine cycle, with the difference of using an organic agent as working fluid. However, unlike the conventional Rankine, the change of fluid allows the energy recovery from low enthalpy sources for work or electricity production. Thus, one of the main research lines realized on this issue is the selection of a suitable working fluid due to its great influence in the design of the process [2-4], [6-10]. Depending on the application, the heat source and the temperature level, the fluid must have optimum thermodynamic properties at the lowest possible temperatures and pressures, and also satisfy several criteria such as being economical, nontoxic, nonflammable, environmentally-friendly, allowing a high utilization of the available energy from the heat source. If all these aspects are considered, a few fluids can be used [2,4-6] and therefore, after an extensive literature review, a preliminary comparison of the previous aspects and the thermodynamic performance obtainable for heat sources up to 100°C with different fluids, R134a was chosen as working fluid. This selection has been done on the basis that R134a: is a nontoxic and nonflammable fluid (belonging to the group A1 based on ASHRAE 34) and its Ozone Depletion Potential (ODP) is zero; there is wide experience of turbomachines and heat exchangers using this fluid; R134a has a high molecular mass (chemical formula: CF₃CH₂F, MM=102kg/kmol), so that turbines work with low enthalpy drops and low mechanical stresses; it has a temperature and critical pressure of 101.1°C and 40.6 bar, respectively, allowing its use in the temperature range of interest, and the condenser operates at a higher pressure than atmospheric, and therefore air in-leakages do not occur. Several researchers have investigated the application and performance of ORC with R134a as a working fluid. In [8], the efficiency of the ORC using benzene, ammonia, R134a, R113, R11 and R12 was analyzed, last two fluids obtaining greater efficiencies, however they are also substances of limited use [11]. An analysis of a regenerative ORC based on the parametric optimization, using R12, R123, R134a, and R717 as working fluids superheated at constant pressure was carried out in [12-13]. Results revealed that selection of a regenerative ORC during overheating using R123 as working fluid appears to be a good system for converting low-grade waste heat to power. In [14-15] a low-temperature solar organic Rankine cycle system was designed and built with R134a as working fluid that works between 35.0°C and 75.8°C for reverse osmosis desalination in Greece. The results showed a system efficiency of about 7% and 4%, respectively. Other studies that have analyzed the use of R134a as working fluid in the ORC cycles for reverse osmosis desalination at an experimental level [16], and also as a theoretical manner [17-22] have presented similar efficiencies as ones previously mentioned. In this same field, [23] showed a simulation to estimate the increase in the efficiency and the energy available for desalination of an upper ORC coupled with a lower ORC with R134a, obtaining an efficiency for the latter of 4.2% and a global of 3%. Other cycles with R134a for applications for geothermal sources are reported by [24-26] and in bottoming cycles with internal combustion engine in [27]. A thermodynamic screening of 31 pure component working fluids for organic Rankine cycle is given in [4] achieving an efficiency of 7.7% with cycles that operate with R134a and temperature of 100.0°C, whereas in [6] from the 20 fluids studied and reported, R134a was found to be the most suitable in terms of yield. Other works that have analyzed the use of R134a as working fluid in ORC cycles of low temperature have been realized by [9] and [28-31].

In view of what has been stated, there is a great interest in the use of this fluid for energy use of sources below 150°C. However, we detected a discrepancy in the literature about the best thermodynamic conditions for its use, because while some studies like those presented in [6,12,13] do not find its overheating interesting, others such as [21] see a positive impact working under this condition. Therefore, this paper has been developed to show in an exhaustive manner, the effective thermodynamic difference with the use of this fluid at saturated and overheating conditions. In addition, the influence of the input temperature in the turbine (in the range of 60°C-150°C) and therefore, the influence of the energy source on the performance and on the net specific work in a basic system and in a system with an Internal Heat Exchanger (IHX) has been studied.

The main contributions of the present paper are based on the scarcity of information and research leading to show the influence of the input temperature and pressure in the turbine (and therefore the energy source), as well as the inclusion of an IHX for the power cycle with R134a as working fluid in low temperature heat sources for power generation. The results show that the efficiency for this fluid is a weak function of temperature, i.e., overheating the inlet fluid to the turbine does not cause a significant change in the efficiency. However, when the pressure ratio in the turbine increases, much larger values of efficiency are obtained, and also, as the input temperature to the turbine rises, the efficiency increases more sharply. Furthermore, the effect of adding an IHX to the cycle was analyzed, giving as result a maximum efficiency of 11% and 14% for the basic cycle and with IHX, respectively.

 

2. Description of the power cycle

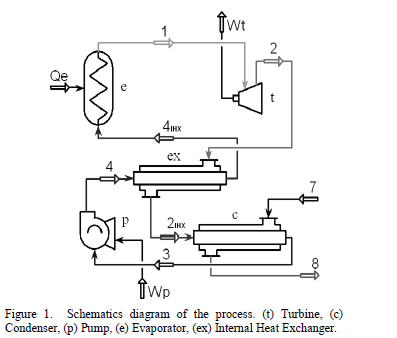
The ORC operation principle is the same as the conventional Rankine cycle. A pump pressurizes the liquid fluid, which is injected into an evaporator (heat source) to produce a vapour that is expanded in a turbine connected to a generator. Finally, the output vapor is condensed and sucked up by the pump to start the new cycle. An IHX can be also included to make even better use of the energy from the expanded vapor, preheating the pump fluid that will enter the evaporator as it is shown in Fig. 1.

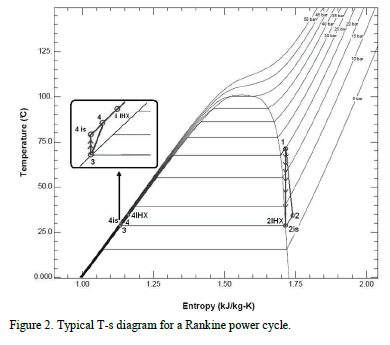
According to the state points displayed in Fig. 1, Fig. 2 shows the power cycle in a T-s-diagram plotted with [32] data. As an example, an ideal cycle process is shown by segments, which are built from the state points 1, 2_is, 3 and 4_is marked with (O). The line segment 1-2_is represents an isentropic expansion with a production of output work. Heat is extracted from 2_is to 3 along a constant subcritical pressure line. Then, an ideal compression of the saturated liquid from pressure at state point 3 to state point 4_is. Finally, the segment 4_is-1 represents the heat addition at constant subcritical pressure to the highest temperature of the cycle at state point 1.

The previous case, but operating under conditions in which the expansion process as well as compression process have a certain efficiency, is represented by the segments built from the state points 1, 2, 3 and 4 marked with (O) in the same Fig. 2, which are also related to Fig. 1. In order to increase the process efficiency, an IHX is introduced (as it can be seen in Fig. 1), in which a portion of the rejected heat, represented by an enthalpy drop from 2 to 2_IHX at constant subcritical pressure, is transferred back to the fluid, raising its enthalpy from 4 to 4_IHX at constant subcritical pressure. Net heat rejection is indicated by the enthalpy drop from 2_IHX to 3 at constant subcritical pressure. State point 3 is at the lowest temperature of the cycle and above the temperature of the heat sink. Net input heat to the cycle occurs from 4 (or 4_IHX) to 1 at constant pressure. Net output work is the difference between the output work from state points 1 to 2 and the input work pump from state points 3 to 4.

 

3. Modelling of the process

The equations used to determine the performance of the different configurations are presented in this section. Using the first law of thermodynamic, the performance of a Rankine cycle can be evaluated under diverse working conditions. For both configurations, the analysis assumes steady state conditions, no pressure drop or heat loss in the evaporator, IHX, condenser or pipes, and the constant isentropic efficiencies of 75% are assumed for the pump as well as for the turbine. The cycle's total energy efficiency is:

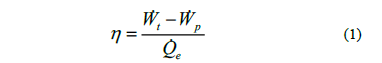
Where 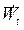is the power out from the turbine; 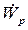is the power input in the pump defined as:

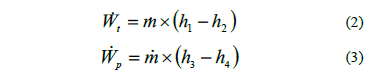
and the 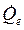is the heat input in the evaporator defined as:

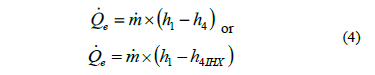
An input temperature of the condensation water T₇=15°C and a minimum working fluid condensation temperature of T₃=25°C have been considered. Otherwise, a pinch point of 10°C is maintained between T₃ and the output temperature of the condensation water (T₈) for both configurations. In the heating process, the overheating of the inlet fluid to the turbine (T₁) is considered from the condition of saturated steam up to its critical temperature. The minimum discharge pressure of the turbine (P₂) is equal to the saturation pressure of the fluid in liquid state (P₃) to the temperature T₃=25°C.

The thermodynamic analysis of the cycle was performed using a process simulator HYSYS^® (Hyprotech Co., Canada). This simulator is useful for thermodynamic analysis, especially at steady state condition, and it has the advantage of including fluid properties and ready to use optimization tools. Its predictions have been compared with the ones from [32] and the results are very similar. The simulation flow diagram is the same as the one presented in Fig. 1, and the method for resolving all the components is widely described in [3,10].

 

4. Results and discussion

This section presents the results obtained in the simulations done with R134a fluid using the method described in section 3. As it was commented in the introduction, this fluid is of interest for the temperature range under study because of its good environmental characteristics, safety and thermophysical properties (temperature and critical pressure, boiling point, etc.).

Furthermore, it must be taken into account that the ideal working fluid for a Rankine cycle is that whose saturated vapor line is parallel to the line of expansion of the turbine. As a consequence, a maximum efficiency is ensured in the turbine when this works in the area of dry steam (as it is shown in Fig. 2). This fluid has a slight negative slope in the saturation curve, and therefore the expansion process can be very close to the line of dry steam.

The procedure for analyzing the behavior of this subcritical cycle consisted of varying the inlet temperature or pressure to the turbine and/or the discharge pressure of the turbine, until these conditions do not allow the fluid to be in the gaseous state neither in the input nor in the exit of the turbine. The results obtained for saturated and overheating conditions are presented in the sections below.

4.1. Saturated conditions
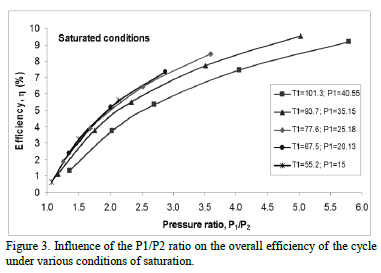
Fig. 3 has been realized to analyze the influence of the P₁/P₂ ratio (in various conditions of saturation) on the efficiency of the cycle for this fluid. The discharge pressure P₂ at five different saturated conditions were studied (7, 10, 15, 20 or 30 bar) maintaining both the inlet temperature to the turbine (in saturated conditions) and the pressure P₁ constant (the latter undoubtedly corresponds to the condition given by saturation temperature), for each curve. Fig. 3 shows that the highest efficiency is achieved when the inlet and the discharge pressure are the highest and lowest respectively, making higher the pressure ratio (i.e, making Dh greater and therefore producing more work). It is interesting to note that for the same pressure ratio, higher efficiencies are obtained for lower temperatures (or what it is, lower pressure P₁); especially in the range from 77°C to 101°C, e.g., for a T₁ of 77°C the efficiency was approximately 1.5% more than for a T₁ of 101°C. For lower temperatures this influence begins to be unappreciable.

4.2. Overheated conditions.
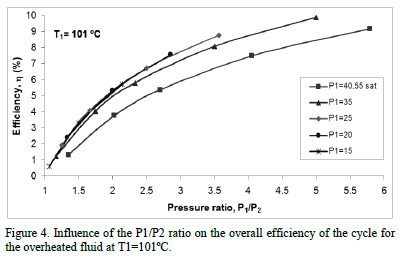
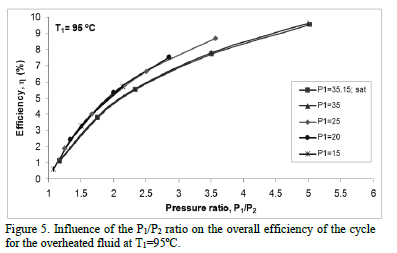
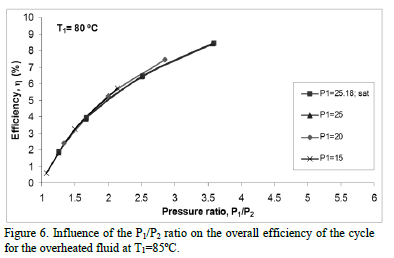
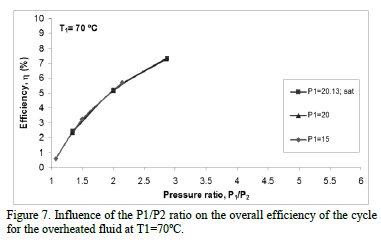
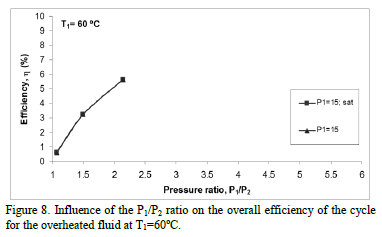
Figures 4 to 8 present the results obtained when the influence of the P₁/P₂ ratio is analyzed with an overheated fluid at constant temperatures of 101°C, 95°C, 80°C, 70°C and 60°C, respectively. The inlet temperature to the turbine, T₁, was kept constant for all the curves, but varying the discharge pressure P₂ and for each of the inlet pressures to the turbine P₁ of 15, 20, 25 and 35 bar, (i.e., analyzing the influence of the P₁/P₂ ratio with the fluid in overheating conditions on the overall efficiency of the cycle). Also the behavior of this cycle with each one of the saturation conditions presented in Fig. 3 was compared to the new conditions of overheating.

Firstly, it can be inferred from Fig. 4 to 8 that the behavior is similar to that discussed for Fig. 3, i.e., higher efficiency is achieved when the inlet and the discharge pressure is the highest and lowest respectively, (with higher pressure ratio, i.e., higher Dh and therefore more work is produced). In addition, for the same pressure ratio higher efficiencies are obtained for lower P₁ (especially in the range of 25 to 40 bar), e.g., the efficiency for a P₁ of 25 bar was approximately 1.5% more than at saturated conditions for a T₁ of 101°C. For pressures less than 25 bar such influence was not very significant.

Also Figs. 4 to 8 show the condition of overheating causes a slight increase in efficiency compared to that achieved at saturation conditions. This occurs because the inlet temperature to the turbine has a wide range of effects on the efficiency of the system depending on the slope of the isobaric curve in the region of overheated steam on the T-s diagram. If a fluid has a significantly steeper slope in the region of high pressure isobaric curve than in the region of low pressure, the system's efficiency increases as the inlet temperature to the turbine increases, otherwise it decreases. In our case, given that the R134a fluid analysis shows a slight negative slope in the saturation curve (Fig. 2), a slight overheating causes a slight increase in h, whereas, when the ratio P₁/P₂ increases, much higher values of this efficiency are obtained and in addition as T₁rises, such h increases more sharply.

Thus, the following section 4.3 discusses how the inlet temperature to the turbine T₁ influences the efficiency of the cycle, at various constant P₁/P₂ ratios.

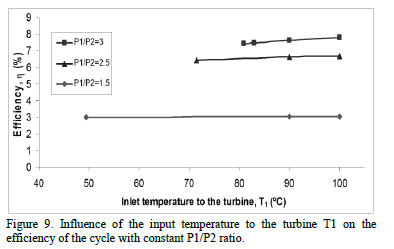
4.3. Influence of the input temperature to the turbine T₁ on the efficiency of the cycle.
In Fig. 9 the results on the h of the cycle by increasing the T₁ at a constant P₁/P₂ ratio are presented. It is obvious that when the P₁/P₂ = 1.5 (which is the lowest of those studied, see Fig. 9) the efficiency, h, increases with T₁. However, it should be noted that h is a weak function of temperature for the case of the fluid studied (as it was

reported in the section 4.2), i.e. overheating the inlet fluid to the turbine does not cause a significant change in h. However, much higher values of h are obtained when the P₁/P₂ ratio increases and also as T₁ rises, h increases more sharply as it is shown in Fig. 9.

4.4. Comparation of basic ORC vs. other with IHX
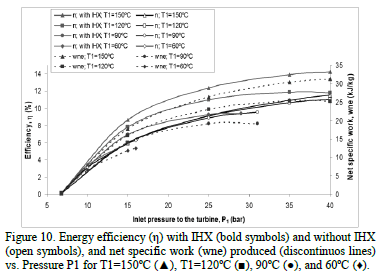
Finally, Fig. 10 presents the results of simulations realized with a basic and with an IHX ORC (Fig. 1). The inlet pressure varies from 7 bar up to its critical pressure at four constant inlet turbine temperatures: 150°C, 120°C, 90°C and 60°C. Also, a pinch point of 5°C is maintained between T₃ and the output temperature of the condensation water (T₈) and a temperature difference (DT) between T₂ and T₄ of at least 5°C for the cycle with IHX. In the heating process, the overheating of the inlet fluid to the turbine (T₁) is considered from the condition of saturated steam up to its critical temperature.

In Fig. 10, the blue tendency lines and the open blue symbols indicate the energy efficiencies of the simple cycle, the green tendency lines and the green bold symbols point to the energy efficiencies of the cycle with IHX and the discontinuous red lines represent the net specific work (wne). On the other hand, symbols represented with a triangle (▲), square (■), circle (●) and rhombus (♦) are linked with the analyzed temperatures of 150°C, 120°C, 90°C and 60°C, respectively.

Fig. 10 shows a behavior where both the h and the wne at all four temperatures increase. There are several reasons for this: noting firstly, that the input temperature and the discharge pressure of the turbine are fixed; second, we assume that the work produced by this device is that given by equation (2); third, if the Mollier diagram of this fluid is analyzed, it can be seen that, for a constant temperature, when the pressure increases, Dh rises, and 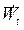along with it, which ensures the increase of both h and the wne of the cycle. It is interesting to note how, for a same inlet pressure to the turbine P₁, there is no appreciable increase in h with increasing temperature in the case of the basic cycle. However, for the cycle with IHX, the difference is more representative, both in the same cycle with IHX at different temperatures, as compared to the basic cycle at the same T₁, except in the latter case, for temperatures of 60°C and 90°C, in which it is not very noticeable the inclusion of an IHX. This occurs because as was mentioned in the preceding sections, in the case of the basic cycle, the overheating of the fluid does not cause an appreciable increase in h, except for pressures close to the maximum allowed by the T₁ studied (i.e. to higher pressure ratios), where this effect starts to be noticeable. As an example for illustrating this, considering an inlet pressure to the turbine of 20 bar, an increase of the inlet temperature to the turbine from 90°C to 150°C, caused a raise in the efficiency of 2.5% for the case of cycle with IHX. For this same pressure and inlet temperature to the turbine of 90°C, the inclusion of the IHX caused an increase in the efficiency of 0.8%, approximately, with respect to the basic cycle.

On the other hand, for the same inlet pressure to the turbine P₁, there is an appreciable increase in h with increasing temperature in the case of a cycle with IHX due to the recovery of energy. As a consequence, the amount of energy required from the heat source decreases and the overall cycle efficiency increases, as can be seen in the same eq. (1).

 

5. Conclusions

Based on the simulations carried out, the system's efficiency proposed is a weak function of temperature, because overheating the inlet fluid to the turbine does not cause a significant change in the overall efficiency of the cycle. However, when the pressure ratio in the turbine increases (obviously limited by the temperature of the heat source), much larger values of efficiency are obtained (≈5% more as maximum for the same temperature T₁) and also, as the inlet temperature to the turbine rises, the efficiency increases more sharply (≈1% more as maximum for the same pressure ratio P₁/P₂). Furthermore, adding an internal heat exchanger to the cycle increases significantly the efficiency values obtained (≈3% more as maximum).

Moreover, considering the energy analysis carried out, it can be concluded that the ORC with R134a as working fluid is suitable for the production of useful energy using low enthalpy heat, as it is possible to operate in relatively low temperature ranges. In addition, many of the aspects taken into account nowadays in these processes, such as environmental issues, safety and efficient and rational use of energy have been satisfied.

 

Acknowledgements

Authors acknowledge all the invaluable comments by Eng. Cecilia Sanz M. from CARTIF. Fredy Vélez. thanks the scholarship awarded by the "Programa Iberoamericano de Ciencia y Tecnología para el Desarrollo", CYTED, CARTIF Technological Center and University of Valladolid in order to carry out his doctoral thesis, on which this paper is based.

 

References

[1] Realpe, A., Diaz-Granados, J.A. and Acevedo, M.T., Electricity generation and wind potential assessment in regions of Colombia. Dyna, vol 171, pp, 116-122, 2012.         [ Links ]

[2] Vélez, F., Segovia, J., Martín, M.C., Antolín, G., Chejne, F. and Quijano, A., A technical, economical and market review of organic Rankine cycles for the conversion of low-grade heat for power generation. Renewable & Sustainable Energy Reviews, vol. 16, pp. 4175–4189, 2012.         [ Links ]

[3] Vélez, F., Chejne, F., Antolín, G. and Quijano, A., Theoretical analysis of a transcritical power cycle for power generation from waste energy at low temperature heat source. Energy Conversion and Management, vol. 60, pp. 188–195, 2012.         [ Links ]

[4] Saleh, B., Koglbauer, G., Wendland, M. and Fischer, J., Working fluids for low temperature organic Rankine cycles. Energy, Vol. 32, pp. 1210–1221, 2007.         [ Links ]

[5] Quolin, S., Declaye, S., Tchange, B.F. and Lemort, V., Thermo-Economic optimization of waste heat recovery organic Rankine cycles. Applied Thermal Engineering, vol. 31, pp. 2885-2893, 2011.         [ Links ]

[6] Tchange, B.F., Papadakis, G., Lambrinos, G. and Frangoudakis, A., Fluid selection for a low-temperature solar organic Rankine cycle. Applied Thermal Engineering, vol. 29, pp. 2468–2476, 2009.         [ Links ]

[7] Quolin, S., Aumann, R., Grill, A., Schuster, A., Lemort, V. and Spliethoff, H., Dynamic modeling and optimal control strategy of waste heat recovery organic Rankine cycles. Applied Energy, vol. 88, pp. 2183–2190, 2011.         [ Links ]

[8] Hung, T.C., Shal, T.Y. and Wang, S.K., A review of organic Rankine cycles (ORC`s) for the recovery of low-grade waste heat. Energy, vol. 22 (7), pp. 661-667, 1997.         [ Links ]

[9] Chen, H., Goswami, Y. and Stefanakos, E., A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renewable & Sustainable Energy Reviews, vol. 14, pp.3059–3067, 2010.         [ Links ]

[10] Vélez, F., Segovia, J., Martín, M.C., Antolín, G., Chejne, F. and Quijano, A., Comparative study of working fluids for a Rankine cycle operating at low temperature. Fuel Processing Technology, vol. 103, pp.71–77, 2012.         [ Links ]

[11] U.S. Environmental Protection Agency. Class I Ozone Depleting Substances. [Online]. [date of reference March 11^th of 2013] Available at: www.epa.gov/ozone/science/ods/classone.html.         [ Links ]

[12] Roy, J.P., Mishra, M.K. and Misra, A., Parametric optimization and performance analysis of a waste heat recovery system using organic Rankine cycle. Energy, vol. 35, pp. 5049-5062, 2010.         [ Links ]

[13] Roy, J.P., Mishra, M.K. and Misra, A., Parametric optimization and performance analysis of a regenerative organic Rankine cycle using low-grade waste heat for power generation. International Journal of Green Energy, vol. 8 (2), pp. 173–196, 2011.         [ Links ]

[14] Manolakos, D., Papadakis, G., Mohamed, E., Kyritsis, S. and Bouzianas, K., Design of an autonomous low-temperature solar Rankine cycle system for reverse osmosis desalination. Desalination, vol. 183, pp. 73–80, 2005.         [ Links ]

[15] Manolakos, D., Papadakis, G., Kyritsis, S. and Bouzianas, K., Experimental evaluation of an autonomous low-temperature solar Rankine cycle system for reverse osmosis desalination. Desalination, vol. 203, pp. 366–374, 2007.         [ Links ]

[16] Manolakos, D., Kosmadakis, G., Kyritsis, S. and Papadakis, G., On site experimental evaluation of a low-temperature solar organic Rankine cycle system for RO desalination. Solar Energy, vol. 83, pp. 646–656, 2009.         [ Links ]

[17] Manolakos, D., Kosmadakis, G., Kyritsis, S. and Papadakis, G., Identification of behaviour and evaluation of performance of small scale, low-temperature organic Rankine cycle system coupled with a RO desalination unit. Energy, vol. 34, pp. 767–774, 2009.         [ Links ]

[18] Bruno, J.C., López-Villada, J., Letelier, E., Romera, S. and Coronas, A., Modelling and optimisation of solar organic Rankine cycle engines for reverse osmosis desalination. Applied Thermal Engineering, vol. 28, pp. 2212–2226, 2008.         [ Links ]

[19] Delgado-Torres, A. and García-Rodríguez, L., Analysis and optimization of the low-temperature solar organic Rankine cycle (ORC). Energy Conversion and Management, vol. 51, pp. 2846–2856, 2010.         [ Links ]

[20] Thanche, B.F., Lambrinos, G., Frangoudakis, A. and Papadakis, G., Exergy analysis of micro-organic Rankine power cycles for a small scale solar driven reverse osmosis desalination system. Applied Energy, vol. 87, pp. 1295–1306, 2010.         [ Links ]

[21] Schuster, A. and Karl, J., Simulation of an innovative stand-alone solar desalination system using an organic Rankine cycle. Int. J. of Thermodynamics, vol. 10(4), pp. 155-163, 2007.         [ Links ]

[22] Karellas, S., Terzis, K. and Manolakos, D., Investigation of an autonomous hybrid solar thermal ORC-PV RO desalination system. The Chalki island case. Renewable Energy, vol. 36, pp. 583-590, 2011.         [ Links ]

[23] Kosmadakis, G., Manolakos, D. and Papakakis, G., Parametric theoretical study of a two-stage solar organic Rankine cycle for RO desalination. Renewable Energy, 35, pp. 989–996, 2010.         [ Links ]

[24] Franco, A. and Villani, M., Optimal design of binary cycle power plants for water-dominated, medium-temperature geothermal fields. Geothermics, vol. 38, pp. 379–391, 2009.         [ Links ]

[25] Aneke, M., Agnew, B. and Underwood, C., Performance analysis of the Chena binary geothermal power plant. Applied Thermal Engineering, vol. 31, pp. 1825-1832, 2011.         [ Links ]

[26] Astolfi, M., Xodo, L., Romano, M. and Macchi, E., Technical and economical analysis of a solar–geothermal hybrid plant based on an organic Rankine cycle. Geothermics, vol. 40, pp. 58–68, 2011.         [ Links ]

[27] Vaja, I. and Gambarotta, A., Internal combustion engine (ICE) bottoming with organic Rankine cycles (ORCs). Energy, vol. 34, pp. 767–774, 2009.         [ Links ]

[28] Schuster, A., Karellas, S., Kakaras, E. and Spliethoff, H., Energetic and economic investigation of organic Rankine cycle applications. Applied Thermal Engineering, vol. 29, pp. 1809–1817, 2009.         [ Links ]

[29] Chen, H., Goswami, Y., Rahman, M. and Stefanakos, E., A supercritical Rankine cycle using zeotropic mixture working fluids for the conversion of low-grade heat into power. Energy, vol. 36, pp. 549-555, 2011.         [ Links ]

[30] Mikielewicz, D. and Mikielewicz, J., A thermodynamic criterion for selection of working fluid for subcritical and supercritical domestic micro CHP. Applied Thermal Engineering, vol. 30, pp. 2357-2362, 2010.         [ Links ]

[31] Lakew, A. and Bolland, O., Working fluids for low temperature heat source. Applied Thermal Engineering, vol. 30, pp. 1262–1268, 2010.         [ Links ]

[32] Lemmon, E.W., Huber, M.L. and Mclinden, M.O., Reference fluid thermodynamic and transport properties (REFPROP). NIST Standard Reference Database, 23, Version 8.0; 2007.         [ Links ]

 

Fredy Vélez. Ph.D in Energetic and Fluid-Mechanical Engineering by University of Valladolid (2011). MSc in Engineer -Emphasis in Chemical Engineering- (2007) and Chemical Engineer (2004), both by Colombian National University, where he was also an Associate Professor at the Energy and Process School. He started to work as researcher in the field of renewable energies in 2004. Since 2007 he is actively working in Energy Department of CARTIF in RTD projects about energy efficiency and integration of renewable energy (solar, geothermal, biomass) for the production of heating and cooling and/or electricity generation in buildings (to achieve zero emission buildings and near-zero energy balance) and industrial processes. He has experience in national and international (European and Latin American) projects, and has published many papers in peer review and technical journals and contributions in conferences about these themes. ORCID 0000-0003-0764-1321

Farid Chejne is a post-doctoral researcher at University Libre of Brussels (1997). He earned a PhD in Energy systems at Technical University of Madrid (1991). BSc in Physic (1989) by University of Antioquia and Mechanical Engineer by University Pontificia Bolivariana (1983). From 1983 to 2002, he worked as Full Professor in the Thermodynamical department in the University Pontificia Bolivariana, starting his career in National University of Colombia in 2002 where he currently continues his work as Full Professor. His research interests includes: modeling and simulation of processes, analysis of energy systems, advanced thermodynamic, energy resources, optimization and rational use of the energy, new technologies, combustion and gasification, management and technology. Furthermore, he has carried out projects for different companies within the power and industrial sectors. He has participated in multiple national and international research projects, contributing in addition in the publication of a large number of publications, including papers in peer review and technical journals, contributions in conferences and books about these themes. He has organized several international workshops, scientific sections and panels at international conferences and conducted various theses.

Ana Quijano. BSc in Environmental Science (2003) and MSc in Research in Engineering for the Agroforestry Development (2010), by the University of Salamanca and University of Valladolid, respectively. She has been working in the Biofuels Area of CARTIF during 2005-2012, leading and participating in several National and European R&D projects on technologies for energy valorisation of biomass. She was nominated as Member of the Action COST "Innovative applications of regenerated wood cellulose fibres" in 2012 for her trajectory in the field of biorefineries. In 2013, she was incorporated to the Energy Area, specializing the execution of FP7 Projects in the field of efficiency and renewable energy generation systems in buildings. Furthermore, she is co-author of 4 articles in scientific journals, 6 articles in dissemination journals and 12 contributions in conferences.