Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.185 Medellín May/June 2014
https://doi.org/10.15446/dyna.v81n185.37718
http://dx.doi.org/10.15446/dyna.v81n185.37718
UV-vis in situ spectrometry data mining through linear and non linear analysis methods
Minería de datos UV-vis in situ con métodos de análisis lineales y no lineales
Liliana López-Kleine a & Andrés Torres b
a Associate Professor, Statistics Department, Universidad Nacional de Colombia, llopezk@unal.edu.co
b Associate Professor, Civil Engineering Department, Pontificia Universidad Javeriana, andres.torres@javeriana.edu.co
Received: April 10th, de 2013. Received in revised form: January 27th, 2014. Accepted: January 31th, 2014.
Abstract:
UV-visible spectrometers are instruments that register the absorbance of emitted light by particles suspended in water for several wavelengths and deliver continuous measurements that can be interpreted as concentrations of parameters commonly used to evaluate physico-chemical status of water bodies. Classical parameters that indicate presence of pollutants are total suspended solids (TSS) and chemical demand of oxygen (CDO). Flexible and efficient methods to relate the instruments's multivariate registers and classical measurements are needed in order to extract useful information for management and monitoring. Analysis methods such as Partial Least Squares (PLS) are used in order to calibrate an instrument for a water matrix taking into account cross-sensitivity. Several authors have shown that it is necessary to undertake specific instrument calibrations for the studied hydro-system and explore linear and non-linear statistical methods for the UV-visible data analysis and its relationship with chemical and physical parameters. In this work we apply classical linear multivariate data analysis and non-linear kernel methods in order to mine UV-vis high dimensional data, which turn out to be useful for detecting relationships between UV-vis data and classical parameters and outliers, as well as revealing non-linear data structures.
Keywords: UV-visible spectrometer, water quality, multivariate data analysis, non-linear data analysis
Resumen:
Los espectrómetros UV-visibles son captores que registran la absorbancia de luz emitida por partículas suspendidas en el agua a diferentes longitudes de onda y proporcionan mediciones en continuo, las cuales pueden ser interpretadas como concentraciones de parámetros comúnmente usados para evaluar el estado físico-químico de cuerpos de agua. Parámetros clásicos usados para detectar la presencia de contaminación en el agua son los sólidos suspendidos totales (TSS) y la demanda química de oxígeno (CDO). Métodos de análisis flexibles y eficientes son necesarios para extraer información útil para fines de gestión y monitoreo a partir de los datos multivariados que proporcionan los captores. Se han usado métodos de calibración de tipo regresión parcial por mínimos cuadrados parciales (PLS). Varios autores han demostrado la necesidad de realizar la calibración para cada tipo de datos y cada cuerpo de agua, así como explorar métodos de análisis lineales y no lineales para el análisis de datos UV-visible y para determinar su relación con parámetros clásicos. En este trabajo se aplican métodos de análisis multivariado lineales y no lineales para la minería de datos UV-vis de alta dimensión, los cuales resultan útiles para la identificación de relaciones entre parámetros y longitudes de onda, la detección de muestras atípicas, así como la detección de estructuras no lineales en los datos.
Palabras clave: Espectrómetro UV-visible, calidad de agua, análisis multivariado, análisis de datos no lineal,
1. Introduction
One of the most recent continuous water quality monitoring measurement techniques, which allows reducing difficulties of traditional sampling and laboratory water quality analysis [20], is UV-Visible in situ spectrometry. UV-Visible spectrometers register the absorbance of emitted light by particles suspended in water. The light is emitted from UV (< 400 nm) to visible wavelengths (> 400 nm). These sensors deliver more or less continuous measurements (approx. one per minute) and can be interpreted as concentrations of parameters commonly used to evaluate the physico-chemical quality of water bodies. Some of these parameters that indicate presence of pollutants are Total Suspended Solids (TSS) and Chemical Oxygen Demand (COD).
The usefulness of these sensors implies constructing functional relationships between absorbance and classical measurement of pollutants concentrations such as TSS and COD in the studied water system taking into account different wavelengths.
Due to the composition of water from urban drainage, which depends on specific properties depending on the urban zone drained (industrial, residential, etc.), the pollutant concentrations vary spatially and temporally [5]. Moreover, the monitoring of residential waste water exhibits a simultaneous presence of several dissolved and suspended particles and leads therefore to an overlapping of absorbances that can induce cross-sensitivities and consequently incorrect results. This situation implies that the construction of a functional relationship between absorbance and classical pollutant measurements is especially challenging and could need application of more sophisticated statistical tools.
In order to find appropriate relationships several linear statistical tools have been applied so far (see e.g. [16], [4]). Chemometric models such as Partial Least Squares (PLS) [5] are used in order to calibrate a sensor for a water matrix taking into account cross-sensitivity [9]. Nevertheless, direct chemometric models can only be used if all components are known and if the Lambert-Beer law is valid, which is not the case when a great number of unknown compounds are involved [9]. Therefore, several authors (see for example [6], [9], [19] have shown that it is necessary to undertake specific sensor calibrations for the studied water system and explore linear and non-linear statistical methods for the UV-Visible data analysis and its relationship with chemical and physical parameters. Some aspects that still need to be addressed are: selection of informative wavelengths, outlier detection, calibration and validation of functional relationships. These aspects are especially relevant for urban drainage, which has particular characteristics [5].
In this work we explore the use of descriptive multivariate (linear) and data mining kernel (non-linear) methods in order to detect data structure and address the above mentioned issues for in situ UV-Vis data analysis. Results are obtained through the analysis of a real-world data set from the influent of the San Fernando Waste Water Treatment Plant, Medellín, Colombia. We found that most of the variable combinations (more than 90%) are linear and can therefore be explained using classical linear statistical methods. Nevertheless, the presence of a slight non-linearity can be revealed using non-linear kernel methods.
2 Materials and Methods
2.1. UV-Visible spectrometry
The spectrometer spectro::lyser, sold by the firm s::can, is a submergible cylindrical sensor (60 cm long, 44 mm diameter) that allows absorbances between 200 nm and 750 nm to be measured at intervals of 2.5 nm. It includes a programmable self-cleaning system (using air or water). This instrument has been used for real time monitoring of different water bodies [8], [5], [3]. Measurements are done in situ without the need of extracting samples, which avoids errors due to standard laboratory procedures [9].
2.2. UV-Vis data used for the analysis
The Medellín river's source is in the Colombian department of Caldas and along its 100 km length (approx.) has 64 tributaries that pass through densely populated urban areas. Before the implementation of the cleaning plan of the Medellín river titled "Programa de Saneamiento del Río Medellín y sus Quebradas Afluentes" [2], these small rivers carried residential, industrial and commercial pollution to the Medellín river without any treatment. The plan has allowed the construction of the San Fernando WWTP (SF-WWTP) (Planta de Tratamiento de Aguas Residuales San Fernando) in the locality of ltagüí (South side of the city of Medellín). SF-WWTP receives waste water from the industrial and residential localities of Envigado, Itagüí, Sabaneta, La Estrella and part of the South of the city of Medellín. The facility has been constructed for a maximum flow rate of 1.8 m3/s. Preliminary, primary and secondary treatment through activated sludges (thickened and stabilized in anaerobic digesters and then dehydrated and sent to a landfill) is undertaken at the WWTP facility [1]. As the result of the secondary treatment, between 80 % and 85% of the pollution is eliminated before the water is returned to the Medellín river. During 2006 the facility treated 39.4 million m3 and produced approx. 36000 tonnes of bio-solids [2].
The data set was obtained from EPM (Empresas Públicas de Medellín), public utility company in charge of Medellin's drainage and treatment systems, at the influent of SF-WWTP and corresponds to UV-Vis absorbance spectra as well as Total Suspended Solids (TSS), Chemical Oxygen Demand (COD) and filtered Chemical Oxygen Demand (fCOD) for 124 samples obtained during dry weather. These samples were obtained in order to get a local calibration of the spectro::lyser sensor at the inlet of the SF-WWTP.
2.2. Statistical analysis
2.2.1. Principal Component Analysis
Principal Component Analysis consists in obtaining axes (PCs) that are linear combinations of all variables and that resume in the first PCs using as much information as possible. The amount of information in each PC is measured as the percentage of variance retained. These axes are constructed by resolving an eigenvalue problem and therefore each new PC is orthogonal to the other PCs generated, assuring that information is not redundant [10]. This is important in the context of UV-Vis measures, as close wavelengths should measure redundant information. So, highly similar wavelengths can be filtered and information can be reduced to some PCs. Moreover correlation to response variables different from UV-Vis measurements can be investigated.
2.2.2. Kernel Methods
Suppose that a group of n objects 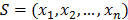 needs to be analyzed. These objects can be of any nature, for example images, texts, water samples, etc. The first step before an analysis is conducted is to represent the objects in a way that is useful for the analysis. Most analyses conduct a transformation of objects, that needs to be known. Kernel methods project objects into a high dimensional space (therefore allowing the determination of non linear relationships) through a mapping
needs to be analyzed. These objects can be of any nature, for example images, texts, water samples, etc. The first step before an analysis is conducted is to represent the objects in a way that is useful for the analysis. Most analyses conduct a transformation of objects, that needs to be known. Kernel methods project objects into a high dimensional space (therefore allowing the determination of non linear relationships) through a mapping 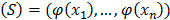 , that does not need to be explicitly known. This mapping is achieved through a kernel function and results in a similarity matrix comparing all objects in pairs
, that does not need to be explicitly known. This mapping is achieved through a kernel function and results in a similarity matrix comparing all objects in pairs 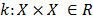 . The resulting matrix has to be semidefinite positive (
. The resulting matrix has to be semidefinite positive (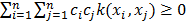 ).
).
This kernel matrix is then used as an entry to different kind of kernel methods, such as Support Vector Machines and Kernel Canonical Correlation Analysis (KCCA). The flexibility of this kind of methods is due to the data representation as pair comparisons, because this does not depend on the data's nature. Moreover, as the same objects are compared independently from the data type, several kernels can then be combined by addition and heterogeneous data types can be integrated to conduct the analysis.
Most simple kernels are linear kernels, constructed obtaining the inner product. Other kernels like Gaussian, polynomial and diffusion kernels have been used for genomic data (Vert et al. 2004). The most common kernel that will also be used here is the Gaussian kernel: 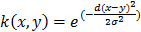 , where d is the Euclidian distance between objects and sigma is a parameter that is chosen via cross-validation.
, where d is the Euclidian distance between objects and sigma is a parameter that is chosen via cross-validation.
2.2.3. Kernel Principal Component Analysis (KPCA)
This is a Principal Component Analysis conducted on kernels (therefore abbreviated kernel-PCA or KPCA). The search of principal components in the high dimensional space H, is based on the mapping 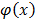 . Objects are assumed to be centered in the original space and in the high dimensional feature space. The new components are found by solving the following problem and finding v and lambda so that the equality
. Objects are assumed to be centered in the original space and in the high dimensional feature space. The new components are found by solving the following problem and finding v and lambda so that the equality 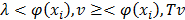 , T being the variance-covariance matrix of the individuals in space H:
, T being the variance-covariance matrix of the individuals in space H: 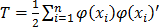 . Writing v as:
. Writing v as: 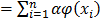 , the system can be rewritten as:
, the system can be rewritten as:

and therefore reduced as in classical PCA to the solution of the following eigenvalue problem: 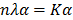 , K being the kernel function. Due to the mapping
, K being the kernel function. Due to the mapping 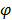 the solution of this eigenvalue problem provides non-linear principal components in the high dimensional space, without knowing
the solution of this eigenvalue problem provides non-linear principal components in the high dimensional space, without knowing  explicitely. The amount of non-linearity is mainly tuned through the kernel hyperparameters, here the parameter sigma of the Gaussian kernel.
explicitely. The amount of non-linearity is mainly tuned through the kernel hyperparameters, here the parameter sigma of the Gaussian kernel.
2.2.4. Kernel-K-means for the detection of outliers
On the non-linear projection of samples obtained after KPCA we conducted a k-means clustering algorithm on three data sets: 1) UV-Vis spectrometry data, 2) Response variables (TSS, COD, fCOD) and 3) UV-Vis and response variables together in order to compare clustering and detect samples that behave differently using these three data sets. Different behaviors should detect samples that show contradictory information between UV-Vis and response variables. The K-means algorithm on non linear projection works the same way as on a linear space. It starts by creating k random clusters (here 3) and reorganizing individuals until within cluster distances to the centroid (mean) of the cluster are as low as possible. At each step individuals are rearranged and centroids recalculated to determine the distance of each individual in the cluster to the centroid [11].
2.2.4. Support Vector Machine Regression
Support Vector Machine regression and classification is very useful in order to detect patterns in complex and non-linear data. The main problem that is resolved by SVM is the adjustment of a function that describes a relationship between objects X and the answer Y (that is binary when classification is done) using S (the data set). If the objects are vectors of dimension P, the relationship is described by 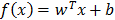 . Primarily, SVM is used for the classification into two categories, where Y is a vector of labels, but an extension to SVM regression exists [18]. SVM classification and regression allow a compromise between parametric and non-parametric approaches. They allow the adjustment of a linear classifier in a high dimensional feature space to the mapped sample:
. Primarily, SVM is used for the classification into two categories, where Y is a vector of labels, but an extension to SVM regression exists [18]. SVM classification and regression allow a compromise between parametric and non-parametric approaches. They allow the adjustment of a linear classifier in a high dimensional feature space to the mapped sample: 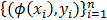 . In this case, the classifier is a hyperplane. The hyperplane, equidistant to the nearest point of each class can be rescaled to 1:
. In this case, the classifier is a hyperplane. The hyperplane, equidistant to the nearest point of each class can be rescaled to 1: 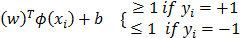 . After rescaling, the distance of the nearest point is 1/|w| and between the two groups is 2/|w|, which is called the margin. In order to maximize it the following optimization problem has to be solved: min |w|2 subject to
. After rescaling, the distance of the nearest point is 1/|w| and between the two groups is 2/|w|, which is called the margin. In order to maximize it the following optimization problem has to be solved: min |w|2 subject to 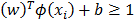 . In order to solve this optimization problem, that apparently has no local minima, and leads to a unique solution, a loss function is introduced:
. In order to solve this optimization problem, that apparently has no local minima, and leads to a unique solution, a loss function is introduced: 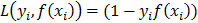 . This function penalizes large values of f(x) with opposite sign of y. Points that are on the boundaries of the classifier and therefore satisfy the equality
. This function penalizes large values of f(x) with opposite sign of y. Points that are on the boundaries of the classifier and therefore satisfy the equality 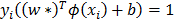 are called the support vectors. The solution consists is though solving the following optimization problem:
are called the support vectors. The solution consists is though solving the following optimization problem: 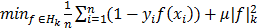 , where Hk is the high dimensional space and µ>0 controls the trade-off the fit of f and the approximation capacity of the space to which f belongs to. The larger µ is, the more restrictive the search space is [12],[18].
, where Hk is the high dimensional space and µ>0 controls the trade-off the fit of f and the approximation capacity of the space to which f belongs to. The larger µ is, the more restrictive the search space is [12],[18].
In SVM regression the loss function differs and a new parameter (e) appears: 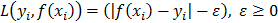 . This loss function ignores errors of size less than e≥0. In classification, when a pattern is far from the margin it does not contribute to the loss function. The basic SV regression seeks to estimate the linear function
. This loss function ignores errors of size less than e≥0. In classification, when a pattern is far from the margin it does not contribute to the loss function. The basic SV regression seeks to estimate the linear function 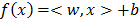 , where x and b are elements of H, the high dimensional space. A function minimizing error is adjusted, controlling training error and model complexity. Small w indicates a flat function in the H space.
, where x and b are elements of H, the high dimensional space. A function minimizing error is adjusted, controlling training error and model complexity. Small w indicates a flat function in the H space.
In nu-SVM regression, e is calculated automatically making a trade-off between model complexity and slack variables (variables added for the optimization to work). If nu>1, necessarily e=0, which is not helpful, because no errors will be considered in the loss function. So, nu should be lower than 1.
Here we used SVM regression to adjust a model for the prediction of response values. Therefore, we divided the samples randomly into approx. 2/3 for training and calibration (82 samples) and approx. 1/3 for validation (41 samples). For the SVM regression the R [15] kernlab [7] package was used. To adjust the sigma parameter based on differential evolution [14] we used the DEoptim package [13]. This procedure was done only for the calibration data, using as the objective function the quadratic differences between observed and SVM-regression estimated data for the water quality parameter (TSS, COD and fCOD) independently.
3. Results and Discussion
Independent intensity values of the data set show a decrease in intensity when wavelength increases. Variability is similar for all wavelengths but is slightly higher for lower wavelengths. Few extreme values are present at the univariate level, but no evidence exists that they could be due to sampling errors and therefore no data filtering was undertaken.
Response variables (TSS, COD, fCOD) have different behaviors, COD being skewed to the left (high frequency of lower values) and the other two showing a normal distribution. Extreme high values are also found at the univariate level, but were not filtered either for the same reasons as before.
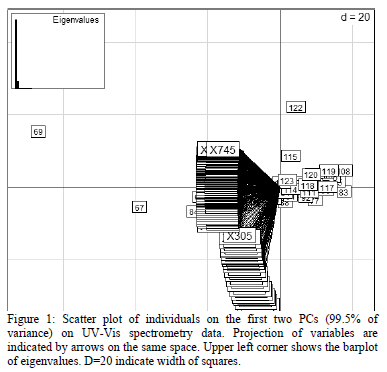
PCA conducted on all UV-Vis data showed that these data are extremely correlated and therefore redundant as they can be resumed in the first PC with 90.1% of variance. The first two PCs resume 99.5% of the variance. The most important variables on the first PC (contributing with highest variance) are the following wavelengths (in nm): 435, 432.5, 437.5, 440, 430, 307.5, 305, 302.5, 300 and 297.5. This result indicates that only with these wavelengths, enough information on samples could be obtained, because approx. 90% of variance is explained using these variables.
Most samples are very similar (showing projections with very similar coordinates on the PC space). Individuals (samples) that behave differently in this sense are 69 and 67 because they separate clearly from the other samples on the first PC (Figure 1). These samples have extreme values on the wavelengths 435 nm, 432.5 nm, 437.5 nm, 440 nm, 430 nm, 307.5 nm, 305 nm, 302.5 nm, 300 nm and 297.5 nm as expected. This can be due to measurement errors or real variations in water quality, observed with more sensitivity at these wavelengths, which could be confirmed by measuring water quality parameters.
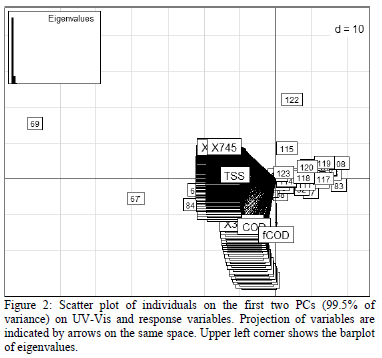
PCA including response variables (TSS, COD, fCOD) does not change the individual structure, meaning that most information is already contained in UV-Vis data. The projection of response variables shows that they are also strongly correlated to the UV-Vis variables, especially TSS as this variable is highly correlated to the first PC (very low angle with PC1 axis) where 90.1 % of the variance is explained. Moreover, COD and fCOD are strongly correlated to the second PC which explains only 9.4 % of variance. These two variables are strongly correlated to each other. Variables most highly correlated to the second PC and therefore to COD and fCOD are (in nm): 205, 207.5, 210, 212.5, 215, 217.5, 220, 222.5, 225, 227.5 (Figure 2). This result indicates clearly that chemical parameters detected at visible wavelengths are related to suspended solids and that parameters related to organic pollution are related to non-visible wavelengths. Moreover, it is possible to conclude that the difference between filtered and non filtered COD is very low, showing similar variance behaviors between them. This does not mean that the COD and the fCOD values are similar but that the information they provide (in terms of variance) is similar.
PCA analysis made it also possible to determine precisely which wavelengths are more related to each of the chemical parameters. TSS is close to wavelengths 435.0 nm, 432.5 nm, 437.5 nm and 440.0 nm, COD to wavelengths 222.5 nm, 220.0 nm, 217.5 nm and 215.0 nm, fCOD differs most from the other response variables and is close to wavelengths 212.5 nm, 210.0 nm, 207.5 nm and 205.0 nm. These results are in accordance with the relationship of wavelengths correlated to PC 1 for TSS and PC2 for COD and fCOD (Figure 2).
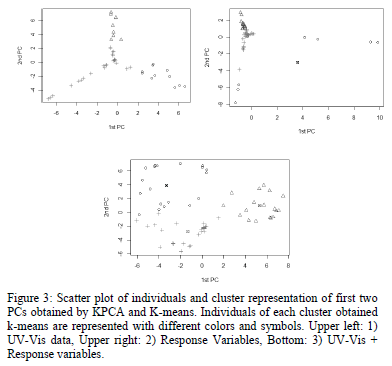
The K-K-means best grouping structure was obtained for 3 clusters on all three data sets (UV-Vis, Response Variables, UV-Vis+Response Variables). Therefore, we worked with 3 clusters. For these data sets, the best Gaussian kernel parameter was sigma= 0.0001. This low value indicates that even though variables are highly linearly correlated as was shown through PCA, some non-linear structure in the data persists and is extracted trough kernel projection on a Hilbert space (Figure 3).
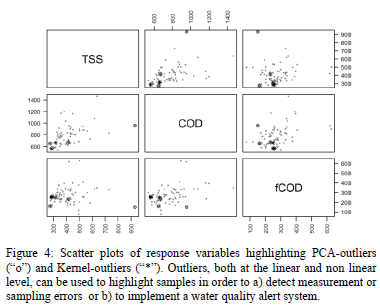
In order to detect samples that behave differently in regard of UV-Vis and response variable data, we compared the three clusters generated with K-K-means and we detected that 6 samples (0.05 %) were systematically placed in a different cluster (13, 14, 27, 52, 75 and 89). For the rest of the individuals, most of them (approx. 80 %) were placed in the same cluster and approx. 20% were placed in two different clusters when UV-Vis alone, UV-Vis and response variables and response variables alone were used. These outlier samples are outliers at a non-linear level and PCA outliers 69 and 67 are outliers at a linear level as had already been detected by PCA (Fig. 4). Notice that samples 67 and 69 have different absorbance fingerprints (Figure 1) but their TSS, COD and fCOD concentration values are exactly the same (931 mg/L, 956 mg/L and 150 mg/L, respectively for both samples 67 and 69, see Fig. 4). This indicates a problem with the data set received and confirms the detections of these samples as outliers. The outliers could have originated due to wrong measurements of the The spectrometer spectro::lyser or the laboratory measurements. Because of the low weight of laboratory measurements (only 3), the outliers are more likely to exist, due to the absorbance measurements.
SVM-regression is much more robust and reliable than linear regression, because it will be less affected by linear outliers that showed to have a very different behavior from the other samples at the linear level (Fig. 2,4) as has been shown in other works [12].
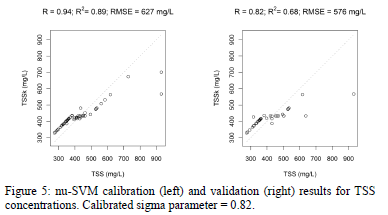
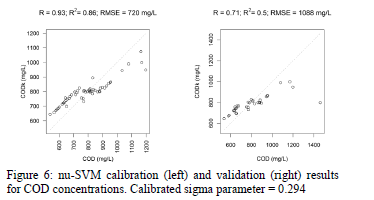
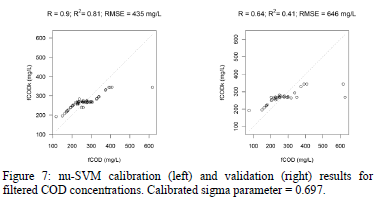
Fig. 5-7 show the results of the SVM regression applied on UV-Vis data in order to model response variables. Predictions on calibration data are very high, but predictions on validation data are not satisfactory for TSS, COD and fCOD.
3. Conclusions
Similar wavelengths of UV-Vis data are highly linearly correlated between each other and to the chemical parameters TSS and COD. This analysis showed that very few wavelengths resume the behavior of all the water-quality measures (less than 5% of all measured wavelengths) and that the wavelengths with the highest variability are visible wavelengths (> 400 nm). This could mean that the spectrometer measures visible pollution in a more accurate way than non-visible pollution or that visible pollution is more variable.
The PCA analysis performed on the spectrometry data coupled with the laboratory measured data (TSS, COD and fCOD), showed that it is possible to detect wavelengths related to each pollutant in relationship with the variance of the Uv-Vis data. Visible wavelengths (432.5 nm to 440.0 nm) were more correlated to TSS and UV wavelengths were more correlated to COD (215.0 nm to 222.5 nm) and fCOD (205.0 nm to 212.5 nm). These results are in accordance with the information given by the constructor of the spectrometer used, spectro::lyser (http://www.s-can.at/). Moreover, a group of wavelengths to be used for prediction could be chosen with the help of a PCA.
The PCA allowed detecting outliers, which is not a standard procedure to detect them, but could be a helpful approach when monitoring water in real time, due to its simple and fast application. The use of kernel-k-means allowed the detection of non-linear outliers, which would have remained undetected using linear analysis methods (PCA, linear clustering, multivariate outlier detection, etc.). This approach opens a new possibility for the use of kernel methods in the advanced identification of outliers for future continuous monitoring of water quality controls (detection of measurement or sampling errors or alert in treatment facilities, valve operation, etc.) and its objective and automatic operation.
Finally, it can be concluded that Support Vector Machine regression allowed a very accurate prediction on calibration data, but predictions on validation data are not satisfactory, especially for TSS. This means that, despite the robustness of the predictions using SVM regression, prediction accuracy needs to be improved, especially for the organic pollution (COD and fCOD variables in this work). In order to improve prediction, a filtering on wavelengths could be performed before calibration. Moreover, other machine learning methods like decision trees or neural networks or even fuzzy classification techniques [17] could be explored.
Acknowledgements
Authors acknowledge Medellín Water and Sewage Company (Empresas Públicas de Medellín – EPM) for providing the data used in this research.
Refrences
[1] Empresas Públicas de Medellín (EPM). Planta de tratamiento de aguas residuales San Fernando premio nacional de ingeniería año 2000. http://xue.unalmed.edu.co/mdrojas/evaluacion/PLANTA%20DE%20TRATAMIENTO%20DE%20AGUAS%20RESIDUALES%20SAN%20FERNADO.pdf, 2007 (accessed 10 January 2012) [ Links ]
[2] Empresas Públicas de Medellín (EPM). EPM y su Programa de saneamiento del río Medellín. http://www.epm.com.co/docs-bid/aguas/Proyectos_Saneamiento_Rio_Medell%C3%ADn_Espa%C3%B1ol.pdf (accessed10January 2012), 2009. [ Links ]
[3] Gamerith, V., High resolution online data in sewer water quality modelling. PhD thesis: Faculty of Civil Engineering, University of Technology Graz (Austria), May 2011, P. 236, þ annexes, 2011. [ Links ]
[4] Gruber G., Bertrand-Krajewski J.-L., de Bénédittis J., Hochedlinger M. and Lettl, W., Practical aspects, experiences and strategies by using UV/VIS sensors for long-term sewer monitoring. Water Practice and Technology (paper doi10.2166/wpt.2006.020), 1(1), P. 8 ISSN 1751-231X, 2006. [ Links ]
[5] Hochedlinger, M., Assessment of combined sewer overflow emissions. PhD thesis: Faculty of Civil Engineering, University of Technology Graz (Austria), June 2005, P.174 þ annexes, 2005. [ Links ]
[6] Hofstaedter, F., Ertl, T., Langergraber, G., Lettl, W. and Weingartner, A., On-line nitrate monitoring in sewers using UV/VIS spectroscopy. In: Wanner, J., Sykora, V. (eds): Proceedings of the 5th International Conference of ACE CR "Odpadni vody – Wastewater 2003", 13–15 May 2003, Olomouc, Czech Republic, pp. 341–344, 2003. [ Links ]
[7] Karatzoglou, A., Smola, A., Hornik, K. and Zeileis, A., kernlab - An S4 Package for Kernel Methods in R. Journal of Statistical Software 11(9), pp. 1-20. URL http://www.jstatsoft.org/v11/i09/, 2011. [ Links ]
[8] Langergraber, G., Fleischmann, N., Hofstaedter, F. and Weingartner, A., Monitoring of a paper mill wastewater treatment plant using UV/VIS spectroscopy. Trends in Sustainable Production, 49(1), pp. 9–14, 2004. [ Links ]
[9] Langergraber, G., Fleischmann, N. and Hofstaedter, F., A multivariate calibration procedure for UV/VIS spectrometric quantification of organic matter and nitrate in wastewater. Water science & technology, 47(2), pp. 63–71, 2003. [ Links ]
[10] Lebart, L., Piron, M. and Morineau, A., Statistique exploratoire multimensionnnelle. Dunod, Paris, 1995. [ Links ]
[11] MacQueen, J. B., Some Methods for classification and Analysis of Multivariate Observations. 1. Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability. University of California Press, 1967. [ Links ]
[12] Moguerza, J.M. and Muñoz, A., Support Vector Machines with Applications. Statistical Science, 21, pp. 322-336, 2006. [ Links ]
[13] Mullen, K., Ardia, D., Gil, D., Windover, D. and Cline, J., 'DEoptim': An R Package for Global Optimization by Differential Evolution. Journal of Statistical Software, 40 (6), 1-26. URL http://www.jstatsoft.org/v40/i06/, 2011. [ Links ]
[14] Price, K.V., Storn, R.M. and Lampinen, J.A., Differential Evolution - A Practical Approach to Global Optimization. Berlin Heidelberg: Springer-Verlag. ISBN 3540209506, 2006. [ Links ]
[15] R Development Core Team R, A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org/, 2012. [ Links ]
[16] Rieger, L., Vanrolleghem, P., Langergraber, G., Kaelin, D. and Siegrist, H., Long-term evaluation of a spectral sensor for nitrite and nitrate. Water Science and Technology. Vol. 57 (10). pp. 1563–1569, 2008. [ Links ]
[17] Soto, S. and Jimenez, C., Aprendizaje supervisado para la discriminación y clasificación difusa. Dyna. Vol. 169. pp. 26-33, 2011. [ Links ]
[18] Schölkopf, B., Smola A. J. Learning with kernels. The MIT Press, Cambridge, Massachusetts, 2002. [ Links ]
[19] Torres, A. and Bertrand-Krajewski, J.L. Partial Least Squares local calibration of a UV-Visible spectrometer used for in situ measurements of COD and TSS concentrations in urban drainage systems. Water Science and Technology 57, pp. 581–588, 2008. [ Links ]
[20] Winkler, S., Bertrand-Krajewski, J.-L., Torres, A. and Saracevic, E., Benefits, limitations and uncertainty of in situ spectrometry. Water science and technology: a journal of the International Association on Water Pollution Research, 57 (10), 1651, 2008. [ Links ]
L. López-Kleine is a biologist from the Universidad Nacional de Colombia – Sede Bogotá. She received her Master's degree in Ecology, Evolution and Biometry from the University of Lyon 1 (France) and her PhD in Biology and applied statistics at AgroParisTech in Paris (France). She is an associate professor at the Statistics Department of the Universidad Nacional de Colombia since 2009. Her main research areas are systems biology and statistical genomics, in which she focuses on applying and developing multivariate and data mining analysis. She is director of the research group "Métodos en Bioestadística".
A. Torres revieved his civil engeneering degree and a specialist degree in management systems in engeneering from the Pontificia Universidad Javeriana, sede Bogotá. He made a MSc in civil engeneering and PhD in urban hydrology at the Institut National des Sciences Appliquées in Lyon, France. He is associate professor at the Pontificia Universidad Javeriana, sede Bogotá and director of the research group "Ciencia e Ingeniería del Agua y el Ambiente (http://190.216.132.131:8080/gruplac/jsp/visualiza/visualizagr.jsp?nro=00000000000048). His main research areas are urban hydrology, especially related to urbain drainage systems, water quality measurements and management of sewer systems.