Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.185 Medellín maio/jun. 2014
https://doi.org/10.15446/dyna.v81n185.38309
http://dx.doi.org/10.15446/dyna.v81n185.38309
Use of a multi-objective teaching-learning algorithm for reduction of power losses in a power test system
Uso de un algoritmo de enseñanza-aprendizaje multi-objetivo para la reducción de pérdidas de energía en un sistema de potencia de prueba
Miguel A. Medina a, Juan M. Ramirez a, Carlos A. Coello b & Swagatam Das c
a CINVESTAV del IPN Unidad Guadalajara, Jal. México. Departamento de Ingeniería Eléctrica, mmedina@gdl.cinvestav.mx jramirez@gdl.cinvestav.mx
b CINVESTAV del IPN unidad Zacatenco, D.F. México. Departamento de Computación, ccoello@cs.cinvestav.mx
c Indian Statistical Institute, Electronics and Communication Sciences Unit, Kolkata, India. Swagatam.das@isical.ac.in
Received: June 1th, 2013. Received in revised form: January 23th, 2014. Accepted: February 26th, 2014.
Abstract
This paper presents a multi-objective teaching learning algorithm based on decomposition for solving the optimal reactive power dispatch problem (ORPD). The effectiveness and performance of the proposed algorithm are compared with respect to a multi-objective evolutionary algorithm based on decomposition (MOEA/D) and the NSGA-II. A benchmark power system model is used to test the algorithms' performance. The results of the power losses reduction as well as the performance metrics indicate that the proposed algorithm is a reliable choice for solving the problem.
Keywords: Multi-objective evolutionary algorithm based on decomposition (MOEA/D), Multi-objective Teaching-learning algorithm, Optimal reactive power dispatch.
Resumen
Este artículo presenta un algoritmo de enseñanza-aprendizaje multi-objetivo basado en descomposición para resolver el problema del despacho óptimo de potencia reactiva (ORPD). La efectividad y el desempeño del algoritmo propuesto son comparados con respecto a un algoritmo evolutivo multi-objetivo basado en descomposición (MOEA/D) y con el NSGA-II. Un modelo de sistema de potencia de referencia se utiliza para probar el desempeño de los algoritmos. Los resultados de la reducción de las pérdidas de energía así como las métricas de desempeño indican que el algoritmo propuesto es una opción fiable para resolver el problema.
Palabras clave: Algoritmo evolutivo multi-objetivo basado en descomposición (MOEA/D), Algoritmo de enseñanza-aprendizaje multi-objetivo, Despacho óptimo de potencia reactiva.
1. Introduction
Optimal reactive power dispatch (ORPD) is a useful tool in modern energy management systems. It plays a significant role for safe operation of power systems. One of the main tasks of a power system operator is to manage the system in such a way that its operation is safe and reliable. Its main aim is to determine the optimal operating capacity and the physical distribution of the compensation devices such as voltage rating of generators, reactive power injection of shunt capacitors/reactors, tap ratios of the tap setting transformers, to ensure a satisfactory voltage profile while minimizing the transmission loss. Due to the continuous growth in the demand for electricity with unmatched generation and transmission capacity expansion, voltage instability is emerging as a new challenge to power system planning and operation. Therefore, the voltage stability index should also be considered as an objective of the ORPD problem.
Many classical optimization techniques such as gradient search (GS) [1], linear programming (LP) [2], Lagrangian approach (LA) [3], quadratic programming (QP) [4], interior point methods (IP) [5] etc., have been successfully applied to solve ORPD problems. However, from the specialized literature, it may be observed that such classical optimization methods exhibit several drawbacks, such as insecure convergence properties and algorithmic complexity. Due the non-differential, non-linearity and non-convex nature of the optimal reactive power dispatch problem, the majority of these techniques converge to a local optimum [8].
In recent years, many meta-heuristic such as evolutionary methods have been implemented to solve the ORPD problem. The advantages of evolutionary algorithms in terms of the modeling and search capabilities have encouraged their application to the ORPD problem. Non-dominated Genetic Algorithm (NSGA-II) [6], particle swarm optimization (PSO) [7], differential evolution (DE) [8], harmony search algorithm (HSA) [9], and general quantum genetic algorithm (GQ-GA) [10], are some of the meta-heuristic methods that have been used to solve the ORPD problem. The majority of the existing multi-objective evolutionary algorithms (MOEAs) aim at producing a number of Pareto-optimal solutions as diverse as possible to approximate the whole Pareto front. Therefore, these methods need some other techniques for ranking solutions (e.g., crowding distance, fitness sharing, niching). However, it has been empirically found that these methods cannot always provide good results, especially when the multi-objective optimization problem is very complicated [11].
Recently, a new framework called multi-objective evolutionary algorithm based on decomposition (MOEA/D) [11], was proposed. This framework decomposes a multi-objective optimization problem into several single-objective optimization sub-problems. In this way, a set of approximate solutions to the Pareto front is achieved by minimizing each sub-problem instead of using Pareto ranking. This has given rise to a new generation of MOEAs.
The teaching-learning based optimization (TLBO) algorithm was recently proposed by Rao et al. [12] as a new meta-heuristic algorithm inspired on the philosophy of teaching-learning process in a class between the teacher and learners (students). This algorithm has emerged as a simple and efficient technique for solving single-objective complex benchmark problems and real world problems. TLBO does not require any specific parameter to be tuned, which facilitates its implementation and use. These are the characteristics of TLBO algorithm that make it suitable to deal with multi-objective optimization problems. Therefore, in this research a teaching-learning algorithm is proposed to deal with multi-objective optimization problems employing a decomposition framework similar to the one adopted by MOEA/D. This framework decomposes a multi-objective problem into several single-objective optimization sub-problems. Thus, a set of Pareto-optimal solutions is achieved by minimizing each sub-problem through neighborhood relationships, instead of using a Pareto ranking method.
The effectiveness of the proposed approach is assessed and compared to a multi-objective evolutionary algorithm based on decomposition MOEA/D [11], which is representative of the sate-of-the-art on the subject. Results are also compared to the NSGA-II algorithm [6], which remains the most popular method based on Pareto ranking. The performance of the methods is investigated on an IEEE 14-bus test system to solve the optimal reactive power dispatch problem by minimizing the transmission losses and a voltage stability index.
The rest of the paper is organized as follows: Section 2 exposes the fundamentals and the general framework of the proposed approach. In Section 3, the problem formulation is summarized. Section 4 presents a brief description of the performance measures. Simulation results and a comparative study are presented in Section 5. Finally, conclusions are provided in Section 6.
2. Fundamentals: methods
2.1. Teaching-learning based optimization
The original teaching learning based optimization (TLBO) algorithm was proposed by Rao et al. [12] to obtain global solutions for continuous non-linear functions. In optimization algorithms, the population consists of different design variables. In TLBO, the design variables are analogous to different subjects offered to learners. The learners' grade is analogous to the 'fitness' as in any other evolutionary algorithm, and the teacher is considered to be the best solution obtained so far [12]. Hence, the performance of TLBO is based on two main phases: the teacher phase, which involves learning from the teacher, and the learner phase, which involves learning through the interaction among learners.
The pseudo-code of the TLBO algorithm can be summarized in the following way.
1: Initialization
2: Evaluation
3: iteration = 1
4: Repeat
5: Teacher Phase
6: Keep the best solutions
7: Learner Phase
8: Keep the best solutions
9: iteration = iteration + 1
10: Until Maximum number of iterations.
Many optimization methods require parameters that affect the performance of the algorithm. For example, differential evolution (DE) primarily depends on the mutation strategy and its intrinsic control parameters such as scale factor (Fs) and crossover rate (Pcr); particle swarm optimizers (PSO) require learning factors, the variation of the inertia weight and the maximum value of the velocity. Unlike other optimization techniques, TLBO does not require any algorithm's parameters to be tuned, which makes the implementation of TLBO simpler.
2.2. Decomposition of a multi-objective optimization problem
A multi-objective optimization problem (MOP) may be formulated as follows:
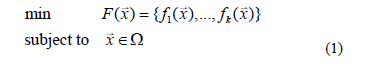
where 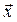 is the vector of decision variables, and W is the feasible region within the decision space.
is the vector of decision variables, and W is the feasible region within the decision space. 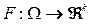 is defined as the mapping of k objective functions.
is defined as the mapping of k objective functions.
In multi-objective optimization, the goal is to find the best possible trade off among the objectives since, frequently, one objective can be improved only at the expense of worsening another. To describe the concept of optimality for problem (1) the following definitions are provided.
Definition 1. Let 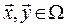 , such that
, such that 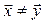 , we say that
, we say that 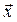 dominates
dominates 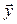 (denoted by
(denoted by 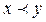 ) if and only if,
) if and only if, 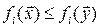 for all i = 1, ..., k.
for all i = 1, ..., k.
Definition 2. Let 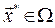 , we say that
, we say that 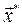 is a Pareto optimal solution, if there is no other solution
is a Pareto optimal solution, if there is no other solution 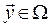 such that
such that 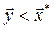 .
.
Definition 3. The Pareto Optimal Set (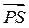 ) is defined by
) is defined by 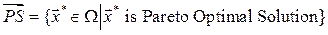 while its image
while its image 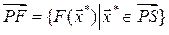 is called the Pareto Optimal Front.
is called the Pareto Optimal Front.
There are several approaches for transforming a MOP into a number of scalar optimization problems, which have been described in detail in [13]. Usually, these methods use a weighted vector to define a scalar function and, under certain assumptions, a Pareto optimal solution is achieved by minimizing such function. In this paper, the Tchebycheff approach is used to decompose a MOP. In this approach, the scalar optimization problem can be stated as [13]:
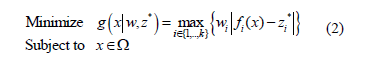
where 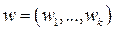 is a weighting vector and
is a weighting vector and 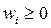 for all
for all 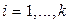 ,
, 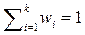 ;
; 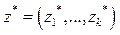 represents the reference point, i.e.,
represents the reference point, i.e., 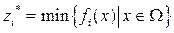 , for
, for 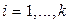 . For each Pareto optimal solution
. For each Pareto optimal solution 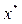 there exists a weighting vector w such that
there exists a weighting vector w such that 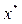 is the optimal solution of (2), and each optimal solution is a Pareto optimal solution for (1). Therefore, it is possible to obtain different Pareto optimal solutions using different weighting vectors w [13].
is the optimal solution of (2), and each optimal solution is a Pareto optimal solution for (1). Therefore, it is possible to obtain different Pareto optimal solutions using different weighting vectors w [13].
2.3. Multi-objective teaching-learning based on decomposition
The proposed Multi-Objective Teaching Learning Algorithm based on Decomposition (MOTLA/D) utilizes the Tchebycheff approach, (2), to decompose the MOP into N scalar optimization sub-problems. Hence, using (2), the objective function of the j-th sub-problem becomes: 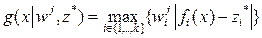 , with
, with 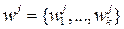 and j = 1… N. The proposed approach looks for the sequential minimization of these sub-problems. Similar to MOEA/D [11], neighborhood relationships among these sub-problems are defined by computing Euclidean distances between weighting vectors.
and j = 1… N. The proposed approach looks for the sequential minimization of these sub-problems. Similar to MOEA/D [11], neighborhood relationships among these sub-problems are defined by computing Euclidean distances between weighting vectors.
In MOTLA/D, for the j-th sub-problem, the size of the neighborhood becomes the number of learners in the class. This class can be expressed as,
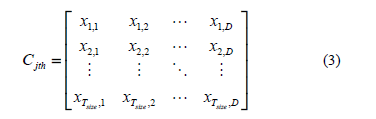
where the subscript D is the number of design variables, and Tsize is the size of the neighborhood WT.
The main steps of the proposed MOTLA/D can be summarized as follows:
Teacher phase: Within the teacher phase, the mean of the class for each design variable is evaluated,
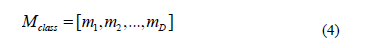
The teacher (Mnew) for the j-th sub-problem represents the best learner of the class Cjth. Thus,
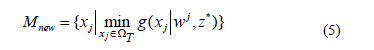
The teacher will try to improve the mean of the class (Mclass) taking it towards its own level (Mnew). The difference between the class (Mclass) and the teacher (Mnew) modifies the j-th learner (xj) in order to generate a new solution (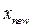 ). Hence, the new solutions generated in this phase are as follows,
). Hence, the new solutions generated in this phase are as follows,
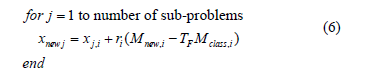
where index j corresponds to the current index of j-th sub-problem, ri is a random number within the range [0, 1]. TF is the teaching factor which value can be either 1 or 2, which is decided randomly with equal probability as TF = round [1 + rand (0, 1)]. The new solution (xnew) is accepted if it gives a better function value.
Learner Phase: The learner phase generates a new solution (xnew) by randomly selecting two learners xi, and xk such that i ≠ k ≠ j. The new solutions generated in this phase are as follows,

Additionally, a polynomial mutation operator is applied to maintain the diversity of solutions. If one or more variables within the new solution (xnew) lies outside W, the i-th value of xnew is reset as follows,
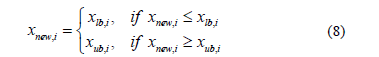
The new solution (xnew) is accepted if it improves the function value and replaces the old solution (xj). The procedure for the implementation of MOTLA/D may be summarized as follows,

3. Problem formulation
In this paper, a reactive power system problem is tackled, which may be stated as an optimization problem where two objective functions are minimized, while satisfying a number of equality and inequality constraints. The following objective functions are minimized: a) the reactive power losses; and b) the voltage stability index Lindex [14].
3.1. Objective functions
3.1.1. Reactive power losses
One important issue in power transmission is the high reactive power losses on the highly loaded lines, with the consequent transmission capacity reduction. Therefore, the reactive power losses minimization is selected as one objective function. The losses are evaluated by the following expression,
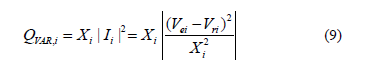
where Vei and Vri are the sending and receiving voltages, respectively; Xi is the line reactance; Ii is the current through the transmission line. Therefore, the objective function for the reactive power losses is expressed as,

where nl is the number of lines. Reducing the reactive power losses enables more active power to be transferred over a single line.
3.1.2. Voltage stability index
There are a variety of indexes that help to assess the steady state voltage stability. In this case, the voltage stability index Lindex is used [14]. This index is able to evaluate the steady state voltage stability margin of each bus. The Lindex value lies between 0 (no load) and 1 (voltage collapse). This value implicitly includes the load effect. The bus with the highest Lindex value will be the most vulnerable, and therefore, this method helps to identify weak areas that require a critical support of reactive power.
For the j-th load bus, the voltage stability index is defined by [14],
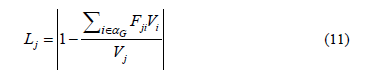
where (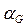 ) represents the set of generator buses; Fji is a term evaluated through the partial inversion of the admittance matrix Ybus, and V represents complex voltages. For stable conditions,
) represents the set of generator buses; Fji is a term evaluated through the partial inversion of the admittance matrix Ybus, and V represents complex voltages. For stable conditions, 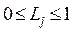 must not be violated for any j. Hence, a global indicator Lindex describing the whole system's stability is defined by [14],
must not be violated for any j. Hence, a global indicator Lindex describing the whole system's stability is defined by [14],
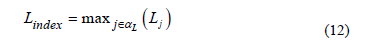
where (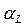 ) is the set of load buses. Pragmatically, Lindex must be lower than a given threshold value. The predetermined threshold value is specified depending on the system configuration and on the utility policy regarding service quality and allowable margin. The Lindex in (12) is associated with the worst bus in the sense of voltage stability. Therefore Lindex is considered as the second objective function for the reactive power dispatch problem addressed in this paper. The minimization of Lindex implies to move such bus toward a less stressed condition.
) is the set of load buses. Pragmatically, Lindex must be lower than a given threshold value. The predetermined threshold value is specified depending on the system configuration and on the utility policy regarding service quality and allowable margin. The Lindex in (12) is associated with the worst bus in the sense of voltage stability. Therefore Lindex is considered as the second objective function for the reactive power dispatch problem addressed in this paper. The minimization of Lindex implies to move such bus toward a less stressed condition.
3.2. Equality constraints
These constraints are the power flow equations as follows:
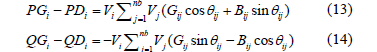
where i=1,..,nb; nb is the number of buses. PGi and QGi are the active and reactive generated powers at the i-th bus, PDi and QDi are the active and reactive demands at the i-th bus, respectively. Vi is the voltage magnitude at the i-th bus. q;ij is the voltage angle difference between buses i and j. Gij and Bij are the mutual conductance and susceptance between buses i and j, respectively.
3.3. Inequality constraints
Generator constraints: Generator reactive power outputs and voltage magnitudes are restricted by their upper and lower bounds as follows:
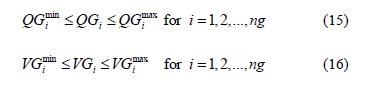
where ng is the number of generating units.
Transformer's tap constraints: Transformer taps are bounded by their related minimum and maximum limits as follows:
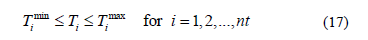
where nt is the number of transformers.
Shunt VAR compensator constraints: The setting of the shunt VAR compensation devices is restricted as follows:
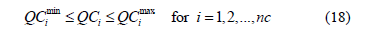
where 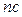 is the number of VAR compensation devices.
is the number of VAR compensation devices.
3.4. Decision variables
The decision variables include the generator voltages VG, and the tap ratio of the transformers (T),
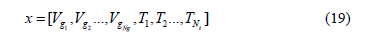
It is worth noting that the decision variables are self-constrained by the optimization algorithm.
3.5. Case study
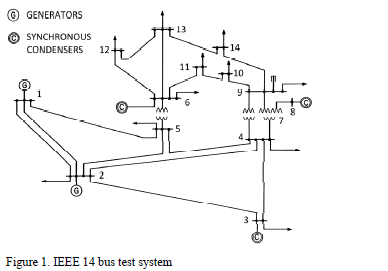
This paper compares the effectiveness and performance of the proposed algorithm with respect to MOEA/D and NSGA-II. Therefore, the algorithms have been applied to a test system composed of 14-buses, 5-generating units, and 20-lines in which three lines have tap changing transformers. The system model and data are summarized in [15]. In this study, 20 independent runs were performed by each algorithm. Fig. 1 shows the bus code diagram of the test power system.
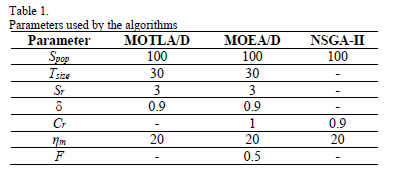
The control parameter settings utilized by the algorithms are summarized in Table 1 where: Spop is the population size, Tsize is the neighborhood size, Sr is the maximum number of solutions replaced, and d is the probability of selecting solutions from the neighborhood. hm is the distribution index used in the polynomial mutation. Cr is the Crossover rate, which determines the quantity of elements to be exchanged by the crossover operator. The parameter Fs is the scale factor associated with MOEA/D, which represents the amount of perturbation added to the main parent. Finally, a mutation rate Pm=1/n is taken into account, where n is the number of decision variables. This parameter indicates the probability that each decision variable has of being changed. It is worth mentioning that the stop condition of each algorithm is the number of function evaluations (25000 for each algorithm).
4. Performance measures
In order to assess the algorithms' performance, two indicators are utilized.
4.1. Coverage of two sets
This performance measure compares two sets of non-dominated solutions (A,B) and outputs the percentage of individuals in one set dominated by the individuals of the other set. This performance measure is defined as [16],
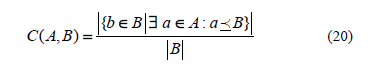
The value C(A,B) = 1 means that all points in B are dominated by or equal to all points in A. The opposite, C(A,B) = 0 represents the situation when none of the solutions in B are covered by the set A. Note that both C(A,B) and C(B,A) have to be considered, since C(A,B) is not necessarily equal to 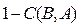 . When C(A,B) = 1 and C(B,A) = 0 then, we say that the solutions in A completely dominate the solutions in B (i.e., this is the best possible performance for A).
. When C(A,B) = 1 and C(B,A) = 0 then, we say that the solutions in A completely dominate the solutions in B (i.e., this is the best possible performance for A).
4.2. Spacing metric
This performance measure quantifies the spread of solutions (i.e., how uniformly distributed are the solutions) along a Pareto front approximation. This performance measure is defined by [17],
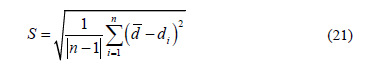
where n is the number of non-dominated solutions, di is the minimum Euclidean distance between objective functions, 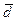 is the mean of all di. A value of zero implies that all solutions are uniformly spread (i.e., the best possible performance).
is the mean of all di. A value of zero implies that all solutions are uniformly spread (i.e., the best possible performance).
5. Results
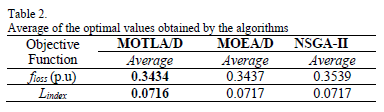
The values of the reactive power losses (floss) and the voltage stability (Lindex) in the base case without optimization are 0.4393 p.u and 0.0767, respectively. Because of the stochastic nature of the tested algorithms, their performance cannot be concluded by the result of a single run. Therefore, the average of the optimal values obtained by the algorithms are shown in Table 2.
According with Table 2, the proposed MOTLA/D estimates in average a 21.83% reduction in reactive power losses and a 6.65% reduction in voltage stability index with respect to the base case. Meanwhile, the MOEA/D algorithm attains in average a 21.76% reduction in reactive power losses and 6.52% reduction in voltage stability index with respect to the base case. Finally, it is observed that the NSGA-II attains in average a 19.44% reduction in reactive power losses and 6.52% reduction in voltage stability index with respect to the base case.
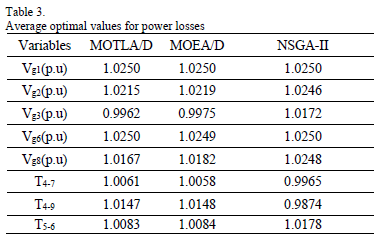
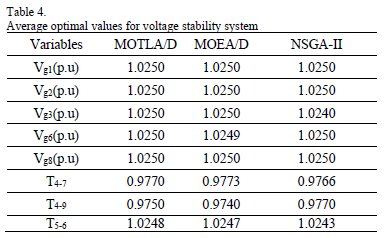
Table 3 shows the average optimal values of the generators' voltages and the tap-position for the transformers of the optimal solution of the objective function (floss) achieved by the algorithms. Likewise, Table 4 indicates the average optimal values of the decision variables (voltages and tap-position) for the optimal solution of the objective function (Lindex) obtained by the algorithms. It means that moving the corresponding elements toward the optimal values specified in Tables 3 and 4, the power system will attain an improved operating condition, more secure, economical, and efficient.
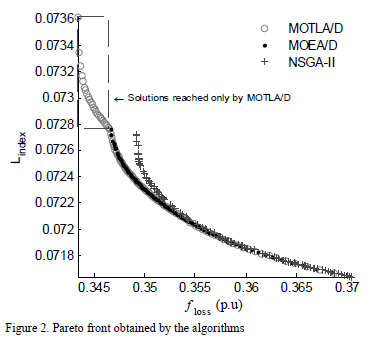
The Pareto fronts obtained by the algorithms are shown in Fig. 2. These figures shows the final set of non-dominated solutions found by each algorithm and correspond to the run with the nearest value of the average of the performance measure (20). It can be clearly seen in Fig. 2, that MOEA/D and NSGA-II only cover a portion of the solutions achieved by MOTLA/D. Therefore, the proposed algorithm is able to achieve more distributed solutions. It is noteworthy that a distribution of the optimal solutions as uniform as possible along the Pareto Front ensures avoid big gaps in the Pareto front and, therefore, all the different type of trade-off solutions are generated. This is relevant, because if big gaps occur, it may happen that the trade-off solution of interest is not produced (i.e., the optimal solution of concern may be located in the missing portion of the Pareto front).
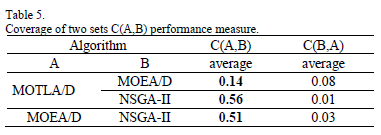
The average results of the coverage of two sets metric obtained by each algorithm is summarized in Table 5. The best results are displayed in boldface.
As noticed in Table 4, the proposed approach (MOTLA/D) outperformed MOEA/D and NSGA-II regarding the coverage of two sets indicator. Moreover, it can be seen that the algorithms based on decomposition have better convergence that the traditional evolutionary technique based on Pareto ranking, NSGA-II. Regarding the spacing metric, the proposed MOTLA/D obtained, in average, a value of 0.0150, meanwhile, MOEA/D and NSGA-II achieved an average value of 0.0156 and 0.0073, respectively. Therefore, NSGA-II attains relatively better results regarding to the spacing metric. However, since convergence has precedence over spread, we can conclude that our proposed MOTLA/D outperformed MOEA/D and NSGA-II in the analyzed case of study.
The convergence time of MOTLA/D, MOEA/D and NSGA-II is, 109.10 s, 246.03 s, and 109.79 s, respectively. Therefore, the proposed MOTLA/D outperformed MOEA/D, and it has a convergence time which is average slightly faster than NSGA-II.
6. Conclusions
This paper presented a multi-objective teaching-learning algorithm based on decomposition for solving the complex problem of optimal reactive power dispatch in power systems. The mechanism of the MOTLA/D is as effective as the MOEA/D and it has the advantage of being easy to comprehend, and simple to implement, so that it can applied to a wide variety of optimization problems. The efficiency of the proposed algorithm is illustrated when solving an IEEE 14 bus test system. Likewise, the effectiveness and performance of MOTLA/D was compared with respect to MOEA/D and NSGA-II. The results of the coverage of two sets metric indicate that the proposed algorithm was able to obtain better solutions than MOEA/D and NSGA-II. According to this metric the optimal solutions obtained by MOTLA/D dominate about 16% of the solutions produced by MOEA/D and 58% of the solutions generated by NSGA-II. In addition, the convergence time proves that MOTLA/D is about twice as fast as MOEA/D and it is slightly faster than NSGA-II. Therefore, MOTLA/D is able to achieve a better handling of reactive power by optimizing the reactive power losses and the voltage stability index. Thus, it may be concluded that our proposed algorithm is a reliable choice for the power test system considered in this study and it may be a promising choice for other test systems because the its simplicity, effectiveness and less computational effort.
References
[1] Yu, D. C., Fagan, J. E., Foote, B. and Aly, A. A. "An optimal load flow study by the generalized reduced gradient approach." Elect Power Syst Res, vol. 10 (1), pp. 47-53, January 1986. [ Links ]
[2] Aoki K, Fan M. and Nishikori, A., "Optimal var planning by approximation method for recursive mixed integer linear programming." IEEE Trans Power Syst, vol. 3 (4), pp. 1741-1747, Nov. 1988. [ Links ]
[3] Sousa V. A., Baptista E. C. and Costa, G. R. M., "Optimal reactive power flow via the modified barrier Lagrangian function approach." Elect Power Syst Res, vol. 84 (1), pp. 159– 164, March 2012. [ Links ]
[4] Lo, K. L. and Zhu, S. P., "A decoupled quadratic programming approach for optimal power dispatch." Elect Power Syst Res, vol. 22 (1), pp. 47–60, September 1991. [ Links ]
[5] Granda, M., Rider, M. J., Mantovani, J. R. S. and Shahidehpour., "A decentralized approach for optimal reactive power dispatch using a Lagrangian decomposition method." Elect Power Syst Res, vol. 89, pp. 148–156, August 2012. [ Links ]
[6] Deb, K., Agrawal, S., Pratab, A. and Merayivan, T., "A fast and elitist multiobjective genetic algorithm: NSGA-II," IEEE Transactions on Evolutionary Computation, vol. 6 (2), pp. 182-197, April 2002. [ Links ]
[7] Yoshida, H., Fukuyama, Y., Kawata, K., Takayama, S. and Nakanishi, Y., "A particle swarm optimization for reactive power and voltage control considering voltage security assessment." IEEE Trans. Power Syst. vol. 15, pp. 1232-1239, 2001. [ Links ]
[8] Abou, A., Ela, E., Abido, M. and Spea, S. R., "Differential evolution algorithm for optimal reactive power dispatch." Electr. Power Syst. Res., vol. 81, pp. 458-64, 2011. [ Links ]
[9] Khazali, A. and Kalantar, M., "Optimal reactive power dispatch based on harmony search algorithm." Electr. Power & Energy Syst., vol. 33, pp. 684-692, 2011. [ Links ]
[10] Vlachogiannis, J. and Ostergard, J., "Reactive power and voltage control based on general quantum genetic algorithms." Expert Syst. Appl., vol. 36, pp. 6118-6126, 2009. [ Links ]
[11] Li, H. and Zhang, Q., "Multiobjective optimization problems with complicate Pareto sets, MOEA/D and NSGA-II." IEEE Transactions on Evolutionary Computation, vol. 13 (2), pp. 284-302, April 2009. [ Links ]
[12] Rao R. V, Savsani, V. J. and Vakharia, D. P., "Teaching-learning based optimization: A novel method for constrained mechanical design optimization problems." Computer-Aided Design, vol. 43 (3), pp. 303-315, Mar. 2011. [ Links ]
[13] Miettinen, K., "Nonlinear Multiobjective Optimization." Kluwer Academic Publishers, Boston. Massachuisetts, 1999. [ Links ]
[14] Kessel, P. and Glavitsch, H., "Estimating the Voltage Stability of a Power System." IEEE Transactions on Power Delivery, vol.1 (3), pp.346-354, July 1986. [ Links ]
[15] System data (2006, December). Available from: <www.ee.washington.edu/research/pstca> [ Links ] .
[16] Zitzler, E., Deb, K. and Thiele, L., "Comparison of Multiobjective Evolutionary Algorithm: Empirical Results." Evolutionary computation, vol. 8(2), pp. 173-195, summer 2000. [ Links ]
[17] Schott, J. R., "Fault Tolerant Design Using Single and Multicriteria Genetic Algorithm Optimization." Master Thesis, Department of Aeronautics and Astronautics, Massachusetts Institute of Technology. May 1995. [ Links ]
Miguel A. Medina was born in Merida. Yuc., MEXICO, on February 5, 1984. He received the B.S. degree in engineering physics from Universidad de Yucatán, Yuc., MEXICO, in 2008 and the MSc degree in electrical engineering from CINVESTAV, Guadalajara, Mexico, in 2010, where he is currently pursuing the PhD degree. His primary area of interest is optimization.
Juan M. Ramirez received the B.S. degree in electrical engineering from Universidad de Guanajuato, Guanajuato, México, in 1984, the M.Sc. degree in electrical engineering from UNAM, D.F., México, in 1987, and the PhD degree in electrical engineering from UANL, Monterrey, México, in 1992. He joined the Department of Electrical Engineering of CINVESTAV, Guadalajara, in 1999, where he is currently a full-time Professor. His areas of interest are in power electronics and smart grid applications.
Carlos A. Coello Coello received the PhD degree in computer science from Tulane University (in the USA) in 1996. He is a full Professor and Chair of the Computer Science Department of CINVESTAV-IPN, in Mexico City, Mexico. He is associate editor of the IEEE Transactions on Evolutionary Computation. His main research interests are evolutionary multiobjective optimization, and constraint-handling techniques for evolutionary algorithms.
Swagatam Das received the PhD degree in engineering from Jadavpur University, India, in 2009. Currently he is serving as an assistant professor at the Electronics and Communication Sciences Unit of Indian Statistical Institute, Kolkata. His research interests include evolutionary computing, pattern recognition, multi-agent systems, and wireless communication. He is the founding co-editor-in-chief of "Swarm and Evolutionary Computation", an international journal from Elsevier. He serves as associate editors of the IEEE Trans. on Systems, Man, and Cybernetics: Systems and Information Sciences (Elsevier). He is an editorial board member of Progress in Artificial Intelligence (Springer), Mathematical Problems in Engineering, International Journal of Artificial Intelligence and Soft Computing, and International Journal of Adaptive and Autonomous Communication Systems. He is the recipient of the 2012 Young Engineer Award from the Indian National Academy of Engineering (INAE).