Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.186 Medellín jul./ago. 2014
https://doi.org/10.15446/dyna.v81n186.36987
http://dx.doi.org/10.15446/dyna.v81n186.36987
Revalidation of Elder's equation for accurate measurements of dispersion coefficients in natural flows
Revalidación de la ecuación de Elder para la medición precisa de coeficientes de dispersión en flujos naturales
Alfredo José Constain-Aragón a
a FLUVIA/HYDROCLORO TECH, SAS, Bogotá, Colombia. alfredoconstain@fluvia.com
Received: February 5th, 2013. Received in revised form: June 16th, 2014. Accepted: June 25th, 2014.
Abstract
One of first practical definitions for numerical solutions of classical model of Advection-Dispersion was the Elder's equation developed in 1959. This relationship based on the theoretical guidance proposed by G.I. Taylor for long, straight pipes, extent successfully the method for the case of ideal prismatic, wide channels in open flow. However, wishing to apply it to real cases with varied geometry the results were not satisfactory due to several reasons which will be examined in this article. This limiting situation for the equation is inconvenient for two reasons: First, whatsoever it is a very used equation due to its simplicity and to the fact that involve geomorphologic parameters, without requiring tracers. Secondly but not the less important, because it is based on fundamental mechanisms that are widely accepted, and then they should not lead to results in conflict with experiments. For these reasons, and also because the study of water quality depends critically on the understanding of these processes, it is interesting to review this subject. It will be tried to show if it is used a longitudinal coefficient function of time it is possible to recover the applicability of equation. For this it is used an extended work of PhD thesis done by H.B. Fischer in the Mc Keck channel of Caltech on behavior of Elder's relationship.
Keywords: Dispersion, Gaussian dynamics, water quality studies
Resumen
Una de las primeras definiciones prácticas para la solución numérica del modelo clásico de Dispersión-Advección fue la ecuación de Elder desarrollada en 1959. Esta relación basada en las guías teóricas propuestas por G.I. Taylor para tubos largos, rectos, extendió exitosamente el método para el caso de canales ideales prismáticos anchos en flujo abierto. Sin embargo al quererse aplicar a casos reales con geometría variada los resultados no fueron satisfactorios por diversas razones que serán analizadas en este artículo. Esta situación limitante para la ecuación es inconveniente por dos razones: Primera, pese a todo es una ecuación muy utilizada hoy en día debido a su sencillez y al hecho de involucrar parámetros de la geomorfología del flujo, sin requerir el uso de trazadores. En segundo lugar, y no menos importante por cuanto está basada en mecanismos fundamentales de los fluidos que se han aceptado como correctos y que por lo tanto no deberían conducir a resultados en conflicto con el experimento. Por estas razones, y además por cuanto el estudio de la calidad del agua depende actualmente en forma crítica del entendimiento de estos procesos, es interesante revisar este tema. Se tratara de mostrar que si se plantea un coeficiente longitudinal función del tiempo se puede recuperar la aplicabilidad de la ecuación. Para esto se aprovecha un extenso trabajo de tesis doctoral realizado por H.B. Fischer en el canal Mc Keck del Caltech sobre el comportamiento de la relación de Elder.
Palabras clave: Dispersión, dinámica Gaussiana, estudios de calidad de agua.
1. Introducción
Siendo un tema de fundamental importancia para el bienestar de las sociedades actuales, el desarrollo de las ciencias del agua es relativamente reciente. El primer estudio importante sobre el transporte dispersivo en los flujos naturales fue realizado por G.I. Taylor en 1954 [1] quien postulo que el principal mecanismo para el esparcimiento aleatorio de solutos en dichos flujos era el efecto cortante generado por las distribuciones de velocidad. Afirmó también que este efecto, bajo ciertas circunstancias, puede representarse mediante una ecuación de Fick mono dimensional. Taylor aplico sus hipótesis a tubos rectos y largos encontrando una definición apropiada para estos casos. Luego, aplicando estos mismos razonamientos J.W. Elder en 1959 obtuvo una definición del coeficiente de transporte para un canal abierto infinitamente ancho. El intento de aplicar posteriormente estas fórmulas a flujos naturales, abiertos e irregulares llevo a una gran dispersión de los valores de estos coeficientes, pensándose que el concepto Fickiano estaba en un error [2] y que los desarrollos de Taylor y Elder deberían circunscribirse a variadas restricciones. El desarrollo de este tema comprende:
1.1. Objetivo
Se plantea mostrar que la Ecuación de Elder apropiadamente interpretada es correcta en sus aplicaciones en los cauces naturales.
1.2. Método general
Se desarrolla un nuevo enfoque teórico del coeficiente de dispersión como función de tiempo que recobra una adecuada operación de las ecuaciones de transporte en flujos naturales. Se aplica luego a la ecuación de Elder y se resuelve en un caso clásico de la literatura técnica desarrollado por H.B. Fischer.
Para concretar este procedimiento se revisan los antecedentes y fundamentos de dicha ecuación y en seguida los argumentos que se usaron para limitar drásticamente (e injustamente) los alcances de Elder, mostrando como ellos a su vez estaban afectados por diversos errores; imposibilitando así su validez como "referencia" válida para descalificarla.
1.3. Resultados generales
La aplicación del método en el caso particular resulta exitosa al concordar bastante bien los datos experimentales con el modelo teórico.
1.4. Conclusiones generales
La técnica desarrollada en este artículo puede aplicarse con gran ventaja en los cauces naturales, permitiendo obtener valores objetivos de la pendiente y la rugosidad.
2. Fundamentos de la ecuación de Elder
La mayoría de los análisis matemáticos de los flujos turbulentos, el transporte de solutos se describe por una ecuación diferencial de balance de masa promediada en el tiempo.
Cuando la difusión vertical y transversal ha ocurrido y el trazador llena uniformemente la sección transversal es más practico plantear el balance como promediado en el espacio y puesto en términos de valores medios, distribuciones y desviaciones, tanto para la velocidad advectiva como para la concentración, medidos sobre el plano móvil asociado a dicha sección transversal [3].

Las distribuciones espaciales de velocidad y concentración son c y u, mientras que las desviaciones espaciales son c' y u'. Los valores medios espaciales son entonces C y U. En este caso el balance se puede poner como sigue (manteniendo solo la difusión turbulenta, ex)
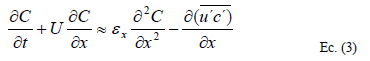
En este punto el esparcimiento aleatorio longitudinal de las partículas de soluto se va a deber primordialmente al efecto cortante de la distribución de velocidades, siendo mucho mayor que el efecto de la difusión turbulenta [4]. Si además se tiene en cuenta la aproximación Fickiana dada por Taylor sobre este tipo de transporte, con E como el Coeficiente de dispersión cortante efectiva:

La ecuación de balance final se puede aproximar como:
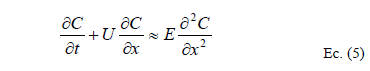
Para deducir un valor específico para el coeficiente de transporte E, Elder se basó en una triple integración sobre el plano móvil, empleada por Taylor previamente [1-5]:
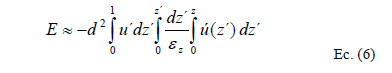
Aquí d es la profundidad media del flujo, ez el coeficiente de transporte vertical y z'= z/d. Se considera que el efecto dispersivo longitudinal se puede describir apropiadamente en función de lo que ocurra con la desviación de velocidad u' y un desarrollo para c' (que desaparece) proporcional al gradiente de C, ya que la operación en Ec. (6) es correspondiente en realidad a la integración espacial de desviaciones implícita en Ec. (4).
Las condiciones impuestas por Taylor para llegar a Ec. (6) Son: A).-Que se cumpla "mezcla completa" en la sección transversal medida por c'<<C. B).- Que el transporte longitudinal debido a la turbulencia sea despreciable. C).- Que los cambios de la concentración promedio C en la sección transversal no sean muy rápidos tal que se pueda establecer a c' como proporcional al gradiente de C (estado estable).
Elder para llegar a un valor concreto de Ec. (6) propone involucrar la analogía de Reynolds con m el esfuerzo cortante y r la densidad del agua Ec. (7) para definir ez; para definir la distribución de velocidades usa la formula (8) de perfil vertical que involucra la constante de Von Kármán, k y la velocidad cortante U* con g aceleración de la gravedad y S la pendiente de fricción del flujo. Ec. (9):
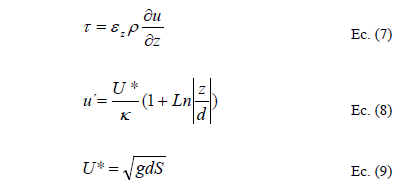
Estas consideraciones llevan a definir el Coeficiente de dispersión longitudinal según Elder como:
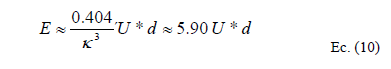
Las condiciones para la validez de esta ecuación práctica son las mismas que se aplicaron para la deducción de los pasos intermedios en el procedimiento de Taylor, Ec. (1) a Ec. (7).
3. Problemas posteriores para la ecuación de dispersión de Elder
Aunque las pruebas iniciales realizadas por Elder correspondieron con precisión con su ecuación:

Posteriores experimentos especialmente en cauces naturales con gran variación de la geomorfología indicaron una gran dispersión con respecto al resultado esperado, del orden de:

Las modelaciones teóricas de las curvas experimentales con base en los coeficientes longitudinales de dispersión derivados de la aplicación de Elder (y de otros investigadores) fueron mostrando errores evidentes especialmente en replicar la asimetría y la "altura" correctas de las curvas [6].
Entre las razones aparentes para explicar la falta de precisión de la fórmula de Elder aplicada a las corrientes naturales se anotan principalmente: La variación del perfil ideal de velocidad vertical y la predominancia de las variaciones laterales de velocidad.
4. Análisis de las aparentes imprecisiones de la fórmula de Elder
Teniendo una fundamentación fijada fuertemente en postulados ampliamente aceptados, a menudo se postula que el motivo fundamental para la falta de precisión de la ecuación de Elder es que las variaciones laterales de velocidad son más significativas que las variaciones verticales. Como se verá, esta objeción es discutible puesto que cada tipo de perfil de velocidad relaciona de manera diferente un mismo tipo de fenómeno. Para explicar esto se pondrá un ejemplo de la termodinámica [7]:
Sea un sistema en el que la variación de energía interna, Ui se deba al ingreso de calor desde el exterior debido a una diferencia de temperatura, DT y a una variación de la energía superficial por variación de la superficie del sistema, DA. Usualmente y dependiendo del tipo de proceso, de la estructura física del sistema y de otros factores, un sumando es predominante sobre el otro.
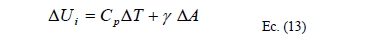
Esto ocurre así por cuanto estas variables son independientes. En el caso de los efectos dispersivos transversales y verticales son en última instancia funciones de la turbulencia, la cual se considera homogénea e isótropa en este tipo de flujos. Por lo tanto, esas dispersiones aunque aparentemente sin conexión, son dependientes y su expresión matemática es en esencia diferente a lo expresado en la Ec. (13). En ese mismo tenor se podría decir que las variaciones laterales de velocidad reflejan una misma realidad que las variaciones verticales. Otra cosa es que se pueda decir que una variación es mayor (más sensible) que la otra [8].
Cualquiera que fuesen las razones para la imprecisión de la fórmula de Elder, la necesidad de disponer de valores concretos del coeficiente de transporte llevó a muchos investigadores a proponer diferentes métodos, la mayoría basados en datos de experimentación con trazadores.
Muy populares en las décadas de 1970 y 1980 fueron las definiciones basadas en la estadística ("variación de momentos") y su ajuste mediante la correlación por Routing [2].
El método de los momentos exige el cálculo de las varianzas para dos curvas secuenciales en función del espacio. Como los datos de concentración son normalmente dados en función del tiempo se debe multiplicar por la velocidad media al cuadrado.
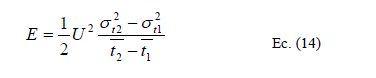
Ahora, cualquiera que sea el valor de E obtenido por la Ec.(14) o por cualquier otro método, lo usual era verificar el resultado por un procedimiento de integración basado en la difusión. Así, si en un tiempo inicial t=0 una distribución inicial de trazador co(x) es observada, entonces por superposición de soluciones elementales se puede obtener la distribución c(x,t) correspondiente a un tiempo posterior. Este resultado se compara en el punto de interés con la distribución experimental real. Si el resultado es satisfactorio se deja el valor de E utilizado, sino se va variando en pasos hasta que se obtenga una convergencia satisfactoria.
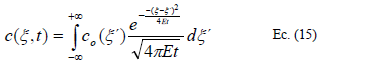
El cálculo de los momentos tiene el problema de que la asimetría de las curvas reales es mayor que la prevista por la teoría difusiva normal, como se explicara posteriormente. El problema con la verificación por Routing es que plantea cálculos muy engorrosos que pueden ser reiterativos en el peor de los casos, sin tenerse una solución completamente satisfactoria.
Por otra parte aunque el autor del método Routing (H. B. Fischer) clama que este ofrece el "mejor coeficiente de dispersión posible" otros autores [9] advierten que si la curva experimental a ser analizada es muy asimétrica el ajuste puede estar en gran error.
5. El coeficiente de transporte longitudinal como función del tiempo
No obstante las diversas objeciones a la fórmula de Elder Se tratará de mostrar como el concepto de coeficiente de transporte función del tiempo puede devolver la validez de la ecuación de Elder, tal como se desarrolla a continuación:
5.1. Velocidad media del flujo en función de los datos del transporte dispersivo
A partir del concepto Browniano del movimiento totalmente aleatorio de las partículas de soluto conservativo en un flujo, se puede establecer una relación mono-dimensional cuadrática entre el tiempo y el desplazamiento característico, D y m [10]:

Por lo tanto se puede establecer una ecuación para la velocidad media advectiva:

Despejando a E:

Debe notarse aquí que el tiempo característico Gaussiano m es diferente a la variable independiente t, ya que la primera se refiere al tiempo en el cual la separación aleatoria de las partículas ocurre mientras esta distancia promedio es D mientras que la escala temporal general se asocia más bien al efecto advectivo de U. La relación entre ambos tiempos se puede establecer si se piensa que el tiempo general se gasta en observar la aparición probabilística de 0, 1, 2...n partículas de trazador que se mueven en su propio marco temporal característico, y teniendo en cuenta que es una dinámica del tipo Svedberg [11].
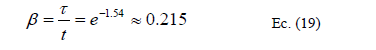
5.2. La descripción de la pluma de soluto vista por diferentes observadores
Aunque la transformación de Galileo para pasar de un sistema inercial a otro se incluye en el argumento exponencial de la ecuación clásica de Fick, con M la masa de soluto y A la sección transversal del flujo:
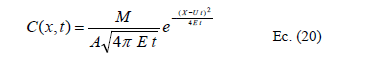
Sin embargo, su implicación física profunda no fue advertida completamente por Taylor en su análisis de la evolución de la pluma en un flujo. En efecto lo que realmente quiere decir esta transformación es que pueden existir diversos observadores inerciales y que ellos tendrán diferentes pinturas del suceso, dependiendo de la composición de velocidades que ellos hagan. Por ejemplo, un observador moviéndose exactamente con U sobre el centro de masa de la pluma describirá su desplazamiento con la ecuación simple:

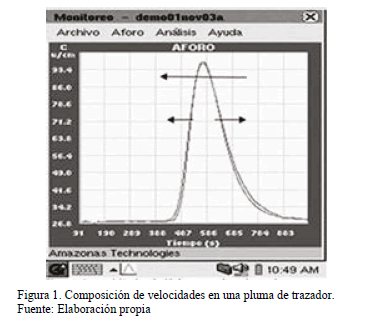
En este sistema inercial particular el observador deberá eliminar la velocidad U pues la pluma no se desplazará con respecto a él, y además esta curva aparecerá simétrica pues el no compondrá U consiguientemente con otras que aparezcan en su descripción (por ejemplo las dos velocidades simétricas de dispersión de la pluma). Fig. 1.
La eliminación de esta velocidad puede ser trabajada en la ecuación diferencial básica de conservación Ec. (5) así:
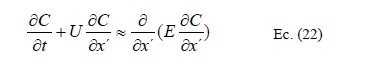
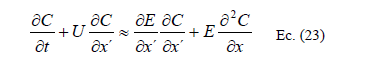
Por lo tanto, para que el término advectivo desaparezca se tiene que:

Esto implica que:

Y si se tiene flujo no uniforme (como ocurre en la práctica) entonces U será función de la distancia x' y por lo tanto del tiempo. Así mismo E será función del tiempo. Entonces, la condición para que el observador móvil sobre la pluma de soluto describa correctamente su visión de este movimiento, es que el coeficiente de transporte sea función del tiempo. Por esta razón quienes aplicaron la ecuación de Fick con E=constante no obtuvieron resultados concordantes con el experimento pues la transformación de Galileo fue solo aplicada parcialmente.
5.3. Una ecuación modificada de Fick para el transporte dispersivoAhora reemplazando la Ec. (18) en la Ec. (20) se tiene con:
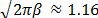
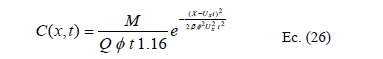
Esta es una ecuación de Fick modificada que tiene en cuenta la dependencia de la velocidad de dispersión con la velocidad media advectiva, tal como se ha explicado anteriormente. La particularidad de esta ecuación es que reproduce bastante bien las curvas experimentales de trazador como se mostrara más adelante.
6. Aplicación del concepto de coeficiente de transporte función del tiempo a un experimento real
Para verificar el nuevo enfoque propuesto fue escogido un experimento detallado en el que se cumplen las condiciones de mezcla y flujo uniforme aproximado.
Este experimento fue realizado por H.B. Fischer en el canal calibrado de 40 metros con pendiente ajustable y recirculación, del W.M Keck Laboratory de Caltech en 1966[1]. El objetivo original del experimento fue analizar la validez de las hipótesis de Taylor y Elder con respecto a la dispersión por efecto cortante.
Este es un canal rectangular de paredes de plástico y lecho de acero inoxidable. Tiene un recorrido uniforme desde 0.0 m hasta los 38.6 m. Para el experimento en cuestión se utilizó una pendiente de 0.0002 ajustada mediante los aparejos mecánicos de precisión del laboratorio. Fig. 2.
Fischer aplico la fórmula de momentos Ec. (13) para determinar E. Así mismo verifico el resultado mediante un procedimiento Routing. Las condiciones anteriores permiten calcular un valor de este coeficiente por la fórmula de Elder y entonces compararla con el dato obtenido por Fischer.
6.1. Consideraciones particulares del experimento
El experimento denominado por su autor como "Series" 2700 consistió en ocho vertimientos con sal común. Cuatro (2700 a 2704) hechos a X1= 14.06 m y otros cuatro (2705-2708) hechos a X2= 25.06 m. Para todos los vertimientos-salvo la distancia-las demás condiciones del experimento fueron mantenidas iguales. Para pasar de una "serie" a otra (de X1 a X2) se movió el dispositivo inyector de trazador, en lugar de mover las sondas para no modificar la calibración. En realidad para cada distancia se promediaron los cuatro vertimientos, así que el dato dado para cada serie es un promedio. Para este experimento se obtuvo una profundidad de la lámina de agua de h= 0.128 m y una velocidad media del flujo de U=0.362 m/s.
La profundidad de cada experimento se controló con un indicador especial colocado sobre la lámina de agua mientras que la velocidad del flujo fue medida con un tubo Pitot tipo Prandlt.
6.2. Método de inyección del trazador
La sustancia trazadora iónica sal común se inyecto al canal súbitamente mediante un aparejo especial que permitió una dispersión completa sobre toda la sección transversal del flujo.
6.3. Método especifico utilizado en el experimento
El experimento de Fischer básicamente estaba orientado a lograr de manera rápida una condición de "Mezcla completa" en el flujo del trazador y obtener una condición de flujo uniforme aproximado. Por lo tanto para el experimento 2700 esta canaleta de la Fig. 2 ocupaba todo el ancho del canal. De esta forma el trazador inyectado alcanzaba mezcla ideal en toda la sección transversal del flujo de manera casi instantánea. La masa de trazador para cada vertimiento fue la misma ya que la canaleta se llenaba en las dos oportunidades con la misma cantidad de solución conductora.
6.4. Datos del Experimento
Los Datos hidráulicos y mecánicos básicos del canal en la "corrida" 2700 se muestran en la Tabla 1.
6.5. Curvas de trazador en los dos sitios de medición
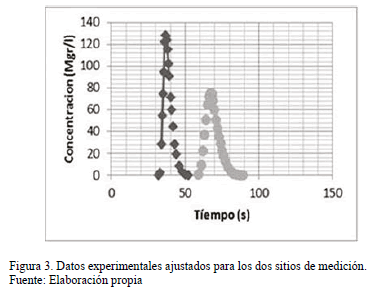
De acuerdo con lo requerido por la ecuación de momentos para el cálculo de E, era necesario tener dos curvas secuenciales con un solo vertimiento. Las gráficas de las dos mediciones se muestran en la Fig. 3. Hay que anotar que H.B. Fischer no documentó la información de la concentración (conductividad) real y solo utilizó datos relativos.
Para poder comparar las diferentes modelaciones que se estudian es necesario tener un valor concreto de masa (que valdrá para todas ellas por igual), por lo que se asume una inyección súbita de sal de M=40,5 gramos, ajustando los datos experimentales correspondientemente a concentraciones absolutas. A partir de estos datos discretos se pueden calcular las varianzas de cada una de las curvas y a partir de ellas por medio de la Ec. (14) calcular el coeficiente de transporte.
7. Análisis y comparaciones de los resultados del experimento utilizando diversos enfoques
7.1. Comparación entre el valor del Coeficiente de dispersión calculado por variación de momentos y la formula de Elder
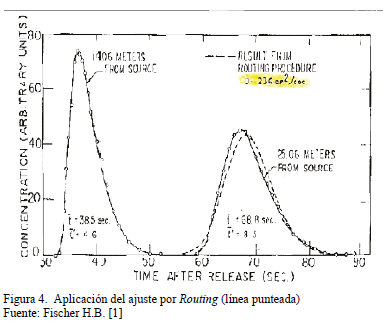
El valor de referencia (verificado por un procedimiento de Routing) es de:
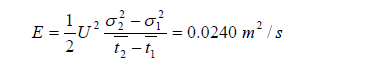
El método Routing de ajuste ofrece un valor bastante parecido al de momentos, E= 0.0236 m2/s. El resultado de la modelación óptima aparece con línea punteada. Fig. 4, tomada del documento original en Ingles de H.B. Fischer [1]. En amarillo se resalta el valor para el Coeficiente Longitudinal de dispersión hallado por este procedimiento.
La aplicación de la fórmula de Elder es como sigue:
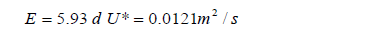
El error porcentual entre los dos valores es de 95% siendo bastante menor el valor de la fórmula de Elder, en concordancia con otros muchos resultados previos en los que esta fórmula minimizaría la dispersión real al no basarse sobre distribuciones laterales de velocidad. [13]
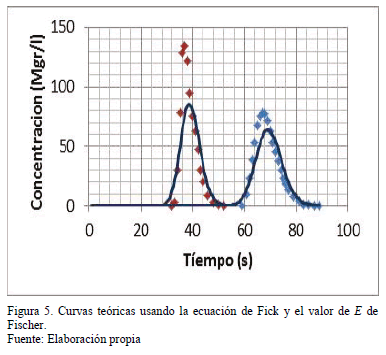
7.2. Modelaciones de las curvas experimentales usando el valor de E de Fischer y la formula de Fick
Modelaciones en la ecuación básica de Fick, Ec. (20) utilizando Excel con el valor de E obtenido por Fischer dan curvas teóricas muy alejadas de sus correspondientes valores experimentales. . 5.
X1=14.06 m
Con E=0.0236 m2/s, A= 0.140 m2 y U=0.362 m/s.
X2= 25.06 m
Con E=0.0236 m2/s, A= 0.140 m2 y U=0.362 m/s.
7.3. Modelaciones de las curvas experimentales usando el coeficiente de dispersión función del tiempo
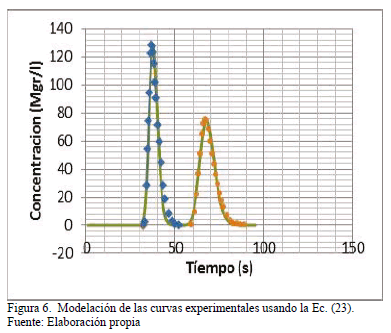
Los datos de las curvas de trazador que son necesarias para la aplicación del nuevo enfoque plasmado en la ecuación modificada de Fick, Ec. (26) se muestran en la Tabla 2 y Fig. 6.
Estos datos se obtienen aplicando el modelo de Fick modificado de la Ec. (20) que sintetiza la metodología del coeficiente de transporte función del tiempo. [14] [15]. En este nuevo procedimiento se corrige el desfasaje entre curvas teóricas y experimentales que resulta de aplicar la metodología corriente con el dato de Elder a partir de su verificación de Routing. Nótese como en la Fig. 5 falla la congruencia obligatoria que debe haber entre un valor hallado por este Routing y el modelo clásico de Fick, que es la base misma del procedimiento de correlación de Fischer. Por el contrario, la congruencia entre teoría y experimento con E(t) es evidente en la Fig. 6.
Es evidente en este caso la correspondencia entre los datos teóricos y experimentales para las curvas del experimento analizado.
7.4. Comparación de los valores de E(t) con el valor calculado con la formula de Elder
Es interesante comparar los valores del coeficiente de transporte función del tiempo con el valor dado por la ecuación de Elder.
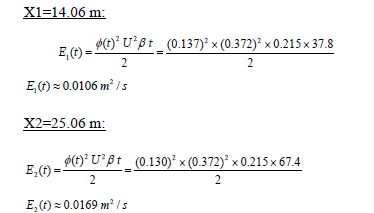
Esto da un valor promedio para E(t)= 0.0138 m2/s, lo que implica un error porcentual del 14% con el resultado de Elder.
7.5. Discusión de los resultados de la aplicación del nuevo método en el experimento clásico de Fischer
Las diferencias entre las curvas teóricas (y su congruencia con los datos experimentales), mostradas en las Figs. 8 y 9 muestran que el método de coeficiente de transporte función del tiempo da resultados mucho mejores que los obtenidos con las teorías convencionales. Pero además de eso, en el desarrollo de los cálculos para el experimento del canal Caltech se obtuvo analíticamente la pendiente utilizada en dicho canal, lo que constituye una gran ventaja en los estudios de calidad de aguas en los que valores congruentes de pendiente son un requisito para el éxito de las modelaciones.
8. Conclusiones específicas
- La ecuación de Elder desarrollada para dar valores concretos del coeficiente longitudinal de dispersión, E en función solo de parámetros de la geomorfología del cauce es analizada en este artículo para un experimento en el canal Caltech en 1966, siendo compatible con los datos experimentales si se utiliza un coeficiente E función del tiempo.
- El procedimiento utilizado por Fischer para caracterizar la dispersión cortante en este canal usa definiciones y ajustes vigentes en la época. Sin embargo sus resultados están muy alejados (por exceso) de los de Elder. Se explica en este artículo las razones por las cuales este punto de vista de Fischer y otros puede estar equivocado.
- De acuerdo con los resultados anteriormente mencionados, la ecuación de Elder da valores de E concordantes con la realidad, dentro del rango esperado de error experimental. Esta es una situación interesante pues la fundamentación teórica de esta ecuación ha sido reconocida como correcta a lo largo de los años y su aparente falla no dejaba de ser un gran interrogante a los especialistas del tema.
- Como quiera que la parte geomorfológica es sumamente importante en los estudios de calidad de aguas [16] ,este método puede entonces ser aplicado con gran ventaja en aquellos casos en los que esta ecuación aporta innegables facilidades, como por ejemplo involucrar la pendiente en los cálculos analíticos.[16]
- Diversas aplicaciones del método a variados cauces indican en principio una buena confidencia del método. [17]
Referencias
[1] Fischer, H.B., Longitudinal dispersion in Laboratory and Natural Streams. Report No. KH-R-12, California Institute of Technology, 1966. [ Links ]
[2] Fischer, H.B., The mechanisms of dispersion in natural streams, Journal of the Hydraulics Division, Proceedings of the ASCE. Nov, pp. 187-215, 1967. [ Links ]
[3] Holley, E.R., Unified view of diffusion and dispersion, Journal of the Hydraulics Division. Proceedings of ASCE, March, pp. 621-631, 1969. [ Links ]
[4] French, R.H., Open channel hydraulics, Chapter 10, New York, Mc Graw-Hill, 1987, pp. 462-507. [ Links ]
[5] Prych, E.A., Effects of density difference on lateral mixing in open-channel flows. Report No. KH-R-21. California Institute of Technology, 1970. [ Links ]
[6] Jobson, H.E., Prediction of travel time and longitudinal dispersion in rivers and streams, USGS report in internet, 1996. [ Links ]
[7] Kikoin, I. y Kikoin, A., Física molecular. Editorial Mir, Moscú, 1971. [ Links ]
[8] Lopatkin A.A. y Spiridonov V.P. Tratamiento matemático de datos fisicoquímicos, Moscú, Editorial Mir, 1973. [ Links ]
[9] Mc Quivey, R.S. and Keefer, T.N., Simple method for predicting dispersion in streams, Journal of the Environmental Engineering Division, August, pp. 996-1011, 1974. [ Links ]
[10] Constain, A.J. y Lemos, R., Una ecuación de velocidad media del flujo en régimen no uniforme, su relación con el fenómeno de dispersión como función del tiempo y su aplicación a los estudios de calidad de agua. Revista Ingeniería Civil CEDEX, 164, pp. 114-135, 2011. [ Links ]
[11] Constain, A.J., Svedberg's number playing a main role in diffusion processes, Presented to Tracer 6, Norway. 2011. [ Links ]
[12] Prigogine, I. and Kondepudi, D., Modern Thermodynamics. New York, Wiley, 1999. [ Links ]
[13] Seo, I.W. and Baek, K.O., Estimation of longitudinal dispersion coefficient for streams, River Flow, Belgium, 2002. [ Links ]
[14] Constain, A. J., Definición y análisis de una función de evolución de solutos dispersivos en flujos naturales, Revista DYNA, 79 (175), pp. 173-181, 2012. [ Links ]
[15] Constain, A. J., Verificación del transporte de trazadores radioactivos usando un coeficiente función del tiempo en cauces naturales, Revista DYNA, 79 (175), pp. 150-157, 2012. [ Links ]
[16] Montelongo, R., Gordillo, A.J., Otazo, E.M., Villagómez, J.R., Acebedo, O.A. y Prieto, F., Modelación de la calidad del agua del Rio Tula, Estado de Hidalgo, México, Revista DYNA, 75 (154), pp. 5-18, 2008. [ Links ]
[17] Hydrocloro Tech SAS., Informe Rio Meta, Documento interno de la empresa, Bogotá, 2014. [ Links ]
A.J. Constaín-Aragón received the Bs. Eng in electronic Engineering by Universidad del Cauca in 1977. He was certified in Telecommunications by the same university. He was professor in Universidad de la Salle, Universidad Javeriana, Universidad Autónoma de Occidente, Universidad del Valle and Universidad del Cauca. In 1993 he was awarded with the Brigard & Castro prize and in 2005with the INNOVA prize. He is currently R&D manager in FLUVIA TECH from Bogota, developing tracer techniques.