Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.186 Medellín jul./ago. 2014
https://doi.org/10.15446/dyna.v81n186.38101
http://dx.doi.org/10.15446/dyna.v81n186.38101
Photorealistic simulated modelling from fractals applied to mined-out pit restoration
Modelo de simulación fotorrealística a partir de fractales aplicados a la restauración de entornos mineros
Iván de Rosario-Amado a, José Santiago Pozo-Antonio b, Gabriel Lorenzo-Salgueiro c, Jorge Feijoo-Conde d & Javier Taboada-Castroe.
a Escuela de Ingenieros de Minas, Universidad de Vigo, España. ivanderosario@gmail.com.
b Escuela de Ingenieros de Minas, Universidad de Vigo, España. ipozo@uvigo.es
c General de Hormigones S.A., España. glorenzos@gedhosa.masaveu.com
d Escuela de Ingenieros de Minas, Universidad de Vigo, España. jorgefeijooconde@gmail.com.
e Escuela de Ingenieros de Minas, Universidad de Vigo, España. jtaboada@uvigo.es.
Received: May 13th, de 2013. Received in revised form: July 14th, 2014. Accepted: July 25th, 2014
Abstract
3D modelling has been used to simulate the restoration of mining environments, mainly due to ease of use. However, this technique poorly models natural structures, such as leaves, coastlines, mountain systems, etc. Recent digital technology innovations have led to the development of fractal geometry software that reiterates geometric objects at different scales. Below we describe how this geometry can be used for environmental restoration and rehabilitation. We present a case study describing an application of fractal geometry to the restoration of a mined-out open pit. We conclude with a discussion of the advantages - mainly realism and the rapid execution time - of using this type of geometry versus 3D modelling for mining restorations.
Keywords: Euclidean geometry, Fractal geometry, Landscape, Mining, Open-pit mine, Landscape integration.
Resumen
A la hora de realizar las restauraciones de entornos mineros, se ha empleado la modelización 3D debido fundamentalmente a su facilidad de manejo. Sin embargo, esta técnica no obtiene buenos resultados cuando genera estructuras naturales, como hojas de árboles, bordes de costa o sistemas montañosos. Gracias al desarrollo de la tecnología digital en los últimos años, nace el empleo de software informáticos basados en la geometría fractal, basada en la repetición continua de diversos objetos geométricos en diferentes escalas.
Este trabajo está constituido por dos secciones diferenciadas. La primera presenta el fundamento de esta geometría orientada a restauraciones y rehabilitaciones medioambientales. La segunda parte presenta un caso práctico de restauración de una corta minera. Finalmente se presentan las ventajas del empleo de este tipo de geometría frente a la modelización 3D en el ámbito de las restauraciones mineras, destacando su realismo y bajo tiempo de ejecución.
Palabras clave: Geometría euclidiana; Geometría fractal; Paisaje; Minería; Corta minera; Integración paisajística.
1. Introduction
Landscape is understood to be the perception or set of sensations (visual, auditory and olfactory) produced by a natural setting in which humans have or have not intervened [18]. Landscape protection policies exist at the European level whose origins lie in two conferences in particular: the 1972 UNESCO World Heritage Convention held in Paris and the 2000 Council of Europe European Landscape Convention held in Florence. Both declare the landscape to play an important public interest role in the cultural, ecological, environmental and social fields [26]. Nonetheless, the lack of reliable and up-to-date information from the European Union related to the type, location, size and conservation status of natural and semi-natural habitats is an obstacle to implementing the Pan-European Biological and Landscape Diversity Strategy [19].
Skãlos and Kaparová [21] discuss - in relation to the European Landscape Convention [26,12] and the case of mining - the issues of identifying and quantifying the values of what are called "ordinary cultural landscapes" and the associated loss of cultural memory, drawing comparisons with the landscapes resulting from farming activities. Uncontrolled and disordered growth of mining infrastructures and operations has altered the landscape resource, greatly affecting perceptions of mine surroundings. As a result of this habitat destruction [7], visual unity is fragmented in small regions isolated from each other [6]. A number of indicators have been developed aimed at assessing the quality of the landscape and quantify its ecological importance [19,26].
1.1. Simulation of mined-out open pits restoration: 3D modelling and fractal geometry
The social and political pressures to restore mined-out open pits has been growing in recent years. 3D modelling has been the technique of choice for simulating the appearance of an area in different seasons of the year through variations in the sun's position and atmospheric conditions, determining how far water would rise in a flood situation and verifying that the restored orography and vegetation would be integrated in the landscape [8, 20]. 3D modelling is also used to study the behaviour of structures that are still in the exploitation-place over time. [32]. However, 3D models represent natural forms (coastlines, tree branches, rocks, mountains, etc.) using Euclidean geometry and so require vast amounts of data for detailed description and representation, not to mention the substantial processing time needed.
Another type of geometry that would simulate more realistic models more rapidly is fractal geometry [4,13], by means of which the structure of objects is repeated in different scales (called fractals). This structure is generated by a recursive or iterative process that is capable of producing similar structures regardless of the viewing scale [16]. An irregular or fragmented geometric element can be subdivided into parts, each of which is approximately a smaller copy of the set [24]. General characteristics of fractals include the following: they have detail at all scales, they are self-similar, they have a simple algorithmic definition and the topological dimension is less than the Hausdorff dimension, which is an extended non-negative real number associated with any metric space. The Hausdorff dimension of an n-dimensional inner product space equals n. This means that the Hausdorff dimension of a point is zero, the Hausdorff dimension of a line is one and the Hausdorff dimension of the plane is two [14].
A number of works describe the use of fractal geometry to describe contours and surfaces in disciplines as diverse as biology, geology, physics, etc., to describe or analyse hydrological systems [15], buildings [22], landscapes [23], etc.
Euclidean geometry, typically used for 3D representation of manmade objects (buildings, rooms, etc.), is based on the measurement of elements such as points, lines, planes and volumes that combine to form specific figures or shapes [17]. 3D modelling can represent coordinates forming meshed structures wrapped by a texture. More complex objects are built from other predefined shapes such as cones, spheres, cylinders, tubes, ring, pyramids etc. via non-uniform rational basis spline (NURBS) curves [28-30]. This geometry is not able to accurately represent forms of nature, however. Natural phenomena like mountains, coastlines, river systems, clouds, leaves, snowflakes, etc. are best described and illustrated by objects whose dimensions are not expressed as integers but as fractions (fractal dimensions). Thus, a straight line has dimension 1, whereas a fractal curve has a dimension whose value lies between 1 and 2, depending on the space occupied in the plane and their relative behaviour [24].
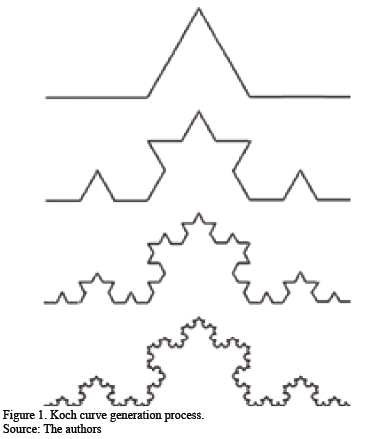
The Koch curve is one of the most common deterministic fractals [5]. Introduced by Helge von Koch in 1904, it is an example of a curve that has no tangent at any point. Figure 1 shows how the Koch curve is constructed, starting from the unit interval (initiator). The central interval of length 1/3 is replaced by two segments of the same length at an angle of 60 degrees so that the generator length is increased to 4/3. This growth factor is associated with each iteration, with the operation repeated in each of the 4 intervals formed, and so on. The Koch curve is the limit of this infinite process. The mathematical expression for calculating the dimension of a fractal is as follows:
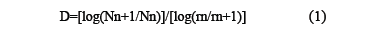
where D is the fractal dimension, Nn is the number of fragments of size rn (the scale).
If the fractal is definite, the length of the line approaches infinity while its area continues to be 0. The Hausdorff dimension for the Koch curve is D = log(4)/log(3)=1.26185, as it is self-similar, with 4 parts similar to the total on the scale 1/3.
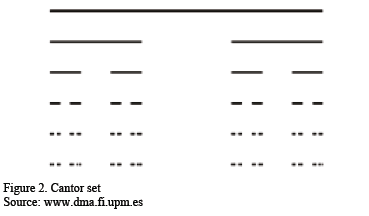
The Cantor set (Figure 2) is a subset of points in the interval [0, 1]. Removed from the unit interval Io is the central open interval of length 1/3, where the intervals are I11=[0,1/3] and I21=[2/3,1], and so on successively, until, in the nth step we have 2n intervals I1n, I2n,..., I2nn of length 1/3n. Reducing the Cantor set by the factor r=1/3 leaves just two equal parts, each measuring 1/2 of the measurement of the Cantor set. The dimension D of a combined set on the scale 1/3 is the number that holds that 1/3D=1/2, i.e. the dimension of similarity (and also the Hausdorff dimension) of the Cantor set is D= log (2)/log(3)=0.6309297.
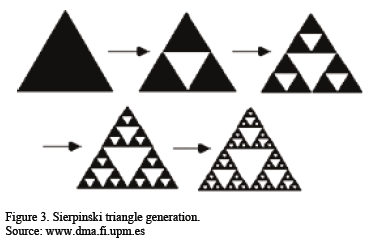
Another example is the Sierpinski triangle (Figure 3). Removed from an equilateral triangle T is a (borderless) triangle resulting from joining the midpoints of the sides of the original triangle. In this first step three new triangles T1, T2 and T3 are obtained, each of which undergoes the same process. Thus, obtained successively are 3, 9, 27, 81, etc. triangles, each a copy at scale 1/2 of the previous stage's triangle, with D=log(3)/log(2)=1.584962.
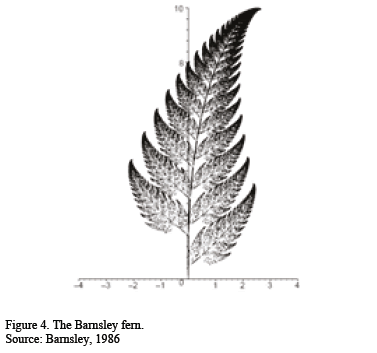
By varying, in each iteration, the points of approximation, the distance (not necessarily 1/2) and the assigned probability in order to choose the apex, different fractals can be obtained, such as the Barnsley fern shown in Figure 4 [2].
It could be said that fractal geometry is the language of nature. Through the repetition of simple instructions (squeezing, stretching, removing, folding, etc.) complex forms and structures are generated whose dimensions do not have to be integers [9,10].
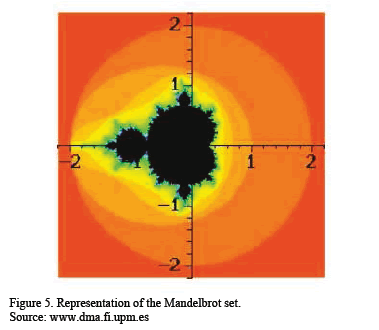
Undoubtedly, the most famous fractal is the Mandelbrot set M, defined as the set of complex numbers c of the complex plane C, for which the associated Julia set of fc is connected (Figure 5). Small perturbation of Julia set values, can cause drastic changes in the sequence of iterated function values.
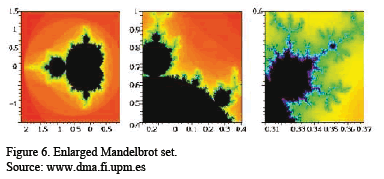
The escape-time algorithm is the tool used to computationally apply fractals. To obtain computer images of the Mandelbrot set, considered is a number N of order 100. For each c of the window to be drawn - choosing increasingly smaller windows with greater zoom, as shown in Figure 6 - the terms of the sequence fck (0) are computed. If the N first terms all confirm that |fck(0)|<2, i.e. they do not leave the circle with center 0 and radius 2, then c belongs to the Mandelbrot set and is painted black. If, however, there exists k≤N with |fck(0)|>2, then the computation is halted for this c as it is outside the
Mandelbrot set, i.e. it has "escaped" from the previous circle. If each number K between 0 and N is assigned a colour and if each number c is represented in the colour corresponding to the first K such that |fck(0)|>2 - i.e. the moment of escape from the enclosed area - then we obtain the typical images of the Mandelbrot set. The escape-time algorithm is used in the fractal image generation [31].
Random fractals also exist, characterized by the random elements involved in their construction [25]. This kind of fractal enables simulation of natural phenomena. A fractal landscape is a representation of a real or imagined landscape produced by fractals [1]. Several approaches can be used to build this type of landscape, but one of the easiest is basically to divide the square where the landscape will be restored into 4 equal parts and then randomly displace the shared central point. This process is repeated recursively in each square until the desired level of detail is obtained.
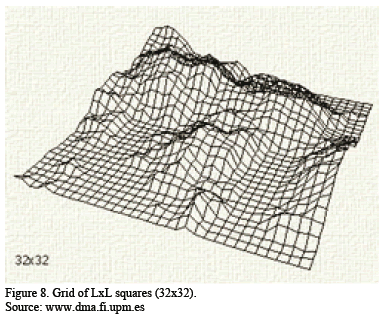
This operation produces 5 new intersections, each assigned a random perturbance over the initial zero height (Figure 7). The process is iterated until a total of LxL squares is obtained (Figure 8). For each iteration the absolute value of the perturbance over the newly generated points is reduced. This is the factor that regulates terrain roughness; thus, larger reduction factors produce smoother surfaces and smaller reduction factors produce rougher surfaces.
It is normal practice in landscape generation programs to set a threshold (sea level).
The aim of this research was to determine whether this new modelling technique could represent an effective alternative to conventional 3D modelling for mining environments, in terms both of the realism of the simulation and the time investment. For this purpose, we performed fractal simulations of the restoration of a mined-out open pit.
2. Methodology
The goal was to visualize the restoration of a mined-out open-pit mine and to verify whether the restoration would suit the terrain and flora of the surroundings and minimize impact on both the environment and the people living in the vicinity. For this purpose, the topographical map of the open-pit mine in .dwg format (Autodesk) was used.
Using the AutoCAD Civil computer code we created a 3D surface bounded by the outer limits of the .dwg topographical map and configuring a square mesh. With the UTM coordinates of the surface correctly georeferenced and scaled, the points of the surface were extracted in a mesh with a stipulated distance between contour lines, in this case 5 m, and an angle between lines of 3.125o. The procedure is described below for Autocad Civil 2010 and summarized in chart form in Figure 11.
- Topographic map: Start with the contour lines (.dwg) for the mined area in UTM coordinates (x,y,z).
- Generate the surface:
- Extract contour line points in ASCII code using the "ExtractPoints" tool.
- Increase the number of contours by linear interpolation.
- Save the set of points representing the surface mesh (Figure 9) as an ENZ formatted file.
- Convert to .txt format: Applying a geostatistical code, process the ENZ file further to improve surface definition using an algorithm for matrix smoothing between the points, with a number n (with a value between 0 and 100) inserted between points.
- Transform from .txt to .ter format using Global Mapper software, so as to be able to work with fractal mathematics in Terragen 2 Deep Edition (Figure 10).
Processing in Terragen started with the loading of the terrain data (.ter) in the workspace. The "node network" tool lists environment variables as follows:
- Terrain height, colour and texture of vegetation cover.
- Terrain slope: stony, angles of over 75 degrees, gneiss hue and texture.
- Shading: moss shades and textures depending on terrain orientation and slope.
- Substrate: mechanical erosion areas with gneiss texture.
- Water: behaviour based on slope and relative heights.
Flora
To correctly assign the flora the application meshes had to be taken into account. Populations of various types of tree, shrub and flower species were inserted through application meshes that could be modified in terms of plant size and density. These objects had certain textures and colours characteristic of the vegetation they represented, so the layer of base colours (called shaders) was not modified. All the flora was taken from the Xfrog library [27] which has an extensive range of trees, plants and flowers that can be uploaded to Terragen. The native species Betula lenta, Abies grandis and Galium aparin were the main species chosen. The slopes of the pit were also planted with native species to improve integration with the landscape.
Atmosphere
To define the atmosphere visual field parameters can be added referring to fog density and height, sky line height and ambient light. Obtaining meteorological parameters for a particular period in the past (year, month, day, hour) enables the atmosphere for that particular day to be reproduced. The atmosphere introduced in our case was fog and, in another simulation, altocumulus.
Lighting
For lighting, which depends directly on the position of the sun, defined were the sun's declination for day d and elevation with respect to the zenith for hour h.
Water
The water behaviour parameters are level, light effects, relative depth, penetrating light attenuation, roughness and wave effect.
Given the characteristics of the mined-out pit, a convenient restoration solution from technical, environmental and socioeconomic perspectives was to create a lake, as water table characteristics permitted this quick restoration solution for a very small investment while equipping the area with a recreational facility:
- Water level 250 m
- Maximum radius: 300 m
- Reflections: 75%
- Transparency 10%
Once all the environmental variables and objects were introduced, a point of view was selected so as to render and create the image of the terrain from that point.
3. Results
Specific weather and environmental conditions were simulated according to different sets of initial parameters.
The renderings resulted in a high degree of realism in the simulations. Furthermore, starting with just the contour lines for the mined-out open pit, the time required was under 30 minutes, including a rendering time of 6 minutes (Pentium (R) Dual-Core CPU T4500 2.3 GHzRAM 3GB and Terragen 2.0 software).
Different simulations of the restoration are reproduced below: a foggy day (Figure 12); if left abandoned (Figures 13 and 14); with a lake (Figure 15); with vegetation at the base (Figure 16). The last two alternatives offered the best landscape integration.
4. Discussion
The main advantages of fractal versus 3D modelling are summarizes as follows:
- Rendering time is shorter.
- Natural objects are better represented.
- Recursive procedures rather than equations are used to model fractal objects.
- Detail is good for all scales of observation.
- Models are easily generated with computers.
- Numerous parameters can be entered and varied rapidly and easily:
- Terrain: roughness, colour, texture etc.
- Water: level, roughness, wave effect, transparency, etc.
- Clouds: size, distribution, density, etc.
- Atmosphere: decay, colour, mean density, etc.
- Lighting: direction, intensity, position of the sun, height, colour, etc.
- Colour (for any variable).
- Photorealism or hyperrealism is achieved, provided all the parameters are well combined.
5. Conclusions
Fractals are apparently complicated geometrical sets but actually require very little information for their description, construction and exploration. The main characteristic of fractal structures is the infinite iteration of a simple process to create an object. They are usually viewed as similar at all levels of magnification, whereas natural objects like clouds, mountains, lightning, shorelines, tree branches, etc. approximate fractals.
Fractal mathematics applied using computer software can be used to simulate different mining environments rapidly and easily. The software allows many variables to be added to the model, resulting in high-resolution images that preserve the real forms of the terrain. This kind of simulation would not be feasible with 3D modelling due to the time required to introduce variables and the lower realism resulting from geometric shapes.
Fractal geometry offers an effective and promising way to model quarries, open-pit mines and other mining environments and restored landscapes.
Acknowledgments
José Santiago Pozo wants to thank to University of Vigo for the financial support given.
References
[1] Anhaia, T.R.S., Luiz, A.M.E., Leitão, K. and Moro, R.S., Pitagui's river upper course landscape in the Parana first Plateau, Brazil. RA'E GA-O Espaco Geografico en Analise, 24, pp. 134-148, 2012. [ Links ]
[2] Barnsley, M.F., Fractal functions and interpolation. Constructive Approximation, 2 (1), pp. 303-329, 1986. [ Links ]
[3] Barnsley, M.F., Massopust, P., Strickland, H. and Sloan, A.D., Fractal modeling of biological structures. Annals of the New York, Academy of Sciences, 504, pp. 179-194, 1987. [ Links ]
[4] Bogachev, M.I., Eichner, J.F. and Bunde, A., Effect of nonlinear correlations on the statics of return intervals in multifractal data sets. Physical Review Letters, 99 (24), pp. 1-4, 2007. [ Links ]
[5] Bunde, A. and Havlin, S., A brief introduction of fractal geometry, Fractals in science. Springer Verlag, 1994. [ Links ]
[6] Chrabra, A., Geist, H.J., Houghton, R.A., Haberl, H., Braimoh, A.K. and Vlek, P.I., Multiple impacts of land-use/cover change. In: Lambin, E.F. and Geist, H.J., Land-use and land-cover change. Local Processes and Global Impacts, Berlin, Sringer-Verlag, 2006, pp. 71-116. [ Links ]
[7] Dirzo, R. and Raven, P.H., Global state of biodiversity and loss. Annual Review of Environmental and Resources, 28, pp. 137-167, 2003. [ Links ]
[8] Fadda, S., Fiori, M. and Matzuzzi, C., Developing rehabilitation design for the abandoned mine excavations in central Sardinia. International Journal of Mining, Reclamation and Environment, 24 (4), pp. 286-306, 2010. [ Links ]
[9] Falconer, K.J., The Hausdorff dimension of some fractals and attractors of overlapping construction. Journal of Statistical Physics, . 47 (1-2), pp. 123-132, 1987. [ Links ]
[10] Falconer, K.J. and Howroyd, J.D., Packing dimensions of projections and dimension profiles. Mathematical Proceedings of the Cambridge Philosophical Society, 121 (2), pp. 269-286, 1997. [ Links ]
[11] Falconer, K.J. and Hu, J., Nonlinear diffusion equations on unbounded fractal domains. Journal of Mathematical Analysis and Applications, 256 (2), pp. 606-624, 2001. [ Links ]
[12] Farina, A. and Bergrano, A., The eco-field hypothesis, toward a cognitive landscape. Landscape Ecology 21, pp. 5-17, 2005. [ Links ]
[13] Lennartz, S. and Bunde, A., Distribution of natural trends in long-term correlated records, A scaling approach. Physical Review E 84, 021129, 2011. [ Links ]
[14] Li, J-J., Wang, X-R., Wang, X-J., Ma, W-C. and Zhang, H., Remote sensing evaluation of urban heat island and its spatial pattern of the Shangai metropolitan area, China. Ecological Complexity, 6 (4), pp. 413-420, 2009. [ Links ]
[15] Livina, V., Kizner, Z., Braun, P., Molnar, T., Bunde, A. and Havlin, S. Temporal scaling comparison of real hydrological data and model runoff records. Journal of Hydrology, vol. 336, pp. 186-198, 2007. [ Links ]
[16] Mandelbrot, B.B., The fractal geometry of nature. W.H. Freman and Co. 1977. [ Links ]
[17] Mandelbrot, B.B., Gefen, Y., Aharony, A. and Peyriere, J., Fractals, their transfer matrices and their eigen-dimensional sequences. Journal of Physics A, Mathematical and General, 18 (2), pp. 335-354, 1985. [ Links ]
[18] Marí-Costa, V., Ecohistory of the agrarian landscape. An application for the Pituso field, pp. 240-250, 2003. [ Links ]
[19] Martínez, S., Ramil, P. and Chuvieco, E., Monitoring loss of biodiversity in cultural landscapes. New methodology based on satellite data. Landscape and Urban Planning, 94, pp. 127-140, 2010. [ Links ]
[20] Pacina, J., Novák, K. and Weiss, L., 3D modeling as a tool for landscape restoration and analysis, IFIP Advances in Information and Communication Technology, 359 AICT, pp. 123-138, 2011. [ Links ]
[21] Skãlos J. and Käsparova, I., Landscape memory and landscape change in relation to mining, Ecological Engineering, 43, pp. 60-69. [ Links ]
[22] Taketomi, T., Sato, T. and Yokoya, N., Real-time and accurate extrinsic camera parameter estimation using feature landmark database for augmented reality, Computer and Graphics, 35, pp. 768-777, 2011. [ Links ]
[23] Tannier, C., Foltête, J.C. and Girardet, X., Assessing the capacity of different urban forms to preserve the connectivity of ecological habitats, Landscape and Urban Planning, 105, pp. 128-139, 2012. [ Links ]
[24] Thomas, I., Frankhauser, P. and Biernacki, C., The morphology of built-up landscapes in Wallonia (Belgium). A classification using fractal indices, Landscape and Urban Planning, 84, pp. 99-115, 2008. [ Links ]
[25] Vlad, M.O., Schönfish, B. and Mackey, M.C., Self-similar potentials in random media, fractal evolutionary landscapes and Kimura's neutral theory of molecular evolution, Physica A, 229, pp. 343-364, 1996. [ Links ]
[26] Déjeant-Pons, M., The European landscape convention. Spatial Planning and Landscape Division, Council of Europe, Europe, France, Landscape Research, 31 (4), pp. 363-384, 2006. [ Links ]
[27] Xfrog. Manual. Xfrog Corporation, 2011. [ Links ]
[28] Yue, Y. and Jia, J., Computing offsets of NURBS curve and surface. In: Tan,R., Sun, J. and Liu, Q., Automatic Manufacturing Systems II, Advanced Materials Research, 542-543, pp. 537-540, 2012. [ Links ]
[29] Zhang, D., Qu, S. and Kang, B., A new digital image hiding approach using multi-image fusion, Proceedings 1st International Workshop on Knowledge Discovery and Data Mining, WKDD, Art. No. 4470458, pp. 553-557, 2008. [ Links ]
[30] Zhang, L-L., Estimation of box dimension for fractal image based on escape time algorithm. Fangzhi Gaoxiao Jichukexue Xuebao, vol. 21 (3), pp. 364-367, 2008. [ Links ]
[31] Zhang, G., Lu, J., Song, K., Zhan, S. and Liang, Y., The change of landscape pattern in Zhenlai Xian, Jilin Province in recent ten years, Shengtai Xuebao/ Acta Ecologica Sinica, 32 (12), pp. 3958-3965, 2012. [ Links ]
[32] Rojas-Sola, J.I., Montalvo-Gil, J.M. and Castro-García, M., 3D modelling and functional analysis of a head frame for mineral extraction. DYNA, 80 (181), pp. 118-125, 2013. [ Links ]
I. De Rosario-Amado, received a Bs. Eng in Mining in 2009, a MSc. degree in Environmental Technology in 2011, all of them from the University of Vigo, España. From 2012 to 2013, he worked in the Department of Natural Resources Engineering and Environment in University of Vigo in several projects related with mining and Conservation and Restoration of Built Heritage.
S. Pozo-Antonio, received a Bs. Eng in Mining in 2009, a MSc. degree in Environmental Technology in 2010, and his PhD. degree in Environmental Technology in 2013, all of them from the University of Vigo, España. From 2010 to 2013, he worked in the Department of Natural Resources Engineering and Environment in University of Vigo in several projects related with mining and Conservation and Restoration of Built Heritage. From 2013-2014 he got an internship in Getty Conservation Institute in Los Angeles (USA). His research interests include: cultural built heritage, mining techniques, landscape management and landscape assessment.
G. Lorenzo-Salgueiro, received a Bs. Eng. in Mining in 2009, a MSc. degree in Environmental Technology, all of them from the University of Vigo, Pontevedra, Spain. In 2007 he presented the first photorealistic simulation modelling process with fractals technology in Vigo's University. From 2009 to 2010, he worked in Explotaciones Mineras del Morrazo, S.L (Spain) on developing environmental projects in opencast mines applying fractal mathematics in 3D designs. In 2010, he worked in a consultory developing european projects over security in mines of Finland, Italy and Spain. From 2011 to actually, he is Technical Lead of quarries and concrete plants in General de Hormigones, S.A. (Masaveu Corporation - Spain). His research interest include: photorealistic simulation, landscape design and environmental restoration and conservation in mining.
J. Feijoo-Conde, finished his university studies in Mining Engineering in 2008, and later a MSc. degree in Environmental Technology in 2011, all of them from the University of Vigo (España), University in which currently he is developing his PhD. degree in Environmental Technology. From 2009 to present day, he works in the Department of Natural Resources Engineering and Environment in University of Vigo in several projects related with mining and Conservation and Restoration of Built Heritage. Currently he is doing a research stay in the Technical University of Denmark (DTU). His research interests include: cultural built heritage, mining techniques, landscape management and landscape assessment.
J. Taboada-Castro, received in 1993 the PhD. degree in Mining Engineering from the University of Oviedo, Spain, for a thesis on the design of underground coal mines. After working in the petroleum and the slates sectors, in 1993 he started working at the University of Vigo, where he is currently a professor. He has more than 60 articles in JCR journals and more than 50 international congresses.