Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.186 Medellín jul./ago. 2014
https://doi.org/10.15446/dyna.v81n186.39190
http://dx.doi.org/10.15446/dyna.v81n186.39190
Molecular dynamics simulation of nanoindentation in Cr, Al layers and Al/Cr bilayers, using a hard spherical nanoindenter
Simulación del proceso de nanoindentación con dinámica molecular en capas de Cr y Al y bicapas de Al/Cr, empleando un nanoindentador esférico
Sebastián Amaya-Roncancio a, Elisabeth Restrepo-Parra b, Diana Marcela Devia-Narvaez b,c, Diego Fernando Arias- Mateus d & Mónica María Gómez-Hermida d
a Universidad Nacional de San Luis , Argentina. sebastianamayaroncancio@gmail.com
b Universidad Nacional de Colombia-sede Manizales, Colombia. erestrepopa@unal.edu.co
c Universidad Tecnológica de Pereira, Colombia. dianadevia@gmail.com
d Universidad Católica de Pereira, Colombia. diegomas@gmail.com, monica.gomez@ucp.edu.co
Received: August 2th, de 2013. Received in revised form: March 10th, 2014. Accepted: April 4th, 2014
Abstract
Three-dimensional molecular dynamics (MD) simulations of a nanoindentation technique using the hard sphere method for Cr (bcc) and Al (fcc) thin films and (Cr/Al)n (n=1,2) systems were carried out. For the model implementation, Morse interatomic potential was used for describing the single crystal interaction and the contact between Cr and Al structures. On the other hand, fixed boundary conditions were used and the repulsive radial potential was employed for modeling the spherical tip, and ideal mechanical properties at 0 K were obtained by simulating load-unload curves. Bilayers presented higher hardness and Young's modulus than Cr and Al layers. Moreover, the region of atoms movement after the unload process shows a continuous parabolic boundary for Al and Cr layers and a discontinuous boundary for the bilayers caused by the interfaces.
Keywords: Hardness; Interface; Morse potential; Nanoindentation; Young's modulus.
Resumen
En este trabajo se realizaron simulaciones empleando dinámica molecular tridimensional aplicada a la técnica de nanoindentación, usando el método de la esfera dura en películas de Cr (bcc), Al (fcc) y sistemas (Cr/Al)n (n=1,2). Se empleó un potencial interatómico de Morse con el fin de describir la interacción en cada cristal y el contacto entre las estructuras de Cr y Al. Se emplearon condiciones de frontera fijas y un potencial radial repulsivo para modelar la punta esférica del indentador. Con estas condiciones se obtuvieron las propiedades mecánicas ideales a 0 K, simulando curvas de carga-descarga. Las bicapas presentaron dureza y módulo de Young altos, comparados con valores obtenidos en capas de Cr y Al. Además, la región de los átomos en movimiento después del proceso de descarga muestra un límite parabólico continuo en las capas de Al y Cr, y limites discontinuos en las bicapas, causados por las interfaces.
Palabras clave: Dureza; Interfase; Modulo de Young; Nanoindentación; Potencial de Morse
1. Introduction
Thin films have been widely used for improving contact surfaces' performance for applications such as magnetic storage devices, hard coatings, microelectromagnetics mechanisms among others [1-4]. Nevertheless, there is a remarkable difference between mechanical properties of materials in bulk and thin films. This difference is higher when films are produced as single thin films and multilayers, the latter presenting better mechanical behavior because of the interface presence. On the other hand, the most useful technique for measuring mechanical properties in systems with low dimensions such as thin films is nanoindentation, as it uses very small loads, in the order of nanonewtons (nN) [5]. This method uses an indenter with a known geometry that comes into contact in a specific place of the surface applying a load. For this type of tests on the nanometer scale, complex and expensive equipment and a long time for analysis are needed. One alternative for studying mechanical properties at a nanometer scale is the use of modeling and simulation techniques that allow understanding the materials behavior in a deeper way. For example, molecular dynamics (MD) is one of the most used methods for this kind of studies [6]. MD simulations are a powerful tool for studying material properties in different fields such as bioscience, chemistry and material science among others [7]. Because of the computational technological developments, now simulations including a hundred million atoms can be developed.
Recently, several works employing MD for simulating the nanoindentation process for studying mechanical properties of thin films and multilayers using different interatomic potentials have been reported. For example A. Ritcher et al. [8] compared experimental and theoretical results of mechanical properties for a nanoindentation method applied to several forms of carbon materials with different mechanical properties, namely diamond, graphite and fullerite films. Molecular dynamics simulations of the indentation process have been performed. Although results were not in the same magnitude because of computing power limitations, the simulations capture the main experimental features of the nanoindentation process showing the elastic deformation that takes place in both materials. In the case of thin films, P. Peng et al. [9] investigated the nanoindentation of aluminum thin film on a silicon substrate by three-dimensional MD simulation, combined with the Lennard-Jones (LJ) potential for describing the interaction at the film-substrate interface. Results showed that the hardness of the film increased with the loading rate. A. K. Nair et al [10] studied the indentation response of Ni thin films of nanoscale thicknesses using molecular dynamics simulations with the embedded atom method (EAM) interatomic potentials. The simulation results for single crystal films show that the contact stress necessary to emit the first dislocation under the indenter is nearly independent of film thickness. In the literature, there are other works showing similar studies to those presented before [11-13]. Regarding multilayers simulation, the literature reports several works that include the influence of the interface presence. T-H Fang et al. [14] applied MD simulations combined with the tight-binding second-moment approximation and Morse potentials for studying the effects of indention deformation, contact, and adhesion on Al, Ni, and Al/Ni multilayered films. Results show that when the indention depth of the sample increased, the maximum load, plastic energy, and adhesion increased. L. Ming-Liang et al. [15] carried out molecular dynamics simulation to investigate the nanoindentation behavior of a Cu(100)/Cu(110) bilayered thin film. It was found that at the indenting stage, the maximum indentation load of the bilayered thin film is lower than that of its constituents; however, they have nearly the same maximum indentation load. Similar studies were carried out by Y. Cao et al. [16]. In these works the indenter was assumed to be a rigid probe with a great number of carbon atoms; nevertheless, considering that the indenter does not present any deformation, it could be considered as a perfect rigid and structureless sphere capable of repulsion of all atoms in contact with it. The spherical shape is not far from the real case, because although in experimental measurements the most used shape of indenter is a pyramid, the indenter vertex has always a finite curvature radius of several tens of nanometers; therefore, it would be reasonable to consider it a spherical indenter, taking into account the scale of MD simulations. This type of indenter has been used by A. V. Bolesta and V.M. Fomin [17] for Cu thin films using the DM code LAMMPS. Nevertheless, this method has not been used for multilayer coatings. In this work we present similarities between mechanical properties in a study of Al, Cr and Al/Cr coatings obtained by MD simulations, combined with Morse potential, and a simple indenter with a spherical shape, and experimental results.
2. Model Description
Molecular dynamics simulations for carrying out nanoindentation tests were carried out for Cr, Al, Al/Cr and (Al/Cr)2 coatings. The indenter was assumed to be a totally rigid and structureless sphere of diamond with diameter of 12 nm [14]. The sample was considered to be films with well-defined atoms in thermal equilibrium at 0 K, orientation in the plane (100) and of equal thickness. The samples size was LxLxd = 20x20x8 nm3 (where L is the dimension in the x-y plane and d is the thickness of each layer). The system construction for the case of two Al/Cr bilayers is present in Fig. 1.
Fixed boundary conditions were considered, but the x-y dimensions were large enough in order to avoid the edges influence on the results obtained. Movement equations combined with the Verlet algorithm with a time interval of 0.92 fs [18] were used. The maximum penetration depth of the tip is 2 nm at a speed of 4.3 m/s, in order to guarantee a The nanoindentation was carried out controlling the spherical indenter position, simulated by means of a repulsive potential with the atoms of the sample surface. The repulsive potential for the indenter is described by: time relaxation between two consecutive simulation steps.

Where A is a constant related to the indenter effective stiffness, R is the indenter radius and ri is the distance between the center of the indenter and the i-th atom belonging to the sample. Values used in this simulation for A and R are 44.14 eV/Å3 and 6 nm respectively. These values were taken evaluated from the work carried out by Lilleodden et al. [19].
The load acting on each individual atom was obtaining by adding two contributions: the first part considers the interaction between the atom and its neighbors; the second part represents the repulsive potential between the atom and the indenter. The Morse potential (Eq. 2) was selected for this simulation because it is computationally simpler and according to several author including Ziegenhain et al. [20] its results are similar to those obtained by using a EAM potential
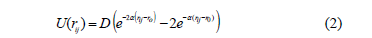
Where D is the dimmer energy, ro is the equilibrium distance and a is the fit of the bulk material modulus and rij is the distance between two atoms in the sample. The interatomic energies for Cr-Cr, Al-Al and Cr-Al were obtained from the Lorentz-Berthelot mixing rule [21]:
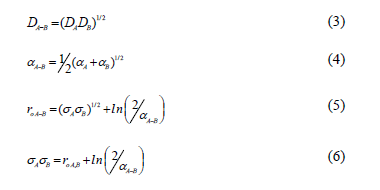
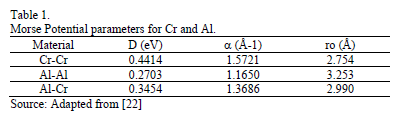
Where DA-B, aA-B and raA-B, are the fit energy, lattice constant and equilibrium distance for A-B compound and DA, DB, aA, aA, raA and raB are the same parameters for A and B elements respectively. The Morse potential parameters for Cr and Al are listed in table 1.
The reduced Young's modulus (E*) is obtained from Eq. (7) which takes into account the combination of the tip and film elastic effects [23].

Where b = 1 for a spherical indenter, S is the slope o f the unload curve initial part and Ac is the projected contact area at a maximum load. The Young's modulus of the sample Es is obtained from the expression:

Where Ei and Es are the indenter and sample Young's moduli, ui and us are Poisson coefficients of the indenter and sample respectively. The contact area, Ac, depends on the indenter radius R and the contact depth hc, and is given by

Where hc can be expressed as:
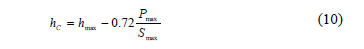
hmax being the maximum penetration depth, Pmax the maximum load and Smax the maximum slope of the unload curve. The material hardness H is defined as the local resistance to the plastic deformation; then, it is determined from the indentation maximum load divided by the contact project area, according to:

3. Results and Discussion
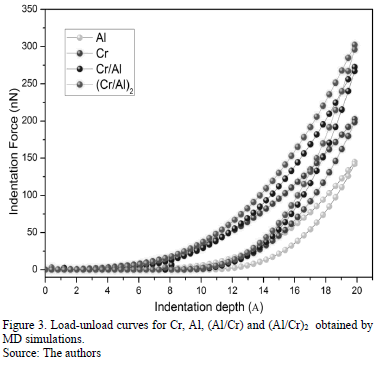
Fig. 3 shows the load-unload curve obtained from indentation simulations for Cr, Al Al/Cr and (Al/Cr)2 at a temperature of 0 K. the maximum load reached by the indentation depth at approximately 2 nm is 144 nN and 202 nN for Al and Cr respectively. For samples with one and two bilayers, the load was increased being 272 nN and 302 nN, respectively.
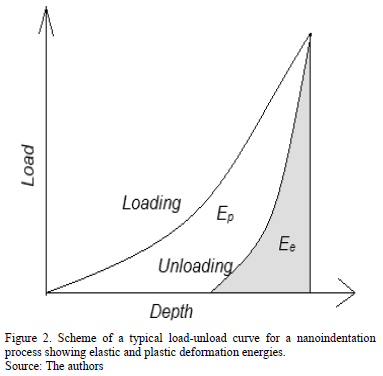
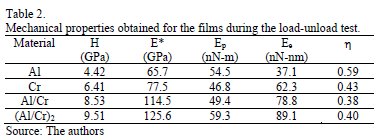
From the load-unload curves of Fig. 3, values of hardness (H), effective Young's modulus (E*=Es/(1-us2)), plastic deformation energy (Ep) and elastic deformation energy (Ee) were obtained. The coefficient of energy dispersion (h), is calculated from the expression h = Ep /(Ee+ Ep). These values are listed in Table 2. Similar results were shown by Saraev and Miller [25].
The hardness value for Al is similar to that reported by Peng et al. [9] using MD. Experimental studies report hardness for Cr of 7 GPa [26], similar to that obtained in this work. Results show higher hardness for Cr than for Al in the case of one and two bilayers, the hardness is increased above the values obtained for single thin films, even greater than the value obtained from the mixing rule (5.41 GPa). This hardness evolution is in agreement with that reported in the literature by using nanoindentation experimental tests for Ag/Ni [27] and Cu/Ni [28] systems. There is a semi-coherent interface generated between the Al substrate and the Cr thin film due to the large mismatch of lattice parameters (fcc-bcc), and misfit dislocation networks formed at the interface accommodating this mismatch. The interface, caused by mismatch of lattice parameters, applies a repulsive force to prevent continuous dislocation slip. With successive emission of dislocations from the indented free surface, more dislocations are propagated toward the interface. It causes a pile up of dislocations on the interface, leading to significant work-hardening of Al/Cr coatings [16].
The Young's modulus of Al obtained was 70 GPa, similar to that reported by Fang et al. [6]. In the case of Cr, no reports for Young's modulus obtained by simulation were found. In experimental tests, a value of 300 GPa was determined, different to the value obtained in our simulations, possibly because in the experimental studies the sample is polycrystalline. The value of h that is associated to the tendency for plastic deformation of the films [29], shows a greater value for Al compared to the other films. The response to the plastic deformation is greater in single layers than in multilayers. The interface creation generates a reduction in the coefficient of energy dissipation; then, multilayer interfaces act as a barrier for the plastic deformation. In other words, interfaces are considered as zones of dissipation energy [30]. In the case of two bilayers, h is also higher than it for one bilayer, possibly because the shear modulus between the materials in contact is similar.
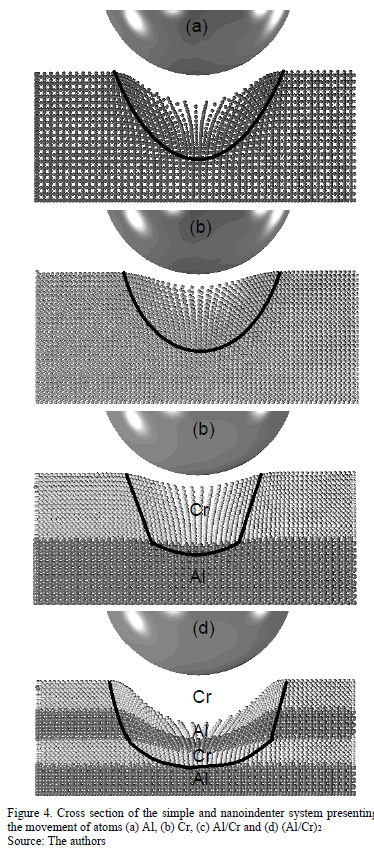
Fig. 4 shows the movement of the atoms driven by dislocations and gliding mechanisms for different samples. The line in the images describes the boundaries of this movement. In Fig. 4 (a) and (b), the movements for Al and Cr layers are presented respectively, describing a parabolic boundary without any discontinuity. On the contrary, For Al/Cr and (Al/Cr)2 (Fig. 4 (c) and (d) respectively) the continuity of the parabola is interrupted by the presence of interfaces, indicating that the atoms' movement decreases as the interfaces appear.
The Cr atoms try to recover their positions after the unload process; nevertheless, the plastic behavior of Al produces dislocations as is shown in Fig. 4 (d).
4. Conclusions
A nanoindentation study for films in single layers, (Al and Cr) and (Al/Cr and (Al/Cr)2), was carried out using molecular dynamics simulations, combined with Morse potential, and using a totally rigid and structureless spherical tip as an indenter. Mechanical properties were evaluated from the load-unload curves, determining the hardness and Young's modulus. The influence of the interface between two different materials on mechanical properties was evaluated. The coefficient of energy dissipation is greater for Al than for other films. The region of atom movement after the unload process describes a parabolic volume for single thin films. In the case of bilayers this zone presents discontinuities caused by the interfaces.
Acknowledgment
The authors gratefully acknowledge the financial support of the Dirección Nacional de Investigaciones of the Universidad Nacional de Colombia, during the course of this research, under projects 18780 and 10719. This work was supported also in part by the Oficina de Investigación de la Universidad Católica de Pereira.
References
[1] Nieto, J., Caicedo, J., Amaya, C., Moreno, H., Aperador, W., Tirado, L. and Bejarano, G., Evaluación de la influencia del voltaje bias sobre la resistencia a la corrosión de películas delgadas de A1-Nb-N. Dyna, 77 (162), p.p. 161-168, 2010. [ Links ]
[2] Muñoz, J. E and Coronado, J. J., Análisis mecánico y tribológico de los recubrimientos Fe-Cr-Ni-C Y Ni-Al-Mo. Dyna, vol. 74 (153), p.p. 111-118, 2007. [ Links ]
[3] Radhakrishnan G., Robertson R. E., Adams P. M. and Cole R. C., Integrated TiC coatings for moving MEMS, Thin Solid Films, vol. 420-421, p.p. 553-564, 2002. [ Links ]
[4] Ashurst, W. R., Carraro, C., Maboudian, R. and Frey, W., Wafer Level Anti-Stiction Coatings for MEMS. Sensors Actuators A, 104, pp. 213-221, 2003. [ Links ]
[5] Meza, J. M., Chaves, C. A. and Vélez, J. M., Técnicas de indentación: Medición de propiedades mecánicas en cerámicas. Dyna, 73 (149), p.p. 81-93, 2006. [ Links ]
[6] Fang, T.-H. Chang, W.-J. and Weng, C.-I., Nanoindentation and nanomachining characteristics of gold and platinum thin films. Materials Science and Engineering: A, 430, p.p. 332-340, 2006. [ Links ]
[7] Hale, J. M., Molecular Dynamics Simulation: Elementary Methods. Wiley-Interscience Publication, 1997. [ Links ]
[8] Richter, A., Ries, R., Smith, R., Henkel, M. and Wolf, B., Nanoindentation of diamond, graphite and fullerene films. Diamond and Related Materials, 9, p.p. 170-184, 2000. [ Links ]
[9] Peng, P., Liao, G., Shi, T., Tanga, Z. and Gao, Y., Molecular dynamic simulations of nanoindentation in aluminum thin film on silicon substrate. Applied Surface Science, 256, p.p. 6284-6290, 2010. [ Links ]
[10] Nair, A. K., Parker, E., Gaudreau, P., Farkas, D. and Kriz, R. D., Size effects in indentation response of thin films at the nanoscale: A molecular dynamics study. International Journal of Plasticity, 24, p.p. 2016-2031, 2008. [ Links ]
[11] Gao, Y., Lu, C., Huynh, N. N., Michal, G., Zhu, H. T. and Tieu, A. K., Molecular dynamics simulation of effect of indenter shape on nanoscratch of Ni. Wear, 267, p.p. 1998-2002, 2009. [ Links ]
[12] Shi, Y. and Falk, M. L., Simulations of nanoindentation in a thin amorphous metal film, Thin Solid Films, 515, p.p. 3179-3182, 2007. [ Links ]
[13] Wang, C.-T., Jian, S.-R., Jang, J. S.-C., Lai, Y.-S. and Yang, P.-F., Multiscale simulation of nanoindentation on Ni (1 0 0) thin film. Applied Surface Science, 255, p.p. 3240-3250, 2008. [ Links ]
[14] Fang, T.-H. and Wu, J.-H., Molecular dynamics simulations on nanoindentation mechanisms of multilayered films. Computational Materials Science, 43, p.p. 785-790, 2008. [ Links ]
[15] Liao, M.-L., Weng, M.-H., Ju, S. P., Chiang, H. J., Molecular Dynamics Simulation on the Nanoindentation Behavior of a Copper Bilayered Thin Film. Chinese Journal of Catalysis, 29, p.p.1122-1126, 2009. [ Links ]
[16] Cao, Y., Zhang, J., Liang, Y., Yu, F. and Sun, T., Mechanical and tribological properties of Ni/Al multilayers-A molecular dynamics study. Applied Surface Science, 257, p.p. 847-851, 2010. [ Links ]
[17] Bolesta, A. V., Fomin, V.M., Molecular dynamics simulation of sphere indentation in a thin copper film. Physical Mesomechanics, 12, p.p. 117-123, 2009. [ Links ]
[18] Haile, J. M., Molecular Dynamics Simulation: Elementary Methods, Wiley, New York, 1992. [ Links ]
[19] Lilleodden, E. T., Zimmerman, J. A., Foiles, S. M. and Nix, W. D., Atomistic simulations of elastic deformation and dislocation nucleation during nanoindentation. Journal of the Mechanics and Physics of Solids, 51, p.p. 901-920, 2003. [ Links ]
[20] Ziegenhain, G., Hartmaier, A. and Urbassek, H. M., Pair vs many-body potentials: Influence on elastic and plastic behavior in nanoindentation of fcc metals. Journal of the Mechanics and Physics of Solids, 57,p.p. 1514-1526, 2009. [ Links ]
[21] Imafuku, M., Sasajima, Y., Yamamoto, R. and Doyama, M., Computer simulations of the structures of the metallic superlattices Au/Ni and Cu/Ni and their elastic moduli. Journal of Physics F: Metal Physics, 16, p.p. 823-829, 1986. [ Links ]
[22] Komanduri, R., Chandrasekaran, N. and Raff, L. M., Molecular dynamics (MD) simulation of uniaxial tension of some single-crystal cubic metals at nanolevel. International Journal of Mechanical Sciences, 43, p.p. 2237-2260, 2001. [ Links ]
[23] Oliver, W. C. and Pharr, G. M., An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. Journal of Materials Research, 7, pp 1564-1583, 1992. [ Links ]
[24] Du, J., Höschen, T., Rasinski, M. and You, J.-H., Interfacial fracture behavior of tungsten wire/tungsten matrix composites with copper-coated interfaces. Materials Science and Engineering: A, 527, p.p. 1623-1629, 2010. [ Links ]
[25] Saraev, D. and Miller, R. E. Atomistic simulation of nanoindentation into copper multilayers. Modelling and Simulation in Materials Science and Engineering, 13, p.p. 1089-1099, 2005. [ Links ]
[26] Romero, J., Esteve, J. and Lousa, A. Period dependence of hardness and microstructure on nanometric Cr/CrN multilayers. Surface and Coatings Technology, 188-189, p.p. 338-343, 2004. [ Links ]
[27] Wen, S.P., Zong, R.L., Zeng, F., Guo, S. and Pan, F. Nanoindentation and nanoscratch behaviors of Ag/Ni multilayers. Applied Surface Science, 255, p.p. 4558-4562, 2009. [ Links ]
[28] Zhu, X.Y., Liua, X.J., Zong, R.L., Zeng, F. and Pan, F., Microstructure and mechanical properties of nanoscale Cu/Ni multilayers. Materials Science and Engineering: A, 527, p.p. 1243-1248, 2010. [ Links ]
[29] Kikuchi, N., Kitagawa, M., Sato, A., Kusano, E., Nanto, H. and Kinbara, A., Elastic and plastic energies in sputtered multilayered Ti-TiN films estimated by nanoindentation. Surface and Coatings Technology, 126, p.p. 131-135, 2000. [ Links ]
[30] Stueber, M., Holleck, H., Leiste, H., Seemann, K., Ulrich, S. and Ziebert, C., Concepts for the design of advanced nanoscale PVD multilayer protective thin films. Journal of Alloys and Compounds, 483, p.p. 321-333, 2009. [ Links ]
Sebastian Amaya-Roncancio, received a Bs. Eng. in Physical Engineering in 2007, and MSc. degree in Physics in 2011. Currently he is a PhD student in Physics at the Universidad Nacional in San Luis, and is a member of the group GEMA of the Universidad Católica de Pereira and PCM Computational Applications of the Universidad Nacional de Colombia sedeManizales. His research interests include: simulation of mechanical properties of materials and physical chemical properties of surfaces
Elisabeth Restrepo-Parra, received a Bs. Eng. in Electrical Engineering in 1990, an MSc degree in Physics in 2000, and her PhD degree in Engineering in 2010. She is a senior professor of the Physics and Chemistry Department, Universidad Nacional de Colombia Sede Manizales and member of the groups: Laboratorio de Física del Plasma and PCM Computational Applications. Her main research areas are: materials processing by plasma assisted techniques, structural, mechanical and morphological characterization of materials and modeling and simulation of physical properties of materials.
Diana Marcela Devia-Narvaez, received her Bs. Eng in Physical Engineering in 2005, an MSc degree in Physics in 2010, and her PhD degree in Engineering in 2012. Currently she is a professor of mathematics in the Universidad Tecnológica de Pereira-UTP, and member of the group Laboratorio de plasma of the Universidad Nacional de Colombia sede Manizales, and Non-linear differential equations "GEDNOL" of the Universidad Tecnológica de Pereira. Her fields of work include: materials processing by plasma assisted techniques, structural, mechanical and morphological characterization of materials and modeling and simulation of physical properties of materials.
Diego Fernando Arias-Mateus, received a Bs. Eng in Chemical Engineering in 1993, an MSc degree in Physics in 2003, and his PhD degree in Engineering in 2012. Currently he is a professor of chemistry, physics and mathematics at the Universidad Católica de Pereira. He is a member of the group GEMA of the Universidad Católica de Pereira and the Laboratorio de plasma of the Universidad Nacional de Colombia, sede Manizales. His fields of work include: materials processing by plasma assisted techniques, structural, mechanical and morphological characterization of materials and simulation of mechanical properties of materials.
Monica Maria Gómez-Hermida, received her Bs. Eng in Physical Engineering in 2004 and MSc degree in Physics in 2009. She is a PhD student in Engineer at the Universidad Nacional de Colombia sede Medellín. Currently she is a professor of physics at the Universidad Católica de Pereira, and member of the group GEMA of the Universidad Católica de Pereira. Her main research areas are: growth of magnetic materials, education pedagogies, study of thermal properties of materials, study of magnetic properties of materials, mathematical simulation and modeling.