http://dx.doi.org/10.15446/dyna.v81n186.45220

An algorithm based on granular tabu search for the problem of balancing public bikes by using multiple vehicles

Un algoritmo basado en búsqueda tabú granular para el problema de balanceo de bicicletas públicas usando múltiples vehículos

 

Rodrigo Linfati ^a, John Willmer Escobar ^b & Bernardo Cuevas ^c

 

^a Departamento de Ingeniería Industrial, Universidad del Bío-Bío, Chile. rlinfati@ubiobio.cl
^b Pontificia Universidad Javeriana, Universidad del Valle, Cali, Colombia. jwescobar@javerianacali.edu.co
^c Departamento de Ingeniería Industrial, Universidad del Bío-Bío, Chile.

 

Received: May 12^th, 2014. Received in revised form: July 1^th, 2014. Accepted: July 28^th, 2014

 

---

Abstract
The use of public bicycle systems has gained great importance in European countries and around the globe; this has led to the need to seek advanced techniques to help decision making. A public bicycle system consists of a set of points where you can pick up and deliver bicycles; a headquarters where a group of vehicles taking leftover bikes and transported to the points where a deficit (the demand exceeds supply) exists. One of the major problems that arise in systems of public bike is balanced, which involves sending bikes from the point where an offer (bicycles left over) to the point where there is a demand (bikes missing) occurs. The way to model this problem is with an adaptation of the vehicle routing problem with pickup and delivery (VRPPD), allowing each route make partial deliveries to customers and limiting the number of customers to visit by each route. In this paper an integer linear programming model is introduced and a metaheuristic based on granular tabu search to find a local optimum. Instances from 15 to 500 customers adapted from the literature are used. The computational results show that the proposed algorithm finds solutions in short computational time.

Keywords: Bike Sharing Problem; Routing; Tabu Search.

Resumen
El uso de sistemas de bicicletas públicas ha cobrado gran importancia en países europeos y alrededor de todo el planeta; esto ha llevado a la necesidad de buscar técnicas avanzadas que ayuden a la toma de decisiones. Un sistema de bicicletas públicas consiste en un conjunto de puntos donde se pueden recoger y entregar bicicletas; un depósito central donde existe un conjunto de vehículos que toma las bicicletas sobrantes y las transportan a los puntos donde exista un déficit (es decir que la demanda supera la oferta). Una de las grandes problemáticas que se presentan en los sistemas de bicicletas públicas es el balanceo, que consiste en enviar bicicletas desde los puntos donde se produce una oferta (bicicletas que sobran) hacia los puntos donde existe una demanda (bicicletas que faltan). La forma de modelar este problema es con una adaptación del problema de ruteo de vehículos con recolección y entrega de mercancías (VRPPD), permitiendo que cada ruta realice entregas parciales a los clientes y limitando el número de clientes a visitar por ruta. En este artículo se introduce un modelo de programación lineal entera mixta y una metaheurística basada en una búsqueda tabú granular para encontrar soluciones. Se usan instancias desde 15 a 500 clientes adaptadas de la literatura. Los resultados computacionales evidencian que el algoritmo propuesto encuentra soluciones en tiempos acotados de cómputo.

Palabras clave: Problema de Bicicletas Publicas, Ruteo de Vehículos, Búsqueda Tabú.

---

 

1.  Introducción

Uno de los problemas más estudiados en la literatura relacionada con la optimización combinatoria es el Problema de ruteo de vehículos (VRP, por su sigla en inglés); esto se debe a la gran importancia que ha tomado en campos como el transporte, la distribución física y logística. Todo lo anterior  debido al  enorme crecimiento que ha vivido la industria en general, obligando a buscar métodos que ayuden a mejorar la eficiencia de los recursos que cada vez son más escasos.

El diseño de un sistema logístico se vuelve cada vez más relevante y las decisiones relativas a la ubicación de los lugares de almacenamiento, las políticas de diseño de esos espacios, el manejo de la flota de vehículos y la entrega final de los productos, son decisiones que requieren un manejo apropiado de todas las variables para obtener la máxima eficiencia posible.

El problema de ruteo de vehículos consiste principalmente en determinar la estructura de las rutas a seguir por una flota de vehículos para llegar de la manera más eficiente a los clientes. En general, los métodos exactos conocidos no son capaces de probar optimalidad para el VRP para instancias que contengan más de 100 clientes en un tiempo de computo reducido; debido a que el esfuerzo y tiempo computacional aumentan exponencialmente con el número de clientes. Por esta razón, el VRP es uno de los problemas de optimización combinatoria y programación entera más desafiante que existe, clasificado en el grupo de problemas NP-Hard [1].

Para este tipo de problemas es a menudo deseable obtener soluciones aproximadas, las cuales pueden ser encontradas en un tiempo computacional reducido y que sean suficientemente buenas para su propósito. Usualmente esta tarea es lograda usando métodos heurísticos, que dependen de cierta visión interna de la naturaleza del problema. El objetivo del presente artículo es proponer para el problema de balanceo de bicicletas públicas una solución aproximada basada en una mateheurística de búsqueda tabú granular, la cual entregue de forma rápida soluciones de buena calidad.

Recientemente se ha considerado el problema llamado "bicicletas públicas" o "bicicletas compartidas"; el cual consiste en el alquiler de bicicletas, las cuales se encuentran ubicadas en una de las muchas estaciones distribuidas dentro de una ciudad para ser utilizadas en viajes cortos y devolverlas en cualquier otra estación. Un factor crucial para el éxito de un sistema de bicicletas públicas es la capacidad de satisfacer la demanda fluctuante de bicicletas en cada estación, además de ser capaz de proporcionar suficientes anclajes vacantes para la devolución de éstas.

Este trabajo modela el problema de bicicletas públicas como una de las variantes del VRP: problema de ruteo de vehículos con recogida y entrega (Vehicle Routing Problem with Pickup and Delivery - VRPPD). El problema VRPPD consiste en equilibrar el sistema (oferta y demanda de bicicletas) mediante un conjunto de vehículos, donde se debe visitar cada una de las estaciones (clientes) que no se encuentren en equilibrio, ya sea porque presentan un número mayor de bicicletas que el deseado (oferta), o porque se encuentran desabastecidas (demanda). En particular, se desea determinar las rutas que minimicen los viajes partiendo desde un depósito sin oferta ni demanda.

El primer programa de bicicletas públicas comenzó en el año 1965 en Ámsterdam con el White Bike Plan o bicicletas blancas; pero desafortunadamente no salió según lo planeado, por lo que el programa se derrumbó en cosa de días. En el año 2007 se da el caso más exitoso cuando en París se lanzó la propuesta Velib, con 15.000 bicicletas de alquiler. El enorme éxito generó un gran interés en este modo de transporte en todo el mundo, donde en 2008 se registraron nuevos programas en Brasil, Chile, China, Nueva Zelanda, Corea del Sur, Taiwán y los EE.UU. [2]

En los últimos años, los sistemas de bicicletas públicas han ido ganando mayor popularidad en los planes de transporte como una estrategia para multiplicar las opciones de viaje, fomentar el uso de modos de transporte activo, disminuir la dependencia del automóvil y, especialmente, reducir las emisiones de gases de efecto invernadero.

1.1.  Bicicletas públicas o compartidas
Son sistemas de alquiler o préstamo gratuito de bicicletas que se pueden encontrar dentro de centros urbanos, impulsados generalmente por la administración pública. Se diferencian de los servicios tradicionales de alquiler de bicicletas, más orientados al ocio o el turismo, por el hecho de prestar un servicio de movilidad práctico, rápido y pensado para el uso cotidiano [3]. Se pueden utilizar para trayectos entre diferentes sectores de una cuidad de manera de evitar el transporte público o como una manera complementaria y de acercamiento a éste, por lo que los sistemas de bicicletas públicas se pueden considerar un modo más de transporte público.

Los sistemas de bicicleta pública, son una idea que tomó fuerza con rapidez en el mundo por los resultados positivos mostrados en ciudades como París, Lyon, Barcelona, Sevilla, Ámsterdam, Berlín, Washington, Nueva York, Santiago de Chile, Río de Janeiro y Ciudad de México, entre otras.

La idea original de los sistemas de bicicletas públicas, pertenece a Laurens (Luud) Maria Hendrikus Schimmelpennink, con el  Plan de Bicicletas Blancas (White Bike Plan),  implementado hacia el año 1965 en Ámsterdam, que consistió en reunir un importante número de bicicletas, pintarlas de blanco y dejarlas en la ciudad para ser utilizadas libremente, con el fin de crear una "ciudad más habitable". Esta iniciativa es realizada siendo miembro del movimiento holandés contractual "Provo" que era integrado por jóvenes que discutían contra las estructuras sociales de la sociedad burguesa y cuyo lema era: "provoquemos reacciones violentas entre la clase gobernante con acciones no violentas" [4].

En esa época se puso a disposición del público una flota de bicicletas sin puntos específicos donde recogerla o dejarla una vez finalizado el desplazamiento, de modo que se podían encontrar en cualquier lugar de la ciudad. Se obtenía un medio de transporte no contaminante, saludable y económico que funcionaba constantemente. Debido a que no se disponía de ningún sistema de seguridad o seguimiento de las bicicletas, los robos y el vandalismo disminuyeron en gran medida la cantidad de bicicletas disponibles por lo que al cabo de unos días el programa fracasó, siendo éste considerado como la primera generación del sistema de bicicletas públicas.

La idea de bicicletas públicas se retomó en los años 90, donde se desarrolló un sistema informatizado, el cual a través de una tarjeta magnética, permitía a los usuarios elegir una bicicleta en un lugar, y dejarla en otro. A este sistema se le dio el nombre de sistema Depo/White Bikey, que era gestionado por la empresa Ytech Innovation Center, dirigida por Luud desde donde se desarrolló la base técnica conceptual de los sistemas actuales de préstamos de bicicletas [5].

Una segunda generación de bicicletas publicas comenzó en 1995, cuando en la ciudad de Copenhague se puso en marcha un servicio de préstamo de bicicletas a gran escala llamado Bycyklen, que tenía como características el uso de bicicletas determinadas para cada estación, uso de colores distintivos y el uso de monedas para el acceso a las bicicletas. A pesar de las mejoras, el problema de este sistema continuo siendo el de los robos, ya que no había registro del usuario ni seguimiento de las bicicletas, y el depósito que se deja a cuenta de utilizar la bicicleta (una moneda) era muy bajo.

En los albores del siglo XXI, los avances de la electrónica y de las telecomunicaciones se aplicaron al concepto de la bicicleta pública exitosamente. En 1998 se implantó en Rennes (Francia) el primer sistema de tercera generación, que incluía registro obligatorio y sistema automático de entrega de bicicletas. Este sistema fue implantado por Clear Channel, que junto a JC Decaux, son las dos empresas de publicidad en el mobiliario urbano que empezaron a ofrecer estos sistemas como parte de sus contratos con algunas ciudades. Estos avances supusieron la contención del vandalismo, al menos hasta valores afrontables económicamente, y la mayor optimización del servicio.

Finalmente se encuentra la cuarta generación de bicicletas que es muy similar a la tercera, pero difieren principalmente en la forma de pago porque incluyen tarjetas de pago para varios servicios e incluso con tarifas integradas a las del resto del transporte público de la ciudad. Estos sistemas también introducen componentes tecnológicos más avanzados (de rastreo de bicicletas, etc.). Aunque no existen sistemas 100 por ciento de cuarta generación, el sistema Alemán Call-a-bike es el que más se les asemeja [6].

1.2.  Bicicletas públicas en el mundo
Europa es el continente con más sistemas de bicicleta pública. Alrededor del 88 por ciento de los sistemas están localizados en el "viejo continente". Por su protagonismo en la tercera generación de bicicletas públicas y por el gran número de sistemas implementados, Francia se ha convertido en uno de los países referentes de la bicicleta pública. Sin embargo, otros países europeos con también gran presencia de bicicleta pública son Alemania, Italia y España.

A pesar de la relevancia de Europa en la historia del sistema de bicicleta pública, en los últimos años este también ha ganado protagonismo más allá de sus fronteras. En América la bicicleta pública está presente desde el 2011 en Chile, Argentina, Brasil, México, Estados Unidos y Canadá representando un cuatro por ciento de los sistemas del mundo. En Latinoamérica son especialmente relevantes los casos de México DF, Sao Paulo, Rio de Janeiro, Buenos Aires y Santiago de Chile por el gran tamaño de sus urbes. En Norteamérica destacan por su tamaño e innovación los sistemas de Montreal y Toronto (en Canadá) y Washington DC (en Estados Unidos). En Toronto y Montreal, el sistema Bixi introdujo como novedad un modelo de estación flexible basada en unas placas de hormigón que no necesitan cimiento ni suministro eléctrico subterráneo. De este modo se evitan las costosas obras de instalación y se deja la puerta abierta a sencillos cambios de localización de las estaciones [7].

Se ha estimado que en Asia están localizados un siete por ciento de los sistemas existentes en el mundo. Así, en Asia existe actualmente un sistema de bicicleta pública en Qatar, Irán, India, dos sistemas en Taiwán y tres sistemas en Corea y Japón. Sin embargo, es China el actual exponente de la bicicleta pública en Asia, no sólo por el número sino también por el tamaño de los sistemas implantados. Destaca especialmente el caso de Hangzhou, que con 50.000 bicicletas se ha convertido en el mayor sistema del mundo superando a Paris.

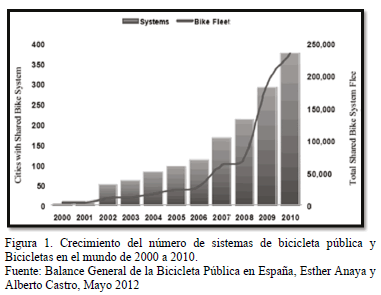
Además del número de sistemas implantados es importante destacar el ritmo con el que se han ido implementando en los últimos años. El número de sistemas de bicicleta pública en el mundo ha crecido exponencialmente desde el año 2000 (ver Fig. 1). Se desconoce por cuánto tiempo continuará este ritmo de crecimiento. Podrían darse dos posibles escenarios futuros. Por una parte, las deficiencias de los sistemas de bicicleta pública pueden hacer que disminuya el "entusiasmo" de las ciudades a la hora de implementar estos sistemas o incluso puede provocar el cierre de algunos de los ya existentes. Por otra parte, la introducción de sistemas públicos en mercados emergentes aún no explorados en profundidad como la India, el Sudeste Asiático, Oriente Medio o África podría contribuir a mantener la expansión mundial de este método de movilidad basado en la bicicleta compartida.

En la Sección 2 se describirá el problema de ruteo de vehículos, luego la variante de recolección y entrega de mercancía, para finalmente explicar la generalización sobre el problema de bicicletas públicas. Luego se presenta el modelo matemático propuesto, el algoritmo de solución inicial y el algoritmo de mejora basado en una búsqueda tabú granular. En la sección 3 de este artículo se presentan los principales resultados obtenidos sobre y en la sección 4 se presenta la discusión, conclusiones y trabajo futuro.

 

2.  Materiales y Métodos

2.1.  Problema de ruteo de vehículos
La planificación de las rutas es uno de los principales problemas en la optimización de las operaciones logísticas, pero su adecuada concepción puede significar grandes ahorros y aumentar el nivel de servicio al cliente. El gran número de aplicaciones al mundo real han demostrado ampliamente que la utilización de procedimientos informáticos para la planificación de los procesos de distribución produce un ahorro sustancial (por lo general entre un 5 y 20 por ciento) en los gastos de transporte globales [8].

En 1959 se presenta el primer problema de VRP, donde Dantzig y Ramser describen una aplicación al servicio de distribución de combustible en estaciones de servicio, proponiendo la primera formulación de programación matemática y un algoritmo de aproximación [9]. Luego, Clarke y Wright propusieron el popular algoritmo de Ahorros que resultó efectivo para su resolución [10].

El estudio y aplicación del ruteo de vehículos se ha desarrollado gracias a la mejora paralela de la tecnología de información y comunicación, lo cual ha permitido reducir el tiempo de ejecución de los algoritmos e integrar información operacional a través de componentes tales como los sistemas de información geográfica.

La función objetivo depende de la tipología y características del problema. Lo más habitual es intentar: minimizar el costo total de operación, minimizar el tiempo total de transporte, minimizar la distancia total recorrida, minimizar el tiempo de espera, maximizar el beneficio total, maximizar el nivel de servicio al cliente, minimizar la utilización de vehículos, equilibrar la utilización de los recursos, etc.

2.2.  Caracterización del VRP
El problema VRP más básico supone la existencia de un depósito que cuenta con una flota de vehículos homogénea y debe atender a un conjunto de clientes geográficamente dispersos, quienes tienen la necesidad de ser abastecidos por algún producto. El objetivo es entregar bienes a este conjunto de clientes con demandas conocidas, al mínimo costo, encontrando las mejores rutas que se inician y terminan en el depósito. Cada cliente es visitado una única vez y los vehículos de transporte llevarán la carga sin exceder su capacidad máxima disponible. [11]

Una ruta es un ciclo simple con origen y destino en el depósito, que representa la secuencia de visitas realizadas por el vehículo que recorre la ruta. El costo de una ruta se obtiene sumando los costos de los arcos que forman el ciclo.

• Así, el objetivo último que persigue este tipo de problemas problema es diseñar un conjunto de rutas de costo mínimo, de modo que: Cada ruta comience y termine en el depósito.
• Cada cliente sea visitado por exactamente una ruta.
• La demanda de los clientes visitados en una misma ruta no supere la capacidad del vehículo  (en el caso de que existan limitaciones de capacidad en el transporte) [12].

2.3.  Problema de ruteo de vehículos con recolección y entrega de mercancía
EL VRPPD (VRP with Pickup and Delivery) es una variante del VRP donde se contempla la posibilidad de que un cliente pueda entregar y recolectar (devoluciones) el producto, por lo tanto, se debe tener en cuenta que los productos que los clientes introducen en el vehículo no deben nunca exceder su capacidad. Esta restricción dificulta aún más el problema de planificación y puede conllevar una mala utilización de la capacidad de los vehículos, incrementar las distancias recorridas o la necesidad de utilizar una flota más amplia [13].

Por consiguiente, es habitual considerar situaciones restrictivas en las que todos los envíos comienzan en el depósito y todas las devoluciones vuelven al depósito central. Así se impide la posibilidad de intercambio de mercancías entre clientes. Una alternativa es la de relajar la restricción de que todos los clientes deben ser visitados al menos una vez. Otra simplificación habitual es la de considerar que cada vehículo debe entregar todos los productos antes de comenzar con las devoluciones.

Así pues, el objetivo es minimizar la flota de vehículos y la suma de los tiempos de transporte con la restricción de que cada vehículo debe tener suficiente capacidad para transportar los productos que van a ser entregados y aquellos que debe recoger en cada cliente para traerlos de vuelta al depósito.

Para que una solución se considere factible, la cantidad total asignada a cada ruta no debe exceder la capacidad del vehículo que sirve esa ruta y dicho vehículo deberá tener suficiente capacidad para recoger las devoluciones que cada cliente tenga en su poder, y con esto se logra que no ocurra que el vehículo tenga mercancías "negativas".

Este problema de ruteo de vehículo con recolección y entrega de mercadería se han ido introduciendo con mayor magnitud en la mente de los investigadores en los últimos tiempos, debido a las grandes aplicaciones que se pueden lograr con este tipo de problema en el área logística [3,5]. Por su complejidad se debe analizar y estudiar bien su método de resolución, el cual está directamente ligado al problema específico del cual se trata.

Existen ciertas consideraciones que se deben tomar al momento de enfrentar un problema de este tipo las cuales son:

• Cada ruta visita el depósito.
• Cada cliente es visitado exactamente por una ruta, es decir por un solo vehículo.
• Cada ruta comienza y termina en el depósito.
• La demanda tanto a entregar como a recoger debe ser atendida por el mismo vehículo.
• La carga del vehículo durante la dura debe ser no negativa y no debe de exceder la capacidad del vehículo [14].

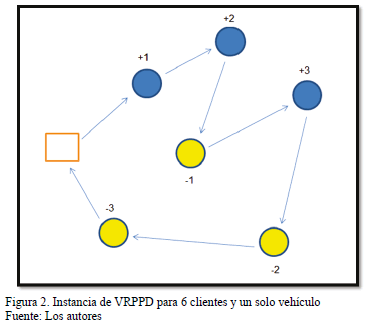
En la Fig. 2, se observa una instancia del VRPPD, con 6 clientes, y una sola ruta. El número que acompaña a cada cliente corresponde a una oferta (número positivo) o una demanda (número negativo). La suma de las ofertas y demandas debe dar cero al completar la ruta, y en cada cliente visitado la capacidad debe estar dentro de los rangos permitidos, sin sobrepasar la capacidad del vehículo y sin quedar con utilización negativa de este.

La optimización de este problema encuentra aplicaciones prácticas en el transporte de un producto entre clientes cuando las unidades de producto no tienen ni un origen ni un destino fijo. Un ejemplo sucede cuando un banco tiene que mover cantidades de dinero en efectivo entre diferentes sucursales; la sucursal principal (el depósito del vehículo) provee el dinero que falta o recoge el dinero sobrante. Otra aplicación importante del VRP ocurre en el contexto de reposición de inventarios. Una serie de minoristas están dispersos por una zona geográfica. A menudo, debido a la naturaleza aleatoria de las demandas, algunos minoristas tienen un exceso de inventario, mientras que otros tienen fuertes ventas y necesitan un stock adicional. En muchos casos, la empresa que suministra a los minoristas de un producto puede decidir mover cantidades de producto de unos minoristas a otros para equilibrar las demandas producidas.

2.4.  Problema de los sistemas de bicicletas públicas
El problema de las bicicletas públicas radica principalmente en el índice de "uso de un sistema" el cual está basado en el equilibrio demanda vs oferta. La demanda es la cantidad de veces que los usuarios acuden al sistema para realizar un préstamo, mientras que la oferta es la cantidad de bicicletas y estaciones que el sistema pone en servicio. Si la demanda es muy alta y la oferta es muy baja, este índice de uso adquirirá valores altos, que cuando son excesivos, pueden producir desajustes en el sistema.

Al existir una excesiva demanda con respecto al número de bicicletas en servicio, el número de bicicletas en movimiento, es decir, circulando entre una estación y otra, aumenta. Esto provoca que el número de bicicletas en estaciones sea menor y que por lo tanto algunas estaciones puedan quedar desabastecidas, o bien puede ocurrir el caso contrario en el cual las estaciones se encuentren saturadas por lo que se tendrá que esperar o estar dispuesto a concurrir a otras estaciones para depositar la bicicleta. Esta consecuencia se traduce en un efecto secundario que es el empeoramiento de la satisfacción del cliente y la imagen del sistema, que a la larga puede afectar a la intensidad de uso.

Una posible medida para eliminar la sobreutilización y el desabastecimiento que se provoca es aumentar la redistribución de las bicicletas entre estaciones.

En particular, se recomienda optimizar la redistribución mediante algoritmos y sistemas de información integrados, de forma que se reduzcan los viajes y que éstos sean más eficientes. Evidentemente, esto supone invertir en la mejora de este aspecto, pero los costos económicos derivados de la evolución técnica y tecnología compensarían los ahorrados por el combustible, el número de vehículos o el personal necesarios para la redistribución.

Otra de las posibles medidas para reducir la sobreutilización y sus efectos es aumentar el número de estaciones y bicicletas disponibles. Sin embargo, la sobreutilización puede llevar a un mayor índice de averías y desequilibrio en el abastecimiento de las bicicletas. Por lo tanto, paralelamente será necesario aumentar el nivel de calidad del mantenimiento y de la disponibilidad del sistema.

Por último, una medida que puede ayudar a disminuir la insatisfacción del usuario en casos de estaciones llenas o vacías es el suministro de información previa o in situ. Si antes de acudir a una estación el usuario puede consultar en internet o en su teléfono móvil el estado de las estaciones, acudirá directamente a aquellas con bicicletas disponibles (para el origen) y anclajes libres (para el destino).

2.5.  Redistribución
Cuando una estación de bicicleta pública está llena, el usuario que quiere devolver una bicicleta prestada no puede hacerlo. La única solución que le queda es desplazarse hasta la estación más próxima y esperar a que algún anclaje esté libre. Cuando ocurre lo contrario, es decir, cuando la estación está vacía, aquel cliente que quiere tomar prestada una bicicleta no puede acceder al servicio. Cuando esto ocurre, el cliente debe desplazarse caminando hasta la estación más próxima esperando que no esté también vacía. Para evitar este desajuste del sistema, el operador se encarga de redistribuir con vehículos las bicicletas desde estaciones llenas a estaciones vacías.

Algunas de las causas que generan el desequilibrio entre las estaciones son las siguientes:

• Baja accesibilidad ciclista: falta de infraestructura ciclista que facilite el acceso.
• Efecto margen: las estaciones situadas cerca de los límites del área suelen tener más baja utilización.
• Baja o alta demanda espacial: estaciones con poca o mucha demanda durante todo el día.
• Baja o alta demanda temporal: estaciones con poca o mucha demanda en un preciso momento del día.
• Excesiva homogeneidad de usos en ciertas estaciones: preponderancia de un uso por encima del resto de usos, por ejemplo, una estación situada en un punto de elevada atracción puntual de viajes, como un campus universitario [7].

La redistribución es uno de los problemas con mayor impacto negativo relacionado a la operación de un sistema de bicicletas públicas. Primeramente, supone un costo importante para el operador. Por ejemplo, Bicing en Barcelona, lo ha declarado en un 30 por ciento de los costos anuales [7]. Segundo, si esa redistribución se produce con vehículos de carburantes fósiles, el municipio debe considerar un aumento significativo de la contaminación ambiental como efecto secundario de la implementación del sistema. Finalmente, la redistribución esconde de fondo otra problemática que es la falta de disponibilidad de bicicletas y anclajes.

Una disponibilidad parcial (no siempre será posible disponer de bicicletas y anclajes en todos los momentos y en todas las ubicaciones) es connatural a un sistema de bicicleta pública con ciertos niveles de uso. La clave es hallar el equilibrio entre un nivel de redistribución que permita  una calidad del servicio aceptable por la mayoría de los usuarios y que a la vez sea coherente con el balance medioambiental y económico del sistema. Para hallar este equilibrio, deben estudiarse los balances ambientales y económicos del sistema, que son particulares en cada caso.

La redistribución es quizá uno de los aspectos más complejos de las bicicletas públicas. Debe tenerse en cuenta desde las fases de planeamiento y preparación del sistema y no abandonarse nunca su vigilancia a través de la recopilación de información, su modelización y sus sistemas de comunicación. Los estudios de logística pueden ser de gran ayuda para optimizar la redistribución. Al ser un transporte individual generado por una red de localizaciones en el espacio, la cantidad y características de los movimientos posibles y reales es abrumadora. Su gestión es, por tanto, compleja, y precisa de estudios de logística específicos. Son muy pocos los sistemas que han llevado a cabo este tipo de estudios, siendo uno de los primeros el Bicing de Barcelona, a finales de 2008. Estudios llevados a cabo sobre este sistema, definieron los clúster, agrupaciones de estaciones que funcionaban con cierta independencia, y descubrieron que respondían a diferentes tipologías. La dinámica de redistribución respondía a las características de los diferentes tipos de clúster, pues los hay receptores, emisores y cambiantes. Otro estudio mostraba la asimetría de las estaciones, es decir la relación entre el número de viajes generados y los atraídos. El índice de asimetría revelaba si la estación era demasiado receptora o emisora de bicicletas, lo cual generaba mayores necesidades de redistribución. Las estaciones con valores situados en los extremos de este índice contribuyen a un mayor desequilibrio del sistema.

Algunos de los factores que causan el desequilibrio de las bicicletas y su redistribución son conocidos. Por lo tanto, ya en el período de diseño del sistema deberían ser descartadas en función del nivel de afectación relativo. Por ejemplo, se deben evitar estaciones en sitios muy altos o muy bajos que requieran un acceso con pendientes excesiva.

Con respecto a las estaciones receptoras, es decir, las que se desequilibran porque hay una gran demanda para devolver la bicicleta, especialmente en ciertos momentos del día, en algunos sistemas se han llegado a estudiar estaciones de gran capacidad en hora punta con intervención de operarios y reposición al momento para conseguir absorber de forma rápida los picos de demanda y oferta en determinados puntos. En cualquier caso, dado que la redistribución va íntimamente ligada a las necesidades de la oferta y la demanda, este es uno de los aspectos clave para determinar la necesidad de ampliación del número de estaciones.

Entre principales estudios en el balanceo de bicicletas públicas, usando técnicas de investigación de operaciones, podemos mencionar los modelos matemáticos propuestos por [5] para la versión dinámica de nuestro problema,  los que son resueltos por generación de columna y técnicas descomposición, siendo capaz de resolver instancias pequeñas, de hasta 100 clientes. La versión estática de nuestro problema es estudiada por [15, 16, 17], en todos ellos se proponen nuevos modelos matemáticos, cada uno con restricciones particulares del problema estudiado, en los trabajos anteriores se proponen técnicas de solución basadas en generación de columna, generaciones de planos de corte y otros, solo logrando resolver instancias pequeñas, de hasta 100 clientes. Los estudios anteriores, basan sus modelos en adaptaciones del VRPPD al problema de balanceo de bicicletas públicas, por la similitud existente entre ambos. Hasta la fecha no existen estudios publicados con algoritmos aproximados que logren encontrar soluciones de buena calidad, en tiempos de cómputo acotado.

 

3.  Método de solución propuesto

El objetivo del modelo propuesto, es encontrar el conjunto óptimo de rutas que cumplan las siguientes restricciones:

• Cada ruta comienza y termina en el depósito.
• Satisfacer la demanda de recogida y entrega de mercadería de todos los clientes.
• En cada punto del recorrido el total de mercancía transportada por el vehículo no exceda su capacidad.
• El vehículo comienza siempre recogiendo mercancía, puesto que inicia vacío.
• Se debe visitar un máximo de clientes por ruta.
• Al regresar al depósito el vehículo no debe llevar mercancía.

El problemas se modela a través de un grafo G = (V, E). El conjunto de nodos V = {v₀, v₁,..., v_n} representa los lugares de la ciudad, que pueden corresponder al depósito, o los clientes. El nodo 0 representa al depósito y los nodos 1,...,n representan clientes. Cada cliente i tiene asociada una oferta representada por O_i con un valor positivo, o una demanda representada por O_i con un valor negativo. Existe un conjunto de vehículos K = {k₀, k₁, ..., k_m}, donde cada uno de ellos podrá realizar una ruta que inicia y termina en el depósito; cada uno de los cuales tiene una capacidad Q positiva. Los vehículos no podrán visitar más de un cierto número de clientes al día lo cual queda determinado por R_max. La existencia de un arco (i, j) ∈ E indica que es posible transportarse desde el sitio representado por i al sitio representado por j. Cada arco (i, j) ∈ E se le asocia un costo C_ij calculado como la distancia de transportarse de i a j.

Se definen las siguientes variables binarias:

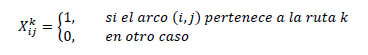
A continuación se dará a conocer el modelo aplicado al problema, que corresponde a una adaptación del VRPPD clásico al problema de las bicicletas compartidas.

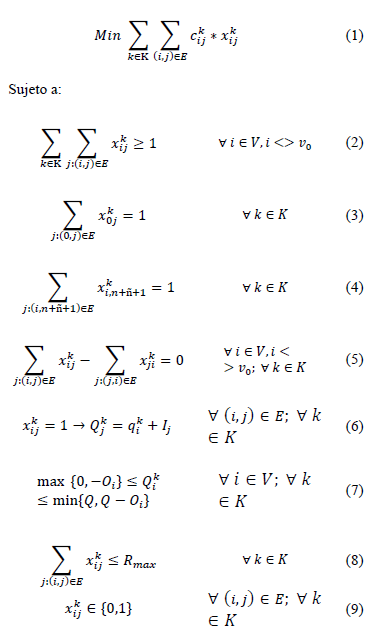
La ecuación (1) corresponde a la función objetivo, la cual es la minimización de la distancia total realizada por los vehículos. La ecuación (2) corresponde a la restricción de que cada cliente debe ser visitado una o más veces. La ecuación (3) corresponde a la restricción que obliga a cada ruta a iniciar en un depósito. La ecuación (4) corresponde a la restricción que obliga a cada ruta a terminar en un depósito. La ecuación (5) corresponde a la restricción de conservación de flujo. La ecuación (6) corresponde a la restricción que calcula la capacidad utilizada del vehículo. La ecuación (7) corresponde a la restricción que establece un mínimo (cero) y un máximo (la capacidad del camión) de carga que puede tener asignada el vehículo en cada cliente, considerando las ofertas y demandas de este. Las ecuaciones (6) y (7) pueden ser transformadas en restricciones lineales por el método de la BigM. La ecuación (8) corresponde a la restricción que establece el número máximo de clientes por ruta. La ecuación (9) corresponde al dominio de las variables binarias. Una de las principales diferencias de nuestro modelo y las presentadas por otros autores, es la inclusión de la restricción (8) y el permitir visitar a cliente por más de una ruta.

Este modelo matemático, resulta difícil de resolver para instancias medianas y grandes, incluso por los más sofisticados algoritmos publicados hasta la fecha [5,15-17], por esto se propone un algoritmo aproximado para su solución.

3.1. Algoritmo basado en búsqueda tabú granular propuesto
Para la solución de la problemática, se propone un algoritmo de dos fases. La primera fase, de inicialización, nos entrega una solución inicial factible por un procedimiento (el algoritmo es descrito en la siguiente sección). La segunda fase, llamada fase de mejoramiento, nos permite mejorar la solución actual por medio de la exploración de vecindarios guiados por una búsqueda tabú granular, (este algoritmo es descrito en la subsiguiente subsección).

3.2.  Fase 1: Solución heurística inicial
Se tiene un depósito central, en el cual estarán los vehículos que participarán y solucionarán el problema de desequilibrio en el sistema de bicicletas públicas. Dichos vehículos visitaran las diferentes estaciones ubicadas aleatoriamente en la cuidad, para ya sea cubrir una demanda o realizar el retiro de las bicicletas sobrantes de las estaciones.

Los vehículos siempre deberán comenzar el recorrido retirando bicicletas puesto que salen vacíos desde el depósito, y la otra condición es que al momento de terminar la ruta no pueden quedar con bicicletas en los vehículos. Las estaciones que serán llamadas clientes, presentaran una demanda (valor negativo) u oferta (valor positivo) conocida de bicicletas.

En primer lugar se tiene una lista con los clientes, sus ubicaciones y sus demandas u ofertas. La sumatoria de las demandas debe ser igual a las de las ofertas.

Se debe definir un valor llamado R_max, que limitará la cantidad de clientes a visitar por cada vehículo dentro de una ruta.

Para encontrar una solución factible del problema es necesario considerar tres elementos importantes:

1. Qué clientes (estaciones) pueden formar parte de una misma ruta.
2. En qué orden deben ubicarse los clientes (estaciones) dentro de la ruta.
3. Que las demandas y oferta de una misma ruta estén equilibradas.

Por lo cual lo primero que se realiza es visitar un cliente o (estación) que presente una oferta de bicicletas de tal manera que el vehículo tenga la capacidad de cubrir alguna demanda, luego buscar clientes de tal manera que se pueda equilibrar las ofertas con las demandas sin sobrepasar el R_max.

Luego de obtener las primeras rutas se deben evaluar la manera de recorrer las estaciones por un vehículo, sin violar la condición de presentar una carga negativa por parte del vehículo.

Luego de realizar los pasos antes mencionados y si aún quedan clientes sin atender se vuelve a buscar un cliente que presente una oferta y se buscan más clientes de manera de cumplir con las condiciones de factibilidad, hasta satisfacer a todos los clientes y equilibrar el sistema.

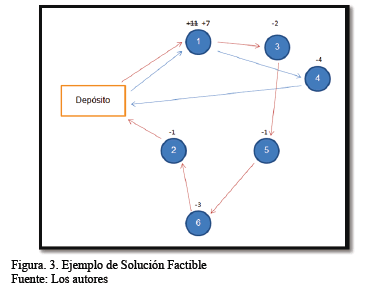
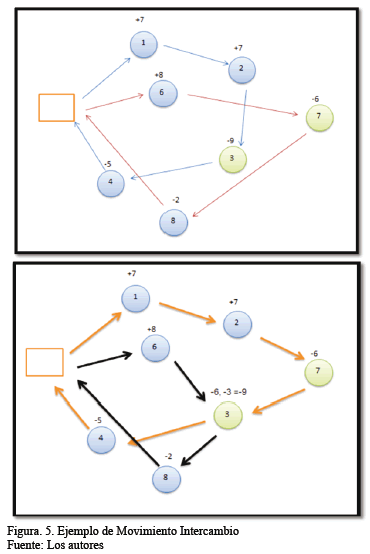
En la Fig. 3, se tiene un depósito, y 6 clientes enumerados desde 1 a 6, sobre el cliente esta anotada la oferta (números positivo) o la demanda respectiva (número negativo). De acuerdo a la Figura 3, el cliente 1 deberá ser visitado más de una vez puesto que su oferta no fue cubierta completamente, quedando aun siete bicicletas por retirar de la estación. Se observa que gracias a esta relajación de las restricciones se logra obtener una solución factible y que no sobrepase el valor del R_max.

3.3.  Fase 2: Algoritmo de mejora basado en búsqueda tabú granular
La búsqueda tabú surge en un intento de dotar de "inteligencia" a los algoritmos de búsqueda local. La búsqueda local consiste en partir de una solución inicial, y teniendo una función objetivo, realizar mejoras, hasta encontrar una solución que no pueda ser mejorada (optimo local). Según Fred Glover [18], la búsqueda tabú es una metaheurística que guía un procedimiento heurístico de búsqueda local en la búsqueda de un óptimo global. Su filosofía se basa en derivar y explotar una colección de estrategias inteligentes para la resolución de problemas, basadas en procedimientos implícitos y explícitos de aprendizaje [19]. Más detalles de la búsqueda tabú pueden ser encontrados en [20].

El algoritmo utiliza un espacio de búsqueda granular [21]. Una característica de la búsqueda tabú es que logra encontrar soluciones de buena calidad, pero para instancias grande el tiempo de computo es elevado, el uso apropiado de una lista de candidatos para obtener un espacio de búsqueda granular logra obtener soluciones de alta calidad, en pequeños tiempos de cómputo para instancias pequeñas, medianas y grandes [21]. El grafo original G = (V, E) se sustituye por un grafo que considera todos los arcos que tienen un costo menor a un umbral de granularidad, los arcos incidentes a los depósitos y los arcos que pertenecen a la mejor solución encontrada durante la búsqueda. Mediante el ajuste del umbral de granularidad se pueden realizar procesos de diversificación (valores grandes) e intensificación (valores pequeños). El umbral de granularidad es ajustado dinámicamente en las iteraciones del algoritmo de la forma sugerida en [21].

Para la búsqueda tabú granular propuesta en el presente estudio se realizan diferentes movimientos que se nombran a continuación.

Fuente: Los autores

• Unir rutas que contengan o visiten clientes en común.
• Unir rutas que no comparten o visiten los mismos clientes.
• Intercambio de clientes dentro de una misma ruta y en diferentes rutas
• 2-Opt en una misma ruta y en diferentes rutas
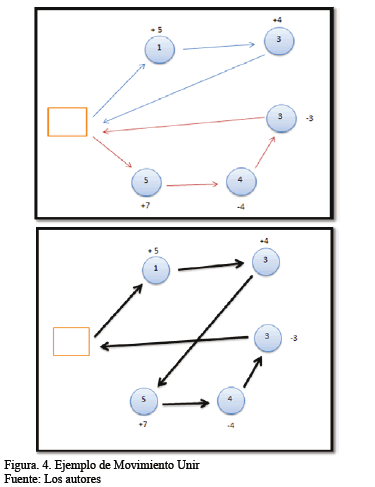
• Los movimientos "Unir" buscan disminuir el número de rutas dentro de las diferentes instancias, para de esta forma obtener el menor número de rutas.

El Movimiento "Intercambio" consta de dos partes: la primera parte intercambia el orden de las visitas a las diferentes estaciones o clientes dentro de una misma ruta, con el fin de encontrar la manera más adecuada de recorrer las rutas lo que favorece la distribución de las bicicletas, mientras que la segunda parte intercambia clientes de diferentes rutas para encontrar las mejores combinaciones de clientes a ser visitados por el mismo vehículo. Los intercambios realizados deben ser rigurosamente revisados, ya que no se pueden realizar todas las combinaciones posibles puesto que se puede caer en soluciones infactibles de recorrido.

El movimiento 2-Opt corresponde al movimiento clásico de VRP, extendido para considerar recolección y entrega de mercadería, además de las características específicas del problema de bicicletas públicas o compartidas.

 

4.  Resultados

Se utilizaron un conjunto de 50 instancias, las cuales se dividirán en secciones de cinco instancias de 15, 25, 50, 75, 100, 150, 200, 300, 400 y 500 clientes cada una. Estas instancias fueron generadas usando la metodología propuesta por [22] para el problema del vendedor viajero, con recogida y entrega de mercadería.

El computador usado para los experimentos computaciones posee un procesador Intel(R) Core(TM) i5-2400 CPU @ 3.10GHz, con 8Gb de memoria RAM, y Linux Ubuntu 12.04 de 64 bits.

Para la selección de parámetros se siguió la metodología propuesta en [23]. Los parámetros que se calibraron fueron:

1. Número de Iteraciones
2. Tamaño de la Lista Tabú

Las instancias fueron separadas en dos tipos, grandes (instancias con más de 100 clientes) y pequeñas (instancias menores o iguales a 100 clientes).

Para las todas las instancias, se probaron diferentes valores para el número de iteraciones, siendo 50 veces el número de clientes, el valor que presenta el mejor desempeño. Para las instancias pequeñas, el tamaño de la lista tabú el mejor desempeño se logra con un valor de 30. Para las instancias grandes, el mejor desempeño del tamaño se logró con una lista tabú de 100 elementos, para evitar ciclos en el corto y mediano plazo.

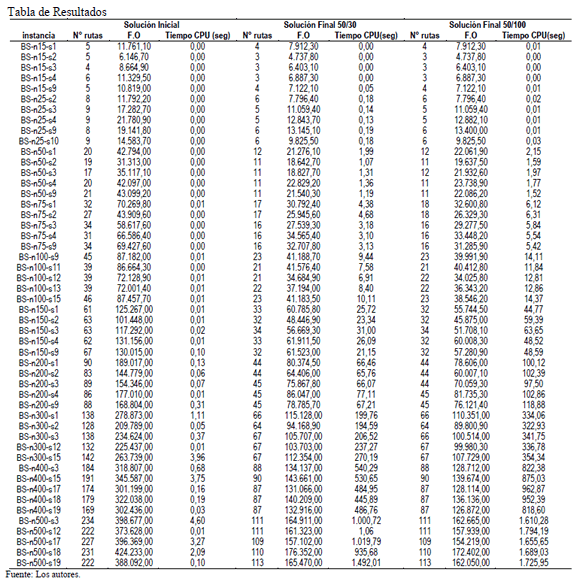
Los resultados finales obtenidos se presentan en la Tabla 1, la primera columna corresponde al nombre de la instancia, luego para la solución inicial, la solución final 50/30 y la solución final 50/100 se reporta el número de rutas generado, el valor de la función objetivo, y el tiempo de cómputo requerido. La solución final 50/30 corresponde a la calibración de las instancias pequeñas, y la solución final 50/100 a la calibración final de las instancias grandes.

 

5.  Discusión y conclusiones

En el presente artículo se desarrolló un algoritmo para resolver el sistema de bicicletas públicas mediante la conceptualización del problema de ruteo de vehículos con entrega y recibido de mercancía, incluyendo las restricciones propias del problema en específico.

Se tratan varios temas relacionados con los VRP, más precisamente relacionados con VRPPD, también se entregó una amplia información sobre los sistemas de bicicletas públicas dentro del mundo. Se formuló un modelo para el el problema de las bicicletas públicas. Se diseñaron algoritmos de solución inicial, algoritmos de mejora y vecindarios para el problema de las bicicletas públicas. El algoritmo de mejora, basado en una búsqueda tabú granular se calibro, buscando los parámetros que potenciaran su funcionamiento, lo que permitió explorar un campo más amplio de soluciones.

Nuestra propuesta de solución logra encontrar soluciones de buena calidad, en tiempos de cómputo reducido para instancias de tamaño pequeñas, medianas y grandes, diferenciando de la propuesta de otros autores donde logran encontrar soluciones optimas, solo para instancias de tamaño pequeño.

Se realizaron diversos experimentos computacionales para comprobar la eficiencia y precisión de los algoritmos propuestos al problema bajo estudio. Dentro de los resultados se aprecia que el enfoque de solución propuesto es capaz de resolver en tiempos computacionales razonables.

Una vez obtenidos los resultados finales para el problema, se muestra un ahorro en costos por distancia recorrida, y existe una disminución en las rutas generadas inicialmente, y por ende de vehículos.

Un trabajo futuro propuesto es estudiar la forma de obtener mejores soluciones iniciales al problema, nuevos vecindarios o movimientos. El modelo exacta propuesto es complejo, y no puede ser resulto por software comerciales como CPLEX que representan el estado del arte en programación lineal entera, se propone estudiar descomposiciones, generación de columna y relajaciones para este modelo.

El algoritmo propuesto podría ser mejorado en futuros desarrollos incluyendo procesos de búsqueda como Algoritmo de recocido simulado, Algoritmo genético, Algoritmo de la colonia de hormiga.

Otro estudio que puede resultar interesante es incorporar a la metodología otras restricciones y parámetros presentes en los clásicos VRP, ya sea tiempos de servicios, calidad, etc.

 

Agradecimientos

Este trabajo ha sido parcialmente financiado por la Pontificia Universidad Javeriana Cali (Colombia) y la Universidad del Bío-Bío (Chile). Esta ayuda es agradecida por los autores.

 

Bibliografía

[1] Vásquez, M., Desarrollo de un Framework para el problema de ruteo de vehículos, Chile, Tesis MSc. en Gestión de Operaciones, Facultad de Ciencias Físicas y Matemáticas, Universidad de Chile, Chile 2007, 23 P.         [ Links ]

[2] Mora-Acero, J., Los sistemas de bicicleta pública vistos desde la relación servicio-producto, Colombia, Facultad de Ciencias Económicas, Universidad Nacional de Colombia, 2011, 54 P.         [ Links ]

[3] DeMaio, P., Bike sharing: Its history, models of provision, and future, Proceedings of Velo City 2009 Conference, 2009.         [ Links ]

[4] Edu Sentis, Bicicletas públicas. [Online]. 2013. [fecha de consulta: December 20th of 2013]. Disponible en: http://edusentis.wordpress.com/category/bicicletas-publicas.         [ Links ]

[5] Contardo, C., Morency, C. and Rousseau, L.M., Balancing a dynamic public Bike-Sharing system. Bureaux de Montréal. Interuniversity research centre on Enterprise networks, Logistics and Transportation, 2012, 34 P.         [ Links ]

[6] Alonso, M.B., Los sistemas de bicicletas públicas urbanas. Tésis de Doctorado en Ingeniería, Departamento de Economía Aplicada, Universidad Autónoma de Barcelona, España, 2009, 76 P.         [ Links ]

[7] Anaya, E. y Castro, A., Balance general de la bicicleta pública en España. IDAE. Curbet Edicions, España, 2012, 30 P.         [ Links ]

[8] Toth, P. and Vigo, D., The vehicle routing problem. Philadelphia: SIAM, USA, 2001.         [ Links ]

[9] Dantzig, G.B. and Ramser, R.H., The truck dispatching problem. Management Science, 6 (1), pp. 80-91, 1959.         [ Links ]

[10] Clarke, G.U. and Wright, J.W., Scheduling of vehicles from a central depot to a number of delivery points. Operations research, 12 (4), pp. 568-581, 1964.         [ Links ]

[11] Suárez, J.G., Análisis, diseño e implementación de un algoritmo e implementación de un algoritmo meta heurístico Grasp que permita resolver el problema de rutas de vehículos con capacidad, Tesis de grado, Facultad de Ciencias e Ingeniería, Pontificia Universidad Católica del Perú, Perú, 2009, 40 P.         [ Links ]

[12] Fumero, A.A., GMOR: Google maps para la optimización de rutas. Escuela de Ingeniería, Universidad de La Laguna, España, 2008.         [ Links ]

[13] Padilla, W. y Díaz, M., Modelo heurístico para el ruteo de vehículos de la empresa Sidauto S.A.. Tesis de Grado, Tecnología en logística, Corporación Universitaria Minuto de Dios, Colombia, 2011.         [ Links ]

[14] Nuño ,T.C., Problema de localización y ruteo con Pickup and Delivery, Tesis de Grado, Facultad de Ciencias Físicas y Matemáticas, Universidad de Chile, Chile, 2012.         [ Links ]

[15] Raviv, T., Tzur, M. and Forma, I.A., Static repositioning in a bike-sharing system: Models and solution approaches. EURO Journal on Transportation and Logistics, 2 (3), pp. 187-229, 2013.         [ Links ]

[16] Chemla, D., Meunier, F. and Wolfler-Calvo R., Balancing a bike-sharing system with multiple vehicles. Proceedings of Congress annual de la société Française de recherche opérationelle et d'aidea la décision, ROADEF2011, Saint-Etienne, France. 2011.         [ Links ]

[17] Chemla, D., Meunier, F., and Wolfler-Calvo, R. ,Bike sharing systems: Solving the static rebalancing problem. Discrete Optimization, 10 (2), pp. 120-146, 2013.         [ Links ]

[18] Glover, F., Future paths for integer programming and links to artificial intelligence. Computers and Operations Research, 13 (5), pp. 533-549. 1986.         [ Links ]

[19] Cámara, J.G., Sistema de un diseño de recogida de residuos urbanos. Tesis de Doctorado en ingeniería, Universidad de Burgos, España, 2010.         [ Links ]

[20] Glover, F. and Laguna, M., Tabu search. Springer, New York, 2013.         [ Links ]

[21] Toth, P. and Vigo, D., The granular tabu search and its application to the vehicle-routing problem, INFORMS Journal on Computing, 15 (4), pp. 333-346, 2003.         [ Links ]

[22] Mosheiov, G., The travelling salesman problem with pick-up and delivery, European Journal of Operational Research, 79 (2), pp. 299-310, 1994.         [ Links ]

[23] Coy, S.P., Golden, B.L., Runger, G.C. and Wasil, E., Using experimental design to find effective parameter settings for heuristics. Journal of Heuristics, 7 (1), pp. 77-97, 2001.         [ Links ]

 

R. Linfati, es Dr. en Investigación de Operaciones de la Universidad de Bologna, Italia. Profesor en el Departamento de Ingeniería Industrial de la Universidad del Bío-Bío, Chile. Sus intereses de investigación incluyen el diseño e implementación de efectivos algoritmos exactos y heurísticos para problemas de optimización combinatoria.

J.W. Escobar, es Dr. en Investigación de Operaciones de Universidad de Bologna, Italia. Docente de programas de Pregrado y Posgrado de la Pontificia Universidad Javeriana y de la Universidad del Valle, Cali Colombia. Sus intereses de investigación incluyen el diseño e implementación de efectivos algoritmos exactos y heurísticos para problemas de optimización combinatoria. 

B. Cuevas, es Ing. Industrial de la Universidad del Bío-Bío, Chile y Asistente de Investigación.