Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.187 Medellín set-/out. 2014
https://doi.org/10.15446/dyna.v81n186.40044
http://dx.doi.org/10.15446/dyna.v81n187.40044
Implementing an evolutionary algorithm for locating container yards of a 3PL provider
Aplicación de un algoritmo evolutivo para la ubicación de patios de contenedores de un operador logístico
Carlos Osorio-Ramírez a, Martín Darío Arango-Serna b & Wilson Adarme-Jaimes a
a Facultad de Ingeniería, Universidad Nacional de Colombia, Colombia,. caosoriora@unal.edu.co
b Facultad de Minas, Universidad Nacional de Colombia, Colombia, mdarango@unal.edu.co
a Facultad de Ingeniería, Universidad Nacional de Colombia, Colombia,. wadarmej@unal.edu.co
Received: September 26th, 2013. Received in revised form: July 9th, 2014. Accepted: July 25th, 2014
Abstract
Defining the facility location is considered as a strategic decision in the context of the supply network management. Often, this decision is made based on minimum cost or best service criteria. However, most of the time these criteria are taken into account separately because the inherent complexity of the multi-objective optimization problems. This study shows the application of the multi-objective evolutionary algorithm known as NSGAII in a real situation faced by a logistics operator in Colombia in order to evaluate different alternatives of distribution for this company.
Keywords: Facilities location, supply network, multi-objective problem, evolutionary algorithm.
Resumen
Definir la ubicación de las instalaciones para una cadena de suministro, es considerada como una decisión de tipo estratégico. A menudo esta decisión se toma con base en criterio de mínimo costo o mejor nivel de servicio o de cobertura. Sin embargo, estos criterios usualmente no son tenidos en cuenta de manera simultánea por la complejidad inherente que pueden tener los problemas de optimización con varios objetivos, los cuales generalmente están en conflicto. El presente trabajo muestra la aplicación del algoritmo evolutivo multi-objetivo NSGAII, en una situación real afrontada por un operador logístico en Colombia, y sirve como punto de partida para dicha empresa para evaluar alternativas de distribución
Palabras clave: Ubicación de instalaciones, cadena de suministro, problema multi-objetivo, algoritmo evolutivo.
1. Introduction
Locating facilities in the supply chain is one of the most important decision making problems in this context, since it determines the shape and configuration of the network itself. In this decision phase, the alternatives are defined along with its associated costs and needed capacity levels to operate the system [1]. The decisions about the location imply the definition of the number, location, and size of the warehouse or production plant to be used, and even the choice of different alternatives of transportation [2]. This set of facilities is represented as nodes in a network, which can be plants, ports, warehouses, or retailers. The development of methodologies for facility location has been a popular research topic within Supply Chain Management, mainly due to the factual characteristics of the problem. Brandeau [3], on one of the first review works related with the topic, proposed alternative ways from the quantitative point of view to face the network location problem. Drezner [4] combines both quantitative and qualitative methodologies to define infrastructure location policies.
A more oriented-focus to customer service is the one proposed by Korpela et al [5] where the network design depends on the demand that must be satisfied. Nozick and Turnquist [6] integrate the concept of location in network design with transportation and distribution activities. The trend of incorporating more formal but also more effective techniques for the studying of the location problem has been growing in the last years. Revelle and Eiselt [7] made a comparative study of the different techniques that have been applied in the last two decades to solve this problem, concluding that one of the great obstacles to overcome, despite the computational advances, consists in the combinatorial complexity whenever there are a considerable number of instances to solve within reasonable times. Furthermore, the combination of depot location and vehicle routing has inspired a growing stream of research because, among other causes, both issues raise two hard combinatorial optimization problems [8]. Although exact algorithms and approximation algorithms for solving these type of problems are increasing their effectiveness and efficiency [9-11], meta-heuristics techniques are still the preferred set of methodologies applied for the solution to these problems and other related to logistics and supply chain management [12].
The appearance of the meta-heuristic optimization techniques has contributed in several ways to the solution of problems that cannot be solved through classical optimization techniques in an efficient and effective way. In the locating facilities case with a considerable number of instances, the problem could become highly combinatorial, so meta-heuristic techniques have to be applied in order to obtain good solutions in reasonable times. (See Badhury et al. [13] in genetic algorithms, Crainic et al. [14] with tabu search and Bouhafs et al. [15] which combine ant colony with simulated annealing).
Generally, the different focuses to tackle the location problem, have in common that their objective function is typically cost minimization. However, depending on the context where the problem is found, it is convenient to include other kind of objective functions, for example, maximizing service levels, or minimizing environmental losses. The presence of additional objectives causes the need of modeling the design of distribution networks or infrastructure location as multi-objective optimization problems. Proof of this, among others, the review article of Farahani et al. [16] present an extensive classification of the different approaches to address and solve this kind of problem. Badri et al. [17] propose a goal programming approach to locate fire stations; Matsui et al [18] suggest a fuzzy model for the location of ambulance stations applying particle swarm optimization (PSO). Bhattacharya [19] presents a max-min approach for the solution of the multi-objective set coverage problem.
Frequently, the objectives of this kind of problems are conflictive. In the network design case, the costs and service levels can be taken into account simultaneously as objectives. The most efficient designs usually do not generate the best service, while the network configurations with excellent service levels require high money investments
2. Formulation of the multi-objective location problem
The infrastructure location optimization models have their origin in the formulation of the transportation problem with a set of origins (supply nodes) that must satisfy the demand from a respective set of destinations (market nodes) at the lowest possible cost. The location of production plants or warehouses has as common objective the fulfilling of a specific demand. The location problems may acquire a binary component, because depending on the specific location of the infrastructure (which is modeled through a binary variable), the network and its related costs may vary.
Nevertheless, the fact of serving and fulfilling the demand has service implications, for instance, the coverage level generated by a given arrangement of the network. Then, the classical linear programming transportation problem is extended inserting the maximum coverage assignment model, which is purely binary [20] and its main objective is to cover the most of the points.
Consequently, the multi-objective location problem can be formulated, according to Villegas et al [21], taking into account the following elements:
2.1. Indexes
- Set of origin nodes (where the infrastructure may be located), i, i = 1, , m
- Set of destination nodes, j, where j = 1, , n
2.2. Parameters
- fi = fixed operation cost of the facility if located at node i.
- Cij = Cost for serving the demand of the node j from facility i.
- Ki = Potential capacity of facility i.
- Dj = Demand of the market node j.
- hij = Distance between nodes i-j that connect after allocation.
- Distmax = Maximum distance that can exist between nodes i and j. This value generally represents a service policy and is linked to the desired coverage level.
2.3. Decision Variables

The optimization model applied to the location problem already mentioned would be expressed in the following way:
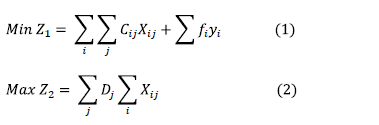
Subject to:

This formulation complements the basic mono-objective approaches [22], since it includes the coverage maximization function to the location problem. It must be noted that these approaches also seek to minimize distances, which are associated to the variable costs of serving demands.
The first objective function (1) corresponds to a cost minimization function, which is formed by the fixed cost of the warehouse and the variable cost to the extent in which this infrastructure is used. The second objective function (2) refers to the maximization of the coverage in terms of the attended demand. The expression (3) guarantees that each market is served from one and only one origin point. The constraint (4) ensures that the served demand does not overcome the capacity of the infrastructure that is used, as long as there is the decision to open business. On the other hand, the constraint (5) makes sure that the distance that exists between a couple of nodes, that are connected because of the choice of the place to locate the infrastructure with its corresponding market to serve, does not exceed a maximum distance that must be previously defined, by the decision maker. Finally, the expression (6) indicates the binary nature of the decision variables.
3. Evolutionary Algorithms
The evolutionary algorithms are a set of meta-heuristic methods which have taken a great importance in the solution of engineering problems during the last decade, due to their efficiency and precision levels that their results provide in real situations of engineering. An evolutionary algorithm is a random- search technique which replicates the evolutionary behavior of species, where the individuals who are better adapted, have bigger chances of surviving. For the replication of an evolutionary process, in every interaction the algorithm keeps a population of chromosomes, where each chromosome represents a solution, which can be feasible or not-feasible. The essential structure of an evolutionary algorithm according to Michalewicz [23] is shown in the Fig. 1
P(t) is the population of solutions (parents) of the generation t, H(t) is the population of solutions (children) of the same generation.
3.1. Application of evolutionary algorithms to the multi-objective infrastructure location problem.
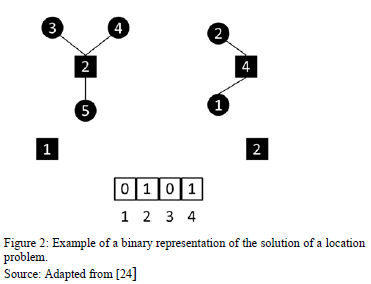
In the development of the implementation of an evolutionary algorithm, the first thing to do is to determine how the codification of the solutions is done. The following procedure was taken from Kratica et al [24] and Villegas et al [21] for the codification of solutions in facility location problems. A codification with a binary string is applied, where the i-th position represents if the corresponding facility is open. Besides, another codification type must be considered, with a representation which indicates the allocation of the supply nodes to the demand nodes.
In Figure 2, an instance of a facility location assignation solution is showed. In this example, the chromosome indicates that the origins marked out in the positions 2 and 4 correspond to those where the infrastructure will be located. As it was previously mentioned, an integer-type auxiliary codification is needed, to indicate how the demand points will be served. In this case, the integer-type chromosome is represented as [4,4,2,2,2]. This means, for example, that markets 3, 4, and 5 are served by the origin 2 and markets 1 and 2 by the source 4. In order to generate the original population, often randomization mechanisms are used. In the binary representation, strings of zeroes and ones, with a length of m, are generated. For the integer codification, a string of integers with a length n is generated. In the case of the evaluation and selection, we must take into account that the problem is multi-objective and hence, the set of dominant chromosomes must be determined over another set of worse solutions.
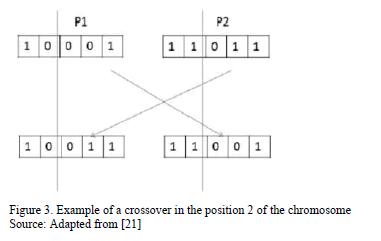
In order to make the parents selection the tournament method may be used, in which two chromosomes are randomly chosen from the population and the chromosome with the best fit is chosen as parent. Nevertheless, in evolutionary algorithms the elitist method of selection has a considerable application, where the best parents are chosen by directly making the evaluation of their fit. To apply the crossover operator, the parents that have been chosen are crossed to obtain the children. This crossover operation can be made in a single point, which consists in randomly selecting a position from the chosen chromosomes, and this position works as a starting point to determine which information will be inherited to the children. This can be better observed in the Fig. 3.
In the mutation operation, the value of certain randomly chosen positions within the chromosome is changed. This operation is executed with a very low probability to avoid the algorithm to work as the local search routines. In order to mutate a binary chromosome, m random numbers, with a uniform distribution between 1 and 0 are generated, and the positions where the value of the pattern is lower than the mutation probability are changed. Since additionally there is an integer representation, for the case of location problems, it is recommended to have other additional mutation operators. In this case, the operator assigns some randomly chosen demand nodes, to other supply nodes which are also randomly chosen.
3.2. NSGAII
The NSGAII algorithm (Non-dominated Sorting Genetic Algorithm) was initially proposed by Deb and Srinivas [25] as the NSGA, and later an improved version, from the computational efficiency point of view was introduced [26]. In this algorithm, the choosing process of the chromosomes is based on the classification of the population in optimal Pareto fronts, more specifically in dominant solution fronts. The first front is structured by the solutions that are not dominated by any single remaining solution among the population; the second front would be formed by those solutions, which hypothetically would belong to the efficient frontier if the ones on the first front didn't exist, and so on, until the whole population is completed.
According to Deb et al [26], initially a size N population is generated in a random manner (P0). Each solution is classified according to its non-dominance level. Later, applying selection, crossover, and mutation mechanisms, an N-size population Q0 of children is generated. Afterwards, a population Rt= Pt∪ Qt, where Rt has a size of 2N, is generated. This population is also arranged according to non-dominance criteria. Consequently, the first optimal front will be integrated by the best solutions of the combined population and must be part of the next generation, Pt+1. If the size of the first front is smaller than N, then all the members of the aforementioned front will make up the next generation. The remaining members of the population Pt+1 will be chosen from the remaining fronts, giving precedence to the second front, then the third front and so on, until the N members of the population are completed. This cycle can be repeated up to T generations. In the Fig.4. the NSGAII algorithm is introduced.
4. Problem description
The situation that was subject of the application of the NSGA II evolutionary technique belongs to a real instance faced by an international logistic operator (freight forwarded -3PL) who has a great operations volume in Colombia (due to confidentiality reasons its name is not provided). One of the reiterative issues and one among those that arise the most difficult during the decision making process, corresponds to the dispatch of containers from the maritime and dry ports, to the different cities of the country where there is the infrastructure to attend the demand, especially at the regional level. Despite this, it has been taken into consideration to centralize the reception and handling of containers in a lower number of ports, compared to the ones that are currently used, because according to the costs and services analysis performed by the company, there is sub-utilization of the installed capacity at the ports, and the fixed operating costs are considerably high, making it really complex to afford them, given the current operation level. The company does not want to neglect its service levels with the centralization of its container handling, because its service policy has represented a competitive advantage in the market and it is acknowledged because of its high standards in terms of accomplishment of promised delivery times to its customers.
The information of the problem, which will be used as input for the optimization model to be solved, is characterized in the following manner:
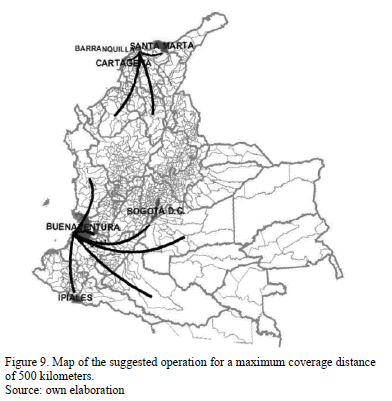
- There are port operations and container yards in seven cities of the country: Barranquilla, Cartagena, Santa Marta, Buenaventura, Cali, Ipiales and Bogotá. Hence, these are the origin or supply nodes in the mathematical model.
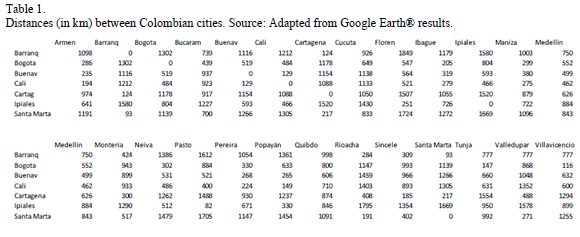
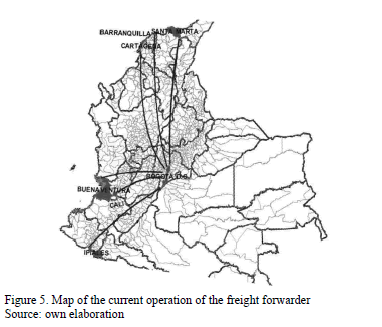
- As receiving centers, 25 points across the country have been considered. These spots are located mainly in the provincial capitals and are considered the destination or market nodes. The distances in kilometers between the origin and destination nodes are introduced in Table 1, where 0 is assumed when origin and destination are the same. In Fig. 5, the map shows the central dispatching from Bogota to the main demand centers.
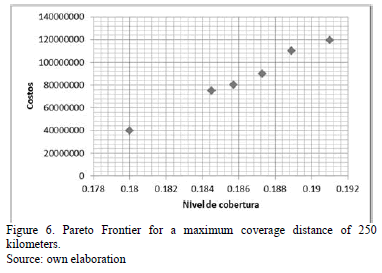
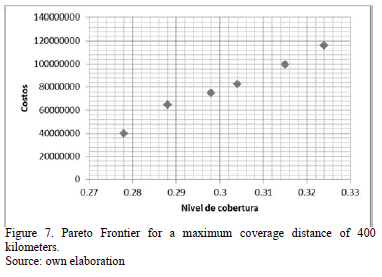
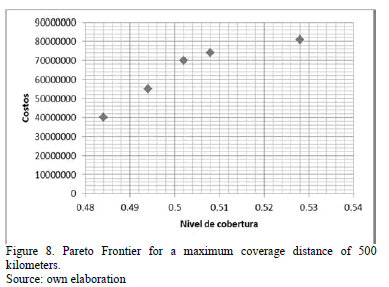
- The demand, capacities, fixed costs, and variable costs, are assumed to be constant and deterministic for the planning period of the problem. This information is also subject to confidentiality agreements. The performance of the algorithm was evaluated for maximum coverage distances of 250, 400, and 500 km.
4.1. Parameters of the implemented algorithm
The following are the values that were implemented as parameters for running the NSGA II model:
Population Size: According to [21], in the multi-objective location problem the results tend to get better as the size of population increases; however, the computational times tend to increase as well, even though in this particular case the number of instances is relatively small. Previous pilot runs were executed with population sizes of 50, 70 and 100 individuals. The latter one showed better results on the tests and was chosen to be implemented in the case study.
Generations: Similar to the population size parameter, the larger the number of generations, larger the probability to get better results. Nevertheless, depends on the size of the problem or number of instances, the probability of getting convergence of the results also increases. Previous pilot runs were executed with 100, 200 and 500 generations. The cases where the number of generations are greater than 100 showed results convergence, so this first value was chosen to be implemented in the model.
Mutation probability: In the mutation operation, the value of certain randomly chosen positions within the chromosome is changed. According to [21], this operator must be executed with low probability values in order to avoid premature convergences to local optima solutions in multi-objective location problem. In the pilot experiments, three different values of mutation probability were used: 0.01, 0.03, and 0.05. As a result of the experiments, 0.01 was the probability implemented as in the other two cases the results showed a significant number of local optima solutions.
Crossover: In this particular case, the single point crossover operator was chosen to be implemented in the final model
For the execution of these runs, the JAVA libraries called JGA © developed by the Universidad de Los Andes (Bogotá, Colombia) to execute Genetic Algorithms were adapted and used, in th multi-objective modes. JGA © is an object oriented-based framework for solving multi-objective optimization models applying evolutionary algorithms. This platform allows to focus on the application's logic by reusing a set of built-in components, as described in [27, 28].
4.2. Achieved results
The parameters that are evaluated correspond mainly to the maximum coverage distance in which the container yards should be located.
It can be observed that the Pareto frontiers for the three evaluated instances have too few points due to the small size of the problem, as illustrated in Figs. 6, 7, 8. It is worth highlighting that for the first two configurations, the solutions are similar in cost terms, but the coverage percentage increases slightly as the maximum distance also increases. These two solution groupings implied that the container yards must be located in Barranquilla, Buenaventura and Cali; nevertheless, this solutions set sacrifices the coverage percentage for those cities that are located inland, as it can be appreciated in the graphic, this coverage hardly reaches 30%. According to the third configuration, the yards should be located in the three aforementioned cities; the difference with the previous configurations lies in that from Buenaventura dispatches to more inland cities can be made, increasing the coverage percentage to 53% in this case.
The interesting side of this last solution is that in terms of costs, it is cheaper than the two first solution sets, for which it could be said that, as the coverage index increases, a better service level will take place, without affecting the costs in a substantial way.
5. Conclusions
In this research the application of meta-heuristic techniques was implemented, to solve multi-objective problems in real world situations in the engineering field. For this case, the NSGA II algorithm was chosen, because of its versatility and implementation efficiency. The problem consisted basically in an assignment or location situation to serve a specific demand, modeling this problem as a network or graph. The implementation of the NSGA II had as results a set of solutions formed in Pareto Fronts, which varied according to the problem instance. Nevertheless, it must be clarified that in this research, metric performance measurements were not evaluated, which help to complement the analysis about the execution of the algorithm.
It is necessary to annotate these results indicate that service and efficiency parameters of the freight forwarder are not aligned, in the sense that the fact of centralizing affects considerably the service levels. The company must evaluate the market that will be affected by the centralization decisions that may be taken, and dimension the impact both in cost and branding terms.
The proposed coverage levels by the model's solution could not be acceptable in practical terms, due to the fact that the market standards can achieve higher levels. Despite this, the scenarios shown by the model allow identifying the cons that the distribution centralization policies would have for the analyzed freight forwarder. Likewise, a representative part of the customers (close to 30%) of this forwarder are really sensitive to the delivery times in their markets (cosmetics and cleansing products), and hence these decisions need to be revised and analyzed really carefully, analyzing the immediate and collateral effects in their customers operational performance.
References
[1] Ballou, R., Business Logistics/supply management: planning, organizing and controlling the supply chain. Prentice-Hall, NY, 2004. [ Links ]
[2] Arango, M.D., Adarme, W. and Zapata, J.A., Commodities distribution using alternative types of transport. A study in the Colombian bread SME's, DYNA, 77 (163), pp. 222-233, 2010. [ Links ]
[3] Brandeau, M., An overview of representative problems in location research, Management Science, 35(6), pp. 645-674, 1989. [ Links ]
[4] Drezner, Z., Facility Location, Springer-Verlag, Nueva York, 1995. [ Links ]
[5] Korpela, J., Lehmusvaara, A. and Tuominen, M., Customer service based design of the supply chain, International Journal of Production Economics, 69, pp. 193-204, 2001. [ Links ]
[6] Nozick, L.K. and Turnquist, M.A., Inventory, transportation, service quality and the location of distribution centers, European Journal of Operations Research, 129, pp. 362-371, 2001. [ Links ]
[7] Revelle, C.S. and Eiselt, H.A., Location analysis: a synthesis and survey, European Journal of Operations Research, 165, pp. 1-19, 2005. [ Links ]
[8] Prodhon, C. and Prins, C., A survey of recent research on location-routing problems, European Journal of Operational Research, 238, pp. 1-17, 2014. [ Links ]
[9] Belenguer, J.-M., Benavent, E., Prins, C., Prodhon, C. and Wolfler-Calvo, R., A branch-and-cut method for the capacitated location-routing problem, Computers and Operations Research, 38 (6), pp. 931-941, 2011 [ Links ]
[10] Baldacci, R., Mingozzi, A. and Wolfler-Calvo, R., An exact method for the capacitated location-routing problem, Operations Research, 59 (5), pp. 1284-1296, 2011. [ Links ]
[11] Harks, T., König, F.G. and Matuschke, J., Approximation algorithms for capacitated location routing, Transportation Science, 47 (1), pp. 3-22, 2013. [ Links ]
[12] Griffis, S.E., Bell, J.E. and Closs, D.J., Metaheuristics in logistics and supply chain management, Journal of Business Logistics, 33 (2), pp. 90-106, 2012. [ Links ]
[13] Badhury, J., Batta, R. and Jaramillo, J., On the use of genetic algorithms to solve location problems, Computers and Operations Research, 29, pp. 761-779, 2002. [ Links ]
[14] Crainic, T.G., Sforza, A. and Sterle, C., Tabu search heuristic for a two-echelon location-routing problem, CIRRELT Technical Report. [Online], 2011, [date of reference: June 14th of 2012], Available at: https://www.cirrelt.ca/DocumentsTravail/CIRRELT-2011-07.pdf [ Links ]
[15] Bouhafs, L., Hajjam, A. and Koukam, A., A Tabu search and ant colony system approach for the capacitated location-routing problem, Proceedings International Conference on Artificial Intelligence and Parallel Computing, pp. 46-54, 2006. [ Links ]
[16] Farahani, R., Steadieseifi, M. and Asgari, N., Multiple criteria facility location problems: A survey, Applied Mathematical Modelling, 34, pp. 1689-1709, 2010. [ Links ]
[17] Badri, M.A., Mortagy, A.K. and Alsayed, A. A multi-objective model for locating fire stations. European Journal of Operations Research, 110, pp. 243-260, 1998. [ Links ]
[18] Matsui, T., Sakawa, M., Kato, K. and Uno, T., Particle swarm optimization for nonlinear 0-1 programming problems, IEEE International Conference on Systems, Man and Cybernetics, pp. 168-173, 2008. [ Links ]
[19] Bhattacharya, U.K., A multi-objective obnoxious facility location model on a plane, American Journal of Operations Research, 1, pp. 39-45, 2011. [ Links ]
[20] Rardin, R., Optimization on Operations Research, Pearson, New York, 1998. [ Links ]
[21] Villegas, J.G., Palacios, F. and Medaglia, A.L., Solution methods for the bi-objective (cost-coverage) unconstrained facility location problem with an illustrative example, Annals of Operations Research, 147 (1), pp. 109-141, 2006. [ Links ]
[22] Daskin, M.S., Network and Discrete Location: Models, Algorithms and Applications, John Wiley & Sons, New York, 1995. [ Links ]
[23] Michalewicz, Z., Genetic Algorithms + Data Structures = Evolution Programs, Springer-Verlag, Berlin, 1996. [ Links ]
[24] Kratica, J. and Filipovic, V., Solving the simple plant location problem by genetic algorithm, RAIRO Operations Research, 35, pp. 127-142, 2001. [ Links ]
[25] Deb, K. and Srinivas, N., Multiobjective optimization using nondominated sorting in genetic algorithms, Evolutionary Computation, 2 (3), pp. 221-248, 1994. [ Links ]
[26] Deb, K., Agrawal, S., Pratap, A. and Meyarivan, T., A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. KanGAL report 200001. Indian Institute of Technology, Kanpur, India, 2000, 11 P. [ Links ]
[27] Medaglia, A.L. and Gutiérrez, E., JGA: An object-oriented framework for rapid development of genetic algorithms. In: Rennard, J.-P., (ed.) Handbook of Research on Nature Inspired Computing for Economics and Management. Idea Group Publishing, Hershey, 2006. [ Links ]
[28] Medaglia A.L., Villegas, J.G. and Rodríguez-Coca, D.M., Hybrid biobjective evolutionary algorithms for the design of a hospital waste management network, Journal of Heuristics, 15, pp. 153-176, 2009 [ Links ]
C. Osorio-Ramírez, holds a Bs. Eng. in Industrial Engineering from the Universidad Industrial de Santander, Colombia and a Graduate Certificate in Logistics and Supply Chain Management from the Massachusetts Institute of Technology, USA. He is currently a PhD candidate in Industry and Organizations Engineering in the Universidad Nacional de Colombia, in Bogotá, Colombia. He is also currently a research associate of the Society, Economy and Productivity research group from the Engineering Faculty of the Universidad Nacional de Colombia.
M. D. Arango-Serna, received the Bs. Eng. in Industrial Engineering in 1991 from the Universidad Nacional de Colombia, Specialist in Finance, Formulation and Evaluation of Projects in 1993 from the Universidad de Antioquia, Colombia, Sp. in Universitary Teaching in 2007 from the Universidad Politécnica de Valencia, Spain. He also holds a MSc. in Systems Engineering in 1997 from the Universidad Nacional de Colombia in Medellín, Colombia and a PhD. in Industrial Engineering in 2001 from the Universidad Politécnica de Valencia, Spain. Is Titular Professor of the Department of Engineering of Organization in the Facultad de Minas of the Universidad Nacional de Colombia. Senior researcher according to Colciencias 2013 classification. Director of the Research Group I+D+i Organizational-Industrial Logistics "GICO".
W. Adarme-Jaimes, holds a Bs. Eng. in Industrial Engineering from the Universidad Industrial de Santander, Colombia, Sp. in Production and MSc. in Industrial Engineering-Logistics from the Universidad del Valle, Colombia and a PhD in Industry and Organizations Engineering in the Universidad Nacional de Colombia. Is Associate Professor of the Engineering at the Universidad Nacional de Colombia, in Bogotá, Colombia. Director of the Society, Economy and Productivity research group of the Universidad Nacional de Colombia.