Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.187 Medellín set-/out. 2014
https://doi.org/10.15446/dyna.v81n186.46761
http://dx.doi.org/10.15446/dyna.v81n187.46761
A modified firefly-inspired algorithm for global computational optimization
Un algoritmo modificado inspirado en luciérnagas para optimización global computacional
Iván Amaya a, Jorge Cruz b & Rodrigo Correa c
a School of Electrical, Electronic and Telecommunication Engineering, Universidad Industrial de Santander, Colombia. ivan.amaya2@correo.uis.edu.co
b School of Electrical, Electronic and Telecommunication Engineering, Universidad Industrial de Santander, Colombia. jorge.cruz1@correo.uis.edu.co
cProfessor, School of Electrical, Electronic and Telecommunication Engineering, Universidad Industrial de Santander, Colombia. crcorrea@uis.edu.co
Received: October 27th, 2013. Received in revised form: April 13th, 2014. Accepted: July 25th, 2014.
Abstract
This article compares the original firefly-Inspired algorithm (FA) against two versions suggested by the authors. It was found that by using some modifications proposed in this document, the convergence time of the algorithm is reduced, while increasing its precision (i.e. it is able to converge with less error). Thus, it is strongly recommended that these variants are further analyzed, especially for the solution of systems of nonlinear equations, since the exploratory test that has been performed yielded good results (i.e. the roots found by the algorithm were quite close to the theoretical one). Moreover, it was also found that the algorithm is dependent on the swarm size, especially when dealing with planar regions.
Keywords: Firefly algorithm; global optimization; standard test functions.
Resumen
Este artículo compara el algoritmo original basado en luciérnagas contra dos versiones sugeridas por los autores. Se encontró que al utilizar algunas modificaciones propuestas en el documento, el tiempo de convergencia del algoritmo se reduce, mientras aumenta su precisión (es decir, converge con menos error). Por tanto, se recomienda fuertemente que estas variantes sean analizadas con más detalle, especialmente para la solución de sistemas de ecuaciones no-lineales, dado que la prueba exploratoria consignada aquí entregó buenos resultados (es decir, las raíces encontradas por el algoritmo se encuentran muy cercanas a los valores teóricos). Además, se encontró que el algoritmo es dependiente del tamaño del enjambre, en especial cuando se trabaja con regiones planas.
Palabras clave: Algoritmo de luciérnagas, optimización global, funciones de prueba estándar.
1. Introduction
The area of global optimization requires theoretical, algorithmic and computational advances in order to address the computation and characterization of global extremes i.e. global minima and maxima, as well as, determine the valid lower and upper bounds on the global extremes. Similarly, global optimization addresses the enclosure of all solutions of nonlinear constrained systems of equations. Until recent years there was only one approach to finding global optima, called deterministic global optimization. This strategy has reasonably well structured mathematical foundations, but requires knowing properties such as differentiability and continuity of the objective function. In recent years a new alternative was proposed, which is known as metaheuristic optimization. In contrast, these strategies make few or no assumptions about the problem being optimized and can efficiently explore the search space in order to find optimal (or near optimal) solutions. A metaheuristic is formally defined as an iterative generation process which guides a subordinate heuristic by combining diverse concepts for exploring and exploiting the search space, without the need of any a priori complicated analytical preparation. Metaheuristic algorithms such as, particle swarm optimization (PSO, [1]), firefly algorithm (FA), simulated annealing [2], spiral algorithm, bat algorithm, for example, are now becoming powerful methods for solving many tough global optimization problems [3]. This article deals with the optimization of an objective function without restrictions, through the original FA algorithm and a couple of variants that are proposed in the following section. Afterwards, some results are shown with standard test functions, analyzing the way in which the swarm size, and one of the proposed factors, can modify the convergence of the strategy. Finally, an example of the use of the algorithm for solving a system of nonlinear equations is shown, and conclusions are drawn.
2. Methodology
During this research, the performance of the original FA, and some modifications proposed in the current paper, will be compared. These variants of the algorithm will be explained below, and the comparison is focused on quality of the answer (i.e. how close is the answer provided by the algorithm to the real one), as well as on the time it took to find it. At first, some results with standard test functions are shown, and then the scope is changed to analyze a nonlinear system of equations.
2.1. An overview on the original algorithm
FA was proposed by Yang in 2010 [4], [5]. According to its author, it is based on the attraction of artificial fireflies via the light they emit. Yang considers that any artificial firefly can attract, or be attracted, by any other one (i.e. they are unisex), as well that their attractiveness is proportional to their brightness, and that the latter one is affected by the landscape of the objective function [6]. This implies, however, that the only function of the light-emission of fireflies is mating, while it could also be used for attracting preys or for intimidating foes, as appears to be the case of real fireflies.
Regarding the algorithm itself, Yang proposes the use of a fixed pair of constants, 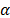 and
and 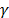 , which relate to the randomness of an artificial firefly's movement and to the dimming of the light emitted by it, as light travels through the search domain, respectively. Striving to not expand too much in the explanation of the algorithm, it will only be said that it can be implemented with the following iterative process:
, which relate to the randomness of an artificial firefly's movement and to the dimming of the light emitted by it, as light travels through the search domain, respectively. Striving to not expand too much in the explanation of the algorithm, it will only be said that it can be implemented with the following iterative process:
- Initialize fireflies
- Calculate each firefly's light (i.e. evaluate the objective function for each firefly)
- Sort fireflies by intensity of light (in ascending order)
- Update fireflies position (i.e. adjust each firefly according to eq. (1) and to the light intensity)
- Check for convergence. If it complies, then exit. If not, then restart the process (skipping the initialization of the elements and using their current position instead).
It is important to remark that in eq. (1), the subscripts 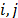 relate to the firefly that is being analyzed, and to the other fireflies, respectively. Also, the superscript
relate to the firefly that is being analyzed, and to the other fireflies, respectively. Also, the superscript 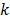 relate to the time step,
relate to the time step, 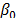 to the attractiveness at distance zero,
to the attractiveness at distance zero, 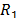 is a random number such that
is a random number such that 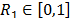 ,
, 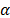 and
and 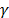 are the previously mentioned constants and
are the previously mentioned constants and 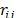 is the Cartesian distance between fireflies.
is the Cartesian distance between fireflies.
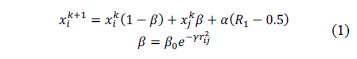
2.2. Proposed modifications
Considering that FA is able to provide good results for test functions [4], but only when 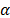 and
and 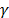 are chosen properly, it was decided to explore the behavior of the algorithm after implementing some modifications, which are now described.
are chosen properly, it was decided to explore the behavior of the algorithm after implementing some modifications, which are now described.
2.2.1. Variable factors
The first and most obvious modification is to allow the constants to vary as the search progresses. However, this variation could be implemented in any number of ways. Since most processes in nature are stochastic, it was decided that the process should behave in the same way (i.e. it should vary stochastically). However, we also require that it decreases through time, since a smaller 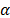 allows random movement in a smaller area, and because a smaller
allows random movement in a smaller area, and because a smaller 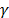 avoids trapping of artificial fireflies in local optima. Thus, the behavior given by eq. (2) was established, where
avoids trapping of artificial fireflies in local optima. Thus, the behavior given by eq. (2) was established, where 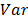 is replaced by each factor (
is replaced by each factor (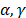 ),
), 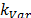 is a proportionality constant that defines how much can a factor (i.e.
is a proportionality constant that defines how much can a factor (i.e. 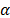 or
or 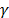 ) be reduced in one iteration, and
) be reduced in one iteration, and 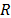 is a random number (uniformly distributed between zero and one).
is a random number (uniformly distributed between zero and one).
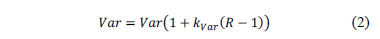
Moreover, if any factor goes below a given limit, it is restarted to a random number (also uniformly distributed) between zero and a maximum value, so the procedure can begin at different points, thus making it a more stochastic-oriented process. During this research, an inferior limit of 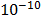 and
and 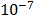 was used for
was used for 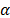 and
and 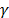 , respectively.
, respectively.
2.2.2. Change of movement equation
Another modification that is proposed in this work, is to change the way in which artificial fireflies travel through the search domain. Here we propose that a firefly (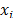 ) is automatically attracted to the vicinity of another one (
) is automatically attracted to the vicinity of another one (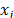 ), by means of eq. (3), striving to speed up the optimization process.
), by means of eq. (3), striving to speed up the optimization process.
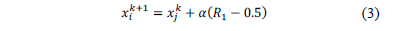
2.2.3. Dividing over the firefly index
Finally, the last change consists of dividing 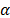 by the index of the attracting firefly, as shown by eq. (4). Since the information of
by the index of the attracting firefly, as shown by eq. (4). Since the information of 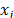 is sorted in an ascending order of
is sorted in an ascending order of 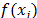 , then the best fireflies (i.e. the ones with higher light emission) have a higher index
, then the best fireflies (i.e. the ones with higher light emission) have a higher index 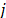 . This means that the fireflies attracted to the best solution found so far, would be located in a smaller vicinity region, thus favoring the intensity of the search.
. This means that the fireflies attracted to the best solution found so far, would be located in a smaller vicinity region, thus favoring the intensity of the search.
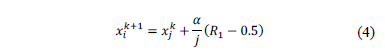
3. Experiments and Results
Most of the tests shown here were run using 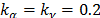 (see eq. (2)), and using the computer described in Table 1. Moreover, some standard test functions were carefully chosen, determined to cover from the most basic one, and up to some of the more difficult ones. Finally, a system of nonlinear equations is solved, via the theorem of real roots [7], [8]. It is important to remark, that results are shown for the original algorithm, as well as for two new versions: one including modifications 2.2.1 and 2.2.2, and other one using all three of them. They will be regarded as "without division" and "with division".
(see eq. (2)), and using the computer described in Table 1. Moreover, some standard test functions were carefully chosen, determined to cover from the most basic one, and up to some of the more difficult ones. Finally, a system of nonlinear equations is solved, via the theorem of real roots [7], [8]. It is important to remark, that results are shown for the original algorithm, as well as for two new versions: one including modifications 2.2.1 and 2.2.2, and other one using all three of them. They will be regarded as "without division" and "with division".
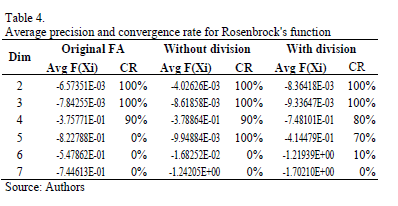
Regarding the tables that will be shown below, it is convenient to stress that they were generated with 10 runs by dimension (unless otherwise stated), that "Avg F(Xi)" relates to the average value of the objective function, and that "CR" is the convergence rate, calculated as the ratio between the number of runs that exited due to convergence (i.e. the answers they found were inside the tolerance margin), and the number of runs per dimension.
3.1. Jong's function
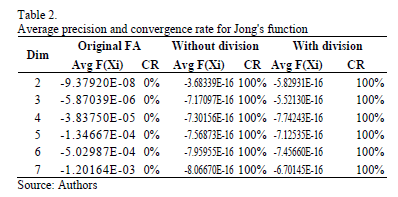
The first test function is a simple one, since it is the summation of quadratic functions, as can be seen from eq. (5). In this case, and due to its simplicity, a precision of 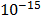 was requested, and 20 artificial fireflies were used, delivering the results from Table 2. It can be seen that the original algorithm is not able to achieve the required level of precision, even though the ones proposed here do it. Moreover, the first proposal is faster than the other two variants, as backed up by Figure 1.
was requested, and 20 artificial fireflies were used, delivering the results from Table 2. It can be seen that the original algorithm is not able to achieve the required level of precision, even though the ones proposed here do it. Moreover, the first proposal is faster than the other two variants, as backed up by Figure 1.
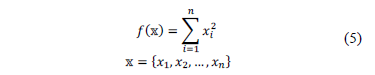
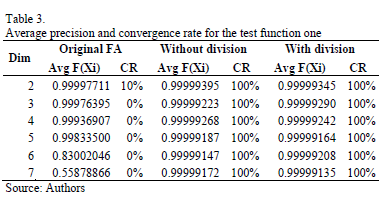
3.2. Test Function one
Its behavior is similar to the one of a parabolic system, and the general equation is shown in eq. (6), which has a global optimum of one, at 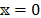 . Results are generated for a desired precision of
. Results are generated for a desired precision of 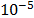 , and
, and
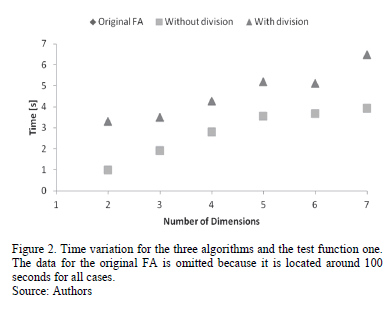
summarizes them for the three versions. It can be seen that the original algorithm is unable to converge on almost every case, whilst both of the versions proposed here converge in all cases. However, the one that does not scale the neighborhood is faster than the one that does it, as can be seen in Figure 2. It is important to stress here that the data of the original FA is omitted because the time values are located around 100 seconds, and they would occlude the visualization of the other ones.
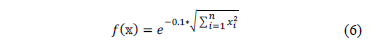
3.3. Rosenbrock's function
As a third approach, and motivated to increase the complexity of the tests, Rosenbrock's function was evaluated, using 30 particles and a precision of 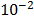 for each run. The general form is given by eq. (7), and the standard search domain is
for each run. The general form is given by eq. (7), and the standard search domain is 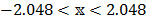 .
.
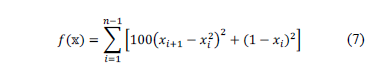
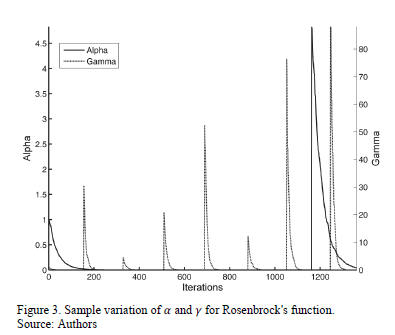
Figure 3 shows a sample variation for 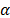 and
and 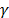 , where it can be seen that the latter restarts several more times than the former, thus allowing a broader combination of the parameters, and increasing the chance of finding a combination that properly optimizes the objective function. In this case,
, where it can be seen that the latter restarts several more times than the former, thus allowing a broader combination of the parameters, and increasing the chance of finding a combination that properly optimizes the objective function. In this case, 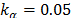 and
and 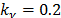 were used.
were used.
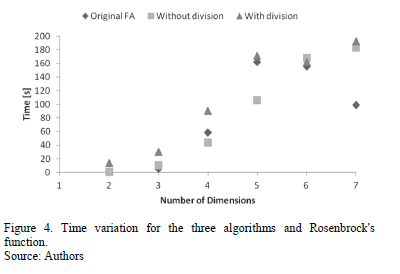
Once again, the tests are summarized in Table 4. In this case, a good convergence rate was achieved for up to five dimensions (restricted, however, to both modifications of the FA, since the original was only able to converge for up to four dimensions), even though for higher dimensions the results were not too far from the results. Besides, and keeping with the behavior of the previous examples, the first proposal is faster than the second one, as can be seen in Figure 4.
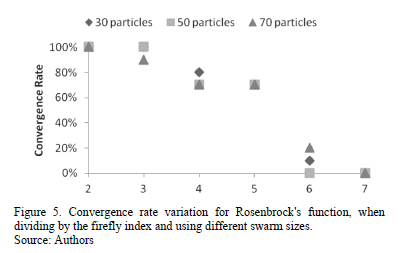
Since the convergence rate was not satisfactory, it was decided to see the effect of the swarm size, as well as how can the value of 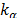 influence the solution. As a first approach, Figure 5 shows the behavior of the convergence rate when varying the population and using
influence the solution. As a first approach, Figure 5 shows the behavior of the convergence rate when varying the population and using 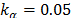 . It can be seen that a higher population can yield a higher value, even though in this case it did not increase too much.
. It can be seen that a higher population can yield a higher value, even though in this case it did not increase too much.
Thus, and considering that the first proposal is the one which has provided the best results, a deeper analysis was performed using this variant. Due to space restrictions, and considering that good data was achieved for lower dimensions, only results between four and seven dimensions will be shown. Figure 6 shows the results for different swarm
sizes. It is important to remark that for these runs, From the previously reported data, it is evident that the convergence of the algorithm is heavily dependent on the initially defined swarm size, especially when dealing with planar regions (such as the one present at Rosenbrock's valley), so special care need to be taken into account when defining this parameter. 3.4. Systems of nonlinear equations 3.4.1. 2x2 System The system that was used is comprised of two equations. After using the theorem of real roots described in [7], the objective function given in eq. (8) is obtained, where the parameters of the system are defined in, following the principles described in the aforementioned theorem, the solution of the system is at the same coordinates that those of the optimum of the objective function. 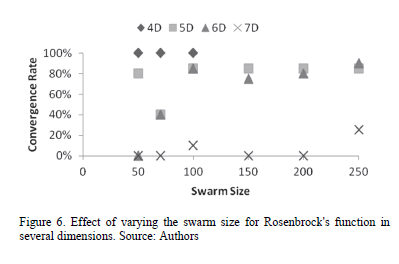
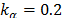 was used, and that in the case of four dimensions, tests were only run for up to 100 particles, since a convergence rate of 100% was always achieved. It can be seen that only when a swarm of 250 artificial fireflies is used, the algorithm is able to deliver a satisfactory answer (i.e. one which complies with the convergence criteria) in 25% of the cases. It is convenient to say that it was also necessary to allow for a generation of a higher
was used, and that in the case of four dimensions, tests were only run for up to 100 particles, since a convergence rate of 100% was always achieved. It can be seen that only when a swarm of 250 artificial fireflies is used, the algorithm is able to deliver a satisfactory answer (i.e. one which complies with the convergence criteria) in 25% of the cases. It is convenient to say that it was also necessary to allow for a generation of a higher 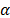 , increasing the limit for up to 100. Since these tests are somewhat more delicate (i.e. they may or may not converge), it was decided to run the algorithm 20 times for each configuration (hence, the possibility of reporting variations of 5% in the convergence rate).
, increasing the limit for up to 100. Since these tests are somewhat more delicate (i.e. they may or may not converge), it was decided to run the algorithm 20 times for each configuration (hence, the possibility of reporting variations of 5% in the convergence rate).
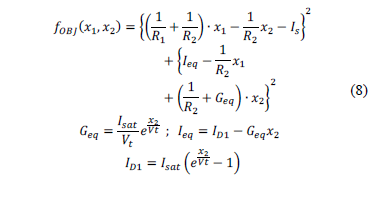
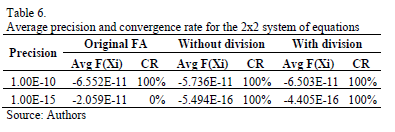
Table 6 summarizes the main results found for the system. It can be seen that for a desired precision of 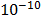 , all three algorithms always converge. However, when asked for somewhat better results (i.e. a precision of
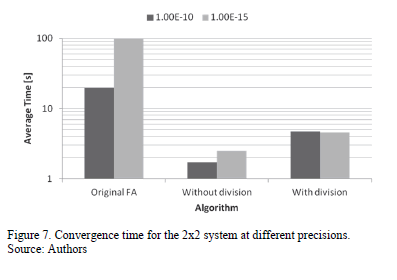
, all three algorithms always converge. However, when asked for somewhat better results (i.e. a precision of 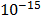 ), the methodology proposed by Jang is unable to converge, as opposed to both of our proposals, which achieve total convergence. It is important to remark that, once again, the algorithm that does not take into account the reduction of the relocation vicinity (i.e. the one called "Without division") is faster than the other proposal, even though the latter one has a more stable behavior, as can be appreciated in Figure 7.
), the methodology proposed by Jang is unable to converge, as opposed to both of our proposals, which achieve total convergence. It is important to remark that, once again, the algorithm that does not take into account the reduction of the relocation vicinity (i.e. the one called "Without division") is faster than the other proposal, even though the latter one has a more stable behavior, as can be appreciated in Figure 7.
4. Conclusions
After a careful review of the tests, it can be concluded that it could be good to develop an intermediate stage that optimizes the behavior of 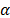 and
and 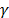 . This needs to be focused on the way of increasing or decreasing them, since higher factors tend to favor exploration and lower ones tend to do so for exploitation. Thus, in order to avoid trapping in local minima, a proper sweep of the search domain should be carried out, e.g. by allowing the generation of an
. This needs to be focused on the way of increasing or decreasing them, since higher factors tend to favor exploration and lower ones tend to do so for exploitation. Thus, in order to avoid trapping in local minima, a proper sweep of the search domain should be carried out, e.g. by allowing the generation of an 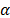 high enough to cover it. On the other hand, it was found that the algorithm's convergence is highly dependent on the swarm size, especially when planar regions are present (such as Rosenbrock's valley), and even more when this phenomena is repeated in several dimensions (e.g. up to seven dimensions as in the current research).
high enough to cover it. On the other hand, it was found that the algorithm's convergence is highly dependent on the swarm size, especially when planar regions are present (such as Rosenbrock's valley), and even more when this phenomena is repeated in several dimensions (e.g. up to seven dimensions as in the current research).
Finally, it was found that the proposed modifications are, in general, good for improving the convergence rate of the original FA. However, the fact of dividing by the index of the artificial firefly, increases the time required for achieving convergence, so unless a proper use for this variant can be found, it would be advisable to only implement the first two novel adjustments. Also, it is strongly recommended to keep using the theorem of real roots to be able to solve a system of equations through an optimization algorithm. Furthermore, it is advisable to perform a deeper analysis with more complex systems, i.e. ones with more unknowns, which can be easily found in nonlinear circuits operating in DC.
References
[1] Parsopoulos, K. E. and Vrahatis, M.N., Particle Swarm optimization and intelligence: Advances and applications. Information Science Reference, Hershey, 2010. [ Links ]
[2] Rao, S.S., Engineering optimization: Theory and practice. John Wiley & Sons, Inc., New Jersey, 2009. [ Links ]
[3] Pirkwieser, S. Hybrid metaheuristics and matheuristics for problems in bioinformatics and transportation, PhD. Dissertation Thesis, Vienna University of Technology, Vienna, Austria, 2012. [ Links ]
[4] Yang, X., Firefly algorithm, Stochastic test functions and design optimisation, International Journal of Bio-Inspired Computation, 2 (2), pp.78-84, 2010. [ Links ]
[5] Yang, X.S., Engineering optimization: An introduction. John Wiley & Sons, New Jersey, 2010. [ Links ]
[6] Yang, X., Firefly algorithms for multimodal optimization, Stochastic algorithms: Foundations and applications, 5792, pp.169-178, 2010. [ Links ]
[7] Amaya, I., Cruz, J. and Correa, R., Real Roots of nonlinear systems of equations through a metaheuristic algorithm, Revista DYNA, 78 (170), pp.15-23, 2011. [ Links ]
[8] Amaya, I., Cruz, J. and Correa, R., solution of the mathematical model of a nonlinear direct current circuit using particle swarm optimization, Revista DYNA, 79 (172), pp.77-84, 2012. [ Links ]
I. Amaya, received his Bs. degree on Mechatronics Engineering from Universidad Autónoma de Bucaramanga, Colombia. Currently, he belongs to the School of Electrical, Electronic and Telecommunication Engineering, and is pursuing his PhD. on Engineering at Universidad Industrial de Santander, Colombia. His research interests include global optimization and microwaves. ORCID: 0000-0002-8821-7137
J. Cruz, received his Bs. degree on Electronic Engineering from Universidad Industrial de Santander, Colombia. Currently, he is with the School of Electrical, Electronic and Telecommunication Engineering, and is pursuing his MSc. on Electronic Engineering at Universidad Industrial de Santander, Colombia. His research interests include global optimization and thermodynamics. ORCID: 0000-0003-4494-7864
R. Correa, received his Bs, degree on Chemical Engineering from Universidad Nacional de Colombia, sede Bogotá, Colombia, and his MSc. degree on Chemical Engineering from Lehigh University, Pensilvania, USA and from Universidad Industrial de Santander, Colombia. He received his PhD. on Polymer Science and Engineering from Lehigh University, Pensilvania, USA and is currently a professor at Universidad Industrial de Santander. His research interests include microwave heating, global optimization, heat transfer and polymers.