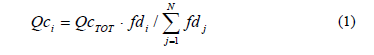Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.187 Medellín set-/out. 2014
https://doi.org/10.15446/dyna.v81n186.40979
http://dx.doi.org/10.15446/dyna.v81n187.40979
Multiobjective optimization of the reactive power compensation in electric distribution systems
Optimización multiobjetivo de la compensación de potencia reactiva en sistemas eléctricos de distribución
Manoel Socorro Santos-Azevedo a, Ignacio Pérez-Abril b, Carlos de León-Benítez c, Jandecy Cabral-Leite d & Ubiratan Holanda-Bezerra e
a Universidad del Estados de Amazonas, Brasil. manoelazevedo@yahoo.com.br
b Centro de Estudios Electroenergéticos, Universidad Central de Las Villas, Cuba. iperez@uclv.edu.cu
c Centro de Estudios Electroenergéticos, Universidad Central de Las Villas, Cuba. charle@uclv.edu.cu
d Instituto de Tecnología y Educación Galileo de la Amazonía, Brasil. jandecycabral@hotmail.com
e Departamento de Ingeniería Eléctrica y Computación, Universidad Federal de Pará, Brasil. bira@ufpa.br
Received: November 25th, de 2013. Received in revised form: March 7th, 2014. Accepted: March 17th, 2014
Abstract
Different methods of optimization have been used for the selection and localization of capacitor banks in distribution circuits. However, it is necessary to consider the distortion taken place by the harmonics of the no-linear loads and the possible appearance of resonances between the inductive elements of the system and the existent capacitor banks. On the other hand, it has not been integrated in a single methodology the use of capacitor banks and of passive harmonic filters to compensate the reactive power in harmonic polluted distribution systems. The present work intends as objective to develop this methodology. The developed program is based on the multi-objective optimization algorithm NSGA-II that it is proven with success in several examples.
Keywords: harmonics; capacitors; passive filters; optimization.
Resumen
Se han empleado diferentes métodos de optimización para la selección y localización de bancos de capacitores en circuitos de distribución. Sin embargo, hay que considerar la distorsión producida por los armónicos de las cargas no-lineales y la posible aparición de resonancias entre los elementos inductivos del sistema y los bancos de capacitores existentes. Por otra parte, no se ha integrado en una sola metodología la utilización de bancos de capacitores y de filtros pasivos de harmónicos para compensar la potencia reactiva en sistemas de distribución contaminados por armónicos. El presente trabajo se propone como objetivo desarrollar dicha metodología. El programa desarrollado se basa en el algoritmo de optimización multiobjetivo NSGA-II que se prueba con éxito en varios ejemplos prácticos.
Palabras clave: armónicos, capacitores, filtros pasivos, optimización.
1. Introducción
La compensación de la potencia reactiva en los sistemas eléctricos de distribución consiste en la selección e instalación de bancos de capacitores en determinados puntos del circuito con el objetivo de reducir sus costos de operación anuales.
Se han empleado diferentes métodos de optimización para la selección y localización de bancos de capacitores en circuitos de distribución que alimentan cargas lineales [1-12]. Algoritmos genéticos [1,2,4], algoritmos de inteligencia colectiva [6,9,10] y aún técnicas heurísticas [5,8,11] se han utilizado para resolver variadas formulaciones de este problema.
Sin embargo, en las condiciones actuales de los circuitos, donde se utilizan cada vez más cargas con comportamiento no-lineal, hay que considerar la distorsión producida por los armónicos de estas cargas y la posible aparición de resonancias entre los elementos inductivos del sistema y los bancos de capacitores existentes.
De esta manera, en un circuito contaminado por armónicos, la variante más económica de localización y selección de capacitores considerando solo los resultados a frecuencia fundamental, puede incrementar los índices de distorsión y por lo tanto ser inviable desde el punto de vista de calidad de la energía [13-16].
Otros medios compensadores de la potencia reactiva más adecuados para circuitos contaminados por armónicos son los filtros pasivos de armónicos, los cuales unen a su acción de filtrado la función de inyección de potencia reactiva a las redes.
Varios trabajos [17-25] se han dedicado a la selección y localización de los filtros pasivos para compensar la distorsión armónica en estos sistemas. No obstante, en la mayoría de estas contribuciones no se consideran los efectos de reducción de pérdidas en la red por la compensación de potencia reactiva lograda por los filtros.
El presente trabajo se propone como objetivo desarrollar una metodología computacional para optimizar la compensación de la potencia reactiva en circuitos de distribución contaminados por armónicos que contemple el uso de bancos de capacitores y de filtros pasivos de armónicos con este fin.
El programa desarrollado se basa en el algoritmo de optimización multiobjetivo NSGA-II que se prueba con éxito en varios ejemplos prácticos.
2. Modelo matemático
Teniendo en cuenta los aspectos expuestos, el presente trabajo formula el problema de optimización de la compensación de potencia reactiva en sistemas eléctricos de distribución contaminados por armónicos como un problema multiobjetivo que persigue la selección y localización de los compensadores necesarios para minimizar:
- El costo de los equipos compensadores seleccionados.
- El costo de operación anual del sistema eléctrico.
- La distorsión total de la tensión en las barras del sistema eléctrico.
El problema de optimización está sujeto al cumplimiento de las restricciones de:
- Las normas de calidad de la energía.
- Las normas de utilización de los equipos compensadores.
2.1. Variables del problema
Las variables independientes del problema de optimización, representadas por el arreglo x, son: el número, localización y parámetros de diseño de los compensadores de potencia reactiva (bancos de capacitores o filtros de armónicos) a instalar en el circuito.
En un algoritmo genético, las características de un individuo (variante de solución) se expresa por el cromosoma que lo define. La representación de las variables del problema se realiza de acuerdo al tipo de codificación que emplea la implementación computacional utilizada, ya sea la clásica codificación binaria u otro tipo de codificación más adecuada para representar las variables. En la mayoría de los casos, lo más cómodo es utilizar una codificación en números reales "real coded GA".
Como el número de compensadores a utilizar es uno de los resultados a obtener, el conjunto de datos que representan una solución es de tamaño variable. De esta manera, cuando se define el problema de optimización a resolver, se va a utilizar un cromosoma que puede representar el número máximo de compensadores que se quieran utilizar.
Una vez definidas sus dimensiones, el cromosoma queda compuesto por los siguientes componentes (Tabla 1).
Partiendo de la estructura del cromosoma utilizado, una vez que este es determinado por el algoritmo genético para una solución dada, el número, localización y parámetros de diseño de los compensadores a instalar quedan determinados directamente con excepción de la potencia reactiva capacitiva de cada compensador, la que se obtiene con el siguiente procedimiento:
1) Se determina la potencia reactiva no estándar del capacitor Qci, proporcional al valor del factor de distribución de potencia reactiva correspondiente:
2) Se determina el número de unidades de tamaño estándar que mejor aproximan el valor de potencia reactiva Qci.
Este procedimiento permite que la distribución de la potencia reactiva entre los distintos compensadores sea determinada por el propio método de optimización a partir de las necesidades del problema. En otras palabras, esta es una forma de resolver el problema de distribuir eficientemente la potencia de los compensadores entre las localizaciones determinadas, sin peligro de que se instale una capacidad total excesiva para el circuito.
Aquí hay que señalar, que las frecuencias de sintonía de los filtros sintonizados se escogen a un 94% del valor de frecuencia fs que se determina en el cromosoma. Esto se hace para evitar la resonancia a una frecuencia indeseada cuando ocurren variaciones en los parámetros del filtro [26-27].
2.2. Funciones objetivo y restricciones
El problema de optimización tratado puede ser formalizado mediante dos funciones objetivo:
- La maximización del valor presente líquido del proyecto de compensación
- La minimización de la distorsión total de los armónicos de tensión.
2.2.1. Costo de inversión de los compensadores
Los compensadores de potencia reactiva, sean capacitores o filtros de diferente tipo, tienen un costo de inversión I(x) compuesto por los costos de: capacitores, reactores y resistores, que se consideran proporcionales a sus respectivas potencias para cada nivel de tensión [28].
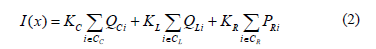
Donde Kc($/kvar), KL($/kvar) y KR($/kW) son los coeficientes de costo de la potencia de capacitores Qc, inductores QL y resistores PR respectivamente, y CC, CL y CR representan los conjuntos de cada uno de estos tipos de elementos.
2.2.2. Costo anual de operación de la red
Las redes eléctricas de distribución de media tensión suministran cargas residenciales, industriales y de edificios comerciales que siguen un patrón de comportamiento diario bastante estable.
Para considerar el efecto de los equipos compensadores de potencia reactiva en el costo de operación de la red, este se acostumbra evaluar mediante dos componentes fundamentales: el costo de la demanda máxima de la carga y el costo de la energía consumida en pérdidas.
El costo de la demanda máxima consiste en los gastos en que incurre la empresa distribuidora en facilitar la capacidad eléctrica (transformadores, líneas, etc.) necesaria para garantizar el suministro de la potencia máxima de la carga. Como la compensación de la potencia reactiva solo modifica las pérdidas de potencia del circuito, este costo se evalúa como proporcional a las pérdidas de potencia en el horario de máxima demanda DPmax.
Por otra parte, el costo de la energía se evalúa como el costo anual de las pérdidas de energía en transformadores, líneas y otros elementos del circuito DEa. Como la carga del circuito varía entre los distintos L estados de carga característicos del mismo, es preciso determinar dichas pérdidas de energía como la sumatoria de las pérdidas que ocurren en cada estado de carga k de duración anual Dtk:
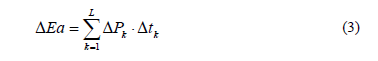
De esta manera, el costo de operación anual de la red se calcula mediante:
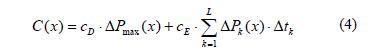
Donde cD($/kW) y cE($/kWh) son los coeficientes de costo correspondientes a cada parte de la función de costo de operación.
2.2.3 Valor presente neto del proyecto
Como la instalación de compensadores de potencia reactiva (capacitores o filtros de armónicos) en un circuito es en definitiva un proyecto de inversión que persigue obtener ganancia a partir de la economía obtenida en el costo de operación de la red, se puede utilizar el valor presente neto VPN como un indicador económico que reúne en una sola función, los costos de inversión y de operación de la red eléctrica.
Considerando un periodo de evaluación de N años con una razón de interés i, el VPN del proyecto de compensación se calcula como:
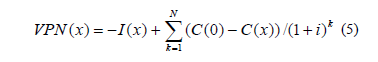
Donde C(0) representa el costo de operación de la red antes de que se instalen los compensadores de reactivo y la diferencia C(0)-C(x) el ahorro anual por concepto de la reducción del costo de operación con la instalación de los compensadores representados por x.
2.2.4. Distorsión armónica total
Los bancos de capacitores son esencialmente equipos compensadores de la potencia reactiva. Sin embargo, los mismos pueden magnificar el efecto de los armónicos de las cargas por la existencia de resonancias serie o paralelo con los elementos inductivos de la red eléctrica.
No obstante, el efecto de los bancos de capacitores sobre la distorsión de la tensión en las barras del sistema depende de la magnitud y localización de los mismos en el circuito, por eso puede existir una solución mediante capacitores que no incremente los indicadores de distorsión o que incluso los reduzca.
Por otra parte, los filtros pasivos de armónicos son primariamente dispositivos de control de armónicos cuya función es evitar la circulación de las corrientes distorsionadas a través de los elementos del sistema y reducir la distorsión de armónicos de tensión en las barras. Por lo tanto una correcta selección y localización de estos compensadores reduce sustancialmente los índices de distorsión de armónicos.
Existen dos indicadores fundamentales de la distorsión de la tensión: la distorsión armónica total THD y la distorsión armónica individual IHDk para un armónico k determinado.
En esta formulación se define como un tercer objetivo la minimización de la distorsión total de la tensión en todas las barras del circuito. Para esto se plantea minimizar el máximo valor de THD del conjunto U de las barras del sistema para el conjunto L de todos los estados de carga considerados.
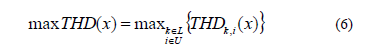
Por lo tanto, el problema de optimización puede formalizarse como:
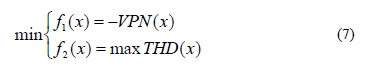
Debe observarse que la minimización de -VPN(x) es equivalente a la maximización de VPN(x).
2.2.5. Restricciones
El conjunto de restricciones del problema considera dos tipos de condiciones fundamentales:
- Las restricciones de calidad de la tensión en las barras del sistema [29].
- Las restricciones al estrés de las componentes de los compensadores [30].
La forma de evaluación de las restricciones de calidad de la tensión depende de la norma adoptada para evaluar los problemas de calidad.
Para lograr que el programa de optimización obtenga soluciones factibles al problema, se define una función de penalidad para las restricciones g(x) que se evalúa como la suma cuadrática de todas las violaciones a las restricciones del problema.
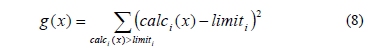
Donde calci y limiti representan el valor calculado y el valor límite del parámetro i acotado por una restricción dada.
Una vez evaluadas todas las restricciones del problema, g(x) tendrá como valor la suma cuadrática de todas las violaciones a las restricciones. Si g(x) tiene valor cero, la solución x es factible, mientras que en caso contrario, la solución no cumple una o varias restricciones.
Para incluir las restricciones como una función de penalidad, el problema se expresa como:
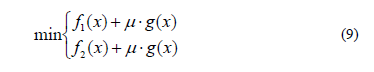
Donde µ es una constante de alto valor que hace atractiva la reducción de g(x) y por lo tanto facilita la búsqueda de una solución factible al problema.
3. Algoritmo de optimización
La optimización multiobjetivo pertenece al área de los problemas de optimización matemática que involucran varias funciones objetivo que deben optimizarse simultáneamente. Normalmente este tipo de optimización se realiza sobre funciones objetivo que pueden tener una naturaleza conflictiva, lo que provoca que las decisiones óptimas tengan que considerar los compromisos existentes entre dos o más objetivos.
A diferencia de los problemas de optimización de un objetivo, normalmente en un problema multiobjetivo no existe una solución única que optimiza todos los objetivos simultáneamente. Cuando eso ocurre, se dice que las funciones son conflictivas y en lugar de una solución existe un conjunto de soluciones para el problema, que se denominan soluciones óptimas de Pareto o soluciones no-dominadas del problema.
Una solución se llama no-dominada si ninguno de los objetivos del problema puede ser mejorado en valor sin empeorar el valor de alguno de los restantes objetivos. Todas las soluciones no-dominadas que integran la frontera de Pareto pueden considerarse igualmente buenas.
Uno de los métodos de mayor éxito en la optimización multiobjetivo es el algoritmo genético de optimización por ordenamiento no-dominado (NSGA-II) [31].
3.1. Características del algoritmo utilizado
Para la realización de este trabajo, se modificó el algoritmo publicado por Sheshadri [32] para incorporar variables enteras además de las variables reales que utiliza esta implementación. De esta manera, se obtuvo un algoritmo de optimización para problemas mixtos en enteros y reales que emplea una codificación del cromosoma en números reales.
3.2. Cálculo de las funciones objetivo y restricciones
El NSGA-II utiliza una función para evaluar todos los objetivos declarados f1(x), fn(x), así como la función de restricciones g(x) a partir del arreglo x de variables independientes del problema (cromosoma). Esta función se define como:
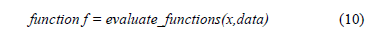
Donde el parámetro data representa los datos adicionales de la red eléctrica y las cargas que son necesarios para determinar el arreglo f de las funciones objetivo.
La citada función emplea el siguiente algoritmo de cálculo:
- Dados los datos del cromosoma x, determina el correspondiente conjunto de compensadores (capacitores o filtros), sus parámetros y su localización en el sistema eléctrico de distribución.
- Calcula el costo de inversión de los compensadores determinados.
- Para todos los L estados de carga considerados, analiza la operación del sistema eléctrico mediante programas de flujo de potencia a frecuencia fundamental y de penetración de armónicos, que han sido desarrollados en Matlab para esta aplicación.
- Con los resultados calculados para todos los estados de carga característicos, calcula el costo de operación de la red: costo de las pérdidas de energía y costo de las pérdidas de potencia en el horario pico.
- Calcula los índices de distorsión de las tensiones en todos los estados de carga y en todas las barras del sistema y determina el máximo valor de THD para evaluar la función objetivo correspondiente.
- Chequea las restricciones de calidad de la energía en todos los estados de carga y en todas las barras y determina el estrés máximo en todos los capacitores. Con estos resultados evalúa la función de restricciones g(x).
3.3. Algoritmo principal de optimización
El algoritmo principal de optimización realiza los siguientes pasos:
- Lee los datos del sistema, las cargas y la descripción del problema de optimización que se quiere resolver.
- Determina el estado de operación inicial del sistema sin equipos compensadores conectados, evalúa el costo de operación inicial y determina los índices de distorsión armónica.
- Definido el tamaño de la población, ejecuta el algoritmo NSGA-II el número de generaciones preestablecidas por el usuario para producir la frontera de Pareto del problema.
- Salva la población final del NSGA-II en un archivo *.mat para el posterior análisis de las soluciones obtenidas.
4. Ejemplo de aplicación
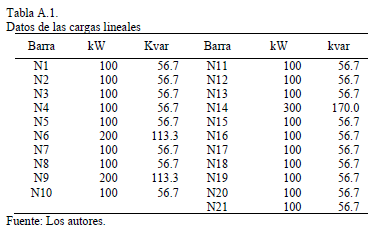
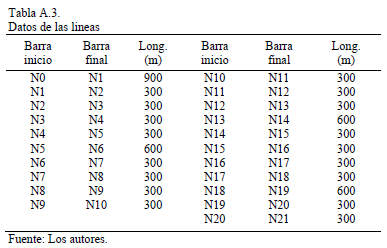
Como ejemplo de aplicación (ver Apéndice) para la presente metodología se utilizó un circuito de distribución formado por un alimentador radial de 13.8 kV que suministra 21 barras de carga en cada una de las cuales hay una mezcla de carga lineal y no-lineal.
La distribución en el circuito de la carga lineal se ofrece en la Tabla A.1 del apéndice, mientras que la carga no-lineal representa un 35% de la carga lineal en cada barra.
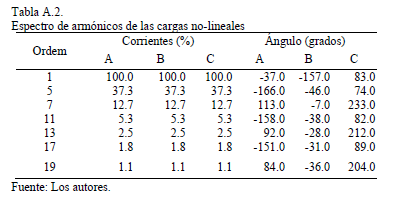
La carga no-lineal se compone de equipos electrodomésticos con un espectro característico que se muestra en la Tabla A.2 del apéndice.
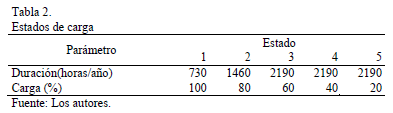
Para probar el comportamiento del sistema se consideran cinco estados de carga posibles en un año característico (Tabla 2).
Por simplicidad, este comportamiento anual se considera igual para todas las cargas lineales y no lineales del circuito.
Todas las barras de media tensión (1 - 21) con excepción de la barra de la fuente (0) se consideran como localizaciones posibles para los equipos compensadores de potencia reactiva a seleccionar.
Para determinar el costo de operación anual del circuito se emplean los coeficientes de costo (Costo de la demanda cD = 120 $/kW y Costo de la energía cE = 0.015 $/kWh).
La evaluación del VPN se realizó para un periodo de 10 años y un interés del 5% anual.
Para formar los compensadores de potencia reactiva se emplean unidades trifásicas de capacitores de 150 kvar. Como datos de costo de los capacitores, inductores y resistores se utilizaron 13 $/kvar, 250 $/kvar y 100 $/kW respectivamente [28].
En todos los casos, se utilizaron los límites de armónicos de tensión de la norma Prodist-módulo 8 [30] como restricciones de calidad de la energía.
Para examinar las posibilidades del programa de optimización, se resolvieron los siguientes casos:
- Compensación con capacitores.
- Compensación con capacitores y filtros sintonizados.
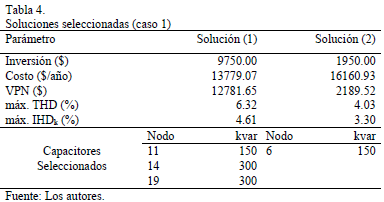
Los resultados iniciales del problema (caso base sin compensadores) se muestran en la Tabla 3.
Según la norma Prodist-Módulo 8, estos índices de distorsión se encuentran dentro de los límites normados para este nivel de tensión.
4.1. Compensación con capacitores
En este caso se quiere determinar la potencia y localización en el circuito de hasta tres bancos de capacitores fijos.
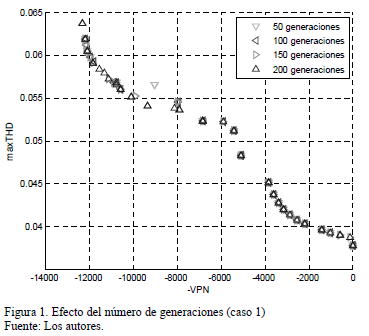
Para determinar de alguna forma el número de generaciones requerido para obtener "buenas" soluciones para el problema, se ejecutaron 200 generaciones del NSGA-II sobre una población de 50 individuos. Las fronteras de Pareto obtenidas por el algoritmo en 50, 100, 150 y 200 generaciones se muestran en la Fig. 1.
Como se aprecia en la Fig. 1, no hay grandes variaciones en las soluciones obtenidas a partir de las 100 generaciones, por lo que se decidió realizar las siguientes corridas solo 150 generaciones.
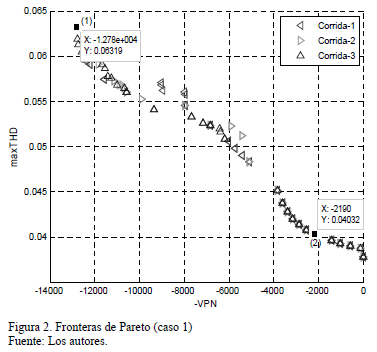
Otro aspecto que se evalúa corrientemente en los algoritmos genéticos es su capacidad para obtener de forma repetida, soluciones semejantes en diversas corridas independientes del programa. En este sentido, se decidió correr tres veces el programa, obteniéndose los resultados que se muestran en la Fig. 2.
Como se puede comprobar en la Fig.2, hay una buena correspondencia entre las tres fronteras de Pareto, lo que habla a favor de la convergencia del algoritmo.
Obtenidas las soluciones de Pareto, pueden utilizarse diferentes criterios para escoger la solución a emplear. Por ejemplo, si se desea la solución de mejor desempeño económico, esta sería la solución (1) que se destaca en la Fig. 2, la que tiene un VPN = $12782 en 10 años. Sin embargo, esta variante es la de peor comportamiento en relación a la distorsión, que alcanza un valor máximo de 6.32%.
Otra variante que se destaca es la solución (2), que consigue un valor positivo del VPN sin prácticamente incrementar la distorsión armónica original del circuito.
La Tabla 4 resume los datos fundamentales de estas soluciones. En la misma se aprecia como en la solución (2), buscando no incrementar la distorsión, el algoritmo modifica la capacidad y localización de los capacitores, con lo que se reduce la eficacia económica de la variante.
4.2. Compensación con capacitores y filtros sintonizados
En este caso se expone la selección y localización de hasta tres capacitores y tres filtros sintonizados.
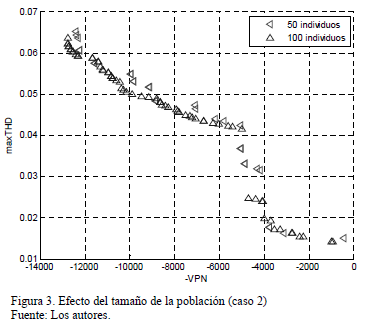
Tras realizar varias pruebas del algoritmo para este nuevo problema, se comprobó la conveniencia de incrementar el tamaño de la población a 100 individuos para determinar con más exactitud la frontera de Pareto del problema (Fig. 3).
Por lo tanto, se efectuaron tres corridas del programa con una población de 100 individuos y 150 generaciones para resolver este nuevo caso.
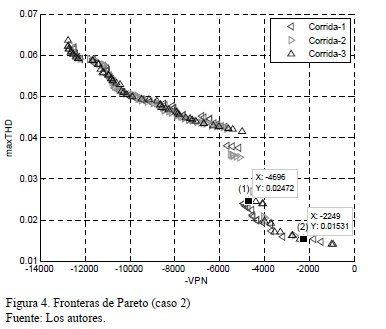
Las fronteras de Pareto resultantes se muestran en la Fig. 4, donde puede verificarse de nuevo la convergencia del algoritmo hacia conjuntos de soluciones semejantes.
En este segundo caso, en que se considera la instalación tanto de capacitores como de filtros de armónicos, se han destacado dos soluciones en la zona de baja distorsión armónica.
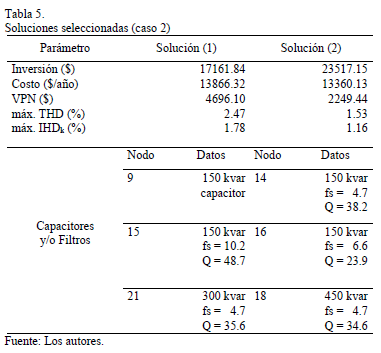
Un resumen de las características de ambas soluciones se ofrece en la Tabla 5, donde en el caso de los filtros se muestran la frecuencia de sintonía fs y el factor de calidad Q resultantes.
Ambas soluciones se logran mediante tres compensadores, la primera con un capacitor y dos filtros sintonizados al 5to y 13vo armónicos y la segunda mediante tres filtros, dos sintonizados al 5to y uno al 7mo armónico.
Aunque la solución (2) es más efectiva desde el punto de vista de calidad de la energía, pudiera escogerse la solución (1) que es el doble de efectiva desde el punto de vista económico.
5. Conclusiones
A partir de los resultados obtenidos en las corridas del programa, se pueden destacar las siguientes conclusiones sobre su uso:
- El algoritmo ha mostrado buena convergencia a soluciones semejantes en diferentes corridas.
- El tamaño de la población y el número de generaciones deben ajustarse para el problema que se pretende resolver.
- Las soluciones que utilizan solo capacitores tienen mejor desempeño económico, pero son inferiores desde el punto de vista de calidad de la energía.
- Las soluciones con filtros sintonizados deben examinarse ante variaciones de los parámetros de los filtros.
6. Apéndice: Datos del ejemplo
Agradecimientos
Al Instituto de Tecnología Galileo de la Amazonía- ITEGAM, a la Fundación para la Investigacióndel Estado de Amazonas - FAPEAM por apoyar financieramente esta investigación.
References
[1] Alencar de-Souza, B. et al., Microgenetic algorithms and fuzzy logic applied to the optimal placement of capacitor banks in distribution networks, IEEE Transactions on Power Systems, 19 (2), pp. 942-947, 2004. [ Links ]
[2] Mendes, A. et al., Capacitor placement in large-sized radial distribution networks, Proc. IEE. Generation, Transmission and Distribution, 152 (4), pp. 496-502, 2005. [ Links ]
[3] Khodr, H.M. et al., Maximum savings approach for location and sizing of capacitors in distribution systems, Electric Power Systems Research 78, pp. 1192-1203, 2008. [ Links ]
[4] Das, D., Optimal placement of capacitors in radial distribution system using a Fuzzy-GA method, Electrical Power and Energy Systems, 30, pp. 361-367, 2008. [ Links ]
[5] Da Silva, C. et al., A heuristic constructive algorithm for capacitor placement on distribution systems, IEEE Transactions on Power Systems, 23 (4), pp. 1619-1626, 2008. [ Links ]
[6] Chang, Ch.F., Reconfiguration and capacitor placement for loss reduction of distribution systems by ant colony search algorithm, IEEE Transactions on Power Systems, 23(4), pp. 1747 - 1755, 2008. [ Links ]
[7] Park, J.Y. et al., Optimal capacitor allocation in a distribution system considering operation costs, IEEE Transactions on Power Systems, 24 (1), pp. 462-468, 2009. [ Links ]
[8] Segura, S. et al., Efficient heuristic algorithm used for optimal capacitor placement in distribution systems, Electrical Power and Energy Systems, 32, pp. 71-78, 2010. [ Links ]
[9] Tabatabaei S.M. and Vahidi, B., Bacterial foraging solution based fuzzy logic decision for optimal capacitor allocation in radial distribution system, Electric Power Systems Research, 81 (4), pp. 1045-1050, 2011. [ Links ]
[10] Singh, S.P. and Rao, A.R., Optimal allocation of capacitors in distribution systems using particle swarm optimization, Electrical Power and Energy Systems, 43, pp. 1267-1275, 2012. [ Links ]
[11] Abul'Wafa, A.R., Optimal capacitor allocation in radial distribution systems for loss reduction: A two stage method, Electric Power Systems Research, 95, pp. 168- 174, 2013. [ Links ]
[12] Ziari, I, Ledwich, G. and Ghosh, A., A new technique for optimal allocation and sizing of capacitors and setting of LTC, Electrical Power and Energy Systems 46, pp. 250-257, 2013. [ Links ]
[13] Ghose, T. and Goswami, S.K., Effects of unbalances and harmonics on optimal capacitor placement in distribution system, Electric Power Systems Research 68, pp. 167-173, 2004. [ Links ]
[14] Teng, A. et al., Planning approaches for the strategic placement of passive harmonic filters in radial distribution networks, IEEE Transactions on Power Delivery, 22 (1), pp. 347-353, 2007. [ Links ]
[15] Abbas-Taher, S., Karimian, K. and Hasani, M., A new method for optimal location and sizing of capacitors in distorted distribution networks using PSO algorithm, Simulation Modelling Practice and Theory, 19, pp. 662-672, 2011. [ Links ]
[16] Chang, G.W. et al., Fuzzy logic and immune-based algorithm for placement and sizing of shunt capacitor banks in a distorted power network, IEEE Transactions on Power Delivery, 26 (4), pp. 2145 - 2153, 2011. [ Links ]
[17] Chang, G.W., Chu, S. Y. and Wang, H.L., A new method of passive harmonic filter planning for controlling voltage distortion in a power system, IEEE Transactions on Power Delivery, 21 (1), pp. 305-312, 2006. [ Links ]
[18] Ghiasi, M., Rashtchi, V. and Hoseini, H., Optimum location and sizing of passive filters in distribution networks using genetic algorithm, International Conference on Emerging Technologies IEEE-ICET, Rawalpindi, Pakistan, 2008. [ Links ]
[19] Zhang R., Yuhong, L. and Yaohua, L., Optimal parameters for filter using improved genetic algorithms. Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing, China, 2008. [ Links ]
[20] Amavel-Luiz, A. and Cardoso-Filho, B.J, Minimum reactive power filter design for high power converters, 13th International Power Electronics and Motion Control Conference, EPE-PEMC, 2008. [ Links ]
[21] Chang, G.W. et al., Passive harmonic filter planning in a power system with considering probabilistic constraints, IEEE Transactions on Power Delivery, 24 (1), pp. 208-218, 2009. [ Links ]
[22] Hong Y.Y. and Chiu, C.S., Passive filter planning using simultaneous perturbation stochastic approximation, IEEE Transactions on Power Delivery, 25(2), pp. 939-946, 2010. [ Links ]
[23] Yue, H. et al., Multi-objective optimal power filter planning in distribution network based on fast nondominated sorting genetic algorithms, in: Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), 2011 4th International Conference on IEEE, pp. 234-240, 2011. [ Links ]
[24] Shengqing, L. et al., Multi-objective optimal design for passive power filters in hybrid power filter system based on multi-island particle swarm optimization, 2012 IEEE 7th International Power Electronics and Motion Control Conference - ECCE Asia, Harbin, China. 2012. [ Links ]
[25] Junpeng, J.I, Haiwa, L., Guang Z., and Jinggang Z., The multi-objective optimization design of passive power filter based on PSO, IEEE Power and Energy Engineering Conference (APPEEC), 2012 Asia-Pacific, pp. 1-4, 2012. [ Links ]
[26] Nassif, A.B. and Xu, W., Passive harmonic filters for medium-voltage industrial systems: Practical considerations and topology analysis, IEEE 39th North American Power Symposium (NAPS 2007), pp. 301-307, 2007. [ Links ]
[27] Nassif, A. B., Xu, W. y Freitas, W., An Investigation on the Selection of Filter Topologies for Passive Filter Applications. IEEE Transactions on Power Delivery, 24(3), 2009. [ Links ]
[28] Kawann, C. y Emanuel, A.E., Passive Shunt Harmonic Filters for Low and Medium Voltage: A Cost Comparison Study, IEEE Trans. on Power Systems, 11(4), 1825-1831, 1996. [ Links ]
[29] Agência Nacional de Energia Elétrica (ANEEL), Procedimentos de Distribuição de Energia Elétrica no Sistema Elétrico Nacional - Prodist: Módulo 8 - Qualidade da Energia Elétrica. 2010. [ Links ]
[30] IEEE Std. 1531-2003, IEEE Guide for Application and Specification of Harmonic Filters, 2003. [ Links ]
[31] Frutos, Mariano et. al, Evolutionary multi-objective scheduling procedures in non-standardized production processes, Dyna: Rev. de la Fac. Nacional de Minas, 79(172), 2003. [ Links ]
[32] Seshadri, A., NSGA-II source code, Available at: http://www.mathworks.com/ matlabcentral/fileexchange/10429-nsga-ii-a-multi-objective-optimization-algorithm/ content/NSGA-II/. [ Links ]
M. S. Santos-Azevedo, graduado en Matemática en 1985, en Procesamiento de Datos en 1999, ambos de la Universidad Federal de Amazonas, Brasil y MSc. en Ingeniería Electrica en 2006, de la Universidad Federal de Campina Grande, Brasil. Es profesor asistente de la Universidad del Estado de Amazonas (UEA), Brasil. Tiene experiencia en el área de Sistemas Computacionales con énfasis en Modelos Analíticos y simulación de sistemas. Es coordinador de proyectos en ITEGAM.
I. Pérez-Abril, graduado en Ingeniería Eléctrica en 1984, Dr. en Ingeniería Eléctrica en 1995, ambos de la Universidad Central de Las Villas, Cuba. Es director del Centro de Estudios Electroenergéticos y profesor de Sistemas Eléctricos Industriales de la Universidad Central de Las Villas, Cuba. Sus área de interés incluyen: calidad de la energía y análisis, diseño y optimización de sistemas eléctricos de potencia.
C. de León-Benítez, graduado en Ingeniería Eléectrica en 1983, Dr. en Ingeniería Eléctrica en 2002, ambos de la Universidad Central de Las Villas, Cuba. Es director del Centro de Estudios Electroenergéticos y profesor de Sistemas Eléctricos Industriales de la Universidad Central de Las Villas, Cuba. Sus áreas de interés incluyen: calidad de la energía y análisis, diseño y optimización de sistemas eléctricos de potencia.
J.Cabral-Leite, graduado en Matemática en 1987 de la Universidad Federal de Rondónia (UNIR), Brasil; en Ingeniería en Producciones Eléctricas, en 2006 de la Fund Centro de Analise Pesq e Inov Tecnologica - FUCAPI, Brasil; MSc. en Ing. Industrial y en Sistemas en 2001, de la Universidad Federal de Santa Catarina (UFSC), Brasil y Dr. en Ing. Eléctrica en 2013, de la Universidad Federal de Pará (UFPA), Brasil. Es Director Presidente e investigador del Instituto de Tecnología y Educación Galileo de la Amazonía (ITEGAM), Brasil. Sus áreas de interés incluyen: calidad de la energía, análisis, diseño y optimización de sistemas eléctricos de potencia.
U. Holanda-Bezerra, graduado en Ingeniería Eléctrica en 1976 de la Universidad Federal de Pará (UFPA), Brasil. MSc. en Ingeniería Eléctrica en 1980, de la Universidad Federal Escuela de Itajubá (EFEI)-MG, Brasil y Dr. en Ingeniería Eléctrica en 1988, de la Universidad Federal de Rio de Janeiro (COPPE/UFRJ), Brasil. Es profesor de la Universidad Federal de Pará, Brasil, desde 1977. Actualmente es profesor en el área de Conversión de Energía. Sus áreas de interés: Seguridad, Calidad de la Energía y Energía Renovable.