Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.187 Medellín set-/out. 2014
https://doi.org/10.15446/dyna.v81n187.40991
http://dx.doi.org/10.15446/dyna.v81n187.40991
Monte Carlo simulation of epitaxial growth of GaInAsSb films
Simulación por el método de Monte Carlo del crecimiento de películas epitaxiales de GaInAsSb
Jheison Alejandro Morales a, Manuel Eduardo Ríos-Olaya b & Liliana Tirado-Mejía c
a Instituto Interdisciplinario de las Ciencias, Grupo de Optoelectrónica, Universidad del Quindío, Colombia. jamoralesv@uqvirtual.edu.co
b Instituto Interdisciplinario de las Ciencias, Grupo de Optoelectrónica, Universidad del Quindío, Colombia. merios@uniquindio.edu.co
c Instituto Interdisciplinario de las Ciencias, Grupo de Optoelectrónica, Universidad del Quindío, Colombia. litirado@uniquindio.edu.co
Received: November 26th, de 2013. Received in revised form: June 9th, 2014. Accepted: June 20th, 2014
Abstract
Material engineering finds an important support on simulation methods. The study of semiconductors growth techniques through simulation allows the determination of the influence of some growth parameters on the film properties. Experimentally, the variations of these parameters are difficult due to the high experimental demands and expenses. In this work we present the numerical simulation of the epitaxial growth of GaInAsSb by three methods. Devices based on this semiconductor material are thermophotovoltaic generators. The solid-on-solid approximation was used, considering the unit cell formed by the four constituent elements, in the establish proportions according to the choose stoichiometry. Through the Kinetic Monte Carlo method we obtained a high coincidence between the simulated film morphology and the obtained in the experimentally grown films.
Keywords: Computational simulation; Kinetic Monte Carlo; Ising model; liquid phase epitaxy; GaInAsSb
Resumen
El estudio de la fabricación de películas semiconductoras por la técnica de Epitaxia en Fase Líquida a través de métodos de simulación es un importante soporte en la ingeniería de estos materiales pues permite determinar la influencia de condiciones de crecimiento sobre las propiedades de las películas epitaxiales, variando a voluntad ciertos parámetros que experimentalmente conllevan exigentes condiciones de crecimiento y altos costos. En este trabajo se presenta la simulación mediante tres diferentes métodos, del crecimiento epitaxial del material GaInAsSb con interesantes aplicaciones en dispositivos de generación de energía termofotovoltaica. Se utilizó la aproximación de sólido sobre sólido suponiendo que la celda unitaria contiene los cuatro elementos precursores en proporciones correspondientes a la estequiometría seleccionada. Se determina que el método de Monte Carlo cinético arroja los mejores resultados, mostrando una buena coincidencia entre la morfología de las películas simuladas con la de películas fabricadas por esta técnica experimental.
Palabras clave: Simulación Computacional; Monte Carlo Cinético; modelo de Ising; Epitaxia en Fase Líquida; GaInAsSb.
1. Introducción
Uno de los elementos principales que han intervenido en el desarrollo de los nuevos materiales utilizados en la electrónica y de los nuevos dispositivos diseñados y fabricados, ha sido el perfeccionamiento de las técnicas de fabricación de capas semiconductoras. Las propiedades electrónicas y ópticas de los dispositivos dependen fuertemente de las características estructurales y de cristalinidad que presenten las capas, y por lo tanto, dependen del control sobre los átomos, moléculas o películas que sea permitido por la técnica de crecimiento utilizada. Es así como las técnicas de fabricación de capas epitaxiales buscan garantizar la formación de capas con un ordenamiento atómico que replica la cristalinidad del sustrato en un crecimiento ordenado (epy: sobre y taxis: orden). Existen varias técnicas de fabricación con la característica mencionada que se diferencian entre sí por la fase en la cual se tiene el material precursor. Por ejemplo, la epitaxia por haces moleculares, en la que los átomos llegan al sustrato a partir de una fase gaseosa, y la epitaxia en fase líquida (EFL), en donde se tiene una solución líquida precursora y a partir de ahí se obtiene el material para formar la fase sólida.
El principio de la técnica de EFL es inducir la formación de la fase sólida sobre un sustrato cristalino, a partir de una solución líquida saturada, cuando se baja la temperatura. A través del diagrama de fases se determina la temperatura a la cual se tiene en equilibrio de fases la solución. Los mecanismos de solidificación que se dan en el proceso dependen principalmente de la rampa de enfriamiento, la calidad superficial del sustrato y la temperatura de contacto. Estos parámetros rigen el posible comportamiento de los adátomos, como es difusión sobre la superficie del sustrato, adsorción y desorción, dando como resultado formaciones particulares de capas, de escalones y de islas coalescentes. En cuanto a la estequiometría de la película, sobre el sustrato se depositan los elementos químicos tal que se forma el compuesto con su estructura cristalina característica. Teniendo en cuenta esta consideración, la simulación en este trabajo se propone como la deposición de unidades conformadas por una molécula neutra, en la aproximación conocida como Sólido sobre Sólido [1]. Por ejemplo, para el Ga1-xInxAsySb1-y se considera la unidad compuesta por los cuatro elementos en una única relación estequiométrica [2-4]. En el crecimiento epitaxial por la técnica EFL, los elementos químicos difunden de la solución líquida hacia el sustrato en un proceso de difusión unidimensional.
La simulación del proceso de crecimiento puede realizarse por diferentes métodos entre los cuales aparecen como dos grandes pilares el método de Monte Carlo (estocástico) y la dinámica molecular (determinista) [5-7], siendo aplicables en situaciones antagónica: mientras que el primero permite simular sistemas de muchas partículas a un costo computacional relativamente bajo, pero sacrificando precisión, el segundo es de alta precisión con alto costo computacional, razón por la cual es útil en sistemas pequeños [8-10]. Una aparente desventaja del método de Monte Carlo con respecto al otro método radica en su incapacidad para describir la evolución del sistema en el tiempo; sin embargo existen variaciones al método de Monte Carlo que suplen esta deficiencia como es el caso del Monte Carlo cinético, que asocia el tiempo con la probabilidad de ocurrencia de un movimiento [11]. En este trabajo se toman el número de partículas que se depositan en la unidad de tiempo sobre el sustrato como un parámetro determinístico, mientras que su ubicación sobre el sustrato y los procesos de los adátomos se toman aleatorios. Estas consideraciones llevan a la aparición de sitios de nucleación que crecen formando islas que finalmente se unen para constituir la capa epitaxial. Se simula la parte correspondiente a la interfaz, partiendo de una solución cuya unidad de deposición es el compuesto estequiométrico, y se obtienen diferentes morfologías de acuerdo al método utilizado, siendo el método de Monte Carlo cinético el que presenta resultados de morfología con mayor similitud a las películas fabricadas experimentalmente.
2. Metodología
Se simula la formación de la película sobre un sustrato, considerando que la unidad que se deposita es una celda formada por los cuatro elementos constitutivos, en una proporción determinada. Se utilizan tres modelos, el primero de los cuales se basa en el modelo de Ising con Metropolis Monte Carlo [1], el segundo incluye la interacción entre partículas utilizando el potencial de Lennard-Jones [12], y el tercero incluye la difusión pero no la interacción de partículas [5]. Para los dos últimos casos se utiliza Monte Carlo cinético. Las diferentes propuestas de simulación se basaron en un número establecido de partículas que se depositan en sitios escogidos aleatoriamente.
Se consideran como parámetros de entrada las temperaturas del sustrato y de la solución, y la razón de deposición, relacionada con el número de partículas para ubicar, por paso. También se definen el tamaño de la retícula y el número de pasos de Monte Carlo. En este trabajo se utilizó un tamaño de retícula de 1000x1000 y el rango para la temperatura fue de 300K a 600K, en pasos de 50K. En todos los casos se utilizó un rango para la razón de deposición que va de uno a diez, en pasos de uno, y para las energías de la superficie plana y de migración se tomaron los valores -3.7 eV y 0.7 eV, respectivamente.
El procedimiento para el primer caso está ampliamente descrito en la literatura, en el que se hace la equivalencia entre la orientación del espín -arriba o abajo- y la ocupación de la retícula -ocupado o vacío-. Se observa la formación de islas con una alta rugosidad. Para el caso del potencial asociado a la retícula, se consideran los primeros próximos vecinos actualizando en cada paso el potencial. En esta simulación se incluye la fluctuación térmica asociada a la difusión de los adátomos, lo que repercute en la morfología de la película resultante. En el Monte Carlo cinético, en términos generales, se ubican aleatoriamente las partículas en la retícula, se analiza la ocupación de sitios próximos vecinos y se clasifican de acuerdo al número de ellos, determinando así las diferentes probabilidades de difundir que tendrá la partícula. Este último algoritmo presenta diversas ventajas frente a los otros modelos, ya que permite estudiar la dinámica del crecimiento tal como se da físicamente el proceso, y además sin recurrir a una matriz de potenciales, haciéndolo más eficiente computacionalmente. Los resultados obtenidos utilizando los tres métodos muestran patrones típicos de películas epitaxiales.
En este trabajo se utiliza la aproximación Sólido sobre Sólido (SOS por sus siglas en inglés) en la que se supone que la superficie está constituida por bloques de construcción o celdas unitarias que se apilan unas sobre otras, permitiendo vacancias o lugares vacíos que se presentan experimentalmente en las interfaces. Cada sitio de la retícula puede estar ocupado por varias celdas unitarias, y esto puede interpretarse como múltiples capas atómicas. Los procesos considerados sobre la superficie, definidos por su probabilidad, son la deposición de átomos nuevos, la desorción de átomos superficiales y la difusión de átomos en la superficie. Además, en el movimiento de los átomos que se depositan y que difunden se consideran cinco eventos relacionados con ocupación de los sitios vecinos y definidos por sus probabilidades de adhesión. Existen varios modelos SOS entre los que se destacan los modelos DGSOS (Discrete Gaussian Solid on Solid), ASOS (Absolute value Solid on Solid) y el modelo XY [1], que comparten la característica de ser interpretados como modelos bidimensionales de espín distribuidos en una retícula, pero considerando la energía potencial de los vecinos y no su orientación del momento magnético. Es decir, un sitio de la retícula puede tomar valores dentro de un conjunto discreto y la energía de interacción es invariante bajo cambios globales.
En muchos casos, la simulación del crecimiento de materiales cristalinos se hace utilizando modelos basados en retículas, obviando las posibles diferencias entre los parámetros de red de la película y el substrato sobre la cual se hace crecer. Estas diferencias provocan compresiones y estrés sobre el cristal, resultando en dislocaciones y otro tipo de defectos que son imposibles de simular a través de modelos SOS [13]. Esta consideración se tiene en cuenta al decidir qué características tendrá el modelo con miras a una aproximación más precisa de los fenómenos simulados. Un criterio que permite decidir entre el uso de modelos basados en retícula y sin retícula resulta del análisis de la coincidencia en los parámetros de red sustrato-película [14]:
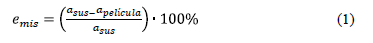
Si emis es menor al 8%, el sistema es un candidato razonable para ser simulado con un modelo basado en retícula. En epitaxia en fase líquida se busca llevar este valor hasta el 3%.
Las consideraciones y aproximaciones utilizadas en las tres diferentes propuestas de simulación se presentan a continuación.
2.1. Metropolis Monte Carlo con modelo de Ising
Utilizando los modelos propuestos de sólido sobre sólido, la primera aproximación consiste en utilizar el método Metropolis para obtener el estado final de la película a determinada temperatura sin conocer la evolución temporal de ésta. Este algoritmo se fundamenta en el modelo de Ising, en el cual se hace la analogía entre el estado del espín (arriba o abajo) con la ocupación de un sitio (ocupado o vacío). Se consideran tres posibles movimientos: adsorción, desorción y desplazamiento de la partícula, que puede interpretarse como difusión. El criterio de aceptación está dado por el paso de Monte Carlo definido por Metropolis:

siendo H el hamiltoniano del sistema, J la energía de interacción, sx y sy indican si los sitios x e y de la retícula están ocupados. El paso de Monte Carlo se define por la expresión:

en donde, para decidir si finalmente aceptar el movimiento o no, se genera un número aleatorio con distribución uniforme y se compara con el valor dado por la distribución exponencial: si el número es mayor entonces se acepta el proceso, en caso contrario se rechaza [5].
2.2. Monte Carlo cinético con potenciales
Para este modelo se tiene en cuenta la interacción entre las partículas y se asocia a cada punto de la retícula un valor de energía potencial. Las variaciones de energía potencial en cada uno de los sitios están basadas en el potencial de Lennard-Jones, teniendo en cuenta la influencia de una partícula frente a los primeros y segundos vecinos. En cada paso de la simulación se depositan N adátamos en sitios aleatorios de la retícula y una vez ubicados, se revisa cada sitio para determinar qué tipo de movimiento se realizará. Se consideran cuatro posibles casos: la desorción, es el caso cuando la partícula ya adherida se desprende de la superficie; la migración o difusión de la partícula por la superficie; la incorporación o adsorción de la partícula a la superficie; y el caso cuando no sucede nada, es decir, cuando la partícula permanece en su posición. Cada movimiento está asociado a umbrales de energía potencial. A diferencia de la simulación previa, en esta simulación es posible realizar varios eventos a la vez, teniendo en cuenta que la frecuencia con la que se revisa cada sitio está relacionada con un intervalo de tiempo en función de la temperatura y en el cual se garantiza que ocurrirá por lo menos algún tipo de movimiento de los mencionados anteriormente. Al considerar los movimientos térmicamente activados, cada celda de la retícula tiene fluctuaciones de energía asociadas a la temperatura estando estas variaciones regidas por la distribución de Boltzmann. Una vez recorrida toda la retícula, se almacenan los movimientos correspondientes a cada sitio en un arreglo en el cual se desordena aleatoriamente para evitar algún tipo de "estructura artificial" en la evolución de la simulación debido al orden con el que se explora la superficie. Una vez actualizados los potenciales en cada sitio de la retícula, se incrementa el tiempo de simulación, siendo E la energía del sitio (i,j) y R un número aleatorio con distribución uniforme.
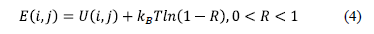
Cada que una partícula se adsorbe, se actualizan los potenciales de los sitios vecinos (primeros y segundos vecinos); la desorción se simula eliminando la partícula de la superficie y revirtiendo su efecto sobre los potenciales en los sitios vecinos. La migración se considera una desorción y una adsorción en sitios inmediatamente vecinos. La incorporación supone que la partícula se introduce dentro de la película y desaparece de la superficie, manejándose de igual manera que la desorción.
La comparación de la energía obtenida a partir de la ec. (4) en cada sitio con los umbrales de energía que debe vencer la partícula para que se dé uno de los movimientos mencionados, se muestra en la Tabla 1. Los subíndices i y m representan la incorporación y la migración, respectivamente, y la U0 es la energía de Lennard-Jonnes.
Para el caso de la desorción, su tasa se define según la ec. (5) en términos del número de enlaces que tenga la partícula con otras (n), la energía de cada enlace (j) y el período de vibración de la partícula ligada al sustrato (to). Para la adsorción simple, con un período de aproximadamente 10-12 s, cada que se aleja la partícula en el ciclo de vibración se considera como un intento de desorción.

Para la migración, ya sea desorción o difusión, la ocurrencia depende de la probabilidad relativa de cada evento. Aquí, la disponibilidad de más de un sitio para la migración se determina por el número de sitios vecinos disponibles. Cuanto mayor es este número, menos profundo es el pozo de potencial, más pequeña la barrera de energía y por lo tanto aumenta la probabilidad de la migración a ese sitio. La ec. (6) determina la posibilidad de ocurrencia de un proceso de difusión, tanto para el modelo Monte Carlo cinético como para el Monte Carlo basado en potenciales.
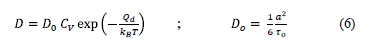
Siendo CV la concentración de las vacancias, a la distancia entre partículas, 1/6 es un factor que depende de la estructura cristalina y Qd es la energía de migración [15]. En las simulaciones realizadas se asumió que el número de sitios posibles a los cuales puede migrar la partícula es constante y no depende de la temperatura. Solo se consideran los primeros vecinos, como sitios posibles. Un salto a una de estas vacancias se considera un evento de difusión. Se utilizaron para Ui y U0 los valores -0.1 y -3.7 eV, respectivamente. El valor de Um se obtiene de la suma de U0, Qd y j, tomando Qd el valor de 0.7 eV.
2.3. Monte Carlo cinético
Una forma de validar los algoritmos es utilizando la teoría de difusión en la que se incluyen los proceso de deposición de átomos nuevos, desorción de átomos superficiales y difusión de átomos en la superficie. Para el caso de difusión superficial, se supone que se tiene una colección de partículas moviéndose en una superficie. En el modelo de gas reticular (LGM lattice gas model), la superficie se modela por una retícula donde cada sitio se marca como ocupado (ni=1) o no ocupado (ni=0). Una aproximación sencilla se hace considerando cada átomo como un "caminante aleatorio" que está limitado por la presencia de otros átomos en la superficie. La difusión consiste en saltos aleatorios hacia sitios vecinos no ocupados; si todos los sitios vecinos están ocupados, el átomo se elimina (desorción). Si la concentración de átomos es muy baja entonces es poco probable encontrar un sitio vecino ocupado, y en este caso el camino medio d es:

para r(t) el vector posición en un tiempo t. Cuando la concentración incrementa se hace más difícil para los átomos encontrar un sitio vecino desocupado y por lo tanto el desplazamiento medio cuadrático de los átomos disminuirá con respecto al caso de baja concentración, según la ecuación de difusión:

donde P(r,t) es la probabilidad de que un átomo esté en la posición r en el tiempo t. En el modelo LGM el coeficiente de difusión D, según ec. (6), está asociado a la concentración de átomos en la superficie [16]. El modelo anterior no toma en cuenta los efectos de la temperatura ni la interacción mutua entre átomos difundiendo y está basado en la llamada teoría de transición de estado, que relaciona dos estados separados por una barrera de energía potencial. La tasa de saltos para cada átomo depende únicamente de sus vecinos cercanos, por lo tanto todos los átomos con igual número de vecinos difunden igual. De nuevo, esto permite agrupar los átomos en cinco diferentes grupos de acuerdo al número de vecinos cercanos. Mientras que en el algoritmo de Metropolis se prueba la aceptación de un evento, en Monte Carlo cinético (KMC por sus siglas en inglés) se escoge el tipo de movimiento, es decir, el tipo de evento seleccionado siempre ocurre (algoritmo n-fold). Para cuando se tiene un total de partículas N y una disponibilidad de movimiento a (grupo de acuerdo al número de vecinos) la razón de deposición está descrita por:

Al multiplicar las razones individuales por el número de átomos que difunden con la misma razón, se obtienen las probabilidades para cualquier tipo de difusión.

En el proceso se genera un número aleatorio r e [0,Rtot] y se selecciona el evento correspondiente; si r < N0k0, se selecciona el evento 0, si N0k0 < r < N1k1 se selecciona el evento 1, y así sucesivamente. Luego se escoge un átomo del grupo y se mueve en dirección aleatoria. En este modelo es posible que un átomo se ubique sobre otro, y el que queda debajo es excluido de la lista de elegibles ya que no puede difundir. Si el átomo de arriba "salta" otra vez, el átomo se incluye nuevamente en la lista. Después de actualizar los grupos se deben revisar los sitios iniciales y finales ya que es posible que un átomo quede cubierto, como consecuencia del salto. Al ocurrir la adhesión de nuevos átomos que se depositan aleatoriamente en la retícula a una razón constante F (monocapas por segundo mc/s), siendo LxL las dimensiones de la retícula, se suman los eventos considerando la adhesión y la difusión.

Cuando el evento "deposición" es seleccionado, se escoge aleatoriamente uno de los sitios de la retícula y se suma un átomo. El incremento del tiempo físico debido a la deposición se calcula de acuerdo la expresión:

La cuantificación de los resultados obtenidos en las simulaciones se realiza a través del coeficiente de rugosidad (Rf). El Rf mide la textura de la superficie de la película a través del rms de las alturas; cuando r = 0 se interpreta como una superficie totalmente plana. Su definición matemática es:

siendo S el número de sitios en la retícula, hi la altura de cada sitio y h el valor medio de la altura.
En general, para calcular cualquier observable físico es necesario obtener el promedio de varias simulaciones independientes ya que el sistema no se encuentra en equilibrio.
3. Resultados
En este trabajo se simuló el crecimiento epitaxial utilizando el modelo de Ising, el Monte Carlo cinético basado en potenciales y en el algortimo n-fold, para establecer las dependencias de la morfología con los parámetros de crecimiento temperatura y razón de deposición. Estos últimos son los parámetros de entrada para los algoritmos. El resultado de la simulación es una superficie que muestra la configuración de las partículas a diferentes instantes de tiempo y su rugosidad. Teniendo en cuenta que en la ref. [17] se reporta una dependencia lineal de la rugosidad con el aumento del tamaño de la retícula, este parámetro se consideró constante.
A continuación se presentan los resultados obtenidos de las simulaciones con los tres métodos escogidos. Para Metropolis, aunque se observa la formación de islas alrededor de los sitios de nucleación similares a las observadas en el proceso experimental de fabricación (Fig. 1); no se calcula la rugosidad por ser éste un parámetro estático puesto que este algoritmo no describe la evolución del sistema según los criterios físicos del crecimiento.
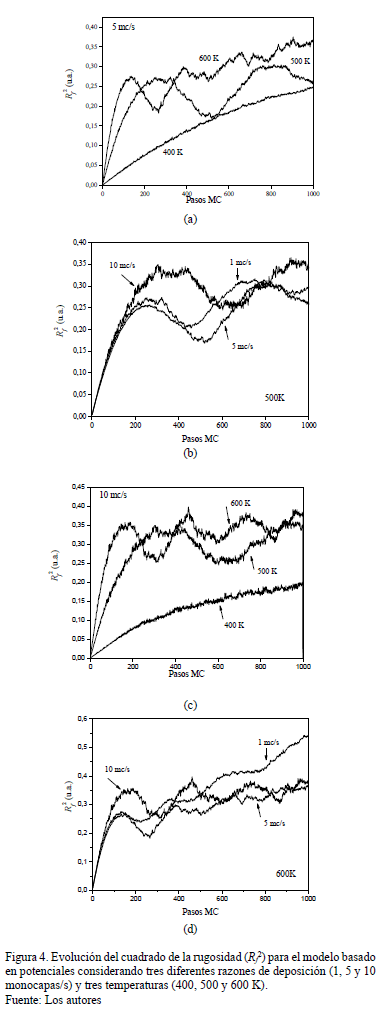
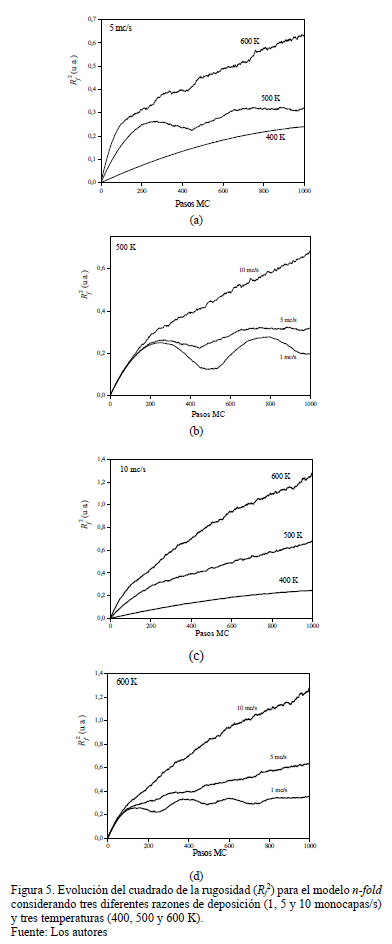
En los resultados utilizando matriz de potenciales y n-fold, se dejan como parámetros constantes el tamaño de la retícula, el número de pasos (relacionado con el tiempo de crecimiento) y las energías de salto. Los parámetros que se varían son la temperatura y la razón de deposición. En las Figs. 2 y 3 se presentan algunas imágenes del estado de la película a distintos momentos del crecimiento utilizando el modelo basado en potenciales y el modelo basado en el algoritmo n-fold, respectivamente.
La comparación de estos resultados muestra que a través del método de los potenciales se obtiene la formación de granos epitaxiales, que coalescen formando películas con morfología similar a las obtenidas experimentalmente. Cuando se utiliza este método se considera que cada unidad depositada es una celda formada por los cuatro elementos constituyentes, en una relación estequiométrica. Las simulaciones realizadas permiten encontrar la morfología superficial, descrita a través de la rugosidad. Se observa cómo evoluciona la rugosidad de la película en el tiempo, y su dependencia con la temperatura de deposición. Analizando este comportamiento se puede extrapolar para predecir el resultado obtenido de un crecimiento, bajo ciertas condiciones de temperatura y concentración de la solución. Aunque la imagen de la película obtenida experimentalmente y la película simulada presentan similitudes en su configuración, las diferencias observadas se atribuyen a que la simulada no ha presentado una completa coalescencia de los agregados. Un aumento en los pasos de MC podría representar de una manera más fiel el resultado experimental.
De los resultados obtenidos referentes a la rugosidad, vemos que la temperatura es un factor determinante en el proceso de difusión de los adátomos y que está vinculada a la razón de deposición. La temperatura favorece la difusión para formar agregados pero, un incremento de ella para una misma razón de deposición, incrementa la rugosidad por el proceso de desorción. El aumento de la razón de deposición disminuye el tiempo de difusión, generando una mayor rugosidad. Cuando se consideran independientemente altas temperaturas, el resultado es una interfaz rugosa mientras que a bajas temperaturas el resultado es una interfaz suave y rígida. Del análisis de las figuras presentadas a continuación se observa un compromiso entre temperatura y razón de deposición.
Se observa en las Figs. 4a, 4c, 5a y 5c para ambos modelos la fuerte influencia de la temperatura para los primeros estadios de crecimiento (100 pasos), mientras que el crecimiento a una misma temperatura (Figs. 4b, 4d, 5b y 5d) no depende de la razón de deposición en los estadios iniciales (por debajo de los 100 pasos).
En el modelo n-fold, para una alta razón de deposición (10 mc/s) no se alcanza la coalescencia de las islas y por lo tanto la rugosidad aumenta monótonamente con los pasos, siendo este efecto más evidente a alta temperatura (600 K). Para una menor razón de deposición (1 mc/s) se observan las oscilaciones asociadas a la formación de capas completas favoreciéndose con altas temperaturas mientras que según el modelo basado en potenciales, sucede lo contrario (Fig. 4.d) describiendo de una manera más cercana el resultado experimental. Si la temperatura no es lo suficientemente alta (400K), los adátomos no tienen mucha oportunidad de difundir y reacomodarse, y por lo tanto se observa una formación lenta de la capa y un crecimiento lento de la rugosidad. Es decir, mientras que en el modelo basado en el algoritmo n-fold crece rápidamente la rugosidad a altas razones de deposición y a altas temperaturas, en el modelo basado en potenciales, se observa cómo la rugosidad alcanza un valor nominal y oscila alrededor de éste debido a la formación de capas (Figs. 4.c y 5.c). Esto muestra que el modelo basado en potenciales permite la coalescencia de islas y la reacomodación de partículas debido a movimientos termoactivados. En general, la rugosidad es mayor para el modelo n-fold que para el de potenciales, debido a la forma de las islas: mientras en el primero los bordes no estan bien definidos, en el segundo modelo la forma de las islas es más compacta.
Uno de las principales dificultades al usar el método de Monte Carlo cinético radica en la necesidad de especificar las tasas de ocurrencia de los eventos, o las barreras de energía relacionadas a cada evento, antes de realizar la simulación. Este método puede ser usado cuando en lugar de la cinética de la termodinámica de equilibrio, dominan los cambios estructurales o de composición en el sistema. Por su parte, el algoritmo de Metropolis tiene la particularidad de generar configuraciones aleatorias de acuerdo a las distribuciones estadísticas deseadas. Aunque permite conocer la configuración final del sistema y estudiar las propiedades de equilibrio (reconstrucción y segregación de la superficie), no contempla el tiempo de ocurrencia de los procesos, resultando en una imposibilidad de estudiar la evolución del sistema. Una diferencia fundamental entre el algoritmo Metropolis y los otros dos métodos considerados en este trabajo (MC cinético y basado en potenciales) radica en la forma como se decide aceptar o rechazar un movimiento. Metropolis se basa en la diferencia de energía entre los estados, mientras Monte Carlo Cinético utilizan tasas que dependen de las barreras de energía entre los estados. Monte Carlo basado en potenciales, al igual que el Monte Carlo cinético, comparten la ventaja de considerar únicamente un pequeño número de reacciones elementales, aumentando la velocidad de los cálculos, a expensas de una menor precisión y menor poder de predicción al no contemplar situaciones que, aunque tienen muy baja probabilidad de ocurrencia, pueden suceder.
Los algoritmos desarrollados nos permiten variar condiciones de crecimiento en el proceso de epitaxia en fase líquida como la razón de deposición asociada a la rampa de enfriamiento, y determinar la dependencia de la morfología con estos parámetros de fabricación.
4. Conclusiones
La simulación del crecimiento epitaxial sobre sustratos monocristalinos se realiza a partir de la consideración de la difusión de celdas unitarias en la superficie del sustrato, semejantes a adátomos. La composición de la celda unitaria se considera fija y los procesos en la superficie del sustrato son de difusión, adsorción y desorción. Se realizaron simulaciones utilizando el algoritmo de Metropolis y el Monte Carlo cinético, con el algoritmo n-fold y el método de potenciales.
El método de Monte Carlo cinético, basado en el algoritmo n-fold no muestra un comportamiento que se aproxime al observado experimentalmente, en cuanto a su dependencia con la temperatura. Aunque aparecen núcleos que forman islas que coalescen, su morfología muestra patrones característicos que bien podrían nombrarse como de tipo fractal alejada de las formas observadas, que son mucho más compactas. Este comportamiento aparentemente anómalo está relacionado también con la energía de barrera para la difusión. Sin embargo, las pruebas realizadas bajo las mismas condiciones y configuraciones, con el algoritmo basado en potenciales muestran comportamientos ligeramente diferentes y más aproximados al comportamiento observado en el experimento físico, presentando coalescencia de islas compactas.
Como se observa en las gráficas, en condiciones apropiadas la rugosidad presenta un comportamiento periódico indicando en los puntos más bajos la formación de monocapas completas, y en los máximos relativos, el proceso inicial de formación. La rugosidad puede ser divergente en casos en los cuales la razón de deposición es muy alta e impide a los adátomos su difusión al ser cubiertos rápidamente por otros adátomos antes de alcanzar una ubicación de menor energía. La temperatura puede ser también un factor importante para la divergencia de la rugosidad, pues al tener mayor energía, los adátomos pueden superar fácilmente las barreras de energía interpuestas por sus vecinos, favoreciendo la desorción y afectando así la permanencia de las islas.
Los algoritmos se escribieron en forma de librerías para su uso con el software GNU Octave, todas las simulaciones se ejecutaron en máquinas sobre GNU Linux, distribución Ubuntu. Se realizaron pruebas con GNU Octave corriendo sobre MS Windows, sin ningún inconveniente evidenciando la portabilidad de las librerías.
Agradecimientos
Este trabajo fue financiado por la Universidad del Quindío, a través del proyecto 589, y por Colciencias a través del programa de Jóvenes Investigadores.
Referencias
[1] Pinn, K. Montecarlo studies of Ising model interfaces and Solid-on-Solid models [Habilitationsschrift], Departamento de Física, Universidad de Münster (WWV), 1995. [ Links ]
[2] Kumar, A. and Dutta. P.S., Liquid phase epitaxial growth of lattice mismatched InSb, GaInAs and GaInAsSb on GaAs substrates using a quaternary melt, J. of Crys. Growth, 310, pp. 1647-1651, 2008. [ Links ]
[3] Rakovics, V., Tóth, A.L., Podor, B., Frigeri, C., Balázs, J. and Horváth, Z.E., Liquid phase epitaxy growth and characterization of Ga1-xInxAsySb1-y quaternary alloys, Materials Science and Engineering, B (91-92), pp. 83-86, 2002. [ Links ]
[4] Denisova, I.A., Lakeenkova, V.M., Mazhorovab, O.S., Popov and Yu, P., Numerical study for liquid phase epitaxy of CdXHg1-XTe solid solution, J. of Crys. Growth, 245, pp. 21-30, 2002. [ Links ]
[5] Carmona, J. and Hoyos B. An improved primitive model for hydrated ions near a metal surface: Monte Carlo simulations. DYNA, 77 (162), pp. 191-203, 2010. [ Links ]
[6] Venables J., Introduction to surface and thin film processes. Cambridge University Press, 2010. [ Links ]
[7] Gilmer, G.H., Huand, H., de la Rubia, T.D., Torre, J.D. and Baumann, F., Lattice Monte Carlo models of thin film deposition. Thin Solids Films, 365 (2), pp. 189-200, 2000. [ Links ]
[8] Landau D., Binder K., A Guide to Monte Carlo simulations in statistical physics. Cambridge University Press, 2005. [ Links ]
[9] Battaile C., The kinetic Monte Carlo method: Foundation, implementation, and application. Computer Methods in Applied Mechanics and Engineering, 197 (41-42), pp. 3386-3398, 2008. [ Links ]
[10] Baskaran A. and Smereka P., Mechanisms of Stranski-Krastanov growth. J. of Appl. Phys., vol.111, pp. 044321-044321-6, 2012. [ Links ]
[11] Kratzer, P., Monte Carlo and kinetic Monte Carlo methods - A tutorial, en: Grotendorst, J., Attig, N., Blügel, S. and Marx, D., Eds. Multiscale simulation methods in molecular sciences, Institute for Advanced Simulation, Forschungszentrum Jülich, NIC Series, Vol. 42, 2009. [ Links ]
[12] Heinbockel, J.H., Outlaw, R.A. and Walker, G.H., A potential-energy scaling model to simulate the initial stages of thin-film growth, NASA Technical Paper 2102, 37 P., 1983. [ Links ]
[13] Biehl, M. and Much, F., Off-lattice kinetic Monte Carlo simulations of Stranski-Krastanov-like growth. Advanced Research Workshop on Quantum Dots: Fundamentals, Applications, and Frontiers. NATO, Proceedings to be published by Kluwer, 2003. [ Links ]
[14] Voter, A., Introduction to the kinetic Monte Carlo Method, [Online], [fecha de consulta: 6 de noviembre de 2013], Available at: http://www.ipam.ucla.edu/publications/matut/matut_5898_preprint.pdf [ Links ]
[15] Sato, K., Takizawa, S. and Mohri, T., On-the-fly kinetic Monte Carlo simulation of atomic Diffusion in L10 structure, Materials Transactions, 52 (3), pp. 391-396, 2011. [ Links ]
[16] Shell, M., CHE210D Principles of modern molecular simulation methods. Universidad de California, [Online], [fecha de consulta: 6 de noviembre de 2013], Available at: http://www.engr.ucsb.edu/~shell/che210d/ [ Links ]
[17] Gangshi, H., Xinyu, Z., Orkoulas, G. and Christofides, P.D., Multiscale modeling and control of porous thin film growth, in: William S. Levine, The Control Handbook, Second Edition, CRC Press, pp. 13.1-13.17, 2010. [ Links ]
J. A. Morales, graduado de Ingeniero Electrónico con calificación meritoria en 2014, de la Universidad del Quindío, Colombia. Ha participado en proyectos de investigación financiados por la Universidad del Quindío y ha presentado resultados en el Simposio de Tratamiento de Señales, Imágenes y Visión Artificial STSIVA, Universidad de Antioquia SIU, en la X Escuela Nacional de Física de la Materia Condensada y en el XXV Congreso Nacional de Física. Realizó en el 2013 el curso "Modelado atomístico en la nanoescala: principios y aplicaciones", ofrecido por la Facultad de Ciencias Químicas de la Universidad Nacional de Córdoba, Argentina. Su perfil está orientado a la planificación, organización, dirección y control de procesos productivos y administrativos. Conocimientos en lenguajes de programación (Matlab, C, C++, Python, VHDL), sistemas operativos (Windows, Linux), metodologías de diseño, planificación y organización de planes de mantenimiento. Diseño de hardware utilizando lenguajes de descripción de hardware o de sistemas basados en microcontrolador.
M. E. Ríos-Olaya, recibió el título de Ingeniero Electrónico en 2008, en la Universidad del Quindío, Colombia. Desde el 2011 hasta el 2013 trabajó como joven investigador de Colciencias, en el Instituto Interdisciplinario de la Ciencia de la Universidad del Quindío, Colombia; específicamente en el grupo de investigación de Optoelectrónica, enfocándose en la simulación computacional de fenómenos físicos correspondientes a técnicas de caracterización óptica de materiales semiconductores y fabricación de dispositivos semiconductores por la técnica de Epitaxia en Fase Líquida. Actualmente es estudiante de Maestría en Ingeniería de Telecomunicaciones de la Universidad de Antioquia, Colombia, donde sus áreas de interés son las redes inalámbricas de área corporal WBAN, seguridad y fiabilidad de dispositivos electrónicos para telemedicina y algunos temas específicos en redes heterogéneas LTE-A.
L. Tirado-Mejía, es licenciada en Educación - Área Mayor Física, en 1984 de la Universidad del Quindío, Colombia. Obtuvo el título de MSc. en Ciencias - Física, en 1989 y Dra. en Ciencias - Física, en 2000, ambos de la Universidad del Valle, Colombia. Profesora de planta de la Universidad del Quindío desde 1998, actualmente en la categoría de Asociado. Hace parte del Grupo de Optoelectrónica y se ha desempeñado en el campo de la investigación en materiales semiconductores con énfasis en las propiedades ópticas y en fabricación de materiales semiconductores por la técnica de Epitaxia en Fase Líquida.