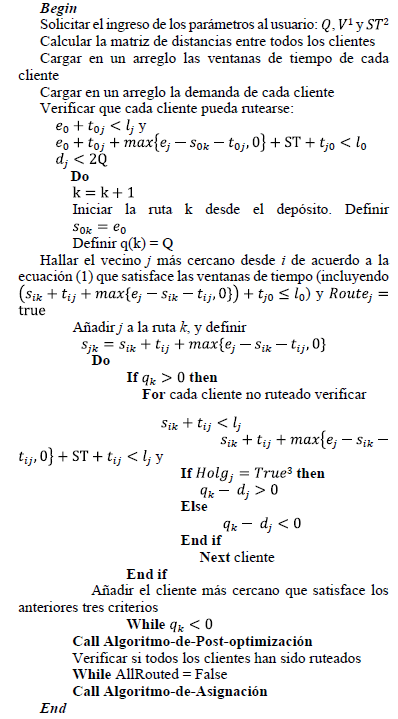Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.187 Medellín Sept./Oct. 2014
https://doi.org/10.15446/dyna.v81n186.46104
http://dx.doi.org/10.15446/dyna.v81n187.46104
An algorithm for the routing problem with split deliveries and time windows (SDVRPTW) applied on retail SME distribution activities
Un algoritmo para el problema de ruteo de vehículos con entregas divididas y ventanas de tiempo (SDVRPTW) aplicado a las actividades de distribución de PYMEs del comercio al por menor
Juan Sepúlveda a, John Wilmer Escobar b & Wilson Adarme-Jaimes c
a Universidad Nacional de Colombia, Bogotá, Colombia. jcsepulvedas@unal.edu.co
b Departamento de Ingeniería Civil e Industrial, Pontificia Universidad Javeriana Cali, Cali, Colombia. jwescobar@javerianacali.edu.co
c Departamento de Ingeniería de Sistemas e Industrial. Universidad Nacional de Colombia. wadarmej@unal.edu.co
Received: May 28th, 2014.Received in revised form: August 25th, 2014.Accepted: September 10th, 2014
Abstract
In this paper, particular conditions of retail trade SMEs was analyzed, identifying not enough financial resources for using powerful tools for solve vehicle routing problem (VRP). On the other hand, in literature revised could not be identified studies about application of current approaches for solving VRP in SMEs. Additionally because of high cost, commercial software do not fit investment budget of those companies. Through a simple insertion heuristic for VRP with split deliveries and time windows (SDVRPTW), developed on an accessible technology platform like Microsoft® Excel™, was validated that SDVRPTW is an appropriate approach for solving vehicle routing problem on retail trade SMEs. Computational results show that the heuristic proposed can reduce about 50% the fleet size.
Keywords: Routing, SME, Distribution, SDVRPTW, Split deliveries
Resumen
En este artículo, se analizan las condiciones particulares de las PYMEs del comercio al por menor, identificando recursos insuficientes en el uso de herramientas robustas para la solución del problema de ruteo de vehículos (VRP). Por otra parte, en la literatura revisada no se encuentra evidencia de estudios sobre la aplicación de enfoques actuales para la solución de VRP en PYMES, y aunque existe software comercial, por su alto costo no se ajustan al presupuesto de inversión de dichas compañías. Mediante una heurística de inserción sencilla para el VRP con entregas divididas y ventanas de tiempo (SDVRPTW), implementada en una plataforma tecnológica de fácil acceso como Microsoft® Excel™, se validó que el SDVRPTW es un enfoque adecuado para abordar la problemática de ruteo de vehículos en compañías PYMEs del sector comercial al por menor. Los resultados computacionales muestran que la heurística propuesta logra reducir aproximadamente en un 50% el número de vehículos empleados.
Palabras clave: Ruteo de, PYME, Distribución, SDVRPTW, Entregas divididas.
1. Introducción
Las pequeñas y medianas empresas (PYMEs) generalmente atienden necesidades específicas y focalizadas de la sociedad y la industria, por lo que sus sistemas de distribución se ajustan a pequeñas cantidades, frecuencias particulares para abastecer a sus clientes y condiciones especiales de transporte. Teniendo en cuenta los mercados que las PYMEs atienden y sus niveles de producción, la cantidad de recursos que invierten para planear y controlar las actividades de distribución son limitados; asimismo la robustez e innovación de sus recursos técnicos y tecnológicos son bajos.
Planear y controlar las actividades de distribución implica necesariamente la toma de decisiones sobre el ruteo de vehículos, además de administrar personas, vehículos, tiempo y otras variables importantes respecto de cómo, cuándo, dónde y a través de qué tipo de vehículo se debe atender algún cliente en el tiempo, de la manera adecuada. Esta toma de decisiones en cualquier aspecto dentro de las compañías, principalmente esta soportada de manera intuitiva por la función de distribución, sin el uso de metodologías cuantitativas. De esta manera se obtienen resultados insatisfactorios o no competitivos afectando su rentabilidad y competitividad.
Algunas metodologías ampliamente conocidas en la literatura en las cuales están basadas las actuales herramientas computacionales para planear las actividades de distribución, son complejas heurísticas y metaheurísticas compuestas por algoritmos computacionales diseñados para proveer soluciones a grandes instancias de ruteo de vehículos en grandes compañías. Ese tipo de métodos de solución fueron bien desarrollados a través de los últimos cincuenta años debido a la creciente complejidad y tamaño de las actividades de distribución alrededor del mundo, los cuales requieren para generar soluciones rápidamente y de calidad, recursos de alta tecnología y personal capacitado para administrar las plataformas y leer los resultados obtenidos. De esa manera las PYMEs tienen algunas desventajas, incluyendo la problemática de no contar con el suficiente dinero para invertir en recursos tecnológicos, ni el personal capacitado para cumplir con los requerimientos de las plataformas y sistemas. Por esta razón la metodología propuesta tiene un gran soporte para el desarrollo logístico de las PYMEs al estar al alcance de las mismas.
1.1. Actividades de distribución de las PYMEs
En [21] se muestra el uso de vehículos alternativos como la bicicleta y motocicleta con tráiler en la distribución de insumos en el subsector de productos de panadería en el área urbana de la ciudad de Palmira-Valle del Cauca. En dicho estudio se encontraron 202 panaderías (registradas en la Cámara de Comercio), que tenían diferente tamaño, necesidades de insumos, frecuencia de pedidos, horarios de trabajo, entre otros. Los investigadores tomaron una muestra de dicha población de clientes (panaderías) y las caracterizaron. Entre otros aspectos relevantes, en dicho estudio se observa que el 80% de los clientes operan desde las 5:00 am hasta las 12 pm. Respecto de la demanda de los clientes, en [21] se calcula la cantidad media para cuatro de los insumos demandados por los clientes en el estudio. Asimismo se caracteriza los dos vehículos referidos arriba, determinando que la velocidad media de la motocicleta con tráiler es de 7.3 Km/h en el centro de la ciudad y de 27.7 Km/h en áreas residenciales y cuenta con una capacidad de 350 Kg. Para la bicicleta la velocidad media es de 6.7 Km/h en el centro de la ciudad y de 8.2 Km/h en áreas residenciales, y cuenta con una capacidad de carga de 100 Kg.
En [14] se analiza el caso de Copacabana, el barrio más densamente poblado de Rio de Janeiro-Brasil. Se encontró que 372 establecimientos (la mayoría de ellos PYMEs) incluyendo farmacias (11%), panaderías (10%), cigarrerías (9%), restaurantes (8%), lavanderías (8%), supermercados (8%) y otros, usan bicicletas para sus actividades de distribución. En particular, 732 bicicletas son usadas, donde el 40% son bicicletas regulares, 30% son bicicletas de carga (bicicletas de doble parrilla) y el 30% triciclos. En promedio, hay dos repartidores de tiempo completo para 31 despachos al día cada uno. En el 29% de los viajes de carga hechos dentro de Copacabana y barrios cercanos (que complementaron el estudio) se realizaron despachos de hasta 25 Kg., el 17% hasta 50 Kg., el 29% hasta 100 Kg., el 21% hasta 200 Kg. y el 4% hasta 250 Kg. Uno de los hallazgos más importantes del estudio realizado por [14] fue que el 42% de los empresarios consultados respondieron que sus negocios simplemente "no podrían funcionar" sin el uso de bicicletas, refiriéndose a la viabilidad económica de sus negocios. La baja rentabilidad de esas PYMEs brasileras convierte a las bicicletas en un factor crítico para la supervivencia de sus negocios, incluso para los repartidores.
En [14] se destacan las ventajas del uso de bicicletas de carga frente a los vehículos motorizados (a menudo furgonetas, camioneras y camiones):
- Los bajos costos asociados a los vehículos (incluyendo la compra, el mantenimiento y los costos operativos).
- Mayor acceso para la distribución de productos. Las bicicletas de carga encuentran parqueaderos sobre la vía mucho más fácilmente que los vehículos motorizados. Incluso durante las horas pico las bicicletas superan a los vehículos motorizados atascados en el tráfico.
- Beneficios medioambientales por la no emisión de gases de efecto invernadero.
- Menores costos de infraestructura. Los vehículos motorizados causan un daño sustancial a las vías y puentes.
- Incremento de la seguridad por la reducción de la cantidad de camiones y furgonetas sobre las vías de la ciudad.
1.2. Métodos cuantitativos para resolver el problema de ruteo de vehículos en PYMEs
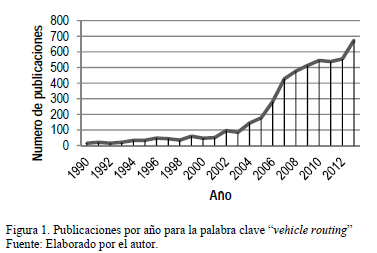
Una búsqueda realizada a través de Scopus® filtrando aquellos artículos publicados entre 1971 y 2013, con la palabra "Vehicle Routing" en el título, resumen y palabras clave, arrojaron un resultado de 5301 artículos. En la Fig. 1 puede observarse un crecimiento exponencial de las publicaciones entre 1990 y 2013, evidenciando un atractivo incremental en este tema especialmente en la última década en este campo del conocimiento.
A pesar del gran número de publicaciones disponibles en la literatura sobre VRP, para el caso de las PYMEs muy pocos artículos fueron encontrados.
En [21] se analiza un algoritmo para el problema de ruteo de vehículos con ventanas de tiempo (VRPTW) basado en la formulación del flujo de los tres índices propuestos en [9], incluyendo un cuarto índice para las rutas. Para la solución de la problemática utilizan el software Logware® 5.0 con un método basado en el algoritmo de los ahorros de Clarke & Wright. El algoritmo propuesto ha sido probado en el problema de distribución de insumos en el subsector del pan en Palmira, Valle del Cauca-Colombia usando motocicletas con tráiler y bicicletas. Se han comparado tres diferentes escenarios, 1) solo bicicletas, 2) solo motocicletas con tráiler (la alternativa más económica) y 3) combinación de bicicletas y motocicletas. En dicho artículo se concluye sobre los beneficios del uso de métodos cuantitativos para la toma de decisiones en actividades de distribución.
En [16] y [13] se reflexiona sobre el rol de la "computación distribuida" especialmente para PYMEs. Debido a que individualmente las PYMEs no podrían acceder fácilmente a recursos de alta tecnología ni a la experticia requerida para resolver complejos como el VRP, se busca que a través de la agrupación de varias compañías se pueda construir una plataforma colaborativa tomando ventaja de las capacidades tecnológicas de las PYMEs. De esta manera se logra generar soluciones de calidad para el VRP mediante la implementación de complejos algoritmos usados por las grandes industrias.
En [12] se aplica la heurística propuesta en [9], la cual es un método del tipo "cluster first - route second", para resolver el problema de ruteo de vehículos de una PYME que distribuye insumos de oficina. En particular, 26 clientes agrupados en tres ciudades son considerados. Las rutas desarrolladas por un solo vehículo en un horizonte de tiempo de 5 días son analizadas. Este artículo presenta una aplicación exitosa de dicha heurística.
En [18] se construye un método heurístico para el VRPTW tomando en cuenta las características administrativas especiales de las PYMEs relacionadas con las capacidades tecnológicas, económicas y humanas. El algoritmo propuesto no requiere de largos tiempos de ejecución (usando tecnología de gama baja y media). El algoritmo incluye variables tradicionales y restricciones del clásico VRPTW. El método de solución desarrollado no usa procedimientos de post-optimización. El algoritmo propuesto es evaluado en instancias propuestas por [20] y es comparado con los resultados de las mejores heurísticas desarrolladas en dicha fecha.
1.3. Características del VRP en PYMEs y el SDVRPTW
De manera opuesta a la realidad de algunas organizaciones y especialmente para las PYMEs, de acuerdo con [1], en muchos problemas de ruteo de vehículos la demanda de los clientes es menor o igual a la capacidad del vehículo y la demanda de cada cliente debe ser satisfecha por solo un vehículo, por lo tanto, hay un supuesto de una sola visita. En [21], se menciona que las PYMEs (especialmente aquellas dedicadas al comercio de insumos al por menor) usan vehículos de baja capacidad, incluyendo bicicletas y motocicletas, por lo que puede ocurrir que la capacidad de algunos de estos vehículos no pueda satisfacer la demanda de algún cliente en una sola visita.
Debido a lo anterior, las PYMEs deberían ser capaces de fraccionar la demanda del cliente en varios vehículos con el propósito de satisfacer los requerimientos del sistema y adicionalmente, reducir el número de rutas y la distancia recorrida por los vehículos. En [22] se menciona que al fraccionar la demanda en múltiples rutas, es posible reducir la distancia recorrida y el número de vehículos empleados. A este punto el problema de ruteo de vehículos para las PYMEs tratan con el Problema de Ruteo de Vehículos con entregas divididas (SDVRP). Sin embargo, las PYMES así como las grandes empresas deben proveer los productos a los clientes dentro de ventanas de tiempo específicas, de tal manera que el problema se puede generalizar a un Problema de Ruteo de Vehículos con entregas divididas y ventanas de tiempo (SDVRPTW).
El SDVRPTW ha sido un problema poco explorado en la literatura según [3]. En [3] se menciona que la única solución heurística para el SDVRPTW ha sido propuesta en [15]. De igual manera en [3] se menciona que muy pocos artículos han sido publicados hasta la fecha. Heurísticas de construcción y mejoramiento han sido propuestas por [10] y [17], métodos exactos basados en "Branch-and-price" ha sido introducido por [11], "Branch-and-price-and-cut" propuesto por [5] y "Branch-and-price-and-cut" mejorado por [2]. En [19] se propone un algoritmo exacto "Branch-and-price" para el Problema de Ruteo de Vehículos con entregas divididas y ventanas de tiempo (SDVRPTW).
El SDVRPTW puede ser definido como:
Dado:
- Un número ilimitado de vehículos homogéneos con capacidad Q localizados en un depósito central.
- Un conjunto de clientes con una demanda de productos (incluso superior a la capacidad de un vehículo).
- Hallar las rutas que:
- Satisfagan la demanda de los clientes (la demanda puede ser fraccionada en varios vehículos, por lo que un cliente puede ser visitado más de una vez).
- Cada ruta empieza y termina en el depósito.
- Cada ruta no puede exceder la capacidad del vehículo asignado.
- Cada ruta debe cumplir las restricciones de ventanas de tiempo.
- La distancia total debe ser minimizada
La heurística para el SDVRPTW desarrollada por [15] consiste en tres etapas. En la primera etapa se genera soluciones iniciales factibles construyendo rutas a través de la inserción del cliente más cercano al último cliente insertado en la ruta, teniendo en cuenta que el tiempo de viaje más el tiempo de espera para atender el siguiente cliente sea mínimo (como puede ser observado en la ecuación (1)). Si la demanda del último cliente excede la capacidad del vehículo, la demanda es fraccionada. En la segunda etapa realiza una búsqueda tabú a partir de la solución inicial para mejorar las rutas y en la tercera etapa se ejecuta un proceso de post-optimización.

A pesar de que los métodos de solución anteriormente descritos han sido desarrollados con éxito para el SDVRPTW, son complejos para las habilidades y conocimientos del personal de las PYMEs y adicionalmente su robustez no es necesaria para los requerimientos de las PYMEs del comercio al por menor. Por lo anterior, un algoritmo sencillo, eficiente y fácil de implementar podría satisfacer las necesidades de ruteo de estas compañías.
2. Datos y métodos
2.1. Caracterización y parametrización del caso de estudio
El grupo de investigación "SEPRO - Logística" de la Universidad Nacional de Colombia desarrolló bajo un esquema de co-financiación con el Departamento Administrativo de Ciencia, Tecnología e Innovación "COLCIENCIAS" una propuesta metodológica para la administración logística de las actividades de abastecimiento/distribución para PYMEs en Colombia, del cual diferentes trabajos de tesis de pregrado, maestría y doctorado han sido derivados. Para dicho proyecto, un conjunto de empresas de diferentes sectores económicos (entre ellos, comercio al por menor, cosméticos, agroindustria y artes gráficas) fueron seleccionadas para su caracterización y para la generación de estrategias o propuestas que ayuden a fortalecer las actividades logísticas y de almacenamiento. Se ha seleccionado el barrio "La Candelaria" como referente en este estudio, donde se ha realizado un estudio de geo-referenciación y caracterización de hábitos de compra de Hoteles y Restaurantes, establecimientos que se constituían como clientes potenciales de las PYMEs de comercio al por menor seleccionada para el estudio realizado por SEPRO.
Las empresas de comercio al por menor de productos perecederos e insumos localizadas en el barrio "La Candelaria" de la ciudad de Bogotá, seleccionadas para la investigación abastecen principalmente restaurantes, cafeterías, fruterías y hoteles. De acuerdo a la investigación mencionada, dichas empresas desean maximizar el uso de transportes alternativos, reducir el impacto ambiental y social de sus actividades de distribución, mejorar sus debilidades en el ordenamiento territorial y mejorar el uso del espacio de almacenamiento así como en unitarización de la carga, entre otras.
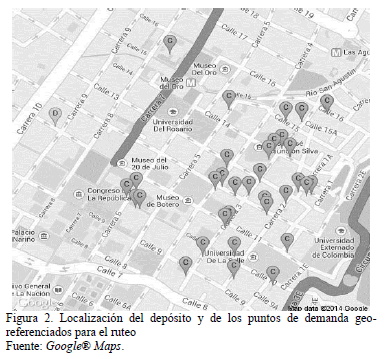
Para la caracterización del caso de estudio se delimitó el área geográfica del barrio "La Candelaria" de acuerdo a los límites propuestos por el Plan de Ordenamiento Territorial. En particular se geo-referenciaron 35 puntos de demanda (Ver Fig. 2) como parámetros del modelo de ruteo, y se diseñaron y aplicaron instrumentos de recolección de información de hábitos de compra a 23 (31,5%) de los 73 establecimientos reportados en la base de datos de la Asociación de Restaurantes de la Candelaria (ARCA).
La información relacionada con los hábitos de compra de los clientes ha sido analizada estadísticamente para caracterizar el caso de estudio y para definir los parámetros del modelo. El 69,6% de los establecimientos encuestados son restaurantes, el 17,4% son hostales y el 13% son hoteles.
Su capacidad promedio es de 58 personas, el establecimiento con menor capacidad es de 24 personas y el de mayor capacidad es de 150. El promedio de tiempo en el mercado para los establecimientos encuestados es de aproximadamente 7 años. El 60,9% de las instalaciones en que operan los establecimientos encuestados son arrendados. El 50% de los establecimientos encuestados mantiene intercambio de información con sus proveedores, de éstos el 81,8% es a nivel de inventarios y el 18,2% restante con base en las ventas realizadas, lo que permite inferir que se aplican estrategias de manejo de inventario por parte del vendedor (Vendor Managed Inventory - VMI). La calidad del producto, seguida del precio son las variables prioritarias por los establecimientos encuestados al momento de seleccionar sus proveedores. De los establecimientos encuestados el 50,8% mantiene una frecuencia de compra semanal y el 51,7% realiza compras vía telefónica para productos perecederos. La demanda promedio de la muestra fue de 67,4 Kg con una desviación estándar de 58,9 y el Lead Time para la recepción de productos alimenticios solicitados al proveedor es en promedio de 1,13 días.
2.2. Formulación matemática
La primera formulación del SDVRPTW ha sido propuesta por [10], quienes tomaron contribuciones del SDVRP realizada por [7,8] y del VRPTW introducida por [6]. Considerando las recientes contribuciones de [22] y [15], la siguiente formulación para el SDVRPTW es analizada:
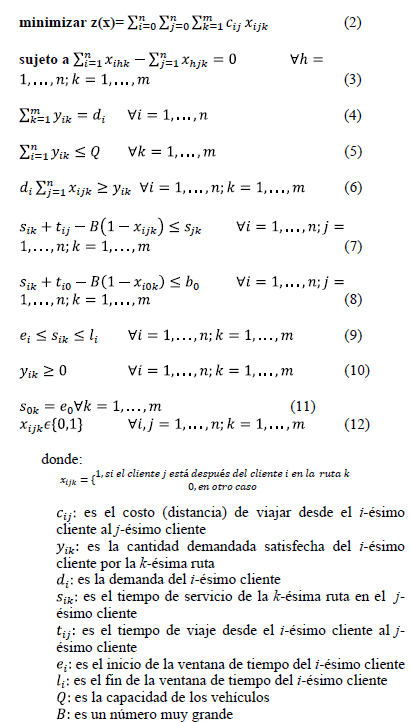
La función objetivo es descrita en la ecuación (2) la cual busca minimizar la distancia recorrida por los vehículos. La ecuación (3) permite la conservación del flujo en las rutas; la ecuación (4) garantiza que la demanda de cada cliente sea satisfecha; la ecuación (5) define que la cantidad de productos distribuidos no exceda la capacidad del vehículo Q; la ecuación (6) establece que un cliente es servido por un vehículo que lo visite; las inecuaciones (7)-(9) establecen que los vehículos deben llegar a cada cliente dentro de su ventana de tiempo, no antes o después de dicho intervalo de tiempo. La ecuación (10) define la no negatividad de las variables empleadas y la ecuación (11) define el inicio del tiempo de servicio en el depósito con el valor del inicio de la ventana de tiempo (punto de inicio para cada ruta).
Para el caso de las PYMEs, considerando el caso de estudio y con el propósito de desarrollar un método de solución fácil de interpretar, fácil de mantener y económico de implementar, en este trabajo se harán algunos supuestos sobre la formulación matemática original:
- Solo hay un tipo de vehículos (p.e. bicicletas).
- Se pueden crear un número ilimitado de rutas con el objetivo de satisfacer los requerimientos.
- Un cliente puede ser visitado hasta dos veces, por lo que su demanda puede ser satisfecha hasta por dos rutas/vehículos.
El último supuesto tiene en cuenta que un cliente no estará dispuesto a atender más de dos vehículos para cumplir sus requerimientos.
2.3. Heurística de inserción
Para resolver el SDVRPTW en las PYMEs analizadas en este trabajo, se propuso una heurística inicial de inserción y un algoritmo de post-optimización integrado con un algoritmo de asignación de vehículos. Los algoritmos construidos en este estudio fueron modelados con el propósito de validar que el enfoque del SDVRPTW es el tipo de problema que se ajusta a los requisitos de las PYMEs bajo estudio y que los métodos cuantitativos son una herramienta poderosa para la toma de decisiones. El algoritmo propuesto no busca competir con los mejores resultados obtenidos en la literatura para el SDVRPTW.
2.3.1. Algoritmo de solución inicial
El algoritmo propuesto tiene en cuenta el criterio de selección de J introducido en [15] para las inserciones de vecinos. Para la inserción de un nuevo cliente en una ruta en construcción, se evalúa que el vehículo pueda regresar al depósito dentro de la ventana de tiempo del depósito y que si un cliente ya fue atendido y tiene un remanente de demanda insatisfecha, la cantidad de productos a distribuir a dicho cliente en el proceso de inserción en la actual ruta en construcción debe satisfacer el remanente de demanda total de dicho cliente; todo esto con el ánimo de usar toda la capacidad disponible de los vehículos y satisfacer las necesidades de los clientes con no más de dos vehículos.
2.3.2. Algoritmo de post-optimización
Construidas todas las rutas necesarias para satisfacer los requerimientos de los clientes, el algoritmo de post-optimización combina aleatoriamente cada posición de cada ruta buscando una mejor solución que minimice la distancia total recorrida en cada ruta y si la encuentra, almacena esa nueva secuencia.
2.3.3. Algoritmo de asignación de vehículos
Finalmente, el algoritmo propuesto asigna cada ruta creada a un vehículo teniendo en cuenta que el tiempo de servicio de cada ruta que se añada al vehículo no tome más tiempo que la ventana de tiempo del depósito. Las ventanas de tiempo de cada cliente visitado en la ruta añadida deben ser satisfechas y el criterio de selección de la ecuación (1) también es tenido en cuenta, añadiendo la siguiente ruta con el mínimo tiempo de espera. De esta manera se itera hasta que todas las rutas hayan sido asignadas a un vehículo.
3. Resultados
El modelo ha sido ejecutado en una computadora 1.3 GHz para 35 puntos de demanda, con los siguientes parámetros generales del modelo:
- Velocidad de los vehículos: 6,7 Km/h (velocidad media de bicicletas de carga)
- Capacidad de carga de los vehículos: 100 Kg (capacidad de bicicletas de carga)
- Tiempo de servicio: 6 min.
Tres escenarios fueron ejecutados con la heurística propuesta para evaluar la validez de la hipótesis que el enfoque SDVRPTW se ajusta mejor que el enfoque VRPTW a las necesidades de las PYMEs para el ruteo de vehículos. Las ventanas de tiempo se ubicaron en un horizonte de planeación entre las 4 AM y 10 PM.
3.1. Escenario VRPTW (demanda menor a capacidad)
En este escenario la demanda fue reducida a la mitad y no se permite despachos fraccionados.
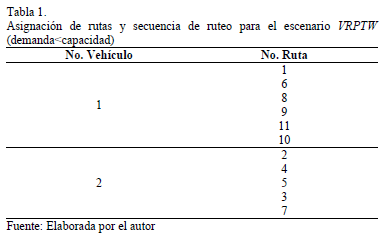
El algoritmo propuesto tomó 2.328 segundos para obtener la solución, dos vehículos fueron necesarios para satisfacer todos los requerimientos de los clientes. Once rutas fueron creadas y la distancia recorrida fue de 22.269 kilómetros.
La Tabla 1 presenta la asignación de rutas y la secuencia de ruteo de los vehículos empleados.
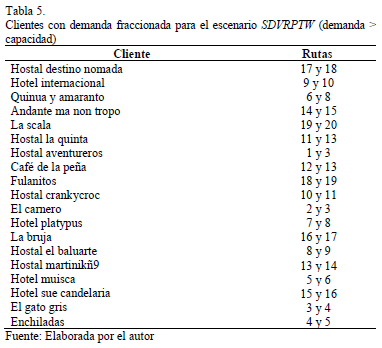
3.2. Escenario SDVRPTW (demanda < capacidad)
En este escenario la demanda fue reducida a la mitad, y las entregas divididas fueron permitidas. Este escenario permite comparar el enfoque VRPTW con el enfoque SDVRPTW cuando la demanda no excede la capacidad de los vehículos.
El algoritmo tardó 2.086 segundos para obtener la solución, solo un vehículo fue necesario para satisfacer los requerimientos de los clientes. Diez rutas fueron creadas y la distancia recorrida fue de 22.383 kilómetros.
La Tabla 2 presenta la secuencia de ruteo del vehículo usado y la Tabla 3 muestra los clientes a los cuales se les fraccionaron la demanda y las rutas en que fueron fraccionadas.
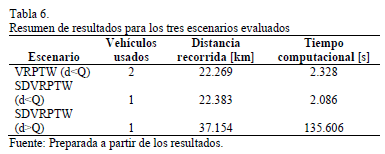
3.3. Escenario SDVRPTW (demanda > capacidad)
En este escenario la demanda es considerada en su totalidad, y las entregas divididas son permitidas. En este caso, la demanda excede la capacidad de los vehículos para algunos clientes, por lo que si las cargas divididas no son permitidas, el problema no tendría solución factible.
Al algoritmo le tomó 135.606 segundos para obtener la solución, solo un vehículo fue necesario para satisfacer los requerimientos de los clientes. Veinte rutas fueron creadas y la distancia recorrida fue de 37.154 kilómetros.
La Tabla 4 presenta la secuencia de ruteo para el vehículo empleado, mientras que la Tabla 5 muestra aquellos clientes a quienes la demanda fue fraccionada y las rutas que satisficieron dichas necesidades.
4. Conclusiones
A pesar de que el ruteo de vehículos ha sido un tema ampliamente estudiado en la literatura desde hace más de 20 años, los estudios recientes se han enfocado en la solución de problemas con características particulares propias de compañías emergentes, las cuales requieren técnicas para planeaciones de procesos de distribución complejas, con un gran número de clientes y con diversos vehículos. Hoy en día existen diversas variantes del VRP así como métodos de solución para resolverlos, aunque con los mercados cambiantes y las condiciones de comercio de la última década, los nuevos métodos de solución responden a las necesidades de las grandes compañías que tienen suficientes recursos para invertir y tienen complejos sistemas de distribución. De igual manera, las PYMEs tambien están expuestas a los mercados cambiantes y están sujetas a una agresiva competencia. Incluso los mercados locales son sumamente competitivos. Las PYMEs Colombianas del sector al comercio al por menor en general usan bicicletas y vehículos pequeños para las actividades de distribución, su planta de personal es de menos de 50 personas y dicho personal no cuenta con suficientes habilidades computacionales y analíticas para administrar los complejos modelos de solución expuestos, entre otras debilidades.
Así, las PYMEs no cuentan con suficientes métodos de solución a la mano, algoritmos y aplicaciones que tengan en cuenta esas características especiales, restricciones y debilidades de las PYMEs, que pudieran habilitarlas para sobrevivir, fortalecer sus capacidades e incrementar su competitividad.
A través del uso de métodos cuantitativos y extendidas herramientas para la toma de decisiones, no solo para las actividades de distribución, las PYMEs podrían reaccionar más rápidamente y de manera más precisa a cualquier cambio en las políticas externas y en las necesidades del mercado que pudieren afectar el desempeño de las empresas y usar de una mejor manera cada recurso que tenga la compañía.
Desarrollando y ofreciendo a las PYMEs herramientas técnicas que apoyen las actividades de distribución, comerciales, operativas y financieras de las PYMEs, estas podrían mejorar sus márgenes de rentabilidad y generar empleo, desarrollo y bienestar para las ciudades y regiones de los países en vías de desarrollo.
Considerando la variante del problema de ruteo de vehículos SDVRPT le proporciona beneficios a las PYMEs en términos de uso de recursos, como puede ser visto en la Tabla 6. Usando el enfoque del SDVRPTW se reduce el número de vehículos usados para satisfacer la demanda de los clientes (Primera función objetivo) y permite usar vehículos con menor capacidad que la demanda de los clientes a través de su fraccionamiento. El método desarrollado en este estudio procura resolver el problema de ruteo de vehículos para las PYMEs con un enfoque no considerado aún en dicho tipo de empresas, dividiendo la demanda de los clientes hasta en dos lotes, usando una heurística de inserción sencilla con un algoritmo de post-optimización primitivo (aleatorizando el orden inicial del conjunto de clientes) y usando una plataforma tecnológica de fácil acceso como Microsoft® Excel™, fácil de entender, fácil de mantener, fácil de implementar y fácil de mejorar. La heurística presentada (y su despliegue en MS Excel™ que contiene una interfaz de usuario amigable y una representación gráfica de las rutas en Google® Maps) son del tipo de herramientas que las PYMEs deberían emplear para la toma de decisiones, que les ayuden a resolver problemas combinatoriales en segundos, respondiendo a problemas de la vida real en cortos periodos de tiempo con cierto grado de precisión.
Referencias
[1] Archetti, C., Savelsbergh, M. and Speranza, M., An optimization-based heuristic for the split delivery vehicle routing problem. Transportation Science, 42 (1), pp. 22-31. 2008. DOI: 10.1287/trsc.1070.0204 [ Links ]
[2] Archetti, C., Bouchart, M. and Desaulniers, G., Enhanced Branch-and-Price-and-Cut for vehicle routing with split deliveries and time windows. Transportation Science 45 (3), pp. 285-298, 2011. DOI: 10.1287/trsc.1100.0363 [ Links ]
[3] Archetti C. and Speranza M., Vehicle routing problems with split deliveries. International Transactions in Operational Research 19, pp. 3-22, 2012. [ Links ]
[4] Dantzig G. and Ramser R., The truck dispatching problem, Management Science, 6, pp. 80-91. 1959. DOI: 10.1111/j.1475-3995.2011.00811.x [ Links ]
[5] Desaulniers G., Branch-and-Price-and-Cut for the split delivery vehicle routing problem with time windows. Operations Research, 58, pp. 179-192, 2010. DOI: 10.1287/opre.1090.0713 [ Links ]
[6] Desrochers M., Lenstra J., Savelsbergh, M. and Soumis F., Vehicle routing with time windows: Optimization and approximation. Vehicle routing: Methods and studies. Elsevier, New York. 1988. [ Links ]
[7] Dror, M. and Trudeau P., Savings by split delivery routing. Transportation Science, 23 (2), pp. 141-145, 1989. [ Links ]
[8] Dror, M. and Trudeau P., Split delivery routing. Naval Res. Logistics, 37, pp. 383-402. 1990. [ Links ]
[9] Fisher. M. and Jaikumar, R., A generalized assignment heuristic for the vehicle routing problem. Networks, 11, pp. 109-124. 1981. [ Links ]
[10] Frizzel, P. and Giffin, J., The split delivery vehicle scheduling problem with time windows and grid network distances. Computers and Operation Research, 22, pp. 655-667, 1995. [ Links ]
[11] Gendreau, M., Dejax, P., Feillet, D. and Guegen, C., Vehicle routing with time windows and split deliveries. Technical Report, 2006-851, Laboratoire Informatique d' Avignon, 2006. [ Links ]
[12] Guerrero, A., Pérez, R. and Olivares, E., Un caso logístico del problema de ruteo vehicular múltiple m-VRP resuelto con la heurística de Fisher & Jaikumar. 4to Taller Latino Iberoamericano de Investigación de Operaciones 2011, Acapulco, Guerrero, México, 2011. [ Links ]
[13] Guimarans, D., Herrero, R., Riera, D., Juan, A. and Ramos, J., Combining constraint programming, Lagrangian relaxation and probabilistic algorithms to solve the vehicle routing problem. In Proceedings of the 17th International RCRA workshop (RCRA 2010): Experimental Evaluation of Algorithms for Solving Problems with Combinatorial Explosion Bologna, Italy, 2010. [ Links ]
[14] Hagen, J., Lobo, Z. and Mendoça, C., The benefits of cargo bikes in Rio de Janeiro: A case of study. 13th World Conference on Transport Research, Rio de Janeiro-Brazil. 2013. [ Links ]
[15] Ho, S. and Haugland, D., A tabu search heuristic for the vehicle routing problem with time windows and split deliveries. Computers and Operations Research, 31, pp. 1947-1964, 2004. DOI: 10.1016/S0305-0548(03)00155-2 [ Links ]
[16] Juan, A., Marull, J., Jorba, J., Hester, J., Marquès, J. and Vilajosana, X., Using agent-based simulation and distributed computing to solve vehicle routing problems. Integrationsaspekte der Simulation: Technik, Organisation und Personal GertZülch & Patricia Stock (Hrsg.) Karlsruhe, KIT Scientific Publishing, 2010. [ Links ]
[17] Mullaseril, P., Dror, M. and Leung, J., Split-delivery routing in livestock feed distribution. Journal of the Operational Research Society, 48, pp. 107-116, 1997. [ Links ]
[18] Nieto, A., García, A. y Crespo, D., ELOCONS un algoritmo de construcción de rutas eficiente para la pequeña y mediana empresa de distribución, Dyna Ingeniería e Industria, 87 (2), pp. 222-228, 2012. DOI: 10.6036/4360 [ Links ]
[19] Salani, M. and Vacca, I., Branch and Prlice for the vehicle routing problem with discrete split deliveries and time windows. European Journal of Operational Research, 213, pp. 470-477, 2011. DOI: 10.1016/j.ejor.2011.03.023 [ Links ]
[20] Solomon, M., Algorithms for the vehicle routing and scheduling problem with time window constraints. Operations Research, 35, pp. 234-265, 1987. [ Links ]
[21] Arango-Serna, M., Adarme-Jaimes, W. and Zapata-Cortes, J., Commodities distribution using alternative types of transport. a study in the colombian bread SME's. DYNA, 77 (163), pp. 222-233. 2010. [ Links ]
[22] Wilck, J. and Cavalier, T., A construction heuristic for the split delivery vehicle routing problem. American Journal of Operations Research, 2, pp. 153-162, 2012 [ Links ]
J.C. Sepúlveda, es Ingeniero Industrial de la Universidad Nacional de Colombia, MSc (c) en Ingeniería - Ingeniería Industrial en la línea de investigación de logística - distribución. Miembro del Grupo de Investigación SEPRO - Logística. Profesional con experiencia en optimización y mejora de procesos productivos, lean manufacturing, sistemas de gestión de la calidad y gerencia de proyectos.
J.W. Escobar, es Dr. en Investigación de Operaciones de Universidad de Bologna, Italia. Docente de programas de Pregrado y Posgrado de la Pontificia Universidad Javeriana y de la Universidad del Valle, Cali Colombia. Sus intereses de investigación incluyen el diseño e implementación de efectivos algoritmos exactos y heurísticos para problemas de optimización combinatoria.
W. Adarme-Jaimes, es Ing. Industrial, Esp. en Gerencia de la Producción, MSc. en Ingeniería, Énfasis en logística, PhD en Ingeniería Industria y Organizaciones - Énfasis en logística. Es Profesor en la Facultad de Ingeniería de la Universidad Nacional de Colombia - Sede Bogotá, Colombia, director del Grupo de Investigación en Logística Sociedad, Economía y Productividad (SEPRO) de la misma universidad. Ha dirigido en los últimos diez años seis investigaciones sobre logística para diferentes sectores de la economía colombiana, con publicación de resultados en revistas indexadas (nueve artículos en los últimos cinco años). Es consultor en política pública sobre logística y sistemas de abastecimiento para los Ministerios de Comercio, Transporte y Salud de Colombia y para la Alcaldía mayor de Bogotá. Director de 14 tesis de Maestría y tres tesis de Doctorado en Logística. Ponente en congresos internacionales sobre logística en Alemania, México, Panamá, Venezuela y Colombia.