Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.188 Medellín Nov./Dec. 2014
https://doi.org/10.15446/dyna.v81n188.38147
http://dx.doi.org/10.15446/dyna.v81n188.38147
Plane geometry drawing tutorial
Tutorial de dibujo geométrico
Eduardo Gutiérrez de Ravé, Francisco J. Jiménez-Hornero & Ana B. Ariza-Villaverde
Deptartamet of Graphic Engineering, University of Córdoba, Córdoba, Spain, eduardo@uco.es
Received: May 18th, 2013. Received in revised form: June 19th, 2013.Accepted: September 25th, 2013.
Abstract
A tutorial has been developed with the aim of making geometry drawing teaching easier. It arises as a helpful tool for lecturers and engineering undergraduate students, with the objective of giving support to theoretical and practical lessons in plane geometry drawing. This easy-to-use tutorial provides users with interactivity, practical videos, self-evaluation, fundamental lessons, and "step by step" teaching due to the different levels of conceptual complexity included in its contents.
Keywords: Plane Geometry, Geometric Design, Geometric constructions, CAGD.
Resumen
Se ha desarrollado un tutorial para facilitar la docencia del dibujo geométrico. Con la idea de servir de apoyo a las explicaciones teóricas y prácticas de los conceptos correspondientes a los trazados geométricos planos necesarios en la ingeniería. Este tutorial es de fácil manejo y permite interactividad con el usuario, animaciones prácticas, autoevaluaciones, explicaciones amplias del temario y la enseñanza "paso a paso" de los conceptos gracias a los diferentes niveles de complejidad conceptual que incluye en su contenido.
Palabras clave: Geometría métrica, Diseño Geométrico, Construcciones Geométrica, CAGD.
1. Introduction
In technical drawing, geometric construction constitutes one of the fundamentals for engineering students. Generally, the main goal of geometry education is to improve spatial skills [1]. Most of this ability is acquired during elementary and high school courses, but some acquisition is left for undergraduate studies [2]. In general, geometry is a discipline which interrelates with other subjects such as computer science, mathematics, computational geometry, computer-aided design and geometric solid modeling [3]. Geometry is necessary for work in various fields such as computer graphics, engineering, architecture, and cartography.
Geometry belongs to school curricula. On the other hand, geometric construction teaching is being abandoned in the training of future engineers due to the incorporation of Computational Geometry (CG) and Dynamic Geometry (DG) teaching, that brings in dynamicity to the traditional ruler-and-compass geometry learning process. During the 1980s several programs were set up for the purpose of simulating geometric constructions carried out with traditional methods [4]. Botana & Valcarce (2002) [5] introduced "Discover", a program for learning and teaching geometry that permits the replacement of the traditional ruler-and-compass by electronic substitutes. During the 1990s, DG has been increasingly used for teaching, mainly in high schools, although the traditional Euclidean tools are still being replaced by virtual tools in computers. Current software DG systems, such as Cabri-Géomètre [6], SketchPad [7], Cinderella [8,9] iGeom [10], and Geometry Expert [11-13] present web-based versions, enabling students to use them worldwide through a web browser. Liu et al. (2007) [14] propose a pen-based intelligent dynamic lecture system for geometry teachers. Plane Geometry plays an important role in learning, research and engineering. Pythagoras is a software simulator for dynamic geometry [15]. The use of Internet and computers can bring great benefits to the teaching of geometry, choosing or creating appropriate programs and methodologies that take advantage of the computer's positive characteristics [16]. DG programs have proven to be an excellent resource for teachers and students [17]. C.a.R. is a dynamic geometry program simulating compass and ruler constructions on a computer [18]. However, on a computer, much more is possible, and as Hoyles & Noss (2003) [19] have shown, Dynamic Geometry systems are ''pedagogic tools finely tuned for the exploration of a mathematical domain''. DG can be understood as being an alternative to traditional ruler-and-compass geometry, which produces static constructions. However, for engineering students and, specifically, mechanical engineering students (designing manufacturing products) [3] it is necessary to learn the fundamentals and step-by-step processes in geometrical construction. Also, they must acquire a knowledge of Geometry and Drawing, which has not been sufficiently promoted in pre-university or university education during recent years [2]. The use of tools that explain underlying processes in a comprehensive way [20] introduces immersive collaborative learning into geometry education and applies 3D dynamic geometry to make it easier. Some authors have understood that it is necessary to gain prior knowledge of plane geometry drawing in order to learn 3D construction, and to improve spatial skills. Computer-Aided Teaching has been of great benefit to teachers and students [14].
In this work, a computer application called PGDT, acronym of Plane Geometry Drawing Tutorial, has been developed based on computational and dynamic geometry with the aim of facilitating the teaching and learning of plane geometry concepts. Thus, the topics included in PGDT are the following ones: 1. Drawing tools, 2. Elementary Geometric Constructions, 3. Working with line segments, 4. Angles, 5. Triangles, 6. Regular Polygons, 7. Tangencies, 8. Quadrilaterals, 9. Circles and connection, 10. Power, 11. Inversive geometry, 12. Scales, 13. Geometric movements, 14. Homothetic transformation and Similarity (geometry), 15. Affinity.
From a total of 225 methods, 26 of them are explicative and do not require any data introduction. All the topics considered here are useful for engineering and they are mainly focused on geometric constructions.
2. Methods
PGDT has been developed under the Windows operating system (WOS) for the purpose of providing the user with a visual, practical and easy-to-use tool for the execution of different Graphical methods. Although Windows is not the only operating system offering those features, it has been chosen because it is one of those most used by students in their personal computers. Delphi is the programming language selected for implementing the application. It is a powerful compiler that easily manages windows and icons of work environments running under WOS.
In PGDT, the following relevant aspects have been taken into account: i) to visualize the parameters of resulting geometric elements (i.e. coordinates, perimeter, area); ii) to set an error control during the step by step learning process of geometric constructions iii) to describe basic mathematic functions and drawing algorithms. These aspects have been developed in the following contents included in PGDT:
- Learning of drawing tool handling by means of videos that explain step by step the use of the ruler-and-compass.
- Theoretical description of each topic: the on-page program structure allows the user to access at each moment to its contents. The subject matter is clearly ordered in chapters, sections, subsections and methods. Each part is explained on the blackboard, where the user is able to visualize and control the method's execution.
- Practices and exercises: These permit the improvement of theoretical and practical knowledge interactively using a dynamic data input.
2.1. Application structure
PGDT has two levels: interface and processing, with three and two independents units, respectively. Those levels are described as follows:
- Interface level including the following units i) Application management: used for controlling user operations such as application closing, resizing and restoring. ii) Lessons index: this shows all the contents and methods of PGDT. iii) Videos: Tutorial videos.
At this level, three windows are available to the user: main, indexes and video windows. These are described below. - Processing level consisting of the next units i) Operations: for videos visualization and lesson-method explanation. ii) Help: On line assessment
2.1.1. Interface level
(PGDT interface has three windows. User can introduce or select parameters and receive some messages by means of dialog boxes.
Main window.
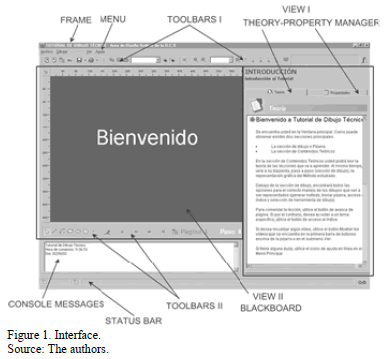
In Fig. 1, the main window components can be observed. This window is used as a system communication and is divided into two views: Theory-Property Manager and Blackboard, the first one showing the theoretical explanation of the selected method as well as input data properties. In the second view, the graphic output of the selected method can be observed.
The program enables the creation of geometric objects, such as points, lines, arcs, circumferences, rectangles, ellipses, by using dynamic measures and the modification of their properties. In addition, options for saving and printing the theory and the graphical methodology are provided, as well as graphic tools like zoom, gridding, rulers or squared patterns. Three colors are used for geometric object representation on the blackboard, red for input, blue for auxiliary construction elements and green for solutions Finally, PGDT includes on-line help.
PGDT main windows contain the following items: i) Window frame, ii) Application menu, iii) Toolbar I, iv) Blackboard, v) Theory and Property manager, vi) Toolbar II, vii) Console message, viii) Status Bar.
- Window frame. The functions of this application facilitate window handling. It is composed of: Title Bar, Menu access (maximization, minimization and restoration of window, movement and resizing and application closing), and fast access to main functions of WOS menu.
- Menu. Includes the following submenus: File (Print and Save in RTF type for text and BMP for blackboard graphics), Draw (this allows graphic object selection), Edition (to copy, cut, paste or delete the graphic objects on the blackboard), Display (with an index showing all the lessons and methods), Videos, Zoom, Rules, Grid, Help on-line and References.
- Toolbar I. Direct access to: forward and backward, index, video, saving, printing, copying, pasting, cutting, deleting, showing grids and rules on the blackboard, graphic object display and zoom tools.
- Blackboard. This is rectangular with the origin of the coordinates in the top left hand corner. Blackboard is used for drawing and showing results.
- Theory and Property manager. Shows theory contents related to the selected method and properties of graphic elements on the blackboard. It is possible to modify properties and geometric parameters of input graphic elements. Theory shows the text, including explicative steps. Property shows characteristics of selected graphic objects, coordinates, color and nomenclature used.
- Toolbar II. This is divided into two sections. In the section on the left the following actions are found: Act/Des, Line, Arc, Rectangle, Ellipse, Circle, Point. In the right hand section the following actions are found: blackboard cleaning, starting method, "backward" and "forward", and ending method and index.
- Console message. This shows messages when user needs to put data on the blackboard.
- Status bar. This shows the actions in progress.
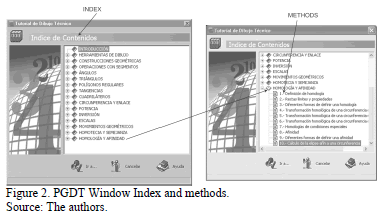
Index window
This window allows the selection of lessons included in PGDT, Fig. 2.
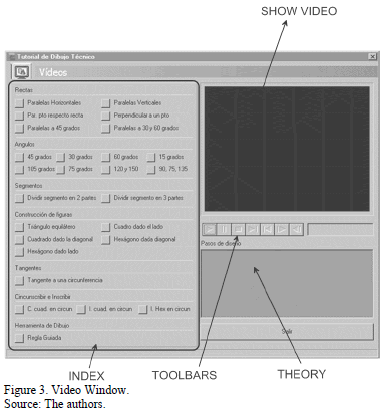
Video window
This window shows videos contained in the tutorial (Fig. 3). These videos are focused on geometric constructions by means of rulers (square and bevel).
2.1.2. Processing level
In this section, PGDT execution procedure is explained. Options described are: i) Video showing ii) Selecting topic- method, iii) Explanation of method selected, iv)
Selecting properties of graphic elements, v) Drawing on the blackboard
- To show a video, the icon access is found in Toolbar I. Moreover, a voice explaining the method shown can be heard.
- Selecting topic-method, this is activated by pressing icon "Muestra el Índice". A window emerges containing 15 tutorial topics and their corresponding methods.
- Explanation of the selected method. The icons "backward" and "forward" are in Toolbar II and permit the user to run through the steps of the method. It is possible to apply the method by introducing new data through the icon "Limpiar dibujo". If the selected method is only a theoretical one, these icons will not be shown in Toolbar II.
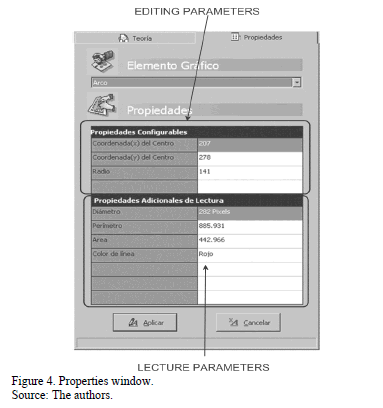
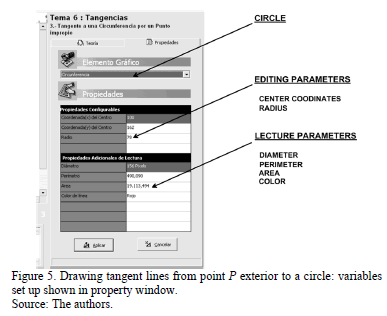
- Selecting properties of graphic objects. This option permits users to choose and change properties of input graphic objects that will be shown in red on the blackboard. Only the configurable properties can be modified (Fig. 4)
- Drawing on the blackboard, by using the mouse.
3. Example of application
The background knowledge related to tangency is a relevant geometry subject in technical design because it is involved in many frequent systems such as rod-crank and gears. For this reason, the drawings of tangent lines to circles have been chosen as examples of application.
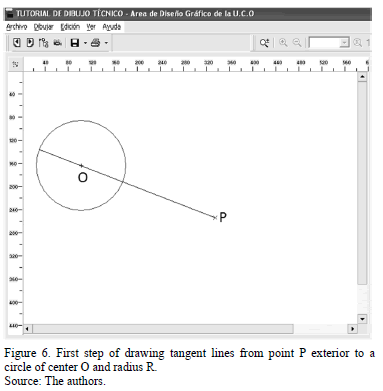
The first example corresponds to drawing tangent lines from point P exterior to a circle. The proposed method is composed of 6 steps. The required graphic object inputs are completed in the first two steps and they are placed on the blackboard. Thus, the circle is introduced by drawing it on the blackboard. Coordinates of its center and radius can be modified through the window properties by the keyboard (Fig. 5).
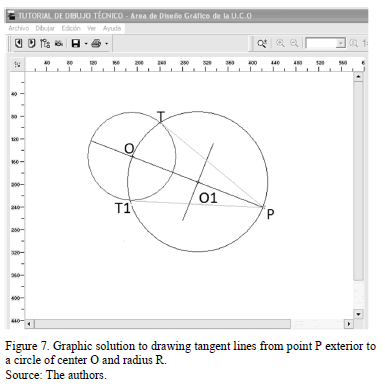
The following steps begin by drawing the line linking point P and center O (Fig. 6) and finish by calculating the geometric solutions shown in Fig. 7.
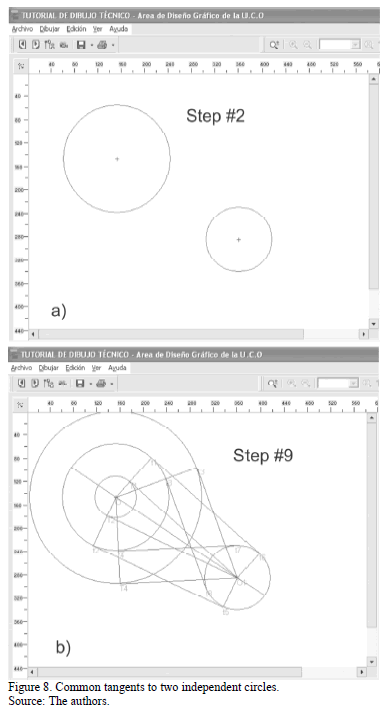
The second application example is shown in Fig. 8. It deals with the calculation of common tangents to two independent circles in 9 steps. Fig. 8a shows the two circles drawn on the board by the user, and Fig. 8b depicts internal and external tangents drawn by the program and the corresponding tangency points
4. Conclusions
This work introduces an application to be used in graphics engineering teaching and learning. One of the main difficulties in encouraging a wider use of DG programs is creating content and evaluating and guiding students during learning activities. This problem is overcome by using the proposed computer application due to the dynamic data entry corresponding to each exercise, and showing the solution step by step. Thereby, teachers can choose the necessary parameters in an easy way. One way to motivate students to think about their own mental models is to allow them to manipulate variables, by changing their values and trying to observe how they behave. It is essential to fulfil this requirement in this kind of computer tool. The application is able to run on computers with low-processing capabilities thus facilitating its required diffusion through e-learning platforms or web.
References
[1] Kaufmann, H. and Schmalstieg, D. Mathematics and geometry education with collaborative augmented reality, Computers & Graphics, 27, pp. 339-345, 2003. http://dx.doi.org/10.1016/S0097-8493(03)00028-1 [ Links ]
[2] Moura, J.G., Branddo, L. O. and Brandao, A. A. F. A Web-based learning management system with automatic assessment resources. Proceedings of the 37th Annual Frontiers in Education Conference, pp. 766-771, 2007. [ Links ]
[3] Lowther, J. L. and Shene, C. K. Computing with geometry as an undergraduate course: A three-year experience, Proceedings of the 32nd Technical Symposium on Computer Science Education. SIGCSE Bulletin, 33 (1), pp. 119-123, 2001. http://dx.doi.org/10.1145/366413.364558 [ Links ]
[4] Ruthven, K., Hennessy, S. and Deaney, R. Constructions of dynamic geometry: A study of the interpretative flexibility of educational software in classroom practice, Computers & Education, 51 (1), pp. 297-317, 2008. http://dx.doi.org/10.1016/j.compedu.2007.05.013 [ Links ]
[5] Botanaa, F. and Valcarce, J. L. A dynamic-symbolic interface for geometric theorem discovery. Computers & Education, 38 (1-3), pp. 21-35, 2002. http://dx.doi.org/10.1016/S0360-1315(01)00089-6 [ Links ]
[6] Bellemain, F. Conception, realisation and experimentation of software for teaching geometry: Cabri-géométre, PhD. dissertation. LSD2-IMAG Laboratory, Grenoble, France, 1992. [ Links ]
[7] Jackiw, R. N. and Finzer, W. F. The geometer's sketchpad: programming by geometry, in Watch what I do: programming by demonstration, Cambridge, MIT Press, 1993. pp. 293-307. [ Links ]
[8] Kortenkamp, U. Foundations of Dynamic Geometry, PhD. dissertation, ETH, Institut für Theoretische Informatik, Zurich, Switzerland, 1999. [ Links ]
[9] Kortenkamp, U. Foundations of Dynamic Geometry, Journal für Mathematik-Didaktik, 21, pp. 161-162, 2000. http://dx.doi.org/10.1007/BF03338916 [ Links ]
[10] Brandão, L. O. iGeom: a free software for dynamic geometry into the web. International Conference on Sciences and Mathematics Education, Rio de Janeiro, Brazil, 2002. [ Links ]
[11] Gao, X. S. Building Dynamic Mathematical Models with Geometry Expert, III. A Geometry Deductive Database, Proceedings of the fourth Asian Technology Conference in Mathematics, pp. 153-162, 1999. [ Links ]
[12] Gao, X. S., Zhu, C. C. and Huang, Y. Building a Dynamic Mathematical Models with Geometry Expert, I. Geometric Transformations, Functions and Plane Curves, Proceedings of the third Asian Technology Conference in Mathematics, pp. 216-224, 1998. [ Links ]
[13] Gao, X. S. Zhu, C. C. and Huang, Y. Building Dynamic Mathematical Models with Geometry Expert, II. Linkages, Proceedings of the third Asian Technology Conference in Mathematics, pp. 15-22, 1998. [ Links ]
[14] Liu, Y., Lin, Q. and Dai, G. PIGP: A Pen-Based Intelligent Dynamic Lecture System for Geometry Teaching in Hui K.-c. et al. Edutainment, LNCS 4469, pp. 381-390, 2007. [ Links ]
[15] Ciobanu, G. and Rusu, D. Pythagoras: An interactive environment for plane geometry. Proceedings of the Intelligent Computer Communication and Processing Conference, pp. 283-286, 2007. [ Links ]
[16] Isotani, S. and Brandão, L. O. An algorithm for automatic checking of exercises in a dynamic geometry system: iGeom. Computers & Education., 51, pp. 1283-1303, 2008. http://dx.doi.org/10.1016/j.compedu.2007.12.004 [ Links ]
[17] Sinclair, M. P. Peer interactions in a computer lab: Reflections on results of a case study involving web-based dynamic geometry sketches. The Journal of Mathematical Behavior, 24, pp. 89-107, 2005. http://dx.doi.org/10.1016/j.jmathb.2004.12.003 [ Links ]
[18] Grothman, R. C.a.R.: Compass and Rules, 1999. Available at http://www.z-u-l.de/doc_en/index.html [ Links ]
[19] Hoyles, C. and Noss, R. What can digital technologies take from and bring to research in mathematics education? in Bishop, A. J. et al. Second International Handbook of Mathematics Education, 2nd edition, Dordrecht, Kluwer Academic, 2003. pp. 323-349. http://dx.doi.org/10.1007/978-94-010-0273-8_11 [ Links ]
[20] Kaufmann, H. and Schmalstieg, D. Designing Immersive Virtual Reality for Geometry Education. Proceedings of the Virtual Reality Conference, pp. 51-58, 2006. [ Links ]
E. Gutiérrez de Ravé obtained his agronomic engineering PhD (1987) from the University of Córdoba (Spain). He is currently full professor in the Department of Graphic Engineering and Geomatics at the University of Córdoba. His research is focused in computer aided design, curves and surfaces and computer graphics.
F.J. Jiménez-Hornero obtained his agronomic engineering PhD (2003) from the University of Córdoba (Spain). He is currently full professor in the Department of Graphic Engineering and Geomatics at the University of Córdoba. His research is focused in computational fluids mechanics, multifractals and computer graphics.
A.B. Ariza-Villaverde obtained her agronomic engineering PhD (2013) from the University of Córdoba (Spain). She is currently developing her research activity as grant holder in the Department of Graphic Engineering and Geomatics at the University of Córdoba. Her research lines are GIS, axial maps, multifractals and computer graphics.