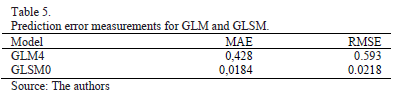Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.189 Medellín Jan./Feb. 2015
https://doi.org/10.15446/dyna.v82n189.42069
http://dx.doi.org/10.15446/dyna.v82n189.42069
Analysis of tailing pond contamination in Galicia using generalized linear spatial models
Análisis de contaminación de balsas mineras en Galicia usando modelos lineales espaciales generalizados
Javier Taboada a, Ángeles Saavedra b, María Paz a, Fernando G. Bastante a & Leandro R. Alejano a
a Department of Natural Resources, University of Vigo, Vigo, Spain, jtaboada@uvigo.es
b Department of Statistics, University of Vigo, Vigo, Spain, saavedra@uvigo.es
a Department of Natural Resources, University of Vigo, Vigo, Spain, mpaz@uvigo.es
a Department of Natural Resources, University of Vigo, Vigo, Spain, bastante@uvigo.es
a Department of Natural Resources, University of Vigo, Spain, alejano@uvigo.es
Received: February 17th, 2014. Received in revised form: August 20th, 2014. Accepted: September 20th, 2014.
Abstract
We statistically analysed the chemical components present in waste water from mines in Galicia (NW Spain). These elements pose a risk to public health and the environment, most particularly in the event of a failure in the containment structure of a pond or dam.
The statistical processing of the data, which started with an analysis of the typical contaminants present in mining ponds and dams, pointed to the potential limitations of using non-spatial models for spatially structured data.
Our results indicate the greater potential of the generalized linear spatial model over the generalized linear model for analysis of spatially structured data. We also show how a misspecification of the model for analysing spatial data can lead to misleading conclusions, which might lead, in turn, to poorly designed protective or corrective measures.
Keywords: tailings pond; environmental risk; generalized linear spatial model; Markov-chain Monte Carlo; spatial statistics.
Resumen
Se analizaron estadísticamente los componentes químicos presentes en las aguas residuales de minas en Galicia (noroeste de España). Estos elementos representan un riesgo para la salud pública y el medio ambiente, muy especialmente en el caso de un fallo en la estructura de contención de un estanque o represa.
El procesamiento estadístico de los datos, que se inició con un análisis de los contaminantes típicos presentes en los estanques y presas mineras, señaló las potenciales limitaciones del uso de modelos no espaciales para datos espacialmente estructurados.
Nuestros resultados indican el gran potencial del modelo lineal espacial generalizado respecto al modelo lineal generalizado para el análisis de datos espacialmente estructurados. También se muestra cómo una mala especificación del modelo en el análisis de datos espaciales puede conducir a conclusiones erróneas, lo que podría dar lugar, a su vez, a un mal diseño de las medidas de protección o correctivas.
Palabras clave: balsa minera; riesgo ambiental; modelo lineal espacial generalizado; Monte Carlo para cadenas de Markov; estadística espacial.
1. Introduction
The disaster that occurred at Aznalcóllar mine (near Seville) in 1998 was one of the most important environmental disasters in Spanish history. A holding dam burst, releasing around five million cubic metres of toxic mine slurry and acidic tailings that affected a surface area of about 4,500 hectares. This accident along with other less serious such accidents, ultimately led to a greater commitment to environmental protection, the implementation of restrictive regulations and the creation of emergency action committees to cope with ecological disasters.
Nonetheless, mining continues to contribute significantly to increasing concentrations of heavy metals in natural ecosystems. According to Laybauer [1], mining increases natural concentrations of copper, iron, aluminium and zinc and also increases acidity, conductivity and suspended solid values. It is therefore important to control contaminant levels in tailing ponds associated with mining activities. Previous researches aiming to classify major sources of water pollution and to analyse the formation of acid mine drainages [2-3] have been carried out.
Analysis of the quality of water used for mining purposes should be considered as the first step in identifying potential sources of contamination. A common error, however, is to exclude analysis of possible geological influences on the presence of chemical elements in water. Statistical techniques have been applied to the study of heavy metals distribution in water, but the potential spatial dependence of the observations has not always been taken into account [4]. A number of multivariate statistical techniques, including cluster analysis and principal component analysis, have been used for similar studies. These techniques, which group similar observations regarding concentrations, are used to identify contaminants which, according to concentration, determine the clustering of observations in homogeneous groups. The geographical location of observations cannot be included in such analyses; however, so valuable information that could explain the presence of certain elements in water is lost. Furthermore, these techniques are not suitable for predicting contaminant concentrations in areas not previously sampled.
To assess the environmental risk posed by mining dams and tailing ponds in Galicia, we statistically analysed the contaminants characteristic of mining waste in both the field and the laboratory so as to statistically study the geological relationship between certain components present in this water and determine, firstly, the real danger implied by the contaminated water and, secondly, the influence of geology on the availability and dispersion of contaminants of anthropogenic origin. These analyses enabled an efficient design for the containment structures and also facilitated further study of measures to reduce contamination when affected by geology.
Used for the purposes of our study were geostatistical methods [5], which have been widely applied to the prediction of stationary processes using linear unbiased estimators with minimum variance. Although conventional geostatistics assumes normality conditions for the stationary process, many of the methods have been generalized to situations where stochastic variation is not Gaussian, for example, [6, 7]. In many of the methods developed and applied to date, model parameter estimates are not usually of interest. However, parameter estimation and inference enables the factors that influence the spatial distribution of the phenomenon of interest to be identified, and this, in turn, helps explain causes.
The generalized linear model (GLM) was developed by Nelder and Wedderburn [8] in order to combine several statistical models within a single theoretical framework. Subsequently developed as an extension to the GLM was the generalized linear mixed model (GLMM), which allows the linear predictor to include random as well as fixed effects [9]. For simplicity sake, it is usually assumed that the random effects follow a Gaussian distribution.
The term 'model-based geostatistics' was first used by Diggle, Tawn and Moyeed [6] to describe an approach to geostatistical problems based on formal statistical models and inference procedures. The generalized linear spatial model (GLSM) is an adaptation of the GLMM to situations where the random effects follow a spatial stationary pattern. Several authors have studied and applied the GLSM [10-14]. The GLSM not only predicts the response variable, it also directs inference to the regression function parameters, the properties of the residuals or the distribution of residuals conditioned to the response variable. For our contaminants project, this approach enabled us to determine locations with high levels of contaminants and also to investigate the factors contributing to contamination.
We used spatial statistical models to assess the impact of known factors and to obtain better predictions of contamination levels for the studied ponds and dams. The aim of our research was to demonstrate how the model-based geostatistical approach developed by Diggle, Tawn and Moyeed [6] and the GLSM could be adapted to contamination analysis.
2. Materials and methods
2.1. The study area and the geographic database
The study population was a set of mining ponds and dams and nearby rivers located in Galicia in NW Spain. Mining in Galicia has a long tradition and is a key source of supply for Spain and for the world. Mining activity in Galicia covers the metal and non-metallic, energy and quarrying sectors; quarrying is particularly important, as Galicia is a key source of ornamental granite and slate. The deposits analysed ranged from settling ponds for solids with direct discharge to the river or sewage system, to closed- or semi-closed-circuit deposits for water used in treatment plants. Water was sampled at authorized discharge points and for ponds and dams that were considered prone to flooding or where there was a risk of collapse of the containment structure. A total of 126 water samples were collected from all four of Galicia's provinces (Pontevedra, Ourense, Lugo and A Coruña).
2.2. Chemical characterization of the water samples
The analytical part of the work was divided into an initial fieldwork phase and a laboratory analysis phase. Firstly, 0.5 L of water was sampled from the main deposits and the corresponding acidity (pH) and redox potential (Eh) values were recorded using a portable Crison PH25 pH-meter. Both pH and Eh reflect the mobility and availability of metals and so are important parameters in determining toxicity. Next, in the laboratory the samples were passed through 0.45-micron nitrocellulose filters and electrical conductivity was measured using a CyberScan CON 1500; this parameter provides information about the possible geological sources of chemicals in water. The samples were frozen until the final phase was implemented, consisting of the chemical analysis of several analytes by the Support Centre for Scientific and Technological Research (CACTI). Aliquots for all the samples were collected to which 2% nitric acid was added for analysis of metals; for the analysis of ions, untreated aliquots were used.
Inductively coupled plasma optical emission spectrometry (ICP-OES) was used to analyse content in calcium, magnesium, sodium, potassium, iron, aluminium, silicon, manganese, zinc, nickel, cobalt, copper, cadmium and lead . Zinc, nickel, cobalt, copper, cadmium and lead are considered highly toxic. The origins are anthropogenic, mainly industrial activities and especially mining activities [15]. Although calcium, magnesium, silicon, aluminium, iron, sodium and potassium do not pose a major pollution risk, they provide information about possible geological sources of chemicals in water; likewise, manganese, nickel and cobalt may also have a geological origin. High-performance liquid chromatography/mass spectrometry (HPLC/MS) was used to analyse content in fluorides, chlorides, nitrates, phosphates and sulfates - all ions that may originate in water treatment procedures based on mining flocculants and coagulants [16].
Since the study refers to mineral deposits in the Galician region, in setting limit values for concentrations of contaminants in waste water discharged into the public water system (including groundwater), we were guided by Order MAM/85/2008 [17], which establishes technical criteria for public water system damage assessment and waste water sampling and residue analyses. Note that maximum levels for aluminium, calcium, potassium, sodium, silicon and Eh are not specified in Order MAM/85/2008 or other legislation.
2.3. Model formulation
In the GLM, a response variable Y=(Y1,Y2,...,Yn) is assumed such that the variables Y1,Y2,...,Yn are mutually independent and with expectation related to a linear predictor E[Y]=g -1(dTb), where b Î Âp is the vector of unknown parameter regressors, d are known explanatory variables, T means transposed and g is a known function called the link function.
GLSMs are GLMMs in which the latent variables are derived from a spatial process. In other words, conditionally on the Gaussian process S(x), the data Yi, i=1, ..., n, follow the classical GLM. In this case the model is as described below.
Consider n distinct locations {x1,...,xn} Ì I Ì Â2 and assume observation of a realization y=(y1,..., yn)T of Y=(Y1,...,Yn)T, where Yi=Y(xi).
Let S={S(x) : x ÎI}, I Ì Â2 be a Gaussian process with a mean function E[S(x)]=d(x)Tb and with covariance cov(S(x), S(x'))=s2r;(x, x'; j) + t21{x=x'}, where b ÎÂp is a vector of unknown regression parameters, d(x) are known explanatory variables with spatial dependence, s2 represents the variance, r;(x,x'; j) is a correlation function in Â2, j is a scaling parameter that controls the rate at which the spatial correlation approaches 0 as the distance between locations grows, and t2 ≥ 0, according to the usual geostatistical terminology, is the nugget effect.
Conditionally on S, the process {Y (x), x ÎI} consists of mutually independent random variables and, for each location x Î I, the distribution of the error [Y (x) |S] has a density that only depends on the conditional mean E[Y (xi)|S(xi)]. A known link function g relates the conditional mean and S(x) in such a way that E[Y (xi)|S(xi)]= g -1(S(xi)).
When the regression parameters b are of interest, it is important to remember that these have a conditional interpretation rather than a marginal interpretation. In particular, E[Yi|S(xi)] and E[Yi] differ in terms of the structural dependence of the explanatory variables d(xi). For this reason, direct comparison cannot be made between the b coefficients of the two models, except when Yi|S(xi) is Gaussian and the link function is identity.
Because the stationary Gaussian process S(x) is not observable, the GLSM parameters are usually approximated by implementing Markov chain Monte Carlo (MCMC) algorithms within a Bayesian framework. See Christensen [18] for further details. This was the approach used for our research, implemented with the geoRglm package, freely available under the open-source R statistical system [19].
3. Results
3.1. Analytical results
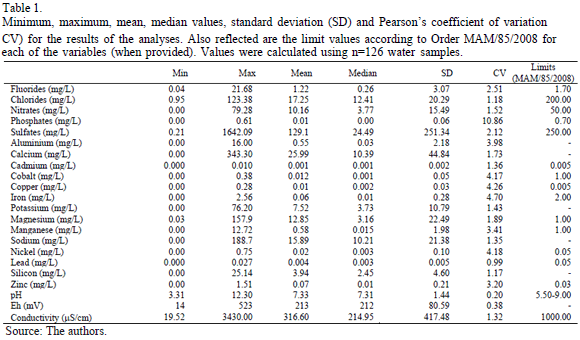
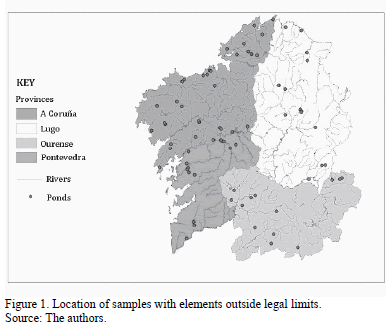
The results of the analysis of the explanatory variables were compared with the maximum values permitted by the legislation [17]. Table 1, which summarizes the analysis results for the 22 variables constituting the study database, shows minimum and maximum values, dispersion parameter values and legislated limit values. Although Table 1 shows data with high standard deviation (SD) values with respect to their means, it was decided to include all the observations in the statistical study since one of the objectives was to quantify the number of samples and mining concessions outside legal limits. Fig. 1 shows the spatial distribution of samples with values outside the legal limits.
The most important distribution and concentration results for the elements analysed in the laboratory are described as follows:
- The values obtained for phosphates and chlorides were below the legal limit.
- Nitrate contamination was infrequent, with only four contaminated samples.
- Fluorides and sulfates with values above the legal limit were encountered in A Coruña samples.
- Cadmium, which is highly toxic, was present in above-limit concentrations in five samples, all taken from locations close to each other.
- Iron was not present as a significant contaminant in the chemical analyses.
- Cobalt and lead levels did not exceed legal limits.
- The pH results indicated that ten ponds and dams had acidic waters; since pH potentially influences the bioavailability of metals, this result implies increased risk for the environment. Moreover, 12 samples showed basic water values above the permitted limits.
- Only seven samples had electrical conductivity values outside the limits, although all the ponds studied had significant variations in conductivity levels.
- Comparison of zinc values with pH and electrical conductivity values indicated that this metal did not appear as a dissolved ion in most of the cases.
- Magnesium was frequently present in the ponds and dams in all four provinces but is likely to be geological in origin.
- Copper also featured frequently in the samples analysed.
- Nickel and manganese contamination occurred mainly in A Coruña.
- Since (as mentioned earlier) no concentration limits have been legally established for aluminium, calcium, sodium, silicon and Eh, no comparisons could be made between our measurements and the legal maximums.
- Concerning the speciation of the metal contaminants, the pH and Eh values indicate that the metals are mainly in forms of higher mobility and availability. This would require additional treatments for controlling the physical properties of the waters of the ponds in order to reduce the mobility and bioavailability of these metals.
3.2. Variable selection
The initial sample database consisted of 126 samples and 22 variables. The response variable was calculated for each sample by quantifying the number of times that explanatory variable values were outside the legal limits established by Order MAM/85/2008. This new variable took values of 0 up to 16, with 0 representing values within the legal limits and other values quantifying increasing levels of contamination.
Preliminary calculations of the correlations between variables were made so as to identify possible linear dependencies between them. This helped determine the quality of the information collected and helped reduce the number of variables to be considered in the statistical study. A preliminary selection of predictors also avoided potential collinearity problems following the application of mathematical models. The study of correlations showed that there were two groups of variables: cluster 1 included conductivity, sulfates, calcium, magnesium, sodium, potassium and chlorides, and cluster 2 included zinc, aluminium, silicon, cobalt, copper, manganese and nickel. Chosen from these two groups were the seven variables that significantly correlated with the variables quantifying contamination, namely, conductivity, sulfates, magnesium, zinc, copper, manganese and nickel. Fluoride, nitrate, cadmium, iron and pH measurements also correlated with the response variable, but new clusters that grouped these together were not detected. Finally, the phosphate, lead and Eh variables showed no significant correlation with any other explanatory variable or with the response variable. Given their poor capacity to explain contamination it was decided to exclude them from the statistical analysis. This preliminary study of correlations led to selection, for modelling purposes, of the following 12 explanatory variables: fluorides, nitrates, sulfates, cadmium, copper, iron, magnesium, manganese, nickel, zinc, pH and electrical conductivity. The recorded values for these variables in the 126 samples were used for the statistical models.
3.3. Fit to a GLM
Assumed in the following cases was that the level of contamination in a given location, Y(xi), could be modelled as a Poisson distribution. Under this hypothesis, the GLM applied was Poisson regression, where the link function is given by the logarithmic function:
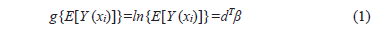
The parameters to be estimated in this model are b=(b0,...,bp), where b0 is the independent term and where b1,..., bp are the regression coefficients for each known regression variable.
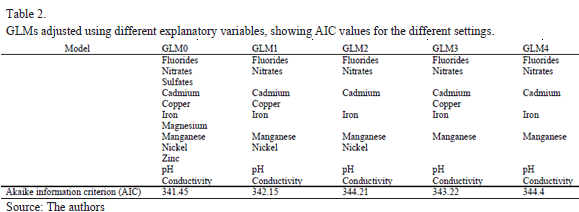
The GLM fitted using 12 explanatory variables and the contamination level as the dependent variable resulted in many of the bi coefficients not being significant. Some of the less significant variables were excluded in a procedure in which different GLMs were fitted, as shown in Table 2.
GLM0 was the model fitted with the 12 variables selected after the preliminary correlation study. GLM4 was a simplified model which only retained conductivity from the cluster 1
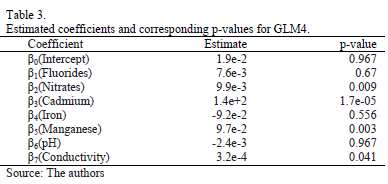
variables and manganese from the cluster 2 variables. Used to measure goodness of fit was the Akaike information criterion (AIC), associated with the concept of entropy; the smaller its value the better the goodness of fit of the estimate. Although the AIC value for GLM0 was the smallest for the five models, all the models had, in fact, very similar values. This was confirmed by a chi-square test to compare GLM0 and GLM4. The p-value for the test was 0.0766, for a significance level of a=0.05, so both models can be considered to be similar. Table 3 shows the coefficients estimated for GLM4 and the corresponding p-values. Although several coefficients continued to feature as not significant, further reduction in the variables produced a significantly poorer fit than for the initial GLM0 model, used to perform the model comparison test. For this reason we chose to perform the statistical analysis with the seven variables listed in Table 3. This selection of variables significantly reduced the dimensionality of the problem, since the initial 12 variables were reduced to seven. This facilitated the interpretation of the fitted parameters of the model and also, thanks to the chi-square test, guaranteed an explanatory power similar to the original GLM0 model with 12 variables.
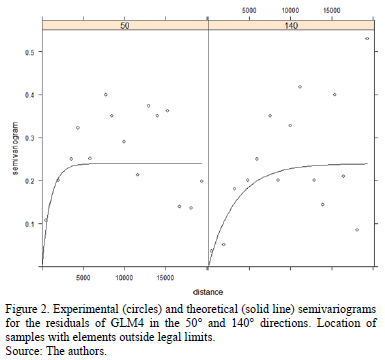
A geostatistical study of the GLM4 residuals showed spatial dependence with geometric anisotropy. Fig. 2 shows the experimental semivariograms (circles) in the 50º and 140º directions. Superimposed on the experimental semivariograms are the theoretical semivariograms (solid line). An exponential model was selected in order to fit the experimental semivariograms, given that this was the parametric model with the lowest fitting error. See Cressie and Diggle et al. [5, 6] for further details of this kind of fit. This graph indicates the existence of a latent spatial process that could not be reflected by the GLM.
3.4. Fit to a GLSM
In fitting the GLSM it was assumed that the conditional distribution of the contamination, i.e. Y(xi)|S(xi), could be modelled as a Poisson distribution. Using again the log function as a link function we now have:
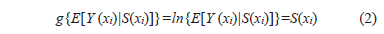
where E[S(x)] =d(x)Tb and cov(S(x), S(x'))=s2r;(x, x'; j) + t21{x=x'} and where an exponential model is assumed for the correlation function. The parameters for estimation in the GLSM are q=(s2, j, t2, b), with b=(b0,...,bp).
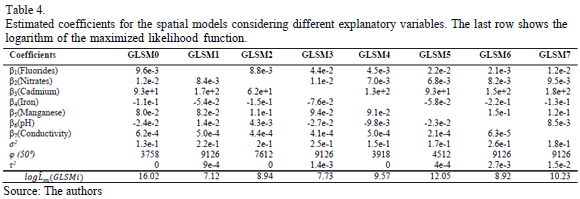
Using the geoRglm software, a spatial model called GLSM0 was fitted so as to model not just the spatial pattern reflected by the residuals of the non-spatial model, but also their anisotropic behaviour. Obtained as an estimator of the vector of coefficients b=(b0,...,b7) were the following values: (1.3e-1, 9.6e-3, 1.2e-2, 9.3e+1, -1.1e-1, 8.0e-2, - 2.4e-2, 6.2e-4). The estimated value of the variance, s2, was 1.3e-1. The scaling parameter, j, was estimated as 3758 in the 50° direction and 12527 in the 140° direction. Finally, the nugget, t2, was considered to have a null value.
To determine the significance of the explanatory variables, the GLSMs were fitted with a single variable removed for each fit. Thus, for example, GLSM1 reflected a spatial model with the fluoride variable removed. Table 4 shows the estimated coefficients for the explanatory variables in the fitted spatial models. The last row shows the logarithm of the value of the likelihood function maximized during the corresponding fit procedure.
We used the log-likelihood ratio test to compare GLSMi, i=1, ..., 7 and the GLSM0 model. According to Mardia et al. [20], the statistic
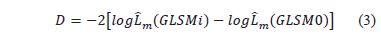
can be approximated by a 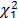 distribution. Therefore, taking a significance level of a=0.05, we could reject the hypothesis that GLSMi and GLSM0 were equivalent if the p-value for the comparison was less than the significance level. For example, comparison between GLSM1 with the fluorides variable excluded and GLSM0 resulted in a value of D=-2 [7.12-16.02]=17.8. Assuming a
distribution. Therefore, taking a significance level of a=0.05, we could reject the hypothesis that GLSMi and GLSM0 were equivalent if the p-value for the comparison was less than the significance level. For example, comparison between GLSM1 with the fluorides variable excluded and GLSM0 resulted in a value of D=-2 [7.12-16.02]=17.8. Assuming a 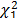 distribution, the p-value was 2.46e-5; hence, for a significance level of a=0.05, we have to reject the null hypothesis that the GLSM0 and GLSM1 models are equivalent and accept that GLSM0 fitted the data better than GLSM1. Using the same reasoning for the other models, the p-value was always less than the significance, so it follows that all the variables were significant in fitting the spatial model.
distribution, the p-value was 2.46e-5; hence, for a significance level of a=0.05, we have to reject the null hypothesis that the GLSM0 and GLSM1 models are equivalent and accept that GLSM0 fitted the data better than GLSM1. Using the same reasoning for the other models, the p-value was always less than the significance, so it follows that all the variables were significant in fitting the spatial model.
It was not possible to design a test that allowed us to compare a spatial model like GLSM0 with a non-spatial model like GLM4. We therefore used cross-validation to test the predictive power of the two models. Thus, eliminating a single case, predictions were made by GLM4 and GLSM0 and errors were recorded. Repeating this procedure for the 126 samples, we calculated the mean absolute error (MAE) and the root mean squared error (RMSE) for both models. Table 5 shows the values obtained; it can be concluded that taking into account the spatial component resulted in a major improvement in predictive capacity.
4. Conclusions
Fitting the data to a GLM revealed the erroneous conclusion that many of the laboratory measurements would be irrelevant when establishing a relationship between the data and the level of contamination recorded during sampling. This conclusion was due to the existence of a latent spatial process which a non-spatial model was unable to identify and isolate.
In the fit to a GLM the spatial correlation of the variables was not taken into account, significantly affecting the quality of the statistical results. It can be concluded that a misspecification of the model can potentially lead to false interpretations regarding the relevance of the explanatory variables.
Although GLSM parameters must be interpreted conditionally to the process space, S, the results indicate the relevance of the explanatory variables in the model fit.
The type and extent of spatial dependence linking the sampling locations were revealed by the values estimated for the spatial process parameters. Moreover, the estimated values for the parameters for the linear part of the model pointed to the variables that were most critical in determining water contamination.
The cross-validation study indicated that the GLSM produced fewer prediction errors than the GLM. What this means is that correctly modelling spatial dependence results in models not only with greater explanatory capacity but also with more reliable prediction capacity.
The geostatistical model verified the existence of spatial dependence between the pond contaminants and local natural geological elements. Thus, for example, certain ponds located in close proximity had similar contamination results for the same elements. The results of the samples analysed indicated a possible spatial influence for magnesium. Independently of the type of mining operation, water samples with high magnesium content were distributed evenly throughout the studied area. At the opposite extreme was cadmium, a non-essential heavy metal that is non-existent in the Galician lithology. The conclusion can only be that cadmium contamination in ponds is the result of human influence. The influence of Galicia's granitic lithology is evident in the mobility of metals. Acidic water favours metal availability and mobility, as corroborated by a cross-analysis between pH and Eh records for certain analysed metals.
Our results show that there is a geological influence on the content in chemicals of mining water samples in Galicia. The results obtained using geostatistical methods have enabled us to assess the impact of the analysed elements and improve the interpretation of the levels of contamination present in tailing ponds. Future research will focus on verifying the elements present in the geological environment for areas where concentration levels are above legal limits, in an endeavour to prevent poor practices by mines and focus on concentrations that are hazardous for health and the environment.
Acknowledgements
This work was funded partly by Xunta de Galicia project INCITE10REM304009PR and by Spanish Ministry of Science and Innovation projects MTM2008-03129 and MTM2012-23204.
References
[1] Laybauer, L., Incremento de metais pesados na drenagem receptora de efluentes de mineraçao - minas do Camaquã, Sul do Brasil, Revista Brasileira de Recursos Hídricos, 3 (3), pp. 29-36, 1998. [ Links ]
[2] Pozo-Antonio, S., Puente-Luna, I., Lagüela-López, S. and Veiga-Ríos, M., Techniques to correct and prevent acid mine drainage: A review, DYNA, 81 (184), pp. 73-80, 2014. http://dx.doi.org/10.15446/dyna.v81n186.38436 [ Links ]
[3] Pérez, B.F. and Espina, J.A., Evaluation of fly ashes for the removal of cu, ni and cd from acidic waters, DYNA, 77 (161), pp. 141-147, 2010. [ Links ]
[4] Nedia, G., Chafai, A., Moncef, S.M. and Chokri, Y., Spatial distribution of heavy metals in the coastal zone of "Sfax-Kerkennah" plateau, Tunisia, Environmental Progress & Sustainable Energy, 30 (2), pp. 221-233, 2011. http://dx.doi.org/10.1002/ep.10462 [ Links ]
[5] Cressie, N., Statistics for spatial data, Wiley, New York, 1993. [ Links ]
[6] Diggle, P.J., Tawn, J. and Moyeed, R., Model-based geostatistics, Journal of Applied Statistics, 47 (3), pp. 299-350, 1998. [ Links ]
[7] Palacios, M.B. and Steel, M.F.J., Non-Gaussian bayesian geostatistical modelling, Journal of the American Statistical Association, 101 (474), pp. 604-618, 2006. http://dx.doi.org/10.1198/016214505000001195 [ Links ]
[8] Nelder, J.A. and Wedderburn, R.W.M., Generalized linear models, Journal of the Royal Statistical Society, Series A, 135 (3), pp.370-384, 1972. http://dx.doi.org/10.2307/2344614 [ Links ]
[9] Breslow, N. and Clayton, D., Approximate inference in generalized linear mixed models, Journal of the American Statistical Association, 88 (421), pp. 9-25, 1993. http://dx.doi.org/10.1080/01621459.1993.10594284, http://dx.doi.org/10.2307/2290687 [ Links ]
[10] Christensen, O. and Waagepetersen, R., Bayesian prediction of spatial count data, Biometrics, 58 (2), pp. 280-286, 2002. http://dx.doi.org/10.1111/j.0006-341X.2002.00280.x [ Links ]
[11] Diggle, P.J., Moyeed, R.A., Rowlingson, B. and Thomson M. Childhood malaria in the Gambia: A case-study in model-based geostatistics, Journal of the Royal Statistical Society: Series C, 51 (4), pp. 493-506, 2002. http://dx.doi.org/10.1111/1467-9876.00283 [ Links ]
[12] Zhang, H., On estimation and prediction for spatial generalised linear mixed models, Biometrics, 58 (1), pp. 129-136, 2002. http://dx.doi.org/10.1111/j.0006-341X.2002.00129.x [ Links ]
[13] Diggle, P.J., Ribeiro, J.P. and Christensen, O.F., An introduction to model-based geostatistics, in Møller, J, (ed) Spatial statistics and computational methods, Springer Verlag, New York, 2003, pp. 43-86. http://dx.doi.org/10.1007/978-0-387-21811-3_2 [ Links ]
[14] Zhang, H., Optimal interpolation and the appropriateness of cross-validating variogram in spatial generalized linear mixed models, Journal of Computational and Graphical Statistics, 12 (3), pp. 698-713, 2003. http://dx.doi.org/10.1198/1061860032265 [ Links ]
[15] Merian, E., Anke, M., Ihnat, M. and Stoeppler, M., Elements and their compounds in the environment: Occurrence, analysis and biological relevance, Wiley, Weinheim, 2004. http://dx.doi.org/10.1002/9783527619634 [ Links ]
[16] Aguila, M.I., Sáez, J., Lloréns, M., Soler, A. y Oruño, J.F., Tratamiento físico-químico de aguas residuales. Coagulación-floculación, University of Murcia, Publishing Service, Murcia, España, 2002. [ Links ]
[17] Orden MAM/85/2008. De 16 de enero por la que se establecen los criterios técnicos para la valoración de los daños al dominio público hidráulico y las normas sobre toma de muestras y análisis de vertidos de aguas residuales, in BOE, 25, España, pp. 5238-5253, 2008. [ Links ]
[18] Christensen, O., Monte Carlo maximum likelihood in model-based geostatistics, Journal of Computational and Graphical Statistics, 13 (3), pp. 702-718, 2004. http://dx.doi.org/10.1198/106186004X2525 [ Links ]
[19] R Development Core Team R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, 2012. [ Links ]
[20] Mardia, K.V., Kent, J.T. and Bibby, J.M. Multivariate analysis, Academic Press, London, 1979. [ Links ]
J. Taboada, received the Bs in Mining Engineering in 1980, from the University of Oviedo, Spain, and received a PhD. degree in Mining Engineering in 1993 from the University of Oviedo, Spain. At present, he's professor of Mining Engineering for the Department of Natural Resources and Environmental Engineering of the University of Vigo, Spain. His research interests include mining, environment and safety.
Á. Saavedra, received the Bs. in Mathematics in 1989, from the University of Santiago de Compostela, Spain and received a PhD degree in Mathematics in 1997 from the University of Oviedo, Spain. At present, she works in the School of Mining Engineering for the Department of Statistics and Operational Research of the University of Vigo, Spain, where she is a member of the group Mining Exploitation. Her research interests include spatial data and data mining.
M. Paz, received the Bs. in Mining Engineering in 2009, from the University of Vigo, Spain and received his MSc. in Environmental Technology in 2012. Her interests include occupational accidents and Bayesian networks. She is currently working on her doctoral thesis.
F.G. Bastante, received the Bs. in Mining Engineering in 1995, from the Technical University of Madrid (UPM), Sapin and received a PhD degree in Mining Engineering in 2002 from the University of Vigo, Spain. He is currently an Associate Professor in the School of Mining Engineering of the University of Vigo. Current research activities include applications of mathematical modelling in mining engineering.
L.R. Alejano, received the Bs. in 1992 and obtained a PhD degree in Mining Engineering in 1996 both in the Universidad Politécnica de Madrid, Spain. He has been teaching and researching in rock mechanics and other mining engineering related disciplines in the Department of Natural Resources and Environmental Engineering at the Universidad de Vigo, Spain, since 1995. He has published more than 40 papers in relevant scientific journals and he has been involved in more than 50 research and consulting projects primarily in the field of rock engineering. He is presently Vice-President of the Spanish Society of Rock Mechanics and Associate Editor of the international Journal of Rock Mechanics & Mining Sciences.