Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.189 Medellín Jan./Feb. 2015
https://doi.org/10.15446/dyna.v82n189.42785
http://dx.doi.org/10.15446/dyna.v82n189.42785
Mixture experiments in industrial formulations
Diseño de mezclas en formulaciones industriales
Diana Cristina Ortega-Pérez a, Moises Oswaldo Bustamante-Rua b, Derly Faviana Gutiérrez-Rôa c & Alexander Alberto Correa-Espinal d
a Gestión Tecnológica, SUMICOL S.A., Medellín, Colombia. dortega@corona.com.co
b Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. mobustam@unal.edu.co
c Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. dfgutierrezr@unal.edu.co
d Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. alcorrea@unal.edu.co
Received: March 26th, 2014. Received in revised form: September 29th, 2014. Accepted: October 17th, 2014.
Abstract
In this paper, we focus on the practical aspects of the formulation of industrial mixtures efficiently. Proposing a working strategy that integrates the design of experiments and the PDCA cycle, from the point of view of the experimenter, rather than from theoretical perspective, develop to define the experimental plan, get the data and adjust a statistically significant and high practical significance model.
Keywords: formulation; design of experiments DOE; mixture experiment; PDCA cycle.
Resumen
En este artículo nos hemos centrado en los aspectos prácticos de la formulación de mezclas industriales de forma eficiente, proponiendo una estrategia de trabajo que integra el diseño de experimentos y el ciclo PHVA, desde el punto de vista del experimentador más que desde una perspectiva teórica elaborada, para definir el plan experimental, obtener los datos y ajustar un modelo estadísticamente significativo y con alto significado práctico.
Palabras clave: formulación; diseño de experimentos; diseño de mezclas; ciclo PHVA.
1. Introducción
Ingenieros, académicos y científicos en muchas ocasiones tienen entre sus objetivos de investigación, el analizar la proporción en que los ingredientes o componentes deben participar en una mezcla, sin importar la cantidad absoluta de ellos, más conocido como formulación de mezclas.
A lo largo de la historia, el problema de la formulación de mezclas ha sido tradicionalmente abordado por el método de ensayo y error, que consiste en formular mezclas donde las proporciones de los materiales utilizados se establecen de manera arbitraria y se selecciona aquella mezcla que mejora las propiedades de interés, sin ser necesariamente la óptima, ya que no se exploran todas las combinaciones posibles de los componentes.
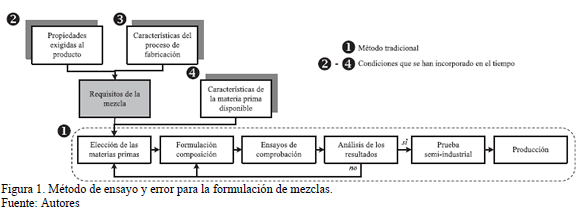
Desde los alquimistas, los metalúrgicos y los ceramistas, las mezclas obtenidas experimentalmente, en una secuencia de ensayo y error o como consecuencia de mezclas accidentales, se plasmaban en "recetas" que eran sigilosamente conservadas y replicadas para obtener los productos deseados, para lo cual se debía garantizar que sus componentes, en proporción y procedencia exactas, sean empleados siguiendo estrictamente el procedimiento establecido. Sin embargo, fue con la llegada de la porcelana a Europa de las manos de Marco Polo, que este método fue alterado, pues se contaba con un producto, más no con la receta que permitía su elaboración, y fue por ello que China mantuvo el monopolio de fabricación de la porcelana desde su invención en el siglo VII hasta el siglo XVII, cuando Johann Friedrich Böttger reinventó el proceso en Europa, tras muchos intentos previos que dieron lugar a los distintos tipos de porcelana que se conocen actualmente. Este hecho agrega una condición al método del ensayo y error, ya que ahora deben ser tenidas en cuenta las propiedades exigidas al producto final, entre los requisitos de la mezcla a formular.
Si bien los componentes, su proporción y procedencia, son la base de las recetas, el procedimiento de elaboración es fundamental para la obtención satisfactoria de las propiedades de interés y lo que subyace tras su éxito, es la tecnología disponible para su fabricación. Se pueden desarrollar recetas sofisticadas que de no contar con tecnologías apropiadas, quedan reducidas a buenas ideas. Entonces, la tecnología y por ende, las características del proceso de fabricación condicionan la formulación de la mezcla, adicionando otra condición al tradicional método de ensayo y error.
Con el correr de los años, la competencia entre industrias que conlleva a la búsqueda incansable de reducción de costos; así como, la escasez de materias primas, demanda una condición adicional al método de ensayo y error tradicional, pues no siempre es posible para las industrias importar la materia prima exigida en la receta y se hace necesario modificar las fórmulas, para incluir las características de la materia prima disponible.
Las distintas condiciones exigidas al método de ensayo y error previamente mencionadas y resumidas en la Fig. 1, lo convierten en un método inviable, costoso y demorado, que ha motivado la consideración de otros métodos experimentales más eficientes para abordar la formulación de mezclas, como la programación lineal [1] y el diseño de experimentos. Cuando se piensa en diseño de experimentos, puede suponerse que se trata de diseños factoriales, que permiten estudiar el efecto sobre la variable respuesta al variar dos o más factores. Sin embargo, si al mantener constante la cantidad total de mezcla, el valor de la variable respuesta cambia cuando se realizan cambios en las proporciones de los componentes que la conforman, se trata de un diseño de mezclas, que es una metodología estadística que surgió a partir de la teoría de mezclas de Scheffé en 1958, y ha sido utilizado en la optimización de formulaciones de alimentos, pinturas, polímeros, asfalto, concreto, vidrio, cerámica, medicamentos, entre otros, obteniéndose excelentes resultados.
Aunque el interés y aplicación del diseño de experimentos con mezclas es creciente, existen dificultades en su implementación e interpretación, que pueden deberse a que no es una metodología muy difundida, pues muchos libros de diseño de experimentos no la mencionan o le otorgan poca relevancia [2].
El objetivo de este artículo es presentar el diseño de experimentos con mezclas desde una perspectiva de procesos que facilite su aplicación en industrias que producen y venden productos elaborados a partir de mezclas; haciendo énfasis en las estrategias que orientan la planificación del experimento, su ejecución, el análisis de los datos experimentales y las acciones que deben emprenderse después de realizar los experimentos, con el ánimo de formular mezclas y obtener conocimiento de ellas. Para ello, se iniciará presentado brevemente una introducción al diseño de mezclas y algunos conceptos básicos relacionados, luego se desarrollarán las estrategias a tener en cuenta en el diseño de experimentos con mezclas.
2. Diseño de experimentos con mezclas
Un diseño de experimentos con mezclas que tienen 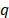 componentes o ingredientes, consiste en un conjunto de experimentos en los que se prueban combinaciones particulares o mezclas de dichos ingredientes. Si se denotan por
componentes o ingredientes, consiste en un conjunto de experimentos en los que se prueban combinaciones particulares o mezclas de dichos ingredientes. Si se denotan por 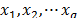 , las proporciones en las que participan los componentes de la mezcla, se deben satisfacer dos restricciones:
, las proporciones en las que participan los componentes de la mezcla, se deben satisfacer dos restricciones: 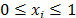 para cada componente
para cada componente 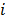 y
y 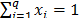 . Estas restricciones indican que la suma de todos los componentes que integran la mezcla debe ser 100%, esto significa que los componentes no pueden ser manipulados independientemente unos de otros, y que sus proporciones deben variar entre 0 y 1.
. Estas restricciones indican que la suma de todos los componentes que integran la mezcla debe ser 100%, esto significa que los componentes no pueden ser manipulados independientemente unos de otros, y que sus proporciones deben variar entre 0 y 1.
Sin embargo, existen situaciones donde algunas proporciones no pueden variar entre 0 y 1, porque algunas o todas las proporciones de los componentes están restringidas por límites inferiores 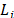 y/o límites superiores
y/o límites superiores 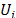 , entonces la restricción puede definirse como:
, entonces la restricción puede definirse como: 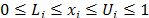 . Además de los límites superiores e inferiores que restringen a los componentes de forma individual, puede que exista cierta dependencia entre dos o más componentes y sea necesario utilizar restricciones lineales de multicomponentes, que ponen límites a las funciones de componentes. Por otro lado, es posible que se desee mantener fija cierta parte de la mezcla, entonces las proporciones deben ser escaladas, de tal forma que sumen la unidad.
. Además de los límites superiores e inferiores que restringen a los componentes de forma individual, puede que exista cierta dependencia entre dos o más componentes y sea necesario utilizar restricciones lineales de multicomponentes, que ponen límites a las funciones de componentes. Por otro lado, es posible que se desee mantener fija cierta parte de la mezcla, entonces las proporciones deben ser escaladas, de tal forma que sumen la unidad.
Al planear un experimento con mezclas se decide, en función del conocimiento no estadístico y el objetivo del problema, las mezclas que conformarán el conjunto de experimentos, pues no se trata de probar las formulaciones que se le ocurran al investigador, ya que se estaría retornando al método de ensayo y error [3]. Los diseños de experimentos con mezclas distribuyen adecuadamente las mezclas en la región experimental, la cual se representa con figuras geométricas de 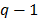 componentes, cuando los componentes de la mezcla pueden variar entre 0 y 1. Así para dos componentes la región experimental es un segmento de recta, para tres un triángulo, para cuatro un tetraedro y para más de cuatro un hipertetraedro.
componentes, cuando los componentes de la mezcla pueden variar entre 0 y 1. Así para dos componentes la región experimental es un segmento de recta, para tres un triángulo, para cuatro un tetraedro y para más de cuatro un hipertetraedro.
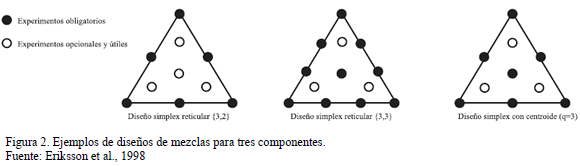
Los dos tipos básicos de diseño son el simplex reticular y simplex con centroide. El diseño simplex reticular 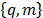 considera
considera 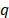 componentes y permite ajustar un modelo estadístico de orden
componentes y permite ajustar un modelo estadístico de orden 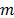 . Los puntos del diseño consisten en todas las posibles mezclas que se forman con
. Los puntos del diseño consisten en todas las posibles mezclas que se forman con 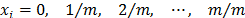 . Este diseño incluye básicamente puntos en los bordes, pero si el investigador desea hacer predicciones en el interior es recomendable agregar el centroide global y las mezclas localizadas entre el centroide y los vértices. El diseño simplex con centroide se aplica cuando se tienen pocos componentes y consiste en
. Este diseño incluye básicamente puntos en los bordes, pero si el investigador desea hacer predicciones en el interior es recomendable agregar el centroide global y las mezclas localizadas entre el centroide y los vértices. El diseño simplex con centroide se aplica cuando se tienen pocos componentes y consiste en 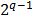 puntos definidos de la siguiente forma: las
puntos definidos de la siguiente forma: las 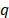 mezclas puras, todos los puntos medios de las aristas definidas por cada dos vértices, los centroides de las caras definidas por cada tres vértices y así hasta obtener el centroide global (ver Fig. 2).
mezclas puras, todos los puntos medios de las aristas definidas por cada dos vértices, los centroides de las caras definidas por cada tres vértices y así hasta obtener el centroide global (ver Fig. 2).
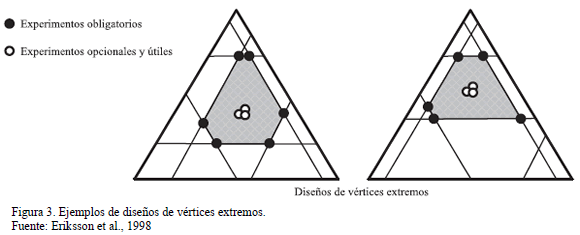
Sin embargo, cuando existen restricciones adicionales, ya sean límites inferiores y/o superiores o restricciones lineales, la región experimental ya no es regular y su forma depende de la ubicación de las restricciones (ver Fig. 3). Los puntos experimentales se colocan en los vértices extremos de la región experimental, utilizando seudocomponentes si la región está completamente al interior del simplex, y algoritmos de otro modo.
Después de recolectar las observaciones definidas en el plan experimental, es necesario ajustarlas a un modelo estadístico para investigar el efecto de los componentes sobre la respuesta. Para ello se utilizan los modelos canónicos de primer, segundo o tercer orden (ver Tabla 1), que resultan de la modificación del modelo de regresión lineal al incluir la restricción 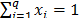 . Los parámetros del modelo se estiman utilizando el método de mínimos cuadrados y el modelo se elige en función de la cantidad de puntos experimentales, la prueba de falta de ajuste y el resumen de estadísticos.
. Los parámetros del modelo se estiman utilizando el método de mínimos cuadrados y el modelo se elige en función de la cantidad de puntos experimentales, la prueba de falta de ajuste y el resumen de estadísticos.
Una vez se tenga modelada la respuesta, el investigador puede predecirla en cualquier formulación posible dentro de la región experimental utilizada para ajustar el modelo; encontrando así, la composición de la mezcla que corresponda a un perfil de respuesta óptima. También puede cuantificar la influencia que tienen los diferentes componentes sobre la respuesta, tanto en forma individual como en su acción conjunta con otros componentes, en cuyo caso, en función de su signo se determinará si existe sinergismo o antagonismo entre los componentes.
3. Estrategias para diseñar experimentos con mezclas
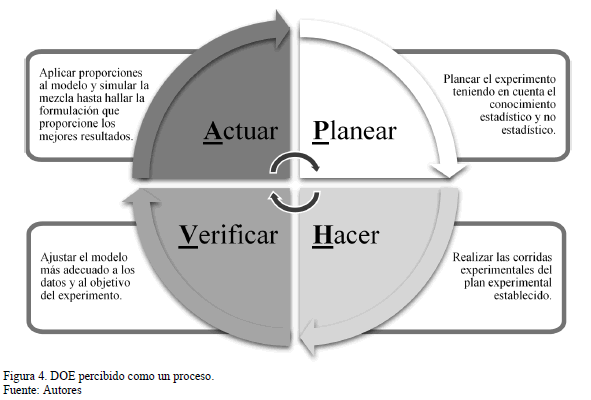
El ciclo PHVA, ideado por Walter A. Shewhart y difundido por Edwards Deming, es un método iterativo de gestión de cuatro etapas: planear, hacer, verificar y actuar; utilizado para el control y la mejora continua de procesos. Un proceso es un conjunto de actividades que interactúan para transformar elementos de entrada en resultados, los cuales a su vez pueden convertirse en entradas de otros procesos. El diseño de experimentos con mezclas visto como un proceso, puede abordarse siguiendo el ciclo PHVA (ver Fig. 4).
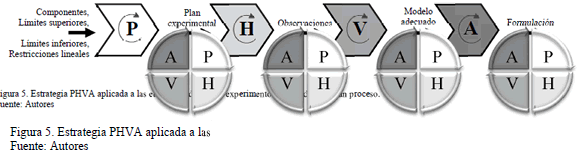
Así mismo, si cada una de estas etapas del ciclo PHVA se analizaran como si fuese un proceso y se aplicara nuevamente el ciclo PHVA a cada uno de ellas (ver Fig. 5), se podría obtener una estrategia a seguir que facilite la forma de encarar el diseño de experimentos con mezclas.
Planear - Planear: Inicie definiendo el objetivo de la experimentación, ya que el orden máximo del modelo estadístico que se podrá ajustar para modelar adecuadamente la superficie de respuesta, depende de él. Un modelo lineal es útil cuando el objetivo es la exploración, o la prueba de robustez; mientras que los cuadráticos y cúbicos son relevantes para la optimización. La exploración se utiliza en las primeras fases de una investigación, sobre todo cuando se tienen muchos componentes y se desea revelar los más importantes. La optimización se utiliza para encontrar la combinación correspondiente a un perfil de respuesta óptimo y la prueba de robustez se utiliza para asegurar el cumplimiento de las especificaciones de un producto. El siguiente paso es especificar el número de componentes. Si la mezcla tiene muchos componentes y se conocen sus efectos, se pueden mantener constantes los menos importantes o algunos de los componentes pueden, a su vez, ser mezclas de otros componentes, teniéndose mezclas dentro de mezclas [4]. Habiéndose definido 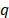 y
y 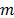 , es posible determinar el número de ensayos o puntos experimentales requeridos (ver Tabla 1). Sin embargo, los experimentos de mezclas con frecuencia requieren un modelo de orden superior al que se había planificado inicialmente. Por lo tanto, es buena idea, en la medida de lo posible, aumentar puntos experimentales más allá del mínimo requerido para ajustar el modelo.
, es posible determinar el número de ensayos o puntos experimentales requeridos (ver Tabla 1). Sin embargo, los experimentos de mezclas con frecuencia requieren un modelo de orden superior al que se había planificado inicialmente. Por lo tanto, es buena idea, en la medida de lo posible, aumentar puntos experimentales más allá del mínimo requerido para ajustar el modelo.
Luego, a partir del conocimiento no estadístico del fenómeno que se analiza, el experimentador debe considerar el uso de límites y/o restricciones para los componentes, comprobar su coherencia y realizar los ajustes que sean necesarios. Sin embargo, es necesario ser cauteloso, porque su presencia tiene impacto decisivo sobre el número de puntos experimentales, ya que la región experimental es altamente mutilada y por tanto irregular, dificultando la obtención de un diseño de mezclas significativo. Si no se tiene conocimiento que oriente la fijación de dichos límites es mejor mantener la región regular o incluir límites en algunos componentes, únicamente cuando la combinación no sea factible o resulte peligrosa, para ello se pueden hacer corridas preliminares, sin caer en el ensayo y error de planes experimentales. En ocasiones, las costumbres en la operación limitan los componentes a un rango muy estrecho o sólo se cuenta con "recetas", sintiéndonos tentados de partir de ellas y ampliar el rango de los componentes en 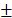 cierto porcentaje, esta situación conlleva a una región irregular que demanda muchos experimentos y puede generar problemas de multicolinealidad. Es aconsejable mantener el espíritu de investigador y por ende de incrédulo, pues los experimentos otorgan soluciones y también generan conocimientos. Así mismo, es importante tener en cuenta que si el rango de variación de un componente es pequeño, por ejemplo menor a 3%, la región experimental será muy pequeña, lo cual derivará en un modelo de regresión débil o con los signos de los coeficientes incorrectos.
cierto porcentaje, esta situación conlleva a una región irregular que demanda muchos experimentos y puede generar problemas de multicolinealidad. Es aconsejable mantener el espíritu de investigador y por ende de incrédulo, pues los experimentos otorgan soluciones y también generan conocimientos. Así mismo, es importante tener en cuenta que si el rango de variación de un componente es pequeño, por ejemplo menor a 3%, la región experimental será muy pequeña, lo cual derivará en un modelo de regresión débil o con los signos de los coeficientes incorrectos.
En función de los límites elegidos se podrán usar distintas estrategias. Cuando uno o todos los componentes tienen límites inferiores, se recomienda utilizar L-pseudocomponentes: 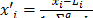 para conformar la región experimental, la cual estará dentro y con sus vértices alineados a los del simplex original. Cuando uno o todos los componentes tienen límites superiores, se recomienda utilizar U-pseudocomponentes:
para conformar la región experimental, la cual estará dentro y con sus vértices alineados a los del simplex original. Cuando uno o todos los componentes tienen límites superiores, se recomienda utilizar U-pseudocomponentes: 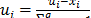 para conformar la región experimental, la cual es un simplex invertido denominado U-simplex, que deberá ser tenido en cuenta cuando se interpreten los coeficientes del modelo que se le ajuste. Si el U-simplex desborda el simplex original
para conformar la región experimental, la cual es un simplex invertido denominado U-simplex, que deberá ser tenido en cuenta cuando se interpreten los coeficientes del modelo que se le ajuste. Si el U-simplex desborda el simplex original 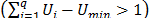 , la región experimental será la intersección con el simplex original y dejará de ser un simplex. Cuando al mismo tiempo los componentes tienen límites inferiores y superiores, la región experimental corresponde a un hiperpoliedro convexo, mucho más compleja que un simplex.
, la región experimental será la intersección con el simplex original y dejará de ser un simplex. Cuando al mismo tiempo los componentes tienen límites inferiores y superiores, la región experimental corresponde a un hiperpoliedro convexo, mucho más compleja que un simplex.
Para definir la forma y el tamaño de regiones experimentales diferentes al simplex es necesario determinar el número de vértices, bordes, caras y demás [5]. Para ajustar el modelo se requieren al menos 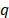 vértices para estimar los
vértices para estimar los 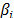 , los puntos medios de al menos
, los puntos medios de al menos 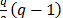 bordes para estimar los
bordes para estimar los 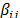 y los centroides de las caras para estimar los
y los centroides de las caras para estimar los 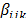 y/o realizar la prueba de ajuste del modelo. Las coordenadas se obtienen con algoritmos como el de Vértices Extremos [6], que utiliza el centroide general en vez de los centroides de las caras; el algoritmo de XVERT [7] o el algoritmo XVERT1 [8].
y/o realizar la prueba de ajuste del modelo. Las coordenadas se obtienen con algoritmos como el de Vértices Extremos [6], que utiliza el centroide general en vez de los centroides de las caras; el algoritmo de XVERT [7] o el algoritmo XVERT1 [8].
Planear - Hacer: Para generar el plan experimental se puede emplear algún programa computacional; sin embargo, se debe tener el conocimiento y la capacidad de anular cualquier plan que sea inapropiado para el problema en cuestión, teniendo en cuenta la forma y el tamaño de la región experimental. Cuando la región experimental es irregular, se recomienda al experimentador generar unos planes experimentales preliminares, libres de límites y restricciones, e introducirlos de uno en uno mientras se evalúa su efecto, pues muchas veces las coordenadas de la región se ciñen a los límites definidos sin tener que recurrir a ellos, lo cual ahorra el número de experimentos. Si esta estrategia no es factible y se hace necesario incluir todos los límites y restricciones, utilice sólo los puntos experimentales necesarios para ajustar el modelo, sin sobredefinirlo. Por otro lado, tenga en cuenta incluir réplicas que permitan obtener los grados de libertad necesarios para la prueba de ajuste del modelo, el centroide general es el punto experimental más utilizado para ello.
Planear - Verificar: El plan experimental obtenido debe revisarse cuidadosamente, verificando que los puntos experimentales sean coherentes y factibles, sobre todo los correspondientes a los centroides, porque suelen estimarse con 4 a 5 cifras decimales que dificultan su puesta en práctica, siendo necesario redondear las proporciones a una cantidad más manejable de decimales y por tanto, más realista.
La ubicación de los puntos en la región experimental influye en la determinación de los coeficientes de regresión o tiene un efecto marcado sobre las estadísticas de resumen del modelo. En un caso extremo, los estimados del parámetro pueden depender más del subconjunto influyente de puntos que de la mayor parte de los datos; lo cual es totalmente indeseable, pues se prefiere un modelo regresión que sea representativo de todas las observaciones y no de algunas. Por lo tanto, se deben localizar estos puntos influyentes y evaluar su impacto en el modelo. El diagnóstico consiste en medir el apalancamiento de la diagonal 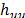 de la matriz sombrero
de la matriz sombrero 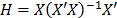 y si
y si 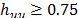 el diseño tiene puntos influyentes, por lo que se sugiere distribuirlos de forma uniforme, a través de réplicas en los puntos experimentales con
el diseño tiene puntos influyentes, por lo que se sugiere distribuirlos de forma uniforme, a través de réplicas en los puntos experimentales con 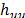 más altos [9].
más altos [9].
Planear - Actuar: Es menester del experimentador juzgar si la región a obtenerse con el plan experimental es científicamente válida y con un alto significado práctico. Si, por cualquier motivo, el plan experimental resulta inadecuado, se debe reconsiderar la configuración de componentes, límites y restricciones, retornando a la primera etapa de la estrategia.
Hacer - Planear: Por muy bueno que sea el plan experimental definido, los modelos que se ajusten a los datos pueden ser débiles si se cometen errores en la ejecución de los experimentos, por ello es importante contener las ansias y no hacerlos hasta que se cuente con un protocolo de experimentación que garantice que todas las variables que puedan tener algún efecto en la respuesta, influyan exactamente igual en todos los experimentos. Por ejemplo, trate que los operarios sean los mismos y que realicen las mismas actividades para todos los experimentos, que los instrumentos y maquinaria empleada sea la misma, que los componentes provengan del mismo lote o si son de lotes distintos que sean mezclados antes del uso, que las condiciones ambientales sean similares, que el tiempo de realización de los experimentos y el que transcurre entre ellos sean lo más similares posibles, que el proceso de experimentación sea el mismo, etc. Si el costo no es muy elevado, realice pruebas con cualquier tratamiento, en las que también participen quienes están planeando el experimento, con miras a detallar más las instrucciones y prever las acciones a emprender frente a posibles contingencias.
Para recolectar los datos diseñe una hoja de trabajo en la que se especifique de manera clara cada prueba, el orden en que será corrida y la forma en que se medirán los resultados o se colectarán los datos. Recuerde que el plan experimental debe realizarse en orden aleatorio para evitar efectos sistemáticos de factores ajenos a la experimentación. Finalmente, asegúrese que se dispone del equipo necesario para llevar a cabo la experimentación: las instalaciones y los servicios, los instrumentos de medición, los componentes en la cantidad necesaria, el personal, el tiempo, el presupuesto económico y los servicios de gestión. Cualquier problema de tipo logístico puede afectar negativamente el desarrollo de los experimentos.
Hacer - Hacer: Durante la ejecución de los experimentos es recomendable registrar en una bitácora cualquier acontecimiento anómalo o situación inesperada, que permita posteriormente explicar la presencia de datos atípicos; así como, las acciones que fueron emprendidas.
Hacer - Verificar: Tan pronto se finalicen los experimentos, es aconsejable verificar la calidad de los datos obtenidos, sometiéndolos a pruebas estadísticas para detectar valores atípicos, pues los coeficientes de regresión y los estadísticos de resumen son muy sensibles a su presencia y de acuerdo con su ubicación, pueden tener efectos moderados a graves.
Hacer - Actuar: Los valores atípicos deben ser cuidadosamente investigados, para ver si existe una razón de su comportamiento extraordinario. A veces, los atípicos se deben a eventos desacostumbrados pero explicables, como errores en la medición o en el registro, falla del instrumento de medición, etc. Si éste es el caso, el atípico debe corregirse, rehaciendo el tratamiento. Si por el contario, el atípico es una observación extraordinaria pero perfectamente factible, puede ser peligroso eliminar el punto porque se estaría perdiendo evidencia valiosa, por una sensación falsa de precisión. Cuando se tienen dudas de si mantener el atípico o quitarlo, se recomienda hacer el análisis con y sin la presunta anomalía, y si se obtienen las mismas conclusiones la disyuntiva deja de tener importancia, caso contrario se deberían recoger más datos o aplicar técnicas específicas para su tratamiento [10,11].
Verificar - Planear: A partir de los datos de un diseño es posible ajustar un modelo de primer o mayor grado, según el tipo de diseño. En esta etapa no hay mucho que planear, pues es una consecuencia de las etapas previas.
Verificar - Hacer: Utilizando un software estadístico, obtenga el análisis de varianza para evaluar la calidad de ajuste del modelo y estime los coeficientes del modelo por mínimos cuadrados, a través de una regresión.
Verificar - Verificar: El análisis de los resultados del diseño de mezclas inicia con el ajuste y selección del modelo adecuado, según el número de puntos experimentales utilizados. Para ello se cuenta con la prueba de bondad de ajuste, el coeficiente de determinación y las estadísticas de resumen. Con el criterio de la prueba de ajuste del modelo, presentada en el ANOVA, normalmente se elige el modelo más simple con un valor-p mayor que 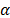 , lo cual conlleva en ocasiones a que todos los modelos sean buenos candidatos, debiéndose entonces recurrir al criterio del coeficiente de determinación
, lo cual conlleva en ocasiones a que todos los modelos sean buenos candidatos, debiéndose entonces recurrir al criterio del coeficiente de determinación 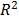 .
.
El 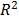 es una medida adimensional cuyo recorrido está acotado entre cero y uno, lo que facilita su cálculo e interpretación y a la vez motiva su uso excesivo, con interpretaciones abusivas y hasta erróneas. Un error frecuente en la interpretación de
es una medida adimensional cuyo recorrido está acotado entre cero y uno, lo que facilita su cálculo e interpretación y a la vez motiva su uso excesivo, con interpretaciones abusivas y hasta erróneas. Un error frecuente en la interpretación de 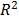 es el de no tener en cuenta que este coeficiente y el número de datos suelen variar de forma inversa; o no recordar que el número de variables explicativas consideradas en el modelo también condicionan su valor, ya que
es el de no tener en cuenta que este coeficiente y el número de datos suelen variar de forma inversa; o no recordar que el número de variables explicativas consideradas en el modelo también condicionan su valor, ya que 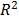 es una función no decreciente del número de variables exógenas o regresoras presentes en el modelo.
es una función no decreciente del número de variables exógenas o regresoras presentes en el modelo.
En ocasiones los investigadores seleccionan el modelo con base en el 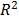 más elevado, lo cual puede conducir a conclusiones no acertadas. El objetivo de un análisis de regresión no es obtener un valor elevado de
más elevado, lo cual puede conducir a conclusiones no acertadas. El objetivo de un análisis de regresión no es obtener un valor elevado de 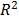 , sino obtener estimadores precisos de los verdaderos coeficientes de la regresión poblacional. En el análisis empírico no es raro encontrar valores altos de
, sino obtener estimadores precisos de los verdaderos coeficientes de la regresión poblacional. En el análisis empírico no es raro encontrar valores altos de 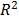 en modelos conformados con coeficientes de regresión que no son estadísticamente significativos o que tienen los signos contrarios a los esperados a priori. El investigador debe preocuparse por la relevancia lógica o teórica que tienen las variables explicativas para la variable endógena y por su significación estadística, considerando qué tanto contribuye cada término a la explicación de la variable respuesta, para de esta forma, eliminar los que tienen poca contribución, que son aquellos cuyo valor-p es mayor que
en modelos conformados con coeficientes de regresión que no son estadísticamente significativos o que tienen los signos contrarios a los esperados a priori. El investigador debe preocuparse por la relevancia lógica o teórica que tienen las variables explicativas para la variable endógena y por su significación estadística, considerando qué tanto contribuye cada término a la explicación de la variable respuesta, para de esta forma, eliminar los que tienen poca contribución, que son aquellos cuyo valor-p es mayor que 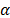 en la prueba t sobre la significancia de los términos del modelo. Sin embargo, esta prueba no es decisiva, debido a que en ocasiones los coeficientes aparentan ser significativos porque sus estimadores están correlacionados con el estimador de otro coeficiente que sí tiene contribución significativa, por lo que se sugiere analizar los efectos en
en la prueba t sobre la significancia de los términos del modelo. Sin embargo, esta prueba no es decisiva, debido a que en ocasiones los coeficientes aparentan ser significativos porque sus estimadores están correlacionados con el estimador de otro coeficiente que sí tiene contribución significativa, por lo que se sugiere analizar los efectos en 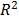 al ir eliminando los coeficientes que tienen menor contribución, retirando definitivamente aquellos coeficientes que al eliminarse mantienen casi invariable
al ir eliminando los coeficientes que tienen menor contribución, retirando definitivamente aquellos coeficientes que al eliminarse mantienen casi invariable 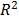 , hasta que sólo queden en el modelo términos significativos.
, hasta que sólo queden en el modelo términos significativos.
Como alternativa de solución al problema del incremento artificial del valor 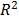 se tiene el coeficiente de determinación ajustado, que tiene la propiedad de ser neutral frente a la introducción de variables adicionales, siendo mejor su uso en lugar de
se tiene el coeficiente de determinación ajustado, que tiene la propiedad de ser neutral frente a la introducción de variables adicionales, siendo mejor su uso en lugar de 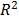 . Ahora bien, el uso de cualquiera de los coeficientes alternativos propuestos, tienen problemas propios de interpretación y no resuelve las deficiencias de
. Ahora bien, el uso de cualquiera de los coeficientes alternativos propuestos, tienen problemas propios de interpretación y no resuelve las deficiencias de 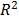 . Aunque el
. Aunque el 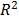 es una de las medidas preferidas para evaluar el grado de ajuste del modelo al conjunto de observaciones, esta medida debe emplearse junto a otras para obtener conclusiones válidas, pues su exclusiva consideración puede conducir a errores importantes en el análisis de regresión.
es una de las medidas preferidas para evaluar el grado de ajuste del modelo al conjunto de observaciones, esta medida debe emplearse junto a otras para obtener conclusiones válidas, pues su exclusiva consideración puede conducir a errores importantes en el análisis de regresión.
Entre las medidas sugeridas está el error estándar de la regresión 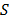 , que representa la dispersión entre las observaciones y el modelo; por lo que cuanto más bajo sea su valor, mejor pronosticará el modelo. Otra medida es la suma de los cuadrados de predicción PRESS, que también evalúa la capacidad predictora del modelo, prefiriéndose los valores pequeños. El factor de inflación de la varianza VIF, que indica en qué medida la multicolinealidad está presente en un análisis de regresión. Si
, que representa la dispersión entre las observaciones y el modelo; por lo que cuanto más bajo sea su valor, mejor pronosticará el modelo. Otra medida es la suma de los cuadrados de predicción PRESS, que también evalúa la capacidad predictora del modelo, prefiriéndose los valores pequeños. El factor de inflación de la varianza VIF, que indica en qué medida la multicolinealidad está presente en un análisis de regresión. Si 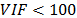 no hay serios problemas de colinealidad, si
no hay serios problemas de colinealidad, si 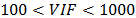 implica moderada a alta colinealidad y
implica moderada a alta colinealidad y 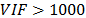 la colinealidad es severa. La multicolinealidad puede influir en forma dramática sobre la capacidad de estimar los coeficientes, haciendo que sean inestables, difíciles de interpretar e incluso con el signo incorrecto [12]. Su presencia se debe a múltiples causas, entre ellas las restricciones muy estrechas y el uso de modelos sobredefinidos. Sin embargo, los diseños de mezclas son propensos a la multicolinealidad, debido a la restricción
la colinealidad es severa. La multicolinealidad puede influir en forma dramática sobre la capacidad de estimar los coeficientes, haciendo que sean inestables, difíciles de interpretar e incluso con el signo incorrecto [12]. Su presencia se debe a múltiples causas, entre ellas las restricciones muy estrechas y el uso de modelos sobredefinidos. Sin embargo, los diseños de mezclas son propensos a la multicolinealidad, debido a la restricción 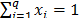 , por lo que debemos aprender a vivir con ella [5], o usar modelos alternativos como la regresión por mínimos cuadrados parciales - PLS, que no asume dependencia matemática entre componentes [13]. Tenga presente que los buenos modelos son aquellos que cumplen más criterios de calidad del ajuste y que siempre existirán circunstancias en las que, al no cumplirse alguno de los criterios, desde el punto de vista práctico no necesariamente harán inviable el modelo; pero, bajo calidad similar en el ajuste de dos modelos, siempre ha de preferirse el más sencillo. Finalmente, la validez de los resultados obtenidos queda supeditado a que los supuestos del modelo (normalidad, varianza constante e independencia de los residuos) se cumplan.
, por lo que debemos aprender a vivir con ella [5], o usar modelos alternativos como la regresión por mínimos cuadrados parciales - PLS, que no asume dependencia matemática entre componentes [13]. Tenga presente que los buenos modelos son aquellos que cumplen más criterios de calidad del ajuste y que siempre existirán circunstancias en las que, al no cumplirse alguno de los criterios, desde el punto de vista práctico no necesariamente harán inviable el modelo; pero, bajo calidad similar en el ajuste de dos modelos, siempre ha de preferirse el más sencillo. Finalmente, la validez de los resultados obtenidos queda supeditado a que los supuestos del modelo (normalidad, varianza constante e independencia de los residuos) se cumplan.
Verificar - Actuar: Si el modelo cumplió los criterios formales de evaluación podrá continuar a la etapa siguiente, caso contrario deberá retornar a la primera etapa de esta estrategia. Si no son satisfactorias las comprobaciones comunes de diagnóstico de adecuación del modelo, se deberá recurrir a las transformaciones.
Actuar - Planear: Aunque la ecuación se ajuste bien a los datos, y pase las pruebas normales de diagnóstico, no hay seguridad de que vaya a predecir con exactitud nuevas observaciones. Se recomienda evaluar la capacidad predictiva del modelo, con corridas de confirmación pertenecientes a la región experimental.
Actuar - Hacer: Realice los experimentos adicionales siguiendo estrictamente todo lo indicado en la etapa Hacer de esta estrategia. Emplee varias repeticiones para que se tenga una buena estimación de lo logrado.
Actuar - Verificar: Confirme la capacidad predictora del modelo ajustado, comparando los resultados experimentales contra los predichos. Si el modelo predice satisfactoriamente continúe el análisis, caso contrario deberá modificar el modelo, ya sea aumentando el diseño o retornando a la etapa inicial de esta estrategia, lo cual no significa que se han perdido recursos, sino que se ha logrado más conocimiento de la mezcla analizada. Saque provecho de lo realizado y trate de entender el fenómeno. Según Ronald Fisher, "el mejor momento para planificar una investigación es después de haberla hecho". No cometa el error de desechar el experimento y valorarlo como un fracaso. Por el contrario, teniendo en cuenta el ciclo PHVA, use el aprendizaje obtenido en el nuevo ciclo.
Además de los criterios formales de evaluación, el investigador debe preguntarse ¿es razonable la ecuación, las magnitudes de sus coeficientes y sus signos?, ¿tienen sentido los regresores en el modelo, considerando su contexto?, ¿los errores estándar son relativamente pequeños?, ¿el modelo obtenido es técnica y económicamente factible? Recuerde que en las industrias pesa más el valor económico que el estadístico, se pueden tener fórmulas estadísticamente válidas pero que por carecer de sentido práctico son abandonadas.
Luego, interprete los coeficientes significativos obtenidos. Debido a la restricción de que la suma de las proporciones siempre es igual a la unidad, el efecto de un componente en un diseño de mezclas es diferente al efecto de un diseño factorial. Cuando el modelo es lineal, la mezcla es estrictamente aditiva. En mezclas no aditivas, dependiendo del signo del coeficiente se tendrá sinergismo o antagonismo entre los componentes. Tenga en cuenta la forma del simplex, especialmente si usó un U-simplex. Finalmente, realice la superficie de respuesta y verifique las tendencias.
Actuar - Actuar: Habiéndose obtenido un modelo estadísticamente válido y con alto significado práctico, es hora de emplearlo para determinar en qué porcentaje debe participar cada uno de los componentes para lograr que la fórmula tenga las propiedades deseadas. Se debe evitar el riesgo de hacer extrapolaciones indiscriminadas con base en el modelo, que van más allá de la región que contienen las observaciones originales. En caso de contar con varias variables respuestas, utilice la optimización simultánea.
Estas estrategias se hacen desde el punto de vista del experimentador, más que desde una perspectiva teórica elaborada y buscan facilitar el uso del diseño de experimentos de mezclas sin pretender constituirse en un manual, por lo que los investigadores deberán ampliar estos conceptos a la hora de aplicarlos.
4. Conclusiones
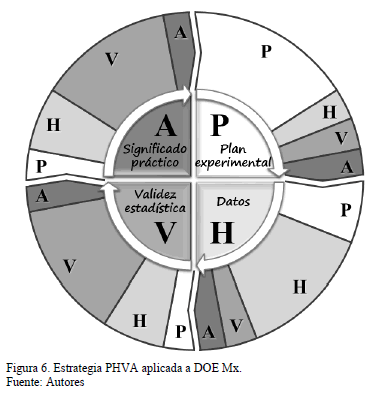
Las bondades del uso del diseño de experimento para la formulación de mezclas industriales son superiores al método tradicional del ensayo y error; sin embargo, es necesario asegurar su correcta aplicación, para ello se puede usar la estrategia del ciclo PHVA para definir el plan experimental, obtener los datos, ajustar un modelo estadísticamente significativo y con alto significado práctico (ver Fig. 6).
Si bien todas las etapas de esta estrategia son importantes, la etapa planificar es la más crítica, pues conocer los límites, las restricciones, la forma y el tamaño de la región experimental facilita la creación del diseño. Ignorar estas dimensiones vulnera al experimentador tornándolo totalmente dependiente de algún programa computacional y sin ninguna garantía de que el número total de experimentos del plan, es el correcto para los objetivos establecidos. Por otro lado, la elección del modelo adecuado, en la etapa verificar no puede supeditarse simplemente al 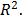 Finalmente, en la industria cobra un gran significado la validez técnica y económica de las formulaciones que se desarrollen. En la Fig. 6, se representa a escala el desarrollo de esta estrategia.
Finalmente, en la industria cobra un gran significado la validez técnica y económica de las formulaciones que se desarrollen. En la Fig. 6, se representa a escala el desarrollo de esta estrategia.
Referencias
[1] Zamora-Morales, B.P., Sánchez-García, P., Volke-Haller, V.H., Espinosa-Victoria, D. y Galvis-Spínola, A., Formulación de mezclas de sustratos mediante programación lineal. Interciencia, 30 (6), pp. 365-369, 2005. [ Links ]
[2] Cafaggi, S., Leardi, R., Parodi, B, Caviglioli, G. and Bignardi, G., An example of application of a mixture design with constraints to a pharmaceutical formulation. Chemometrics and Intelligent Laboratory Systems, 65 (1), pp. 139-147, 2003. doi: 10.1016/S0169-7439(02)00045-X [ Links ]
[3] Gutiérrez-Pulido, H. y De la Vara-Salazar R., Análisis y diseño de experimentos. Segunda edición. México: McGrawHill, 2008. 483 P. [ Links ]
[4] Eriksson, L., Johansson, E. and Wikstrom, C., Mixture design - design generation, PLS analysis, and model usage. Chemometrics and Intelligent Laboratory Systems, 43, pp. 1-24, 1998. doi: 10.1016/S0169-7439(98)00126-9 [ Links ]
[5] Cornell, J.A., Experiments with mixtures. Tercera edición. Nueva York: John Wiley & Sons, 2002. [ Links ]
[6] cLean, R.A. and Anderson, V.L., Extreme vertices design of mixture experiments. Technometrics, 8, pp. 447-454, 1966. doi: 10.1080/00401706.1966.10490378 [ Links ]
[7] Snee, R.D. and Marquardt, D.W., Extreme vertices design for linear mixture models. Technometrics, 16, pp. 399-408, 1974. doi: 10.2307/1267670 [ Links ]
[8] Nigam, A.K., Gupta, S.C. and Gupta, S., A new algorithm for extreme vertices designs for linear mixture models. Technometrics, 25, pp. 367-371, 1983. doi: 10.2307/1267858 [ Links ]
[9] Montgomery, D.C. and Voth, S.R., Multicollinearity and leverage in mixture design. Journal of Quality Technology, 26, pp. 96-108, 1994. [ Links ]
[10] Barnett, V. and Lewis, T., Outliers in statistical data. Segunda edición. Nueva York: Wiley, 1994. [ Links ]
[11] Myers, R.H., Classical and modern regression with aplications. Segunda edición. Boston: Publishers P-K, USA. 1990. [ Links ]
[12] Akay, K.U., A Note on model selection in mixture experiments. Journal of Mathematics and Statistics, 3 (3), pp. 93-99, 2007. doi: 10.3844/jmssp.2007.93.99 [ Links ]
[13] Muteki, K., MacGregor, J.F. and Ueda, T., Mixture designs and models for the simultaneous selection of ingredients and their ratios. Chemometrics and Intelligent Laboratory Systems, 86 (1), pp. 17-25, 2007. doi: 10.1016/j.chemolab.2006.08.003 [ Links ]
D.C. Ortega-Pérez, graduada de Geología en 1991, de la Universidad EAFIT, Colombia, Esp. en Técnicas de Microscopía Electrónica del Instituto Eduardo Torroja, España, MSc. en Ingeniería de Minerales de la Universidad de Exeter, Inglaterra y candidata a Dr. en Ingeniería, Ciencia y Tecnología de Materiales de la Universidad Nacional de Colombia.
M.O. Bustamente-Rua, graduado de Ingeniería de Minas y Metalurgia en 1986, de la Universidad Nacional de Colombia, Esp. en Minería y Metalurgia en 1988, MSc. en Minería y Metalurgia en 1991 y Dr en Minería y Metalurgia en 1999, todos ellos de la Universidad de Concepción, Chile.
D.F. Gutiérrez-Rôa, graduada de Ingeniería Industrial en 2004 de la Universidad Mayor de San Simón, Bolivia, Esp. en Sistemas de Gestión de Calidad en 2006 y Magíster en Ingeniería Administrativa en 2010, ambos de la Universidad Nacional de Colombia.
A.A. Correa-Espinal, graduado de Ingeniería Industrial en 1995 de la Universidad Nacional de Colombia, MSc. en Ingeniería Industrial en 1999 de la Universidad de los Andes y Dr. en Estadística e Investigación Operativa en 2007, de la Universidad Politécnica de Cataluña, España. Profesor de tiempo completo del Departamento de Ingeniería de la Organización, Facultad de Minas, Universidad Nacional de Colombia.