Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.189 Medellín Jan./Feb. 2015
https://doi.org/10.15446/dyna.v82n189.48552
http://dx.doi.org/10.15446/dyna.v82n189.48552
A hybrid metaheuristic algorithm for the capacitated location routing problem
Un algoritmo metaheurístico híbrido para el problema de localización y ruteo con restricciones de capacidad
John Willmer Escobar a, Rodrigo Linfati b & Wilson Adarme-Jaimes c
a Departamento de Ingeniería Civil e Industrial, Pontificia Universidad Javeriana, Cali, Colombia. jwescobar@javerianacali.edu.co
b Departamento de Ingeniería Industrial, Universidad del Bío-Bío, Concepción, Chile. rlinfati@ubiobio.cl
c Departamento de Ingeniería de Sistemas e Industrial, Universidad Nacional de Colombia, Bogotá, Colombia. wadarmej@unal.edu.co
Received: June 22th, 2014. Received in revised form: June 17th, 2014. Accepted: June 18th, 2014.
Abstract
This paper addresses the Capacitated Location-Routing Problem (CLRP) in which the aim is to determine the depots to be opened, the customers to be assigned to each open depot, and the routes to be performed to fulfill the demand of the customers. The objective is to minimize the sum of the cost of the open depots, of the used vehicle costs, and of the variable costs associated with the distance traveled by the performed routes. In this paper, a Granular Tabu Search (GTS) with different diversification strategies within a Iterated Local Search (ILS) is proposed to solve the CLRP. A shaking procedure is applied whenever the best solution found so far is not improved for a given number of iterations. Computational experiments on benchmark instances taken from the literature show that the proposed approach is able to obtain, within short computing times, high quality solutions illustrating its effectiveness.
Keywords: Location Routing Problem (LRP), Iterated Local Search (ILS), Granular Tabu Search (GTS), Metaheuristic Algorithms.
Resumen
Este artículo considera el problema de localización y ruteo con restricciones de capacidad (CLRP), en el cual la meta es determinar los depósitos a ser abiertos, los clientes a ser asignados a cada depósito abierto y las rutas a ser desarrolladas para satisfacer la demanda de los clientes. El objetivo es minimizar la suma de los costos fijos de los depósitos abiertos, el costo del uso de los vehículos, y los costos variables asociados con la distancia recorrida por las rutas. En este artículo, una búsqueda tabú granular (GTS) con diferentes estrategias de diversificación contenida en una búsqueda iterativa local (ILS) es propuesta para resolver el CLRP. Un procedimiento de perturbación es aplicado cuando la mejor solución encontrada no se puede mejorar por un número determinado de iteraciones. Experimentos computacionales sobre instancias de benchmarking tomadas de la literatura muestran que el algoritmo propuesto es capaz de obtener, con tiempos computacionales reducidos, soluciones de alta calidad mostrando su efectividad.
Palabras clave: Problema de Localización y Ruteo (LRP), Búsqueda Iterativa Local (ILS), Búsqueda Tabú Granular (GTS), Algoritmos Metaheuristicos.
1. Introducción
El problema de localización y ruteo con restricciones de capacidad (CLRP) puede ser modelado como el siguiente problema de grafos: Sea 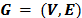 un grafo indirecto, donde
un grafo indirecto, donde 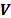 es un conjunto de nodos que contienen un subconjunto
es un conjunto de nodos que contienen un subconjunto 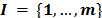 de depósitos potenciales y un subconjunto
de depósitos potenciales y un subconjunto 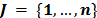 de clientes. Cada depósito potencial
de clientes. Cada depósito potencial 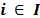 tiene una capacidad
tiene una capacidad 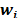 y un costo de apertura
y un costo de apertura 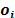 . Cada cliente
. Cada cliente 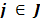 tiene una demanda
tiene una demanda 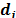 la cual debe ser satisfecha por un depósito abierto. Un conjunto de vehículos idénticos, cada uno con capacidad
la cual debe ser satisfecha por un depósito abierto. Un conjunto de vehículos idénticos, cada uno con capacidad 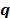 y costo fijo
y costo fijo 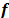 , está disponible en cada depósito
, está disponible en cada depósito 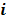 . Cada arco
. Cada arco 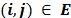 es asociado con un costo de viaje
es asociado con un costo de viaje 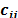 . La meta del CLRP es determinar los depósitos a ser abiertos, los clientes a ser asignados a cada depósito abierto y las rutas a ser desarrolladas para satisfacer las demandas de los clientes. Las siguientes restricciones son impuestas:
. La meta del CLRP es determinar los depósitos a ser abiertos, los clientes a ser asignados a cada depósito abierto y las rutas a ser desarrolladas para satisfacer las demandas de los clientes. Las siguientes restricciones son impuestas:
- Cada ruta debe comenzar y finalizar en el mismo depósito;
- Cada cliente debe ser visitado exactamente una vez por una sola ruta;
- La carga total de cada ruta debe no exceder la capacidad del vehículo
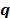 ;
; - La carga total de las rutas asignadas a un depósito abierto i no debe exceder su capacidad
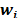 .
.
La función objetivo del CLRP está determinada por la suma de los costos de apertura, de los costos de viaje y de los costos fijos asociados con los vehículos usados. El CLRP es conocido por ser un problema NP-hard, desde que este es una generalización de dos problemas NP-hard: el problema de localización de instalaciones con restricciones de capacidad (CFLP) y el problema de ruteo de vehículos con múltiples depósitos (MDVRP).
Algoritmos exactos han sido propuestos para resolver el CLRP en [1-3]. Estas aproximaciones han sido capaces de probar optimalidad en instancias de tamaño mediano (menores o iguales a 150 clientes). Debido a esto, heurísticas y metaheurísticas han sido propuestas para resolver exitosamente instancias de CLRP de gran tamaño.
En [4] se propone una búsqueda tabú de dos fases para resolver el CLRP. La búsqueda tabú de dos fases itera entre la etapa de localización y la etapa de ruteo, en aras de obtener mejores soluciones para instancias de gran tamaño. En este trabajo, resultados para instancias de hasta 200 clientes son reportados. Otro algoritmo basado en una aproximación de dos fases ha sido propuesto por [5]. En la primera fase (fase de localización), los clientes son agregados en nodos llamados "súper-clientes" y el problema de localización con restricciones de capacidad es resuelto a través de una relajación Langragiana. En la segunda fase (fase de ruteo), una búsqueda tabú granular (GTS) con un vecindario es usado para resolver el correspondiente problema de ruteo de vehículos (VRP) para cada depósito.
Métodos basados en agrupación han sido propuesto por [6]. Estos métodos consideran tres etapas. En la primera etapa, el conjunto de clientes son divididos en grupos de acuerdo a la capacidad de vehículos. En la segunda etapa, un problema de viajero de negocios (TSP) es resuelto para cada grupo. Finalmente, en la tercer etapa, cada tour TSP es agrupado en "súper-clientes" para resolver el correspondiente problema de localización de instalaciones con restricciones de capacidad (CFLP).
En [7] se propone un procedimiento aleatorio goloso (GRASP) con una estrategia de conectividad de soluciones de alta calidad para el CLRP. Los mismos autores (ver [8]) han propuesto una algoritmo memético con administración de la población.
Recientemente, varios algoritmos metaheurísticos han sido propuestos por [9-13]. En [9], una búsqueda de vecindario variable con siete vecindarios ha sido propuesto. En el segundo trabajo ([10]), se propone una metaheurística basada en un GRASP híbrido con una búsqueda local evolutiva (ELS). En [11] se propone un algoritmo basado en recocido simulado con tres vecindarios aleatorios para el CLRP. En [12] se han introducido una búsqueda de vecindario variable para el problema de localización y ruteo periódico con restricciones de capacidad (PLRP) y para el CLRP. En este trabajo, una combinación de una búsqueda de vecindario variable (VNS) pura con la solución de varios ILPs es considerada para la solución del CLRP. Finalmente, en [13] se ha propuesto un algoritmo exitoso de dos fases, el cual es capaz de encontrar soluciones de alta calidad dentro de tiempos computacionales cortos.
En este artículo, se introduce una metaheurística basada en una búsqueda tabú granular dentro de una búsqueda iterativa local para el CLRP. El algoritmo propuesto explota la potencialidad de la búsqueda local iterativa que ha sido estudiada en [14] y la búsqueda tabú eficiente propuesta en [15]. En la literatura revisada hasta el momento no se ha hallado la combinación del GTS dentro de un esquema de ILS. El artículo está organizado de la siguiente forma. En la sección 2 el marco general del algoritmo es detallado. Sección 3 presenta el algoritmo propuesto, denominado GITS. Experimentos computacionales en las instancias de benchmarking son mostradas en Sección 4. Finalmente, sección 5 detalla las conclusiones e investigación futura.
2. Marco general del algoritmo
2.1. Esquema de la Búsqueda Local Iterativa (ILS)
Esta técnica ha sido propuesta a principios de los años 1980 ([16]). La búsqueda local iterativa es principalmente una versión mejorada del algoritmo Ascenso de Colina (Hill Climbing) con reinicios aleatorios. Este método realiza una búsqueda de óptimos locales, ya que realiza un tour desde un óptimo local a otro.
La ILS se basa en dos principios. Primero, el ILS no escoge un reinicio aleatorio al azar, sino que busca un punto de reinicio lo suficientemente lejano para obtener un óptimo local diferente al actual, pero a su vez, suficientemente cerca para que no ser una búsqueda aleatoria de óptimos locales. Segundo, cuando encuentra un nuevo óptimo local debe decidir si utilizarlo como nuevo punto de partida para el reinicio o no, en caso de escoger siempre el nuevo óptimo local se estaría en presencia de una caminata aleatoria, si sólo se seleccionan óptimos locales nuevos mejores que el anterior, se estaría haciendo un proceso de Ascenso de Colina (Hill Climbing). La ILS escoge un punto intermedio entre ambos extremos.
2.2. Espacio de búsqueda granular
El algoritmo propuesto utiliza la idea de un espacio de búsqueda granular introducida por [15], el cual está basado en la utilización de un grafo incompleto que contiene los arcos incidentes a los depósitos, los arcos que pertenecen a las mejores soluciones encontradas durante la búsqueda y los arcos cuyo costo es menor que un valor de 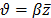 , donde
, donde 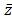 , es el costo promedio de los arcos de la mejor solución factible encontrada durante la búsqueda y
, es el costo promedio de los arcos de la mejor solución factible encontrada durante la búsqueda y 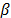 es un factor de esparsificación, actualizado dinámicamente durante la búsqueda. La modificación dinámica del grafo incompleto permite al algoritmo alternar entre etapas extensas de intensificación y etapas breves de diversificación. Un valor pequeño de
es un factor de esparsificación, actualizado dinámicamente durante la búsqueda. La modificación dinámica del grafo incompleto permite al algoritmo alternar entre etapas extensas de intensificación y etapas breves de diversificación. Un valor pequeño de 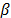 es asociado con etapas de intensificación, mientras que un valor alto de
es asociado con etapas de intensificación, mientras que un valor alto de 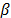 es asociado con etapas de diversificación. La idea general de la búsqueda tabú granular es encontrar soluciones de gran calidad, conservando las características de la búsqueda tabú original, dentro de tiempos de computación cortos.
es asociado con etapas de diversificación. La idea general de la búsqueda tabú granular es encontrar soluciones de gran calidad, conservando las características de la búsqueda tabú original, dentro de tiempos de computación cortos.
2.3. Procedimiento de solución inicial
La solución inicial 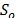 es construida usando un algoritmo híbrido propuesto por [13]. Este algoritmo es usado para construir la solución inicial, debido a la capacidad de obtener buenas soluciones factibles dentro de tiempos de computación razonables. Primero, un tour TSP gigante es construido conteniendo todos los clientes mediante la conocida heurística Lin-Kernighan (LKH) ([17]). Luego el tour gigante es partido en varios grupos para cada uno de los cuales, la capacidad del vehículo es satisfecha.
es construida usando un algoritmo híbrido propuesto por [13]. Este algoritmo es usado para construir la solución inicial, debido a la capacidad de obtener buenas soluciones factibles dentro de tiempos de computación razonables. Primero, un tour TSP gigante es construido conteniendo todos los clientes mediante la conocida heurística Lin-Kernighan (LKH) ([17]). Luego el tour gigante es partido en varios grupos para cada uno de los cuales, la capacidad del vehículo es satisfecha.
Para cada depósito 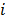 y cada grupo
y cada grupo 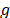 , un TSP tour es ejecutado para obtener la distancia real de asignar el depósito
, un TSP tour es ejecutado para obtener la distancia real de asignar el depósito 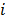 al cluster
al cluster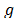 . Luego, los depósitos son asignados a los grupos resolviendo un modelo de programación entera mixta correspondiente al bien conocido problema de localización con restricciones de capacidad y fuente única (ver, e.g. [18] y [19]).
. Luego, los depósitos son asignados a los grupos resolviendo un modelo de programación entera mixta correspondiente al bien conocido problema de localización con restricciones de capacidad y fuente única (ver, e.g. [18] y [19]).
Note que el procedimiento de solución inicial es repetido 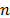 veces (donde
veces (donde 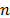 es el número de clientes) seleccionando cada vértice como vértice inicial para dividir el tour gigante. Finalmente, un procedimiento de división es aplicado para reducir el costo de la distancia recorrida por las rutas adicionando nuevas rutas y asignándolas a diferentes depósitos [13]. El procedimiento de división es aplicado dos veces manteniendo la solución mejor solución factible encontrada.
es el número de clientes) seleccionando cada vértice como vértice inicial para dividir el tour gigante. Finalmente, un procedimiento de división es aplicado para reducir el costo de la distancia recorrida por las rutas adicionando nuevas rutas y asignándolas a diferentes depósitos [13]. El procedimiento de división es aplicado dos veces manteniendo la solución mejor solución factible encontrada.
2.4. Vecindarios
El algoritmo propuesto permite soluciones infactibles con respecto a las capacidades de los vehículos y de los depósitos. Dada una solución factible S durante la búsqueda tabú granular, se asigna un valor de la función objetivo 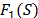 . El valor de
. El valor de 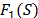 es igual a la suma de los costos fijos de los depósitos abiertos, del costo de la distancia recorrida por los arcos que pertenecen a las rutas de la solución
es igual a la suma de los costos fijos de los depósitos abiertos, del costo de la distancia recorrida por los arcos que pertenecen a las rutas de la solución 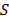 , y del costo fijo de los vehículos usados en
, y del costo fijo de los vehículos usados en 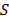 . En adición, para cada solución infactible
. En adición, para cada solución infactible 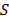 con respecto a la capacidad del depósito, se adiciona a
con respecto a la capacidad del depósito, se adiciona a 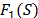 un término de penalización obtenido por la multiplicación de la capacidad extra del depósito por un parámetro de penalización dinámicamente actualizado durante la búsqueda
un término de penalización obtenido por la multiplicación de la capacidad extra del depósito por un parámetro de penalización dinámicamente actualizado durante la búsqueda 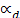 . De esta manera, el valor de la función objetivo
. De esta manera, el valor de la función objetivo 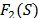 es obtenido. Un procedimiento similar es aplicado al valor de la función objetivo para cualquier solución
es obtenido. Un procedimiento similar es aplicado al valor de la función objetivo para cualquier solución 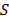 infactible con respecto a la capacidad de los vehículos usando un factor de penalización
infactible con respecto a la capacidad de los vehículos usando un factor de penalización 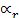 . Note que si la solución
. Note que si la solución 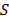 es factible
es factible 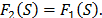
En particular, si se han encontrado soluciones infactibles respecto a la capacidad del depósito durante 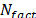 iteraciones, el valor del factor de penalización
iteraciones, el valor del factor de penalización 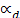 es calculado como el
es calculado como el 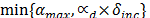 , donde
, donde 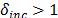 . De lo contrario, si soluciones factibles se han encontrado con respecto a la capacidad del depósito durante
. De lo contrario, si soluciones factibles se han encontrado con respecto a la capacidad del depósito durante 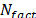 iteraciones, el valor del factor de penalización
iteraciones, el valor del factor de penalización 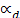 es calculado como
es calculado como 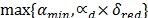 , donde
, donde 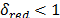 .
. 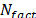 ,
, 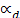 ,
, 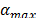 ,
, 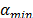 ,
, 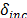 y
y 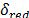 son parámetros ajustados. Una aproximación similar es aplicada para calcular el valor del factor de penalización
son parámetros ajustados. Una aproximación similar es aplicada para calcular el valor del factor de penalización 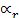 . El algoritmo metaheurístico aplica movimientos entre rutas y al interior de las rutas correspondiente a los siguientes vecindarios:
. El algoritmo metaheurístico aplica movimientos entre rutas y al interior de las rutas correspondiente a los siguientes vecindarios:
- Inserción: Un cliente es transferido de su posición actual a otra posición, dentro de la misma ruta o en una ruta diferente (que pertenece al mismo depósito o a otro diferente).
- Intercambio: Un par de clientes son intercambiados al mismo tiempo en la misma ruta o en una ruta diferente (que pertenece al mismo depósito o a otro diferente).
- Two-opt: Esta es una extensión del movimiento tradicional Two opt. Si los dos clientes pertenecen a la misma ruta, el movimiento es considerado como el bien conocido movimiento intra ruta Two-opt ([17]). Si los clientes pertenecen a una ruta diferente que pertenece a un mismo depósito, el movimiento es similar al tradicional Two-opt en el problema de ruteo de vehículos (VRP). De lo contrario, si cada par de clientes pertenecen a depósitos diferentes, es necesario desarrollar un movimiento adicional con los arcos incidentes a los depósitos para reconectar las rutas de forma correcta.
- Doble inserción: Dos clientes son transferidos de su posición actual a otra posición manteniendo el arco que los conectan. Los clientes pueden ser insertados en la ruta actual o en una ruta diferente (perteneciendo al mismo depósito o a uno diferente).
- Doble intercambio: Un par de arcos son intercambiados al mismo tiempo. Los arcos puedes estar en la misma ruta o en una ruta diferente (que pertenece al mismo depósito o a otro diferente).
Un movimiento es realizado sólo si los nuevos arcos insertados en la solución están en el espacio de búsqueda granular.
3. Descripción del algoritmo propuesto
Esta sección presenta la discusión del algoritmo desarrollado (GITS) para la solución del CLRP. El algoritmo propuesto utiliza una búsqueda tabú granular (GTS) internamente dentro de una búsqueda iterativa local (ILS) para las estructuras de vecindario descritas en la sección anterior. En particular, ILS controla la búsqueda global; mientras que el GTS guía el proceso de búsqueda local usando los diferentes vecindarios y el eficiente espacio de búsqueda descrito en la sección 2.2.
En particular, después de construir la solución inicial 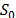 (mediante el procedimiento descrito en la sección 2.3), GITS itera a través de diferentes vecindarios para mejorar la mejor solución factible encontrada durante la búsqueda. El algoritmo propuesto selecciona un vecindario de las estructuras descritas en la sección 2.4, y aplica una búsqueda tabú granular (GTS) en el vecindario seleccionado hasta que un mínimo local es encontrado. Luego el vecindario es reiniciado aleatoriamente y de nuevo el procedimiento GTS es aplicado. El algoritmo es ejecutado por
(mediante el procedimiento descrito en la sección 2.3), GITS itera a través de diferentes vecindarios para mejorar la mejor solución factible encontrada durante la búsqueda. El algoritmo propuesto selecciona un vecindario de las estructuras descritas en la sección 2.4, y aplica una búsqueda tabú granular (GTS) en el vecindario seleccionado hasta que un mínimo local es encontrado. Luego el vecindario es reiniciado aleatoriamente y de nuevo el procedimiento GTS es aplicado. El algoritmo es ejecutado por 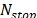 iteraciones (donde
iteraciones (donde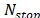 es un parámetro dado).
es un parámetro dado).
El procedimiento GTS explora el espacio de solución moviéndose en cada iteración de una solución 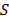 a la mejor solución (solución con el menor valor en el vecindario
a la mejor solución (solución con el menor valor en el vecindario 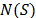 , de
, de 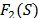 , inclusive si esta es infactible). El último movimiento es declarado como tabú. El tamaño de la lista tabú es aleatoriamente ajustado en el intervalo
, inclusive si esta es infactible). El último movimiento es declarado como tabú. El tamaño de la lista tabú es aleatoriamente ajustado en el intervalo 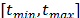 , donde
, donde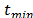 y
y 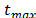 son paramétricos.
son paramétricos.
El GTS considera tres estrategias de diversificación. La primera estrategia está basada en la diversificación granular propuesta por [15]. Inicialmente el factor de esparsificación es ajustado a un valor pequeño 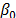 . Cuando la mejor solución factible no es mejorada después de
. Cuando la mejor solución factible no es mejorada después de 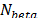 iteraciones, el factor de esparsificación
iteraciones, el factor de esparsificación 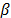 es incrementado a
es incrementado a 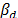 . Luego un nuevo grafo es calculado, y
. Luego un nuevo grafo es calculado, y 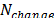 iteraciones son desarrollados comenzando de la mejor solución factible encontrada. Finalmente, el factor de esparsificación es reseteado a su valor original
iteraciones son desarrollados comenzando de la mejor solución factible encontrada. Finalmente, el factor de esparsificación es reseteado a su valor original 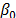 y la búsqueda continua.
y la búsqueda continua. 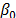 ,
, 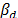 ,
, 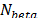 y
y 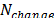 son paramétricos.
son paramétricos.
La segunda estrategia de diversificación está basada en un esquema de penalización: en la selección del mejor movimiento a ser desarrollado para cualquier solución infactible 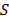 , un término extra de penalidad
, un término extra de penalidad 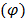 es adiccionado al valor de la función objetivo
es adiccionado al valor de la función objetivo 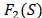 . El valor de
. El valor de 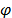 es igual al producto de la diferencia absoluta
es igual al producto de la diferencia absoluta 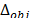 entre dos valores sucesivos de la función objetivo, de la raíz cuadrada del número de rutas
entre dos valores sucesivos de la función objetivo, de la raíz cuadrada del número de rutas 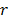 , y del factor de escala
, y del factor de escala 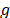 ( [20]). Finalmente, la última estrategia de diversificación determina cada
( [20]). Finalmente, la última estrategia de diversificación determina cada 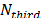 iteraciones (donde
iteraciones (donde 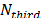 es un parámetro dado) una solución factible usando el procedimiento VRPH propuesto por [13] para el problema del CLRP.
es un parámetro dado) una solución factible usando el procedimiento VRPH propuesto por [13] para el problema del CLRP.
Finalmente, un procedimiento de perturbación es aplicado cuando el GTS se mantiene en óptimo local por un 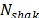 número de iteraciones (donde
número de iteraciones (donde 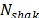 es un parámetro dado). En particular, este procedimiento aplica el movimiento de inserción considerando tres rutas aleatorias al mismo tiempo (por mayores detalles ver [21]). En particular, nosotros consideramos un procedimiento aleatorio de selección de las rutas a ser perturbadas. El algoritmo selecciona la primera ruta (k1) aleatoriamente. La segunda ruta (k2) es el vecino más cercano de k1, y la tercera ruta (k3) es el vecino más cercano de k2, diferente a k1. La evaluación de la distancia entre rutas se calcula teniendo en cuenta su ''centro de gravedad''.
es un parámetro dado). En particular, este procedimiento aplica el movimiento de inserción considerando tres rutas aleatorias al mismo tiempo (por mayores detalles ver [21]). En particular, nosotros consideramos un procedimiento aleatorio de selección de las rutas a ser perturbadas. El algoritmo selecciona la primera ruta (k1) aleatoriamente. La segunda ruta (k2) es el vecino más cercano de k1, y la tercera ruta (k3) es el vecino más cercano de k2, diferente a k1. La evaluación de la distancia entre rutas se calcula teniendo en cuenta su ''centro de gravedad''.
Para cada cliente i1 de la ruta k1, cada cliente i2 de la ruta k2, cada arco (h2,j2) de la ruta k2 (con h2≠i2 y j2≠i2), y cada arco (h3,j3) de la ruta k3, se obtiene una nueva solución S considerando los siguientes movimientos: 1) remover cliente i1 de ruta k1 e insertarlo entre vértices h2 y j2 en ruta k2; 2) eliminar cliente i2 de ruta k2 e insertarlo entre vértices h3 y j3 en ruta k3. El movimiento asociado con el valor mínimo de la función objetivo es implementado. El procedimiento de perturbación permite al algoritmo explorar nuevas regiones del espacio de solución.
3.1. Pseudocódigo del algoritmo propuesto

4. Descripción del algoritmo propuesto
El algoritmo propuesto (GITS) fue implementado en C++ y los experimentos han sido desarrollados en una Intel Core Duo (un solo core ha sido usado) CPU (2.00 Ghz) bajo Linux Ubuntu 11.04 con 2 GB de memoria. El desarrollo del algoritmo propuesto ha sido testeado en tres conjuntos de instancias propuestas en [4,22,23]. En todos los conjuntos, los clientes y los depósitos son representados por puntos en el plano. De esta manera, el costo de un arco es calculado como la distancia euclidiana, multiplicada por 100 y calculado como un entero (ver [22]), o calculado como número real de doble precisión (ver [4,23]).
El conjunto de datos propuesto por [23] considera 36 instancias con depósitos sin restricciones de capacidad. El número de clientes es ajustado en el intervalo (100, 200), y el número de depósitos potenciales está entre 10 o 20. La capacidad del vehículo es ajustado a 150. El conjunto de datos propuesto en [22] considera 30 instancias. El número de clientes es ajustado en el intervalo [20, 200], y el número de depósitos potenciales es 5 o 10. La capacidad del vehículo es 70 o 150. Finalmente, el conjunto de datos propuesto en [4] contiene 13 instancias obtenidas desde problemas clásicos del VRP adicionando nuevos depósitos con sus correspondientes capacidades y costos fijos. El número de clientes está entre 21 a 150, y el número de depósitos potenciales de 5 a 10.
4.1. Ajuste de parámetros
En particular, para cada instancia, una corrida del algoritmo ha sido ejecutada. Los mejores resultados del algoritmo son reportados en Tablas 1-4. El siguiente set de parámetros ha sido obtenido después de varias corridas en los tres set de instancias: 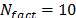 ,
, 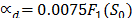 ,
, 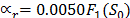 ,
, 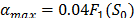 ,
, 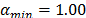 ,
, 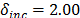 ,
, 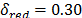 ,
, 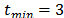 ,
, 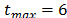 ,
, 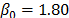 ,
, 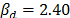 ,
, 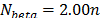 ,
, 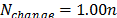 ,
, 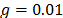 ,
, 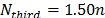 ,
, 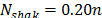 , y
, y 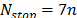 . Estos valores han sido usados para las soluciones de las instancias consideradas.
. Estos valores han sido usados para las soluciones de las instancias consideradas.
4.2. Estudio comparativo
El algoritmo propuesto ha sido comparado con los siguientes algoritmos publicados para el CLRP: GRASP ([7]), MA|PM ([8]), LRGTS ([5]), GRASP+ELS ([10]), SALRP ([11]), VNS+VLNS ([12]) y 2-Phase HGTS ([13]). Los resultados se presentan según aparecen en la literatura. Note que los resultados promedio no están disponibles para
todos los algoritmos. Los resultados reportados para GRASP, MA|PM, LRGTS, SALRP, y 2-Phase HGTS corresponde a una sola corrida del algoritmo asociado. VNS+VLNS ha sido ejecutado 30 veces para cada instancia, y el costo reportado y tiempo computacional corresponde al costo promedio y tiempo promedio sobre las corridas. Finalmente, GRASP+ELS ha sido ejecutado cinco veces considerando cinco diferentes semillas, y los costos reportados corresponden a las mejores soluciones sobre las corridas y el tiempo computacional requerido para alcanzar dichas soluciones. En Tablas 1-4, la siguiente notación es usada:
Instancia nombre de la instancia;
n número de clientes;
m número de depósitos potenciales;
Costo costo de la solución obtenida por cada método (en una sola corrida o la mejor corrida);
BR costo del mejor resultado entre los algoritmos considerados;
CPU CPU usado por cada algoritmo;
Índice CPU Passmark performance test para cada CPU;
Tiempo CPU tiempo de ejecución en segundos en la CPU usada por cada algoritmo;
Gap BR porcentaje gap del costo de la solución encontrada por cada algoritmo con respecto al BR;
NBR número de BR obtenidos por cada algoritmo.
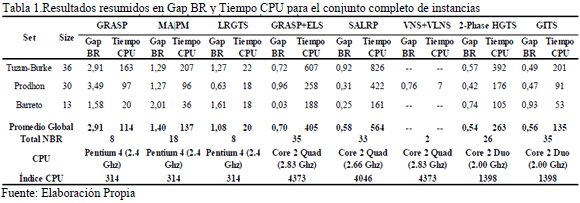
En Tablas 2-4, los valores para los cuales cada algoritmo es capaz de encontrar el valor de BR, son escritos en negrilla. Cuando el algoritmo propuesto (GITS) mejora el valor de BR, este resultado es subrayado. Finalmente, el índice CPU es obtenido por el Passmark Performance Test[1]. Este es un bien conocido benchmark test. Una CPU es más rápida cuando el índice CPU índex es alto. En Tabla 1, se reporta un resumen de resultados obtenidos por los algoritmos considerados para el set completo de instancias. En particular, valores promedio del Gap BR, CPU time, Total NBR y CPU índex son reportados. Tabla 1 muestra que el algoritmo propuesto provee el valor promedio más pequeño de Gap BR que el reportado por GRASP, MA|PM, LRGTS, GRASP+ELS, SALRP y VNS+VLNS. Solamente algoritmo 2-Phase HGTS provee, con mayores CPU times, ligeramente mejores valores promedio de Gap BR.
En cuanto al tiempo de CPU, GITS es más rápido que GRASP+ELS, SALRP y 2-Phase HGTS, los cuales han sido los algoritmos previamente publicados que han sido capaces de obtener los mejores resultados. Es de notar que el CPU time usado por algoritmo GRASP+ELS no representa el tiempo global requerido para encontrar la mejor solución, desde que este corresponde al tiempo de CPU utilizado para encontrar la mejor solución en su respectiva corrida. Por otro lado, algoritmos GRASP, MA|PM, LRGTS and VNS+VLNS toman menos CPU time, pero ellos parecen ser menos robustos que el algoritmo propuesto en términos de la calidad de solución.
Además, el algoritmo propuesto junto con el GRASP+ELS son capaces de obtener el mayor número de BKS. El algoritmo propuesto ha sido capaz de alcanzar 35 BR de 79 instancias consideradas en este artículo.
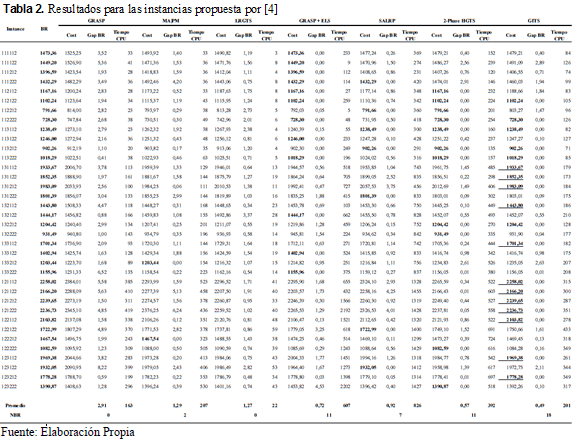
Los resultados para el conjunto de datos propuesto en [4] son reportados en Tabla 2. Los resultados muestran que el algoritmo propuesto es capaz de producir 18 BR sobre 36 instancias; de las cuales 12 corresponden a nuevos valores de BR. En este conjunto de datos, se puede observar que el algoritmo supera todas las otras heurísticas en términos del promedio Gap BR y número global de soluciones de BR encontradas.
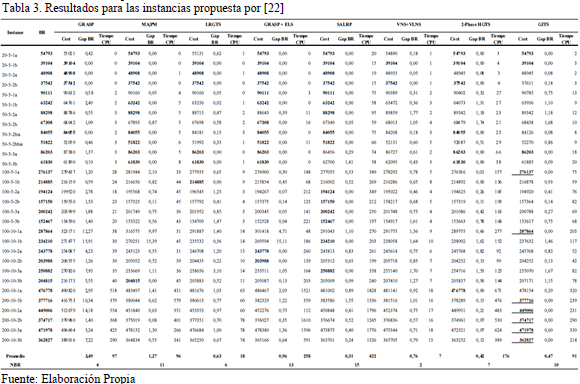
Los resultados para el conjunto de datos propuestos en [22] son detallados en Tabla 3. En promedio, el algoritmo propuesto es capaz de obtener mejores resultados que GRASP, MA|PM, LRGTS, GRASP+ELS y VNS+VLNS. Sólo, SALRP y 2-Phase HGTS proveen también con tiempos computacionales mayores, ligeramente mejores resultados de Gap BR.
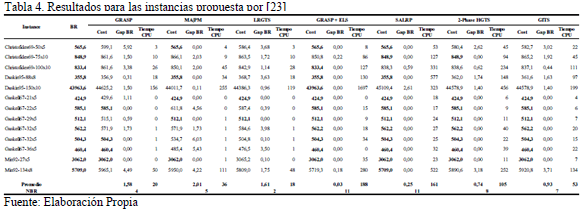
Finalmente, Tabla 4 reporta los resultados obtenidos para el set de instancias propuestas en Barreto [23]. Los resultados muestran que el algoritmo propuesto es competitivo en términos de la calidad de la solución. Algoritmo GITS es capaz de obtener mejores resultados promedios que GRASP, MA|PM y LRGTS, pero es superado por algoritmos GRASP+ELS, SALRP y 2-Phase HGTS.
5. Conclusiones y futuras investigaciones
En este artículo se propone un algoritmo efectivo para el problema de localización y ruteo con restricciones de capacidad (CLRP). El desarrollo del algoritmo propuesto ha sido evaluado considerando instancias de benchmarking propuestas en la literatura. Los resultados computacionales muestran el algoritmo propuesto es capaz de producir, dentro de tiempos computacionales cortos, varias soluciones obtenidas por los métodos previamente publicados y algunas nuevas mejores soluciones. Los resultados obtenidos sugieren que el algoritmo propuesto es competitivo con los algoritmos previamente publicados. El algoritmo propuesto podría ser aplicado a otros problemas de ruteo con múltiples depósitos como el problema de ruteo de vehículos con múltiples depósitos (MDVRP), el problema de localización y ruteo con restricciones de periodicidad (PLRP), etc.
Agradecimientos
Este trabajo ha sido parcialmente soportado por la Pontificia Universidad Javeriana, Cali, la Universidad del Bío-Bío, Chile y la Universidad Nacional de Colombia. Este soporte es gratamente agradecido.
Bibliografía
[1] Laporte, G., Nobert, Y. and Arpin, D., An exact algorithm for solving a capacitated location-routing problem. Annals of Operations Research, 6 (9), pp. 291-310, 1986. http://dx.doi.org/10.1007/BF02023807 [ Links ]
[2] Contardo, C., Gendron, B. and Cordeau, J.F., A branch-and-cut-and-price algorithm for the capacitated location-routing problem. CIRRELT, 2011. [ Links ]
[3] Belenguer, J.M., Benavent, E., Prins, C., Prodhon, C. and Calvo, R.W., A branch-and-cut method for the capacitated location-routing problem. Computers & Operations Research, 38 (6), pp. 931-941, 2011. http://dx.doi.org/10.1016/j.cor.2010.09.019 [ Links ]
[4] Tuzun, D. and Burke, L.I., A two-phase tabu search approach to the location routing problem. European Journal of Operational Research, 116 (1), pp. 87-99, 1999. http://dx.doi.org/10.1016/S0377-2217(98)00107-6 [ Links ]
[5] Prins, C., Prodhon, C., Ruiz, A., Soriano, P. and Calvo, R.W., Solving the capacitated location-routing problem by a cooperative Lagrangean relaxation-granular tabu search heuristic. Transportation Science, 41 (4), pp. 470-483, 2007. http://dx.doi.org/10.1287/trsc.1060.0187 [ Links ]
[6] Barreto, S., Ferreira, C., Paixao, J. and Santos, B.S., Using clustering analysis in a capacitated location-routing problem. European Journal of Operational Research, 179 (3), pp. 968-977, 2007. http://dx.doi.org/10.1016/j.ejor.2005.06.074 [ Links ]
[7] Prins, C., Prodhon, C. and Calvo, R.W., Solving the capacitated location-routing problem by a GRASP complemented by a learning process and a path relinking. 4OR: A Quarterly Journal of Operations Research, 4 (3), pp. 221-238, 2006a. [ Links ]
[8] Prins, C., Prodhon, C. and Calvo, R.W., A memetic algorithm with population management (MA|PM) for the capacitated location-routing problem. Lecture Notes on Computer Science, 3906, pp. 183-194, 2006b. http://dx.doi.org/10.1007/11730095_16 [ Links ]
[9] Jabal-Ameli, M.S., Aryanezhad, M.B. and Ghaffari-Nasab, N., A variable neighborhood descent based heuristic to solve the capacitated location-routing problem. International Journal of Industrial Engineering Computations, 2 (1), pp. 141-154, 2011. http://dx.doi.org/10.5267/j.ijiec.2010.06.003 [ Links ]
[10] Duhamel, C., Lacomme, P., Prins, C. and Prodhon, C., A GRASP× ELS approach for the capacitated location-routing problem. Computers & Operations Research, 37 (11), pp. 1912-1923, 2010. http://dx.doi.org/10.1016/j.cor.2009.07.004 [ Links ]
[11] Yu, V.F., Lin, S.W., Lee, W. and Ting, C.J., A simulated annealing heuristic for the capacitated location routing problem. Computers & Industrial Engineering, 58 (2), pp. 288-299, 2010. http://dx.doi.org/10.1016/j.cie.2009.10.007 [ Links ]
[12] Pirkwieser, S. and Raidl, G.R., Variable neighborhood search coupled with ILP-based very large neighborhood searches for the (periodic) location-routing problem. In Hybrid Metaheuristics, Springer Berlin Heidelberg, pp. 174-189, 2010. http://dx.doi.org/10.1007/978-3-642-16054-7_13 [ Links ]
[13] Escobar, J.W., Linfati, R. and Toth, P., A two-phase hybrid heuristic algorithm for the capacitated location-routing problem. Computers & Operations Research, 40 (1), pp. 70-79, 2012. http://dx.doi.org/10.1016/j.cor.2012.05.008 [ Links ]
[14] Gendreau, M. and Potvin, J.Y., Handbook of metaheuristics. Vol. 2. New York, Springer, 2010. http://dx.doi.org/10.1007/978-1-4419-1665-5 [ Links ]
[15] Toth, P. and Vigo, D., The granular tabu search and its application to the vehicle-routing problem, INFORMS Journal on Computing, 15 (4), pp.333-346, 2003. http://dx.doi.org/10.1287/ijoc.15.4.333.24890 [ Links ]
[16] Baxter, J., Local optima avoidance in depot location. Journal of the Operational Research Society, 32 (9), pp. 815-819, 1981. http://dx.doi.org/10.1057/jors.1981.159 http://dx.doi.org/10.2307/2581397 [ Links ]
[17] Lin, S. and Kernighan, B.W.m An effective heuristic algorithm for the traveling-salesman problem. Operations Research, 21 (2), pp. 498-516, 1973. http://dx.doi.org/10.1287/opre.21.2.498 [ Links ]
[18] Barcelo, J. and Casanovas, J., A heuristic Lagrangean algorithm for the capacitated plant location problem. European Journal of Operational Research, 15 (2), pp. 212-226, 1984. http://dx.doi.org/10.1016/0377-2217(84)90211-X [ Links ]
[19] Klincewicz, J. and Luss, H., A Lagrangian relaxation heuristic for capacitated facility location with single-source constraints. Journal of the Operational Research Society, 37 (5), pp. 495-500, 1986. http://dx.doi.org/10.1057/jors.1986.84 http://dx.doi.org/10.2307/2582672 [ Links ]
[20] Taillard, E., Parallel iterative search methods for vehicle routing problems. Networks, 3 (8), pp. 661-673, 1993. http://dx.doi.org/10.1002/net.3230230804 [ Links ]
[21] Renaud, J., Laporte, G. and Boctor, F., A tabu search heuristic for the multi-depot vehicle routing problem. Computers & Operations Research 23 (3), pp. 229-235, 1996. http://dx.doi.org/10.1016/0305-0548(95)O0026-P [ Links ]
[22] Prins, C., Prodhon, C. and Wolfler-Calvo, R., Nouveaux algorithmes pour le probleme de localisation et routage sous contraintes de capacite. MOSIM., 4e'me Conference Francophone de Modelisation et Simulation, Nantes, France, 4, pp. 1115-122. 2004. [ Links ]
[23] Barreto, S., Analise e modelizacao de problemas de localizacao distribuicao, PhD. Thesis, University of Aveiro, Aveiro, Portugal, 2004. [ Links ]
J.W. Escobar, es Dr. en Investigación de Operaciones de la Universidad de Bologna, Italia. Docente de programas de Pregrado y Posgrado de la Pontificia Universidad Javeriana y Universidad del Valle, Colombia. Sus intereses de investigación incluyen el diseño e implementación de efectivos algoritmos exactos y heurísticos para problemas de optimización combinatoria.
R. Linfati, es Dr en Investigación de Operaciones de la Universidad de Bologna, Italia. Profesor en el Departamento de Ingeniería Industrial de la Universidad del Bío-Bío, Chile. Sus intereses de investigación incluyen el diseño e implementación de efectivos algoritmos exactos y heurísticos para problemas de optimización combinatoria.
W. Adarme-Jaimes, recibió el grado de Ing. Industrial en 1993 de la Universidad Industrial de Santander, Colombia; es Esp. en Ingeniería de la Producción y Mejoramiento Continuo en 1997 de la Universidad Pedagógica y Tecnológica de Colombia, Colombia, es MSc. en Ingeniería con énfasis Logística en 2007 de la Universidad del Valle, Colombia, Dr. en Ingeniería, Industria y Organizaciones en 2011 de la Universidad Nacional de Colombia, Bogotá, Colombia. Profesor en la Facultad de Ingeniería de la Universidad Nacional de Colombia, Sede Bogotá. Director del grupo de investigación en Logística Sociedad, Economía y Productividad (SEPRO). Ha dirigido en los últimos diez años seis investigaciones sobre logística para diferentes sectores de la economía colombiana, con publicación de resultados en revistas indexadas. Es consultor en política pública sobre logística y sistemas de abastecimiento para los Ministerios de Comercio, Transporte y Salud de Colombia y Alcaldía mayor de Bogotá. Director de 14 tesis de maestría y tres tesis de Doctorado en Logística. Ponente en congresos internacionales sobre logística en Alemania, México, Panamá, Venezuela y Colombia.