Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.190 Medellín mar./abr. 2015
https://doi.org/10.15446/dyna.v82n190.48730
DOI: http://dx.doi.org/10.15446/dyna.v82n190.48730
The importance of being chemical affinity. Part VI: The harvest
La importancia de llamarse afinidad química. Parte VI: La cosecha
Guillermo Salas-Banuet a, José Ramírez-Vieyra b, Oscar Restrepo-Baena c, María Noguez-Amaya d & Bryan Cockrell e
a Universidad Nacional Autónoma de México, salasb@unam.mx
b Universidad Nacional Autónoma de México, jgrv@unam.mx
c Universidad Nacional de Colombia, ojestre@unal.edu.co
d Universidad Nacional Autónoma de México, nogueza@unam.mx
e University of California, Berkeley, bryan.cockrell@berkeley.edu
Received: September 5th, 2014. Received in revised form: November 3th, 2014. Accepted: November 25th, 2014.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
The quantitative scale of electronegativity, obtained by Linus Pauling, as a result of qualitative electron affinity background, generated multiple different and interesting proposals until today, which have proved to be the effort of ingenuity to get a universal concept of affinity, which has resulted incomplete. Thermodynamics, specifically its thermochemical branch, has offered an explanation, which has been accepted by The International Union of Pure and Applied Chemistry (IUPAC), as incomplete as the former. In both cases, it is thought that the error is in regard to affinity as a property, rather than a behavior.
Keywords: Affinity, Electronegativity, chemistry, history, thermodynamics.
Resumen
La escala cuantitativa de electronegatividad obtenida por Linus Pauling, como resultado de aquellas antecedentes cualitativas de electroafinidad, generó múltiples propuestas diferentes e interesantes, hasta el día de hoy, lo que ha mostrado ser el esfuerzo del ingenio por conseguir un concepto universal de afinidad, que ha resultado incompleto. La termodinámica, específicamente su rama termoquímica, ha ofrecido una explicación, tampoco universal, que ha sido aceptada por la Unión Internacional de Química Pura y Aplicada (IUPAC, por sus siglas en inglés), igual de incompleta. En ambos casos, se piensa que el error está en considerar a la afinidad como una propiedad, en vez de un comportamiento.
Palabras clave: Afinidad, electronegatividad, química, historia, termodinámica.
1. Introducción
Si se considera cierta la afirmación de que Antoine Lavoisier es el padre de la química, entonces esta nace en 1789 cuando publica su libro Traité Élémentaire de Chimie. Con ello, su gestación estaría en la búsqueda de una teoría congruente que explicara la afinidad química, su proceso de parto en el desarrollo de los conceptos tempranos de electricidad y calor y su primer alimento en el de estructura atómica.
Después, la química continuaría buscando explicaciones para la afinidad a través del concepto de electronegatividad -desencadenando una serie de propuestas de escalas sostenidas en diversos intentos para explicar su razón lógica- y la termodinámica lo haría usando los conceptos de energía y entropía.
2. Antecedentes.
En la visión histórica occidental, la primera manera de explicar el mundo y sus transformaciones fue la hierofánica; se piensa que el concepto intuitivo de afinidad química estuvo presente en las mentes de algunos -seguramente pocos- de los hombres que -desde la Prehistoria y durante decenas de miles de años- transformaron las rocas, usando fogatas y hornos, en cerámicas y metales. Esa experiencia permitió que, al iniciarse el periodo de la Historia, se desarrollara un conocimiento práctico y óptimo, en Mesopotamia (antigua Irak y el noreste de Siria), Egipto y Persia (actualmente Irán) [1]. Ese conocimiento fue tomado y repensado por los griegos, libre de influencias religiosas, entre los siglos VI y II a.C. [2]. Como resultado de este ejercicio, a finales de ese tiempo y en el ambiente de las ciencias exactas del Museo Alejandrino, nació la alquimia científica. El pensamiento griego permanecería inmutable hasta el siglo IX, cuando los musulmanes de Bagdad, Damasco y Toledo lo modificaron -dando origen a una alquimia más mágica que científica- y lo difundieron; hacia finales del siglo XIII llegaría a gran parte de Europa, donde se asimilaría y propagaría a otras partes del mundo [3]. El conocimiento práctico de los materiales fue tomado por los romanos, hasta el siglo V d. C. cuando se derrumbó su imperio. Con él quedó un vacío de poder que dejó a una Europa medieval sumida en constantes luchas, hasta que fue llenado por la dominante Iglesia Cristiana de Roma, la cual presionó a los creyentes para que se utilizara su pensamiento religioso para definir y explicar todo, incluso a la naturaleza; a partir del siglo IX, algunos de sus integrantes comenzaron a luchar por su propia independencia de pensamiento. En el siglo XII, en Europa se descubrieron, tradujeron y difundieron los textos de los pensadores griegos clásicos, con lo cual surgió el Renacimiento, en el siglo XV, y la Ilustración, a finales del siglo XVII. En este siglo, Robert Boyle le dio la espalda a algunas teorías alquímicas y estableció hipótesis químicas -usando las ideas de los griegos, las suyas propias y las de sus contemporáneos- con las que fundó los estudios sobre la afinidad química; entre estos, destacan la propuesta de tablas cualitativas de afinidad. Es en el siglo XVIII cuando la química se consolida como una ciencia, gracias al trabajo de Antoine Lavoisier y sus varios colaboradores [4]. A partir del siglo XIX, la nueva ciencia se enriquece y evoluciona debido desarrollos intelectuales y experimentales diversos -de la propia área y de otras- como los relativos a la electricidad, el calor y el átomo, lo que permitió, en el primer tercio del siglo XX, que Linus Pauling presentara una tabla cuantitativa de electronegatividad (de afinidad), cimentada en la determinación del porcentaje del carácter iónico de los enlaces covalentes -obtenido con las energías de algunos enlaces químicos, a través de la medición de los calores de formación de varios compuestos- y una definición de la misma [5].
3. Explicaciones químicas para la afinidad.
Con la propuesta de Linus Pauling, se inicia la presentación de una multiplicidad de escalas, conceptos y definiciones de electronegatividad, X, que intentan explicar la afinidad de elementos y compuestos. En la primera mitad del siglo XX se dieron las primeras [5].
3.1. La afinidad química en la 2ª mitad del siglo XX.
Raymond Iczkowski y John Margrave [6] usaron la energía atómica -tomada como las energías de los iones positivo y negativo relativas a los átomos neutros- expresada en una serie de potencias en N (cuyos coeficientes se determinan por potenciales de ionización sucesivos), en la forma de N = n - Z, donde n es el número de electrones alrededor del núcleo en un estado de ionización dado y Z es el número atómico del núcleo. Definieron la electronegatividad de un átomo neutro en fase gaseosa:
X = (-dE/dN)N = 0 donde dE es el cambio de energía que acompaña al cambio en la carga, dN. Indicaron que al usar el primer potencial de ionización y la afinidad del primer electrón, su X era equivalente a la relación de Mulliken; así, enfatizaron la la cercanía a esa relación y asentaron que las unidades de la X deberían ser de energía por electrón; por supuesto, compararon exitosamente su escala con la de Mulliken [5]. Que la X sea igual a (-dE/dN) quiere decir que después de juntarse dos átomos se obtendrá una disminución en la energía, si los electrones se transfieren al átomo, para el cual el descenso de energía total (dE) excede al incremento total en la energía del átomo del que se remueven esos electrones; ese descenso de la energía total se debe a la ganancia de una carga electrónica fraccional, dN [7]. Allen [8] subrayó que con esto se estableció a la X como un concepto de transferencia de carga.
En un trabajo que llegó a ser clásico, Robert Parr et al. [9] revisaron el concepto de X desde el punto de vista de la teoría de la densidad funcional. Esta viene de dos teoremas de Hohenberg y Kohn, los cuales establecen que la densidad electrónica (r) determina todas las propiedades de un átomo o una molécula en un estado neutro no degenerado y la energía de un átomo para un estado neutro degenerado. La teoría define que el potencial químico electrónico m es igual a (∂E/∂N)n, donde n es una constante del potencial externo debido a las cargas nucleares establecidas (el potencial del núcleo); tanto la cantidad de E (la energía electrónica) como de N (el número de electrones) son funciones de r. Parr y sus compañeros comentaron que encontraron que la X era la misma para todos los orbitales naturales en un átomo o molécula en sus estados neutros (el potencial químico); precisaron el concepto de la X como el potencial químico negativo, con lo que X = - m = (∂E/∂N)n = ½(I + A); como la conexión con la definición de Mulliken [5] era inmediata, se le calificó de absoluta. Esto significa que cuando dos átomos A y B, con un mA diferente a mB, se unen químicamente, el sistema se equilibrará a un nuevo valor común de m, diferente a los de A y B. Con X = -m y la analogía existente entre m y la energía libre de Gibbs, se implicaba una igualdad de la X para cualquier cantidad de átomos enlazados, con lo que se validó el principio igualador de Sanderson; y explican: la diferencia de electronegatividad en los estados de valencia, produce la transferencia de electrones entre los átomos de la molécula en formación, así, los electrones se distribuyen entre los orbitales para igualar el potencial químico de orbital a orbital. Allen [8] comenta que el trabajo de Parr et al. fue citado en más de 300 artículos, en algunos de los cuales se cita también a Sanderson. Bartolotti [10] subraya que con el trabajo de Parr se conectó a X con la mecánica cuántica y que m fue introducido en la teoría de la densidad funcional como un multiplicador de Lagrange, para asegurar que el número de partículas sería conservado al minimizarse la energía. En otro comentario, Ralph Pearson [11] hace notar que m es una cantidad que caracteriza a cualquier sistema químico, átomo, radical, ión o molécula; que es constante en cualquier parte del sistema; que mide la tendencia de los electrones a escapar del sistema; y que, como es una propiedad sólo de sistemas al equilibrio, lo es de estados neutros. Señala que la electronegatividad de Pauling (XP) -y las otras electronegatividades similares- difiere bastante de la absoluta de Parr, ya que, para esta última, es una propiedad de un átomo libre en el estado neutro y no de uno en su estado de valencia excitado, adecuado para tomar parte en una molécula. Indica que la aplicación de la escala de Pauling es útil para estimar las polaridades de los enlaces y, en algún grado, las resistencias de los enlaces entre átomos diferentes; mientras que la absoluta es una medida de la reactividad química del átomo, radical, ión o molécula, cuya aplicación típica está en: a) estimar la interacción inicial entre dos de ellos; b) dar la dirección del flujo electrónico; y c) proporcionar un estimado de la cantidad inicial de la densidad electrónica transferida, relacionada a su vez a las barreras de energía para la reacción y, en algunos casos, a la resistencia del enlace coordinado formado; pero que no es una medida confiable de la polaridad final del enlace. También advierte que la X absoluta no satisface la definición de XP, como la propiedad de un átomo en una molécula, pero sí en la idea esencial de atraer y mantener electrones, y que no existe una razón que obligue a restringir su aplicación a átomos combinados. Dice que se ha mostrado que las escalas pueden ser comparables y que sólo sus aplicaciones son diferentes, por lo que el asunto no es preguntarse cuál escala es la más correcta porque cada escala es más apropiada en su propia área de uso. Pearson apoya al principio igualador de Sanderson al decir que, aunque no está probado por ninguna teoría, es intuitivamente interesante.
Al presentar su electronegatividad espectroscópica, Xespec, [12], Allen comentó que -usando la Figura 6 (y su texto) de otro artículo suyo [13]- se contrastó la energía de la expresión (I + A)/2, usada por Parr, para hacer la aproximación del potencial químico electrónico (m) al comportamiento de la Xespec, encontrando que eran muy diferentes. Además, calcula y presenta los valores de las diferencias promedio de las energías de Hartree, de la capa de valencia entre los átomos libres de F, O y N y el átomo de H, para los átomos relativos al H y referidos a cero, obteniendo: -0.450, -0.162 y -0.630, respectivamente, y los de los mismos átomos en sus hidruros relativos al H en el H2 y referidos a cero, FH, OH2 y NH3, obteniendo: -0.055, -0.028 y -0.010, respectivamente. Allen explica que si el potencial químico, m, fuese calculado de la misma forma, los valores obtenidos para los átomos libres serían aproximadamente los mismos, mientras que los de los hidruros estarían todos en un solo punto (el del H2), contraviniendo la observación empírica que indica que los átomos mantienen su identidad cuando se combinan en moléculas o sólidos. Así, concluye, la igualación de la X no acontece y el potencial químico electrónico, m, tal como fue desarrollado por Parr, Pearson, y otros, resulta una cantidad química totalmente diferente a la X. Posteriormente, Allen [8] presenta la idea de que con X = - m = (∂E/∂N)n -en la formulación de la densidad funcional- se implica la frase "la tendencia de los electrones a escapar" (describiendo la XM) y que, más que una transferencia de carga o esa "tendencia a escapar", la electronegatividad es un concepto de enlazamiento estático, tal como los potenciales de ionización que la definen: la energía de un electrón en un átomo o, más precisamente, la energía promedio de los electrones de valencia en un átomo. Afirma que esta interpretación no destruye para nada la idea coloquial de la X como "atraer" o el "poder de jalar" electrones, ya que si la energía promedio de los electrones en el átomo A es más baja que la energía promedio de los electrones en el átomo B, entonces el átomo A atraerá los electrones del átomo B, cuando A y B se unan.
Más tarde [13], Lelan Allen estableció que la X es una propiedad íntima de la Tabla Periódica y una definición para ella: la energía promedio de un electrón, de los de la capa de valencia, para átomos libres en su estado basal, indicando que las energías del electrón pueden ser determinadas directamente con los datos espectroscópicos, de ahí el nombre para su electronegatividad, y que esta descripción llevaba a una definición mejorada de la X de grupo (o de sustituyentes), así como a la extensión y refinamiento en el uso de las perturbaciones de la X en la teoría orbital molecular cualitativa y semicuantitativa y al entendimiento del orden de las reglas de la X orbital híbrida, tales como que
sp > sp2 > sp3. Estableció la Xespec como (mep + nes)/(m + n), para elementos representativos, en donde ep y es son las energías de ionización s y p; m y n son el número de electrones de p y s. Afirmó que los valores de la Xespec se ajustan (comparando gráficas) bastante a los de las ampliamente aceptadas escalas de Pauling [14] y de Allred y Rochow [15], lo que, para él, es de primera importancia. Precisa que la Xespec permite racionalizar dos aspectos: 1) la separación diagonal de la Tabla Periódica entre metales y no metales -estableciendo a los elementos B, Si, Ge, As, Sb, Te, Bi y Po como los metaloides- y 2) la formación de moléculas a partir de los gases nobles. Para él, estos gases son el punto primordial de la Tabla Periódica porque sus Xs presentan dos caras: tienen altos valores, con lo que muestran su capacidad para retener a sus electrones, pero ningún valor para atraer a otros. Afirma que la X es la energía de activación para el enlace y que: 1. con la diferencia de las electronegatividades espectroscópicas, DXespec, entre dos átomos diferentes, es posible sistematizar las propiedades de un amplio grupo de materiales conocidos: sólidos iónicos, moléculas covalentes, metales, minerales, polímeros inorgánicos y orgánicos, semiconductores, etc. e identificar el carácter iónico (la polaridad del enlace) de esos átomos; y 2. la X de los metales de transición no puede ser determinada de manera simple debido a la naturaleza de las distribuciones radiales del orbital d y que esto se nota en el poco uso que de ella hacen los químicos de esos metales. Comparó su escala con las de Allred y Rochow, Boyd y Edgecombe, Mulliken y Pauling:
XP = 1.75 x 103 Xespec (Kj/mol) o XP = 0.69Xespec (eV).
El mayor valor de Xespec la presenta el Ne = 4.783, seguido por los elementos: F = 4.193, He = 4.16, O = 3.61 y Ar = 3.242. Su método tiene la ventaja de poder estimar las electronegatividades de elementos que no pueden ser obtenidas por otros medios, como la del Francio, al que Allen asigna un valor de 0.67.
3.2. Escalas de X para los elementos en sus diferentes estados de valencia u oxidación.
Existen tres antecedentes de estas escalas: 1) Mulliken [16] determinó la X de sólo 11 elementos en diferentes estados de valencia usando valores de I y A, porque no existían valores de A para el resto de los elementos; encontró que la X de un átomo se incrementaba con el aumento de la valencia; 2) Allred [17] usó el método de Pauling para calcular las Xs en diferentes estados de oxidación, para un puñado de elementos de los que existían datos disponibles: Mo, Fe, Tl, Sn y Pb; y 3) Sanderson [18] propuso un método para calcular la X de elementos en diferentes estados de valencia, basado en las cargas parciales y las energías de enlace; su método estaba limitado a los metales de transición.
Keyan Li y Dongfeng Xue [19] estimaron los valores de electronegatividad, XLX, para proponer una escala para 82 elementos, en diferentes estados de valencia y con los números de coordinación más comunes. Los calcularon basándose en el potencial químico efectivo, definido por la energía de ionización y el radio iónico, es decir, en términos del potencial iónico efectivo (j), j = n*(Im/R)1/2/ri, donde n* es el número cuántico principal efectivo, Im es la energía de ionización última (numéricamente igual a la de la afinidad electrónica de un catión dado), R = 13.6 eV (la constante de Rydberg) y ri es el radio iónico. Ellos explicaron que, para el momento de escribir su trabajo, la X era una propiedad invariante, la cual no dependía del ambiente químico del átomo (v.gr: el estado de la valencia y el número de coordinación); y que, hasta donde sabían, no existía esta información completa, por lo que decidieron construirla. Encontraron que para un catión determinado, la X se incrementaba de acuerdo al aumento del estado de oxidación, disminuía con el aumento del número de coordinación y que existía una una perfecta correlación lineal con la escala de Luo [20], basada en el potencial covalente, debido a que la teoría de la X absoluta de Parr es el soporte teórico de ambas. Compararon su escala con la de Pauling: XP=0.105XLX+0.863.
3.3. Las otras escalas de electronegatividad.
Desde la primera propuesta de Pauling hasta la fecha de elaboración de este trabajo (periodo de más de 80 años) se han encontrado, entre las revistas occidentales más consultadas, múltiples trabajos enfocados a proponer una escala de X, sobre todo haciendo relaciones entre propiedades; de estos, sólo 26 presentan alguna originalidad. Las diversas escalas se fundamentan en características atómicas -principalmente- y moleculares, tanto de la estructura (radios atómicos, longitudes de enlace, etc.) como de las propiedades (potenciales de ionización, carga eléctrica, etc.). Es posible distinguir que cerca del 80% de los autores comparan su escala con alguna otra; más del 70% lo hace directa (62%) o indirectamente (8%) con la de Pauling; el 20% que agrupa a las que tienen un origen en la mecánica cuántica no hace comparaciones, o las hace con alguna que tiene su mismo fundamento. Durante las comparaciones y al ajustar los valores de una escala al rango de los de la de Pauling, surgió el concepto de las Unidades Pauling (UP). Aunque el empirismo y el fundamento de la escala de Pauling se señalan como erróneos por muchos autores, la mayoría de ellos validan su propia escala al compararla con ella (sigue siendo la más famosa y utilizada, sobre todo en la educación) y, al hablar de X, mantienen el concepto de "atraer electrones". Todos los trabajos parten del planteamiento de una hipótesis, aunque sólo Pauling y Malone las comprueban con experimentación propia; algunos autores toman alguna experimentación previa y calculan la X con el método que proponen y el resto deriva su comprobación matemáticamente. Las propuestas tienen dos características comunes: son conceptos sencillos y se usan fácilmente, lo cual es esencial en la ciencia y la educación.
3.4. Evaluar y reglamentar la X.
Mullay [21] realizó un análisis para evaluar el desarrollo de las escalas de X y planteó tres etapas: la primera involucró la búsqueda del método apropiado para calcular o medir las Xs atómicas; en la segunda se cambió el énfasis hacia el cálculo de la X de grupo y la carga atómica, y se exploraron y clarificaron los efectos de la carga atómica sobre la X; y, en la tercera, se propició la profundización del concepto básico, principalmente a través del uso de la teoría de la densidad funcional [9]. Sin embargo, de ahí en adelante se han publicado indistintamente trabajos del tipo de las tres etapas planteadas. Por decenio, el número de trabajos publicados durante el siglo XX fue de 3 durante los años 30, 2 en los 40, 3 en los 50, 6 en los 60, 6 en los 70, 10 en los 80, 1 en los 90 y 6 en los primeros 8 años del siglo XXI; aun sumando los trabajos que se dejaron fuera (menores en cantidad), el incremento no es comparable al número de químicos investigando y publicando en el mismo periodo de tiempo.
Gordon Sproul [22] pensó que se podían evaluar 15 escalas de X usando los triángulos del enlace. Graficó la X promedio versus la diferencia de electronegatividades para 311 compuestos binarios, bien identificados por A. F. Wells [23] por su tipo de enlace, utilizando sólo parámetros físicos y químicos medibles y evitando emplear la X. Concluyó que todas las escalas dan gráficas triangulares que segregan efectivamente los compuestos considerados, en tres regiones relativas al tipo de enlace iónico, metálico y covalente; y que las escalas que proveen la mejor segregación de los compuestos son la de Allen [13] y la de Nagle [24], con un acierto superior al 96%. Esto provocó que Peter G. Nelson publicara un comentario [25] en el que señalaba, entre otros detalles, que el tipo de enlace no es una propiedad medible y que en las ediciones previas del texto de A. F. Wells, se da la impresión de haber utilizado la X para realizar algunas de sus asignaciones. Sproul [26] contestó, entre otras cosas, que Wells no menciona, en el texto de referencia, la posibilidad de usar a la X para determinar tipos de enlace, sino que utilizó algunos fenómenos subjetivos como conductividad/resistencia eléctrica, puntos de fusión y características estructurales, tales como iones aislados, anillos, cadenas, moléculas separadas, etc.
Murphy et al. [27] -entre ellos Leland Allen- establecieron 9 reglas que, a su criterio, todas las escalas de X deberían de obedecer: 1. Las Xs atómicas necesitan ser obtenidas de las propiedades de los átomos libres. 2. Es necesaria una precisión de tres números (unidad, décima y centésima). 3. La X es una energía por electrón. 4. Todos los electrones de valencia deben ser incluidos en la definición de X. 5. Tres requerimientos del grupo principal están interrelacionados: a) la identificación de la X con el poder atrayente de un átomo por electrones es generalmente igual a su poder para retenerlos; b) los átomos de los gases nobles sólo tienen la habilidad para retenerlos; y c) las magnitudes de la X deben, paralelamente, establecer limitaciones de oxidación. 6. Los valores de X de los ocho elementos semimetálicos (B, Si, Ge, As, Sb, Te, Bi y Po) no deben traslaparse con los de los metales y los no metales; se debe respetar la regla del Si: todos los metales deben tener valores de X menores o, cuando mucho, iguales al del Si. 7. Para los compuestos binarios, AB, las electronegatividades de A y de B deben de calificar y definir los tipos de enlace como iónico, covalente o metálico. 8. La X debe tener una definición mecánica cuántica viable. 9. La escala de X debe mostrar un incremento sistemático de izquierda a derecha a través de los periodos. Cabe notar, que esta última regla no la cumple la escala de Allen, específicamente para los metales de transición. Los autores aplicaron estas reglas a la escala de XP y dictaminaron que sólo satisface las reglas 4 y 5 del criterio. Además, indican algunos errores de Pauling que, según ellos, han influido fuertemente en la actitud negativa de los químicos hacia la X: 1. Forzó a que la X tuviera unidades de (eV)1/2, en aras de ajustar mejor unos pocos enlaces más en su relación energía de enlace-polaridad de enlace original, con lo que se ha confundido a los químicos innecesariamente; 2. Las electronegatividades de varios metales de transición violan la regla del Si, haciendo que los químicos se cuestionen si la X es realmente aplicable a esta clase de átomos; 3. Su definición de X [14] "la atracción por electrones de un átomo neutro en moléculas estables" ha sido mal interpretada por el 15-20% de los autores de los textos que discuten su escala, cuando explican que la X es una propiedad molecular intrínseca, aun cuando Pauling lo niega implícitamente, en la siguiente frase del mismo texto; y 4. La definición de Pauling no es viable en la mecánica cuántica porque está construida sobre propiedades termodinámicas y no sobre electrónicas, lo que implica una falta de capacidad para designar las electronegatividades de 18 elementos.
Leland Allen [8] había proporcionado cinco criterios para establecer una definición coherente de X: 1. La X debe ser una cantidad de un átomo libre. 2. Debe responderse al problema de porqué la X no se puede medir en el laboratorio. 3. Una escala correcta de X debe ser cercanamente compatible con los valores de X empleados por los químicos prácticos al racionalizar sus resultados experimentales durante los últimos 70 (ahora casi 100) años. 4. Se cree que alguna función de las energías de ionización de los electrones de valencia atómica es el mejor candidato para ser la propiedad física medible necesaria para definirla. 5. Una definición correcta de la X debe ser totalmente compatible y hacer una conexión directa con los métodos de investigación de la mecánica cuántica, usados por los científicos profesionales para sus predicciones y explicaciones detalladas sobre la química contemporánea y los problemas de la física del estado sólido. Referente al criterio 4, Pauling [14] afirma: La propiedad de la electronegatividad de un átomo en una molécula es diferente del potencial de ionización del átomo y de su afinidad electrónica aunque está relacionada a esas propiedades en una manera general.
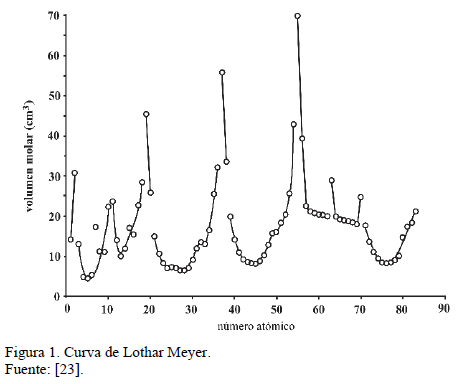
Boeyens [28] estableció sólo una regla, al explicar que la forma moderna en la que se grafica la curva de Lothar Meyer (Figura 1) del volumen atómico (V = M/r, la masa atómica en gramos y la densidad de los elementos sólidos) presentado como una función de Z (el número atómico), demuestra convincentemente la periodicidad elemental y expresa la X atómica. Boeyens indica que si se interrumpe la curva en los puntos donde se sabe que se completan los niveles de energía s, p, d y f -en vez de conectar todos los puntos en la secuencia de Z-, esta se fragmenta en regiones formadas por 2 u 8 elementos, excepto para los de las tierras raras, pero que si se toman junto con el par de elementos precedentes (Cs y Ba) y se separa el segmento en el Sm, la curva queda dividida en dos segmentos de 8 elementos cada uno. Ahora, todos los segmentos son curvas que tienen, alternadamente, una pendiente positiva y otra negativa, que se relacionan a los elementos tradicionalmente considerados como electropositivos y electronegativos.
Esta noción teórica, dice Boeyens, provee una definición precisa de X y permite afirmar que las escalas que no reflejen esta periodicidad deben considerarse inapropiadas. Es notorio que no define un significado.
De todo lo anterior, es posible distinguir tres acuerdos generales: la X es una propiedad; indica la capacidad de atraer y conservar electrones; y, en un enlace, los electrones se comparten en forma desigual.
Es notorio el gran esfuerzo realizado para tratar de derivar valores universales cuantitativos de X, lo que ha permitido observar: la confusión que existe de la imagen física que corresponde al concepto de X; que el concepto de X no se ha definido exactamente, por lo que sigue siendo ambiguo; que la X no es una propiedad de un átomo aislado que pueda medirse, como el número atómico, la masa o la energía de ionización; que al determinar la X, en realidad se están midiendo propiedades que dependen de la distribución electrónica o de la estructura atómica, todas diferentes. Así, la X ha quedado como un concepto inherentemente confuso, con bajo contenido de información.
Aquí se considera que la dificultad encontrada para su medición radica en que la X no es una propiedad, sino un comportamiento. Las propiedades se relacionan a algún nivel o tipo de estructura, con lo que son medibles. Los comportamientos se deducen de la comparación de los datos medidos, por lo que siempre son cualitativos. De ahí la imposibilidad de obtener una escala de X cuantitativa y una definición exacta para ella, universalmente válidas, y, por lo tanto, para la afinidad química.
4. La termodinámica en el problema de la afinidad.
El concepto de afinidad estuvo íntimamente relacionado al calor generado por las reacciones químicas. Mientras, la termodinámica nace y se desarrolla del estudio del calor producido por la máquina, desde el inicio de la revolución industrial. Sin embargo, no es sino hasta que se aprecia que uno de los conceptos importantes relativos al calor en la máquina, es aplicable al de reacción química -dando una medida de la afinidad- que se da origen a la termoquímica, uniendo a las dos ciencias.
4.1 El calor
Durante el periodo de oro del pensamiento griego, entre los siglos V y III a.C., las ideas sobre el calor y la mecánica surgieron en caminos paralelos. En la Sicilia del siglo V a.C., Empédocles de Agrigento postuló la existencia de cuatro raíces elementales: fuego, aire, agua y tierra, los que al unirse asumían las formas de todos los cuerpos de la naturaleza; como demostró experimentalmente que el aire era una substancia [2], extendió el concepto a los tres elementos restantes, asignándoles las características de pequeños e indivisibles. Para el año 360 a.C. a través del diálogo Timeo, Platón filosofa -tratando de explicar el calor- que el fuego y el aire son partículas muy pequeñas, más que los intersticios de las estructuras de la tierra y el agua, con lo que tienen mucho espacio para entrar en ellas y moverse, sobre todo el fuego; y agrega: no debemos olvidar que la figura original de fuego (la pirámide), más que cualquier otra forma, tiene un poder de dividir que corta el cuerpo en trozos pequeños y, por lo tanto, produce naturalmente el afecto que llamamos calor [29]. Las primeras interpretaciones alquímicas sobre la naturaleza del calor se confundían con aquellas sobre la combustión; tal vez por ello, en el siglo XVII, el alquimista y físico alemán Johann Joachim Becher (1635-1682) estableció una teoría que duraría un siglo, la cual fue defendida por su compatriota el médico y químico Georg Stahl (1659-1734). Proponía un principio inflamable, con la existencia de un fluido sutil hipotético (el flogisto), que estaba en los cuerpos y se desprendía en la combustión.
En 1780 se publicó en Londres, aunque en francés, el primer libro de termoquímica Essai sur la nouvelle théorie du feu élémentaire, et de la chaleur des corps [30] del portugués João Jacinto de Magalhães (1722-1790) -un espía del gobierno francés en cuestiones industriales- que contenía, entre muchas otras cosas: a) una tabla de calores específicos construida con los datos obtenidos por el químico irlandés Richard Kirwan (1733-1812); b) los conceptos: capacidad para el calor (ahora conocido como capacidad de calor específico) y calor latente -creados por Joseph Black (1728-1799), médico, físico y químico escocés, basándose en sus trabajos experimentales- usados para explicar por qué se mantenía constante la temperatura en los cambios de estado y para aclarar la diferencia conceptual entre temperatura q y cantidad de calor Q; también definió una caloría como la cantidad de calor que necesita 1g de agua para aumentar su temperatura en 1°C; c) las investigaciones realizadas en la década de 1770 por William Irvine (1743-1787), químico y médico escocés, alumno de Black, sobre el calor específico, con las que esbozó el concepto de calor absoluto; d) así como los conceptos de capacidad calorífica específica de las sustancias y calor de las reacciones químicas, nombrados por Adair Crawford (1748-1795), un químico y médico irlandés, quien utilizó métodos calorimétricos desarrollados por él mismo.
Como en el último cuarto del siglo XVIII aún no se había esclarecido la naturaleza del calor, Antoine Lavoisier (1743-1794) invitó al astrónomo, físico y matemático francés Pierre Laplace (1749-1827) a trabajar con él en torno al problema de su cuantificación, porque cuando un científico no entiende, mide. Se proponía determinar las condiciones bajo las cuales se pueden vaporizar diferentes fluidos, medir la dilatabilidad de algunas sustancias y presentar un nuevo método basado en un calorímetro diseñado por Laplace, un novedoso instrumento para medir la transferencia de calor en numerosos fenómenos. Cabe mencionar que Lavoisier y Laplace conocían el libro de Magalhães, por lo que Lavoisier utilizó el concepto del calor latente durante la fusión del hielo usado en el calorímetro de Laplace, para medir el calor emitido por varias sustancias cuando se quemaban en oxígeno. Con los resultados definieron una unidad cuantitativa de calórico -un patrón- como la cantidad que derretiría una libra francesa (489,6 gramos, medida adoptada en el año 800 por Carlomagno) de hielo. Obtuvieron resultados para tres sustancias elementales, fósforo, carbón e hidrógeno, reportadas en libras de hielo fundido por libra de elemento quemado. La caloría, unidad usada hoy, se definiría después de la revolución francesa, tal como Black la había estipulado, aunque acotada al rango de 14.5 a 15.5°C. Entre 1777 y 1783, los dos sabios colaboraron en tres ocasiones; los resultados de sus investigaciones están en cuatro escritos contenidos en los famosos escritos: Mémoire sur la chaleur [31] y De l'action du calorique sur les corps solides, principalement sur le verre et sur les métaux [32].
Ya Lavoisier había ideado una nueva explicación de la combustión en términos de la existencia del gas oxígeno. En su memoria Réflexions sur le phlogistique (1777), Lavoisier afirmó que la teoría del flogisto era incompatible con sus resultados experimentales, con lo que propuso la existencia de otro fluido sutil, el calórico que, al impregnar la materia, sería la sustancia responsable del aumento de su calor. Para él: todos los cuerpos naturales obedecen a dos fuerzas, el fluido ígneo, el asunto del fuego, que tiende continuamente a separar a las moléculas, y la atracción, que contrabalancea esa fuerza. En tanto que la última de estas fuerzas, la atracción, sea victoriosa, el cuerpo permanece en estado sólido; si estas dos fuerzas están en un estado de equilibrio, el cuerpo se vuelve líquido; finalmente, cuando la fuerza del calor expansivo prevalece, el cuerpo toma el estado gaseoso. El fluido calórico se haría visible en las llamas, que estarían formadas en su mayor parte por dicho calórico desprendiéndose de los cuerpos y sería el responsable del calor de la materia [33]. El concepto central de la teoría calórica era que el calor, al ser una sustancia elemental, se conservaba; su cantidad total permanecía intacta. No podía ser creada o destruida. El modelo calórico fue ampliamente aceptado -temporal y geográficamente- ya que explicaba las características y los efectos del calor, tales como su difusión por contacto entre los cuerpos, la expansión de estos, el trabajo producido al expandirse el vapor, los distintos estados de agregación de la materia, las quemaduras producidas por congelación (el calórico causaba los mismos daños en la piel al entrar y al salir del cuerpo); cada sustancia presentaría una distinta solubilidad para el calórico, lo que explicaría el calor específico de cada cuerpo; e interpretaba los resultados experimentales que evidenciaban la equivalencia entre calor y trabajo del inglés James Prescott Joule (1818-1889), al plantear que, durante la fricción de un cuerpo contra otro, se romperían las vesículas microscópicas contenedoras del calórico, liberando calor. Fue esta idea la que le causó problemas a la teoría del calórico, ya que algunas personas la interpretaban de forma diferente: Platón había dicho que el calor y el fuego son engendrados por la fricción y el impacto, y esto es movimiento; Robert Hooke (1635-1703), había afirmado que el calor es, nada más, una agitación muy vigorosa y vehemente de las partes de un cuerpo [34]; al apreciar la producción de calor debida a la fricción y el violento movimiento de los líquidos en ebullición, el inglés Francis Bacon (1561-1626) concluyó que la verdadera esencia del calor es el movimiento y nada más [35]; Galileo Galilei (1564-1642), Christiaan Huygens (1629-1695) [36], Isaac Newton (1643-1727) [37] y John Locke (1632-1704) [38] compartían la misma visión. Esto llevó al planteamiento de la teoría cinética del calor.
La primer persona que intentó una formulación matemática de la clase de energía que está conectada con el movimiento (energía cinética) fue Gottfried Wilhelm Leibniz (1646-1716), quien trabajó en este asunto de 1676 a 1689; se dio cuenta de que en muchos sistemas mecánicos de varias masas, cada uno con una velocidad, la energía se conservaba, siempre que las masas no interactuaran. Llamó a esta cantidad la vis viva o fuerza viva del sistema [39]. El principio representa una declaración exacta de la conservación aproximada de la energía cinética en situaciones donde no hay fricción.
La duda mayor sobre el calórico vino de un joven que se encontraba supervisando la fabricación de cañones en Baviera. En el proceso de taladrar el centro de los cañones, Benjamín Thomson (1753-1814), conocido como el conde de Rumford, observó que se producía un aumento de temperatura en la estructura del cañón, en las virutas metálicas y en el propio taladrador, de modo que parecía generarse calor continuamente, en lugar de conservarse como decía la teoría del fluido calórico.
Rumford dirigió una serie de experimentos para medir el cambio de temperatura que ocurría. En uno de ellos utilizó agua para refrigerar el taladrador y la estructura del cañón y midió el aumento de temperatura del agua, observando que el ésta llegaba a hervir sin ningún fuego; entonces concluyó que el calor no podía ser una sustancia material, ya que parecía no tener límite. Más bien parecía que el movimiento mecánico se podría convertir en calor y, más importante, que la conversión era cuantitativa y se podría predecir permitiendo una constante de conversión universal entre la energía cinética y el calor. Cuando el científico británico Thomas Young (1773-1829) trabajó realizando ensayos de tracción y propuso la medida actualmente utilizada para la rigidez de los materiales, en 1807, utilizó el término energía para designar la vis viva, el cual se utiliza desde entonces. El principio de equivalencia mecánica se afirmó por primera vez en su forma moderna por el cirujano alemán Julius Robert von Mayer en 1842 [40]. Mayer llegó a su conclusión en un viaje a las Indias Orientales Holandesas, donde se encontró con que la sangre de sus pacientes era de un rojo más profundo porque consumían menos oxígeno, y por lo tanto menos energía, para mantener su temperatura corporal en un clima más caliente. Él descubrió que el calor y el trabajo mecánico eran formas de energía, publicó una monografía donde declaró una relación cuantitativa entre ellos.
En 1837, en un trabajo publicado por Karl Friedrich Mohr (1806-1879) se encuentra una de las afirmaciones generales más tempranas de la conservación de la energía: además de los 54 elementos químicos conocidos que hay en el mundo físico un agente único, y esto se llama Kraft (energía o trabajo). Puede parecer, según las circunstancias, como el movimiento, la afinidad química, la cohesión, la electricidad, la luz y el magnetismo; y de cualquiera de estas formas puede ser transformado en cualquiera de los otros [41].
Germain Henri Hess (1802-1850) fue un químico y médico suizo que, en 1840, al demostrar que el calor generado en las transformaciones químicas no dependía de la ruta de la reacción, formuló la Ley de la suma constante del calor (Ley de Hess), uno de los primeros principios de la termoquímica. Hess decía: Cuando se produce una reacción química, no sólo hay una transformación de unas sustancias en otras, sino que también tiene lugar un cambio energético. Este cambio es tal, que la reacción consume o produce energía, ya sea en forma de calor, trabajo mecánico, trabajo eléctrico o energía luminosa; lo que significa que la ley es la aplicación a las reacciones químicas del primer principio de la termodinámica. Puede enunciarse diciendo que la variación de la energía térmica de una reacción se puede obtener sumando algebraicamente las entalpías de otras reacciones varias, relacionadas con la que nos interesa. Esta ley resulta de gran utilidad para estimar en forma indirecta una entalpía de reacción desconocida, resultando factible calcular las energías térmicas de muchas reacciones cuya medición directa no es posible o deseable realizar.
Poco después, en 1843, el físico inglés James Prescott Joule (1818-1889) verificó que al fluir una corriente eléctrica a través de un conductor, éste experimentaba un incremento de temperatura; a partir de ahí dedujo que si la fuente de energía eléctrica es una pila electroquímica, la energía habría de proceder de la transformación llevada a cabo por las reacciones químicas, que la convertirían en energía eléctrica y que esta se transformaría en calor. Si en el circuito se introduce un motor eléctrico, se origina energía mecánica; una de las mayores generalizaciones de la ciencia. También realizó otra serie de experimentos. En el más famoso, que ahora se llama el aparato Joule, un peso descendente es atado a una cuerda la cual causa que una rueda de paletas gire y agite el agua en la que se encuentra sumergida, dentro de un calorímetro; el aumento de la temperatura es medida por un termómetro. Joule demostró que la energía potencial gravitatoria perdida por el peso descendente era igual a la energía interna adquirida por el agua a través de la fricción con las paletas; esto es, midió el equivalente mecánico del calor. Ahora, el término calor se reserva sólo para la energía térmica transferida cuando dos cuerpos con diferente temperatura están en contacto.
Dado que la energía se conserva, un cuerpo no puede ganarla a menos que otro se la transfiera incrementando su energía térmica, porque fluyó desde él debido a que estaba más caliente, o porque le ejerció trabajo mecánico. Así, la primera ley de la termodinámica (de la conservación de la energía, establecida por el médico y físico alemán Herman von Helmholtz (1821-1894), en 1847, dice que el cambio neto en la energía en un cuerpo (DE) será igual a la energía que le sea transferida -a través del flujo neto de calor (Q), más la cantidad neta del trabajo realizado sobre el cuerpo (W)- o retirada, con lo que Q y W pueden ser negativos. La primera ley dice cómo medir cualquier cambio de energía en un cuerpo, pero nada dice acerca de cuánta energía hay en el cuerpo, respuesta que se obtiene con la relación de Einstein, que especifica que la cantidad de energía en un cuerpo (E) es igual a su masa (m), multiplicada por el cuadrado de la velocidad de la luz (c2), lo que resulta en muchísima energía (sólo que aún no se conoce cómo obtenerla, salvo para materiales radiactivos).
4.2. La segunda ley de la termodinámica.
Esta implica la existencia de una propiedad adicional de la materia, llamada entropía, la cual, al igual que la energía térmica de la primera ley, puede ser determinada en el laboratorio. Así como la primera ley establece que la energía del universo se conserva, la segunda establece que la entropía del Universo no se conserva sino que su cantidad total nunca decrece, sólo se mantiene o aumenta. La declaración de que es imposible para un dispositivo que opera cíclicamente convertir energía térmica en mecánica, sin perder algo de la térmica en los alrededores fríos, es llamada la segunda ley de la termodinámica, según lo estableció William Thomson Kelvin (1824-1907) en 1848, al publicar la creación de una escala termodinámica para la temperatura, de carácter absoluto [42].
En 1824, Nicolas Léonard Sadi Carnot (1796-1832), un físico e ingeniero francés, quien fue pionero en el estudio de la Termodinámica, publicó su obra maestra Reflexiones sobre la potencia motriz del fuego y sobre las máquinas adecuadas para desarrollar esta potencia [43], donde expuso las ideas que llevarían al segundo principio de la termodinámica, al descubrir una relación entre las temperaturas de los focos calientes (la máquina) y frío (los alrededores) y el rendimiento de la máquina. Experimentalmente probó que, en una máquina caliente, la descarga de calor hacia los alrededores fríos es inevitable, por lo que ninguna máquina real alcanza el rendimiento teórico de Carnot -el cual se obtiene siguiendo el ciclo de Carnot, al que llegó usando las leyes de la mecánica en ausencia de fricción- que es el máximo posible para esa diferencia de temperaturas.
Rudolf Julius Emmanuel Clausius (1822-1888) fue un físico y matemático alemán, considerado uno de los fundadores centrales de la ciencia de la termodinámica. En su trabajo más importante sobre la teoría mecánica del calor, publicado en 1850 [44], estableció por primera vez las ideas básicas de la segunda ley de la termodinámica y formuló de manera novedosa el principio de Sadi Carnot, demostrando que podía interpretarse como la equivalencia de calor y trabajo. Clausius enunció y bautizó, en 1854, la 2a Ley de la Termodinámica para procesos irreversibles como dS ³ dQ/dT y a partir de 1865 entropía, del griego entrοpίa que significa transformación o evolución.
En 1884, el físicoquímico holandés Jacobus Henricus Van't Hoff (1852-1911) propuso que el trabajo externo máximo obtenido al llevar a cabo isotérmicamente una reacción química reversible, era una medida de la afinidad química [45]. En este sentido, el matemático y físico belga Théophile Ernest de Donder (1872-1957) propuso, en 1922 [46], una relación termodinámica entre la afinidad química y la energía libre de Gibbs, para los sistemas que, no estando en equilibrio, no se encuentran muy lejos de él (termodinámica irreversible). A partir de la desigualdad de Clausius, De Donder hizo equivalente la afinidad de la reacción, A, a la derivada parcial negativa de la energía libre de Gibbs, G, con respecto a la extensión de la reacción, x, a presión y temperatura constantes:
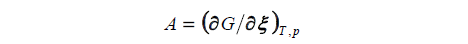
Un corolario de utilizar esta definición, en cinética, es que la velocidad de una reacción cercana al equilibrio es proporcional a la afinidad de la reacción.
En 1954, Ilya Progogine y Raymond Defay [47] definieron la misma afinidad, sustituyendo la derivada parcial de la energía libre de Gibbs por la del calor incompensado, Q', tanto para los sistemas en equilibrio como para los que no. Esta definición es la actualmente aceptada por la IUPAC.
Como puede verse, la propuesta termodinámica para definir la afinidad está acotada para condiciones específicas. Además, la medición de la energía de la reacción es equivalente a la medición del calor de reacción realizada por Pauling [5], aunque con más fundamento teórico y precisión experimental.
5. Conclusión
Pareciera que la química y la termodinámica siguieron caminos separados; sin embargo son similares pues durante su desarrollo, básicamente usaron los mismos conceptos y consideraron a la afinidad como una propiedad y no como un comportamiento. Por eso, aún con las incontables intuiciones, razonamientos y racionalizaciones -relacionados a infinidad de esfuerzos y trabajos de múltiples personas, durante cientos de años- el concepto de afinidad es y seguirá siendo un espejismo: aunque parezca cercano, es inalcanzable.
Referencias
[1] Salas, G., Ramírez, J., Restrepo, O., Cockrell, B. y Noguez, M. La Importancia de llamarse afinidad química. Parte I: La semilla. DYNA, 79 (173), pp. 135-144, 2012. [ Links ]
[2] Salas, G., Ramírez, J., Restrepo, O., Noguez, M. y Cockrell, B. La Importancia de llamarse afinidad química. Parte II: La semilla germina. DYNA, 80 (177), pp. 162-170, 2013. [ Links ]
[3] Salas, G., Ramírez, J., Restrepo, O., Noguez, M. y Cockrell, B. La Importancia de llamarse afinidad química. Parte III: El crecimiento vano. DYNA, 80 (181), pp. 219-227, 2013. [ Links ]
[4] Salas, G., Ramírez, J., Restrepo, O., Noguez, M y Cockrell, B. La Importancia de llamarse afinidad química. Parte IV: Las primeras flores. DYNA, 81 (184), pp. 225-232, 2014. http://dx.doi.org/10.15446/dyna.v81n187.46092 [ Links ]
[5] Salas, G., Ramírez, J., Restrepo, O., Noguez, M. y Cockrell, B. La Importancia de llamarse afinidad química. Parte V: Los frutos. DYNA, 81 (187), pp. 267-275, 2014. http://dx.doi.org/10.15446/dyna.v81n187.46092 [ Links ]
[6] Izcowzki, R.P. and Margrave, J.L., Electronegativity, Journal of the American Chemical Society, 83 (17), pp. 3547-3551, 1961. http://dx.doi.org/10.1021/ja01478a001 [ Links ]
[7] Mortier, W.J., Electronegativity Equalization and its Applications, en Sen, K. and Jørgensen, C.K. eds., Electronegativity, pp. 125-143, Heidelberg, Springer-Verlag, 1987. [ Links ]
[8] Allen, L.C., Chemistry and Electronegativity, International Journal of Quantum Chemistry, 49 (3), pp. 253-277, 1994. [ Links ]
[9] Parr, R.G., Donnelly, R.A., Levy, M. y Palke, W.E., Electronegativity: The density functional viewpoint, Journal of Chemical Physics, 68 (8), pp. 3801-3807, 1978. http://dx.doi.org/10.1063/1.436185 [ Links ]
[10] Bartolotti, L.J., Absolute Electronegativities as Determined from Khon-Sham Theory, en Sen, K. and Jørgensen, C.K. (editors), Electronegativity, pp. 27-40, Heidelberg, Springer-Verlag, 1987. [ Links ]
[11] Pearson, R.G., Electronegativity Scales, Accounts of Chemical Research, 23 (1), pp. 1-2, 1990. [ Links ]
[12] Allen, L.C., Electronegativity Scales, Accounts of Chemical Research, 23, pp. 175-176, 1990. [ Links ]
[13] Allen, L.C., Electronegativity Is the Average One-Electron Energy of the Valence-Shell Electrons in Ground-State Free Atoms, Journal of the American Chemical Society, 111 (25), pp. 9003-9014, 1989. [ Links ]
[14] Pauling, L., The Nature of Chemical Bond, Ithaca, Cornell University Press, 1960. [ Links ]
[15] Allred, A.L. and Rochow, E.G., A scale of Electronegativity Based on Electrostatic Force, Journal of Inorganic Nuclear Chemistry, 5 (4), pp. 264-268, 1958. http://dx.doi.org/10.1016/0022-1902(58)80003-2 [ Links ]
[16] Mulliken, R.S., A New Electroaffinity Scale; Together with Data on Valence States and on Valence Ionization Potentials and Electron Affinities, Journal of Chemical Physics, 2 (11), pp. 782-793, 1934. http://dx.doi.org/10.1063/1.1749394 [ Links ]
[17] Allred, A.L., Electronegativity Values from Thermochemical Data, Journal of Inorganic Nuclear Chemistry, 17 (3-4), pp. 215-221, 1961. http://dx.doi.org/10.1016/0022-1902(61)80142-5 [ Links ]
[18] Sanderson, R.T., Principles of Electronegativity. II. Applications, Journal of Chemical Education, 65 (3), pp. 227-231, 1988. http://dx.doi.org/10.1021/ed065p227 [ Links ]
[19] Keyan, L. and Xue, D., Estimation of Electronegativity Values of Elements in Different Valence States, Journal of Physical Chemistry A, 110 (39), pp. 11332-11337, 2006. http://dx.doi.org/10.1021/jp062886k [ Links ]
[20] Luo, Y. and Pacey, P.D., Theoretical support for a new electronegativity scale, Journal of the American Chemical Society, 113 (4), 1465-1466, 1991. http://dx.doi.org/10.1021/ja00004a087 [ Links ]
[21] Mullay, J., Estimation of Atomic and Group Electronegativities, en Sen, K. and Jørgensen, C.K. (editores), Electronegativity, pp. 1-26, Heidelberg, Springer-Verlag, 1987. [ Links ]
[22] Sproul, G., Electronegativity and Bond Type. 2. Evaluation of Electronegativity Scales, Journal of Physical Chemistry, 98 (27), pp. 6699-6703, 1994. http://dx.doi.org/10.1021/j100078a009 [ Links ]
[23] Wells, A. F., Structural inorganic chemistry, Oxford, Clarendon Press, 1945. [ Links ]
[24] Nagle, J.K., Atomic Polarizability and Electronegativity, Journal of the American Chemical Society, 112 (12), pp. 4741-4747, 1990. [ Links ]
[25] Nelson, P.G., Comment on Sproul's Evaluation of Electronegativity Scales, Journal of Physical Chemistry, 99 (39), pp. 14570, 1995. [ Links ]
[26] Sproul, G.D., Reply to "Comment on Sproul's Evaluation of Electronegativity Scales", Journal of Physical Chemistry, 99 (39), pp. 14571, 1995. http://dx.doi.org/10.1021/j100039a054 [ Links ]
[27] Murphy, L.R., Meek, T.L., Allred, A.l. and Allen, L.C., Evaluation and Test of Pauling's Electronegativity Scale, Journal of Physical Chemistry, 104 (24), pp. 5867-5871, 2000. [ Links ]
[28] Boeyens, J.C.A., The Periodic Electronegativity Table, Zeitschrift für Naturforschung, 63b, pp. 199-209, 2008. [ Links ]
[29] Platón, Timeo, Serrano, R y Díaz, M. (editores), Madrid, Consejo Superior de Investigaciones Científicas, 2012. [ Links ]
[30] De Magalhães, J.J., Essai sur la nouvelle Théorie du Feu élémentaire et de la Chaleur des Corps, London, W. Richardson, 1780. [ Links ]
[31] Lavoisier, A.L. et Laplace, P.S. Mémoire sur la chaleur. pp. 283-333, 1780 [ Links ]
[32] De l'action du calorique sur les corps solides, principalement sur le verre et sur les métaux, pp. 739-764, Mémoires de l'Académie des Sciences, 1783. [ Links ]
[33] Lavoisier, A.L., Réflexions sur le phlogistique, pour servir de développement à la théorie de la combustion & de la calcination, publiée en 1777, Paris, Académie des sciences, 1783. [ Links ]
[34] Hooke, R., Micrographia or, Some physiological descriptions of minute bodies made by magnifying glasses, London, J. Martyn and J. Allestry, 1665. [ Links ]
[35] Bacon, F., Novum Organum (traducción al inglés), London, Clarendon Press, 1878. [ Links ]
[36] Huygens, C., Traité de la lumière, Pierre Vander A, 1690. [ Links ]
[37] Newton, I., Il Saggiatore, Roma, Giacomo Mascardi, 1623. [ Links ]
[38] Locke, J., An Essay Concerning Human Understanding, London, Eliz. Holt, for Thomas Basset, 1690. [ Links ]
[39] Leibniz, G.W., Specimen Dynamicum, en Loemker, L.E. Ed., Philosophical Papers and Letters, pp. 435-452, D. Reidel-Springer, Netherlands, 1976. [ Links ]
[40] Mayer, J.R., Annalen der Chemie und Pharmacie 43 (2), pp. 233-240, 1842. http://dx.doi.org/10.1002/jlac.18420430208 http://dx.doi.org/10.1002/jlac.18420420212 [ Links ]
[41] Chisholm, H. Ed., Mohr, Karl Friedrich. Encyclopædia Britannica, Cambridge University Press, 1911. [ Links ]
[42] Goldstein, M. y Goldstein, F.I., The refrigerator and the Universe, Cambridge, Harvard University Press, 1993. [ Links ]
[43] Sadi, N.L., Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance, París, Bachelier, 1824. [ Links ]
[44] Clausius, R., Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen, Annalen der Physik, 155 (4), pp. 500-524, 1850. http://dx.doi.org/10.1002/andp.18501550403 [ Links ]
[45] Van't Hoff, J.H., Studies in Chemical Dynamics, Amsterdam, Frederik Muller and Co., 1896. [ Links ]
[46] De Donder, T.E., L'Affinitié. Applications auz gaz parfaits. Mémoires de la Classe des Sciences, Académie Royale de Belgique, 5th series, 7, pp. 197-205, 1922. [ Links ]
[47] Prigogine, I. and Defay, R., Chemical Thermodynamics, New York, John Wiley & Sons, 1954. [ Links ]
G. Salas-Banuet, es Ingeniero Químico Metalúrgico con título de postgrado, ambos de la Universidad Nacional Autónoma de México - UNAM, México. Profesor Titular en la Facultad de Química de la misma universidad, donde ha trabajado en docencia, investigación y divulgación. Su área principal de trabajo está en los metales; otros campos de interés son el pensamiento, las ideas, la historia, arqueología, desarrollo humano. Ha publicado en revistas nacionales e internacionales indexadas. Así mismo ha enviado trabajos a conferencias y eventos científicos.
J. Ramírez-Vieyra, obtuvo su diploma en Ingeniería Metalúrgica en la Universidad Nacional Autónoma de México - UNAM, México, donde también obtuvo su Maestría en Ingeniería. Fue profesor adjunto y ha sido Investigador Asistente. Adicionalmente, actúa como Profesor Asistente en la Facultad de Química de la UNAM, México. Ha colaborado en algunos proyectos de investigación en la elaboración de artículos y ha participado en congresos y publicado artículos en sus temas de interés: Metalurgia física, Arqueometalurgia, Educación en ingeniería y Materiales y ambiente.
O. Restrepo-Baena, es Ingeniero de Minas y Metalurgia de la Universidad Nacional de Colombia; Magister en Evaluación de Impactos Ambientales y Doctor en Metalurgia y Materiales de la Universidad de Oviedo, España. Trabaja en la Facultad de Minas de la Universidad Nacional de Colombia, Sede Medellín y su área de trabajo se centra en Metalurgia extractiva y Materiales de Ingeniería: Cementos, Cerámicos, Pigmentos.
M. Noguez-Amaya, es Ingeniera Química Metalúrgica de la Facultad de Química, Universidad Nacional Autónoma de México - UNAM, México. MSc. en Ingeniería Metalúrgica de la School of Engineering, University of Pittsburgh, USA. Actualmente profesora de tiempo completo en la Facultad de Química de la UNAM; ganó el premio "Ernesto Rios del Castillo" y el premio "Sor Juana Inés de la Cruz" a la mujer universitaria de la UNAM. Sus áreas de interés son: Metalurgia física, Educación en ingeniería y Materiales y ambiente.
B.R. Cockrell, recibió su PhD. en Antropología (Arqueología) en la UC, Berkeley, USA. Su área de investigación actual está en el análisis de metales del Cenote Sagrado de Chichen Itza en Yucatán, México, en colaboración con investigadores de la UNAM, México. Actualmente enseña en el Departamento de Antropología de UC Berkeley y en SF State University. Sus intereses incluyen la metalurgia de los antiguos pueblos americanos así como la arqueometría y arqueología de Mesoamérica.