Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.190 Medellín Mar./Apr. 2015
https://doi.org/10.15446/dyna.v82n190.42016
DOI: http://dx.doi.org/10.15446/dyna.v82n190.42016
Review of mathematical models to describe the food salting process
Revisión de modelos matemáticos para describir el salado de alimentos
Julián Andrés Gómez-Salazar a, Gabriela Clemente-Polo b, & Neus Sanjuán-Pelliccer b
a Escuela de Agronomía, Universidad de la Salle Bajío, León, México, jgomezs@delasalle.edu.mx
b Departamento de Tecnología de Alimentos, Universitat Politècnica de València, Valencia, España, gclemen@tal.upv.es
Received: February 11th, 2014. Received in revised form: January 28th, 2014. Accepted: February 11th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
Salting and subsequent curing are part of the traditional processing method used in the meat and fish industry. Different preserving agents (sodium chloride, nitrite, nitrate, among others) are added in this process. Nowadays, more attention is paid to the amount of salts added and the salting time employed. For this reason, it is important to know the factors governing salt penetration and the most convenient process conditions. The transfer mechanism of the salts through the structure is an interesting aspect in meat and fish processing technology. Mathematical models are the best way to discover the factors, which govern this process, which may represent and explain the observed data and predict the behaviour under different conditions. The objective of this review is to describe the use of the mathematical models to simulate meat and fish salting and the benefits derived from their use. Most of the models used to describe the salting process are diffusional, based on Fick's second law, although empirical ones are also used. For modelling purposes a good description of the experimental results should be guaranteed. The complexity of the model will depend on the objective to be reached and will be analysed in each case.
Keywords: meat, fish, salting, curing, modelling
Resumen
El salado y posterior curado forman parte del procesado tradicional de conservación de carne y pescado. En él se añaden diferentes conservantes (cloruro sódico, nitritos, nitratos, entre otros). En la actualidad se está aumentando el control sobre la cantidad de sales añadidas y el tiempo de salado. Por ello es importante conocer los factores que controlan la penetración de sal y las condiciones de proceso más adecuadas. Los mecanismos de transferencia de las sales en el sólido son aspectos muy interesantes a considerar en las industrias de procesado de carne y pescado. Los modelos matemáticos son la mejor manera de conocer los factores controlantes en estos procesos. Éstos representan y explican los datos observados y predicen el comportamiento bajo diferentes condiciones. El objetivo de este trabajo es describir el uso de modelos matemáticos para similar el salado de carne y pescado y los beneficios derivados de su uso. La mayoría de los modelos utilizados para describir el proceso de salado son difusionales, basados en la segunda ley de Fick, aunque también son utilizados los modelos empíricos. Para propósitos de modelización debe ser garantizada una buena descripción de los resultados experimentales. La complejidad del modelo dependerá del objetivo a alcanzar será analizado en cada caso.
Palabras clave: carne, pescado, salado, curado, modelización
1. Introduction
The process of salting is traditional in the meat and fish industry. Sodium chloride is an essential ingredient of salting that provides different functionalities: providing flavour, solubilizing proteins, dehydrating and altering osmotic pressure so as to inhibit bacterial growth and subsequent spoilage. Nitrate and nitrites are also added to the meat in this process. They are basic ingredients in meat products. Nitrates, which are reduced to nitrites by bacterial action, produce an antimicrobial effect, while nitrites inhibit the growth of Clostridium botulinum and, thereby, the formation of the neurotoxic proteins. Nitrites also contribute to the development of flavour in cured meat products and are responsible for the formation of the characteristic pink/red colour in cured and smoked products. Over the last few years, changing consumer demands and increasing global competition have led the meat sector to embrace new ingredient systems and new processing technologies. In the case of curing salts, consumers are demanding healthier products that are low in salt. The use of salts in meat is seen to be a cause of the increased risk of chronic diseases, such as obesity, cancer and strokes [1]. In this regard, what has been proposed is the control of and reduction in the level of salts added to meat products. Likewise, it is also important to increase knowledge about the reactions that take place and the process conditions.
It is essential to carry out an exhaustive control of the salting process in order to develop high quality fish and meat products. This involves a good distribution of the salts in the product and an estimation of the salting time. In order to control both aspects, it is important to know the main factors governing salt penetration. The transport phenomena involved in salting, defined by salt and water transfer, are complex and depend on aspects such as brine concentration, temperature or pH, among other things. One of the best ways to gain knowledge of the factors governing this process is the use of mathematical models, which may represent processes, explain the observed data and predict the behaviour of the process under different conditions [2]. This paper presents a review of the development and use of mathematical models describing mass transfer during the salting and curing of meat and fish.
2. The salting process
Meat and fish are traditionally preserved by being treated with salts, such as sodium chloride, sodium nitrite and sodium nitrate. Salt reduces water activity and lends specific organoleptic and sensory characteristics to the products. The forms of adding salts differ depending on the final product to be obtained. Salting is performed either by dry, brine or injection salting or a combination of these methods.
Traditional dry salting consists of covering or rubbing the raw material with solid salt; this is partially dissolved and drained during the process by fluid effluent from the product as a consequence of the osmotic and diffusional mechanisms [3].
Brine salting is based on the immersion of the meat or fish pieces in a water and salt solution. In dry and brine salting, counter current salt and water mass transfer take place between the brine (or dry salt) and the meat. Barat et al. [3] did not find any significant differences between these two processes in terms of the physicochemical and sensory parameters, but noted that dry salting is more favourable to dehydration, while brine salting favours the entry of salt. However, brine salting has several advantages over dry salting, including shorter processing times due to higher salt uptake and higher weight yields due to a better control over the rate of salt uptake and water loss in the muscle [4-6].
Injection-salting is a method that also introduces salt into the muscle tissue, but differently from dry and brine salting. In this case, the brine is forced to distribute itself into the muscle tissue through an injection system. Likewise, over the last few years, various technologies have been tested for the purposes of accelerating the penetration of the salt in the food, such as massage, ultrasound, centrifugation, vacuum, freezing, electric current, pressure and alternating pressure and vacuum [7].
Salting changes the composition and structure of the tissue and the extent of these changes may affect the mass transfer kinetics and sensorial properties of the final product. The gradual increase of salt concentration in the meat muscle leads to changes in its functional properties. All of the salting procedures bring about the salt saturation of the liquid phase of the products. Proteins are strongly aggregated at high salt concentrations, leading to a reduction in the water holding capacity of the muscle [8]. This implies a strong bond between water and salt and the concurrent dehydration of the protein [9].
Two main simultaneous flows are usually generated during salting, water loss and salt uptake. Salt ions diffuse through the aqueous phase of the product, which is distributed by means of a complex network of microscopic channels within the dry matter matrix. At the same time, the liquid phase of the product does not remain constant when the salt is dissolved in it. Water molecules migrate outside the product, which causes resistance to diffusion [10].
Salt diffusion is related to the change between the salt concentration in the interior of the food and that in the external brine solution, where the mass transfer rates do not cease until equilibrium is reached. Equilibrium is the end of the diffusion process, that is, when the net rate of mass transfer is zero. The diffusion rate necessary to reach equilibrium depends on the concentration gradient (chemical potential) between the brine and the product. During salting, a marked increase in the concentration of salt in the muscle may be observed in the first few hours due to the large concentration gradient at the beginning of the process. Likewise, a great decrease in moisture in the muscle can be observed [11]. Thereafter, the diffusion decreases until the equilibrium concentration is reached [12].
3. Modelling of salting process
Mathematical modelling has become a common practice when analysing the salting phenomena due to the cost and time involved in experimental studies [13-16]. These models usually contain a food system description and the mechanisms and rate equations of changes. Models can be used to improve the understanding of the process dynamics and to develop a control strategy for a new process [13]. The complexity needed in a model depends on the objective to be reached. In general, the simpler the model, the easier its mathematical solution. Nevertheless, the model equations must be a good approximation to the real process [17]. The models can give realistic representations of a process, explain the observed data and predict the behaviour under different conditions [18]. These can be used for process optimization, for example to reduce the cost of the process or the processing time without the need to carry out experiments. However, models are an approximation to reality, which may not provide an accurate description of the system resulting in poor prediction. Moreover, simulation using complex models can require the use of complex mathematical algorithms, which can increase the calculation time. Models can be classified as theoretical and empirical. Theoretical models are developed using the principles of chemistry, physics and biology. Theoretical models are derived from mass and energy balances. Among the theoretical models that have been applied to mass transfer, the diffusional ones are the most widely used. For this reason, they are explained in detail in section 3.1. In section 3.2, the empirical models are presented.
3.1. Diffusional models
Diffusion is the predominant transport mechanism involved in salting. It is a spontaneous phenomenon of mass transfer caused by the random motion of the molecules under a concentration gradient. For the purposes of modelling the diffusion in salting processes, authors commonly consider water diffusion and salt diffusion separately [12,14,15].
The key equation describing diffusion is Fick's second law (Equation 1).
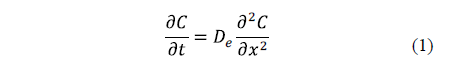
Eq. 1 is based on the hypothesis that the transfer rate of a diffusing substance through a unit area is proportional to the concentration gradient measured normally to the section [19]. Diffusion alone does not usually occur. For this reason, the calculation of an effective diffusion coefficient that covers all real phenomena can be useful [2].
Effective diffusivity is a property that determines the velocity of mass propagation through the material. In the case of salting, this property defines the penetration velocity of salt and water loss in a food [20]. The estimation of this property allows both the mass flux and the processing time to be predicted or controlled [9].
The analytical solutions of Fick's diffusion equation for predicting D in salting for classical geometries has been widely used for different geometries: planar with transport in one direction (Equation 2), cylindrical (Equation 3), spherical (Equation 4), and parallelepipedic with multidirectional transport (Equation 5) [11,16,21-32].
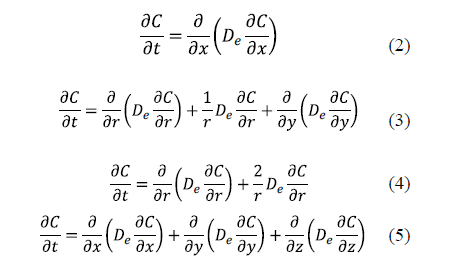
The solution of these equations depends on the boundary conditions. The number of boundary conditions required is determined by the order of the highest derivatives appearing in each independent variable in the governing differential equations. Thus, a transient process governed by a first derivative respect to time will require one boundary condition related to this variable, usually one initial condition. The initial condition refers to the distribution of salt at the beginning of the salting process. For example, for a slab geometry it can be expressed as (Eq. 6).

Eq. 6 indicates that at the beginning of the salting process the total salt concentration in the product is the same and equal to the initial concentration.
Since the governing equation for each spatial dimension is of the second order, two boundary conditions are needed for each dimension. A symmetry condition and a surface condition are usually formulated. For an infinite slab, the symmetry condition is expressed in equation 7. Generally speaking, a symmetry condition must be formulated for each spatial dimension.
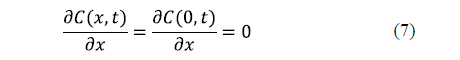
As regards the surface condition, two considerations can be made depending on whether the external resistance to mass transfer is negligible or not. If the external resistance to mass transfer is negligible, it is assumed that the equilibrium concentration of salt is reached on the surface of the solid from the beginning of the process. This condition is expressed by equation 8 for an infinite slab of thickness, 2L.
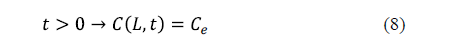
The industrial salting process is not carried out under conditions of strong agitation. For that reason, the external resistance to mass transfer can sometimes be considered. In this case, a mass transfer coefficient (kc) is included in the surface boundary condition. Equation 9 shows the surface condition under this hypothesis for an infinite slab of thickness, 2L [25].
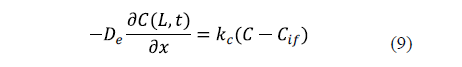
Previous diffusion equations (Eqs. 2 to 5) took into account the local concentration of salt in the sample. Since the experimental values are determined as average concentrations, these equations are integrated to calculate the average salt content of the sample and to model the average concentrations in order to compare the experimental and calculated results.
Mass transport phenomena during salting can be assumed as the diffusion of ionic species in a multicomponent electrolyte solution. Mass transfer in electrolytic solutions requires a description of the movement of mobile ionic species, material balances, current flow, electroneutrality and fluid mechanics. Solutes do not diffuse independently; a diffusion potential is established and ions interact with it [9]. Thus, the description of the process by means of the generalized Stefan-Maxwell equation [33] is more rigorous than that achieved using the previously described Fick equation [34].
Pinotti et al. [9] analysed the effect of NaCl concentration on the diffusion coefficients of NaNO2 and KNO3 in pork meat. They applied the Stefan-Maxwell theory in electrolyte solutions to calculate the diffusion coefficients. Costa-Corredor et al. [34] simulated simultaneous water and salt diffusion in dry fermented sausage by means of the generalized Stefan-Maxwell theory. They converted this equation into the multicomponent Fick equation for the simulation. Pakowski et al. [35] simulated the evolution of water and salt profiles during the dry curing of Spanish ham in a similar way.
3.1.1. Factors influencing diffusion
The diffusion of salt and water in meat is influenced by several factors. These factors can be used as implicit functions in models [36].
3.1.1.1. Water content
Since water is the main component of meat and fish, the interaction between water molecules and other macromolecules determines the water retention capacity [37]. Water retention capacity is an important factor in the diffusion of salts during the salting process, inasmuch as salts-due to their high degree of solubility-are mobilized into the aqueous phase of meat and fish [38]. Thus, the transport rate of salt falls as the water content of food decreases during processing [20,39].
3.1.1.2. Brine concentration
The rates of salt and water diffusion are positively correlated with the increasing salt concentration of the brine [40]. Different authors have studied the influence of brine concentration on the salt and water diffusion coefficients in meat from multiple regression models [41-43]. Corzo and Bracho [23] modeled the effect of salt concentration and temperature on the water diffusion coefficient of sardine sheets. They used a multiple linear regression to fit the diffusion coefficient as a function of absolute temperature (1/T) and brine concentration (C).
3.1.1.3. Meat fibre direction
The influence of meat fibre direction on the diffusion of salt and water in salted products has been widely studied [24, 36, 44-46]. All of these studies have found that both salt and water diffusion behave in an anisotropic way in fish and meat muscles. For instance, Gisbert [45] studied the salting of pork loin and found a higher salt and water diffusivity when the diffusion occurred parallel to the meat fibres.
3.1.1.4. Operating temperature
The diffusivity is significantly affected by temperature. An increase in temperature raises the thermal energy of molecules, leading to an increase in their diffusion rate. [9,23,28]. Thus, the relationship between salt and water diffusivity and temperature is generally described by the Arrhenius equation (Eq. 10).
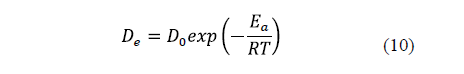
3.1.1.5. Shrinkage
During salting, moisture loss leads to the tightening of the solid structure of the product and local shrinkage. Isotropic shrinkage is when the dimensions of the product change in equal proportions in every direction. Clemente et al. [47] found a linear relationship between the quotients "radius/initial radius" and "volume/initial volume" and the moisture content for the drying of salted pork meat. Other relationships were described by Comaposada [48] to determine the effect of shrinkage on water diffusion in the salted muscle of pork ham, and by Corzo and Bracho [49] to determine the shrinkage of salted sardine sheets.
3.1.1.6. pH
The pH of the meat has a significant effect on the diffusion of curing salts and water because this factor controls the water retention capacity. Studies by Cierach and Modzelewska-Kapitula [50] on salted pork meat, show that meat with low pH values, from 5.4 to 5.5 (PSE meat, Pale Soft and Exudative), reached a higher concentration and achieved a greater salt diffusion compared to meat with high pH values of between 6.2 and 6.8 (DFD meat, Dark, Firm and Dry). Arnau et al. [51] studied the effect of pH on the salt content in hams obtaining similar results.
3.1.2. Improvement of diffusional models
Several aspects are important in the development of better models with which to describe the salting process. One of them is the precise measurement of the salt and moisture content at every point of the food and its surroundings during processing [11]. In this direction, the greatest advances have been made by using non-destructive testing methods, such as X-ray tomography, ultrasounds and NMR [31,52-54]. Another aspect is the adequate thermodynamic definition of the food and its surroundings [55], identifying the components, phases and driving forces that exist, both in pile and brine salting processes. In the same fashion, an adequate resolution of the rigorous equations allows a better approximation of the models with which to describe the real process. Assuming constant diffusion coefficients, regardless of the time, distance or food composition, and that the external resistance to mass transfer is neglected [25], facilitates the solution of the model. Nevertheless, sometimes this means that the model does not provide close fitting results [56].
3.2. Empirical models
Empirical models are obtained by fitting experimental data; thus, these models only describe systems under specific conditions. Empirical models present some advantages, such as the ability to model water losses and solid uptake, as well as the physical-chemical and sensory properties of the food material. These models ignore the internal resistance to mass transfer, for which reason they are limited to obtaining a general expression of the mass transport phenomena experienced during the process [57]. Shi and Le Maguer [58] described some important aspects related to the application of these models. There are several empirical equations used to model the mass transfer kinetics during salting, which are useful for the purposes of optimizing the process itself. Although not derived from any physical laws or diffusion theories, their application during the study of salting kinetics has been demonstrated.
3.2.1. Azuara's model
Azuara et al. [59] proposed a model, which avoided the limitations of Fick's diffusion model for practical purposes, and succeeded in predicting mass transport during osmotic dehydration accurately [60]. Both water loss and salt uptake are modelled. This model can be written as:
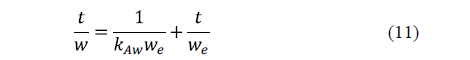
Similarly, for solid uptake, it can also be written as:

This model does not consider the size, shape and structure of the material. Its greatest advantage is that equilibrium does not have to be reached in order to predict water loss and salt gain.
3.2.2. Peleg's model
Peleg's model [61] is a two-parameter model widely used in food processing. The linearized equation for water loss is:
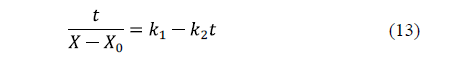
Similarly, for salt uptake, Peleg's model can also be written as:
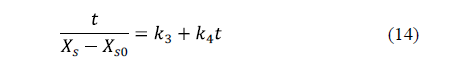
Corzo et al. [60] applied Peleg's and Azuara's models for the purposes of describing mass transfer during pile salting of goat meat sheets using different mixtures of NaCl, KCl, CaCl2 and MgCl2. High coefficients of determination and low mean relative errors indicated that both models are able to represent the moisture loss and salt uptake during pile salting. The equilibrium moisture and salt contents estimated by Peleg's model were lower than those estimated by Azuara's model.
3.2.3. Zugarramurdi and Lupin's model
This mathematical model is an exponential approach to the equilibrium value of sodium chloride and water concentrations. The acceptability of the model has been verified through experiments on various fish species. The authors concluded that the behaviour of the system under consideration is general and may be applied to any species [62-64]. The equations for the model are equation 15 for water loss and equation 16 for sodium chloride uptake.
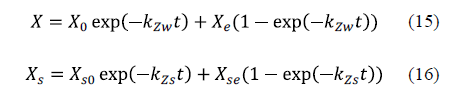
Corzo et al. [65] considered applying Zugarramurdi and Lupin's model during the pile salting of goat meat sheets in order to study not only the equilibrium, but also the kinetics of the process. A good agreement between the experimental and calculated results was obtained. Chabbouh et al. [14] applied both Zugarramundi and Lupin and Peleg's models for the description of water exudation and salt uptake by beef meat. Both models displayed a good fit to the experimental data for sodium chloride uptake and water exudation. Bellagha et al. [62] used Zugarramundi and Lupin's model in the modelling of the salting kinetics of sardine. They obtained good agreement between the experimental values and those calculated by means of the model for both brine and dry salting.
4. Conclusions
Using models to describe meat and fish salting is highly useful for industrial purposes; for example, in the prediction of the salting time and the brine concentration necessary to reach a certain salt concentration in a piece of meat or fish.
The diffusion of salt and water in meat and fish is influenced by several factors. It is necessary to develop mathematical equations, which take all of those aspects and the physical properties into account in order both to improve our understanding and to describe the salting kinetics adequately.
Most of the models used to describe the salting process are diffusional, based on Fick's second law. In the case of salting, the most commonly applied equations are diffusional for regular shapes. In order to improve diffusional models, additional details of the physical and chemical processes that take place during salting should be incorporated. Other models used for salting are the empirical ones, such as Azuara's model, Peleg's model and Zugarramurdi and Lupin's model.
The level of complexity needed in a model depends on the objective to be reached. In general, the easier the model, the easier is its solution. Nevertheless, a good description of the experimental results should be guaranteed. For this reason, the model to be used will be analysed in each case.

Acknowledgements
The authors of this paper acknowledge the financial support from CONSOLIDER INGENIO 2010 (CSD2007-00016), Spain.
References
[1] Weiss, J., Gibis, M., Schuh, V. and Salminen, H., Advances in ingredient and processing systems for meat and meat products, Meat Science, 86 (1), pp. 196-213, 2010. http://dx.doi.org/ 10.1016/j.meatsci.2010.05.008 [ Links ]
[2] Mulet, A., Drying modeling and water diffusivity in carrots and patatoes, Journal of Food Engineering, 22 (1-4), pp. 329-348, 1994. http://dx.doi.org/10.1016/0260-8774(94)90038-8 [ Links ]
[3] Barat, J.M., Rodriguez-Barona, S., Andres, A. and Fito, P., Cod salting manufacturing analysis, Food Research International, 36 (5), pp. 447-453, 2003. http://dx.doi.org/10.1016/S0963-9969(02)00178-3 [ Links ]
[4] Andrés, A., Rodríguez-Barona, S., Barat, J. M. and Fito, P., Salted cod manufacturing: Influence of salting procedure on process yield and product characteristics, Journal of Food Engineering, 69 (4), pp. 467-471, 2005. http://dx.doi.org/ 10.1016/j.jfoodeng.2004.08.040 [ Links ]
[5] Beraquet, N.J., Iaderoza, M., Jardim, D.C.P. and Lindo, M.K.K., Salting of mackerel (Scomber japonicas) II. Comparison between brining and mixed salting in relation to quality and salt uptake, Coletaneado Instituto de Technologia de Alimentos, 13, pp. 175-198, 1983. [ Links ]
[6] Thorarinsdottir, K.A., Arason, S., Bogason, S.G. and Kristbergsson, K., The effects of various salt concentrations during brine curing of cod (Gadus morhua), International Journal of Food Science and Technology, 39 (1), pp. 79-89, 2004. http://dx.doi.org/ 10.1046/j.0950-5423.2003.00757.x [ Links ]
[7] Vandendriessche, F., Tecnologías centroeuropeas de elaboración de jamón curado. III Congreso Mundial del Jamón. Ed. Consejo Regulador de la Denominación de Origen "Jamón de Teruel", pp. 192-212, 2005. [ Links ]
[8] Thorarinsdottir, K.A., Arason, S., Sigurgisladottir, S., Gunnlaugsson, V.N., Johannsdottir, J. and Tornberg, E., The effects of salt-curing and salting procedures on the microstructure of cod (Gadus morhua) muscle, Food Chemistry, 126 (1), pp. 109-115, 2011. http://dx.doi.org/ 10.1016/j.foodchem.2010.10.085 [ Links ]
[9] Pinotti, A., Graiver, N., Califano, A. and Zaritzky, N., Diffusion of nitrite and nitrate salts in pork tissue in the presence of sodium chloride, Journal of Food Science, 67 (6), pp. 2165-2171, 2002. http://dx.doi.org/10.1111/j.1365-2621.2002.tb09521.x [ Links ]
[10] Andrés, A.I. y Ruiz J., Tecnología del salazonado del jamón ibérico, En cap. VIII de Tecnología del jamón ibérico, de los sistemas tradicionales a la explotación racional del sabor y el aroma". Coordinador J. Ventanas. Ediciones Mundi Prensa. Madrid, 2001. [ Links ]
[11] Barat, J.M., Baigts, D., Aliño, M., Fernandez, F.J. and Perez-García, V.M., Kinetics studies during NaCl and KCl pork meat brining, Journal of Food Engineering, 106 (1), pp. 102-110, 2011. http://dx.doi.org/10.1016/j.jfoodeng.2011.04.022 [ Links ]
[12] Volpato, G., Michielin, E.M.Z., Ferreira, S.R.S. and Petrus, J.C.C., Kinetics of the diffusion of sodium chloride in chicken breast (Pectoralis major) during curing, Journal of Food Engineering, 79 (3), pp. 779-785, 2007. http://dx.doi.org/10.1016/j.jfoodeng.2006.02.043 [ Links ]
[13] Vodyanova, I.V., Storro, I., Olsen, A. and Rustad, T., Mathematical modelling of mixing of salt in minced meat by bowl-cutter, Journal of Food Engineering, 112 (3), pp. 144-151, 2012. http://dx.doi.org/10.1016/j.jfoodeng.2012.03.020 [ Links ]
[14] Chabbouh, M., Ahmed, S.B.H., Farhat, A., Sahli, A. and Bellagha, S., Studies on the salting step of Tunisian kaddid meat: Experimental kinetics, modeling and quality, Food and Bioprocess Technology, 5 (5), pp. 1882-1895, 2012. http://dx.doi.org/10.1007/s11947-011-0635-2 [ Links ]
[15] Uribe, E., Miranda, M., Vega-Galvez, A., Quispe, I., Claveria, R. and Di Scala, K., Mass transfer modelling during osmotic dehydration of jumbo squid (Dosidicus gigas): Influence of temperature on diffusion coefficients and kinetic parameters, Food and Bioprocess Technology, 4 (2), pp. 320-326, 2011. http://dx.doi.org/10.1007/s11947-010-0336-2 [ Links ]
[16] Graiver, N., Pinotti, A., Califano, A. and Zaritzky, N., Mathematical modeling of the uptake of curing salts in pork meat, Journal of Food Engineering, 95 (4), pp. 533-540, 2009 http://dx.doi.org/10.1016/j.jfoodeng.2009.06.027 [ Links ]
[17] Katekawa, M.E. and Silva, M.A., A review of drying models including shrinkage effects, Drying Technology, 24 (1), pp. 5-20, 2006. http://dx.doi.org/10.1080/07373930500538519 [ Links ]
[18] Gómez, J., Sanjuán, N., Bonb, J., Arnauc, J., Clemente, G., Effect of temperature on nitrite and water diffusion in pork meat, Journal of Food Engineering, 149, pp. 188-194, 2015 http://dx.doi.org/10.1016/j.jfoodeng.2014.10.008 [ Links ]
[19] Crank J., The Mathematics of Diffusion. London: Oxford University Press. 66 P., 1957. [ Links ]
[20] Costa-Corredor, A., Munoz, I., Arnau, J. and Gou, P., Ion uptakes and diffusivities in pork meat brine-salted with NaCl and K-lactate, LWT-Food Science and Technology, 43 (8), pp. 1226-1233, 2010. http://dx.doi.org/10.1016/j.lwt.2010.03.018 [ Links ]
[21] Corzo, O. and Bracho, N. Determination of water effective diffusion coefficient of sardine sheets during vacuum pulse osmotic dehydration, LWT-Food Science and Technology, 40 (8), pp. 1452-1458, 2007. http://dx.doi.org/10.1016/j.lwt.2006.04.008 [ Links ]
[22] Torregroza-Espinosa, A., Montes-Montes, E., Ávila-Gómez, A. and Remolina-López, J., Kinetic modelling of drying of three varieties of yucca industrial. DYNA, 81 (186), pp. 184-192, 2014. http://dx.doi.org/10.15446/dyna.v81n186.39923 [ Links ]
[23] Corzo, O. and Bracho, N., Water effective diffusion coefficient of sardine sheets during osmotic dehydration at different brine concentrations and temperatures, Journal of Food Engineering, 80 (2), pp. 497-502, 2007. http://dx.doi.org/10.1016/j.jfoodeng.2006.06.008 [ Links ]
[24] Gou, P., Comaposada, J. and Arnau, J. Meat pH and meat fibre direction effects on moisture diffusivity in salted ham muscles dried at 5ºC, Meat Science, 61 (1), pp. 25-31, 2002. http://dx.doi.org/10.1016/j.jfoodeng.2006.06.008 [ Links ]
[25] Gou, P., Comaposada, J. and Arnau, J., NaCl content and temperature effects on moisture diffusivity in the Gluteus medius muscle of pork ham, Meat Science, 63 (1), pp. 29-34, 2003. http://dx.doi.org/10.1016/S0309-1740(01)00158-9 [ Links ]
[26] Graiver, N., Pinotti, A., Califano, A. and Zaritzky, N., Diffusion of sodium chrloride in meat pork: Influence on its microstructure, Scanning, 27 (2), pp. 76-77, 2005. [ Links ]
[27] Graiver, N., Pinotti, A., Califano, A. and Zaritzky, N., Diffusion of sodium chloride in pork tissue, Journal of Food Engineering, 77 (4), pp. 910-918, 2006. http://dx.doi.org/10.1016/j.jfoodeng.2005.08.018 [ Links ]
[28] Telis, V.R.N., Romanelli, P.F., Gabas, A.L. and Telis-Romero, J., Salting kinetics and salt diffusivities in farmed Pantanal caiman muscle, Pesquisa Agropecuaria Brasileira, 38 (4), pp. 529-535, 2003. http://dx.doi.org/10.1590/S0100-204X2003000400012 [ Links ]
[29] Van Nguyen, M., Arason, S., Thorarinsdottir, K.A., Thorkelsson, G. and Gudmundsdottir, A., Influence of salt concentration on the salting kinetics of cod loin (Gadus morhua) during brine salting, Journal of Food Engineering, 100 (2), pp. 225-231, 2010. http://dx.doi.org/ 10.1016/j.jfoodeng.2010.04.003 [ Links ]
[30] Vestergaard, C., Andersen, B.L. and Adler-Nissen, J., Sodium diffusion in cured pork determined by 22Na radiology, Meat Science, 76 (2), pp. 258-265, 2007. http://dx.doi.org/10.1016/j.jfoodeng.2010.04.003 [ Links ]
[31] Vestergaard, C., Risum, J. and Adler-Nissen, J., Quantification of salt concentrations in cured pork by computed tomography, Meat Science, 68 (1), pp. 107-113, 2004. http://dx.doi.org/10.1016/j.meatsci.2006.11.007 [ Links ]
[32] Wang, D.H., Tang, J.M. and Correia, L.R., Salt diffusivities and salt diffusion in farmed Atlantic salmon muscle as influenced by rigor mortis, Journal of Food Engineering, 43 (2), pp. 115-123, 2000. http://dx.doi.org/10.1016/S0260-8774(99)00140-5 [ Links ]
[33] Taylor, R. and Krishna, R., Multicomponent Mass Transfer. New York: John Wiley and Sons, Inc.P, pp. 37-43, 1983. [ Links ]
[34] Costa-Corredor, A., Pakowski, Z., Lenczewski, T. and Gou, P., Simulation of simultaneous water and salt diffusion in dry fermented sausages by the Stefan-Maxwell equation, Journal of Food Engineering, 97 (3), pp. 311-318, 2010. http://dx.doi.org/ 10.1016/j.jfoodeng.2009.10.021 [ Links ]
[35] Pakowski, Z., Gou, P., Comaposada, J. and Arnau, J., Simultaneous water and salt diffusion in meat during drying and curing of ham. Drying 2004 - Proceedings of the 14th International Drying Symposium (IDS 2004). São Paulo, Brazil, 22-25 August 2004, vol. A, pp. 518-525, 2004. [ Links ]
[36] Zhang, Q., Xiong, S., Liu, R., Xu, J. and Zhao, S., Diffusion kinetics of sodium chloride in Grass carp muscle and its diffusion anisotropy, Journal of Food Engineering, 107 (3-4), pp.311-318, 2011. http://dx.doi.org/10.1016/j.jfoodeng.2011.07.011 [ Links ]
[37] Renou, J.P., Foucat, L., and Bonny, J.M., Magnetic resonance imaging studies of water interactions in meat, Food Chemistry, 82 (1), pp. 35-39, 2003. http://dx.doi.org/10.1016/S0308-8146(02)00582-4 [ Links ]
[38] Honike, K.O., The use and control of nitrate and nitrite for the processing of meat products, Meat Science, 78 (1-2), pp. 68-76, 2008. http://dx.doi.org/10.1016/j.meatsci.2007.05.030 [ Links ]
[39] Boudhrioua, N., Bonazzi, C. and Daudin, J.D., Moisture and salt transfers during constant temperature drying of gelatin gels: Effects of composition and of water flux intensity, Chemical Engineering Research and Design, 81 (A9), pp. 1113-1122, 2003. http://dx.doi.org/10.1205/026387603770866263 [ Links ]
[40] Offer, G. and Trinick, J., On the mechanism of water holding in meat: The swelling and shrinking of myofibrils, Meat Science, 8 (4), pp. 245-281, 1983. [ Links ]
[41] Aliño, M., Grau, R., Fernández-Sánchez, A., Arnold, A., and Barat, J.M., Influence of brine concentration on swelling pressure of pork meat throughout salting, Meat Science, 86 (3), pp. 600-606, 2010. http://dx.doi.org/10.1016/j.meatsci.2010.04.010 [ Links ]
[42] Aliño, M., Grau, R., Baigts, D. and Barat, J.M., Influence of sodium replacement on the salting kinetics of pork loin, Journal of Food Engineering, 95 (4), pp. 551-557, 2009 http://dx.doi.org/10.1016/j.jfoodeng.2009.06.016 [ Links ]
[43] Birkeland, S., Akse, L., Joensen, S., Tobiassen, T. and Skara, T., Injection-salting of pre rigor fillets of Atlantic salmon (Salmo salar), Journal of Food Science, 72 (1), 2007. http://dx.doi.org/10.1111/j.1750-3841.2006.00211.x [ Links ]
[44] Foucat, L., Benderbous, S., Bielicki, G., Zanca, M. and Renou, J.P., Effect of brine injection on water dynamics on postmortem muscle: Study of T2 and diffusion coefficients by MR microscopy, Magnetic Resonance Imaging, 13 (2), 1995. http://dx.doi.org/10.1016/0730-725X(94)00094-J [ Links ]
[45] Gisbert, M., Influencia de las variables de proceso en la evolución físco-química y bioquímica del lomo embuchado. Tesis Doctoral. Universidad Politécnica de Valencia, 2001. [ Links ]
[46] Hansen, C.L., van der Berg, F., Ringgaard, S., Stodkilde-Jorgensen, H. and Karlsson, A.H., Diffusion of NaCl in meat studied by H-1 and Na-23 magnetic resonance imaging, Meat Science, 80 (3), pp. 851-856, 2008. http://dx.doi.org/10.1016/j.meatsci.2008.04.003 [ Links ]
[47] Clemente, G., Bon, J., Sanjuan, N. and Mulet, A., Determination of shrinkage function for pork meat drying, Drying Technology, 27 (1), pp. 143-148, 2009. http://dx.doi.org/10.1080/07373930802566051 [ Links ]
[48] Comaposada, J., Sorption isotherms and water diffusivity in muscles of pork ham at different NaCl contents. PhD Thesis. Universitat Politècnica de Catalunya, 1999. [ Links ]
[49] Corzo, O. and Bracho, N., Shrinkage of osmotically dehydrated sardine sheets at changing moisture contents, Journal of Food Engineering, 65(3), 2004. http://dx.doi.org/10.1016/j.jfoodeng.2004.01.030 [ Links ]
[50] Cierach, M. and Modzelewska-Kapitula, M., Effects of pH values and fat content on sodium chloride diffusion rate in pork, Journal of Food Processing and Preservation, 35 (2), pp. 129-142, 2011. http://dx.doi.org/10.1111/j.1745-4549.2009.00465.x [ Links ]
[51] Arnau, J., Guerrero, L., Casademont, G. and Gou, P., Physical and chemical changes in different zones of normal and PSE dry-cured ham during processing, Food Chemistry, 52 (1), pp. 63-69, 1995. http://dx.doi.org/10.1016/0308-8146(94)P4182-F [ Links ]
[52] Bertram, H.C., Engelsen, S.B., Busk, H., Karlsson, A.H. and Andersen, H.J., Water properties during cooking of pork studied by low-field NMR relaxation: Effects of curing and the RN-gene, Meat Science, 66 (2), pp. 437-446, 2004. http://dx.doi.org/10.1016/S0309-1740(03)00132-3 [ Links ]
[53] Fortin, A., Tong, A.K.W., Robertson, W.M., Zawadski, S.M., Landry, S. . and Robinson, D.J., A novel approach to grading pork carcasses: Computer vision and ultrasound, Meat Science, 63 (4), pp. 451-462, 2003. http://dx.doi.org/10.1016/S0309-1740(02)00104-3 [ Links ]
[54] Kent, M., Peymann, A., Gabriel, C. and Knight, A., Determination of added water in pork products using microwave dielectric spectroscopy, Food Control, 13 (3), pp. 143-149, 2002. http://dx.doi.org/10.1016/S0956-7135(01)00066-4 [ Links ]
[55] Barat, J.M., Grau, R., Ibáñez-Company, J.B. y Fito, P., Métodos de salazonado convencionales e innovadores, captación y difusión de la sal, CDrom II Congreso Mundial del Jamón. Coordinador Jesús Ventanas. Edita Universidad de Extremadura, 2003. [ Links ]
[56] Clemente, G., Bon, J., Sanjuán, N. and Mulet, A., Drying modelling of defrosted pork meat under forced convection conditions, Meat Science, 88 (3), 374-378, 2011. http://dx.doi.org/10.1016/j.meatsci.2011.01.012 [ Links ]
[57] Quintero-Chávez, R., Quintero-Ramos, A., Jiménez-Castro, J., Barnard, J., Márquez-Meléndez, R., Zazueta-Morales, J.d.J. and Balandrán-Quintana, R.R., Modeling of total soluble solid and NaCl uptake during osmotic treatment of bell peppers under different infusion pressures, Food and Bioprocess Technology, 5 (1), pp. 184-192, 2012. http://dx.doi.org/10.1007/s11947-010-0358-9 [ Links ]
[58] Shi, J. and Le Maguer, M., Osmotic dehydration of foods: Mass transfer and modeling aspects, Food Reviews International, 18 (4), pp. 305-335, 2002. http://dx.doi.org/10.1081/FRI-120016208 [ Links ]
[59] Azuara, E., Cortes, R., Garcia, H.S. and Beristain, C.I., Kinetic-model for osmotic dehydration and its relationship with Fick 2nd law, International Journal of Food Science and Technology, 27 (4), pp. 409-418, 1992. http://dx.doi.org/10.1111/j.1365-2621.1992.tb01206.x [ Links ]
[60] Corzo, O., Bracho, N. and Rodríguez, J., Comparison of Peleg and Azuara et al. models in the modeling mass transfer during pile salting of goat sheets, LWT-Food Science and Technology, 46 (2), pp. 448-452, 2012. http://dx.doi.org/10.1016/j.lwt.2011.12.002 [ Links ]
[61] Peleg, M., An empirical-model for the description of moisture sorption curves, Journal of Food Science, 53 (4), pp.1216, 1988. [ Links ]
[62] Bellagha, S., Sahli, A., Farhat, A., Kechaou, N. and Glenza, A., Studies on salting and drying of sardine (Sardinella aurita): Experimental kinetics and modeling, Journal of Food Engineering, 78 (3), pp. 947-952, 2007. http://dx.doi.org/10.1016/j.jfoodeng.2005.12.008 [ Links ]
[63] Corzo, O. and Bracho, N., Osmotic dehydration kinetics of sardine sheets using Zugarramurdi and Lupin's model. Journal of Food Engineering, 66, pp. 51-56, 2005. http://dx.doi.org/10.1016/j.jfoodeng.2004.02.033 [ Links ]
[64] Corzo, O. and Bracho, N., Equilibrium water and salt contents of sardine sheet during osmotic dehydration. LWT-Food Science and Technology, 39, pp. 357-363, 2006. http://dx.doi.org/10.1016/j.lwt.2005.02.008 [ Links ]
[65] Corzo, O., Bracho, N. and Rodriguez, J., Pile salting kinetics of goat sheets using Zugarramurdi and Lupin's model, Journal of Food Processing and Preservation, 37, pp. 615-620, 2013. http://dx.doi.org/10.1111/j.1745-4549.2012.00695.x [ Links ]
J. Gómez-Salazar, completed a BSc. Eng in Food Engineering in 2006 at Universidad de Caldas, Manizales, Colombia and a PhD degree in Science and Food Technology in 2013 at Universidad Politécnica de Valencia, España. He is a professor in the school of Agronomy, in the Universidad de la Salle Bajío, León, Guanajuato, and Mexico. His research interests include: preservation and food processing.
G. Clemente-Polo completed a BSc. Eng in Agronomy in 1997 at Universidad Politécnica de Valencia, Valencia, España and a PhD degree in Science and Food Technology in 2004 at the Universidad Politécnica de Valencia. She is a professor in the food technology department, in the Universidad Politécnica de Valencia. Her research interests include: preservation, food technology and Life cycle analysis (LCA).
N. Sanjuán-Pelliccer, completed a BSc. Eng in Agronomy in 1991 at Universidad Politécnica de Valencia, Valencia, España and a PhD degree in agronomy engineer in 2008 at Universidad Politécnica de Valencia. She is a professor in the food technology department, in the Universidad Politécnica de Valencia. Her research interests include: preservation, food technology and Life cycle analysis (LCA).













