Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.190 Medellín mar./abr. 2015
https://doi.org/10.15446/dyna.v82n190.42311
DOI: http://dx.doi.org/10.15446/dyna.v82n190.42311
Container stacking revenue management system: A fuzzy-based strategy for Valparaiso port
Sistema de gestión de ingreso para el aparcamiento de contenedores: Una estrategia fuzzy para el puerto de Valparaíso
Héctor Valdés-González a, Lorenzo Reyes-Bozo a, Eduardo Vyhmeister b, José Luis Salazar c, Juan Pedro Sepúlveda d & Marco Mosca-Arestizábal e
a Facultad de Ingeniería, Universidad Andrés Bello, Santiago, Chile. hvaldes@unab.cl, lreyes@unab.cl
b Departamento de Ciencias de la Energía y Mecánica, Universidad de las Fuerzas Armadas - ESPE sede Latacunga, Ecuador, eduardo.vyhmeister@gmail.com
c Departamento de Ingeniería Química, Universidad de Santiago de Chile, Santiago, Chile, jose.salazar@usach.cl
d Departamento de Ingeniería Industrial, Universidad de Santiago de Chile, Santiago, Chile, juan.sepulveda@usach.cl
e Inacap, Vitacura, Chile. planea.mmosca@gmail.com
Received: February 27th, de 2014. Received in revised form: July 23th, 2014. Accepted: December 30th, 2014
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
This article presents an intelligent system for container stacking based on fuzzy logic. The method establishes a defined criterion for accepting or rejecting in real time an entry request to the stacking areas of the port in Valparaiso, Chile. A case study based on expert knowledge illustrates the proposed method with real data. First, the optimum solution is determined for a problem of maximization of entries, based on historical records from the traffic and information center of Valparaiso Port. Second, this solution is used to establish a strategy for making "the best possible decisions." The combination of the optimization and the fuzzy results (which consider the type of cargo, prices, and capacity) is performed at two levels. First, the optimization results are used as feed for the fuzzy system to determinate a ratio of future acceptances. Second, the optimization results are compared to the fuzzy system results in order to estimate a parameter to establish the minimal percentage value for accepting a request. As a result, a proper use of the stacking area is achieved, which results in an increase of profits and revenue management.
Keywords: fuzzy logic; revenue management; stacking, containers; capacity; demand.
Resumen
Este artículo presenta un sistema inteligente de aparcamiento de contenedores basado en lógica difusa. El método establece un criterio definido para aceptar o rechazar en tiempo real una solicitud de entrada a las zonas de aparcamiento del puerto de Valparaíso, Chile. Estudio de caso basado en conocimiento experto, ilustra el método propuesto con datos reales. En primer lugar, la solución óptima se determina para un problema de maximización de prestaciones a partir de los registros históricos del centro de información de tráfico y del puerto de Valparaíso. En segundo lugar, se utiliza esta solución para establecer una estrategia para tomar "la mejor decisión posible." La combinación de la optimización y los resultados difusos (que consideran el tipo de carga, los precios, y la capacidad) se lleva a cabo en dos niveles. En primer lugar, los resultados de optimización se utilizan como alimentación del sistema difuso para determinar una proporción de aceptaciones futuras. En segundo lugar, los resultados de la optimización se comparan con los resultados del sistema difuso, con el fin de estimar un parámetro para establecer el valor del porcentaje mínimo que permita aceptar una solicitud. Como resultado, se consigue un uso adecuado de la zona de apilamiento o aparcamiento de contenedores, lo que resulta en un aumento de los beneficios y la gestión de ingresos.
Palabras clave: lógica difusa, gestión de ingreso, apilamiento, contenedores, capacidad, demanda.
1. Introduction
One of the geographical features of Chile is that it has over 4,000 km of coast. There are 11 state-administered ports and 26 private ports. State ports load 60.7% of cargo. Of these, Valparaiso port moves the most container cargo, 33% of the total. Moreover, it is the number one port for exports, recording the transfer of 8,457,122 metric tons in 2011 [1] and an annual growth of over 20%, and thereby plays a significant role in the Chilean economy [2].
The continued development of Valparaiso port activity has involved the ZEAL (Zona de Extensión de Apoyo Logístico - Extension Zone for Logistic Support) taking measures to increase the competitiveness of the port. To this end, ZEAL has carried out an audit and documentation of loads transferred by the port. This contributes to the decongestion of the port and its access routes, which, in turn, increases rotation of load transfer. However, the logistical operations between ZEAL and the terminals require constant planning and control. Other agents are also involved in these operations: EPV (Empresa Portuaria de Valparaíso - Valparaiso Port Company) as the port authority; concessionaries such as TPS (Terminal Pacífico Sur - South Pacific Terminal) and ZSC (ZEAL Sociedad Concesionaria - ZEAL Concessionaire); state organizations such as Customs and SAG (Servicio Agrícola y Ganadero - Agricultural and Livestock Service); Sernapesca; and other exporters and transporters [3].
From a theoretical point of view of the management of the supply chain, the current administration measures are insufficient, particularly because the global objective should be sought over local objectives, or those of each member of the chain [4]. The creation of ZEAL is an important step but it is limited by the fact that it concentrates on the documentation operations prior to entry to the port and does not consider the operations related to cargo reception in the stacking areas.
The need for the present study arises principally from growth in port activities. A steady increase in the volume of transfers, year after year, has meant that the terminals, and in particular TPS, exceed their maximum capacity at certain periods. This does not just occur in seasons when there is a high demand for horticultural products, but throughout the year and especially on weekends. Similarly, there are also periods with low capacity use [1,5].
Given this context, this research aims to incorporate an element of judgment for the reception of containerized cargo through the management of demand for cargo transfers, by focusing on matching the offer of port services with exporters' cargo demands. Specifically, an intelligent system for container stacking based on fuzzy logic is proposed. The system decides whether to accept or reject the request of a defined criterion for each type of load and gives a response in "real time." This would enable the company to increase its revenue and reduce the variable costs for hiring external storage in periods of high demand.
2. Revenue management and fuzzy optimization
Revenue Management is a form of management for maximizing revenue in activities with capacity constraints [6]. This technique has been used in various sectors, although mostly in companies with perishable products and services that manage demand with price changes over time [7].
Revenue Management, also called Yield Management, consists of adapting the demand to the existing supply, based on prices and inventory management, in order to maximize revenue [8]. In other words, revenue management aims to "sell the correct unit of the inventory" to the "right client" at the "right time" [9,10].
Revenue management has its origin in studies undertaken by Littlewood [11] at BOAC (now British Airways) where customers who reserved flights earlier were offered lower prices; this innovation considerably increased revenue as the percentage of flights with empty seats decreased significantly. Subsequently, several complementary studies and more complex models allowed problems closer to reality to be solved. Nowadays, revenue management is used by almost all airlines, and extensively in the service industry, for example in hotels, theaters and restaurants. Four fundamental areas of study are focused on in the literature: demand forecast, reservations (overbooking), seat inventory control and pricing [12].
Below is a description of the necessary conditions for applying a model to maximize profits in ports according to revenue management. This model enables the construction of fuzzy rule bases for the "best possible decisions."
2.1. Necessary conditions for applying revenue management
According to Kimes [13], in order to apply revenue management to a company or organization, 5 conditions need to be met (Limited Capacity, Market Segmentation, Demand Uncertainty, Perishable Inventory, and High Fixed Costs). These conditions are explained in-depth in the literature and will not be explained here.
2.2. Theory and methodology of fuzzy optimization
Studies, applications, theory and methodology of fuzzy optimization have been active since the proposal by Bellman and Zadeh in the 1970s [14]. In fact, many models and approaches to fuzzy linear programming [15, 16], fuzzy multi-objective programming [17,18], fuzzy integer programming [19, 20], fuzzy dynamic programming [21], and fuzzy nonlinear programming [22, 23] have been developed over the years by several researchers. In the meantime, fuzzy ranking [24], fuzzy set operation, sensitivity analysis [25] and fuzzy dual theory [24], as well as the application of fuzzy optimization to practical problems, also represent important topics [26]. Previous applications to practical problems are part of the basis for the work presented in this paper.
There isn't enough scope here to review the abundant literature on fuzzy optimization. For one of the latest surveys on fuzzy linear programming from a practical point of view, the reader is encouraged to look into, for example, [26-28].
3. Foundations of fuzzy logic
Fuzzy logic is the logic used by expressions that are neither completely true nor false. That is to say, it is the logic applied to concepts that can have any value of accuracy within a set of values between two extremes: absolutely true and absolutely false [2]. Fuzzy logic enables us to deal with imprecise information [29,30], such as "medium height" or "low temperature," in terms of fuzzy sets that are combined in rules for defining action. For example: "If the temperature is high, cool." Thus, control systems based on fuzzy logic combine input variables defined in terms of fuzzy sets via groups of rules that produce one or several output values [31].
3.1. Fuzzy sets and membership function
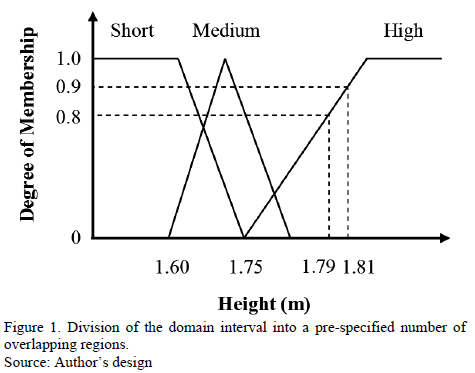
Owing to the fact that the study includes a fuzzy rule-based system, both fuzzy logic [32] and fuzzy rule-based systems will be discussed first. Fuzziness is inherent in many problems of knowledge representation. High-level managers or complex decision processes often deal with generalized concepts and linguistic expressions, which are generally fuzzy in nature. The first time the concept of fuzzy logic was illustrated, it was by the engineer Zadeh [32]. The membership degree is defined in fuzzy terms with a membership function (Fig.1). The function 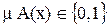 , represents the membership degree of an input "x" to fuzzy set A [33]. The most typically used functions include triangular, trapezoidal, sigmoidal, gauss, gamma, p, etc.
, represents the membership degree of an input "x" to fuzzy set A [33]. The most typically used functions include triangular, trapezoidal, sigmoidal, gauss, gamma, p, etc.
3.2. Mamdani Fuzzy control systems
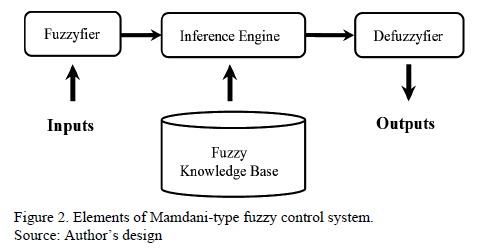
Fuzzy control systems are based on expressions of fuzzy logic for formulating rules for system control [2]. The elements that make up a Mamdani fuzzy control system [34] are presented in Fig. 2.
3.2.1. Fuzzyfier
The input for a Mamdani fuzzy logic system is normally a numeric value coming from, for example, a sensor. In order for the system to be able to process this value, it is necessary to convert it into "language" that the inference mechanisms can use, i.e. membership functions. This is the function of the fuzzyfier (Fig. 3.).
3.2.2. Inference mechanism and fuzzy rule base
The role of the inference mechanism is to take the membership functions and, using the rule base, generate the fuzzy system output. The rule base is the way the fuzzy system resolves the problem for which it has been designed. The structure of Mamdani-type fuzzy logic rule is expressed as follows [35]: IF x is A THEN y is B, where x is input variable and y is the output variable. A and B are the linguistic terms (for example, S - Short; M - Medium; H - High) used for the fuzzy subsets (membership function distributions) of the corresponding input and output variables, respectively.
3.2.3. Defuzzifier
The output generated by the inference mechanism is a fuzzy output, which means that it cannot be interpreted by an external element that can only deal with numerical information (a controller, for example). The process of converting the fuzzy output from the inference mechanism into a numerical value is realized by the defuzzifier. Some of the methods used are Centroid, Bisector, MOM (Middle of Max.), LOM (Largest of Max.) and SOM (Smallest of Max.) [35].
4. Proposed model: Intelligent system for container stacking
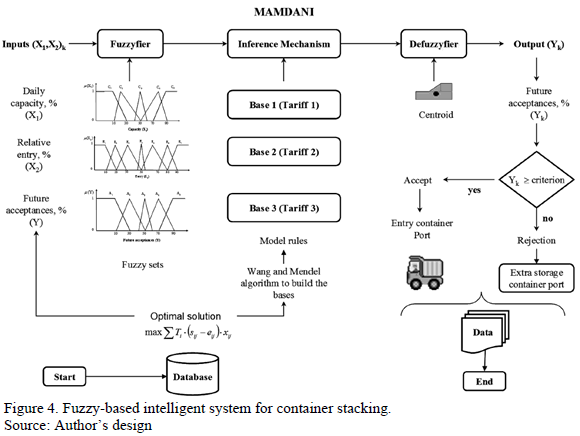
The model proposed for intelligent container stacking was created by combining a non-linear optimization problem and the results obtained by the experience and historical records (gathered from the traffic and information center, CTI - Centro de Tráfico e Informaciones del Puerto [3]), which are represented in the inference mechanism of the Fuzzy Logic system. The combination of both parts is performed at two levels. First, the optimization results are used as feed of the fuzzy system to determine a ratio of future acceptances. Second, the optimization results are compared to the fuzzy system results in order to estimate a parameter to establish the minimal percentage value for accepting a request. The optimization uses real time information of the stacking capacity to estimate the most suitable conditions of the space use (which can be used as import, export and transit cargo) and it must be taken into account that more than one cargo request could exist at the same time.
The problem was solved for different scenarios of stacking capacities (1,000, 7,000, 15,000 and 30,000), which are equivalent to a day, a week, 15 days and a month of evaluation (time interval for cargo reception).
Fig. 4. summaries the information flow of the fuzzy-based intelligent system for container stacking. The intelligent system for container stacking allows us to decide whether to accept or reject a request to enter the port in "real time" in order to increase revenue. The system is based on fuzzy rules using a model that maximizes profits through revenue management, which provides the "best possible decisions" [26,36].
4.1. Profit maximization model
The model for maximization is based on the historical records for the CTI [3]. The elements of the model are described below:
Parameters: Ti, Tariff i (i = 1, 2, 3 with T1 ≥ T2 ≥ T3); C: Total available stacking area capacity.
The tariffs are determined according to the type of cargo; the values are those in the Service Manual of the TPS (Terminal Pacífico Sur - South Pacific Terminal) [37]. Thus, tariff 1 corresponds to load type "Embarkation" (exportation); tariff 2 to load type "Disembarkation" (importation), and tariff 3 to "Transit" and "Port" (empty cargo that will be set on the load area).
Decision variable: xij: Binary variable the entry and use (or not) of a space in the stacking area by a cargo j that has arrived and has a tariff i.
Objective Function: The objective function is the profit maximization which can be obtained by the multiplication of the tariff and the total cargo in the stacking area (existing and incorporated cargo). The stacking area is therefore constantly modified; the decision variable by itself will not describe a dynamic representation for the possibilities of cargos leaving the stacking area. Auxiliary parameters were used and can be observed in Eq. 1, where ej is binary value that assumes a 1 if the request j has been incorporated into the stacking area; liq represents a cargo q that already existed in the stacking area with tariff i; sj and sq are binary values that assume a 1 if the request j (or q) leaves the stacking area:
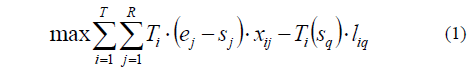
It can be highlighted that the values of s and e are constants that do not change once they assume a value of 1, which implies that the cargo that was accepted to use a space in the cargo area do not affect the objective function anymore (i.e., the value assumed by the decision variable is irrelevant once the cargo has left the stacking area). This equation was simplified by ignoring the space used by the existing cargo at the moment of running the optimization problem, which implies that only the available stacking area (and not total area) was used on the model programming.
Eq. 2 describes the final objective function used:
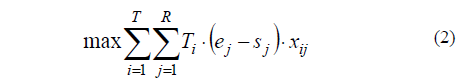
Restrictions: As previously mentioned, given the simplification, only the total available capacity is used as a restriction:
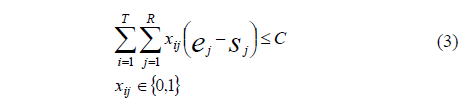
Further complex restrictions could be implemented (such as maximum time in stacking area, obligatorily acceptance of cargos into the stacking area, etc.), but the incorporation and analyses of such restrictions are out of the scope of the present work.
4.2. Variables of the stacking container system
From the optimal solution for the maximization model and the input (eij) and output (sij) of each accepted cargo (which can be used as a historic record of the stacking area cargo movement), it is possible to determine the available capacity, the relative input/entries, and the percentage accepted for each instant and each type of tariff. These variables enable us to construct the rule base for the fuzzy system:
The porcentual available capacity X1, can be calculated as represented in Eq. 4:
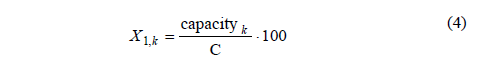
The porcentual relative entry for each request type X2, is described in Eq. (5):
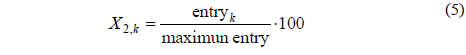
The percentage of future acceptances "Y" (%), is calculated in Eq. (6):
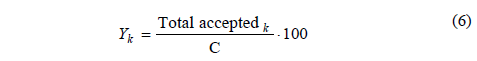
Where "capacityk" corresponds to the capacity at the moment of arrival of request type k. "entryk" corresponds to the entry of request type k. "Total acceptedk" is the total requests accepted after the request k with tariffs lower than or equal to "i."
4.3. Intelligent system for container stacking
This system is based on a Mamdani-type control system, using Matlab 7 software and in particular a Matlab Fuzzy Logic Toolbox. The elements of the system are described below:
4.3.1. Fuzzyfier
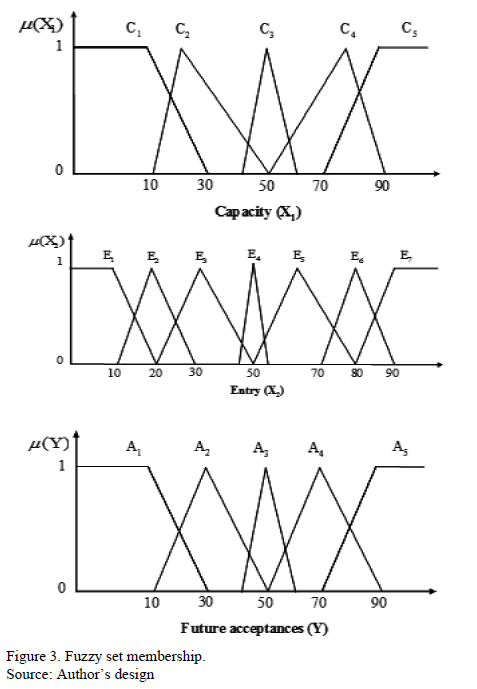
In this section, the different fuzzy sets are described for each variable of the system: 2 inputs "Available capacity" X1 and "Relative input" X2, as well as the output "Future acceptances" Y. The fuzzy sets corresponding to the variables are as follows:
Where C1, C2, C3, C4 and C5 are the fuzzy sets "Very low capacity," "Low capacity," "Medium capacity," "High capacity" and "Very high capacity," respectively. E1, E2, E3, E4, E5, E6 and E7 correspond to the fuzzy sets "Very low entry," "Low entry," "Low-medium entry," "Medium entry" "Medium-high entry," "High entry" and "Very high entry," respectively. Finally A1, A2, A3, A4 and A5 represent the fuzzy sets "Very few accepted," "Few accepted," "Medium-amount accepted," "Many accepted" and "Very many accepted," respectively. The linguistic variables, the membership functions, and the representation of the expert knowledge were determined by an expert committee in the company. This committee comprised the CEO and a group of engineers with more than ten years of experience in the field. Additionally, data gathered from 10 years of staking processes was used to build the proposed model.
4.3.2. Inference mechanism
The inference mechanism has 3 rule bases, one for each type of tariff. It is constructed on the basis of the fuzzy sets described above, using the algorithm proposed by Wang and Medel [36].
4.3.3. Defuzzyfier
A centroid method is used which has greater statistical information and a single output; these features are necessary given the complexity of the system with regard to the number of variables involved (Matlab Fuzzy Logic Toolbox).
4.4. Criterion for accepting or rejecting a request
The output of the system is the value of the variable "future acceptances," Y, for each entry request to the port (Fig. 3).
Therefore, the defined criterion (ai) is a minimal percentage value for accepting a request. In order to determine the values of each criterion (a1; a2; a3) for each type of tariff (T1; T2; T3) respectively, the optimal solution for each case is used, established by the Eq. (7). " Tariff "i":
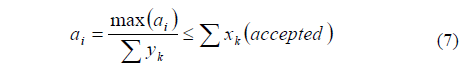
Where "yk" is the value of the variable "future acceptances" for each request k, and "xk" is the value of the decision corresponding to the maximization model for each request k. In simplest terms, the total acceptances of the systems must not be greater than the total number accepted by the optimal solution; if not, the capacity restrictions will be exceeded.
5. Results
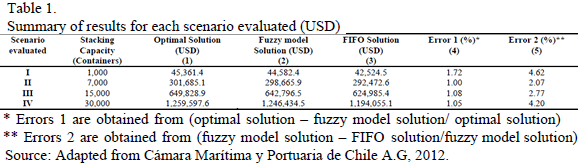
The results obtained for the scenarios and the different capacities considered are presented in Table 1. The capacity restrictions of 1,000, 7,000, 15,000 and 30,000 containers are equivalent to 1 day, 1 week, 15 days and one month of evaluation (time interval for cargo reception), respectively.
For each scenario evaluated, the information used was from the CTI of the Valparaiso port [3]. The error analysis that may exist in the representation of the entry or exit of containers from the stacking area due to probabilistic estimations is beyond the scope of this research. However, the results for each scenario are very close to the optimal solution with a percentage error lower than 1.8% (see Table 1).
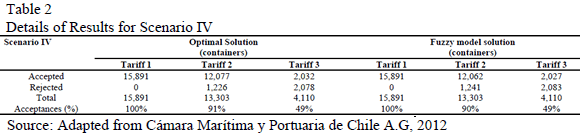
These results are better than those from the current procedure for cargo reception (FIFO solution). In addition, additional revenue is generated at 4.0% (5), equivalent to USD $600,000 annually (Table 2).
6. Conclusions
The main advantage of the proposed fuzzy-based container stacking system is that it enables decisions about entry requests for a container to Valparaiso port to be taken in "real time." Moreover, the system structure allows the rule base to be modified or updated at any time, thereby increasing its efficiency. As the results obtained are superior to those from the current procedures, this would improve profits for the port company, thereby meeting another objective of this paper.
Future research should mainly aim to facilitate the constant updating of the rule base for the system. Furthermore, since the current research has only focused on three of the most representative types of cargo, it would be useful to incorporate other less common types of cargo to better represent reality.
References
[1] Cámara Marítima y Portuaria de Chile A.G. Estadísticas de carga de comercio exterior vía marítima año 2011, 2012 [en línea]. [fecha de consulta Noviembre 3 de 2012]. Disponible en: http://www.camport.cl [ Links ]
[2] Combettes, P.L., The foundations of set theoretic estimation, IEEE Proceeding, 81 (2), pp. 182-208, 1993. http://dx.doi.org/10.1109/5.214546 [ Links ]
[3] SI-ZEAL, Sistema de información de Puerto de Valparaíso - Information system for Valparíso port, 2012 [en línea]. [fecha de consulta Diciembre 15 de 2012]. Dsiponible en: http://sizeal.sizeal.cl/EpvZealWeb. [ Links ]
[4] Huo, B., The impact of supply chain integration on company performance: An organizational capability perspective, Supply Chain Management: An international Journal, 17 (6), pp. 596-610, 2012. http://dx.doi.org/10.1108/13598541211269210 [ Links ]
[5] Alessandri, A., Cervellera, C., Cuneo, M., Gaggero, M. and Soncin, G., Modeling and feedback control for resource allocation and performance analysis in container terminals. IEEE Transactions on Intelligent Transportation Systems, 9 (4), pp. 601-614, 2008. http://dx.doi.org/10.1109/TITS.2008.2006737 [ Links ]
[6] Li, B., Modelling for cruise two-dimensional online revenue management system. International Journal of Digital Content Technology and its Applications, 4 (6), pp. 72-76, 2010. http://dx.doi.org/10.4156/jdcta.vol4.issue6.7 [ Links ]
[7] Wen-Chyuan, C., Chen, J.C.H. and Xu, X., An overview of research on revenue management: Current issues and future research. International Journal of Revenue Management, 1 (1), pp. 97-128, 2007. http://dx.doi.org/10.1504/IJRM.2007.011196 [ Links ]
[8] Heo, C.Y. and Lee, S., Application of revenue management practices to the theme park industry. International Journal of Hospitality Management, 28 (3), pp. 446-453, 2009. http://dx.doi.org/10.1016/j.ijhm.2009.02.001 [ Links ]
[9] Ottjes, J.A., Veeke, H.P.M., Duinkerken, M.B., Rijsenbrij, J.C. and Lodewijks, G., Simulation of a multiterminal system for container handling. In K.H. Kim and H. Gunther (Eds.), Container terminals and cargo systems, Springer, 2007, pp. 15-36. http://dx.doi.org/10.1007/978-3-540-49550-5_2 [ Links ]
[10] Weatherford, L.R. and Bodily, S.E., A taxonomy and research overview of perishable-asset revenue management: Yield management, overbooking, and pricing. Operations Research, 40, pp. 831-844, 1992. http://dx.doi.org/10.1287/opre.40.5.831 [ Links ]
[11] Littlewood, K., Forecasting and Control of Passenger Bookings, AGIFORS Symposium Proc. 12, Nathanya, Israel, 1972. [ Links ]
[12] McGill, J. and Van Ryzin, G., Revenue management: Research overview and prospects. Transportation Science, 33 (2), pp. 233-256, 1999. http://dx.doi.org/10.1287/trsc.33.2.233 [ Links ]
[13] Kimes, S., Yield management: A tool for capacity constrained service firms. Journal of Operational Management, 8, pp. 348-363, 1989. http://dx.doi.org/10.1016/0272-6963(89)90035-1 [ Links ]
[14] Bellman, R.E. and Zadeh, L.A., Decision making in a fuzzy environment. Management Science, 17, pp. 141-164, 1970. http://dx.doi.org/10.1287/mnsc.17.4.B141 [ Links ]
[15] Fang, S.C., Hu, C.F., Wang, H.F., Wu, S.Y., Linear programming with fuzzy coefficients in constraints. Computers and Mathematics with Applications, 37 (10), pp. 63-76, 1999. http://dx.doi.org/10.1016/S0898-1221(99)00126-1 [ Links ]
[16] Wang, D. and Fang, S.C., A genetic-based approach for aggregate production planning in fuzzy environment. IEEE Trans. on SMC (Part A), 12 (5), 636-645, 1997 [ Links ]
[17] Sakawa, M. and Yano, H., An interactive fuzzy satisficing method for multiobjective nonlinear programming problems with fuzzy parameters. Fuzzy Sets and Systems, 30 (10), pp. 221-238, 1989. http://dx.doi.org/10.1016/0165-0114(89)90017-1 [ Links ]
[18] Sakawa, M. and Yano, H., Fuzzy dual decomposition method for large-scale multiobjective non-linear programming problem. Fuzzy Sets and Systems, 67, pp. 19-27, 1994. http://dx.doi.org/10.1016/0165-0114(94)90205-4 [ Links ]
[19] Chanas, S. and Kuchta, D., Discrete fuzzy optimization, in Fuzzy Sets in: Decision Analysis Operations Research and Statistics -The Handbook of Fuzzy Sets Series (Slowinski, Ed.,) Kluwer Academic, Dordrecht, pp. 249-276, 1998. [ Links ]
[20] M. Stoica, et al., Fuzzy integer programming, in: Zimmermann, H.-J., Zadeh, L.A. and Gaines, B.R., Eds. Fuzzy Sets and Decision Analysis, North-Holland, Amsterdam, pp. 123-132, 1984. [ Links ]
[21] Kacprzyk, J. and Esogbue, A.O., Fuzzy dynamic programming: Main developments and applications, Fuzzy Sets and Systems, 81 (1), pp. 31-46, 1996. http://dx.doi.org/10.1016/0165-0114(95)00239-1 [ Links ]
[22] Liu, J. and Fang, S.C., Solving nonlinear optimization problems with fuzzy relation equation constraints. Fuzzy Sets and Systems, 119, pp. 1-20, 2001. http://dx.doi.org/10.1016/S0165-0114(98)00471-0 [ Links ]
[23] Trappey, J.F.C., Liu C.R. and Chang, T.C., Fuzzy non-linear programming: Theory and application in manufacturing. International Journal of Production Research, 26 (5), pp. 975-985, 1988. http://dx.doi.org/10.1080/00207548808947912 [ Links ]
[24] Verdegay, J.L., A dual approach to solve the fuzzy linear programming problems. Fuzzy Sets and Systems, 14 (2), pp. 131-141, 1984. http://dx.doi.org/10.1016/0165-0114(84)90096-4 [ Links ]
[25] Ostermark, R., Sensitivity analysis of fuzzy linear programs: An approach to parametric interdependence. Kybernetes, 16, pp. 113-120, 1987. http://dx.doi.org/10.1108/eb005762 [ Links ]
[26] Brinkmann, B., Operations systems of container terminals: A compendious overview. In: Böse, J.W. (Eds.), Handbook of terminal planning, operations research/computer science interfaces, series 49, Springer Science+Business Media, LLC, pp. 25-39, 2011. http://dx.doi.org/10.1007/978-1-4419-8408-1_2 [ Links ]
[27] Inuiguchi, M. and Ramik, J., Possibility linear programming: A brief review of fuzzy mathematical programming and a comparison with stochastic programming in portfolio selection problem. Fuzzy Sets and Systems, 111, pp. 3-28, 2000. http://dx.doi.org/10.1016/S0165-0114(98)00449-7 [ Links ]
[28] Tang, J., Wang, D.W., Fung, R.Y.K., Yung, K.-L., Understanding of fuzzy optimization: Theories and methods. Journal of Systems Science and Complexity, 17 (1), pp. 117-136, 2004. Available at: http://www.sysmath.com/jweb_xtkxyfzx/EN/Y2004/V17/I1/117 [ Links ]
[29] Available at: http://www.scielo.org.co/scielo.php?pid=S0012-73532011000500003&script=sci_arttext [ Links ]
[30] Martín del Brío, B. and Sanz Molina, A., Redes Neuronales y Sistemas Difusos, Ed. Alfaomega, México D.F, 2005. [ Links ]
[31] Zadeh, L.A., Fuzzy Sets. Information and Control, 8 (3), pp. 338-353, 1965. http://dx.doi.org/10.1016/S0019-9958(65)90241-X [ Links ]
[32] Brubaker, D.I., Everything you always wanted to know about fuzzy logic. (EDN-Design Feature). EDN. Canon Communications LLC, 1993, pp. 103-106. [ Links ]
[33] Ustundag, A., Serdar Kilinç, M. and Cevikcan, E., Fuzzy rule-based system for the economic analysis of RFID investments. Expert Systems with Applications, 37 (7), pp. 5300-5306, 2010. http://dx.doi.org/10.1016/j.eswa.2010.01.009 [ Links ]
[34] Soto, C. and Jiménez, C., Supervised learning for fuzzy discrimantion and classification. DYNA, 78 (169), pp. 26-33, 2011. [ Links ]
[35] Mamdani, E.H., Odtengaard, J.J. and Lembessis, E., Use of fuzzy logic for implementing rule-based control of industrial processes. In: Paul P. Wang (Eds.), Advances in Fuzzy sets, possibility theory, and applications, New York: Plenum Press, 1983, pp. 307-323. http://dx.doi.org/10.1007/978-1-4613-3754-6_19 [ Links ]
[36] Nandi, A.K. and Davim, J.P., A study of drilling performances with minimum quantity of lubricant using fuzzy logic rules. Mechatronics, 19 (2), pp. 218-232, 2008. http://dx.doi.org/10.1016/j.mechatronics.2008.08.004 [ Links ]
[37] Wang, L.X. and Mendel, J.M., Generating fuzzy rules by learning from examples. IEEE Transactions on Systems, Man and Cybernetics, 22 (6), pp. 1414-1427, 1992. http://dx.doi.org/10.1109/21.199466 [ Links ]
[38] TPS, Terminal Pacífico Sur Valparaíso S.A. Manual de Servicios, 2012. Valparaíso, Chile, 2012. [ Links ]
H. Valdés-González, completed his BSc and MSc degrees in Electrical Engineering in 1994 and 1997 respectively, from the Universidad de Santiago de Chile, Chile and a PhD degree in Automatic Control in 2002, from Université Joseph Fourier, France. Since 2009, he has worked for the Universidad Andrés Bello, Chile, where he is an Associate Professor. His research interests include simulation, modeling, process control, optimization and metaheuristics.
L. Reyes-Bozo, completed his MSc and PhD degrees in Engineering Sciences in 2006 and 2011, respectively, both of them from the Pontificia Universidad Católica de Chile, Chile. Since 2008, he has been a Full Professor and Researcher in the Engineering Science Department, Universidad Andrés Bello. He has worked on programs and projects in the mining field, with emphasis on environmental management. His research interests include: use of industrial ecology strategies and cleaner production concepts in industrial process; assessment of biodegradable substances as froth flotation agents to concentrate sulfide ores; modeling, simulation and process control.
E. Vyhmeister, completed his BSc and MSc degrees in Chemical Engineering in 2001 and 2003 respectively, from the Universidad de Santiago de Chile, Chile and a PhD degree in Chemical Engineering automatic from the Universidad de Puerto Rico in 1999. His research interests include: simulation, modeling, non-linear optimization and thermodynamics.
J.L. Salazar, completed his BSc degree in Chemical Engineering in 2003, from the Universidad de Santiago de Chile and a PhD degree in Process Engineering in 2014, from Universidad de Santiago de Chile, Chile. His research interests include simulation, modeling, process control, and optimization.
J.P. Sepúlveda, completed his BSc and MSc degrees in Industrial Engineering in 1996 and 2002 respectively, from the Universidad de Santiago de Chile, Chile and a PhD degree in Industrial Engineering in 2005from Institut National Polytechnique de Grenoble, France. Since 2012, he has worked for the Universidad Andrés Bello, Chile. His research interests include supply chain management, logistics, optimization and operations management.
M. Mosca- Arestizábal, completed his BSc and MBA in 1998 and 2003, respectively, both of them from the Pontificia Universidad Católica de Chile, Chile. Since 2010, he has been the director at Inacap, Santiago of Chile.