Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.190 Medellín mar./abr. 2015
https://doi.org/10.15446/dyna.v82n190.43137
DOI: http://dx.doi.org/10.15446/dyna.v82n190.43137
A hybrid genetic algorithm for ROADEF'05-like complex production problems
Algoritmo genético híbrido para problemas complejos de producción tipo ROADEF'05
Mariano Frutos a, Ana Carolina Olivera b & Fernando Tohmé c
a Department of Engineering, Universidad Nacional del Sur and CONICET, Bahía Blanca, Argentina. mfrutos@uns.edu.ar
b Department of Exact and Natural Sciences, Universidad Nacional de la Patagonia Austral and CONICET, Comodoro Rivadavia, Argentina. aco@cs.uns.edu.ar
c Department of Economics, Universidad Nacional del Sur and CONICET, Bahía Blanca, Argentina. ftohme@criba.edu.ar
Received: April 25th, de 2014. Received in revised form: October 30th, 2014. Accepted: November 13th, 2014
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
In this work, we present a hybrid technique that combines a Genetic Algorithm with meta-heuristics to solve a problem in RENAULT France's production plants. The method starts with an initial solution obtained by means of a GRASP (Greedy Randomized Adaptive Search Procedure) used as an input for a Genetic Algorithm complemented by a Simulated Annealing procedure of population improvement. We establish a comparison point among the different techniques used in the method. Their performances are evaluated as well as that of the entire method. The conclusion is that hybrid methods have clear advantages for the treatment of production planning problems.
Keywords: multi-objective optimization, hybrid algorithms, car sequencing.
Resumen
En este trabajo se presenta una técnica híbrida que combina un Algoritmo Genético con meta-heurísticas para la resolución de un problema en las plantas productivas de RENAULT Francia. El método comienza con una solución inicial por medio de GRASP (Greedy Randomized Adaptive Search Procedure), que es utilizada como entrada por un Algoritmo Genético complementado por un procedimiento de Simulated Annealing para mejorar las poblaciones. Se establece un punto de comparación entre las diferentes técnicas. El desempeño de las mismas es evaluado así como el de todo el método. La conclusión es que los métodos híbridos tienen claras ventajas para el tratamiento de problemas de planificación de la producción.
Palabras clave: optimización multi-objetivo, algoritmos híbridos, secuenciamiento de vehículos.
1 Introduction
Scheduling and programming problems at the core of the SFROAD (Société Française de Recherche Opérationnelle et d'Aide à la Décision) 2005 focus on the problems that have arisen at the RENAULT, France production plants. They present ROADEF'05 with the challenge of finding a solution to a real world extension of the classical car sequencing problem [1], the goal of which is to schedule cars along an assembly line while satisfying several capacity constraints. The particular problem addressed by SFROAD differs from the standard one since, besides capacity constraints imposed by the assembly shop, it introduces paint batching constraints involving the minimization of the consumption of solvents in the paint shop. Our analysis focuses on the phase of arrangement of daily sequences in production problems [2]. Here it is necessary to take into account different, even conflicting factors. The main goal is to develop a hybrid technique to tackle this problem and evaluate its performance compared to other traditionally used methods. Usual techniques intended to find approximate optimal solutions to similar problems are, greedy search [3], GRASP [4], GISMOO Algorithm [5], local search [6,7], hybrid variable neighborhood search [8], among others. The Hybrid Genetic Algorithm (HGA) presented in this work amalgamates constructive procedures like the Greedy Randomized Adaptive Search Procedure (GRASP) [9], and Genetic Algorithms (GAs) [10] with search methods like Simulated Annealing (SA) [11].
The paper is structured as follows: First, the ROADEF'05 problem is introduced. Then, the proposed Hybrid Genetic Algorithm (HGA) is described in detail. Then, comparisons between the HGA and other methods are presented. Finally, we analyze the results of running the HGA and present the conclusions.
2. ROADEF'05
The problem consists in determining the scheduling order of vehicles in a production day that best satisfies the assembly line and paint shop requirements [1]. The paint shop goal is to minimize the consumption of paint solvent. Therefore, it requires grouping vehicles according to their colors as well as minimizing the number of spray gun washes, i.e. to schedule the longest paint color batches that are possible. Paint color batches have a limitation on the upper batch size due to the need for frequent washing of the spray guns even when there is no need for paint color changes. This limitation constitutes a hard constraint.
In order to lighten the workload in the assembly line, vehicles that require special assembling operations have to be evenly distributed throughout the total processed cars. These vehicles are considered to be "hard to assemble". There are two classes of ratio constraints, high priority level and low priority level ones. High priority level ratio constraints ensue from car characteristics that require heavy workloads in the assembly line. Low priority level ratio constraints, instead, result from car features that cause small inconveniences in the production process.
Given the heterogeneities involved in the problem, multi-objective optimization constitutes a natural approach to the problem [12-14]. The objectives are, from the highest to the lowest priority level with no compensation between them: (a) the minimization of paint color changes (eq. 1); (b) minimization of the number of violations of high priority level ratio constraints (eq. 2); (c) the minimization of violations of low priority level ratio constraints (eq. 3).
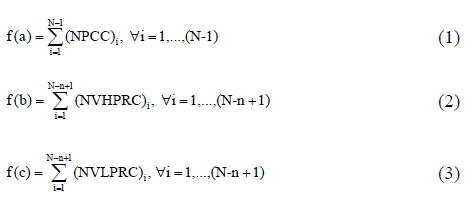
Here NPCCi is the number of paint color changes in the sequence i, NVHPRCi and NVLPRCi are the number of violations of high priority ratio constrains and low priority ratio constrains, respectively in sequence i. On the other hand, N is the number of sequences and n the number of sub-sequences. The fitness (f) is defined for each of the three objectives. In what follows, we assume that the values of a, b and d are given (a=1.000.000, b=1.000 y d=1) and that the full model is captured by eq. (4) and eq. (5). In eq. (4), objective one (obj one) corresponds with (a) or (b), objective two (obj two) is (a), (b) or (c), and objective three (obj three) is (a) or (c). Of course, the "or" in the definition of the objectives are exclusive, i.e. only one of the alternatives will be the case. In this way eq. (4) is directly related to the possible scenarios that frame the problem. Eq. 5 restricts the number of vehicles of the same color in each sub-sequence.
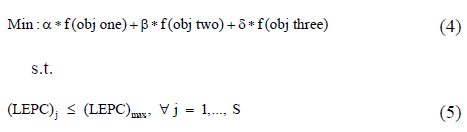
Here LEPCj is the amount of cars of the same color in the sub-sequence j, LEPCmax is the maximum allowable number of cars of the same color and S is the number of sub-sequences of equal color.
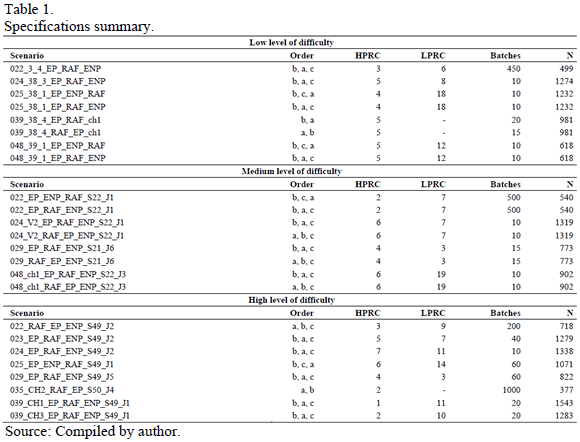
Table 1 specifies the level of complexity, scenario, number of high priority level constraints (HPRC), number of low priority level constraints (LPRC), limit of paint color batches (batches) and number of vehicles in a production day (N). The priorities of the objectives (a), (b) and (c) are shown in the Order column.
3. Hybrid Genetic Algorithm
The Hybrid Genetic Algorithm (HGA) presented here has two main stages, each with a different clear objective: the first one constructs an initial solution set with GRASP [9,15], while the second one, using it, follows the evolution of the population by means of the Genetic Algorithm (GA) [10,16] combined with Simulated Annealing (SA) [11]. In the GA stage, the SA module is introduced to improve the children from one generation to the other. Fig. 1 shows the layout of the Hybrid Genetic Algorithm.
3.1. Greedy Randomized Adaptive Search Procedures
The GRASP algorithm is, in turn, structured in two phases: a constructive one whose product is a good but not necessarily locally optimal solution; and a local search procedure that examines solution neighborhoods until a local optimum is found. The procedure begins by taking a random vehicle as the first element in the sequence. While not all vehicles are in the sequence, the closest match for place i is chosen. Each element of the candidate list is assigned a probability to be chosen. These probabilities are weighed with respect to a partial fitness value.
When the sequence is complete, an n permutation of vehicle-pairs is repeated m times. The objective is to look for a local optimum in the neighborhood of the solution. The values of m and n are input parameters of the algorithm. In Fig. 2 the layout of the GRASP algorithm is observed. Tables 2 (Solution: 17 5 4 10 9 8 2 6 3) and 3 (Solution: 1 7 5 4 10 9 8 3 2 6) show the construction of a feasible and a non feasible solution with the GRASP.
3.2. Genetic Algorithm Stage
The genetic stage works on the basis of the individuals produced by the GRASP stage. Each individual is a list of integers that represents the order in sequence of production. An individual in the population is a chain of integers. Each integer represents a vehicle.
The chromosome of the individual indicates the order of production sequence, in one day of work, from left to right. The initial population is a set of solutions received from the GRASP stage. Ranking selection is used to choose the parents that will construct the next population. An empirical analysis allows us to conclude that a population of between 90 and 100 individuals constitute a large enough sample.
3.2.1. Crossover
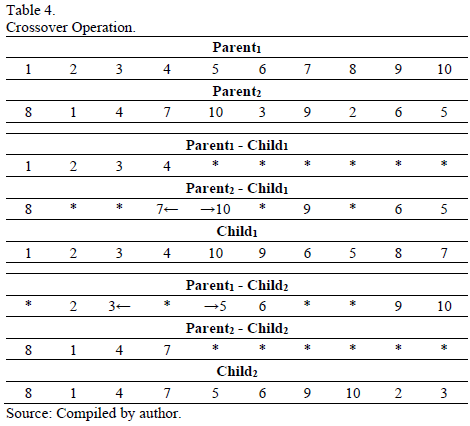
The GA is implemented with one point crossover. The operator randomly chooses a point to cross the parents. The simple crossover is applied here. Table 4 shows the crossover between Parent1 = (1 2 3 4 5 6 7 8 9 10) and Parent2 = (8 1 4 7 10 3 9 2 6 5) to obtain Child1 = (1 2 3 4 10 9 6 5 8 7) and Child2 = (8 1 4 7 5 6 9 10 2 3).
As an example, let us start from parents Parent1 = (1 2 3 4 / 5 6 7 8 9 10) and Parent2 = (8 1 4 7 / 10 3 9 2 6 5), where the slashes are split points. First, we obtain Child1 = (1 2 3 4 * * * * * *) and Child2 = (8 1 4 7 * * * * * *), preserving the first sub sequence of the respective split point for Parent1 and Parent2. Then, starting from the split point, the vehicles in Parent2 that are not in Child1 are used to complete the vehicles in Child1. In this case, the list of vehicles in Parent2 starting from the second split point is: (10 3 9 2 6 5), but when the vehicles that belong already to Child1 (i. e., 3 2) are eliminated, the sub-sequence becomes (10 9 6 5 8 7). These vehicles are added to Child1, starting from the split point. When the end is reached, the remaining cars are added at the initial part of Child1.
3.2.2. Mutation
The mutation operator generates one value for each vehicle in an individual solution. This value indicates whether the vehicle must change its position in the sequence. If this is the case, a new value is generated. The new number indicates the new position of the vehicle in the sequence. Table 5 (Child1: 1 2 3 4 10 9 6 5 8 7, Mutation: 1 2 5 4 10 9 6 3 8 7) shows an example of a child mutation.
3.2.3. Simulated Annealing
The goal of a "simulated annealing phase" is to improve the quality of children between generations. The key factor consists in defining an initial parameter l, the initial temperature (Ti), a cooling speed (w), the number of iterations (M) for each temperature (T), and the final temperature (Tf). For all children ch in a generation we select ch for the initialization of Sa and given Ti, greater than Tf , Simulated Annealing runs through two nested cycles. The first cycle is associated with T. The second is related to M, which varies depending on the actual state of T and parameter w. The second cycle generates the new sequence Sc. Sc is constructed taking into account the pair permutations of vehicles in Sa. If f(Sc) < f(Sa), Sc replaces Sa. Otherwise, it is associated a probability of accepting to Sc. The objective is to escape from a local optimum. When the nested cycle terminates, T is actualized considering a and initial parameter l. The algorithm returns Sa, the last sequence of vehicles found. In Fig. 3 we show the layout of SA.
4. Experiments
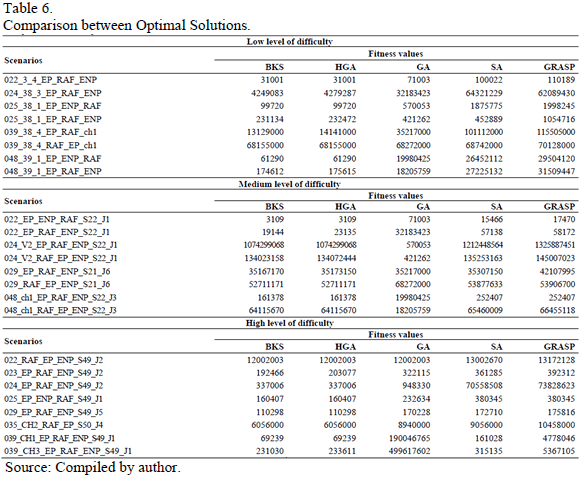
Preliminary essays lead to the adoption of the following parameters: Size of the Population: 250, Number of Generations: 500, Probability of Crossing: 0.80, Probability of Mutation: 0.01, Initial Temperature for SA: 850, Final Temperature for SA: 0.01, Cooling Factor for SA: 0.95, CPU: 3.00 GHZ, RAM: 4.00 GB. Each algorithm had 30 runs. Table 6 shows the best known solution for each problem (BKS) and the best results reached with each meta-heuristic [9-11].
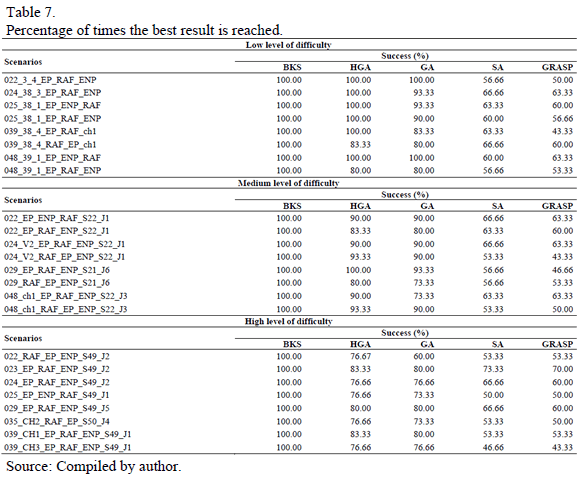
In addition, the third column in Table 6 presents the best results per HGA. Table 7 shows the proportion of the 30 runs in which the best result was reached (Success (%)). Running times were always short of 300 seconds. Taking the average running time for HGA, GA took 21.2% less time than that, SA 38.5% less, while GRASP ran for 62.8% less time.
For the problems pertaining to low levels of difficulty, HGA reaches the best result (on average) 95.4% of runs, while GA, SA and GRASP reach the best results at 89,9%, 61,6% and 56,2%, of the runs, respectively. On problems pertaining to medium levels of difficulty, HGA achieves the best results at an average of 89.9% of its runs, while GA, SA and GRASP achieve them at 84,9%, 59,9% and 55,4% of the runs, respectively. Finally, in terms of high levels of difficulty problems, HGA reaches optimum results at a n average of 78.7% of its runs, while GA, SA and GRASP achieve them at 74,9%, 57,9% and 54,9% of their corresponding runs.
5. Conclusions
In this work we presented a novel approach to the solution of ROADEF'05, combining different procedures. They were adapted on the basis of the structure, number of variables and complexity of each scenario. Individual analyses of the Greedy Randomized Adaptive Search Procedure (GRASP), a Genetic Algorithm (GA) and Simulated Annealing (SA) returned satisfactory results. Moreover, in most scenarios GRASP and SA generated solutions with similar features. However, GA converges to better quality results than SA and GRASP. It is interesting to note that GA reaches superior results when the initial individual population is obtained by means of the GRASP. In this context, the Hybrid Genetic Algorithm (HGA) efficiently amalgamates the desirable characteristics of the three meta-heuristics, GRASP, GAs and SA. The experiments sustain this claim since the results achieved with the hybrid technique are better than those obtained by each technique by itself.
Acknowledgments
This work was funded by two research grants: PICT-2011-0396 of the Fondo para la Investigación Científica y Tecnológica (FONCyT) of the Agencia Nacional de Promoción Científica y Tecnológica (AGENCIA) and PGI 24/J056 of the Universidad Nacional del Sur.
References
[1] Solnon, C., Cung, V.D., Nguyen A. and Artigues C., The car sequencing problem: Overview of state-of-the-art methods and industrial case-study of the ROADEF'2005 challenge problem. European Journal of Operational Research, 191 (3), pp. 912-927, 2008. DOI: 10.1016/j.ejor.2007.04.033. [ Links ]
[2] Gagne, C. and Zinflou, A., An hybrid algorithm for the industrial car sequecing problem. Proceedings of IEEE Congress on Evolutionary Computation, 1, (1-8), 2012. DOI: 10.1109/CEC.2012.6256122. [ Links ]
[3] Briant, O., Naddef, D. and Mouni, G., Greedy approach and multi-criteria simulated annealing for the car sequencing problem. European Journal of Operational Research, 191 (3), pp. 993-1003, 2008. DOI: 10.1016/j.ejor.2007.04.052. [ Links ]
[4] Bautista, J., Pereira, J. and Adenso-Díaz, B., A GRASP approach for the extended car sequencing problem. Journal of Scheduling, 11, pp. 3-16, 2008. DOI: 10.1007/s10951-007-0046-4. [ Links ]
[5] Zinflou, A. and Gagné, C., Tackling the industrial car sequencing problem using GISMOO algorithm. In assembly line - theory and practice, W. Grzechca, Ed., Ed: I-Tech Education and Publishing, pp. 85-106, 2011.DOI: 10.5772/21113. [ Links ]
[6] Estellon, B., Gardi, F. and Nouioua, K., Two local search approaches for solving real-life car sequencing problems. European Journal of Operational Research, 191 (3), pp. 928-944, 2008. DOI: 10.1016/j.ejor.2007.04.043. [ Links ]
[7] Gavranovic, H., Local search and suffix tree for car-sequencing problem with colors. European Journal of Operational Research, 191 (3), pp. 972-980, 2008. DOI: 10.1016/j.ejor.2007.04.051. [ Links ]
[8] Prandtstetter, M. and Raidl, G.R., An integer linear programming approach and a hybrid variable neighborhood search for the car sequencing problem. European Journal of Operational Research, 191 (3), pp. 1004-1022, 2008. DOI: 10.1016/j.ejor.2007.04.044. [ Links ]
[9] Frutos, M., Olivera, A.C. y Casal, R., Estudio sobre distintas estrategias utilizadas para establecer secuencias detalladas en entornos productivos. Proceedings of XII International Conference on Industrial Engineering and Operations Management, XXVI Encuentro Nacional Engenharia de Produção 1, pp. 136, 2006. [ Links ]
[10] Olivera, A.C., Frutos, M. y Casal, R., Algoritmos Genéticos: Una estrategia clave para abordar problemas de secuenciamiento en gran escala. Proceedings of XXXIV Jornadas Argentinas de Informática e Investigación Operativa, pp 1-9, 2006. [ Links ]
[11] Olivera, A.C., Frutos, M. and Casal R., Métodos para determinar secuencias de producción en un ambiente productivo complejo. Proceedings of XIII Congreso Latino-Iberoamericano de Investigación Operativa, pp.1-6, 2006. [ Links ]
[12] Fonseca, C.M. and Fleming, P.J., Overview of evolutionary algorithms in multiobjective optimization. Evolutionary Computation, 3 (1), pp. 1-16, 1995. DOI: 10. [ Links ]1162/evco.1995.3.1.1.
[13] Hanne, T., Global multiobjective optimization using evolutionary algorithms. Journal of Heuristics, 6 (3), pp. 347-360, 2000. DOI: 10.1023/A:1009630531634. [ Links ]
[14] Ribeiro, C.C., Aloise, D., Noronha, T.F., Rocha, C. and Urrutia, S., A hybrid heuristic for a multi-objective real-life car sequencing problem with painting and assembly line constraints. European Journal of Operational Research, 191 (3), pp. 981-992, 2008. DOI: 10.1016/j.ejor.2007.04.034. [ Links ]
[15] Resende, M. and González Velarde, J.L,. GRASP: Procedimientos de búsqueda miopes aleatorizados y adaptativos. Revista Iberoamericana de Inteligencia Artificial, 19, pp. 61-76, 2003. [ Links ]
[16] Goldberg, D.E., Genetic algorithms in search, Optimization and machine learning. Addison Wesley Publishing Company, Inc, 1989. [ Links ]
M. Frutos, is an Assistant Researcher of CONICET (National Research Council of Argentina) and Teaching Assistant at the Department of Engineering of the Universidad Nacional del Sur, in Bahía Blanca, Argentina. He completed his undergraduate degree in Industrial Engineering and MSc and PhD in Engineering at his home university. His research focuses on scheduling problems in production and their treatment through metaheuristic methods. He has published in Operational Research, Annals of Operations Research, Dyna, and American Journal of Operations Research among others. He participates actively in the Operations Research community in Latin America.
A.C. Olivera, is an Assistant Researcher of CONICET (National Research Council of Argentina) stationed at the Department of Exact and Natural Sciences of the Universidad Nacional de la Patagonia Austral, Comodoro Rivadavia, Argentina. She has a PhD in Computer Science from the Universidad Nacional del Sur, Bahía Blanca, Argentina and held a post-doctoral position at the University of Malaga, Malaga, Spain. Her research focuses on urban traffic and production chain optimization problems using bio-inspired algorithms. She has published book chapters and several papers in indexed journals and proceedings of refereed international conferences.
F. Tohmé, is a Principal Researcher of CONICET (National Research Council of Argentina) and Full Professor at the Department of Economics of the Universidad Nacional del Sur, in Bahía Blanca, Argentina. A former Fulbright Scholar, he held visiting positions at U.C. Berkeley, Washington University in St. Louis and Endicott College, USA. He holds an undergraduate degree in Mathematics and a PhD in Economics. His research has focused on decision problems, game theory and optimization in the socio-economic settings. He has published in Theory and Decision, Mathematics of Social Sciences, Artificial Intelligence, Mathematical and Computational Modeling, and Annals of Operations Research among others.