Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.191 Medellín maio/jun. 2015
https://doi.org/10.15446/dyna.v82n191.51146
DOI: http://dx.doi.org/10.15446/dyna.v82n191.51146
A genetic algorithm to solve a three-echelon capacitated location problem for a distribution center within a solid waste management system in the northern region of Veracruz, Mexico
Algoritmo genético para resolver el problema de localización de instalaciones capacitado en una cadena de tres eslabones para un centro de distribución dentro de un sistema de gestión de residuos sólidos en la región norte de Veracruz, México
María del Rosario Pérez-Salazar a, Nicolás Francisco Mateo-Díaz b, Rogelio García-Rodríguez c, Carlos Eusebio Mar-Orozco d & Lidilia Cruz-Rivero e
a División de Posgrado e Investigación, Instituto Tecnológico Superior de Tantoyuca Veracruz, México, rosario.perez.salazar@gmail.com
b División de Ingeniería en Gestión Empresarial, Instituto Tecnológico Superior de Tantoyuca Veracruz, México, pacomatthew06@gmail.com
c División de Ingeniería en Sistemas Computacionales, Instituto Tecnológico Superior de Tantoyuca Veracruz, México, rgarciardz@gmail.com
d División de Posgrado e Investigación, Instituto Tecnológico Superior de Tantoyuca Veracruz, México, carlos.mar.orozco@gmail.com
e División de Posgrado e Investigación, Instituto Tecnológico Superior de Tantoyuca Veracruz, México, lilirivero@gmail.com
Received: January 28th, 2015. Received in revised form: March 26th, 2015. Accepted: April 30th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
Mexico is the world's third largest consumer of Polyethylene Terephthalate (PET), only preceded by the United States and China. PET is commonly used in plastic containers such as beverage bottles and food packaging. It can be argued that the main problem regarding pollution generated by PET waste lies in the lack of appropriate solid waste management. The decision regarding facility location is the central issue in solid waste management. A mixed integer linear programming model of the capacitated facility location problem is proposed and then a genetic algorithm is designed to optimize the model. The problem is described as follows: given the quantities of PET generated in the northern region of Veracruz, Mexico, by considering five cities and each as a single generation source, a collection center has to be selected among a set of pre-identified locations in the town of Tempoal, Veracruz; in order to serve a set of demand points in the re-use market; demands are assumed to be uncertain. The aim is to minimize the system's overall cost.
Keywords: genetic algorithm, solid waste management; capacitated location problem.
Resumen
México es el tercer consumidor mundial de Tereftalato de Polietileno (PET), sólo después de Estados Unidos y China. El PET es utilizado comúnmente para fabricar recipientes de plástico tales como botellas para bebidas y empaques para alimentos. Se puede argumentar que el principal problema con respecto a la contaminación generada por los residuos de PET radica en una inadecuada gestión de residuos sólidos. Proponemos un modelo de programación entera mixta del problema de localización de instalaciones capacitado y luego un algoritmo genético es desarrollado para optimizar este modelo. El problema se describe de la siguiente manera: dada la cantidad de PET generado en la región norte de Veracruz, México, considerando cinco ciudades y cada una como una fuente de generación única, un centro de recolección tiene que ser seleccionado entre un conjunto de lugares previamente determinados en la ciudad de Tempoal, Veracruz; con el fin de servir a un conjunto de puntos de demanda en el mercado re-uso; se asume que las demandas como parámetros de incertidumbre. El objetivo es minimizar el costo total del sistema.
Palabras clave: algoritmo genético; gestión de residuos sólido; problema de localización capacitado.
1. Deciding the location of solid waste system facilities
Decisions regarding the location of facilities can be considered as a strategic issue with an inherent risk for almost every company. The problem of locating facilities establishes alternatives in order to evaluate the conditions for the proper management of transportation and inventory levels, considering the company's ability to manufacture and market its products.
The capacitated facility location problem (CFLP) is a well-known variant of the FLP, and has been studied by several authors. According to the list above we can find multiple examples in scientific literature regarding CFLP; discrete [24] and continuous [4], multi-facility [6, 30], multi-echelon [13,28], single source [3,23] and multi- source [1], multi-commodity [24], and dynamic [9, 27].
The modeling process that requires the facility location decisions has to consider the fluctuation and inherent stochastic nature of the parameters involved in the problem analysis [12,24]. Costs, demands, travel times, supplies, and other inputs to classical facility location models may be highly uncertain; these input data are based on a forecast that results in taking into account uncertain parameters whose values are governed by probability distributions that are known by the decision maker, and, hence, are likely to be more realistic. Otherwise, if input data is assumed to be known with certainty, deterministic models are considered [24,25]. The random parameters can be either continuous, in which case they are generally assumed to be statistically independent of one another, or described by discrete scenarios, each with a fixed probability [17,20,24,29,31].
There are different methods to find the optimal solution to the problem regarding the location of facilities within network design, such as multi-criteria programming, branch and bound algorithm, dynamic programming, among others, mixed integer linear programming (MIP) being one of the most popular methods used in commercial location models [2]. Linear programming based techniques have been applied successfully to uncapacitated facility locations problems to obtain constant factor approximation algorithms for these problems; however, linear programming based techniques have not been successful when dealing with capacitated FLP. Continuing with this analysis of the type of solution methodology that has been used for solving the FLP, many variants of this problem have been studied extensively from the perspective of approximation algorithms, one of the most recently proposed is heuristics [1,4,8,22,28].
Regarding multicriteria analysis and optimization, a combined methodology based on multicriteria decision analysis and optimization for the distribution centers location problem, this model provides a set of relevant quantitative and qualitative attributes used for the decision of locating distribution centers [32].
A waste is something that has no value of use. Solid waste (SW), commonly known as trash or garbage consists of everyday items such as product packaging, grass clippings, furniture, clothing, bottles, food scraps, newspapers, appliances, paint and batteries [10]. A solid waste collection system is concerned with the collection of waste from sources, routing to trucks within the region, the frequency of collection, crew size, truck sizes, number of operating trucks, transportation of collected waste to a transfer station, an intermediate processing facility or a landfill and a host of other problems [14].
Within solid waste management (SWM), we can identify some key activities such as the selection of the number and locations of transfer stations, intermediate processing facilities, landfill sites, their capacities, capacity expansion strategies and routing of the waste across point sources (district or counties within the region) and routing of the waste through the facilities to ultimate disposal on a macroscopic level. Regarding these two routing choices, we recognize two perspectives in SWM, regional and by district [14]. Limited suitable land area and resources, growing public opposition, and deterioration of environmental conditions are invariably the main constraints for the proper functioning of an SWM. In this context, SWM has often been viewed from the narrow perspective of counties or districts rather than a regional perspective [18]. Some applications and examples have been observed in literature [10].
The phases of SWM can be divided into four distinct phases [12]: pre-collection, collection, transportation and treatment. The pre-collection is the proper storage, handling, sorting and presentation of waste suitable for collection and transfer conditions. This phase is essential for the accurate functioning of the following stages. Collection and transportation stages are often the most costly and hence require careful planning. Fifty to 70 % of the transport and disposal of solid waste was spent on the collection phase [19]. Waste is compacted and transported directly to the points of treatment or transfer plants. Treatment includes disposal operations or use of the materials contained in the waste.
One of the main issues in SWM involves facility capacity location, where a related optimization analysis will typically require the use of integer variables to carry out the decision process of locating a particular facility development or expansion options to be used. Thus, MIP techniques are useful for this purpose [15].
Uncertainty is an important issue to discuss in SWM, primarily in waste generation and economic criteria. Waste generation is a function of population distribution and growth, and per capita waste generation rates, while economic estimates are a function of the technology used, economies of scale, land availability, and local labor and equipment prices. Deterministic and stochastic mathematical programming models have been applied for SWM [18]. Some of the approaches concerning deterministic models are linear programming, MIP, dynamic programming, and multi - objective programming; in contrast, techniques used for stochastic models involve probability, fuzzy and grey system theory [5]. A probabilistic approach is also presented in an algorithm for probabilistic analysis of unbalanced three-phase weakly-meshed distribution systems is presented; this algorithm uses the technique of Two-Point Estimate Method for calculating the probabilistic behavior of the system random variables [33].
Regarding MIP techniques and incorporating stochastic parameters, a MSW capacity planning problem formulation has been proposed to be solved in three main stages [18]; first the formulation of a MIP model for the given MSW management planning problem providing the optimal solutions as bases for decision making, then a modeling for generating alternative methods was used for generating a near-optimal alternative, and finally a simulation technique was used for incorporating random waste generation in order to compare optimal solutions and simulation results.
2. Model formulation
Model formulation for the multiple-source, capacitated facility location problem is described as follow: given a number of sources that generate quantities of SW, a collection center has to be selected among a set of locations, in order to serve a set of demand points. The objective is to locate the collection center that minimizes the fixed and variable cost of handling and transport products through the selected network. The index, parameters and variables of this model are shown in Table 1, Table 2 and Table 3.
The mathematical formulation is as follows:
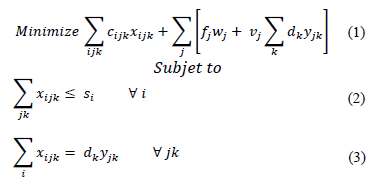
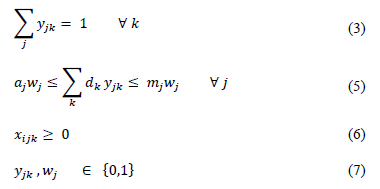
The objective function (1) aims to minimize fixed costs and variable costs. The supply constraint states that available supply cannot be exceeded (2), and the demand of all demands points (3) must be satisfied. Regarding operability of the collection center, each customer must be served only by one collection center (4). Also, for each collection center there should be a minimal activity in order to begin operation and a maximum activity as well, set by the established capacity (5).
3. Situations description
Mexico is the world's third largest consumer of Polyethylene Terephthalate (PET), only preceded by the United States and China. PET is commonly used in plastic containers such as beverage bottles and food packaging. In Mexico, every person uses an average of 225 bottles per year, additionally around 800 thousand tons of PET is consumed per year, with an annual growth of 13%. Due to the problem of SW and PET contamination, new public policies have been created in the country; for example, in Veracruz, the program for the prevention and integrated waste management uses the public policy in addition to good management. Approximately 4451 tons of SW is collected on a daily basis in the state of Veracruz, which represents 5% of the national collection. The country houses 241 collection centers and in Veracruz, there are only 5 towns with such centers. To supply the demand for PET bottles in Mexico, there are 5 manufacturing plants and about 190 bottling plants, serving nearly one million outlets [4]. The generation of SW has increased over the past few years growing by 25% between 2003 and 2011. In 2011, Veracruz was the fourth largest producer of SW, nationwide, with 5.5%, just after Estado de Mexico (16%), Distrito Federal (12%) and Jalisco (7%), and Nuevo Leon (5%).
For this work, a basic generic supply chain network is considered. The source echelon is represented by five towns, the next echelon is denoted by the three pre-determined locations for the collection center selection, and finally the customer echelon consists of three identified demand points. Fig. 1 depicts a three echelon supply chain network.
Due to the fact that the evaluation zone for this project is developed in the north of Veracruz, specifically in the town of Tempoal, we considered five towns as possible sources: el Higo (S1), Tantoyuca (S2), Platón Sánchez (S3), Huejutla (S4) and Tempoal (S5). The productions per town are 4000, 18300, 4400, 32920 and 7700 tons per year, respectively. From these amounts only 2% from each town corresponds to PET and other plastics [4]; hence, the amounts to be considered as parameter the "Amount of solid waste supplied by each source," which for this case are 80, 366, 88, 658, 154 tons per year, respectively. These amounts increase by 13% per year [3]; thus, the increase was calculated over a period of 5 years.
To determine the cost of transportation from source to the collection center, the distance between the two points is determined, and then divided between the performance of vehicle 1 to be used, and then multiplied by the current cost of gasoline.[1] ($12.9 liter) and finally is multiplied by 2, which represents the back and forth of the vehicle from alternative 1 (A1) to the sources of the waste, similarly we determined the cost for each source (S1, S2, S3, S4 and S5) and alternative (A1, A2 and A3). Considering an increase of gasoline of $ 0.11 per month, the transportation costs were obtained from the source to the collection center and from the distribution center to the customer annually with a 5 year projection. Unlike other models of storage location or facilities, whereby the location is chosen according to the sources of supply, the model for this research takes into account three previously established potential sites by which the nature of the problem is which alternative to choose between these three possible locations for storage centers: two outside the town of Tempoal (A1 and A2), Veracruz, and the third in the town of Huejutla, Hidalgo (A3). To determine the fixed costs of each collection center the following concepts were observed: Initial investment, labor, electricity, water, telephone, whose amounts were A1 = $ 2, 668,000 A2 = $ 3, 173,000 and A3 = 4, 176,000, of these amounts, annual operating costs are A1 = 168,000, A2 = 173,000 and A3 = 176,000, where the capacity of each of the collection centers are 7,000, 17,000, 34,000 tons per year, respectively. Thus the variable costs per ton of material handled within the distribution center are $ 381.14, $ 186.64, $ 122.82, respectively.
Three potential customers for the re-use of PET were established taking into account the volume of purchase (demand), the cost of transportation, cost of processing, storage capacity and fixed costs. For this case, a customer located in the city of Tampico (C1), another in the city of Madero (C2), and the third in Altamira (C3) in the state of Tamaulipas were selected. The demand data were collected through a field study in which random customers were taken in the state of Tamaulipas, specifically in the towns of Tampico and Altamira. The data obtained were analyzed and it was observed that the three sets of data follow a normal distribution. These parameters allowed us to obtain the annual growth rate, which was estimated by calculating the percentage change for each year and then taking absolute values averaged when they showed a decrease in demand. In this way, the percentages estimated regarding the demand growth rates per customer are: C1 = 13.99%, C2 = 13.72% and C3 = 14.27%, these values allowed us to calculate the increase in demand over a period of 5 years. The same procedure is used to determine the cost of transport from source to the collection center and from the collection center to the customer, in this case from A1, A2, and A3 to C1, C2, and C3.
4. Genetic algorithm principles
Genetic algorithms (GAs) are mathematical optimization techniques that simulate a natural evolution process. GAs constitute one of the artificial intelligence exhaustive searching techniques; they are stochastic algorithms whose search methods model some natural phenomena: genetic inheritance and Darwin strife for survival [27]. Their search procedure consists of maintaining a population of potential solutions while conducting a parallel investigation for non-dominated solutions [22]. Considering network strategy design, which contemplates the logistic chain network problem formulated by a MIP model, GAs have been applied as an alternative procedure for generating optimal or near-optimal solutions to location problems [7,16,26].
The GA implemented in this study uses quite common genetic operators. The proposed GA procedure implies the following steps:
Encoding of solutions. Solutions were encoded by dividing the chromosome, i.e. a complete set of coded variables, into two parts. The first part represents the continuous variables represented by the trailers assignment percentage at six locations proposed in the case study. The second part of the chromosome represents the assignment of trailers (crates and cages) to planned destinations.
Initial population creation. The procedure of creating the initial population corresponds to random sampling of each decision variable within its specific range of variation. This strategy guarantees a population various enough to explore large zones of the search area.
Fitness Evaluation. The criteria for each optimization model are to minimize total cost. If one restriction isn't satisfied, the solution is marked as not feasible.
Selection Procedure: The selection procedure consists of random sampling of pairs of individuals in the roulette wheel, one individual at a time. Individuals presenting higher fitness values have larger probability of propagating to next generation.
Crossover: Two selected parents are submitted to the crossover operator to produce two children. The crossover is carried out with an assigned probability, which is generally rather high. If a number randomly sampled is superior to the probability, the crossover is performed. Otherwise, the children are copies of the parents. In case of a discrete variable, this is copied for the parents. For continuous variables, the child takes the value of both parents; the first child takes 80% of parent one and 20% of parent two, and the second child takes 20% of parent one and 80% of parent two.
Mutation: The genetic mutation introduces diversity in the population by an occasional random replacement of the individuals. The mutation is performed on the basis of an assigned probability. A random number is used to determine whether a new individual will be produced to substitute the one generated by crossover. The mutation procedure consists of replacing one of the decision variable values of an individual, while keeping the remaining variables unchanged. The replaced variable is randomly chosen, and its new value is calculated by randomly sampling within its specific range. The new value is determined adjusting the old value; the adjustment is a low percentage of the old value that never causes an infeasible individual.
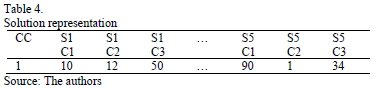
The encoding solution is an array of values that describes one solution to the problem. The first value represents the location selected for the collection center. The subsequent values indicate the amount of units of SW from sources to customer.
Table 4 shows one solution of the GA. The solution indicates that the best location for the collection center is A1. Moreover, the solution indicates that the amount of units of SW from source 1 to customer 1 is 10. It can be noted that transporting units of SW from S1 to C2 is more suitable than transport units from S5 to C2.
Each instance of the problem consists of a file with all the information described in section 4, such as the number of sources, number of customers and corresponding demand; and in reference to the collection center locations information such as the initial investment for construction, annual operating cost, and minimum and maximum capacity. Each file represents one year of the 5 year planning horizon.
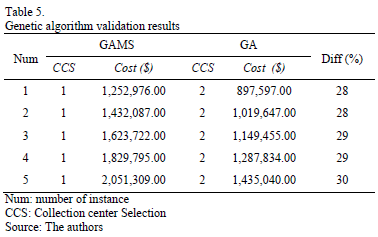
Initially, instances are considered without uncertainty. Customer demand is known and doesn't change over time. Each instance of the problem was executed 30 times with the GA, and the solutions were compared with the results obtained by GAMS. GAMS (General Algebraic Modeling System) is a high-level software tool for modeling and solving optimization problems and mathematical programming. The comparative process was used to tune the GA. Population size and percentage of mutation was set to 100 and 1%. A tournament selection process was carried out. Fig 2 shows the code of the genetic algorithm.
The runtime in all cases was less than 1.5 seconds and it is noted that runtime was not relevant in finding the best solution.
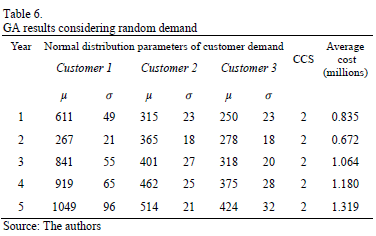
The second group of instances included uncertainty regarding customer demand, represented by a normal distribution. The second group of instances includes uncertainty regarding customer demand, represented by a normal distribution. In order to obtain the parameters of the probability distribution, goodness of fit tests were executed.
5. Results
Table 5 shows the execution results along with the number set of the collection center selected to be open. GAMS results indicate to open the collection center in A1, while the GA proposed to open the collection center in A2. The average cost for each instance is presented. Analyzing the outcome, we can see that in all 5 instances of the problem, the GA gives better results than GAMS decreasing up to 30% in the overall cost, thus validating the GA.
Then, 30 iterations of the GA were executed for every year considered in the planning horizon, taking into account the uncertainty representing the variation of the 3 demand points modeled by normal probability distribution (see Table 6) along with the number set of the collection center selected to be open and the average cost.
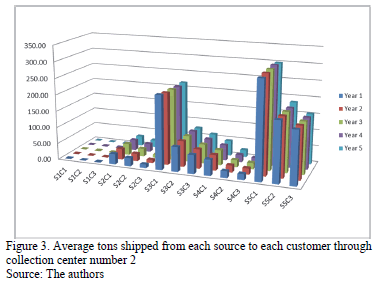
Also, the GA gives the average amount of units to be shipped from sources to customers for each year. Fig 3 shows the average tons shipped from each source to each customer through the selected collection center that represents lower cost. We can infer important decisions based on this graph; for example, that we should not ship units from S1 to C1, but that it is convenient to ship units from S5 to C1.
The mathematical model is optimized through genetic algorithm presented in this section. The optimization is performed subject to random demand to determine which collection center to open and the corresponding calculations of cost.
6. Conclusions
Within the Mexican environmental context, a priority issue is that of creating solid waste treatment facilities due to the considerable increase in waste in recent years. There are several techniques regarding decisions on the location of solid waste system facilities.
The overall objective of the work presented in this paper was to develop a facility location problem to assist decision makers in the selection of a collection center among three pre-identified locations given by the local government. Considering the overall cost of the network, we identify a three-echelon, multi-source, capacitated facility location problem for the consideration of transferring PET waste generation in five towns in the northern region of Veracruz through the selected collection center to meet three demand points in the re-use market. The facility location problem was modeled using a mixed integer programming technique. The mathematical model is optimized through genetic algorithm. The optimization is performed subject to random demand to determine which collection center to open and the corresponding calculations of cost.
References
[1] Avella, P. and Boccia, M., A cutting plane algorithm for the capacitated facility location problem. Computational Optimization and Applications, 43 (1), pp. 39-65, 2009. DOI: 10.1007/s10589-007-9125-x [ Links ]
[2] Ballou, R.H., Logística: administración de la cadena de suministro. Pearson Educación, 2004. [ Links ]
[3] Cabrera, G., Cabrera, E., Soto, R., Rubio, L., Crawford, B. and Paredes, F., A hybrid approach using an artificial bee algorithm with mixed integer programming applied to a large-scale capacitated facility location problem. Mathematical Problems in Engineering, 2012. DOI: 10.1155/2012/954249 [ Links ]
[4] Carlo, H.J., Aldarondo, F., Saavedra, P.M. and Torres, S.N., Capacitated continuous facility location problem with unknown number of facilities. Engineering Management Journal, 24 (3), pp. 24-31, 2012. DOI: 10.1080/10429247.2012.11431944 [ Links ]
[5] Chi, G., Integrated planning of a solid waste management system in the City of Regina. Doctoral Thesis, University of Regina, Canadá 1997. [ Links ]
[6] Chudak, F.A. and Williamson, D.P., Improved approximation algorithms for capacitated facility location problems. In Integer programming and combinatorial optimization, Springer Berlin Heidelberg, 1999, pp. 99-113. DOI: 10.1007/3-540-48777-8_8 [ Links ]
[7] Correa, E.S., Steiner, M.T., Freitas, A.A. and Carnieri, C., A genetic algorithm for solving a capacitated p-median problem. Numerical Algorithms, 35 (2-4), pp. 373-388, 2004. DOI: 10.1023/B:NUMA.0000021767.42899.31 [ Links ]
[8] Dias, J.M., Captivo, M.E. and Clímaco, J., Dynamic location problems with discrete expansion and reduction sizes of available capacities. InvestigaçãoOperacional, 27 (2), pp. 107-130, 2007. [ Links ]
[9] Dias, J.M., Captivo, M.E. and Clímaco, J., Capacitated dynamic location problems with opening, closure and reopening of facilities. IMA Journal of Management Mathematics, 17 (4), 317-348, 2006. DOI: 10.1093/imaman/dpl003 [ Links ]
[10] Erkut, E., Karagiannidis, A., Perkoulidis, G. and Tjandra, S.A., A multicriteria facility location model for municipal solid waste management in North Greece. European Journal of Operational Research, 187 (3), pp. 1402-1421, 2008. DOI: 10.1016/j.ejor.2006.09.021 [ Links ]
[11] Farahani, R.Z., SteadieSeifi, M. and Asgari, N., Multiple criteria facility location problems: A survey. Applied Mathematical Modelling, 34 (7), pp. 1689-1709, 2010. DOI: 10.1016/j.apm.2009.10.005 [ Links ]
[12] García, F.J.A. and Tena, C., Gestión de residuos sólidos urbanos: Análisis económico y políticas públicas. Cuadernos Económicos de ICE, (71), pp. 71-91, 2006. [ Links ]
[13] Gendron, B., and Semet, F., Formulations and relaxations for a multi-echelon capacitated location-distribution problem. Computers & Operations Research, 36 (5), pp. 1335-1355, 2009. DOI: 10.1016/j.cor.2008.02.009 [ Links ]
[14] Gottinger, H.W., A computational model for solid waste management with application. European Journal of Operational Research, 35 (3), pp. 350-364, 1998. DOI: 10.1016/0377-2217(88)90225-1 [ Links ]
[15] Huang, G.G.H., Huaicheng, G. and Guangming, Z., A mixed integer linear programming approach for municipal solid waste management. Journal of enviromanetal sciences China-English Edition, 9, pp. 431-445, 1997. [ Links ]
[16] Kratica, J., Toic, D., Filipović, V. and Ljubić, I., Solving the simple plant location problem by genetic algorithm. RAIRO-Operations Research, 35 (01), pp. 127-142, 2001. DOI: 10.1051/ro:2001107 [ Links ]
[17] Listeş, O. and Dekker, R., A stochastic approach to a case study for product recovery network design. European Journal of Operational Research, 160 (1), pp. 268-287, 2005. DOI: 10.1016/j.ejor.2001.12.001 [ Links ]
[18] Najm, M.A., El-Fadel, M., Ayoub, G., El-Taha, M. and Al-Awar, F., An optimization model for regional integrated solid waste management I. Model formulation. Waste management & research, 20 (1), pp. 37-45, 2002. DOI: 10.1177/0734242X0202000105 [ Links ]
[19] Noche, B., Rhoma, F.A., Chinakupt, T. and Jawale, M., Optimization model for solid waste management system network design case study. In Computer and Automation Engineering (ICCAE) The 2nd International Conferenceon 5, pp. 230-236, IEEE, 2010. [ Links ]
[20] Shafia, M.A., Rahmaniani, R., Rezai, A. and Rahmaniani, M., Robust optimization model for the capacitated facility location and transportation network design problem. International Conference on Industrial Engineering and Operations Management, Istanbul, 2012. [ Links ]
[21] Shepherd, S. and Sumalee, A., A genetic algorithm based approach to optimal toll level and location problems. Networks and Spatial Economics, 4 (2), pp. 161-179, 2004. DOI: 10.1023/B:NETS.0000027771.13826.3a [ Links ]
[22] Silva, C.M. and Biscaia, E.C., Genetic algorithm development for multi-objetive optimization of Batch Free radical polymerization reactors. Computers & Chemical Engineering, 27, pp 1329-1344, 2003. DOI: 10.1016/S0098-1354(03)00056-5 [ Links ]
[23] Silva, F.J.F. and De la Figuera, D.S., A capacitated facility location problem with constrained backlogging probabilities. International journal of production research, 45 (21), pp. 5117-5134, 2007. DOI: 10.1080/00207540600823195 [ Links ]
[24] Snyder, L.V. Facility location under uncertainty: A review. IIE Transactions, 38 (7), pp. 547-564, 2006. DOI: 10.1080/07408170500216480 [ Links ]
[25] Snyder, L.V., Daskin, M.S. and Teo, C.P., The stochastic location model with risk pooling. European Journal of Operational Research, 179 (3), pp.1221-1238, 2007. DOI: 10.1016/j.ejor.2005.03.076 [ Links ]
[26] Syarif, A., Yun, Y. and Gen, M., Study on multi-stage logistic chain network: A spanning tree-based genetic algorithm approach. Computers & Industrial Engineering, 43 (1), pp. 299-314, 2002. DOI: 10.1016/S0360-8352(02)00076-1 [ Links ]
[27] Torres-Soto, J.E. and Üster, H., Dynamic-demand capacitated facility location problems with and without relocation. International Journal of Production Research, 49 (13), pp. 3979-4005, 2011. DOI: 10.1080/00207543.2010.505588 [ Links ]
[28] Tragantalerngsak, S., Holt, J. and Rönnqvist, M., An exact method for the two-echelon, single-source, capacitated facility location problem. European Journal of Operational Research, 123 (3), pp. 473-489, 2000. DOI: 10.1016/S0377-2217(99)00105-8 [ Links ]
[29] Wagner, M.R., Bhadury, J. and Peng, S., Risk management in uncapacitated facility location models with random demands. Computers & Operations Research, 36 (4), pp. 1002-1011, 2009. DOI: 10.1016/j.cor.2007.12.008 [ Links ]
[30] Wu, L.Y., Zhang X.S. and Zhang, J.L., Capacitated facility location problem with general setup cost. Computers & Operations Research, 33 (5), pp. 1226-1241, 2006. DOI: 10.1016/j.cor.2004.09.012 [ Links ]
[31] Zhou, J. and Liu, B., New stochastic models for capacitated location-allocation problem. Computers & industrial engineering, 45 (1), pp. 111-125, 2003. DOI: 10.1016/S0360-8352(03)00021-4 [ Links ]
[32] Soto-de la Vega, D., Vidal-Vieira, J.G. and Vitor-Toso, E.A., Methodology for distribution centers location through multicriteria analysis and optimization. DYNA [on line]. 81 (184), pp. 28-35, 2014. Available at: http://dyna.medellin.unal.edu.co/en/ediciones/184/articulos/v81n184a03/v81n184a03.pdf [ Links ]
[33] Peñuela, C., Granada, M. and Sanches, J.R., Algorithm for probabilistic analysis of distribution systems with distributed generation. DYNA, [on line]. 78 (169), pp. 79-87, 2011. Available at: http://dyna.medellin.unal.edu.co/en/ediciones/169/articulos/a09v78n169/a09v78n169.pdf [ Links ]
M. del R. Pérez-Salazar, completed her BSc Eng in Electronic Engineering in 2007 at the Instituto Tecnológico de Puebla and her MSc degree in Industrial Engineering in 2011 at the Instituto Politécnico Nacional, from which she gratuated with honors. From 2009 to 2010, she was a member of the Instituto Politécnico Nacional Institutional Research Training Program. Since 2011, she has been a Full Professor at the Industrial Engineering Department, Instituto Tecnológico Superior de Tantoyuca. She is currently the coordinator of the Industrial Engineering Graduate Program, Instituto Tecnológico Superior de Tantoyuca. Her research interests include discrete event simulation, supply chain mamagement, enterprise information systems, artificial intelligence applied to risk analysis and decision making.
N.F. Mateo-Díaz, completed his BSc Eng in Industrial Engineering in 2009, his MSc degree in Industrial Engineering in 2013, both at the Instituto Tecnológico Superior de Tantoyuca. He worked on projects regarding finacial investment modeling, wining third place at the Second Latin American Financial Modeling contest using Risk Simulator software in 2013. Currently, he is a Full Professor at the Industrial Engineering Department, Instituto Tecnológico Superior de Tantoyuca.
R. García-Rodríguez, completed his BSc. Eng in Computer Systems Engineering in 2005, his MSc degree in Computer Science in 2010, both at the Instituto Tecnológico de Ciudad Madero. Since 2011, he has been a Full Professor at the Computer Systems Department, Instituto Tecnológico Superior de Tantoyuca. His research interests include software engineering, intelligent optimization and mathematical modeling.
C.E. Mar-Orozco, completed his BSc Eng in Industrial Engineering in 2009 at the Instituto Tecnológico de Ciudad Madero and his MSc degree in Industrial Management in 2012 at the Universidad Autonoma de Tamaulipas. His work experience includes both, manufacturing and services organizations. He has won several prizes in investment projects contests. Currently, he is a Full Professor at the Industrial Engineering Department, Instituto Tecnológico Superior de Tantoyuca.
L. Cruz-Rivero, completed her BSc Eng in Industrial Engineering in 2002 at the Instituto Tecnológico de Ciudad Madero and her MSc degree in Business Administration in 2008 at the Universidad Valle del Bravo Campus Tampico, graduated Magna Cum Laude. She collaborated with the petrochemical sector in Petrocel-Temex as an assistant in the maintenance project to improve productivity. Since 2011, she has been a Full Professor at the Industrial Engineering Department, Instituto Tecnológico Superior de Tantoyuca. Her research area is design and development of products and services as a TRIZ practitioner by Altshuller Institute.