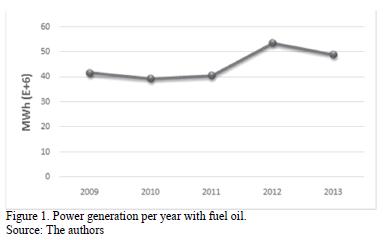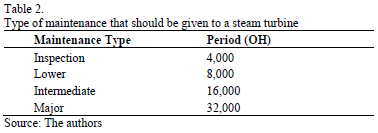Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.191 Medellín maio/jun. 2015
DOI: http://dx.doi.org/10.15446/dyna.v82n191.51152
Technical efficiency of thermal power units through a stochastic frontier
Eficiencia técnica de unidades de generación termoeléctrica mediante una frontera estocástica
José Antonio Marmolejo-Saucedo a, Román Rodríguez-Aguilar b, Miguel Gastón Cedillo-Campos c & María Soledad Salazar-Martínez d
a Facultad de Ingeniería, Universidad Anáhuac México Norte, México D.F., México. jose.marmolejo@anahuac.mx
b Escuela Superior de Economía, Instituto Politécnico Nacional, México D.F., México. roman.rodriguez@ipn.mx
c Instituto Mexicano del Transporte, Querétaro, México. gaston.cedillo@imt.mx
d Universidad Nacional Autónoma de México, México D.F., México. s.salazar@unam.mx
Received: January 28th, 2015. Received in revised form: March 26th, 2015. Accepted: April 30th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
This work presents a model to obtain a stochastic frontier production function of a Mexican power generation company. The stochastic frontier allows us to evaluate the technical efficiency of an energy producer according of the level of inputs. Electricity generation based on thermal generation is highly expensive due to operational inefficiency of thermal power plants. At the moment, in Mexico, technical efficiency of thermal power units has not been studied for the national electricity system. Therefore, in order to know the productivity levels of thermal generation, an empirical application of the stochastic frontier model is obtained using a panel data of thermoelectric units from the Mexican electricity system for the 2009-2013 period.
Keywords: Stochastic frontier; thermal generation; technical efficiency.
Resumen
Este trabajo presenta un modelo para obtener la frontera estocástica de la función de producción de una empresa mexicana de generación eléctrica. La frontera estocástica permite evaluar los niveles de eficiencia técnica del productor de energía respecto de los insumos utilizados. La generación eléctrica obtenida mediante generación térmica es muy costosa debido a la ineficiencia operativa de las centrales termoeléctricas. Hasta el momento, en México, la eficiencia técnica de las centrales termoeléctricas no ha sido estudiada para el Sistema Eléctrico Nacional. Por lo tanto, con la finalidad de conocer los niveles de productividad de la generación térmica, se realizó una aplicación de un modelo de frontera estocástica utilizando datos de panel de las centrales termoeléctricas del Sistema Eléctrico Mexicano para el periodo 2009-2013.
Palabras clave: Frontera estocástica; generación térmica; eficiencia técnica.
1. Power generation: the case of the Mexican electricity system
The generation of electricity using fossil fuels in Mexico is a process with broad participation; in 2011, the plants that only used fossil fuels accounted for 72.6% of the total electricity produced and are expected to remain broad in participation to meet the future electricity demand [1].
The use of fossil fuels for power generation has been severely questioned as the production of carbon dioxide (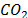 ) contributes to the accumulation of greenhouse gases (GHGs) emitted into the atmosphere.
) contributes to the accumulation of greenhouse gases (GHGs) emitted into the atmosphere.
Therefore, there are two prospective scenarios of capacity expansion for the 2013-2027 period. The first is the planned expansion of the public power generation companies with a share of 31.9% with the use of clean technologies in 2027. An 18.4% of hydro capacity, 4.1 % wind power, nuclear 1.8% and a remaining 2.4% with geothermal, solar and biogas capacity. In the alternative scenario, the expansion program is aligned to the goals set in local laws, seeking to increase its generation with non-fossil sources to a 35 % in 2027 [2].
This means that, although fossil fuel generation will be reduced, its use will be located in the worst case at 65% in 2027 [3]. Therefore, the total elimination of fossil fuels for power generation is nearly impossible, because it still represents one of the economic lower cost options in Mexico.
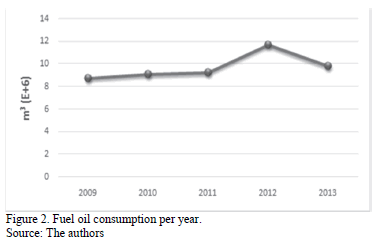
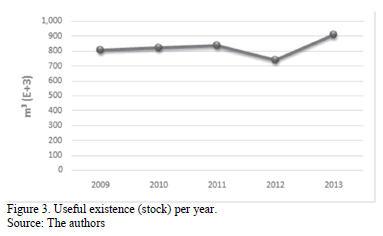
Figs. 1, 2 and, 3 show the behavior of thermal power generation, fuel oil consumption, and useful existence (stock of fuel oil) from 2009 to 2013.
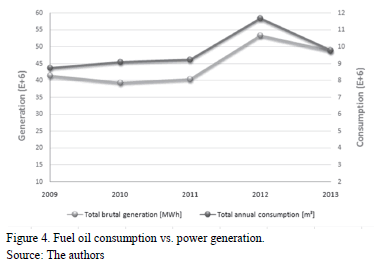
Fig. 4 shows that the behavior of the fuel oil consumption of power plants over time is directly related to the behavior of generation; i.e. power generation is a function of the consumption.
Both behaviors follow the same trend but they do not match on the same points throughout the timeline. For example, there are differences between consumption and generation since in some years, the points almost coincide and the graphical difference is very low, but in other years this difference increases and the points are apart from each other.
It could be concluded that when the points of consumption and generation are far apart, we have a period of technical inefficiency.
In 2013, the production of generation per unit volume (m3) increased. It is the lowest difference that can be seen. A total of 4.9 MWh/m3 was generated in 2013; while in 2010, it was of 4.3 MWh/m3.
Ideally, the points must coincide throughout the timeline, i.e. 100% of technical efficiency.
Regarding the level of fuel oil inventory (useful existence), we can mention that it is a policy concerning the reduction of the risk of not meeting the demand of electricity.
Indeed, the public power generation company must ensure at all times that the fuel oil supply to the thermal plants is guaranteed for any contingency.
2. Technical efficiency
The efficiency analysis is based on microeconomic analysis, through maximizing a given production function using a set of inputs and technology. There are two approaches to the optimization of a production function either through the maximization of production or cost minimization given a certain level of production.
In [4], two conceptual visions of economic efficiency were proposed:
- Technical efficiency: The ability of a production unit to obtain the highest level of product, a given level of inputs and technology.
- Allocative efficiency: The ability of a production unit to use the inputs in optimal proportions, given a price level and technological level.
The usefulness of technical efficiency lies in generating information to improve the management capacity of the production units, and to know the information of input used and generation of production over to define optimal strategies for improvement. There are several methods of estimating technical efficiency: parametric, non-parametric, deterministic, and stochastic.
- Parametric: Assume a functional form of the production function.
- Nonparametric: Do not assume any functional form of the production function.
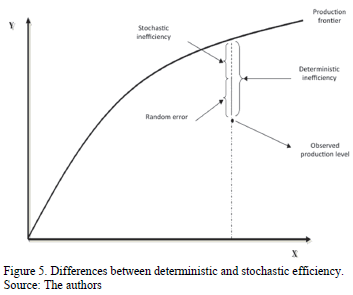
- Deterministic: Part of the approach that all distance between the border of production and production value observed for a productive unit corresponds to technical inefficiency.
- Stochastic: The production has a random component representing the technical efficiency as part of the deviation from the optimum production units.
Techniques for estimating technical efficiency according to the adopted approach can be classified among the primal and dual approaches. In the case of primal approach, technical efficiency is estimated based on maximizing production or minimizing function costs. In the case of a dual approach, technical efficiency for both functions is estimated [16-18]. Models can also be categorized in terms of temporality, in cross section or panel data models.
The nonparametric models generally used are estimates based on Data Envelopment Analysis (DEA) methodologies based on mathematical programming. The great advantage of using DEA methodologies is that a specific functional form of the production function is not required. On the other hand, the main disadvantage is that they are deterministic models that can be affected by the number of inputs used as well as by the presence of outliers [14, 15].
2.1. Stochastic frontier
In 1977, [5,6] simultaneously proposed a stochastic frontier. The initial specification was a cross-sectional model with an error term composed of two factors: one that measured the random effect and another that measured the technical inefficiency. [7-10] present developments of stochastic frontier models in various applications. In [11], a model was proposed for the inefficiency effects of the stochastic frontier production function. This model is applied in the analysis of data on electricity generation during different time periods.
The most important thing in terms of the methodology of estimation of stochastic frontiers is that the treatment of error terms does not assume that all errors are attributable to a random factor, and that a segment of these is attributable to technical inefficiency. Fig. 5 shows the comparison between deterministic and stochastic methods for estimating technical inefficiency for a production function.
A number of empirical studies have estimated stochastic frontiers and predicted firm level efficiencies using these estimated functions and then regressed the predicted efficiencies upon firm specific variables in an attempt to identify some of the reasons for differences in predicted efficiencies between firms in an industry.
The two stages estimation procedure is inconsistent in its assumptions regarding the independence of the inefficiency effects in the two estimation stages. This estimation procedure is unlikely to provide estimates that are as efficient as those that could be obtained using as single stage estimation procedure.
This issue was addressed in [11,12] where the authors proposed stochastic frontier models in which the inefficiency effects are expressed as an explicit function of a vector of firm specific variables and a random error. [13,14] proposed a model, which is equivalent to the [12] specification, with the exceptions that allocative efficiency is imposed, the first order profit maximizing conditions is removed, and panel data is permitted. The model specification may be expressed as:
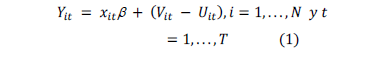
Where:
is a logarithm of the production of the i-th firm in the t-th time period
is a kx1 vector of transformation of the input quantities for the i-th firm in the t-th time period
is a vector of unknown parameters
is a random variable which is assumed to be iid
)
is a non negative random variable assumed to account for technical inefficiency in production and to be independently distributed as truncations at zero of the
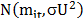
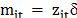
is a px1 vector of variables which influences the efficiency of a firm and
is an 1xp vector of parameters to be estimated.
2.2. Efficiency predictions
The measures of technical efficiency relative to the production frontier are defined as:
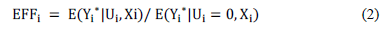
Where 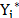 is the production of the i-th firm, which will be equal to
is the production of the i-th firm, which will be equal to 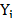 when the dependent variable is in original units and will be equal to exp (
when the dependent variable is in original units and will be equal to exp (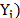 when the independent variable is in logarithms. In the case of a production frontier,
when the independent variable is in logarithms. In the case of a production frontier, 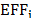 will take a value between zero and one, while it will take a value between one and infinity in the cost function case.
will take a value between zero and one, while it will take a value between one and infinity in the cost function case.
3. Stochastic frontier model to measure efficiency in Mexican power Generation Company
The study includes data for a group of 21 thermoelectric units. Annual average gross electricity generation, level of consumption, and useful existence of fuel oil are analyzed. A balanced panel data for 21 thermoelectric units was built for the 2009-2013 period. The useful existence and consumption of fuel oil are expressed as an annual average in cubic meters and annual average gross generation of electrical energy in MWh.
The objective of measuring technical efficiency in the production of electrical energy is to assess whether levels of consumption and useful existence correspond with the level of production of each thermoelectric, assuming a given technology.
The goal is to evaluate the interaction between the inputs to generate electric power and congruence of results. Two specifications of production function were tested: Trans-logarithmic and Cobb-Douglas. The Cobb-Douglas production function was chosen because it generates better estimates, so all variables are expressed in logarithmic fashion.
The advantage of having a series of panel data is that this allows the evaluation of the technical efficiency of thermoelectric units over time to capture the dynamic performance of each production unit. The functional form of the model is presented in equation (3).
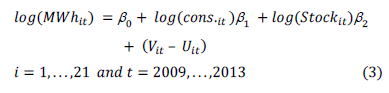
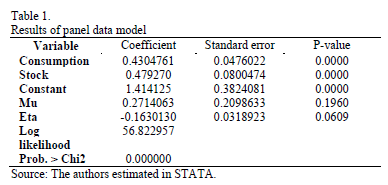
A fixed effects model was estimated by the maximum likelihood method, considering fuel oil consumption and useful existence as independent variables and power generation as dependent variable. Technical efficiency was considered a variable over time. The results obtained for the proposed model are presented in Table 1.
The model results show that general model and the inputs considered are statistically significant. The values of the estimated parameters of inputs considered are consistent with expectations, i.e. both inputs positively involved in the generation of electricity.
The first test (Mu) states that the average truncated normal is zero. It can be seen that at the 5% significance level the null hypothesis is not rejected. The null hypothesis of the second test is that inefficiency is time invariant (Eta). The values of the null hypothesis are located at the limit to 95% significance. The hypothesis that inefficiency is time invariant is rejected to 90% significance, and shall be deemed inefficiency dynamic over time.
Based on the model parameters estimated, we calculated the level of efficiency according to equation (2). The level of technical efficiency estimated is between 0 and 1, where 1 means that the production unit is efficient and values below 1 indicate that the unit is inefficient. When the distance from 1 is greater, it means the unit presents greater inefficiency.
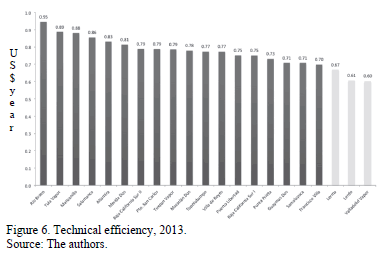
Fig. 6 shows the estimation of efficiency for 2013 of all thermoelectric units considered in the analysis. It is noted that Rio Bravo, Tula Steam and Manzanillo are the most efficient thermoelectric units. By contrast Lerma, Lerdo and Valladolid Vapor are the worst performers in terms of thermoelectric units.
Of the 21 thermoelectric units analyzed, only four have an efficiency of 90%, ten have an efficiency of 80% and seven shows an efficiency level below 70%. It is noteworthy that only four thermoelectric units show efficiency levels of around 90%. This implies that strictly speaking 81% of the thermoelectric units operate inefficiently.
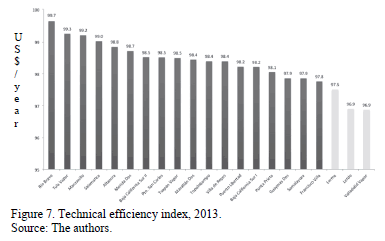
An efficiency rating was calculated based on estimates of efficiency technical for each thermoelectric in the period of analysis, using 2009 as base year. The index shows the evolution of efficiency for each thermoelectric in time. Values greater than 100 indicate that the efficiency has been improved, and values below 100 indicate that the efficiency is worse.
Fig. 7 shows the evolution of efficiency index of each unit analyzed for 2013. It is noted that in general the level of efficiency of all units has decreased since 2009. Especially for the three thermoelectric units with worst performance, their level of inefficiency has fallen on average by 3% in the period of analysis.
The results show that 81% of the thermoelectric units are inefficient, considering threshold efficiency values of at least 90%, observing the evolution of efficiency in time, all thermoelectric units have decreased levels of efficiency.
The estimated level of efficiency is an indicator to analyze in more detail the operation of thermoelectric units with lower levels of efficiency. It is also useful to evaluate overall performance of the electric power sector. These results show the need to assess in more detail the operation of 81% of the thermoelectric plants in Mexico.
3.1. Cause analysis of inefficiency
There are several factors that affect the productivity of the systems; for example, technical efficiency, which can be incorporated in the stochastic frontier. One of the reasons for technical efficiency to show a downward trend in all thermoelectric plants, could be the wear and tear of the generating units, given that in many cases the right kind of maintenance determined by the number of operation hours (inspection, minor, intermediate and major) is not given, mainly due to limited budget or other political factors.
The diagnosis of the operation of an energy system is to discover and interpret the signs of malfunction of equipment that compose and quantify their effects in terms of additional consumption of resources; i.e. where, how and how much the overall consumption of resources can be saved, holding constant the quantity and product specifications of the system.
For thermoelectric plants a malfunction of certain equipment such as boilers, will have a major economic impact, even for small deviations in their performance with respect to what is expected by design.
A good diagnosis of the operation must be preceded by a conceptual development that explains the origin of the increase.
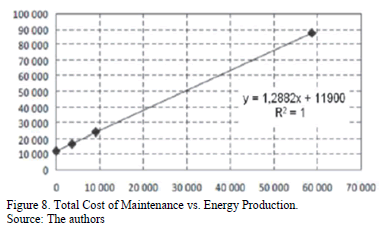
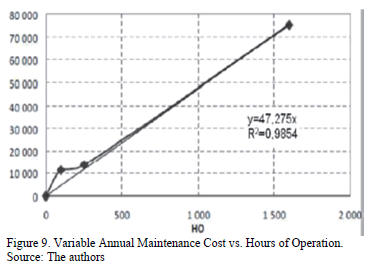
In Figs. 8 and 9 we see an example of the relationship between the total cost of maintenance per year and the relationship between the Variable Annual Maintenance Cost (CVM) and the operation time (HO), respectively.
Thus, considering the age of most power plants, the maintenance represents a considerable budget, which often cannot be covered in a timely manner, minimizing technical efficiency.
4. Conclusions
The stochastic frontier of production function shown in this work allows an efficiency study of different thermal generation plants. Additionally, the analysis of panel data allows the evaluation of the variation in time of the technical inefficiency of electrical production.
In general, 81% of the thermoelectric units are technically inefficient in their operation; one reason for this technical inefficiency is related to maintenance levels.
The evaluation of technical efficiency is a useful indicator for monitoring the operation of thermoelectric units and evaluating their performance, in order to identify which units require particular attention to achieve maximum performance in their operation. Therefore, it is important to conduct a proper diagnosis with (conventional, energy simulation and thermoeconomics) existing methods for the proper functioning of the energy system.
Acknowledgements
The authors thank Flora Hammer for comments and suggestions that improved this paper. At the same time, we acknowledge all the support provided by the National Council of Science and Technology of Mexico (CONACYT) throughout the research program "Redes Temáticas de Investigación," as well as by the Mexican Logistics and Supply Chain Association (AML) and the Mexican Institute of Transportation (IMT).
References
[1] Salazar, M.S., Una estrategia para mejorar la administración de los inventarios de diesel en las centrales termoeléctricas: un estudio de caso, MSc. Thesis, Engineering Systems Department, National Autonomous University of Mexico, Mexico, 100 P, 2015. [ Links ]
[2] Secretaría de Energía. Prospectiva del sector eléctrico 2013-2027, Mexico, 2013. [Online], [date of reference December 19th of 2014]. Available at: http://sener.gob.mx/res/PE_y_DT/pub/2013/Prospectiva_del_Sector_Electrico_2013-2027.pdf [ Links ]
[3] González-Santaló, J.M., La generación eléctrica a partir de combustibles fósiles. Boletin IIE. Octubre-diciembre 2009. [Online], [date of reference December 19th of 2014]. Available at: http://www.iie.org.mx/boletin042009/divulga.pdf [ Links ]
[4] Farrell, M., The measurement of productive efficiency. Journal of the Royal Statistical Society, 120 (3), pp. 253-290, 1957. DOI: 10.2307/2343100 [ Links ]
[5] Meeusen, W. and Van den Broeck, J., Efficiency estimation from Cobb-Douglas production functions with composed error. International Economic Review, 18, pp. 435-444, 1977. DOI: 10.2307/2525757 [ Links ]
[6] Aigner D., Lovell C., and Schmidt, P., Formulation and estimation of stochastic frontier production function models. Journal of Econometrics, 6, pp. 21-37, 1977. DOI: 10.1016/0304-4076(77)90052-5 [ Links ]
[7] Forsund, F., Lovell, C. and Schmidt, P., A survey of frontier production functions and of their relationship to efficiency measurement. Journal of Econometrics, 13, pp.5-25, 1980. DOI: 10.1016/0304-4076(80)90040-8 [ Links ]
[8] Schmidt, P., Frontier production functions. Econometric Reviews, 4, pp. 289-328, 1986. DOI: 10.1080/07474938608800089 [ Links ]
[9] Bauer, P., Recent developments in the econometric estimation of frontiers. Journal of Econometrics, 46, pp.36-56, 1990. DOI: 10.1016/0304-4076(90)90046-V [ Links ]
[10] Greene, W., The econometric approach to efficiency analysis. In H. Fried, Lovell, C. and Schmidt, S (Eds.), The Measurement of Productive Efficiency. New York: Oxford University Press, 1993. [ Links ]
[11] Reifschneider, D. and Stevenson, R., Systematic departures from the frontier: A framework for the analysis of firm inefficiency. International Economic Review, 32 (3), pp.715-23, 1991. DOI: 10.2307/2527115 [ Links ]
[12] Battese, G. and Coelli, T., A stochastic frontier production function incorporating a model for technical inefficiency effects. Working Papers in Econometrics and Applied Statistics. Department of Econometrics, University of New England, 69, pp. 1-22, 1995. [ Links ]
[13] Battese, G. and Coelli, T., A Model for Technical Inefficiency Effects in a Stochastic Frontier Production Function for Panel Data. Empirical Economics, 20, pp. 325-332, 1995. DOI: 0.1007/BF01205442 [ Links ]
[14] Berndt, E.R. and Wood, D.O., Technology, prices and the derived demand for energy, Econ. Statist. 57, pp. 259-268, 1975. DOI: 10.2307/1923910 [ Links ]
[15] Díaz-Serna, F.J., Optimización de la operación y evaluación de la eficiencia técnica de una empresa de generación hidroeléctrica en mercados de corto plazo. PhD Thesis, Universidad Nacional de Colombia. Medellín, 186 P, 2011. [Online], [date of reference December 19th of 2014]. Available at: http://www.bdigital.unal.edu.co/3683/#sthash.KcLJiF0R.dpuf [ Links ]
[16] Garzón, P. and Pellicer, E., Organizational efficiency of consulting engineering firms: Proposal of a performance indicator. DYNA, 76 (160), pp. 17-26, 2010. [Online], [date of reference December 19th of 2014]. Available at: http://www.revistas.unal.edu.co/index.php/dyna/article/view/13463/14365 [ Links ]
[17] Calderero-Gutierrez, A., Fernandez-Macho J., Kuittinen H. et al., Innovacion en las regiones europeas. Una alternativa metodologica y actualizada del Ris. DYNA, 84 (6), pp.501-516, 2009. [ Links ]
[18] Diaz, J., La eficiencia técnica como un nuevo criterio de optimización para la generación hidroeléctrica a corto plazo. DYNA, 76 (157), pp. 91-100, 2009. [Online], [date of reference December 19th of 2014]. Available at: http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=S0012-73532009000100009&lng=es&nrm=iso [ Links ]
J.A. Marmolejo-Saucedo, is professor in the Faculty of Engineering at Universidad Anahuac Mexico Norte, Mexico. He has a PhD. in Engineering with a specialization in Operations Research from the National Autonomous University of Mexico (UNAM), Mexico and is currently a member of the National System of Researchers of the National Council of Science and Technology (CONACYT) of Mexico. He is on the Board of the Mexican Society of Operations Research, and member of the Scientific Committee of the International Congress on Logistics and Supply Chain (CiLOG) organized by the Mexican Logistics and Supply Chain Association (AML). His areas of interest are large-scale optimization and mathematical modeling in power systems and logistical problems in the supply chain.
R. Rodriguez-Aguilar, is PhD. in Economics with a specialization in mathematical finance from the School of Economics at the National Polytechnic Institute, Mexico. He has a MSc. degree in Engineering and Statistics granted by the National Autonomous University of Mexico, a MSc. degree in Public Policy Institute of Technology and Research superiors of Monterrey, Mexico. Dr. Rodriguez is a member of the Mexican Mathematical Society, the National Association of Economists and Economic Modeling Network EcoMod. His areas of interest are stochastic optimization, mathematical finance and econometrics.
M.G. Cedillo-Campos, is a Professor in Logistics Systems Dynamics and Founding Chairman of the Mexican Logistics and Supply Chain Association (AML), Mexico. Dr. Cedillo is National Researcher (National Council of Science and Technology of Mexico - CONACYT), Innovation Award 2012 (UANL-FIME) and National Logistics Award 2012. In 2004, he received with honors a PhD. in Logistics Systems Dynamics from the University of Paris, France. Recently, he collaborated as a Visiting Researcher at Zaragoza Logistics Center as well as Georgia Tech Panama. He works in logistics systems analysis and modeling, risk analysis, and supply chain management, which are the subjects he teaches and researches in different prestigious universities in Mexico and abroad. Dr. Cedillo is the Scientific Chairman of the International Congress on Logistics and Supply Chain (CiLOG) organized by the Mexican Logistics and Supply Chain Association (AML), and coordinator of the National Logistics Research Network in Mexico supported by CONACYT.
M.S. Salazar-Martínez, has a degree in Electrical Electronic Engineering from the National Autonomous University of Mexico. Currently, she is working in the Federal Electricity Commission in Mexico. Her functions include planning and supply of diesel and fuel oil-fired to power thermoelectric plants to the National Electric Network by forecasting methods. Her areas of interest are modeling problems using advanced techniques of planning systems.