Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.191 Medellín maio/jun. 2015
https://doi.org/10.15446/dyna.v82n191.51153
DOI: http://dx.doi.org/10.15446/dyna.v82n191.51153
Optimization of the distribution of steel pipes using a mathematical model
Optimización de la distribución de tubería de acero mediante un modelo matemático
Miguel Mata-Pérez a & Jania Astrid Saucedo-Martínez b
a Posgrado en Logística y Cadena de Suministro, Universidad Autónoma de Nuevo León, México. miguel.matapr@uanl.edu.mx
b Posgrado en Logística y Cadena de Suministro, Universidad Autónoma de Nuevo León, México. jania.saucedomrt@uanl.edu.mx
Received: January 28th, 2015. Received in revised form: March 26th, 2015. Accepted: April 30th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
Distribution is one of the most important processes in a supply chain, given that it represents up to two thirds of company logistics costs and up to 20% of the total cost of products. For that reason, it is essential to optimize the costs of distribution. A steel producer located in Monterrey distributes their products to different parts of Mexico. Currently, the distribution is carried out through empirical knowledge, underusing resources and generating unnecessary costs. The aim is to undertake the distribution process more efficiently. This paper presents an optimization model based on vehicle routing problem (VRP), for the distribution of heavy pipes taking into account the company's own characteristics, such as: rented heterogeneous fleet, multiple shipments of products, split deliveries and open cycles (meaning that the routes may not necessarily end in the depot).
Keywords: Vehicle Routing Problem (VRP); combinatorial optimization; distribution of heavy pipes.
Resumen
El proceso de distribución suele representar más de dos terceras partes de los costos logísticos de la compañía y más del 20% del costo total de los bienes transportados. Es por ello que es vital para la empresa optimizar dicho costo. Una empresa productora de aceros ubicada en Monterrey, debe distribuir sus productos a múltiples clientes localizados a lo largo del país. En la actualidad dicha actividad es realizada mediante conocimientos empíricos, ocasionando que se subutilicen los recursos y generando altos costos de distribución. La empresa requiere realizar dicho proceso en forma más eficiente. Este artículo presenta un modelo de optimización basado en el problema de ruteo de vehículos (VRP), para la distribución de tubería pesada tomando en cuenta las características propias de la empresa, tales como: flota heterogénea y rentada, embarque de múltiples productos, entregas divididas y ciclos abiertos (las rutas no necesariamente terminan en el depósito).
Palabras clave: Problema de ruteo de vehículos (VRP); optimización combinatoria; distribución de tubería pesada.
1. Introduction
Transport operations and product distribution represent up to two-thirds of company logistics costs [2] and up to 20% of the total cost of transported products [13]. In many cases, the transport networks are too stiff and unable to absorb market variations in demand [2]. This has prompted outsourcing to transportation and distribution businesses, offering greater flexibility and more efficient deliveries management at competitive prices.
Given a set of products and of customers with well-defined demands, the distribution process consist in the company having to decide whether the deliveries can be complete or whether they need to be split, the best times for the deliveries, the kinds of vehicles to be used, the complete supply path, among other possible decisions. The distribution process of every company usually entails special characteristics in accordance with the individual features of each company.
It is important to note that the optimal distribution configuration is affected by variety configuration for the distribution, which, in turn, is affected by the variety of destinations, the diversity of products offered, and demand variability. Hence, it is common in practice to find problems such as underuse of transport, inefficient routes, and extra costs for loading and unloading.
Therefore, route planning is one of the main problems in the optimization of transport logistics operations, whose main objective is to find the appropriate balance between the cost of this activity and its contribution to the level of service specified by the company.
In this work, we present a combinatorial optimization model based on VRP for optimization in a real distribution company that supplies its products all over the country.
2. Description of the problem
A steel producer located in Monterrey-which distributes its products nationally-welds pipes from hot or cold rolled steel sheet, with different thicknesses and hardnesses to provide different products such as mechanical tubing, driving, conduit, oil, thin wall, etc. (See Fig. 1).
The company focuses its operations in a plant. In this paper, we focus on the distribution of the steel pipe all over the country, so that all the vehicles used must start their routes in this plant.
By company policies, Mexico is divided into thirteen areas, each composed of one or more states (see Fig. 2). According to these areas, the route for each vehicle must not go beyond a single zone.
The company does not have a fleet for distribution; instead they rent the necessary vehicles from several freight companies. This presupposes that the availability of vehicles is unlimited. Since the vehicles are not company property, they have no obligation to return to the plant once they finish their routes.
Another important feature of the fleet of vehicles is that they have different load capacities (9 vehicle types each with a capacity of 3.5, 6, 15, 22, 27, 28, 30, 32 and 36 Tons respectively). It must also be taken into account that some
vehicles cannot visit certain areas due transport authority regulations regarding the kind of road or due to physical restrictions a customer may present to receiving a certain kind of vehicle on their premises.
One of the features of our problem is that the company does not stick to delivery schedules and simplifies the solution by discarding penalties for partial or late deliveries. This also allows each customer order to be carried on more than one vehicle regardless of its characteristics. This is known as a "split delivery."
The fixed cost per trip includes three deliveries; however, the same vehicle can make more than three deliveries, incurring an additional cost for each one.
Pipelines being very heavy, it is important to maximize the load capacity of each vehicle in terms of weight, whereas the volume of the material is not a restriction for the arrangement inside the vehicle.
3. Background
Transportation problems are a diverse set of cases that some authors have attempted to group according to the most important characteristics; this allows the formulation of mathematical models to facilitate decision-making in companies that use a kind of transport. Furthermore, by adopting models, their solution usually has a significant impact on the cost and the level of customer service.
The transportation problems consist basically in assigning routes to vehicles to deliver or pick up products. The well-known Vehicle Routing Problem (VRP) generalizes a large set of problems concerning the distribution of products or services to a set of clients located in specific points.
The VRP has been studied extensively in the literature. For a deeper review of VRP, see [9,10].
It is important to mention that the VRP is NP-Hard [9]. There are many exact methods [11] for solving the VRP and an increasing number of heuristics methods for approximate the optimal solution [8,12].
All VRPs are determined by the functional constraints that must be satisfied by the vehicles and the conditions and operating standards of the enterprises. Depending on their characteristics, [4, 6] introduces the following VRP types:
- Size of fleet: a single vehicle or a limited or unlimited number of vehicles.
- Demand: stochastic, deterministic, dynamic, partially satisfied, fixed for all clients or variable depending on the client.
- Multiple products or a single product type.
- Schedule: unrestricted, with time windows (just beginning, end only, beginning and end, flexible, multiple).
- Fleet Type: homogeneous or heterogeneous.
- Depots: single, multiple, replenishment intermediate.
- End of route: return to the depot (closed cycle) or not (open cycle).
- Network communication: if there is a direct path between two clients, or whether these should be considered different routes.
- Costs: fixed or variable.
- Capacity of vehicles: limited and singular, limited and different, and unlimited.
- Number of routes per vehicle: limited to a single route, limited to a certain number, and unlimited.
- Objective: minimize costs, minimize number of vehicles, minimizing distance traveled and minimize time.
Thus, the combination of different characteristics determines an appropriate model for any possible specific situation. The study of the basic models has allowed the development of techniques that are applicable to cases that are increasingly complex.
For their historical significance, below is a summary of some of the most important routing problems. One of the first studies that treated this problem dates back to 1959 and it treated a problem involving dispatch service trucks applied to fuel distribution stations [5].
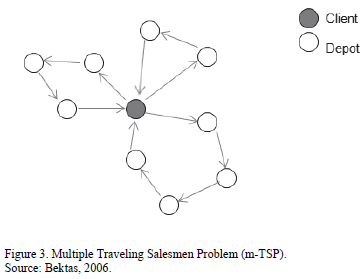
One of the best known is the Traveling Salesman Problem (TSP), in which a salesman must visit a particular number of customers once, and then return to where he started his trip [1]. Later, a variant appeared, known as m-TSP (Multiple Traveling Salesmen Problem), in which there are m sellers who must attend a certain number of clients that can be visited only once, and each seller must return to the starting point when her or his trip is finished [3]. See an illustration of the m-TSP in Fig. 3.
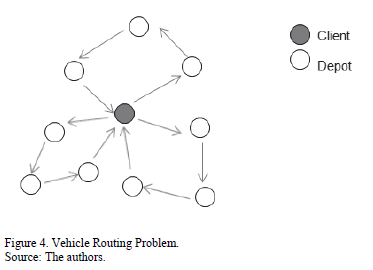
The Vehicle Routing Problem (VRP) is a generalization of the m-TSP, where a demand is associated for each customer and a capacity is defined for each vehicle. In the easier VRP, there exists a fleet of identical vehicles to make deliveries to customers from a single depot (See Fig. 4).
The following list presents some of the highlights of the VRP problems. For a more comprehensive list see [14].
- Asymmetric Vehicle Routing Problem (AVRP): The duration of the trip or the distance between two points depends on the direction of the path.
- Capacitated Vehicle Routing Problem (CVRP): The vehicle has a carrying capacity that must not be exceeded.
- Fleet Size and Mix Vehicle Routing Problem (FSMVRP): Handling fixed costs depending on the type of vehicle. The variable costs are the same for all vehicles. The problem does not impose restrictions on the number of vehicles.
- Vehicle Routing Problem with Heterogeneous Fleet (VRPHE): Fixed costs and dependent variables of the vehicle type. The problem does not impose restrictions on the number of vehicles.
- Pickup and Delivery Problem (PDP): The same vehicle must pick up and carry the goods from one place to another network.
- Min-max Vehicle Routing Problem (VRP Min-max): Try to minimize the length of the longest path.
- Vehicle Routing Problem with Precedence Constraints (VRPPC): Before visiting a particular client, the vehicle must visit a previous set of them.
- Multiple Depot Vehicle Routing Problem (MDVRP): There are several depots, from which the vehicles assigned to them depart and return.
- Open Vehicle Routing Problem (OVRP): When transportation is outsourced, the vehicles have no reason to return to the plant.
- Dynamic Vehicle Routing Problem (DVRP): Set of problems where some parameters depend on the time variable.
- Stochastic Vehicle Routing Problem (SVRP): Set of problems where some parameters have some uncertainty.
- Vehicle Routing Problem with Multiple Use of Vehicles (VRPM): Each vehicle can take more than one route over a period of time.
- Vehicle Routing Problem with Split Delivery (VRPSDV): A client's demand can be covered by several vehicles.
- Vehicle Routing Problem with Time Windows (VRPTW): Every customer has a distribution or delivery schedule. Schedules are also presented in the plants.
Concerning our problem, in the literature we found similarities with other VRP that have already been formulated; however, none of them include all of the company characteristics. That is why a custom mathematical model is required.
Our problem presents a heterogeneous fleet, because the company rents different kinds of vehicles according to its needs. The deliveries can be split due to the fact that it is not uncommon for the demands to exceed vehicle capacity. The company offers multiple products, and because the fleet is hired, it is not necessary for the vehicles to return to the depot (open cycles).
4. Mathematical model proposed
Imitating the terminology from classical models (see, for example [7]), we called our proposed model Open Vehicle Routing Problem with Heterogeneous Fleet, Split Deliveries and Multiple Products (OVRPHFSDMP).
It will be assumed that all data are integers and not negative numbers. The mathematical model for the OVRPHFSDMP is as follows.
4.1. Parameters

4.2. Variables

4.2. Model

Eq. (1) represents the objective function that minimizes the sum of the total cost for all used vehicles. The constraint represented for eq. (2) calculates the price that the company needs to pay to use the vehicle from the plant to the farthest destination taking into account the fixed costs and the extra costs. Eq. (3) estimates the number of customers that the vehicle must visit, and eq. (4) calculates the number of extra deliveries 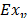 when the vehicle visits more than three clients. Eq. (5) ensures that all vehicles used start their routes at the plant but do not need to return to it as well as ensuring that each customer is visited at most once by the same vehicle. Eq. (6) allows the entry and exit of vehicles from a point k on the condition that a trip is not made from a place that has not been previously visited. Eq. (7) assigns packages on the vehicles that will be used. Eq. (8) ensures that customer demand is satisfied. Eq. (9) ensures that the weight carried on a vehicle does not exceed its capacity. Eq. (10) states that the vehicles will be assigned only to customers that the vehicles can access (i.e. due to infrastructure or transport authority regulations). Eq. (11) ensures that vehicles do not perform cycles.
when the vehicle visits more than three clients. Eq. (5) ensures that all vehicles used start their routes at the plant but do not need to return to it as well as ensuring that each customer is visited at most once by the same vehicle. Eq. (6) allows the entry and exit of vehicles from a point k on the condition that a trip is not made from a place that has not been previously visited. Eq. (7) assigns packages on the vehicles that will be used. Eq. (8) ensures that customer demand is satisfied. Eq. (9) ensures that the weight carried on a vehicle does not exceed its capacity. Eq. (10) states that the vehicles will be assigned only to customers that the vehicles can access (i.e. due to infrastructure or transport authority regulations). Eq. (11) ensures that vehicles do not perform cycles.
5. Computational experimentation
To test the model, 60 test cases have been proposed, 10 of them were from the history of the company and 50 others were probabilistically generated taking into account the behavior of real case studies.
To solve all the cases, we used GAMS (version 23.7.3) running on a Precision R5400 Rack Workstation Dell computer with 2 Quad Core Xeon Processor E5420 2.50 GHz and RAM 4 GB.
It is important to remember that the company has divided the country into thirteen different areas to facilitate the distribution, so that, if in one day all the areas are addressed, we split the problem into 13 independent problems and then integrate the results.
For reasons of confidentiality, we were not able to use the actual prices of the vehicles, instead assigning rates that behave similarly (variation between the vehicle costs).
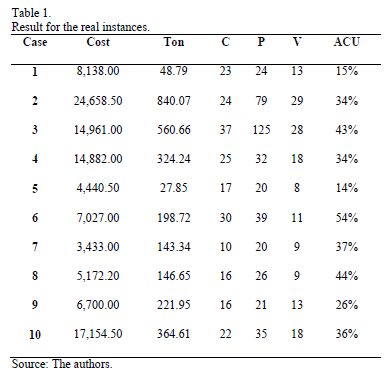
In Table 1, we present the results for the real cases. The first column represents the number of cases, the second shows the total costs obtained, the third column presents the total tonnes to be sent, the fourth, fifth and sixth columns represent the number of customers, packages and vehicles involved in the case respectively, and the seventh column shows the average capacity used (ACU) of the vehicles in the solution.
Usually when the company receives an order, it sends a vehicle to satisfy the demand regardless of the size of the order or the average vehicle capacity. Although for such cases, we do not have the company routing at our disposal, we know that the ACU in the historic data is around 30%, meaning that the routing that model offers, represents an improvement of around 4% in ACU.
Therefore, based on these results, we proposed that the company consolidate its orders due to the fact that the ACU was low. This is possible given that the customers do not penalize the company for deliveries delayed up to one week. In the simulated cases, we suppose that the orders can be consolidated, that is why the ACU is significantly improved.
We created a random generator of cases based on data from real cases to determine the demand by probability functions.
For each client and each type package a random real number is generated 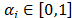 . Then the demand
. Then the demand 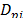 is assigned as follow:
is assigned as follow:
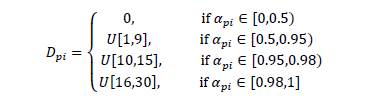
Where:
is a random integer number between a and b.
The quantities for the demands and the threshold for the partitioning in demands have been selected imitating the frequencies found in practice.
We proposed five types of cases, gradually varying the number of clients, packages and vehicles, (see Table 2).
Table 3 shows twenty representative cases (four of each kind). The first column represents the case number; the second column shows the size of case (Clients/Package/Vehicles); the third column indicates the total weight to be sent; the fifth column shows the average capacity used in the solution; finally, the fifth column present the computation time in seconds to solve each case.
We expected the time to increase according to the number of the clients, kind of package and vehicles used, but with respect to the ACU we were not able to determine anything.
Note that all the solutions (Table 3.) found for the 50 cases are optimal but, as can also be seen, the computation time increases exponentially as the size of the case increases.
6. Conclusions
The problem studied in this work has great practical significance because the distribution process is one of the principal components of any supply chain, and because it is directly related to costs, productivity and business performance in enterprises.
The main contribution of this work is the creation of a mathematical model that helps the decision maker to adapt to different scenarios investing less time and producing better solutions. The mathematical tool developed is a model of mixed integer linear programming for solving vehicle routing problems with heterogeneous fleet not belonging of the company, split deliveries and multiple products (OVRPHFSDMP for Open Vehicle Routing Problem with Heterogeneous Fleet, Split Deliveries and Multiple Products).
The model has been tested in real cases, in an important company, which produces and distributes steel pipes across the country, demonstrating that it adequately simulates reality, offering effective solutions and a plausible profit in the distribution costs for the company.
References
[1] Applegate, D.L., Bixby, R.M., Chvátal, V. and Cook, W.J.. The traveling salesman problem. Journal of Computer and System Sciences, 72 (4), pp. 509-546, 2006. [ Links ]
[2] Ballou, R., Business logistics management: Supply chain management. Planning, Organizing, and Controlling the Supply Chain. Weatherhead, United Kingdom: Prentice-Hall International, 2004. [ Links ]
[3] Bektas, T., The multiple traveling salesman problem: An overview of formulations and solution procedures. Omega, 34, pp. 209-219, 2006. DOI: 10.1016/j.omega.2004.10.004 [ Links ]
[4] Bodin, L. and Golden, B., Routing and scheduling: Classification in vehicle routing and scheduling. Networks, 11, pp. 97-108, 1981. DOI: 10.1002/net.3230110204 [ Links ]
[5] Dantzig, G.B. and Ramser, J.H., The truck dispatching problem. Management Science, 6 (1), pp. 80-91, 1959. DOI: 10.1287/mnsc.6.1.80 [ Links ]
[6] Desrochers, M., Lenstra, J.K. and Savelsbergh, M.W.P., A classification scheme for vehicle routing and scheduling problems. European Journal of Operational Research, 47, pp.75-85, 1990. DOI: 10.1016/0377-2217(90)90007-x [ Links ]
[7] Dror, M. and Trudeau, P., Split delivery routing. Naval Research Logistics, 37, pp. 383-402. 1990. DOI: 10.1002/nav.3800370304 [ Links ]
[8] Galván, S., Arias, J. y Lamos H., Optimización por simulación basado en EPSO para el problema de ruteo de vehículos con demandas estocásticas. DYNA, 80 (179), pp. 60-69, 2013. [ Links ]
[9] Laporte, G., Fifty years of vehicle routing. Journal of Transportation Science, 43 (4), pp. 408-416, 2009. DOI: 10.1287/trsc.1090.0301 [ Links ]
[10] Laporte, G. The vehicle routing problem: An overview of exact and approximate algorithms. European Journal of Operational Research 59, pp. 345-358, 1992. DOI: 10.1016/0377-2217(92)90192-C [ Links ]
[11] Laporte, G. and Nobert, Y., Exact algorithms for the vehicle routing problem. Annals of Discrete Mathematics 31, pp. 147-184, 1987. DOI: 10.1016/s0304-0208(08)73235-3 [ Links ]
[12] Sepúlveda, J, Escobar, J.W. and Adarme-Jaimes, W., An algorithm for the routing problem with split deliveries and time windows (SDVRPTW) applied on retail SME distribution activities. DYNA, 81 (187), pp. 223-231, 2014. DOI: 10.15446/dyna.v81n187.46104 [ Links ]
[13] Toth P. and Vigo D., Models, relaxations and exact approaches for the capacitated vehicle routing. Bologna: Ediciones SIAM, 2002. [ Links ]
[14] Yepes, V., Las redes de distribución como elementos de ventaja competitiva. Qualitas Hodie 76, pp. 30-33, 2002. [ Links ]
M. Mata-Pérez, completed a BSc in Applied Mathematics at UAQ, Mexico in 2002, and a MSc. degree and PhD. in Engineering Systems at the UANL, Mexico. He is an expert in mathematical modeling and optimization of large-scale systems. He is currently a full professor in the Logistics and Supply Chain Program of UANL, Mexico.
J.A. Saucedo-Martínez, completed her BSc. In Mathematics at UANL, Mexico in 2005, a MSc. degree in Engineering Systems at UANL, Mexico, and a PhD in Applied Mathematics at UNESP, Brazil, in 2012. She is an expert in mathematical modeling and optimization of large-scale systems. She is full professor in the Logistics and Supply Chain Program at UANL, Mexico.