Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.191 Medellín May/June 2015
https://doi.org/10.15446/dyna.v82n191.45513
DOI: http://dx.doi.org/10.15446/dyna.v82n191.45513
Matrix multiplication with a hypercube algorithm on multi-core processor cluster
Multiplicación de matrices con un algoritmo hipercubo en un cluster con procesadores multi-core
José Crispín Zavala-Díaz a, Joaquín Pérez-Ortega b, Efraín Salazar-Reséndiz b & Luis César Guadarrama-Rogel b
a Facultad de Contaduría, Administración e Informática, Universidad Autónoma del Estado de Morelos, Cuernavaca, México. crispin_zavala@uaem.mx
b Departamento de Ciencias Computacionales, Centro Nacional de Investigación y Desarrollo Tecnológico, Cuernavaca, México. jpo_cenidet@yahoo.com.mx, efras.salazar@cenidet.edu.mx, cesarguadarrama@cenidet.edu.mx
Received: September 10th, 2014. Received in revised form: March 9th, 2015. Accepted: March 17th, 2015
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
The algorithm of multiplication of matrices of Dekel, Nassimi and Sahani or Hypercube is analysed, modified and implemented on multi-core processor cluster, where the number of processors used is less than that required by the algorithm n3. 23, 43 and 83 processing units are used to multiply matrices of the order of 10x10, 102x102 and 103X103. The results of the mathematical model of the modified algorithm and those obtained from the computational experiments show that it is possible to reach acceptable speedup and parallel efficiencies, based on the number of used processor units. It also shows that the influence of the external communication link among the nodes is reduced if a combination of the available communication channels among the cores in a multi-core cluster is used.
Keywords: Hypercube algorithm; multi-core processor cluster; Matrix multiplication
Resumen
Se analiza, modifica e implementa el algoritmo de multiplicación de matrices de Dekel, Nassimi y Sahani o hipercubo en un cluster de procesadores multi-core, donde el número de procesadores utilizado es menor al requerido por el algoritmo de n3. Se utilizan 23, 43 y 83 unidades procesadoras para multiplicar matrices de orden de magnitud de 10X10, 102X102 y 103X103. Los resultados del modelo matemático del algoritmo modificado y los obtenidos de la experimentación computacional muestran que es posible alcanzar rapidez y eficiencias paralelas aceptables, en función del número de unidades procesadoras utilizadas. También se muestra que la influencia del enlace externo de comunicación entre los nodos disminuye si se utiliza una combinación de los canales de comunicación disponibles entre los núcleos en un cluster multi-core.
Palabras Clave: Algoritmo Hipercubo, cluster de procesadores multi-core, Multiplicación de matrices
1. Introduction
The multicore clusters are formed by either nodes or processors, often heterogeneous, connected with architecture of dynamic configuration, high speed bus; it allows point to point connections among each processing unit. The nodes are composed of processors and the processors in turn are composed of multiple cores, where each of them has the ability to run more than one process at a time [1]. These features allow us to propose solutions to various problems using computing parallel and concurrent [2,3], such as the one presented in this work: The matrix multiplication with the DNS algorithm (Dekel, Nassimi, Sahani or hypercube) on a multicore cluster.
The execution time of the DNS or Hypercube algorithm for multiplying nxn matrices is polylogarithmic T∞(logn) and requires a polynomial number of processors Hw(n3), these two parameters classify it as an efficiently parallelizable algorithm [4]. But, in its implementation in a multicore cluster the following limitations are presented: First, the number of processing units available is finite and is lesser than those required by the hypercube algorithm for matrice sizes given Hw(n3); Second, the processing units are spread over various nodes and processors. Where the speed of the communication links among the cores is different, they can be on the same processor, in the same node, either in different nodes or processors.
Similar modifications [5] are proposed to implement the hypercube algorithm on multicore clusters. In the modification proposed in this work the number of processing units remains constant, leaving as a variable the grain size or the number of the subarrays that divides the nxn matrices. Contrary to what is proposed by [5], where the number of processing units is determined by the size of the input.
The implementation of the algorithm is made by the library Message Passing Interface MPI, where MPI processes are assigned to the cores. If an MPI process is assigned to a core, then it will be parallel computation; but if more than one MPI process is assigned to the same core, then it will be concurrent computation. Computational experiments took place in the ioevolution multicore cluster. Where nxn matrices are multiplied by 8, 64 and 512 processing units, the matrix's size is a multiple of 72, from 72 x 72 up to 2304 x 2304 items.
Theoretical and experimental results show that the solution proposed in this work allows to multiply matrices of size multiples 1,000X1,000 in multi-core cluster, using a smaller number of processors than required processors by original algorithm; with modifications proposed, it is possible to achieve acceptable speedup and good parallel efficiencies, depending on the number of processing units used; the developed mathematical model of the modified DNS algorithm predicts the behavior of the parallel implementation on a multi-core cluster.
The article consists of the following parts: in the second the methodology and foundations of the Hypercube algorithm are presented; in the same section the analysis of its running time on a MIMD computer, of memory and distributed computation, is presented. Based on this analysis, the modifications to multiply matrices on a multi-core cluster are presented. The third part contains the computational experiments and analysis of results. Finally, in the fourth section the conclusions that come out of this work are presented.
2. Methodology
Algorithms for matrix multiplication based on the model Simple Instruction Multiple Data (SIMD) has been developed since the beginning of the parallel computation, such as: Systolic Array or Mesh of Processors, Cannon, Fox, DNS method (Dekel, Nassimi, Sahani) or hypercube and meshes of trees [4-8]. In all of them, except for DNS, the parallel process of solution consists of sequential steps of data distribution and computing. In general, in the first stage the data between processor units are distributed. In the second, each processor performs the multiplication of elements allocated. In the third, the first and second steps are repeated until all columns and rows of the matrices are rotated and multiplied. In the fourth stage the resulting elements are added. In contrast, in either the DNS or Hypercube algorithm, the distribution and multiplying of elements run only once, the first and second stages, and similarly to the other algorithms the fourth stage is executed once.
Then the DNS or Hypercube algorithm is described.
2.1. Hypercube algorithm
The algorithm is based on multiplying two nxn matrices using the model Simple Instruction Multiple Data (SIMD), the execution time is q(logn) and requires n3 processors. This consists of q steps to distribute and rotate the data among the processor units, the number of stages is given by 5q = 5 logn and the matrix size by n3 = 23q[4].
The solution strategy is: distribute and rotate the elements of the matrices (aik, bik) in the computer nodes, connected by hypercube architecture. Once the rotation and distribution of elements is performed, each processing unit has the pair (aik, bki), then they are multiplied. After the multiplication, the products are sent to be added and get the cijelements.
The matrix multiplication algorithm SIMD Hypercube comprises three phases: In the first, the elements are distributed and rotated in the processing units; in the second phase the elements are multiplied; and in the third, the products are summed to obtain the solution matrix.
2.2. Runtime hypercube algorithm in a multi-core cluster
For the execution time on a multi-core cluster it is necessary to introduce the factors that influence its implementation, such as: time used: calculation Tcal, communications Tcomm, wait Twait and local operations Tlocal [9]. The Twait and Tlocaltimes are assumed to be zero for the following reasons: First, each processing unit receives the data and immediately executes the next operation (Twait = 0); Second, the processor units do not perform local operations for the distribution of the data (Tlocal = 0). Since the beginning of the process, the units neighbouring for sending are defined. Therefore, parallel execution time is determined by:
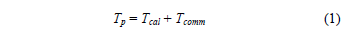
To be able to add the Tcal and Tcomm times, they must be expressed in the same units: runtime or in the number of operations of the processing unit, so it is necessary to standardize the communication time. To this end the constant g, eq. (2) [10], is introduced.
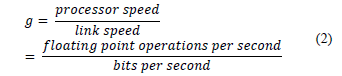
The constant calculates the communication time depending on processor operations [10]. Therefore, the communication time is determined by the expression:
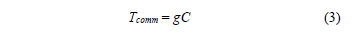
To calculate the execution time in a parallel computer of distributed memory and distributed process the Tcal and Tcomm times are entered in the algorithm of Fig. 1. The execution time of the phases of Hypercube algorithm is shown in Table 1.
Whereas q = logn time parallel execution is:
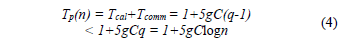
If eq. (4) is compared with equation unmodified Tp(n) = 1 + 5logn [4], it shows that the time of the parallel execution, eq. (4), grows approximately gC multiple, because normally g > 1 and C is always greater than 1. This indicates that the parallel algorithm is faster than the sequential for the matrix's certain size. For example, if g = 2 and C is equal to 64 bits, the matrix of size 14x14 is needed for which the modified hypercube parallel algorithm is going to be faster than the sequential. Additionally, 2,744 processing units are required to implement it.
Multiplying matrices of dimensions 1,000X1,000 in a multi-core cluster with this algorithm has the following drawback: the number of processing units is not available. Consequently, it needs to be modified in order to multiply matrices of this size, because the number of available processing units is less than n3.
2.3. Amendments to the DNS algorithm to it runs on a multi-core computer
The modification is to increase the grain size, as follows: to replace the scalar by sub matrices and that they follow the same procedure for the distribution and rotation of elements aijand bij. Consequently, the distribution and rotation of sub matrices will be a function of the q variable equal to logn. The value of the variable is determined by the number that divides the matrices to multiply. If the n dimension of the matrix is divided into k parts to generate submatrices 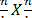 , then q is equal to logk. The number of submatrices generated is 23q = k3 and the number of processors is given by p = k3. The k variable can define the size of the submatrices and the number of processing units that are required.
, then q is equal to logk. The number of submatrices generated is 23q = k3 and the number of processors is given by p = k3. The k variable can define the size of the submatrices and the number of processing units that are required.
The necessary modifications to the algorithm in Fig. 1 below:
- Replace to aij by Aij
- Replace to bij by Bij
- Replace to cij by Cij
- Replace to aikbkj by
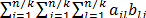
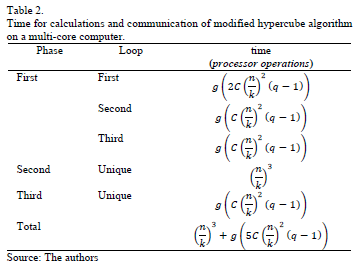
The computation and communication times of the modified algorithm are shown in Table 2.
The execution time of the parallel algorithm is determined by:
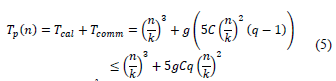
Whereas p = k3 and q = log k the expression (5) is reduced to:
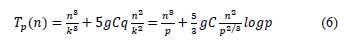
The C variable, in the expression (6), is the type of data that is sent and g is given by eq. (2). Table 3 shows the results of eq. (6) for a value of g = 1 and 2, C = 32 and a number of processing units 8, 64 and 512 (k = 2, 4 and 8). The results are presented in Table 3 based on the parallel speedup Sp = (T1/Tp).
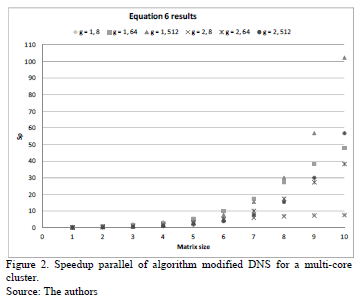
The results of the eq. (6) shows that when g = 1 runtimes are smallest. This indicates that the algorithm is sensitive to the characteristics of the communication link. Regarding the parallel speedup, it is best using eight processing units for multiplying matrices smaller than 1,000X1,000, from 64 to matrices of smaller sizes than 10,000X10,000 and 512 for multiplying matrices over 10,000X10,000. Fig. 2 plots the data of Table 3.
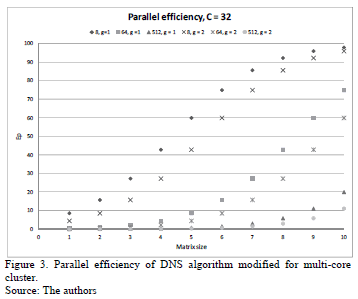
As seen in Fig. 2, the largest differences occur in large arrays, the multiplication matrix is faster when more processing units are used. When using as a reference the parallel efficiency Ep = (Sp/p)X100, the better efficiencies are obtained when less processing units are used, as shown in Fig. 3.
As is shown in Fig. 3, the best efficiency is attained when the minor number of parallel processing units are used, about 100% for the larger matrices. However, the parallel efficiency decreases when more processing units are used, at best by 20%. Although the trend is that the efficiency will increase as the size of the matrix increases. This indicates that for 512 parallel processing units will reach its asymptotic value for a given size of matrices.
The parallel efficiency low is related to the time spent on communications, it grows exponentially when the number of processing units is higher and, consequently, the data sent concurrently among processing units.
3. Computational experiments in the multi-core cluster
The computational experiment was conducted on a multi-core cluster with a finite number of processors and memory units. In consequence the size of the matrices of the computational experiment was limited.
In view of the fact that the cores can be programmed as independent units [1]. The algorithm was encoded in ANSI C and for sending data the MPI library was used. The MPI-processes are assigned to the cores. If only one of them is assigned to a core, then it will work with parallel computing. But, if more than one is assigned, then it will work with parallel and concurrent computing. All nodes in the multi-core cluster are used in the experimentation, each node has the same load in all tests, for which the same number of MPI-processes to each processing unit is assigned.
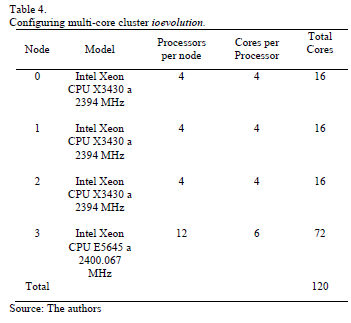
3.1. Description of multi-core cluster ioevolution
The multi-core cluster used has the following characteristics:
Features cluster shows that there are different g constants. The first is when two processes are assigned to the same core; the second is when the cores are in the same processor; the third corresponds to the communication between processors in the same node; and the fourth is for communication between nodes in the cluster. Of these, it is considered the external link between nodes, it is by means of fibre optics with a bandwidth of 1 Gbit per second, and with the speed of nuclei the g ≈ 2.4 is obtained.
3.2. Computational test on cluster ioevolution
The computational tests consist of multiplying matrices without gaps and in different sizes. Its elements are real, 32-bit floating number, and are generated randomly. During each execution of the program different matrices are used.
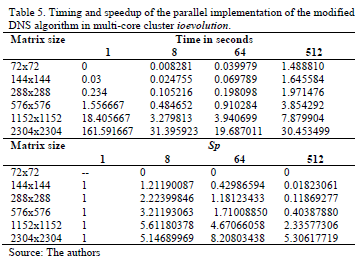
The sizes of the matrices are multiples of the number 72, because this is a number divisible by k values (2, 4 and 8). Table 5 shows the average execution time obtained in 30 runs and the speedup of the parallel implementation is presented.
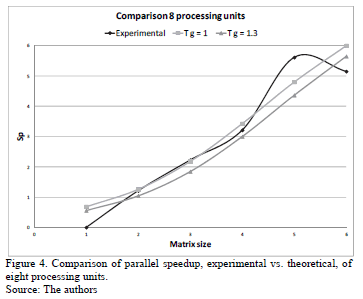
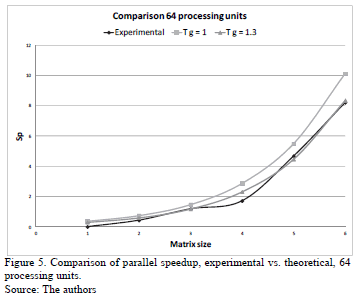
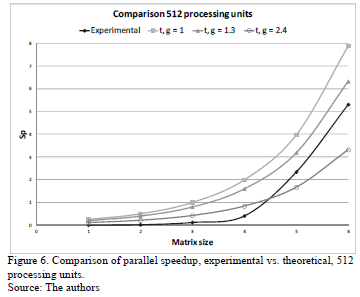
If the theoretical results of Table 3 and experimental results of Table 5 are compared, it is noted that the experimental values of speedup are closer to those calculated when g = 1. In order to determine the value of the g constant that most approximates the theoretical results to results experimentally, tests were performed with different values of g, of them the closest to the experimental is when g = 1.3. This is shown in Figs. 4, 5 and 6.
The three Figs. 4, 5 and 6 show experimental results, they are closer to the theoretical when g = 1.3, this value is lower than the g calculated by the external link (g = 2.4). The obtained value of g = 1.3 indicates that the use of the combination of the different communication channels of multi-core cluster improves the parallel implementation.
The most approximate experimental results to the theoretical are when 8 and 64 processing units are used. However, when 512 units of processing are used, the more approximate experimental results to the theoretical is when the matrix's size is higher than 1,000X1,000.
In Fig. 6 the values obtained with g = 2.4 are also plotted. It is observed that for matrices with a size smaller than 1,000X1,000 the experimental speedup is lower than those calculated using the external link. In contrast to the matrix size bigger than 1,000X1,000, the experimental speedup is better than the theoretical considering that same link. At this size the experimental results follow the trend of theoretical with a g = 1.3. This shows that there are factors that influence in the reduction of parallel speedup.
Establishing communication among the processing units is one of the factors influencing the parallel speedup. It follows the above with the following, for the same size of matrices and different number of processor units the changes made are: the size of the sub matrices and the number of simultaneous communications. The subarrays are bigger when eight processing units are used and a lesser number of concurrent communications are performed. In contrast, the subarrays are the smallest with 512 processing units and the largest number of simultaneous communications of the three tested cases are performed. The time difference, between the theoretical and the experimental, increases as the number of simultaneous communications increases, although smaller matrices are sent, Figs. 4 and 6. This reveals that in sending data from one processing unit to another there is a mechanism for communication, which requires processor runtime.
Another factor that influences the running time is the number of processes that are calculated in each core. When 8 and 64 processing units are used, a process is assigned to each core and all processes are communicated simultaneously. The communication channel will be a function of where the process will be allocated on either the same processor or node.
On the other hand, when 512 processes are assigned to the cores, each one of them runs more of a process. In this case the transmission of data among processes may be sequential. Sequentially because there is a means of communication among the cores, and it is used for various processes. Therefore, when a process sends its data using the communication channel, other processes assigned to the same core have to wait their turn. This sequentiality is reflected in the experimental results, they follow the trend given by g = 1.3 and not given by g = 2.4.
It shows that from size matrices 1,152X1,152 the speedup maximum is obtained when eight processor units are used, for bigger matrices the speedup parallel rapidly diminishes. With this value a parallel efficiency of 70.15% is obtained. For the other tested cases, 64 and 512, the execution time of parallel implementation continued to improve. This coincides with the theoretical results, the best parallel efficiencies are obtained with 8 processors and matrices smaller than 1,000X1,000
4. Conclusions
It is concluded that:
- With the proposed changes to DNS or hypercube algorithm can multiply matrices of different orders of magnitude in a multi-core cluster, using a number of processors lesser than n3.
- The influence of the external communication link between nodes in the cluster decreases, if a combination of communication channels available among the cores of a multi-core cluster is used.
- The amendment proposed in this paper, the number of processing units, is a function of the number of submatrices in that the matrix is divided.
- For larger problems it was shown that the influence of data access between processors affects parallel efficiency, rather than smaller problems. It is expected that new designs of processors [11, 12] will optimize access to data and consequently the best parallel efficiencies will be obtained.
References
[1] Rauber, T. and Rünger, G., Parallel programming for multicore and cluster systems. Springer Heidelberg Dordrecht London New York 2010. DOI 10.1007/978-3-642-04818-0. [ Links ]
[2] Muhammad, A. I., Talat, A. and Mirza, S.H., Parallel matrix multiplication on multi-core processors using SPC3 PM, Proceedings of International Conference on Latest Computational Technologies (ICLCT'2012), Bangkok, March 17-18, 2012 [ Links ]
[3] L'Excellent, J.-Y. and Sid-Lakhdar, W.M., A study of shared-memory parallelism in a multifrontal solver, Parallel Computing 40 (3-4), pp 34-46, 2014. DOI 10.1016/j.parco.2014.02.003 [ Links ]
[4] Quinn, M.J., Parallel computing (2nd ed.): Theory and practice. McGraw-Hill, Inc. New York, NY, USA 1994. [ Links ]
[5] Gupta, A. and Kumar, V., Scalability of parallel algorithms for matrix multiplication, Proceedings of International Conference on Parallel Processing, 3, pp. 115-123, 1991. DOI 10.1109/ICPP.1993.160. [ Links ]
[6] Alqadi, Z.A.A., Aqel, M. and El Emary, I.M.M., Performance analysis and evaluation of parallel matrix multiplication algorithms, World Applied Sciences Journal 5 (2), pp. 211-214, 2008. [ Links ]
[7] J. Choi, A new parallel matrix multiplication algorithm on distributed-memory concurrent computers, Technical Report CRPC-TR97758, Center for Research on Parallel Computation Rice University, [On line] 1997. Aviable at http://citeseerx.ist.psu.edu/viewdoc/download?DOI=10.1.1.15.4213&rep=rep1&type=pdf. [ Links ]
[8] Solomonik, E. and Demmel, J., Communication-optimal parallel 2.5D matrix multiplication and LU factorization algorithms, Proceeding Euro-Par'11 Proceedings of the 17th international conference on Parallel processing, Heidelberg, Volume Part II, Springer-Verlag Berlin, Heidelberg, 2011. [ Links ]
[9] Zavala-Díaz, J.C., Optimización con cómputo paralelo, teoría y aplicaciones, México, Ed. AmEditores, 2013. [ Links ]
[10] Sánchez, J. and Barral, H., Multiprocessor implementation models for adaptative algorithms, Journal IEEE Transactions on Signal Processing, USA, 44 (9), pp. 2319-2331, 1996. [ Links ]
[11] Un Nuevo Proyecto Financiado con Fondos Europeos trata de Lograr los Primeros Chips de Silicio para RAM Óptica de 100 Gbps.Dyna 87 (1), pp. 24, 2012. [ Links ]
[12] La Politécnica de Valencia Patenta Mejoras en Procesadores. Dyna, 83 (8), pp. 155 2008. [ Links ]
J.C. Zavala-Díaz, received the PhD. degree in Computational Science at Monterrey Institute of Technology and Higher Education (ITESM), Mexico, in 1999, since 1999 he is a research professor at the Autonomous University of the State of Morelos, Mexico. He worked in Research Electrical Institute (IIE), México 1986-1994. His research interests include: parallel computing; modeling and problem solving of discrete and linear optimization; and optimization using metaheuristics.
J. Pérez-Ortega, received the PhD. degree in Computational Science at Monterrey Institute of Technology and Higher Education (ITESM), Mexico in 1999, since 2001 he is a research of National Research and Technological Development (CENIDET). He worked in Research Electrical Institute (IIE), México 1985-2001. His research interests include: optimization using metaheuristics; NP-problems; combinatorial optimization; distributed systems; and software engineering.
E. Salazar-Reséndiz, received the MSc. degree in Computational Science at National Research and Technological Development (CENIDET) in 2014. he works in Research Electrical Institute (IIE).
C. Guadarrama-Rogel, received the MSc. degree in Computational Science at National Research and Technological Development (CENIDET) in 2014. he works in Research Electrical Institute (IIE).