Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.192 Medellín July/Aug. 2015
https://doi.org/10.15446/dyna.v82n192.48565
DOI: http://dx.doi.org/10.15446/dyna.v82n192.48565
Loads Characterization using the instantaneous power tensor theory
Caracterización de cargas usando la teoría instantánea del tensor de potencia
Odair Augusto Trujillo-Orozco a, Yeison Alberto Garcés-Gómez b, Armando Jaime Ustariz-Farfán c & Eduardo Antonio Cano-Plata d
Facultad de Ingeniería y Arquitectura, Universidad Nacional de Colombia - Sede Manizales, Manizales, Colombia a oatrujilloo@unal.edu.co, b yagarsesg@unal.edu.co, c ajustarizf@unal.edu.co, d eacanopl@unal.edu.co
Received: April, 29th of 2014. Received in revised form: February 13th of 2015. Accepted: June 30th of 2015
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
This paper presents a novel methodology to characterize loads using the instantaneous power tensor theory in three-phase three-wire or four-wire systems. Tensor theory is based on the dyadic product between voltage and current instantaneous vectors; this definition allows us to represent the phenomena of power quality produced by loads operation, through the deformation of a cube and the trajectory of one of its three-dimensional vectors. This new way of characterization could help researchers to construct better models of three-phase loads, or to achieve a better monitoring and machines diagnosis. Results are reached by implementing simulations in MATLAB® and endorsed with experimental measurements.
Keywords: Power quality, vector trajectory, paths, current-voltage characteristic, characterizing loads, harmonics, Lissajous, diagnosis.
Resumen
Este artículo presenta una novedosa metodología para caracterizar cargas usando la teoría instantánea del tensor de potencia en sistemas trifásicos de tres y cuatro hilos. La teoría tensorial está basada en el producto diádico entre los vectores instantáneos de corriente y tensión; esta definición permite representar los fenómenos de calidad de la potencia que produce la operación de la carga, a través de la deformación de un cubo y la trayectoria de uno de sus vectores tridimensionales. Esta nueva forma de caracterización podría ayudar a investigadores a construir mejores modelos de cargas trifásicas, o a realizar un mejor monitoreo y diagnóstico de máquinas. Los resultados son alcanzados implementando simulaciones en MATLAB® y son validados con mediciones experimentales.
Palabras clave: Calidad de la potencia, trayectoria del vector, caminos, característica corriente-tensión, caracterización de cargas, armónicos, Lissajous, diagnóstico.
1. Introduction
Characterization of loads has been a useful tool for several applications like dimensioning of facilities, loads modeling, power conservation and energy efficiency [1], diagnosis of machines [2-4], even real time monitoring [5], etc. Modeling is the most important part in the simulation analysis; also a good characterization of loads is a useful input for network operation and planning [6]. Some methods use data analysis [7], or Lissajous patterns that involve the voltage and current time functions [8,9]; but most of such methods only apply for single phase loads; those that are suitable for three-phase systems do not involve voltage and current at the same time [5]. This paper proposes a new way for characterizing loads, using three-dimensional trajectories (3-D paths) for three-phase power, instead of single-phase voltages or currents diagrams, using the instantaneous power tensor theory.
The paper is arranged as follows. First, a background of other methods is presented in such a way that comparisons can be made between them. Second, the proposed method is introduced as a methodology consisting of five steps. Third, simulation results using synthetic signals are presented. Fourth, experimental results with measurements of two real loads are exposed. Finally, conclusions and future work are raised.
2. Background of Other Methods
2.1. Current - Voltage Lissajous Patterns
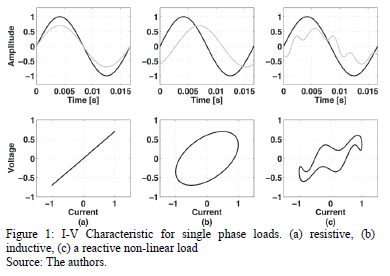
Traditionally, for single phase loads, the current-voltage characteristic or Lissajous patterns has been the most popular method for characterizing loads [1,8,9]; even on three-phase systems it is still used, graphing the I-V characteristic for each phase. The Lissajous patterns describe the "complex harmonic motion" of a system with parametric equations given by (1), where the ratio w1/w2 and the value of a determines the shape of the pattern.
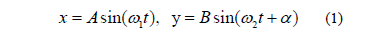
In Fig. 1 three typical single-phase I-V characteristic curves can be seen corresponding to (a) a resistive load, (b) an inductive load, and (c) a reactive non-linear load. It is worth noticing here that for the pure resistive load a straight line or linear I-V relationship is obtained.
This is not a suitable approach for characterizing three-phase loads, because it is not possible to see the whole three-phase effect caused by such load operation. Also, it is difficult to determine which harmonic is imposing the load to the network.
The main feature of this method is the advantage that can be seen in the relationship between voltage and current signals.
2.2. Alpha - Beta Patterns
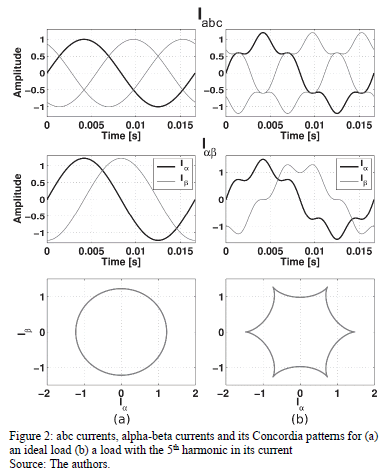
Due to the need of characterizing three-phase loads on a single diagram, for a better understanding and analysis, some authors have proposed the a-b frame [4,5]. This approach uses the Clarke's Transform for a-b components, and their paths or Concordia patterns to draw the three-phase voltage or current vector.
The Clarke's transform is given by (2). It takes the measurements of a three-phase system and leads it to a two axes coordinate frame of reference (a-b frame), allowing us to obtain the two-dimensional patterns useful for characterizing load or machine diagnosis.
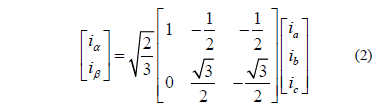
Fig. 2 shows the abc currents, the ab currents and the generated patterns of (a) a three-phase load without unbalances, neither harmonics nor reactive power; (b) a load that causes three-phase current with the 5th harmonic. The pattern from (a) could be taken as a reference or ideal condition.
2.3. Characteristic Trajectory of the Instantaneous Power Tensor
A more recent approach, based on the tensor theory has been published in [10]. It uses the dyadic product of the voltage and current instantaneous vectors, to get the Instantaneous Power Tensor. It also describes all the phenomena of power quality just analyzing the different characteristic values of the obtained matrix. The following equation defines the power tensor.
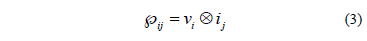
Then, for a three-phase system, the power tensor can be written as:
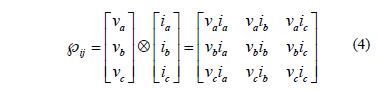
In order to be able to draw the patterns used in loads characterization, it is necessary to get a spatial vector derived from the power tensor. For that reason it is desirable to reduce the order of the tensor. This spatial vector allows us to describe the characteristic trajectory of the power tensor in the R3 space.
Reduction of the power tensor order is described in [10]. Here, it is shown that it is possible to find a vector xj (a first order tensor), which matches with the following equation:
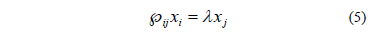
Where, l and xjare the eigenvalues and eigenvectors of the power tensor, respectively.
The matrix representation of the instantaneous power tensor, allows us to calculate its eigenvalues and eigenvectors through the following equation system:
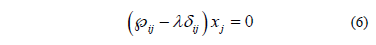
Where, 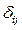 is the "Kronecker's delta" tensor. The roots of the characteristic equation given by (7) are the eigenvalues stated in (8).
is the "Kronecker's delta" tensor. The roots of the characteristic equation given by (7) are the eigenvalues stated in (8).
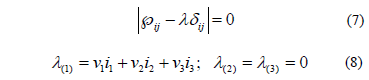
There is a unique eigenvector xj for each l in (6). As an example, a possible combination of eigenvectors associated to each eigenvalue, may be:
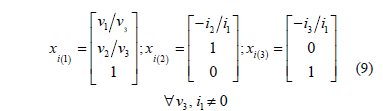
With these results it is possible to obtain the trajectories that describe the internal products between the power tensor and its eigenvectors. Considering that l2= l3=0, the only one possible trajectory is:
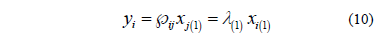
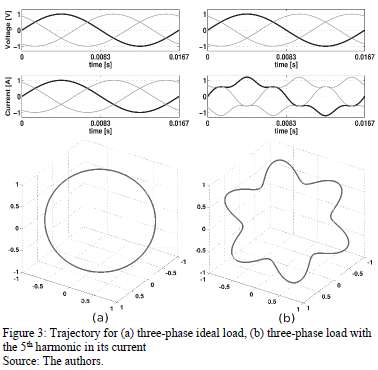
Fig. 3 (a), shows the trajectory generated by the vector stated in (10), corresponding to the operation of an ideal load, i.e. the matrix 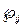 is formed by instantaneous vectors of voltage and current with positive sequence, fundamental component and perfectly in phase. Fig. 3 (b) shows another trajectory for a three-phase load with the 5th harmonic in its current. Here the number of bumps is equal to n+1, where n is the harmonic order.
is formed by instantaneous vectors of voltage and current with positive sequence, fundamental component and perfectly in phase. Fig. 3 (b) shows another trajectory for a three-phase load with the 5th harmonic in its current. Here the number of bumps is equal to n+1, where n is the harmonic order.
Notice that in this approach, the drown trajectory describes the behavior of the instantaneous power, i.e. takes into account the voltage and current signals at the same time.
Although this method takes into account the relationship between the three-phase voltage and current vectors, it cannot draw trajectories generated by reactive power, neither 3rd harmonic, nor its multiples. Thus, it is necessary to use another concept of the instantaneous power tensor, which enables us to draw the corresponding trajectories caused by the mentioned phenomena. This alternative methodology is described in the next section.
3. Proposed methodology for loads characterization
The following methodology uses the instantaneous power tensor theory proposed in [10] for characterizing loads, but using the definition of the power distortion tensor, instead of the characteristic trajectory. The process begins when the voltage and current vectors are stored in a computer or in a DSP based system. Thus, if a DSP based system is used, it is possible to do it in real time. On the contrary, the use of a computer based software like Matlab® or another one that allows making matrix operations and plotting the results of the measurements, is needed.
Assuming instantaneous values, the methodology is described as follows:
- Step 1: Obtain the power tensor of the real system
This is done by applying the definition in (4) for the voltage and current vectors. Then, the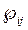 tensor is obtained.
tensor is obtained.
- Step 2: Obtain the ideal power tensor
The ideal power tensor is formed by instantaneous voltage and current vectors at fundamental frequency, positive sequence and perfectly in phase.
- Step 3: Obtain the distortion tensor and the distortion cube
The distortion tensor represents exclusively all the phenomena of power quality in the power trade of the system. The distortion cube is the R3 spatial representation of the distortion tensor.
- Step 4: Visualization process
From the distortion cube, choose the three-dimensional vector path generator and trace the path with each spatial coordinate.
- Step 5: Identify the power issues
Using the different views of the plotted path for one cycle of the signals on steady stage; look at the characteristics of the closed path (i.e. bumps, loops, plane unsubscription). And then, conclude about the load operation.
In the next subsections the necessary foundations to implement this methodology, are described.
3.1. The ideal power tensor
It represents the ideal power transference corresponding to the conditions of a circuit with a sinusoidal source at fundamental frequency, without either unbalances or reactive power, feeding a resistive load. The equation is given by:
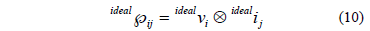
The voltage and current vectors could be gathered by extracting the fundamental components at positive sequence from the voltage and current signals, using the preferred method. Here, the method depicted in [11] was used.
3.2. The instantaneous power distortion tensor
The instantaneous power distortion tensor ∂ij describes exclusively the deviation of the power quality in respect to the ideal conditions of the system, and it is depicted by this equation:
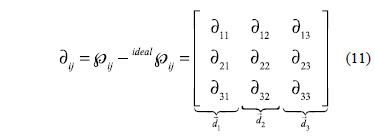
Having a load that draws sinusoidal balanced voltages and currents signals and perfectly in phase, all the elements of ∂ij will equal zero.
3.3. Spatial representation of ∂ij
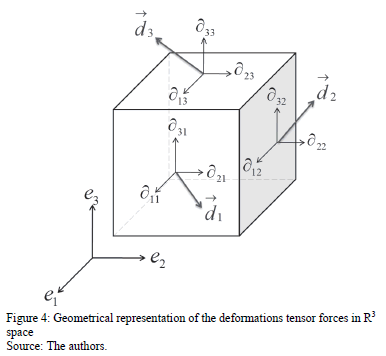
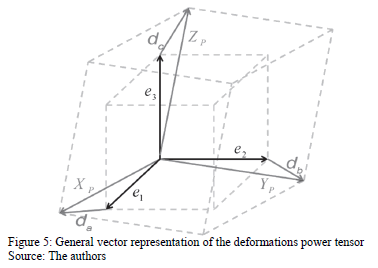
In this approach, it is possible to construct a unitary cube having three director vectors given by the reference axes, 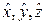 named e1,e2,e3, respectively. The column vectors
named e1,e2,e3, respectively. The column vectors 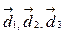 exert deforming forces to each external cube face, depending on their components, i.e., depending on the deviations of the power trade in the system. This cube is named as the deformation cube and its formulation is sketched in Fig. 4.
exert deforming forces to each external cube face, depending on their components, i.e., depending on the deviations of the power trade in the system. This cube is named as the deformation cube and its formulation is sketched in Fig. 4.
The condition for these deformations to match with reality is that they have to be infinitesimal quantities. Thus, in order to be able to see such deformations it is necessary to scale it by a real positive number greater than one.
3.4. Visualization process
The final goal is to visualize the paths generated by the distortion cube, identify their shape, and with this, characterize the load. Accordingly, it is necessary to write some software applying vector algebra.
Due to the fact that the deformations are infinitesimal quantities, it is possible to shift the column vectors of the tensor ∂ij from their original position to the corners of the unitary cube, as depicted in Fig. 5.
Then, having the vectors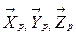 , if the values of the distortion tensor are different from zero, an instantaneous deforming cube can be plotted, with origin in (-1,-1,0); otherwise, the distortion cube will be the same unitary cube used as reference.
, if the values of the distortion tensor are different from zero, an instantaneous deforming cube can be plotted, with origin in (-1,-1,0); otherwise, the distortion cube will be the same unitary cube used as reference.
3.5. Vector path generator
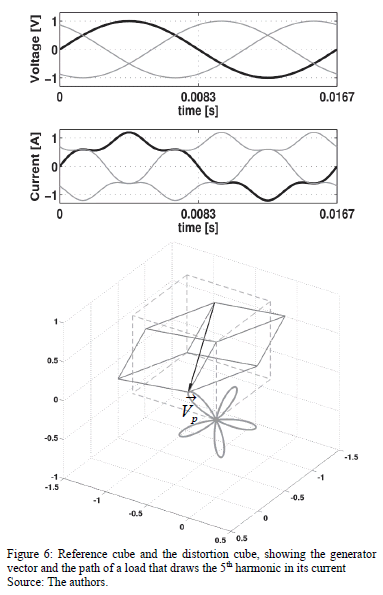
In order to obtain the three-dimensional paths, it is necessary to choose a vector of the distortion cube, which allows drawing the paths corresponding to the deviations, imposed by the load operation. Fig. 6 shows the chosen vector and, for simplicity, the resultant path corresponding to a load drawing three-phase current with the 5th harmonic.
In Fig. 6, the unitary cube using dashed lines and the deformed one using solid lines can be seen. This last one is where the generator vector comes. This vector does not follow a trajectory with an ideal load operation, because it is static due to the zero values in ∂ij.
The trajectory drawn by the vector 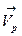 can be gathered with either single or a combination of different loads (linear and non-linear).
can be gathered with either single or a combination of different loads (linear and non-linear).
4. Simulation Results
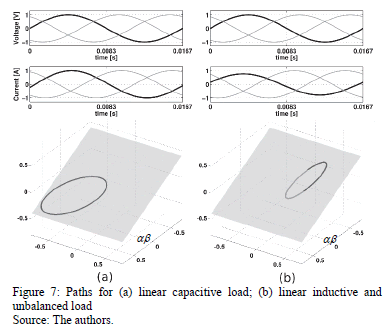
In Fig. 7 (a), a linear balanced, three-phase capacitive load has been characterized. Due to the fact that the load is capacitive, the generated path is an ellipse oriented to the left. In Fig. 7 (b), a linear unbalanced, three-phase inductive load, has been characterized. Given that the load is inductive, the ellipse is oriented to the right. Notice that this method is able to show zero sequence components, meaning unbalance, or the 3th harmonic (and its multiples) in other cases. For this reason, and for convenience, but not being necessary, a semitransparent ab plane has been used, since the zero sequence components cause the path to unsubscribe from the ab plane.
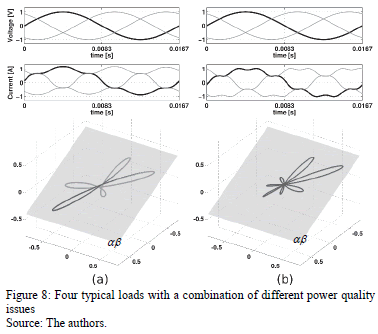
Fig. 8 (a) shows the paths corresponding to a three-phase load that causes the 5th and 7th harmonics in its current; with the 5th harmonic predomination, unbalance (zero-sequence). Fig. 8 (b) shows a three-phase load with the 5th and 7th harmonics in its current, with the 7th harmonic predomination; also lagging displacement factor.
Here the zero-sequence components cause path unsubscribing. Also, it can be seen that the predominant harmonic order establishes the number of bumps of the path, and the nature of the reactive power, establishes the orientation of the path.
Moreover, it is possible to characterize loads with a complex combination of power issues, which is done by looking at the whole 3-D view of the generated trajectory. Additionally, it can be seen on the 2-D views and be comparing the paths with the known ones for making additional inferences.
4. Experimental Results
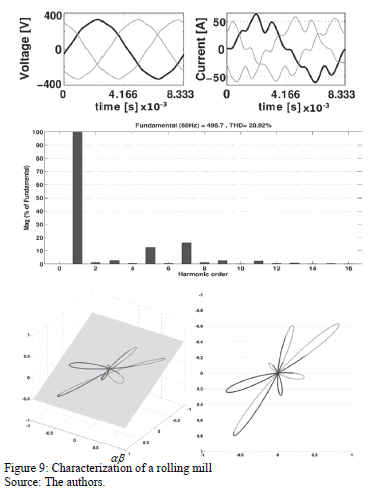
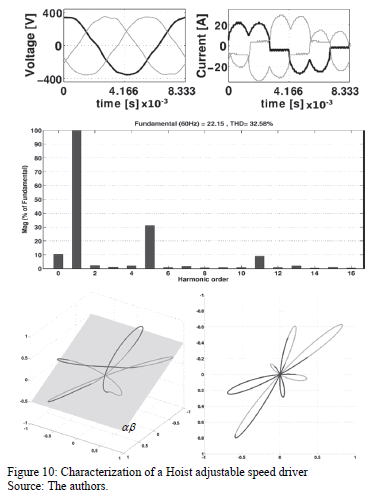
Two real industrial loads with several power issues have been characterized. Measurements have been done with the AEMC Power Pad-3945, and processed with MATLAB®, using the proposed methodology.
Fig. 9 shows the characterization of a rolling mill; measurements have been taken from the terminal block. This is a three-phase load with several harmonics, the 7th harmonic predomination. (The frequency spectrum of the A phase current is shown, which allows comparisons). Anew, the predominant harmonic order establishes the number of bumps; in the bottom right corner of Fig. 9, a zoom to the X-Y view was performed and seven bumps can be counted. The soft trace parts are due to the fact that the path is crossing the plane, which means a presence of a 3rd harmonic or unbalance.
Fig. 10 shows the characterization of a three-phase adjustable speed drive, connected to a hoist. This load draws the 5th harmonic predomination and evidence of zero-sequence due to the path unsubscribing. In the bottom right corner of Fig. 10, a zoom to the X-Y view was performed and it can be seen that the 11th harmonic is just taken away from the symmetry to the whole trajectory, but five bumps, corresponding to the predominant harmonic order can be counted.
It is important to clarify that plotting the voltage and current signals, or the frequency spectrum is not needed. Only the path is needed to characterize the load.
Conclusions
The proposed methodology is capable of depicting many phenomena due to the operation of three-phase loads; odd harmonics are depicted more precisely with nbumps as with harmonic order. Also it is the only one that is able to depict zero sequence evidence, and can give information about harmonic content when a load imposes several harmonics, establishing the dominant harmonic order with no need of the Fourier Transform.
With this methodology it is possible to characterize reactive non-linear and unbalanced loads. Loads with a more complex combination of power issues can be characterized, even for a system with different loads having different characteristics on each phase or having voltage distortion.
Although the proposed methodology needs the extraction of the fundamental components of voltage and current signals for constructing the ideal tensor, it does not mean that it loses its instantaneous character, because it can be supposed that the fundamental components do not change frequency or phase angle during the load operation, i.e. the ideal tensor remains approximately constant.
In this paper, only current distortion effects were taken into account; due to the fact that it is more common to have very low voltage distortion at the load side. But with the increase of low impedance non-linear loads, the voltage distortion may increase considerably. Therefore, taking into account voltage distortion, is necessary future work.
Another future work is to use the capabilities of the proposed methodology to make some experiments and benchmarking, in the areas of machines diagnosis and electric systems monitoring.
Bibliography
[1] Yi, D., Liang, D., Bin, L., Harley, R.G. and Habetler, T.G., A review of identification and monitoring methods for electric loads in commercial and residential buildings. Energy Conversion Congress and Exposition (ECCE), 2010 IEEE, pp.4527-4533, 12-16 Sept. 2010. [ Links ]
[2] Milanez, D.L. and Emmanuel, D.L., The instantaneous-space phasor a powerful diagnosis tool. IEEE Trans. on Instr. and Meas. 52 (1), pp. 143-148, 2003. DOI: 10.1109/TIM.2003.809069 [ Links ]
[3] Zidani, F.M., Benbouzid, E.H., Diallo, D. and Nait-Said, M.S., Induction motor stator faults diagnosis by a current Concordia pattern based fuzzy decision system. IEEE Trans. Energy Convers. 18 (4), pp. 469-475, 2003. DOI: 10.1109/TEC.2003.815832 [ Links ]
[4] Verucchi C.J. y Acosta G.G., Técnicas de detección y diagnóstico de fallos en máquinas eléctricas de inducción. IEEE Latin America Transactions, 5 (1), March 2007. [ Links ]
[5] Gilreath, P., Peterson, M. and Singh, B.N., A Novel technique for identification and condition monitoring of nonlinear loads in power systems, power electronics, drives and energy systems. PEDES '06. International Conference, pp.1-7, 12-15 Dec. 2006. [ Links ]
[6] Chao-Shun, Ch., Tsung-Hsien, W., Chung-Chieh, L. and Yenn-Minn, T., The application of load models of electric appliances to distribution system analysis. Power Systems, IEEE Transactions. 10 (3), pp.1376-1382, Aug 1995. [ Links ]
[7] Figueiredo, V., Rodrigues, F., Vale, Z. and Gouveia, J.B., An electric energy consumer characterization framework based on data mining techniques. Power Systems, IEEE Transactions. 20 (2), pp.596-602, May, 2005 [ Links ]
[8] Cano-Plata, E.A., Aplicaciones de la transformada ondita y la teoría de la potencia instantánea a la detección y clasificación de problemas de calidad de la potencia, PhD Tesis, Universidad de Buenos Aires, Buenos Aires, Argentina, 2006. [ Links ]
[9] Jagiela, K., Rak, J., Gala, M. and Kepinski, M., Identification of electric power parameters of AC arc furnace low voltage system. IEEE Conference Proceeding, 26-29 Sept. 2010, pp. 1-7, ISBN 978-1-4244-7244-4. DOI: 10.1109/ichqp.2010.5625439 [ Links ]
[10] Ustariz-Farfán, A.J., Formulación de una teoría tensorial de la potencia eléctrica: aplicaciones al estudio de la calidad de la energía, Ph.D. Tesis, Universidad Nacional de Colombia, Sede Manizales, Colombia, 2011. [ Links ]
[11] Ustariz-Farfán, A.J., Cano-Plata, E.A., and Tacca, H.E., New deviation factor of power quality using tensor analysis and wavelet packet transform, International Conference on Power Systems Transients (IPST2011). Delft, Netherlands. June 14-17, 2011. [ Links ]
O.A. Trujillo-Orozco, was born in Fresno Tolima Colombia, in November 1979. He received the BSc. Engineering degree in 2013 from the Universidad Nacional de Colombia, Manizales campus, in Electrical Engineering. He's currently working on his MSc degree in Engineering, Electrical Engineering at the Universidad Nacional de Colombia, Manizales campus.
Y.A. Garces-Gomez, was born in Manzanares-Caldas, Colombia, in 1983. He received the BSc. In Engineering Electronic in 2009 from the Universidad Nacional de Colombia, Manizales campus. Between 2009 and 2011 he held a "Colciencias" scholarship for postgraduate studies in engineering - industrial automation at the Universidad Nacional de Colombia. He is currently working for a PhD degree in engineering in the Universidad Nacional de Colombia.
A.J. Ustariz-Farfán, was born in Urumita, Colombia in 1973. He received a BSc degree in Electrical Engineer in 1997, and a MSc in Electric Power in 2000 from the Universidad Industrial de Santander, Colombia. He received the PhD. degree in Electrical Engineering at the Universidad Nacional de Colombia, in 2011. He is a research and associated professor with the Electrical, Electronic and Computer Engineering Department, Universidad Nacional de Colombia, Manizales campus.
E.A. Cano-Plata, was born in Neiva, Colombia, in 1967. He received the BSc. and Sp. Engineering degree in 1990 and 1994 from Universidad Nacional de Colombia, Manizales, both in Electrical Engineering. Between 1996 and 1998 he had a DAAD scholarship for postgraduate studies in Electrical Engineering at the Universidad Nacional de San Juan, Argentina. He received the Dr. degree in Engineering in 2006 from the Universidad de Buenos Aires, Argentina. Since 1994, he is a titular professor at the Universidad Nacional de Colombia in Manizales, Colombia.