Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.192 Medellín July/Aug. 2015
https://doi.org/10.15446/dyna.v82n192.48574
DOI: http://dx.doi.org/10.15446/dyna.v82n192.48574
Representation of electric power systems by complex networks with applications to risk vulnerability assessment
Representación de los sistemas eléctricos de potencia mediante redes complejas con aplicación a la evaluación de vulnerabilidad de riesgos
Gabriel Jaime Correa-Henao a & José María Yusta-Loyo b
a Facultad de Ingenierías, Fundación Universitaria Luis Amigó, Medellín, Colombia. gabriel.correahe@amigo.edu.co
b Departamento de Ingeniería Eléctrica, Universidad de Zaragoza, Zaragoza, España. jmyusta@unizar.es
Received: March 27th, 2014. Received in revised form: May 14th, 2015. Accepted: July 02nd, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
The occurrence of impact events (e.g. blackouts with vast geographic coverage) into electrical critic infrastructure systems usually require the analysis of cascade failure root causes through the conduction of structural vulnerability studies, with well-defined methodologies that may guide decision-making for the implementation of prevention actions and for operation recovery of the power system (e.g. N-1 and N-t contingency studies). This technical contribution provides some alternative techniques based upon complex networks and graph theory, which in the last few years, have been proposed as useful methodologies for analysis of physical behavior of electric power systems. Vulnerability assessment is achieved by testing their performance into random risks and deliberate attack threat scenarios. Results shown in this proposal lead to conclusions on the use of complex networks for contingency analysis by means of studies of those events that result in cascade failures and consumer disconnections.
Keywords: critical infrastructure protection; vulnerability analysis; cascade failures; homeland security; risk analysis
Resumen
La ocurrencia de eventos de alto impacto (e.g., apagón con alcance geográfico) en sistemas eléctricos usualmente se diagnostica a través de técnicas de análisis estructural de vulnerabilidad, constituidas por metodologías definidas que permiten guiar la toma de decisiones en acciones de prevención y recuperación de la normalidad en la red (e.g., contingencias N-1 y N-t). En esta contribución técnica se presenta una metodología alternativa frente a las herramientas clásicas de análisis de contingencias (teoría de grafos), que últimamente se ha validado como método útil en el análisis físico de sistemas de potencia. Se realiza una valoración de la vulnerabilidad en redes de prueba IEEE, mediante cuantificación de su comportamiento ante escenarios de riesgos de tipo aleatorio o de ataques deliberados. Estos resultados permiten concluir la viabilidad de redes complejas para análisis de contingencias, mediante el estudio de eventos desencadenantes de fallos en cascada y desconexión de consumidores.
Palabras clave: protección de infraestructura crítica; análisis de vulnerabilidad; fallos en cascada; seguridad nacional; análisis de riegos.
1. Introduction
Critical infrastructure is described by many governments as the whole set of assets that are essential for the functioning of a society and its economy. In recent years, the European Commission (EC), the United States (US) Department of Homeland Security, and others have been concerned about the security of their country infrastructure. The Council of the European Union adopted Directive 114/08/EC in 2008 [1], giving rise to the European Program for Critical Infrastructure Protection (EPCIP). In 2009, the US National Infrastructure Protection Plan (NIPP) was launched and later updated in 2013 as an effort to guide decision-making under threat scenarios [2]. Such protection plans can be framed as a risk management plan involving six steps: establishing safety goals, identification of resources, risk assessment, prioritization of actions, implementation of protection programs, and measuring of their effectiveness [3,4].
Power systems have always been regarded as one of the most important critical infrastructures in relation to social, economic and military issues in a country. In order to analyze the electric system's vulnerability to threats, some new concepts have arisen in an attempt to describe the grid performance [5]. The resilience concept suggests that a system can adapt to reach a new stable position, after suffering a disturbance or contingency in one or more of its elements. Additionally, robustness implies that the system will operate its undamaged infrastructure, despite being exposed to perturbations [5]. Therefore, a robust and resilient network is equivalent to a low vulnerability network.
In order to evaluate the stated vulnerability, it is important to point out the importance of threat quantification required by NIPP's steps of identification and assessment. Therefore, it is possible to determine high-impact incidents that may lead to cascade failure events into critical infrastructures, in this case, electric power systems. Such studies, usually referred to as Structural Vulnerability Analysis [6], provide important data about the performance of the power grid when exposed to perturbations and disruptions, requiring suitable methodologies to precise detection of anomalies and perturbations in power systems [6]. Among these techniques, N-1 and N-t contingency studies [7-9] are the most used criteria in the power industry.
On the other hand, the first definition of scale-free networks compared the infrastructure systems to complex networks [10-13]. Ever since then, graph theory has provided a new perspective on the study of power systems. Furthermore, concepts of resilience and robustness in scale-free networks have been applied to both power grids and computer networks [12]. They have proved to be a good approach to understanding the grid's dynamic behaviors that generally lead to cascade effect failures. As a result, when applied to power systems, structural vulnerability analysis focuses on the performance of complex networks when they're exposed to disruptions, either randomly (tolerance against errors or faults) or deliberately (tolerance against attacks) [12,14,15].
The way the nodes are removed from a scale-free network depends on graph statistical measures. Some studies suggest node removal according to their degree of connection [7,14,16-18]. Other studies suggest node removal based on their betweenness [19-21]. Besides, considering random node removals or degree-based node attacks, some authors also propose recalculation of degree distribution at each iteration, after every node disruption [7,19].
In this technical contribution, authors show the usefulness of scale-free graph measures as an accurate tool to assess the vulnerability of power transmission grids. This is undertaken by comparing operational indexes in traditional AC electric power flow measurements versus scale-free graph indexes, by assessing vulnerability to both deliberate attack and random error network tolerance. This shows the validation of a faster method than AC power flow, as it is graph theory modeling, and provides acceptable results for understanding the complex nature of electric critical infrastructure and their response against threats that may disrupt the normal operation of the power grid.
The paper has the following arrangement: Section 2 introduces scale-free graphs and their equivalence for power electric systems, and Section 3 describes appropriate indexes to quantify vulnerability in power grid disruptions. Section 4 proposes an algorithm for risk scenarios of random error and deliberate attack vulnerability assessment on the basis of illustrative examples based upon IEEE test power networks, using N-1 contingency analysis and N-t dynamic simulation model for cascade failure events. Section 5 shows the results of the proposed model on selected IEEE testing networks (14, 30, 300 bus). Discussion and conclusions on practical applicability of scale-free graph modeling under risk scenarios is also provided at the end of the paper.
The purpose of the technical contribution focuses on the comparison of the relative vulnerability between networks. This is very useful to guide decision-making concerning the effectiveness and impact of expansion plans, e.g., providing greater robustness to the electric network (improvement of the mesh and higher degree of connectivity of buses) and their responses in both random risk scenarios and intentional attack threats.
2. Topology representation in power networks
The fields of application of graph theory, also known as complex network theory [22], are characterized by the fact that they make it easy to perform an abstract representation of a system as a network topology with statistical measures. This leads to evaluate the effects of the changes in topology on the robustness of the system when subjected to different types of attacks and failures.
Electric power networks resemble scale-free graphs [10], which enable the representation of most of the assets that conform the power grid. Such representation may be simplified as a complex network where substations are specified as nodes and electric lines are sketched as links [7,8,12,15,18-20]. In those cases, it is easy to calculate cluster measures (triangles) in order to determine the graph vulnerability [12].
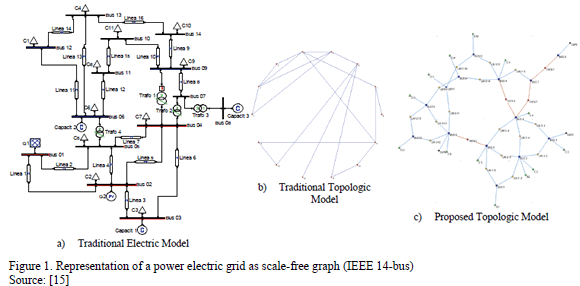
The herein proposed representation looks for a topology where both transformers and electric towers are also taken into account as assets susceptible to be removed due to attacks or errors in the power grid. Fig. 1 shows the proposed topological representation of a 14-bus electric network, compared to the traditional representation (which only considers buses and links). Thus, the resulting IEEE 14-bus network is constituted by a graph of 50 nodes and 56 links. This way, it is possible to provide a more realistic sketch of the power system as a scale-free graph, where the set of towers that hold power lines as well as the set of transformers are considered as nodes in the graph [26].
Such representation is very useful when assessing random error related risks, since randomly disruption of any node, may relate to one of low connectivity degree. In statistical terms, those nodes with less connectivity are the most likely to disrupt [12,18,23,24].
3. Definitions on indexes for topological representation of the power network
Representation of power systems as scale-free networks has been well documented [7,23,24]. As previously exposed in Section 2, the topological sketch of an electric power grid would consist of a set of assets such as transmission lines and cables representing graph edges, whereas substations, transformers, generators, loads and electric towers represent graph nodes [12,15].
Mathematically, a graph corresponds to an adjacency matrix composed by a pair of sets G = (N, E), where N(G) is the set of nodes and E(G) is the set of edges. An edge corresponds to a connection between pairs of nodes with the form (i, j) such that i, j Î E. The link (i, j) is denoted as ij. An edge connecting two nodes denotes Gij= 1 (corresponding to the location of a pair of nodes) and Gij = 0 otherwise [5,7,20].
Studying the properties of a graph leads to the analysis of the adjacency matrix properties [25]. The nodal degree (ki) is the set of converging edges (Ei) to a particular node (Ni):

where:

In order to illustrate this definition, please refer to generators and loads that are connected through a single link to the power grid, meaning that their nodal degree is k = 1.
The definitions in (1) and (2) constitute the basis to determine statistical measures of the scale-free graph (i.e. their robustness and their connectivity). It is important to point out that scale-free graph representation implies that few nodes are highly connected. This means that such nodes have a larger number of edges compared to other nodes, even though the degree of connection throughout the scale-free graph is quite low. Such graphs are closer to reality, since the network will grow preferentially based on the nodes of greater connectivity [10,16], as happens in real infrastructures. A more detailed explanation on this characterization may be consulted in [3,7,12,15].
3.1. Graph's geodesic distance ('d)
Based on the analysis of the scale-free graph adjacency matrix G = (N, E), it is possible to determine inferences on the evolution of the network when it is exposed to successive node removal (disintegration of the network). These statistic measures lead to the construction of indexes that reveal an equivalence between power load shedding and graph disintegration [7,12,15].
Graph geodesic distance dij describes how compact a network is. The shortest geodesic distance between two nodes dij is calculated by counting the minimum number of nodes in the path between a pair of nodes i and j [25]. The graph average distance'd is determined as a function of the network's geodesic distance dij and the total number of nodes N [19], as shown in Eq. (3):

Calculation of the geodesic distances in (3) may be performed through Dijkstra, Bellman-Ford, Floyd-Warshall and Johnson algorithms [25] that are well documented in literature.
The following definitions relate to the analysis of the adjacency matrix G = (N, E) of a scale-free graph. The graph evolves as it is exposed to disintegration due to node disruptions (cascade failure evolution).
3.2. Network connectivity (K)
The connectivity of network K is determined in any graph representing the power grid by counting the amount of nodes that are connected to a scale-free graph [22], as shown in Eq. (4):

NLC: amount of nodes connected on the remaining scale-free graph, after a node disruption under contingency events.
N: Base-case: total amount of nodes in the original scale-free graph
3.3. Geodesic strength ('gs)
From Eq. (3) the Average Efficiency ('e) is formulated as [21]:

Index eij is usually calculated as the inverse of geodesic distances, and it allows the quantification about how efficiently flows can be exchanged within a network. If there were no connection between two nodes: dij » ¥ , eij = 0 [15, 17,24].
From Eq. (5), we define the geodesic strength 'gs as a parameter that measures the functionality of a network when exposed to node disruptions. Index in Eq. (6) standardizes geodesic efficiency as formulated by [17,26,27] and enables vulnerability assessments into a network due to effects of iterative cascade failure events [10].

dij LC: shortest path between a pair of nodes of the scale-free graph, after a node disruption under contingency events.
dij BC: Base-case: shortest path between a pair of nodes in the original scale-free graph
Index'gs in (6) varies between one and zero. The lower strength index value'gs, the greater impact on the graph. It describes flow bottlenecks into the network as some geodesic paths are disrupted. This is equivalent to a power grid fragmentation due to isolation of power loads into the system.
Consequently, it is possible to substitute onerous computational techniques (e.g. power flow routines) with more efficient procedures (e.g. graph theory statistics) in order to perform structural vulnerability analysis, depending on the incidents that trigger cascade failure events [10].
The convenience of merging power flow models and scale-free graph statistics has been previously demonstrated in [12,15,16] through the calculation of the responses in different IEEE networks. This is performed by contrasting the results of traditional electrical engineering parameters, referred to as a portion of disconnected loads or power load shedding [28-31], with geodesic strength 'gs, and thus allowing comparisons between different power systems to determine the most vulnerable. This validation implies an important advantage when combining traditional methodologies of electric power flows and graph theory statistics in order to study perturbations, disruptions and black-out events [12].
3.4. Power grid load (PGL)
Even though structural vulnerability analysis can be achieved by calculating evolution of indexes in Eq. (4) and (6), it is not clear that this evaluation method may be reliable, since electric parameters of the power grid are not involved in these calculations. Therefore, traditional power flow parameters need to be considered in order to compare the effectiveness of graph theory indexes.
Power flow indexes documented in literature are mainly used to determine the impact of N-1 contingencies in the power grid: Maximum Load Conditions [9], Comprehensive Information System, Power System Loss [31], and Index of Severity [8]. A good measure of functionality for the power grid network would be the consumer loads that remain connected to the electrical service after a disruption event. An intuitive power flow index to understand evolution of cascade failure events corresponds to Power Grid Load (PGL), which is also useful to quantify the load shedding condition in a power grid, as proposed in [9,28,31].
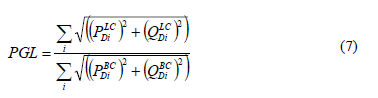
PDiLC: active power load that remains electrically connected, after a node disruption under contingency events.
QDiLC: reactive power load that remains electrically connected, after a node disruption under contingency events.
PDiBC: Base-case: Total active power load in testing network.
QDiBC: Base-case: Total reactive power load in testing network.
PGL in Eq. (7) is calculated as a percentage of the load that keeps connected to the remaining electric grid at each node removal iteration, in order to avoid cascade outage. Its range varies between zero and one. The higher PGL index value, the lower impact on non-supplied energy.
PGL in Eq. (7) is computed by means of Standard Power Flow (SPF) routine [30] (corresponding to nonlinear equations that are solved iteratively using Newton's Method [8,9]).
3.5. Severity index (S.I)
Even though Severity Index (S.I.) is well documented for N-1 contingency analysis [8], the index might be useful for measuring in cascade failure events, as quoted in technical studies [9, 28]. The Severity Index is referred to as a common method of contingency analysis based on power flow methodologies in order to establish the load level of both lines and transformers after a certain incident event. Severity Index is defined as follows [8]:

PDiLC: active power load that remains electrically connected, after a node disruption under contingency events.
N: Base-case: total number of nodes representing substations, lines, and transformers in the scale-free graph.
PDiBC: Base-case: Total active power load in testing network
4. Algorithm design for vulnerability assessment on the power grid under risk scenarios
This section explains the procedure for computational analysis, considering a first approach through N-1 contingency analysis and extending it to random errors and deliberate attacks tolerance with an N-t dynamic cascade failure simulation model. Even though the disruption strategies are explained in detail in Section 5, it is worth mentioning that Deliberate Attacks node removal means that the most connected nodes are removed at each contingency event.
4.1. N-1 contingency analysis model and n-t dynamic failure model simulation
Cascade failure events resembles a graph disintegration, taking first into account the estimation of the parameters from a power grid that operates under steady state conditions (base case) [12]. Such cascade failure events are determined by the interdiction of network's nodes according to certain removal strategies. A node disruption implies the elimination of all edges connected to it and therefore, its corresponding connected links also disappear. A first approach to determine the most critical assets on the power grid consists in N-1 contingency analysis. The results provide information about the nodes that require the most important attention in terms of their protection, due to the effects exerted on them throughout the network when they are interdicted from the system [9].
The described technique can be extended to a dynamic simulation model, which is equivalent to successive contingency N-1 and N-t iterations over a constantly changing topology structure. Since power flows can only be performed based upon the existence of the reference (slack) bus generator, removal of nodes is handled around the reference slack generator bus (this means that the slack generator must always be present in the network and cannot be removed). The algorithm has been designed to measure parameters only with components that remain connected to the network as it disintegrates. Generator outages are considered in random failure routines, since generators are treated as nodes in the scale-free graph that may be subject to disruptions.
The proposed N-t cascade failure dynamic model takes into account two different scenarios in which multiple samplings are performed for random error phenomena, unlike deliberate attacks that run only one sample [12]. Since error distribution is highly asymmetric in N-t analysis, we propose taking the suggestion of the Central Limit Theorem, implying the normal distribution of data for a sufficiently large number of independent random values. Such approximation is good enough when more than 30 samples are collected [25].
The described algorithm has been implemented in Matlab®. Its programming takes into account power flow algorithms provided by PSAT (Power System Analysis Toolbox) [30]. Furthermore, the script incorporates features of MatlabBGL graph theory toolbox [31]. Geodesic distances dij in Eq. (3) are calculated according to Bellman-Ford shortest-paths algorithm [25].
4.2. Algorithm implementation and processing time
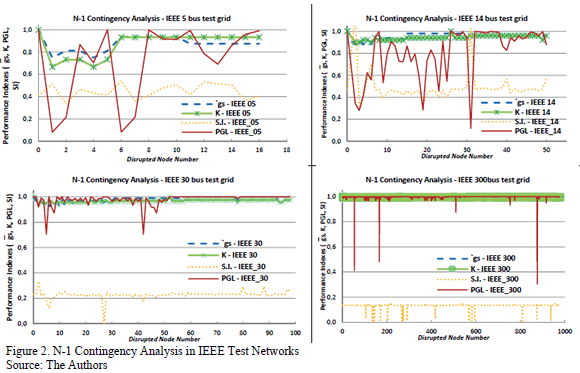
Realistic scenarios have been applied in order to prove the usefulness of graph theory models, especially for N-t contingency analysis. They correspond to IEEE Testing Networks of 5, 14, 24, 30, 57, 118 and 300 buses, whose iterative processes are shown in Table 1. The data can be accessed through flat text files [15]. Table 1 shows the iterations required to perform the proposed dynamic cascade failure model, for N-t contingency analysis.
In N-t contingency analysis, the structure of the network has to rearrange constantly, since it is exposed to successive node interdictions. This fact may turn out in divergences on the power flow results when executing a Standard Power Flow (SPF) routine [8]. In cases where the SPF routine does not converge, a convenient PSAT feature provides a Continuation Power Flow (CPF) routine [31], an efficient method for solving ill-conditioned cases.
The algorithm has been implemented in Matlab®. The script completes its execution until it may not be possible to disrupt any other node from the network, either because all nodes are isolated, or because there are no more electric circuits to perform power flows routines. The designed algorithm is able to calculate graph theory indexes previously defined in Eq. (4), (6) and electric power flow indexes previously exposed in Eq. (7), (8). Table 1 also shows some relevant statistics that concern the simulation of deliberate attacks and random errors on IEEE testing networks. Note that the number of iterations per sample is greater in random disruptions than node degree-based attacks.
5. Simulation results according to interdiction strategies
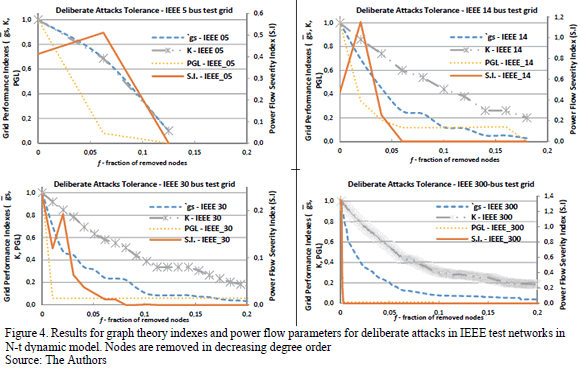
The results of the simulation are shown in Fig. 2 for N-1 contingency analysis, whereas Fig. 3 shows the results for the N-t dynamic model simulation for random error node removal strategy, and Fig. 4 for deliberate attack node removal strategy.
In order to keep the illustrations clear in both figures, the results of only three bus networks have been plotted, corresponding to IEEE testing networks of 5, 14, 30 and 300 buses (considered a good representation of the methodology).
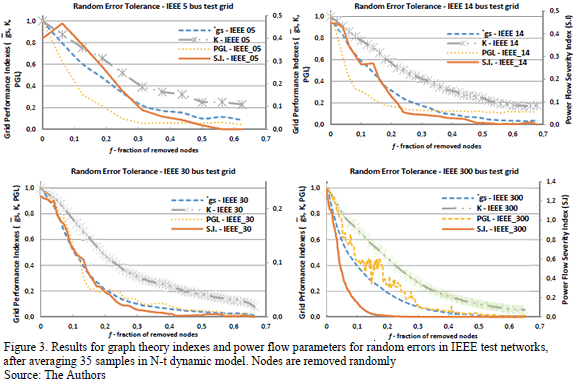
In Fig. 2 the x-axis refers to the node name failed on an N-1 contingency (unfortunately it is not possible to display all of those names). Scales for all indexes are indicated in per-unit values. The "most critical" nodes may be identified in the equivalent scale-free graph of the power grid, by just determining the higher values of the I.S parameter, or the lowest values of the PGL parameter, related to the node disruption.
5.1. N-1 contingency analysis
The study of N-1 contingency analysis refers to those events that occur when a network element is removed or taken out of service due to unforeseen circumstances. For every grid's disruption, power flows are redistributed throughout the network and voltage bars change. As a result, there may be overloaded lines and transformers [7].
Fig. 2 shows the results for both power grid load index (Eq. 7) and severity index (Eq. 8) compared to geodesic strength and connectivity index (Eq. 4 and Eq. 6) for N-1 contingency analysis in IEEE test networks of 5, 14, 30 and 300 buses. The analysis is performed through the successive execution of the Standard Power Flow Newton-Raphson algorithm [7,30,31]. As explained in Eq. (7) and Eq. (8) the contingency results are compared to the base case, i.e., the network operating under normal conditions. Hence, N-1 contingency analysis allows the identification of the most vulnerable nodes in the power network, which is the first step for decision-making in critical infrastructure protection.
Graph theory indexes 'gs in Eq. (6) and K in Eq. (4) show that in all cases the greatest impact on the network occurs through the removal or isolation of nodes with a higher degree of connectivity, especially buses. However, networks with less nodes (such as generators, capacitors and loads) have a minimal impact on both connectivity and geodesic strength indexes. N-1 contingency analysis provides a more realistic scenario when calculating PGL index of Eq. (7), since it relates to the power grid operating parameters. The most critical nodes may be identified as those whose removal leads to the lowest impact on either connectivity or geodesic strength.
In the particular case of the IEEE 30 bus network, made up by 98 nodes, the isolation of its generators in either node 5 or node 42 implies the decoupling of system loads, configuring a blackout event that affects almost 30% of the power grid. Furthermore, disruption of node 2 may cause a significant overload in lines and transformers as implied by the quantification of S.I. (43% greater than the base case). In the IEEE 300 bus test network, even though there are no nodes that lead to a total breakdown, in a few cases (nodes 54, 166 and 876) the PGL index may decrease down to a range of 30% to 50% on the system connected load in the power grid.
5.2. Dynamic N-t model for random error tolerance
A network may become a target in different risk scenarios either by deliberate attacks or random errors. This fact can be studied assuming that from a connected scale-free graph of N nodes, there might be a fraction f of nodes that may be removed. This section compares vulnerability results using both graph theory indexes and classic power flow indicators, in several realistic scenarios. In this section, nodes interdiction strategies are related to random perturbations, which cause the failure of some other nodes (natural disasters, equipment faults, procedure failures). Thus, the first mechanism to be studied is the removal of randomly selected nodes. The numerical simulations in Fig. 3 indicate that scale-free networks display a topological robustness against random node failures (since low degree nodes are far more abundant than high degree ones).
From Fig. 3, random error risk scenarios cause a total collapse of the network service (blackout) after the removal of 20% of the nodes. The PGL index evolution shows that in all cases, the IEEE bus test network completely collapses with the removal of about 20% of the nodes. The comparison between results of graph connectivity index K and PGL in Fig. 3 show that nodal connectivity is not proportionally related to the grid's electrical condition. This means that the PGL electrical index evolves at a different bias rate than the impact on connectivity graph index K.
The use of the average geodesic strength 'gs index, shown in Fig. 3, does really facilitate contrasting of results between classic electrical parameters and topological indicators, since the results of the geodesic strength 'gs match with the forecasts obtained through electric index PGL from Eq. (7).
A graphic comparison between PGL and'gs for events of random error disruptions (Fig. 3) shows that the 300 bus test-network is the most vulnerable, followed by 57 and 24 bus test-networks.
Severity Index S.I. from Eq. (8) has also been sketched in a secondary axis, in order to understand the evolution on loading of both transformers and transmission lines, as node removing takes place during cascade failure events. It can be noticed that these elements of the network discharge their loads as long as the PGL index evolves in similar trends. One interesting observation relates to the remarkable bias on the 'gs index when compared to the S.I parameter.
5.3. Dynamic N-t model for deliberate attack tolerance
Another realistic risk scenario is given by deliberate attacks, consisting of those risks caused by antagonist attackers on the power grid, i.e. emulating an intentional attack on the network [16].
This second removal strategy, in which the most highly connected nodes are removed at each contingency event, is the most damaging scenario to the integrity of the system [32]. In the case of an intentional attack, when the nodes with the highest number of edges are targeted, the network breaks down faster than in the case of random node removal.
The PGL index evolution in Fig. 3 shows that, under deliberate attacks, the removal of only 1% of the nodes in the plotted bus-test networks causes a blackout (100% of loads are isolated from the power grid). Furthermore, I.S. evolution shows that the loads are quickly discharged from transformers and transmission lines.
This fact demonstrates the reason why scale-free networks may be fragile to intentional attacks, since the removal of the nodes with higher connectivity has a dramatic disruptive effect on the network, and this can be observed in Fig. 4. The slight recovery of the I.S parameter when about 2% of the nodes are removed in both IEEE 5 and IEEE 14 bus test network is explained by the fact that there is an electrically connected circuit around the slack generator, which allows the circulation of power flows.
Taking into account the results shown, the networks are completely isolated when removing 2% and 25% of nodes respectively at deliberate attacks (Fig. 4) and random error (Fig. 3) removal strategies. Results for deliberate attack disruptions (Fig. 4) show the existence of a better correlation between geodesic strength index 'gs (5) and PGL parameter (7), than network connectivity index K (4). When the geodesic strength 'gs has a value close to zero, this implies a greater disintegration of the network, and hence flows between generators and loads need to step over more paths.
6. Discussion
It would be worth determining the dependence among electric parameters (PGL, S.I.), relating to graph theory indexes (K, 'gs), so it is possible to estimate the benefit of using the mechanisms of graph theory, instead of power transfer capacity between generators and loads, in order to perform vulnerability analysis. A practical measure to establish such dependence is the Pearson correlation coefficient r, which is obtained via division of the covariance of two variables by the product of their standard deviations s, as exposed in Eq. (9).
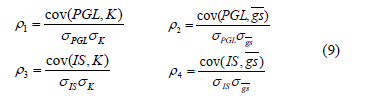
ri: Correlation between electric index (PGL, IS) and graph theory index (K, 'gs)
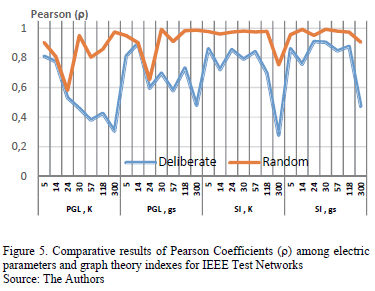
Fig. 5 reveals the results for correlations between indexes of Eq. (9).
Note that for random error node removal strategy, the Pearson correlation r2 is closer to +1, which implies a positive linear relationship between the PGL index and geodesic strength 'gs. According to this comparison, the'gs parameter would also be useful to determine the disconnected electric load PDi out of the power grid during cascade failures events.
On the other hand, comparison for connectivity index K shows lower correlation r1 with electrical index PGL. This means that it should not be considered as a precise indicator to assess the vulnerability of electric networks. Therefore, this correlation confirms the comparisons of the bias trend between index 'gs (6) and PGL (7) shown in Fig. 3 and Fig. 4.
In deliberate attacks, correlation r2 for parameter 'gs is weaker than r1 for index K. Thus, average geodesic strength'gs is of interest to make comparisons between different power systems and determine which one is the most vulnerable.
A final comment relates to the correlation between I.S and graph theory indexes (r3, r4) that are quite close to +1 for random disruption strategies in all test networks. This means that both parameters may be useful to infer the impact on the loadability of the power system.
Results on Pearson correlations allow an inference on the advantage of using graph theory based models, since there are faster performances when applied to IEEE test systems compared to traditional AC Power Flows. This issue is critical in order to recover a power system from a serious disturbance such as blackouts, transmission lines outages, and terrorist attacks.
7. Conclusion
The proposal herein explained allows the comparison of numerical indexes of graph theory (K,'gs) and power flow techniques (PGL, IS) in order to assess vulnerability for any power grid. The usefulness of combining scale-free graph statistics and power flow model parameters has been validated, making it possible to substitute laborious computational tools (i.e. classic power flow techniques) with more efficient techniques (i.e. graph theory statistics) to perform structural vulnerability analysis of any electric network, depending on the events that trigger cascade failures (random risks or deliberate threats).
The convenience of N-1 contingency analysis to identify the most vulnerable nodes in the power system has been validated. This is the first step for decision-making in the protection of these assets. It has also been proven that scale-free graph indexes can be used to qualify the vulnerability of a power grid topology compared to another one, especially for N-t dynamic cascade failure events. Hence, this feature is a great advantage since it is not necessary to run power flow routines to compare the vulnerability among different power systems. This result also demonstrates the computational efficiency of the proposed method.
References
[1] Council of the European Communities, On the identification and designation of European critical infrastructures and the assessment of the need to improve their protection, Council Directive 114 December/2008, Official Journal of the European Communities, Brussels, Belgium, 2008, 75 P. [ Links ]
[2] NIPP, National Infrastructure Protection Plan, Washington DC (USA), U.S. Department of Homeland Security, 2013, 175 P. http://www.dhs.gov/national-infrastructure-protection-plan [ Links ]
[3] Yusta-Loyo, J.M., Correa-Henao, G.J. and Lacal-Arántegui, R., Methodologies and applications for critical infrastructure protection: State-of-the-art, Energy Policy, 39, pp. 6100-6119, 2011, DOI: 10.1016/j.enpol.2011.07.010 [ Links ]
[4] Correa-Henao G.J. and Yusta-Loyo, J.M., Seguridad energética y protección de infraestructuras críticas, Lámpsakos, [Online]. 10, pp. 92-108, 2013. Available at: http://www.funlam.edu.co/revistas/index.php/lampsakos/article/view/1312 [ Links ]
[5] Correa-Henao G.J., and Yusta-Loyo, J.M., Structural vulnerability in transmission systems: Cases of Colombia and Spain, Energy Conversion and Management, 77, pp. 408-418, 2013. DOI: 10.1016/j.enconman.2013.10.011 [ Links ]
[6] Gil-Montoya, F., Manzano-Agugliaro, F., Gómez-López J. and Sánchez-Alguacil, P., Técnicas de investigación en calidad eléctrica: ventajas e inconvenientes, DYNA, 79 (173-I), pp 66-74, 2012. [ Links ]
[7] Holmgren, Å.J., Using graph models to analyze the vulnerability of electric power networks, Risk Analysis, 26, pp. 955-969, 2006. DOI: 10.1111/j.1539-6924.2006.00791.x [ Links ]
[8] Gómez-Expósito, A., Análisis y operación de sistemas de energía eléctrica, Madrid, Spain. McGraw-Hill, 2002. ISBN: 94-4g1-3592-X. [ Links ]
[9] Milano, F., Pricing system security in electricity market models with inclusion of voltage stability constraints, Dr. Thesis in Electrical Engineering, University of Genova, Italy, 218 P., 2003. [ Links ]
[10] Qiming, C. and McCalley, J.D, Identifying high risk N-k contingencies for online security assessment, IEEE Transactions on Power Systems, 20, pp. 823-834, 2005. DOI: 10.1109/TPWRS.2005.846065 [ Links ]
[11] Barabási, A. and Albert, R., Emergence of scaling in random networks, Science, 286, pp. 509-512, 1999. DOI: 10.1126/science.286.5439.509 [ Links ]
[12] Correa-Henao, G.J. and Yusta-Loyo, J.M., Grid vulnerability analysis based on scale-free graphs versus power flow models, Electric Power Systems Research, 101, pp. 71-79, 2013. DOI: 10.1016/j.epsr.2013.04.003 [ Links ]
[13] Ángel-Restrepo P.L. y Marín-Sepulveda, L.F., Un método computacional para la obtención de rutas óptimas en sistemas viales, Dyna, 78 (167), pp. 112-121, 2011. [ Links ]
[14] Albert, R. and Barabási, L., Statistical mechanics of complex networks, Review Modern Physics, 74, pp. 47-97, 2002. DOI: 10.1103/RevModPhys.74.47 [ Links ]
[15] Correa-Henao, G.J. y Yusta-Loyo, J.M., Seguridad en infraestructuras de transporte de electricidad, [Online]. Editorial Académica Española, 304 P, 2014, ISBN 978-3-659-01249-5. Available at: http://amzn.to/1BeXB3U [ Links ]
[16] Correa-Henao, G.J., Yusta-Loyo, J.M. and Lacal-Arántegui, R., Using interconnected risk maps to assess the threats faced by electricity infrastructures, International Journal of Critical Infrastructure Protection, 6, pp. 197-216, 2014. DOI: 10.1016/j.ijcip.2013.10.002 [ Links ]
[17] Motter, A. and Lai, Y., Cascade-based attacks on complex networks, Physical Review E, 66, pp. 065-102, 2002. DOI: 10.1103/PhysRevE.66.065102 [ Links ]
[18] Jelenius, E., Graph models of infrastructures and the robustness of power grids, MSc. Of Science in Physics Engineering Thesis., Royal Institute of Technology (KTH), Stockholm, Sweden, 89 P., 2004. [ Links ]
[19] Chen, G., Dong, Z.Y., Hill, D.J., Zhang, G.H. and Hua, K.Q., Attack structural vulnerability of power grids: A hybrid approach based on complex networks, Physica A: Statistical Mechanics and its Applications, 389, pp. 595-603, 2010. DOI: 10.1016/j.physa.2009.09.039 [ Links ]
[20] Johansson, J., Risk and vulnerability analysis of interdependent technical infrastructures, Dr. Thesis in Industrial Electrical Engineering, University of Lund, Sweden, 189 P., 2010. [ Links ]
[21] Wang, K., Zhang, B.H., Zhang, Z., Yin, X.G. and Wang, B., An electrical betweenness approach for vulnerability assessment of power grids considering the capacity of generators and load, Physica A: Statistical Mechanics and its Applications, 390, pp. 4692-4701, DOI: 10.1016/j.physa.2011.07.031 [ Links ]
[22] Newman, M.E.J., The structure and function of complex networks, SIAM Review, 45, pp. 167-256, 2003. DOI: 10.1137/S003614450342480 [ Links ]
[23] Solé, R., Rosas-Casals, M., Corominas-Murtra, B. and Valverde, S., Robustness of the European power grids under intentional attack, Physical Review E 77 (2), pp. 026102, 2008. DOI: 10.1103/PhysRevE.77.026102 [ Links ]
[24] Murray, A., Matisziw, T. and Grubesic, T., Critical network infrastructure analysis: interdiction and system flow, Journal of Geographical Systems, 9, pp. 103-117, 2007. DOI: 10.1007/s10109-006-0039-4 [ Links ]
[25] Gross, J.L. and Yellen, J., Handbook of graph theory, Chapman and Hall/CRC, [Online]. 2nd ed, 800 P, 2005, ISBN 978-1584885054. Available at: http://amzn.to/1zOFKW4 [ Links ]
[26] Crucitti, P., Latora, V., Marchiori M. and Rapisarda, A., Error and attack tolerance of complex networks, Physica A: Statistical Mechanics and its Applications, 340, pp. 388-394, 2004. DOI: 10.1016/j.physa.2004.04.031 [ Links ]
[27] Latora, V. and Marchiori, M., Efficient behavior of small-world networks, Physical Review Letters, 87 (19), p. 198701, 2001. DOI: 10.1103/PhysRevLett.87.198701 [ Links ]
[28] Salmeron, J., Wood, K. and Baldick. R., Analysis of electric grid security under terrorist threat, IEEE Transactions on Power Systems, 19 (1), pp. 905-912, 2004. DOI: 10.1109/TPWRS.2004.825888 [ Links ]
[29] Donde, V., López, V., Lesieutre. B., Pinar, A., Chao, Y. and Meza, J., Severe multiple contingency screening in electric power systems, IEEE Transactions on Power Systems, 23 (2), pp. 406-417, 2008. DOI: 10.1109/TPWRS.2008.919243 [ Links ]
[30] Milano, F., An open source power system analysis toolbox, IEEE Transactions on Power Systems, 20 (3) pp. 1199-1206, 2005. DOI: 10.1109/TPWRS.2005.851911 [ Links ]
[31] Gleich, D., MATLAB_BGL: Graph theory toolbox, [Online]. Purdue University, Palo Alto CA, USA, 2008. Available at: http://www.mathworks.com/matlabcentral/fileexchange/10922 [ Links ]
[32] Holmgren, A.J., Jenelius, E. and Westin, J., Evaluating strategies for defending electric power networks against antagonistic attacks, IEEE Transactions on Power Systems, 22 (1), pp. 76-84, 2007. DOI: 10.1109/TPWRS.2006.889080 [ Links ]
G.J. Correa-Henao, received the Electrical Engineer degree in 2001, the MSc. degree in Computer Science in 2004, from Universidad Nacional de Colombia, Medellín, Colombia, and the MSc. degree in Business Administration in 2007 from Universidad San Pablo, Madrid, Spain. He also received the PhD degree in Renewable Energy and Energetic Efficiency from Universidad de Zaragoza, Spain in 2012. He is currently a lecturer and researcher at the Faculty of Engineering in Fundación Universitaria Luis Amigó, in Medellín, Colombia, with research interests in distributed generation, power system security analysis and decision-making methodologies.
J.M. Yusta-Loyo, received a degree in Industrial Engineering in 1994 and a PhD. in Electrical Engineering in 2000 from Universidad de Zaragoza, Spain. He is currently a senior lecturer at the Department of Electrical Engineering of Universidad de Zaragoza, España. From 2004 to 2007 he was Vicedean of the Faculty of Engineering at Universidad de Zaragoza, España. His research interests include technical and economic issues in electric distribution systems, power systems security analysis, and the demand side of electricity markets.