Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.192 Medellín July/Aug. 2015
https://doi.org/10.15446/dyna.v82n192.48578
DOI: http://dx.doi.org/10.15446/dyna.v82n192.48578
Vulnerability assessment of power systems to intentional attacks using a specialized genetic algorithm
Valoración de la vulnerabilidad de sistemas de potencia ante ataques intencionales usando un algoritmo genético especializado
Laura Agudelo a, Jesús María López-Lezama b & Nicolás Muñoz-Galeano b
a Interconexión Eléctrica S.A (ISA), Medellín, Colombia. laura.agudelo@gmail.com
b Departamento de Ingeniería Eléctrica, Facultad de Ingeniería, Universidad de Antioquia, Medellín, Colombia jmaria.lopez@udea.edu.co; micolas.munoz@udea.edu.co
Received: April 29th, 2014. Received in revised form: February 17th, 2015. Accepted: July 10th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
A specialized genetic algorithm applied to the solution of the electric grid interdiction problem is presented in this paper. This problem consists in the interaction of a disruptive agent who aims at maximizing damage of the power system (measured as load shed), and the system operator, who implements corrective actions to minimize system load shed. This problem, also known as "the terrorist threat problem", is formulated in a bi-level programming structure and solved by means of a genetic algorithm. The solution identifies the most vulnerable links of the network in terms of a terrorist attack, providing signals for future reinforcement of the network or more strict surveillance of critical elements. The proposed approach has been tested on three case studies: a didactic five-bus power system, a prototype of the Colombian power system and the IEEE Reliability Test System. Results show the robustness and applicability of the proposed approach.
Keywords: bilevel programming; power system vulnerability; genetic algorithms, intentional attacks.
Resumen
En este artículo se presenta un algoritmo genético especializado aplicado a la solución del problema de interdicción. Este problema consiste en la interacción de un agente disruptivo que pretende maximizar el daño al sistema de potencia (medido en deslastre de carga), y el operador del sistema que implementa acciones correctivas para minimizar el deslastre de carga. Este problema, también conocido como "el problema del terrorista," es formulado en una estructura de programación binivel y solucionado mediante un algoritmo genético. La solución identifica los corredores más vulnerables de la red en términos de un ataque terrorista, suministrando señales para futuros refuerzos de la red o vigilancia más estricta de activos críticos. El enfoque propuesto ha sido probado en tres casos de estudio: un sistema didáctico de 5 barras, un prototipo del sistema colombiano y el sistema de pruebas de confiabilidad IEEE. Los resultados muestran la robustez y aplicabilidad de la metodología propuesta.
Palabras clave: programación binivel; vulnerabilidad de sistemas de potencia; algoritmos genéticos; ataques intencionales.
1. Introduction
The constant growth of power demand, along with stronger environmental regulation, that in most cases delay the building of new transmission lines, have forced most power systems in industrialized countries to operate near their static and dynamic limits. Under this scenario, electric power systems are more vulnerable to intentional attacks [1]. Some of the most important effects of such attacks include load shedding and higher operational costs associated to repairing towers and transmission lines [2].
The traditional approach for power system vulnerability is based on the study of credible contingencies (N-1 and N-2 criteria) [3]-[4]. However, such studies require exhaustive simulation and therefore, they are associated with a high computational burden; on the other hand, only natural-occurring outages are taken into account. Currently, it is well known that electric power systems are exposed not only to natural random phenomena, but also to malicious attacks. That is the case of the Colombian interconnected power system which has undergone the effects of terrorist attacks for several decades. As a matter of fact, only between 1999 and 2010 the National Interconnected System (NIS) faced as many as 200 terrorist attacks per year [2].
The electric grid interdiction problem, also known as the "terrorist threat problem" has been the focus of several studies in the last decade. This problem was first formulated in [5] as a max-min attacker-defender model. In such models the terrorist maximizes load shedding, while the system operator minimizes it. In [6] and [7] this problem is solved by using linearization and applying duality properties. First, the nonlinear expressions were recast as linear constraints; then, the inner optimization problem was replaced by its dual, turning the max-min bi-level optimization problem into a max-max bi-level optimization problem. Such a model is equivalent to a single-level maximization problem solvable via branch and cut methods. In [8] Arroyo and Galiana generalized the terrorist threat problem proposed by Salmeron, Wood and Baldick in [5]. The modeling approach of the problem proposed in [8] allows defining different objective functions for the terrorist and system operator. Also, it permits the imposition of new constraints in the outer optimization problem that might depend on both, inner and outer variables. As regards the terrorist's interests, different objectives can be considered. For example: i) to minimize the number of system components to be attacked, in order to achieve a given load shed, or ii) to maximize the load shed for a given number of system components that can be attacked.
In [9] the authors present a Mixed Integer Linear Programming approach for the analysis of the electric grid interdiction problem. In this case the bi-level programming problem is first turned into a one-level mixed-integer nonlinear programming program by using the fundamental duality theorem of linear programming [10]; then, disjunctive constraints are used to eliminate the nonlinearities of the problem. The resulting problem can be solved by using commercially available software. In [11] a worst-case interdiction analysis of the terrorist threat problem is performed by a generalization of Benders decomposition. In [12] the electric grid interdiction problem is formulated including line switching, which means that, after a terrorist attack, the system operator has also the option of switching some lines in order to reduce load shedding.
In this paper the authors propose a novel Genetic Algorithm (GA) approach to address the electric grid interdiction problem. Instead of turning the model into a one-level mixed-integer linear programming problem, the problem is solved in its original form as a mixed-integer non-linear programming problem. Results of the proposed algorithm are validated with studies reported in the specialized literature, showing its capability to attain globally optimal or near-optimal solutions.
2. Mathematical Formulation
The mathematical formulation of the electric grid interdiction problem is provided in equations (1) to (9) [8]. In this case the objective of the disruptive agent consists on maximizing the total load shedding that can be attained given a fixed number of elements (lines or transformers) under attack.
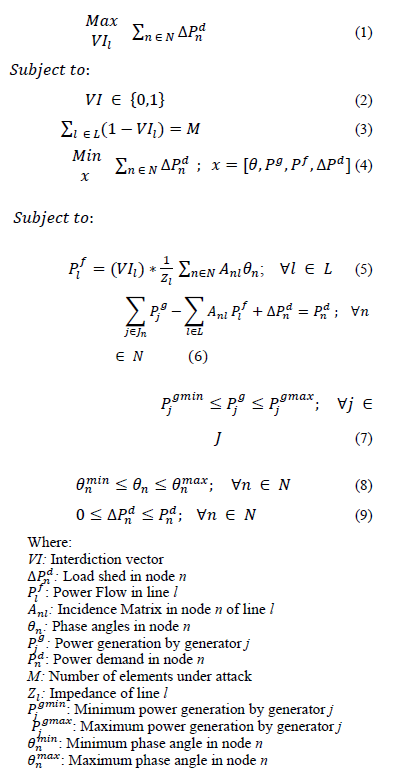
The interdiction vector consists of a binary array in which every position indicates the state of the element. If the position is equal to one it indicates an element on service; conversely, if the position is zero it indicates an element out of service (under attack). Equations (1) to (3) represent the upper level optimization problem (disruptive agent problem). For a given number of system components that could be attacked (M), the disruptive agent must maximize the load shedding of the system. Such a problem is at the same time restricted by the reaction of the system operator (equations (4) to (9)). For a given interdiction vector, the system operator must perform a re-dispatch of generation in order to minimize load shedding. Note that equations (4) to (9) correspond to an optimal DC power flow; furthermore, for a given interdiction vector, the inner optimization problem is a linear programming problem.
3. Specialized Genetic Algorithm
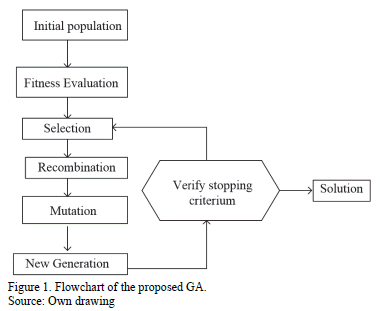
The strategy proposed in this paper to approach the electric grid interdiction problem consists of using a Genetic Algorithm (GA); however, any other metaheursistic technique could be applied. The methodology proposed in this paper takes advantage of the fact that, for a given interdiction vector, the equivalent problem is a DC optimal power flow. In this case, a number of interdiction vectors are randomly generated as initial candidate solutions and are modified in each generation according to the GA's rules. The objective of the GA is to find the maximum load shedding if a fixed number of elements are under attack. The flowchart of the proposed algorithm is presented in Fig. 1.
3.1. Problem codification
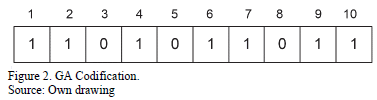
As stated above, every solution candidate of the GA consists of a binary chain representing the interdiction vector. Fig. 2 illustrates an interdiction vector for a power system of 10 elements over which the elements 3, 5 and 8 are under attack.
3.2. Initial Population
The initial population is randomly generated and consists of a set of different interdiction vectors (every interdiction vector must have the same number of elements under attack). For each interdiction vector a DC optimal power flow is run in order to determine the load shedding (which is the fitness function of the GA). With such information the individuals are ready to proceed for the next GA steps.
3.2. GA's Operators
The selection operator of the GA is performed by choosing the best solutions after applying a series of tournaments with a given number of elements. In this case, the number of candidates selected for the next step (recombination) is the same number of parents. The recombination is performed at a single point randomly selected. Every individual generates two new ones; in this stage two times the initial population is created. The mutation makes a minimal change in some of the individuals. The mutation is performed using a mutation factor (with a low probability) with every bit of the interdiction vector. If mutation or recombination leads to non feasible candidates, such candidates are penalized in the objective function. Finally, to keep the number of candidate solutions constant, only the best solutions are kept in each iteration.
4. Test and Results
The proposed methodology was tested using three different power systems: a didactic 5 bus power system, the solution of which has already been provided in [8], a prototype of the Colombian power system and the IEEE Reliability Test System.
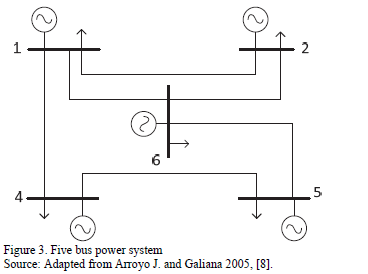
4.1. Case A. Five bus Power System
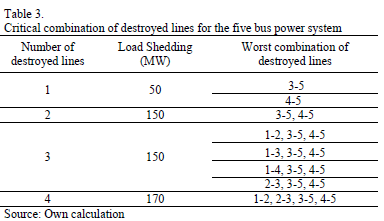
The first test is performed with the 5 bus power system illustrated in Fig. 3. This system has been used only for comparison purposes, and to illustrate that the proposed GA is able to reach global optimal solutions. The data for this system is provided in Tables 1 and 2.
It can be observed that for a single line under attack, the maximum load shedding obtained is 50 MW. In this case the line under attack must be either line 3-5 or line 4-5. Any other single attacked line would not result in load shedding. On the other hand, for two lines under attack there is only one strategy to obtain maximum load shedding (attacking lines 3-5 and 4-5 simultaneously). For a maximum of three lines under attack there are three possible interdiction vectors that would render a maximum load shedding of 150 MW. Finally, if only 4 lines could be taken down simultaneously, the maximum load shedding would be 170 MW.
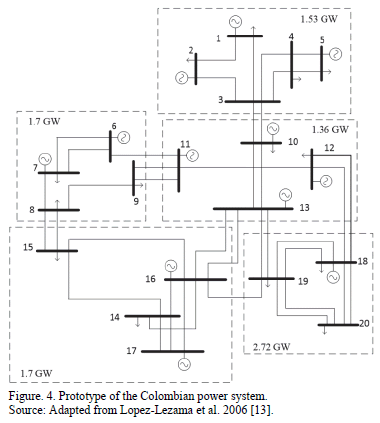
4.2. Case B. Prototype of the Colombian Power System
To show the applicability of the proposed approach in real power systems, a prototype of the Colombian power system was considered. Due to security reasons, a real
Colombian system with actual data cannot be displayed. Fig. 4 illustrates the system under study. This system has 20 nodes and 40 lines and is distributed in 5 sub-areas. The total demand of the system is 9010 MW and the installed capacity is 12850 MW. Specific line, load and generation data for this system can be consulted in [13]. Three different scneraios were considered:
- Scennario A: Considering all generation units available.
- Scenario B: Limiting generation in sub-area 5. The generation availabe in node 18 was reduced to 42% (1500MW).
- Scenario C: Limiting generation in sub-area 3. The generation available in node 13 was reduced to 25% (500 MW).
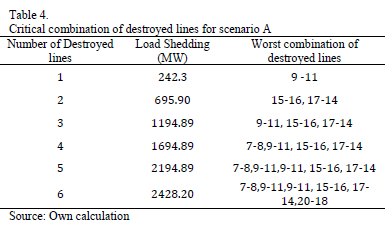
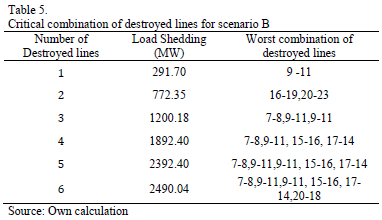
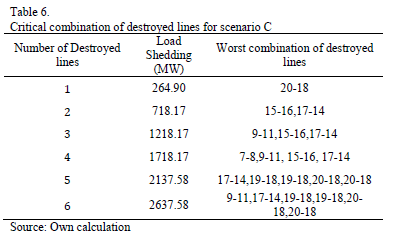
Several tests were performed in each scenario, for different numbers of circuits under attack, to find the worst combination of destroyed lines. The GA was developed in Matlab and was run in a computer with CORE I3 processor and 2Gb of RAM memory. The mutation rate was set to 5% and 100 parents were used in the initial population. The best results were found in only ten generations and around 300 seconds. Results are shown in Tables 4, 5 and 6.
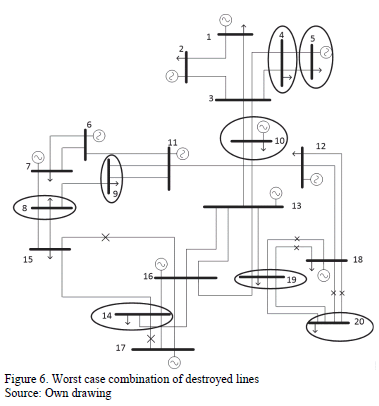
Results show that Scenario C with 6 destroyed lines is the worst possible case in terms of load shedding. It causes 2637.58 MW of load shed, 29.27% of the total system demand. This attack would cause a bottling up of energy in bus 18 and load shedding in buses 4, 5, 8, 9, 10, 14, 19 and 20. Fig. 6 illustrates the lines and buses affected.
The tests also revealed that sub-area 4 is the most sensitive to load shedding, especially buses 14 and 15. This is due to the fact that in this area the load is higher than the installed generation. Furthermore, such generation is mainly thermal which is the most expensive.
4.2. Case C. IEEE Reliability Test System
Several tests were also performed with the 24 bus IEEE Reliability Test System [14]. This test system is composed of 24 buses, 38 lines, 32 generators and 17 loads. The load profile selected for this study corresponds to a winter weekday at 6:00 pm (2850 MW).
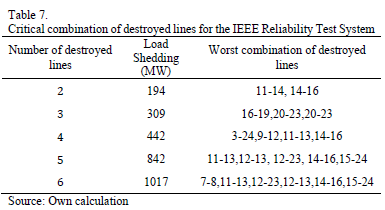
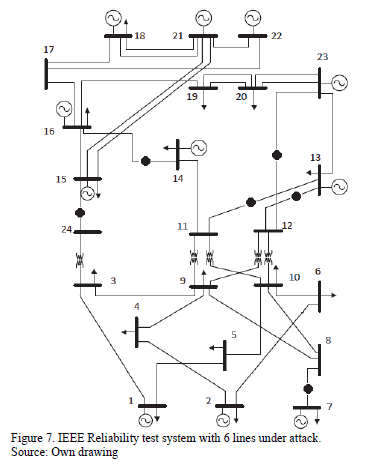
For the sake of simplicity, and without loss of generality, lines in the same corridor are treated independently; which means that the failure of a line does not necessarily imply the unavailability of the remaining lines in the same corridor. Several tests were performed with the GA, considering an increasing number of destroyed lines. Table 7 shows the worst combination of destroyed lines and the corresponding load shedding for this system. It can be observed that the simultaneous attack of 6 lines results in the loss of 1017 MW that represents 35.7% of the total demand. However, attacking a single line does not result in any loss of load.
In the IEEE Reliability Test System most of the generation is located in the upper part of the network, while most of the load is distributed in the nodes of the lower part of the system. As a consequence, the simultaneous attack of 5 or 6 lines focusses on dividing the system in two islands, separating generation from load. Fig. 7 depicts the simultaneous attack of 6 lines (marked with blackened circles). As a consequence of this attack the system is split into two islands i) the upper area with excess of generation capacity and no load shedding and ii) the lower area with deficit of generation and all the loss of load.
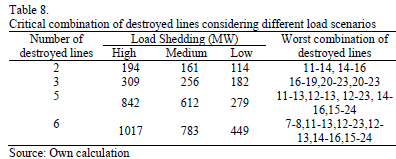
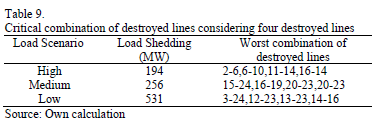
Table 8 shows the results obtained considering high, medium and low load scenarios. For the high load scenario the previously defined demand of 2850 MW was considered; for the medium load scenario a winter weekday at 9:00 pm with a total load of 2365 MW was considered; and finally for the low load scenario a summer weekday at 5:00 am with a total demand of 1653 MW was taken into account.
As is expected, the load shedding is significantly less in the low load scenario when compared with the medium and high load scenarios. It was also found that the worst combination of destroyed lines is the same for 2, 3, 5 and 6 destroyed lines; however, with 4 lines under attack there is a different solution for each of the load scenarios. The worst combination of destroyed lines, considering 4 circuits is presented in Table 9.
5. Conclusions
A specialized genetic algorithm for vulnerability assessment of power systems to intentional attacks was presented in this paper. The proposed approach is robust and efficient and can be applied to real power systems. The tests carried out with a prototype of the Colombian power system and the IEEE reliability test system allows the most vulnerable lines in terms of terrorist attacks to be identified.
The main advantage of using a GA for solving the electric grid interdiction problem is the possibility of having a set of high quality solutions instead of a single one solution. This gives the system operator more information about its most vulnerable elements and provides signals for future reinforcements of the network or more strict surveillance on critical elements.
With the use of a GA instead of classical mathematical programming, there is no need to bring into play duality theory or linearization schemes to transform the electric grid interdiction problem into a single-level optimization problem. This opens the possibility to approach the interdiction problem with a more accurate modeling of the network, such as an AC optimal power flow. This will be the focus of further work.
Acknowledgments
The authors would like to thank the Sustainability Program 2014-2015 of the University of Antioquia for financial support.
References
[1] Leffler L., The NERC program for the electricity sector critical Infrastructure protection, Proceedings of Power Engineering Society Winter Meeting, pp. 95-97, 2001. DOI: 10.1109/pesw.2001.916871 [ Links ]
[2] Corredor, P. and Ruiz, M., Against all odds. IEEE Power & Energy Magazine, 9 (2), pp. 59-66, 2011. [ Links ]
[3] Arragada, G., Evaluación de confiabilidad en sistemas eléctricos de distribución, M.S. Thesis, Department of Electrical Engineering, Pontificia Universidad Católica de Chile, Santiago de Chile, 1994. [ Links ]
[4] Kinney R., Crucitti P., Albert, R. and Latora, V., Modeling cascading failures in the North American power grid. The European Physical Journal, 46 (1), pp. 101-107, 2005. DOI: 10.1140/epjb/e2005-00237-9 [ Links ]
[5] Salmeron, J., Wood, K. and Baldick, R., Analysis of electric grid security under terrorist threat. IEEE Transactions on Power Systems, 19 (2), pp. 905-912, 2004. DOI: 10.1109/TPWRS.2004.825888 [ Links ]
[6] Álvarez, R. E., Interdicting electrical power grids, MSc. Thesis, Naval Posgraduate School, Monterey, C.A, Mexico, 2004. [ Links ]
[7] Salmerón, J., Wood, K., and Baldick, R., Optimizing electric grid design under asymmetric threat (II), Tech. Rep. Naval Postgraduate School, Monterey, C.A., 2004. [ Links ]
[8] Arroyo, J. and Galiana, F., On the solution of the bilevel programming formulation of the terrorist threat problem. IEEE Transactions on Power Systems, 20 (2), pp. 789-797, 2005. DOI: 10.1109/TPWRS.2005.846198 [ Links ]
[9] Motto, L., Arroyo, J. and Galiana, F., A mixed-integer LP procedure for the analysis of electric grid security under disruptive threat. IEEE Transactions on Power Systems, 20 (3), pp. 1357-1365, 2005. DOI: 10.1109/TPWRS.2005.851942 [ Links ]
[10] Bertsimas, D. and Tsitsiklis, J., Introduction to Linear Optimization Belmont, MA: Athena Scientific, 1997. [ Links ]
[11] Salmeron, J., Wood, K. and Baldick, R., Worst-case interdiction analysis of large-scale electric power grids, IEEE Transactions on Power Systems, 24 (1), pp. 96-104, 2009. DOI: 10.1109/TPWRS.2008.2004825 [ Links ]
[12] Arroyo, M. and Fernandez, J.F., A genetic algorithm approach for the analysis of electric grid interdiction with line switching, Proceedings of the 15th International Conference on Intelligent System Applications to Power Systems (ISAP), Curitiba, Brazil, Nov. 2009. DOI: 10.1109/isap.2009.5352849 [ Links ]
[13] López-Lezama, J.M., Murillo-Sanchez, C.E., Zuluaga L.J. and Gutierrez-Gomez, J.F., A contingency-based security-constraint optimal power flow model for revealing the marginal cost of a blackout risk equalizing policy in the Colombian energy market, Proceedings of the IEEE PES Transmission and Distribution Conference and Exposition, Caracas, Venezuela, 2006. [ Links ]
[14] Grigg C., Wong P., Albrecht P., Allan R., Bhavaraju M., Billinton R., Chen Q., Fong C., Haddat S., Kuruganty S., Li W., Mukerji R., Patton D., Rau N., Reppen D., Schneider A., Shahidehpour M., and Singh C., The IEEE Reliability Test System-1996. IEEE Transactions on Power Systems, 14 (3), pp.1010-1020, 1999. DOI: 10.1109/59.780914 [ Links ]
L. Agudelo, studied electrical engineering and currently she is studying a Masters in Engineering at the Universidad de Antioquia, Medellín, Colombia. She works in the operation department at Interconexión Eléctrica S.A. Utility (ISA) in Medellin, Colombia. Her interests include power systems optimization and real time operation.
J.M. Lopéz-Lezama, studied electrical engineering at Universidad Nacional de Colombia, Medellin, Colombia, where he also obtained a MSc. Degree. He obtained a PhD. degree from the UNESP in Sao Paulo, Brazil. Currently he works at the Department of Electrical Engineering in the Universidad of Antioquia in Medellin, Colombia. His interests include power systems optimization and distributed generation.
N. Muñoz-Galeano, studied electrical engineering at the Universidad de Antioquia in Medellín, Colombia. He obtained a PhD degree from the Universidad Politécnica de Valencia. Currently he works as an Assistant professor at the Department of Electrical Engineering in the Universidad de Antioquia in Medellin, Colombia. His interests include power system electronics and electrical machines.