Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.192 Medellín July/Aug. 2015
https://doi.org/10.15446/dyna.v82n192.48580
DOI: http://dx.doi.org/10.15446/dyna.v82n192.48580
Spinning reserve analysis in a microgrid
Análisis de reserva rodante en una microred
Luis Ernesto Luna-Ramírez a, Horacio Torres-Sánchez b & Fabio Andrés Pavas-Martínez c
a Programa de Investigación Adquisición y Análisis de Señales PAAS, Universidad Nacional de Colombia, Bogotá, Colombia. lelunar@unal.edu.co
b Programa de Investigación Adquisición y Análisis de Señales PAAS, Universidad Nacional de Colombia, Bogotá, Colombia. htorress@unal.edu.co
c Programa de Investigación Adquisición y Análisis de Señales PAAS, Universidad Nacional de Colombia, Bogotá, Colombia. fapavasm@unal.edu.co
Received: April 29th, 2014. Received in revised form: February 19th, 2015. Accepted: June 16th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
This paper proposes a methodology to model and analyze the security scheme required by a microgrid that considers the participation of renewable energy sources. This security scheme is represented by an up and down spinning reserve, which allows to drive the system frequency to a steady state after the occurrence of events associated not only to forecast errors in the electricity demand (as traditional schemes do), but also to forecast errors in the power availability of the intermittent energy sources. The proposed methodology was implemented on a real microgrid that considers the interconnection of a photovoltaic generator. From this, it was concluded that the security scheme designed for the microgrid efficiently ensured the relation between generation and demand, at each study hour.
Keywords: microgrid; security scheme; spinning reserve; photovoltaic generation; forecasting techniques.
Resumen
Este artículo propone una metodología para modelar y analizar el esquema de seguridad requerido por una microred que considera la participación de fuentes renovables de energía. Este esquema de seguridad está representado por una reserva rodante hacia arriba y hacia abajo, la cual permite llevar la frecuencia del sistema a un estado estable después de la ocurrencia de eventos asociados no sólo a errores en el pronóstico de la demanda (tal como lo hacen los esquemas tradicionales), sino también a errores en el pronóstico de la disponibilidad de potencia de las fuentes intermitentes de energía. La metodología propuesta se implementó en una microred real que considera la interconexión de un generador fotovoltaico. A partir de ello, se concluyó que el esquema de seguridad diseñado para la microred garantizó eficientemente la relación entre generación y demanda, para cada hora de análisis.
Palabras clave: microred; esquema de seguridad; reserva rodante; generación fotovoltaica; técnicas de pronóstico.
1. Introduction
In recent years, the electricity sector has experienced significant changes due to the introduction of a business oriented market structure. Such structure pretends to achieve higher efficiencies in the electricity supply, i.e. prices that reflect efficient costs and ensure the fulfillment of the quality, reliability and security criteria.
The advances achieved in the electricity sector, along with the high levels of demand growth and the concerns over the management of non-sustainable energy resources have led to the implementation of new generation technology alternatives. These new technologies consider a rational and efficient use of the energy, in such a manner that they have a minimal impact on the environment and contribute to ensure energy availability for future generations. In addition, the development of these technologies (usually of small scale) becomes important again with the installation of power plants near to the consumption centers, this time with the power system backup. This is an alternative of high penetration in the electricity sector and is commonly known as Distributed Generation (DG) [1].
The integration of DG within electrical systems and the incentive to optimize energy resources has gained strength in the last years. Accordingly, some countries have adjusted their regulatory policies in order to encourage the DG participation in the electrical systems [2].
Certainly, these regulatory policies have allowed an increase in the DG participation in the electricity basket. The increase of the DG penetration, the presence of multiple nearby sources, the implementation of demand response programs and the continued evolution of distribution networks into smart grids have led to the concept of microgrids [3]. A microgrid is an active distribution network that considers the coordinated operation and control of DG sources together with storage devices and controllable loads [4].
According to IEEE 1547-4 [5], microgrids are expected to satisfy the security requirements that allow these grids to operate in a secure way for any unexpected power requirement. In most cases, this security scheme is represented by a spinning reserve. This reserve represents one of the most important economic dispatch constraints in a microgrid, because it allows the system frequency to be driven to a steady state after the occurrence of an event [6-8].
Microgrids consider the participation of Renewable Energy Sources (RESs), such as Photovoltaic Generators (PVGs) and Wind Generators (WGs). The power output of the RESs behaves intermittently due to the variable nature of their primary resources (solar radiation and temperature for PVGs, and wind velocity for WGs), and they may even cause security problems in the microgrid. Therefore, it is necessary to design a security scheme for the microgrid, which can respond not only to the statistical forecast errors in the electricity demand (as traditional schemes do), but also to the statistical forecast errors in the power availability of the RESs [9-11].
The usual practice is to minimize these statistical errors by means of appropriate forecasting techniques in order to reduce the implementation costs of a microgrid security scheme [12].
There are different forecasting techniques to analyze time series. The technique based on structural models is one of the most interesting tools to forecast the hourly behavior of the electricity demand and the primary resources of the intermittent energy sources. This technique represents a widely accepted manner to model these kinds of time series of high density or frequency, seasonal and highly stochastic [13].
This paper proposes a novel security scheme that considers the intermittency of the RESs. In section 2, a methodology is proposed to quantify and analyze the up and down spinning reserve level required by a microgrid to satisfy the security requirements demanded by this type of grid. In section 3, the microgrid is described in which the proposed methodology is applied. In section 4, the methodology implementation is presented in the microgrid and also the results of this implementation are discussed. Finally, the conclusions are shown in section 5.
2. Proposed methodology
The proposed methodology allows the security scheme required by a microgrid that considers the participation of intermittent energy sources to be modeled. The security scheme is represented by an up and down spinning reserve located in the generators of the microgrid with controllable power output.
The methodology consists of performing a four stage analysis at each study hour of the next day. In the first stage a generation analysis is performed, evaluating the uncertainty in the forecast power availability of the RESs. A demand analysis is carried out at the second stage, which evaluates the uncertainty in the forecast electricity demand. The third stage consists of a net demand analysis, which quantifies and evaluates the up and down spinning reserve required by the microgrid. This reserve ensures the relation between generation and demand after the occurrence of events associated with forecast errors in both the electricity demand and the power availability of the RESs. At the fourth stage a validation analysis is performed, that verifies the proper sizing of the up and down spinning reserve.
The demand and the power availability of the intermittent energy sources are forecast using the statistical software OxMetrics 6.3 - module STAMP (Structural Time Series Analyser, Modeller and Predictor) and the time series technique based on structural models.
The next steps implement the methodology:
2.1. Generation analysis
1. Acquiring and managing the hourly historical information of the primary resources (solar radiation and temperature for PVGs, and wind velocity for WGs) in the area where the RES is located.
2. Forecasting the behavior of the primary resources, at each study hour of the next day.
3. Identifying the up and down standard deviation (statistical error) in the forecast primary resources, at each study hour of the next day.
4. Developing the mathematical model of the RES. This model has as input variables the primary resources, and it has as an output variable the AC power availability.
5. Acquiring the technical parameters of the RES interconnected to the microgrid.
6. Forecasting the behavior of the power availability of the RES, at each study hour of the next day (pFgt). For this, it is required that the forecast values of the primary resources are entered into the mathematical model of the RES interconnected to the microgrid.
7. Calculating the up and down standard deviation in the forecast power availability of the RES, at each study hour of the next day (spUgt, spDgt). For this, it is required that the values of the up and down standard deviation bounds in the forecast primary resources are entered into the mathematical model of the RES interconnected to the microgrid.
8. If there is another RES interconnected to the microgrid, it is necessary to go back to item 1. If there is not another RES, it is necessary to continue.
It is considered that the forecast power availability of each RES is assumed to follow a normal distribution with expectation pFgt and standard deviation spUgt, spDgt. Due to this condition, the forecast power availability of all the RESs grouped also follow a normal distribution with the next parameters:
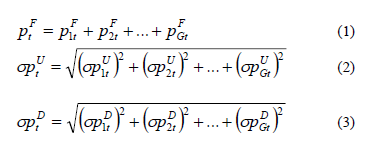
Where,
G: Total number of RES interconnected to the microgrid.
pFt: Forecast power availability [W] of the RESs grouped, at the tth hour of the next day.
spUt: Up standard deviation [W] in the forecast power availability of the RESs grouped, at the tth hour of the next day.
spDt: Down standard deviation [W] in the forecast power availability of the RESs grouped, at the tth hour of the next day.
2.1. Demand analysis
9. Acquiring and managing the hourly historical information of the electricity demand in the microgrid.
10. Forecasting the behavior of the demand, at each study hour of the next day (dFt).
11. Identifying the up and down standard deviation in the forecast demand, at each study hour of the next day (sdUt, sdDt).
It is considered that the forecast demand follow a normal distribution with the expectation of dFt and standard deviation sdUt, sdDt. The normality assumption of the forecast demand is a common practice, as can be seen in the literature [14]. It is justified through the wide diversity of the electricity demand across geographical areas and consumer classes combined with an invocation of the central limit theorem [15].
2.2. Net demand analysis
12. Determining the forecast net demand at each study hour of the next day. The following equation presents the mathematical procedure to calculate the net demand, which represents the difference between the forecast demand and the forecast power availability of the RESs, because the RESs are characterized as negative loads.
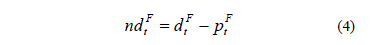
Where,
ndFt: Forecast net demand [W], at the tth hour of the next day.
dFt: Forecast demand [W], at the tth hour of the next day.
13. Determine the up and down spinning reserve required by the microgrid, at each study hour of the next day. This reserve allows counterbalancing the uncertainty in both the electricity demand and the power availability of the RESs. The up and down spinning reserve represent the up and down standard deviation in the forecast net demand, respectively. The following equations present the mathematical procedure to calculate these values, at each study hour of the next day.
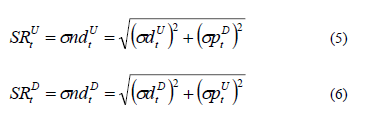
Where,
sdUt: Up standard deviation [W] in the forecast electricity demand, at the tth hour of the next day.
sdDt: Down standard deviation [W] in the forecast electricity demand, at the tth hour of the next day.
sndUt: Up standard deviation [W] in the forecast net demand, at the tth hour of the next day.
sndDt: Down standard deviation [W] in the forecast net demand, at the tth hour of the next day.
SRUt: Up spinning reserve [W], at the tth hour of the next day.
SRDt: Down spinning reserve [W], at the tth hour of the next day.
It is considered that both the forecast electricity demand and the forecast power availability of each RES follow a normal distribution. Due to this condition, the forecast net demand follows a normal distribution with expectation ndFt and standard deviation SRUt, SRDt.
2.3. Validation analysis
14. Verifying the proper sizing of the up and down spinning reserve, at each study hour of the next day. The following equations present the mathematical procedure to validate the up and down spinning reserve.
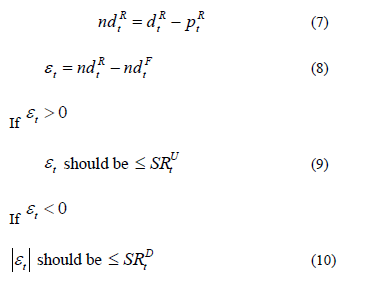
Where,
pRt: Real power availability [W] of the RESs, at the tth hour of the next day.
dRt: Real electricity demand [W], at the tth hour of the next day.
ndRt: Real net demand [W], at the tth hour of the next day.
et: forecast error in the net demand [W], at the tth hour of the next day.
The forecast error in the net demand follows a normal distribution with expectation zero and standard deviation described by the up spinning reserve (SRUt) and down spinning reserve (SRDt). The 68 % of the forecast errors should be located between the up spinning reserve and down spinning reserve, because these two reserves are calculated considering only one standard deviation. Different numbers of standard deviations in the spinning reserve calculation could be considered, depending on the risk aversion of the system operator.
2.4. Methodology Considerations
- The up spinning reserve allows the system frequency to be driven to a steady state after the occurrence of events associated with: excess in the real demand with respect to the forecast demand, and/or deficit in the real power availability of the RESs with respect to the forecast power availability.
- The down spinning reserve allows to drive the system frequency to a steady state after the occurrence of events associated with: deficit in the real demand with respect to the forecast demand, and/or excess in the real power availability of the RESs with respect to the forecast power availability.
- The electricity demand is directly proportional to the use of spinning reserve, i.e. an increase in the real demand with respect to the forecast demand implies that the generators with spinning reserve capacity should increase their generation (up spinning reserve application).
- The RESs are represented as negative loads. Therefore, the power availability of the RESs is inversely proportional to the use of spinning reserve, i.e. an increase in the real power availability of a RES with respect to the forecast power availability implies that the generators with spinning reserve capacity should decrease their generation (down spinning reserve application).
This methodology permits to model, quantify, analyze and verify the security scheme required by a microgrid. The security scheme ensures efficiently the frequency stability of the microgrid, after the occurrence of events associated with forecast errors in both the electricity demand and the power availability of the RESs.
The proposed methodology was applied on a real microgrid located at the Universidad Nacional de Colombia's campus (latitude 04°38' N, longitude 74°05' W and elevation 2556 m.a.s.l.). This microgrid is described in the following section.
3. Description of the microgrid
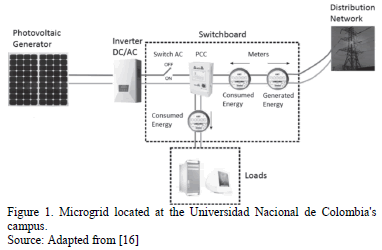
The microgrid [16] is a low voltage system (208/120V) connected to the existing electricity distribution network. This grid considers, among others, a RES, AC loads, computer applications, a real-time database system, bi- directional energy meter and a switching system. By means of these elements the energy resources can be managed under the scheme of microgrids, which promotes the efficient use of the energy, improves the power quality, the reliability, the security, and increases the system flexibility as well.
The microgrid incorporates a PVG with a power capacity of 3640 Wp, which maintains the concept of BIPVS (Building Integrated Photovoltaic Systems). The PVG uses an electronic power inverter to connect it to the AC electric network. This PVG is coupled to two phases of the microgrid due to its two-phase output condition, which is standard for this type of small-scale generation.
The microgrid considers the strategic installation of meters, which allow the dynamic behavior of bi-directional power flow caused by the RES introduction in this grid to be registered. The measurement scheme is presented in Fig. 1.
The microgrid also has an automation system composed by a monitoring and a control system. This automation system allows voltage, power and frequency to be registered and to perform control strategies, which will permit in the future the assignment of energy resources based on technical and economic considerations.
4. Implementation of the proposed methodology
For implementing the proposed methodology, the electricity demand and the power availability of the PVG was first analyzed and forecast. From this information, the spinning reserve required by the microgrid was determined and validated.
4.1. Generation analysis
First, it was necessary to acquire and analyze the available historical data of the solar radiation and temperature in the area where the PVG is located. For that, a database of weather information recorded every hour during the year 2012 was obtained. This database only considers 12 of the 24 hours of a day (from 6:00 to 17:59), because during this period there is significant solar radiation.
From this database, it was possible to model the behavior of the solar radiation and temperature, to forecast their availability and to identify the up and down standard deviation in their forecast, at each study hour of the next day. This was carried out using the time series technique based on structural models [13].
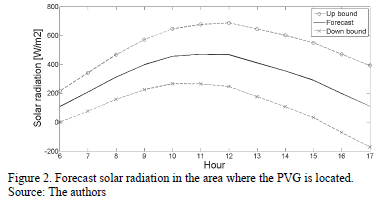
The results of the solar radiation analysis are presented in Fig. 2.
Fig. 2 shows that the forecast solar radiation for the next day starts with a value of 108.56 W/m2 at hour 6. This value increases to 471.31 W/m2 at hour 11. Finally, the forecast solar radiation decreases to a value of 111.31 W/m2 at hour 17.
Fig. 2 also allows us to see that the up and down standard deviation in the forecast solar radiation increases their amplitude as the forecast horizon becomes larger. The up and down standard deviation starts with a value of 107.05 W/m2 at hour 6, this value increases to 281.40 W/m2 at hour 17.
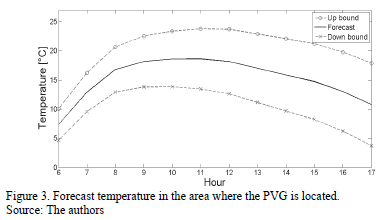
The results of the temperature analysis are presented in Fig. 3.
Fig. 3 shows that the forecast temperature for the next day starts with a value of 7.35 °C at hour 6. This value increases to 18.63 °C at hour 11. Finally, the forecast temperature decreases to a value of 10.81 °C at hour 17.
Fig. 3 also allows us to see that the up and down standard deviation in the forecast temperature increases their amplitude as the forecast horizon becomes larger. The up and down standard deviation starts with a value of 2.70 °C at hour 6, this value increases to 7.08 °C at hour 17.
Next, the electric behavior of a PVG was modeled using MATLAB®. For that purpose, the mathematical model proposed in [17] for the PVG generator was employed.
Then, the technical parameters of the PVG interconnected to the microgrid were identified. These parameters are described in Table 1.
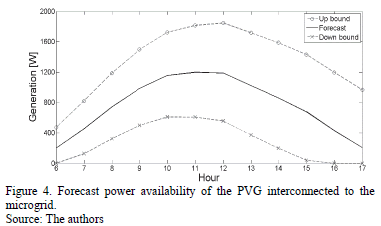
Afterwards, it was possible to forecast the power availability of the PVG interconnected to the microgrid and to identify the up and down standard deviation in its forecast, at each study hour of the next day. This was realized using the mathematical model of a PVG, its technical parameters and the hourly forecast of its primary resources (solar radiation and temperature). The results of the generation analysis are presented in Fig. 4.
Fig. 4 allows us to analyze the forecast power availability of the PVG (pFt), which is represented by the solid line. This figure shows that the pFt for the next day starts with a value of 199.71 W at hour 6. This value increases to 1197.80 W at hour 11. Finally, the pFt decreases to a value of 205.40 W at hour 17.
Fig. 4 shows the up and down standard deviation bounds in the forecast power availability of the PVG, which are represented by the dotted lines.
This figure allows us to analyze that the up standard deviation in the forecast power availability of the PVG (spUt), which increases its amplitude as the forecast horizon becomes larger, i.e. the forecast uncertainty increases as the forecast period becomes larger. The spUt starts with a value of 272.01 W at hour 6. This value increases to 761.60 W at hour 17.
This figure also allows us to see that the down standard deviation in the forecast power availability of the PVG (spDt) increases its amplitude as the forecast horizon becomes larger. However, it starts to decrease its amplitude from hour 15. The spDt starts with a value of 199.71 W at hour 6. This value increases to 659.89 W at hour 14. Finally, the spDt decreases to a value of 205.40 W at hour 17.
The decreasing behavior of the spDt during the last forecast hours is due to two aspects: The down standard deviation bound in the forecast solar radiation has negative values during the last forecast hours; the mathematical model of the PVG interconnected to the microgrid support negative values of neither solar radiation nor temperature. These two aspects led to represent the down standard deviation bound in the forecast power availability of the PVG with a value of zero, at those hours where the down standard deviation bound in the forecast solar radiation is lower than zero.
It is important to note that the standard deviation in the forecast power availability of the PVG is asymmetric, i.e. the up standard deviation is different to the down standard deviation. This asymmetry is due to both the aspects described above and because the efficiency of the PVG inverter varies exponentially with the DC power input.
4.2. Demand analysis
Initially, it was necessary to acquire and analyze the available historical data of the electricity demand in the microgrid. For that, a database of demand information recorded every hour along the last trimester of the year 2012 was obtained. This database only considers 12 of the 24 hours of a day (from 6:00 to 17:59), because during this period there is significant electricity consumption in the microgrid.
From this database, it was possible to model the behavior of the demand, to forecast its availability and to identify the up and down standard deviation in its forecast, at each study hour of the next day. This was realized using the time series technique based on structural models [13].
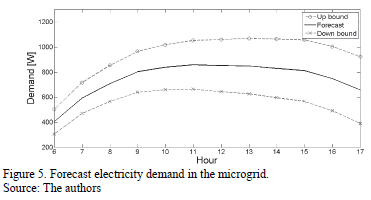
The results of the demand analysis are presented in Fig. 5.
Fig. 5 shows that the forecast demand (dFt) for the next day starts with a value of 403.28 W at hour 6. This value increases to 858.23 W at hour 11. Finally, the dFt decreases to a value of 656.33 W at hour 17.
Fig. 5 allows us to analyze that the up and down standard deviation in the forecast demand (sdUt and sdDt) increases their amplitude as the forecast horizon becomes larger. The sdUt and sdDt start with a value of 98.52 W at hour 6. This value increases to 267.13 W at hour 17.
It is important to note that this standard deviation is symmetric, i.e. the up standard deviation is equal to the down standard deviation.
4.3. Net demand analysis
From the generation and demand analysis, it was possible to determine the forecast net demand and to identify the up and down standard deviation in its forecast, at each study hour of the next day, using the equations (4-6). This up and down standard deviation represents the up and down spinning reserve required by the microgrid, respectively. 68% of the net demand should be located between the up spinning reserve and down spinning reserve, because these two reserves are calculated considering only one standard deviation.
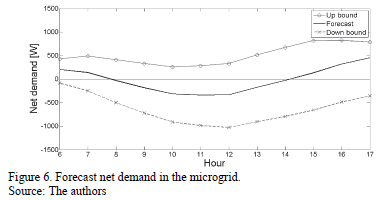
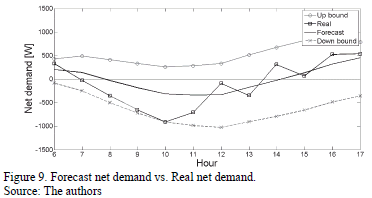
The results of the net demand analysis are presented in Fig. 6.
Fig. 6 shows that the forecast net demand (ndFt) for the next day starts with a value of 203.57 W at hour 6. This value starts to decrease. The microgrid goes from consuming energy of the distribution system to delivering surplus energy to the same system at hour 8. This surplus energy increases to 339.57 W at hour 11, because at this time the maximum level of forecast solar radiation and temperature are reached, and therefore the maximum level of forecast power availability of the PVG is reached. This value starts to decrease. The microgrid goes from delivering surplus energy to the distribution system to consuming energy of the same system at hour 14. This energy consumption increases to 450.93 W at hour 17.
Fig. 6 shows the up and down spinning reserve bounds.
This figure shows that the up spinning reserve required by the microgrid (SRUt) increases its amplitude as the forecast horizon becomes larger. However, it starts to decrease its amplitude from hour 15. The SRUt starts with a value of 222.69 W at hour 6. This value increases to 700.15 W at hour 14. Finally, the SRUt decreases to a value of 336.97 W at hour 17.
This figure also allows us to see that the down spinning reserve required by the microgrid (SRDt) increases its amplitude as the forecast horizon becomes larger. The SRDt starts with a value of 289.30 W at hour 6. This value increases to 807.09 W at hour 17.
The SRUt and SRDt allow the uncertainty in both the electricity demand and the power availability of the PVG interconnected to the microgrid to be countered. This reserve should be located in future generators of the microgrid with controllable power output.
4.4. Validation analysis
In order to validate the proper sizing of the up and down spinning reserve, it was necessary to acquire and manage both the real electricity demand in the microgrid (dRt) and the real power availability of the PVG interconnected to the microgrid (pRt), at each study hour.
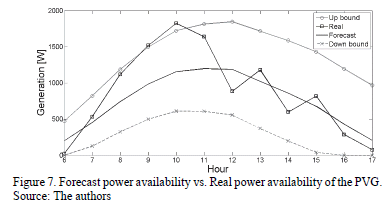
From this information, it was possible to develop a comparative analysis between the pRt and the forecast power availability of the PVG (pFt). The results of this analysis are presented in Fig. 7.
Fig. 7 shows that the pRt behavior is located within the standard deviation bounds in the forecast power availability of the PVG, during much of the forecast horizon. However, the pRt exceeds the up standard deviation bound at the hours 9 and 10 in 19.93 W and 101.01 W, respectively.
These results verify that the time series technique used represents in a proper way the primary resources of the PVG (solar radiation and temperature). However, forecasting these variables with high precision is quite a demanding task due to their high stochastic behavior.
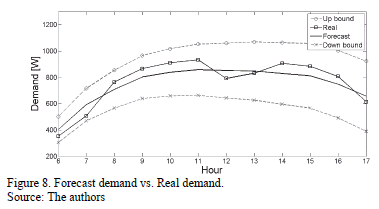
Nonetheless, it was possible to develop a comparative analysis between the dRt and the forecast demand (dFt). The results of this analysis are presented in Fig. 8.
Fig. 8 shows that the dRt behavior is located within the standard deviation bounds in the forecast demand, during the whole forecast horizon.
Additionally, it was possible to determine the real net demand (ndRt) using the equation (7), and to develop a comparative analysis between the ndRt and the forecast net demand (ndFt). The results of this analysis are presented in Fig. 9.
Fig. 9 shows that the ndRt behavior is located within the spinning reserve bounds, during the whole forecast horizon.
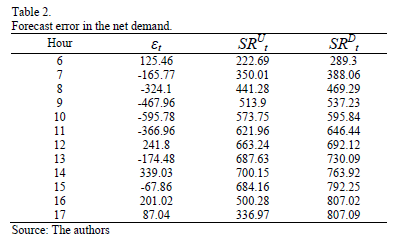
The comparative analysis presented in Fig. 9 served to determine the forecast error in the net demand, using the equation (8). The results of the validation analysis are presented in Table 2.
Table 2 shows that et is lower than SRUt for positive values of et, which is in accordance with equation (9). This table also shows that |et| is lower than SRDt for negative values of et, which is in accordance with equation (10).
It is worth noting that the pRt has a significant increase in its value with respect to the pFt at hours 9 and 10. However, the dRt also increases its value with respect to the dFt at these hours. This means that the et does not exceed the SRDt at these hours.
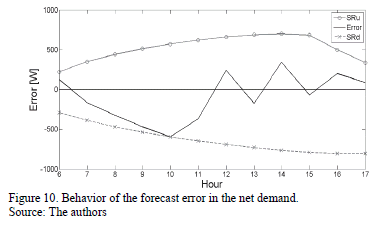
The behavior of et at each study hour can be clearly observed in Fig. 10.
Fig. 10 shows that the et is located within the security bounds represented by the SRUt and SRDt, during the whole forecast horizon. The security scheme designed allowed us to ensure the frequency stability of the microgrid at each study hour, after the occurrence of events associated with forecast errors in both the electricity demand and the power availability of the PVG.
5. Conclusions
The main contribution of this paper is the development of a methodology capable of modeling the security scheme required by a microgrid that considers the participation of intermittent energy sources. The security scheme is represented by an up and down spinning reserve located in the generators of the microgrid with controllable power output.
The methodology consists of performing a four stage analysis at each study hour of the next day: a generation analysis, that evaluates the uncertainty in the forecast power availability of the RES; a demand analysis, which evaluates the uncertainty in the forecast electricity demand; a net demand analysis, which quantifies and evaluates the up and down spinning reserve required by the microgrid to ensure the frequency stability; and a validation analysis, that verifies the proper sizing of the up and down spinning reserve.
In order to implement the proposed methodology, a forecasting technique was employed based on structural models, by means of the statistical software OxMetrics 6.3 - module STAMP.
The proposed methodology was implemented on a real microgrid located at the Universidad Nacional de Colombia's campus, that considers the interconnection of a PVG. From this, it was concluded that the time series technique used represents in a proper way the electricity demand and the primary resources of the PVG (solar radiation and temperature).
The security scheme designed for the microgrid allowed us to efficiently ensure the relationship between generation and demand at each study hour, after the occurrence of events associated with forecast errors in both the electricity demand and the power availability of the PVG.
It is clear that the interconnection of RESs in a microgrid significantly changes the security conditions of this grid, but it represents a challenge for the near future that needs to be assumed and evaluated with appropriate methodologies to ensure the microgrid stability.
Acknowledgments
The authors would like to thank the SILICE group, and the Universidad Nacional de Colombia, for their support and suggestions. The authors would also like to thank the statistical consulting group for their invaluable assistance in the time series analysis.
References
[1] Luna, L.E. and Parra, E.E., Methodology for assessing the feasibility of interconnecting distributed generation, Proceedings of IEEE PES PowerTech, 2011. [ Links ]
[2] Luna, L.E. and Parra, E.E., Methodology for assessing the impacts of distributed generation interconnection. Revista Ingeniería e Investigación, 31 (2), pp. 36-44, 2011. [ Links ]
[3] Hatziargyriou, N., Asano, H., Iravani, R. and Marnay, C., Microgrids. IEEE Power & Energy Magazine, 5 (4), pp. 78-94, 2007. DOI: 10.1109/MPAE.2007.376583 [ Links ]
[4] IEEE, Smart Grid Research. IEEE Vision for smart grid controls: 2030 and beyond. Institute of Electrical and Electronics Engineers, ISBN: 978-0-7381-8458-6, 2013. [ Links ]
[5] Standard IEEE 1547.4., IEEE guide for design, operation, and integration of distributed resource island systems with electric power systems. IEEE Standards Coordinating Committee 21 on Fuel Cells, Photovoltaics, Dispersed Generation, and Energy Storage, 2011. [ Links ]
[6] Bouffard, F., Galiana, F.D. and Conejo, A.J., Market-clearing with stochastic security - Part I: Formulation. IEEE Transactions on Power Systems, 20 (4), pp. 1818-1826, 2005. DOI: 10.1109/TPWRS.2005.857016, 10.1109/TPWRS.2005.857015 [ Links ]
[7] Bouffard, F., Galiana, F.D. and Conejo, A.J., Market-clearing with stochastic security - Part II: Case studies. IEEE Transactions on Power Systems, 20 (4), pp. 1827-1835, 2005. DOI: 10.1109/TPWRS.2005.857016, 10.1109/TPWRS.2005.857015 [ Links ]
[8] Ortega-Vazquez, M. and Kirschen, D., Optimizing the Spinning Reserve Requirements Using a Cost/Benefit Analysis. IEEE Transactions on Power Systems, 22 (1), pp. 24-33, 2007. DOI: 10.1109/TPWRS.2006.888951 [ Links ]
[9] Bouffard, F. and Galiana, F.D., Stochastic security for operations planning with significant wind power generation. IEEE Transactions on Power Systems, 23 (2), pp. 306-316, 2008. DOI: 10.1109/TPWRS.2008.919318 [ Links ]
[10] Ortega-Vazquez, M. and Kirschen, D., Assessing the impact of wind power generation on operating costs. IEEE Transactions on Smart Grid, 1 (3), pp. 295-301, 2010. DOI: 10.1109/TSG.2010.2081386 [ Links ]
[11] Wang, M. and Gooi, H., Spinning reserve estimation in microgrids. IEEE Transactions on Power Systems, 26 (3), pp. 1164-1174, 2011. DOI: 10.1109/TPWRS.2010.2100414 [ Links ]
[12] Morales, J.M., Conejo, A.J., Madsen, H., Pinson, P. and Zugno, M., Integrating renewables in electricity markets: Operational problems. New York: Springer, 2014. DOI: 10.1007/978-1-4614-9411-9 [ Links ]
[13] Lutkepohl, H., New introduction to multiple time series analysis. New York: Springer, 2005. DOI: 10.1007/978-3-540-27752-1 [ Links ]
[14] Gross G. and Galiana F.D., Short-term load forecasting, Proceedings of IEEE, 75 (12), pp. 1558-1573, 1987. DOI: 10.1109/PROC.1987.13927 [ Links ]
[15] Papoulis, A., Probability, random variables, and stochastic processes, 3rd edition. Boston, MA: McGraw-Hill, 1991. [ Links ]
[16] Hernández, J., Luna, L.E. and Blanco, A.M., Design and installation of a smart grid with distributed generation. A pilot case in the Colombian networks, Proceedings of IEEE Photovoltaic Specialists Conference, 2012. DOI: 10.1109/pvsc.2012.6317677 [ Links ]
[17] Hernández, J., Gordillo, G. and Vallejo, W., Predicting the behavior of a grid-connected photovoltaic system from measurements of solar radiation and ambient temperature. Applied Energy Journal, 104, pp. 527-537, 2013. DOI: 10.1016/j.apenergy.2012.10.022 [ Links ]
L.E. Luna-Ramírez, received the BSc. Eng degree in Electrical Engineering from the Escuela Colombiana de Ingeniería "Julio Garavito", Bogotá, Colombia, in 2007, and the MSc. degree in Electrical Engineering from the Universidad Nacional de Colombia, Bogotá, Colombia, in 2011. He is currently pursuing the PhD. degree at the Universidad Nacional de Colombia. He is a junior research of the PAAS-UN Group and he was recently a visiting scholar at the National Renewable Energy Center (CENER), Sarriguren, Spain. His research interests include power systems economics, reliability and stochastic programming.
H. Torres-Sánchez, received the BSc. Eng and MSc. degrees in Electrical Engineering from the Universidad Nacional de Colombia, Bogotá, Colombia, in 1976 and 1982, respectively, and realized PhD. studies at the Technical University of Darmstadt, Darmstadt, Germany (1978-1982). He is currently a professor at the Universidad Nacional de Colombia, Bogotá Colombia and the head of the PAAS-UN Group. His research interests include power quality, electromagnetic compatibility and probabilistic aspects of power quality.
F.A. Pavas-Martínez, received the BSc. Eng, MSc. and PhD. degrees in Electrical Engineering from the Universidad Nacional de Colombia, Bogotá, Colombia, in 2003, 2005 and 2013, respectively. He is currently a professor at the Universidad Nacional de Colombia and a researcher in the PAAS-UN Group. His research interests include power quality, electromagnetic compatibility and probabilistic aspects of power quality.