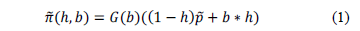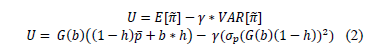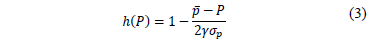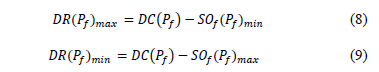Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.192 Medellín July/Aug. 2015
https://doi.org/10.15446/dyna.v82n192.48612
DOI: http://dx.doi.org/10.15446/dyna.v82n192.48612
Modeling dynamic procurement auctions of standardized supply contracts in electricity markets including bidders adaptation
Modelado de subastas dinámicas para compra de contratos estandarizados en el mercado eléctrico incluyendo la adaptación de los participantes
Henry Camilo Torres-Valderrama a & Luis Eduardo Gallego-Vega b
a Departamento de Ing. Eléctrica y Electrónica, Universidad Nacional de Colombia, Bogotá, Colombia. hctorresv@unal.edu.co
b Departamento de Ingeniería Eléctrica y Electrónica, Universidad Nacional de Colombia, Bogotá, Colombia. lgallegov@unal.edu.co
Received: May 9th, 2014. Received in revised form: February 20th, 2015. Accepted: July 7th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
Descendant Clock Auctions have been increasingly used in power markets. Traditional approaches are focused on discovering the bidders' best response but neglecting the bidders' adaptation. This paper presents an algorithm based on decision theory to estimate the bidders' behavior throughout the auction. The proposed model uses portfolio concepts and historical data of spot markets to estimate a long-term contract supply curve. This model was applied to evaluate the Colombia's Organized Market (MOR). Demand curve parameters and round size were varied to evaluate their impact over auction outputs. Results show that the demand curve has a quite small impact over bidders' decisions and round size management is useful to avoid non-competitive bidders' behavior. In addition, it is shown that auction's starting prices strongly influence auction's clearing prices. These results are extremely helpful to design market structures in power markets.
Keywords: Dynamic Auction Model, Descending Clock Auction, Electric Energy Regulation, Colombian Electric Energy Market.
Resumen
Las subastas de reloj descendente han incrementado su uso en los mercados de energía eléctrica. Las aproximaciones tradicionales a estas subastas se han enfocado en encontrar la mejor respuesta de los postores pero desconociendo la adaptación de ellos a lo largo de la subasta. Este artículo presenta un algoritmo basado en la teoría de decisión para estimar el comportamiento de los postores a lo largo de la subasta. El modelo propuesto usa conceptos de portafolios financieros y datos históricos sobre el mercado spot de energía eléctrica para estimar una curva de oferta de contrato de los generadores. El modelo fue utilizado para evaluar el Mercado Organizado (MOR) en Colombia. Los parámetros de la curva de demanda y el tamaño de la cada ronda, fueron variados para evaluar el impacto sobre la salida de la subasta. Los resultados muestran que la curva de demanda tiene un pequeña impacto sobre la adaptación de los pujadores y que el tamaño de ronda es útil para evitar los comportamientos no competitivos. Adicionalmente se muestra que los precios de inicio de la subasta tienen una gran influencia sobre los precios de cierre. Los resultados aquí presentados son útiles para el diseño de estructuras de mercado en el sector eléctrico.
Palabras clave: Modelo de Subasta Dinámica, Subasta de reloj descendente, Regulación de Energía Eléctrica, Mercado Eléctrico Colombiano
1. The problem
Auctions are an important allocation mechanism, and they have been employed to trade many goods for a long time. Nowadays, auctions are employed in many fields as one of the most important allocation mechanisms. This has increased the researchers' interest about enlarging auction's understanding. In fact, auction modeling has been deeply explored in many areas of economics and engineering.
The first approach to auction modeling comes from economic theory, using mathematical models to determine equilibrium strategies for different types of auctions [1]. These models are useful to understand bidders' behavior and some auction's features; however, mathematical models have limitations because strong assumptions are necessary to obtain a model's equilibrium.
Nowadays, computational models allow some of the mathematical model's limitations to be overcome. There are many examples of computational agent-based models useful for auction design, comparison and performance evaluation.
About design auction, in [4] an auction mechanism is settled by using an agent-based model. In [5] an agent-based model is proposed not only for an auction but for a fully automated negotiation system.
About evaluation of auctions' performance, many works have been carried out based on agent-based models. Several features have been studied, for example Shanshan Wang worked on the advantages of combinatorial auctions [6], Kim on the effect of auction repetition [7], Akkaya on the format of online auctions [8] and Sow on risk-prone evaluation by using agent-based models [9].
Moreover, these computational models have been employed to compare different auction formats. In [10] discriminatory and uniform price auctions are compared by using an experimental analysis based on a multi-agents model, and in [11] a similar comparison is done using learning agents.
In power markets, auctions are commonly used since deregulation became a trend. In the Colombian case, there is an electricity market composed of two mechanisms: bilateral financial contracts and a spot market, which is a uniform price auction. A sealed bid auction, like a uniform price auction, is the most common auction format in electricity markets and has been widely modeled even with agent-based learning in the Colombian case [2,3,12].
Espinoza compared different formats of sealed bid auctions by determining an equilibrium strategy for each format using econometric models [13]. Moreover, Gallego determined the bidders strategies by exploring the historical data about Colombian wholesale market and employed a learning algorithm. [14].
Recently, a new kind of auction has been included in electricity markets: multi-round (dynamic) auctions. These kinds of auctions show a distinctive feature when compared to traditional auctions: bidders adjust their bids throughout the auction so the analytic solution problem is harder to solve than sealed bid auctions. Nevertheless, it is possible to find examples of modeling dynamic auctions using computational techniques, as is shown in [15], where a multi-round English auction is modeled using genetic network programming.
Furthermore, some spot electricity markets have used dynamic auctions, but the principal purpose of dynamic auctions is to trade Long Term Supply Contracts (LTSCs) [16,17]. In LTSCs auctions, it is especially important to avoid the so-called winner's curse; this happens in common value auctions when the winner overpays because his estimate is higher than the other bidders' average estimate. Thus, dynamic auctions are often used to trade LTSCs, given that they allow bidders to fit their bids along the auction and thereby they reduce possible overpayment [18].
Despite some LTSCs' auctions using a static format, like Chilean [19] and Peruvian [20] electricity markets, most of LTSCs' auctions are dynamic (New Jersey [21], Illinois [22] and New England [23]), Brazil [19], Spain [24] and Colombia [25]).
In addition, LTSCs' auctions differ from sealed bid auctions because the bidders' decision making involves additional aspects such as financial risk (due to spot prices' volatility) and generation uncertainty. Roubik [26] worked on generators' strategic behavior in LTSCs auctions by using portfolio concepts. Four variables were proposed to be able to understand the generators' Azevedo's who also used Bayesian equilibrium but to analyze bilateral contract auction carried out in Brazil in 2003 [28] and Garcia-Gonzales' who modeled the bidding strategy of a wind power producer in a Descending Clock Auction [29].
A Descending Clock Auction is a dynamic procurement auction that has been recently introduced in several power markets. In short, this auction works as follows. The auctioneer calls bids in successive rounds. Each round has a maximum and a minimum price. The round's maximum price is equal to previous round's minimum price. Hence, the bid price is always descending. In every round the auctioneer adds all bids and announces the total aggregate supply. Auction ends when aggregate supply is equal or less than total demand [30].
From an economic approach, Ausbel & Cramton [31] and Milgrom [32] are the main references. They used a Lyapunov Function to find an equilibrium strategy and their main conclusion is that sincere bidding by the bidders is an equilibrium of the auction game, and, starting from any price vector, the outcome converges to the competitive equilibrium. However, these models are based on strong assumptions about rationality, continuity, and others that allow the easing of the analytic solution. Moreover, Ausbel, Cramton and Milgrom say that the most important feature of a dynamic auction is that the winner's curse is weakened, given that bidders can fit their bids along the auction [33]; however, the model used to demonstrate the equilibrium strategy is static and the adjustment is not evident.
From an engineering approach, models about descending clock auctions are pretty scarce. In [34], Barroso established an optimization model for a price-taker hydrothermal GENCO to devise bidding strategies in multi-item dynamic auctions for long-term contracts.
In order to fill the absence of auction's models from an engineering perspective, this paper presents a methodology that models the bidder's decision in every round in order to maximize their revenues. For this purpose, a MATLAB program based on decision theory [35] and microeconomic theory [36,37], was developed. This allows for the bidders behavior along the auction to be simulated. The bidders model uses portfolio concepts [26] and historical information about their preferences in the spot market.
This paper is organized as follows. In Section II the proposed model is presented, first the bidder model and then the scenarios faced by the bidders in the auction and the possible rewards to a chosen strategy are presented. In Section III the model is applied to the Colombian Energy Market. Section IV presents some results of model implementation. Finally, Section V summarizes the main conclusions.
2. Proposed model
In this section, the proposed descending clock auction model is presented. This model fits an auction mechanism in the Colombian power market known as MOR, including two main parts:
- The Bidders Model: This part focuses on representing the bidder's valuations about the product to be auctioned: a long-term energy supply contract (LTSC). Since historic information about energy contracts is not available due to reasons of confidentiality, it was necessary to design a methodology to set the valuations from the spot market's bids and financial portfolio concepts.
- Decision Making: In this part the decision making is modeled based on a set of scenarios, a set of bidding strategies and a set of rewards.
Below, both parts will be described.
2.1. Bidders model
In a descending clock auction, the auctioneer asks bidders about their bids at every round price, i.e. bidders disclose the supply curve point by point. In fact, bidders' behavior is based on this supply curve as a representation of their LTSC valuations.
In order to calculate their LTSC's valuations this paper proposes a methodology that consists of three stages: 1) Summarize the spot market information through an statistic supply curve 2) Estimate the GENCO's risk aversion and finally 3) Calculate the LTSC's valuation by using a utility function that includes expected generation (obtained from spot market information), risk aversion and variables about the commitment period of LTSCs (expected spot price, variance spot price).
Moreover, the information about LTSC bids is not available, but the information about bids on the spot market is plentiful given that GENCOs offer a supply curve on a daily basis for this market. This curve is formed from individual generation plants' bids that must be ordered by price in such a way that the accumulated quantity is determined by adding every unit's offered quantity.
Based on every GENCO's daily bid, a statistical supply curve can be obtained by ordering every daily supply curve as follows:
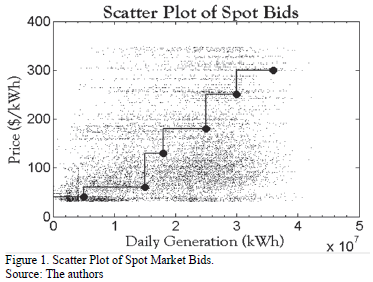
- Steps in supply curves are represented by points in a scatter plot (Fig. 1).
- Next, these points are clustered by price ranges. For each cluster a set of statistical measurements are calculated (i.e. mean, max, min, quartiles) with the aim of building different statistical supply curves.
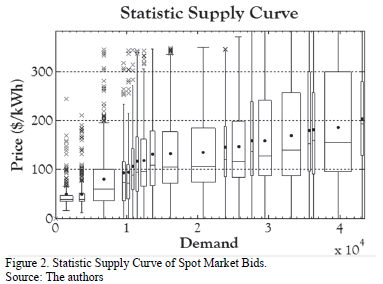
- Finally, clusters are combined in such a way that every cluster's mean is greater than the previous one in order to ensure the supply curve's monotonicity (Fig. 2).
Now, the resulting expected values for each price can be understood as the expected supply curve or expected generation function (G(P)). It is important to note that G(P) represents the total generation (MW) allocated in both markets, spot and contracts rather than only the generation power allocated in the spot market. The amount to be sold in the spot market is calculated from subtracting GENCO's contract obligations.
Also, an optimal hedge level for a given contract price can be determined by using portfolio concepts, [26] as follows:
- First, it is necessary to represent hedge preferences by utility functions as are commonly used in portfolio evaluations. This utility function allows two objectives to be balanced: the expected earnings maximization and financial risk mitigation. In general terms, GENCO's revenue is calculated using equation 1 where b is the contract price, G(b) is the expected generation at contract price b, h is the hedge level (contract sales), (1 - h) is the spot market sales and
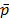 is the mean spot price.
is the mean spot price.
- ii. Now, the expected value for the GENCO's revenue and its involved risk (understood as the revenue variance) can be balanced by using a Linear Mean-Variance Utility Function (LMVUF) having a risk aversion constant (g) (equation 2)
- iii. From the LMVUF's derivative with respect to h, the optimal hedge level can be found. This optimal hedge level depends on the estimated average spot price, its variance and the GENCO's risk preferences (g), as is stated in equation 3.
- iv. Next, it is possible to estimate a hedge curve by calculating the optimal hedge level for several prices using equation 3.
Finally, a Contract Supply Curve (CSC) is calculated by multiplying G(P) and the obtained hedge curve as it was described in step 4. However, some assumptions were necessary to calculate this curve. First, the generators are able to make good estimations about average and variance of spot price, otherwise, it is a mistake to use the historical data to calculate g. Second, risk aversion does not present meaningful changes between commitment periods. Last but not least, generators plan their risk hedge using a LMVFU to represent their risk preferences.
Formally, the Contract Supply Curve is calculated as follows:
- By choosing a period of time and getting its spot market historical information.
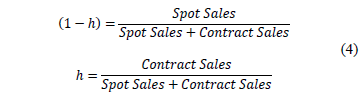
- By determining contract sales, spot sales and weighing them using equation 4.
- By calculating the spot price mean (
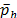 ), the spot price variance (
), the spot price variance (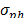 ) and assuming a contract price (b) (i.e. the average price of the contracts for the entire power market).
) and assuming a contract price (b) (i.e. the average price of the contracts for the entire power market). - By calculating risk aversion by clearing (g) from equation 3 as it is stated in equation 5.
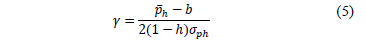
- By predicting the mean (
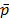 ) and variance spot price (
) and variance spot price (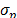 ) for the commitment period of contract.
) for the commitment period of contract. - By calculating the hedge curve (h(P)) as shown in equation 6.
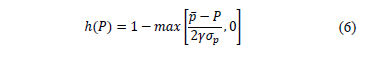
- By determining the expected generation as a function of price (G(P)) for the commitment period of contract.
- By calculating the Contract Supply Curve (CSC(P)) by multiplying point by point curves h(P) and G(P)
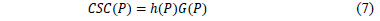
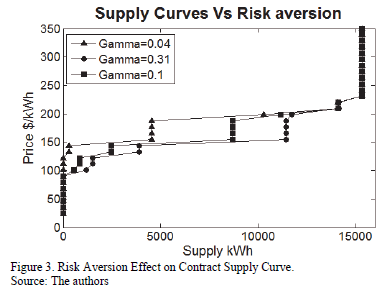
One of the most important contributions of the proposed methodology is that once a Contract Supply Curve is estimated, it is also possible to estimate the effect of the risk aversion in the Contract Supply Curve. Fig. 3 shows the risk aversion effect on a contract supply curve. The three shown Contract Supply Curves were estimated with the following parameters: 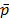 =200 $/kWh,
=200 $/kWh, 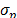 = 1000 and
= 1000 and 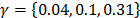 . This figure shows that the higher the risk aversion, the larger the amount of energy to be allocated in contracts for the same price.
. This figure shows that the higher the risk aversion, the larger the amount of energy to be allocated in contracts for the same price.
2.2. Decision making: Scenarios, strategies and rewards
Unlike sealed bid auctions, in a descending clock auction the allocations and payments not only depend on a single bid, but on bids sent in previous rounds; consequently, finding an equilibrium strategy using game theory is more difficult in this kind of auctions. Thus, decision-making was based on an alternative theoretical framework: decision theory.
Decision theory is a set of criteria that allows someone to choose among different strategies under several feasible scenarios. When the scenarios' probabilities are known, it is called decision under risk, and, consequently, decision-making is based on the expected strategy revenue. The most common criterion in this kind of decision making is the expected value criterion. This criterion weights rewards by the scenario's probability of finding the strategy's expected value [35].
In every round in a descending clock auction, bidders face two scenarios:
- The next round in the auction will be the last one.
- The next round in the auction will not be the last one.
These two scenarios are enough to understand the decision making. On one hand, if bidders have certainty that next round is not the last one, they will strategically bid to improve their position in the auction. On the other hand, if bidders have certainty that next round is the last one, they will bid in order to maximize their revenue.
In fact, bidders can choose among many possible bids, but to limit the choices it is important to balance the results accurately and the time spent to get them. Therefore, it is proposed that the bidders' choices can be grouped in three strategies as follows:
- Bidding a quantity of energy according their CSC curves.
- Bidding a larger quantity of energy than the one set by their CSC curves.
- Bidding a smaller quantity of energy than the one set by their CSC curves.
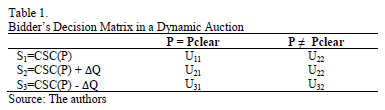
Now, for each scenario-strategy there is an associated reward, i.e. for strategy i and scenario j the associated reward is Uij. When next round is the last one (Scenario 1), the reward (Ui1) is calculated from equation 2 with b equal to the round price (Pa), given that payment is actually achieved in the final round.
In scenario 2 (the next round is not the last one), rewards are not real revenues given that there is no payment. However, bidders choose an optimal strategy to drive the auction toward a convenient point where they can maximize their revenues at the end of the auction. Therefore, the strategy's reward is the expected revenue derived from the current strategy.
In addition, if an auction has interdependent estimations, bidders may be motivated to send bids that differ from their real valuations. In other words, if each bidder's estimate is partially based on rivals' information, one bidder offering small quantities might induce his/her rivals to decrease their valuations and, consequently, they may leave the auction. Furthermore, bidders may also have incentives to hold their bids. A bidder inflates their valuations in the hopes of exhausting the competitors' limited budgets. Then, a bidder shifts to bid its real valuation for these goods, now facing weakened competition [30]. The chosen strategy depends on the expected strategy's impact on aggregate supply. This impact depends on bidder's market power.
Assuming that all bidders have historical information about other bidders, they can estimate the aggregate supply for each price based on the aggregate supply for the previous round price and the historical offers for the same price. Next, based on a supply curve estimate and a demand curve, the residual demand (DR) is calculated [36]. Once the bidder has the auction situation summarized in the residual demand, it is easy to estimate the expected revenues for a given strategy.
In order to estimate the expected revenue for a given strategy, an algorithm was implemented in MATLAB. This algorithm follows these steps:
- Calculate the probability that the current aggregate supply curve be greater than the historical aggregate supply curve for the current round price.
- Estimate other bidders' aggregate supply (SO) for the next round price based on historical data and the probability found at step one.
- For the three possible strategies (si), calculate the aggregate supply for next round price ASr+1|si by adding SO and si.
- Calculate the probability that ASr+1|si be greater than the historical aggregate supply for next round price.
- Estimate other bidders' aggregate supply for the future price rounds (SOf (Pf)). SOf (Pf) based on two limits: (SOf (Pf)max) and (SOf (Pf)min).
- SOf(Pf)max is other bidders' maximum aggregate offer at a future round price (Pf ). For every Pf value, SOf(Pf)max it is such that the probability of SOf(Pf)max is greater or equal to other bidders' historical aggregate supply, which is equal to Prb.
- SOf(Pf)min is the other bidders' minimum aggregate offer at a future round price (Pf), and is estimated by taking the other bidders' minimum historical aggregate supply at price Pf.
- Estimate maximum (DRmax) and minimum (DRmin) residual demand from SOf (Pf)min, SOf (Pf)max and the demand curve (DC(Pf)) as follows:
- Determine the set of possible clearing prices from DR(Pf)min, DR(Pf )max and the range of possible own bids.
- Calculate the expected reward (Ui2) based on the obtained set of possible clearing prices.
Based on expected rewards a decision matrix can be written (Table 1). Once this matrix is established, it is necessary to estimate the probability of each scenario in order to use the expected value criterion to choose the most convenient strategy under the feasible scenarios.
The probability of scenario 1 (Probsc1) (next round being the last), is estimated based on the historical data about the clearing price. The probability of scenario 2 is calculated as (1-Probsc1).
3. Model application
The proposed model was applied in the Colombian power market and specifically to a new market auction scheme proposed in the last 5 years. The following sections describes this application
3.1. Colombian electricity wholesale market
The Colombian power market (known as MEM) was created in 1995 as a competitive environment for the generation and energy retail activities. This market structure assures the existence of enough sellers and buyers avoiding any direct influence of any agent over the final energy tariffs [12]. In addition, MEM allows the trading of energy by means of a spot market or bilateral contracts, and both choices might be represented as an energy portfolio to manage the suppliers' revenue risk. In this market, hiring 100% of power generation lets suppliers know the expected annual revenues, implying lower levels of risk. Nevertheless, the average spot price is usually higher than the average contract price, so, hiring 0 % of power generation maximizes the expected revenue. Consequently, an optimal hedge level must be determined in order to maximize the revenue at an acceptable risk level.
In addition, there are two kinds of final customers: regulated and non-regulated customers. The regulated customers pay a tariff that is fixed by the regulator. This tariff transfers the purchase energy cost that was paid by its incumbent retailer. On the other hand, non-regulated customers buy energy through a competitive scheme.
3.2. Organized market (MOR)
Five years ago, a new scheme to trade energy for the regulated customers has been designed: the Organized Market (MOR). MOR is a descending clock auction where standard long term energy supply obligations are traded. In other words, the auction product is a standardized contract with a fixed commitment period (one year). According to this new market structure, suppliers/retailers who want/need to sell/buy energy to regulated customers must bid exclusively through this new market scheme (MOR).
Retailers have a passive role in MOR, the auctioneer asks them for the energy needed and sets an aggregate demand curve by adding the retailers' requests. Moreover, the auctioneer fix two prices: PP1 and PP2. PP1 is the maximum price that the auctioneer is willing to buy for the total energy demand while PP2 is the maximum price that the auctioneer is willing to buy only for any fraction of the demand.
Before the auction takes place, the available information is limited. PP2 is known, PP1 is unknown, and a range of values for the possible total demand is given instead of an accurate total demand. Thereby, bidders do not know the real demand curve. Instead they have an expectation that can be represented by lower and upper limits.
During an auction, the auctioneer sets a range of prices for which the bidders are able to offer. This range sets a variable called round size. For each round, the auctioneer sets the round size in order to balance the auction's transaction costs and the available time to fit the bidders' bids. Additionally, a suitable handling of this round size allows the chances of exercising market power to be limited.
Finally, the auction ends when the aggregate supply meets the total demand curve. Then, the auctioneer discloses the final allocations.
3.3. Simulation parameters
The proposed model was applied to MOR in order to evaluate the impact of varying its parameters: PP2, PP1 and round size.
Six generators were modeled and their main features are presented in Table 2. These agents choose one of the following three strategies in every round:
- Bid according to their CSC at round price
- Bid according 25th percentile of their historical bids at round price
- Bid according 75th percentile of their historical bids at round price
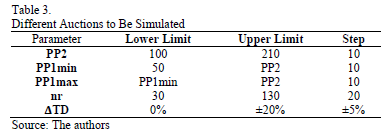
The simulation was set with the following values: average spot price (87 $/kWh), spot price variance (1000 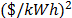 ), PP2 was varied between 100 and 210 $/kWh and PP1 between 50 and 210 $/kWh. All these values were chosen from the historical data about Colombia's spot market.
), PP2 was varied between 100 and 210 $/kWh and PP1 between 50 and 210 $/kWh. All these values were chosen from the historical data about Colombia's spot market.
In order to vary the round size, an additional parameter was introduced: a maximum number of rounds (nr). Thus, round size is calculated by dividing the difference between the auction's starting price and minimum price over nr. Thereby, the higher the maximum number of rounds, the smaller the size of the rounds.
The simulation scenarios are composed of 5 variables: price PP2, maximum number of rounds (nr), total demand uncertainty (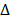 TD) and the two PP1's limits: PP1max and PP1min.
TD) and the two PP1's limits: PP1max and PP1min.
Table 3 shows the parameters for the simulated auctions using the MATLAB algorithm described above. In all the auctions, more than 15.000 scenarios were simulated.
4. Results and Discussion
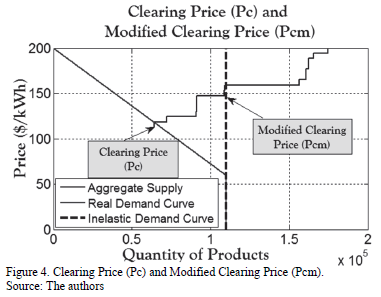
The main model's output is the auction's clearing price (Pc). However, Pc is impacted by the demand curve shape, as is shown in Fig. 4. To avoid this possible bias in the analysis, a Modified Clearing Price (Pcm) was introduced to filter this effect and accordingly, to identify the direct parameters' impact over bidders' decision throughout the auction.
Then the parameters' impact over Pc and Pcm is evaluated by applying the Pearson's coefficient to the simulation's outputs. Table 4 summarizes the results.
From table 4, some conclusions can be inferred:
- PP2 has the greatest impact over Pc and Pcm. Thus, PP2 price influences the clearing price, and also it directly influences bidders' decision-making processes.
- PP1 has an impact over Pc but not over Pcm. Thus, despite PP1 having an impact over the clearing price it doesn't have an impact over bidders' decisions.
- The remaining parameters do not have a strong influence over the auction's outputs.
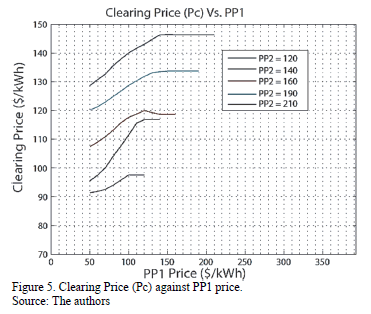
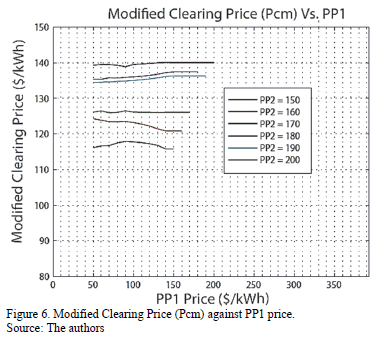
Fig. 5 shows a sensitivity analysis of auction outputs against PP1 with different PP2 values. This figure supports the conclusion about the greater impact that PP2 has over clearing prices and hence, over bidder's decisions. As well, Fig. 5 is helpful to understand that PP1 impact is limited; PP1 only impacts the auction output given that PP1 defines the demand curve shape and hence only Pc has a direct relation with PP1. Finally, an additional conclusion can be stated: PP1 doesn't influence bidder's decisions throughout the auction. Fig. 6 shows this fact.
5. Contributions and conclusions
Two of the paper's contributions must be highlighted. First, this paper proposes a methodology to obtain a GENCO's contract supply curve from historical data about spot prices. Barroso [34] presented a similar methodology; however, the proposed methodology in this paper summarizes the GENCOs' risk preference in one constant (g) instead of a piecewise function. Roubik's work [26] proposed a methodology to establish the hiring level based on the GENCOs' risk preference; however, this paper contributes to Roubik's work in the extend that it proposes a methodology to calculate the expected generation from spot market historical data and so, GENCO's hiring profile is calculated from spot market information. This paper proposes a methodology to summarize spot market historical data in a statistic supply curve, which allows for statistic information about GENCO's bidding profile to be obtained.
The paper's second important contribution is the modeling of GENCO's strategic behavior throughout a dynamic auction. Models like Barroso's obtain the GENCOs' best response to the auction, but this response is independent of the auction's development. Instead, this paper presents a methodology to get the GENCOs' best response for the next round that allows the bidders' adaptation along the auction to be understood. This modeling feature is extremely helpful to understand bidding behaviors for the purpose of future power market designs.
Regarding the Colombian power market (MOR), some conclusions emerge from the application of the proposed model. This model allows the auction sensitivity of several demand curve parameters and round sizes to be evaluated. This sensitivity analysis allows the following conclusions to be stated:
- The auction's starting price PP2 has the strongest impact on the auction's clearing price.
- Under MOR's rules, PP1 price does not influence bidders' decisions. However, PP1 has an important effect on clearing prices because PP1 modifies the demand curve and consequently, the equilibrium price.
- The round size strongly influences bidders' decisions throughout the auction. Hence, suitable round size management is helpful to prevent anticompetitive behaviors among bidders. However, the round size impact over auction's clearing price is low due to the strong relation between staring price and clearing price.
These conclusions are extremely helpful to design market structures in power markets, given that it allows emerging behaviors along the proposed auctions to be modeled.
References
[1] Krishna, V., Auction theory, publisher by: Elsevier Science, 2009. [ Links ]
[2] Gallego, L., Duarte, O. and Delgadillo, A., Strategic bidding in Colombian electricity market using a multi-agent learning approach, Proceedings of Transmission and Distribution Conference Latin America, pp.1-7, 2008. DOI: 10.1109/tdc-la.2008.4641706 [ Links ]
[3] Delgadillo, A., Gallego, L., Duarte, O., Jimenez, D. and Camargo, M., Agent learning methodology for generators in an electricity market, Proceedings of IEEE Power and Energy Society General Meeting, pp.1-7, 2008. DOI: 10.1109/pes.2008.4596279 [ Links ]
[4] Xing, L. and Lan, Z., A method based on iterative combinatorial auction mechanism for resource allocation in grid multi-agent systems, Proceedings of IEEE International Conference on Intelligent Human-Machine Systems and Cybernetics IHMSC '09, pp. 36-39, 2009. DOI: 10.1109/ihmsc.2009.17 [ Links ]
[5] Arai, S. and Miura, T., An intelligent agent for combinatorial auction, Proceedings of IEEE International Conference on Hybrid Intelligent Systems (HIS), pp.34-39, 2011. DOI: 10.1109/his.2011.6122076 [ Links ]
[6] Wang, S. and Song, H., A multi-agent based combinational auction model for collaborative e-procurement, Proceedings of IEEE International Conference on Industrial Engineering and Engineering Management (IEEM) , pp.1108-1112, 2008. [ Links ]
[7] Tae I1, K., Bilsel, R.U., Kumara, S.RT., A reinforcement learning approach for dynamic supplier selection, Proceedings of IEEE International Conference on Service Operations and Logistics, and Informatics (SOLI), pp. 1-6, 2007. [ Links ]
[8] Akkaya, Y., Badur, B. and Darcan, O.N., A study on internet auctions using agent based modeling approach, Proceedings of IEEE International Conference on Management of Engineering and Technology (PICMET), pp. 1772-1778, 2009. DOI: 10.1109/picmet.2009.5261945 [ Links ]
[9] Sow, J., Anthony, P. and Mun-Ho, Ch., Competition among intelligent agents and standard bidders with different risk behaviors in simulated English auction marketplace, Proceedings of IEEE International Conference on Systems Man and Cybernetics (SMC), pp. 1022-1028, 2010. DOI: 10.1109/icsmc.2010.5641740 [ Links ]
[10] Liu, X. and Cao, H., Uniform price versus discriminatory auctions in bond markets: A experimental analysis based on multi-agents system, Artificial Intelligence, Proceedings of IEEE International Conference on Management Science and Electronic Commerce (AIMSEC), pp. 1791-1794, 2011. [ Links ]
[11] Cincotti, S., Guerci, E., Ivaldi, S. and Raberto, M., Discriminatory versus uniform electricity auctions in a duopolistic competition scenario with learning agents, Proceedings of IEEE International Congress on Evolutionary Computation, pp. 2571-2578, 2006. DOI: 10.1109/cec.2006.1688629 [ Links ]
[12] Camargo, M., Jimenez, D. and Gallego, L., Using of data mining and soft computing techniques for modeling bidding prices in power markets, Proceedings of IEEE International Conference on Intelligent System Applications to Power Systems (ISAP), pp. 1-6, 2009. DOI: 10.1109/isap.2009.5352872 [ Links ]
[13] Espinosa, M., Una aproximación al problema de optimalidad y eficiencia en el sector eléctrico colombiano, Documentos CEDE Feb. 2009, Ediciones Uniandes, pp. 1-58, 2009. [ Links ]
[14] Gallego, L. and Duarte, O., Modeling of bidding prices using soft computing techniques, Proceedings of IEEE International Conference on Transmission and Distribution: Latin America, pp. 1-7, 2008. DOI: 10.1109/tdc-la.2008.4641757 [ Links ]
[15] Yue, Ch., Mabu, S., Chen, Y., Wang, Y. and Hirasawa, K., Agent bidding strategy of multiple round english auction based on genetic network programming, Proceedings of IEEE International Joint Conference ICCAS-SICE, pp- 3857-3862, 2009. [ Links ]
[16] Batlle, C. and Rodilla, P., Policy and regulatory design on security of electricity generation supply in a market-oriented environment. Problem fundamentals and analysis of regulatory mechanisms, España, Instituto de Investigaciòn Tecnológica, 2009. [ Links ]
[17] Moreno, R., Bezerra, B., Mocarquer, S., Barroso, L. and Rudnick, H., Auctioning adequacy in South America through Long-Term contracts and options: From classic Pay-as-Bid to Multi-Item dynamic auctions, Proceedings of the IEEE PES General Meeting, pp. 1-8, 2009. DOI: 10.1109/pes.2009.5275658 [ Links ]
[18] Cramton, P. and Sujarittanonta, P., Pricing rule in a clock auction, decision analysis [Online], 2009. [date of reference November 2nd of 2013]. Avaible at: http://pubsonline.informs.org/doi/abs/10.1287/deca.1090.0161?journalCode=deca [ Links ]
[19] Mocarquer, S., Barroso, L., Rudnick, H., Bezerra, B. and Pereira, M., ¿Energy policy in Latin America: the need for a balanced approach?, IEEE Power and Energy Magazine, 7 (4) , pp. 26-34, 2009. DOI: 10.1109/MPE.2009.933417 [ Links ]
[20] Camac, D., Ormeño, V. and Espinoza, L., Assuring the efficient development of electricity generation in Peru, Proceedings of IEEE General Meeting, pp. 1-5, 2006. DOI: 10.1109/pes.2006.1708977 [ Links ]
[21] La-Casse, C. and Wininger, T., Maryland versus New Jersey: Is there a "Best" competitive bid process?, The Electricity Journal, 20 (3), pp. 46-59, 2007. DOI: 10.1016/j.tej.2007.03.002 [ Links ]
[22] de Castro, L., Negrete-Pincetic, M. and Gross, G., Product definition for future electricity supply auctions: The 2006 Illinois experience, The Electricity Journal, 21 (7), pp. 50-62, 2008. DOI: 10.1016/j.tej.2008.08.008 [ Links ]
[23] Cramton, P. and Stoft, S., A capacity market that makes sens, The Electricity Journal, 18 (7), pp. 43-54, 2005. DOI: 10.1016/j.tej.2005.07.003 [ Links ]
[24] Gener, A., Modelo de gestión del riesgo del suministro de último recurso de electricidad en agentes verticalmente integrados, Tesis, Universidad Pontificia de Comillas, Madrid, España. 2010. [ Links ]
[25] Cramton, P. and Stoft, S., Colombia firm energy market, Proceedings of Hawaii International Conference on System Sciences, pp. 1-11, 2007. DOI: 10.1109/hicss.2007.133 [ Links ]
[26] Roubik, E. and Rudnick, H., Assessment of generators strategic behavior in long term supply contract auctions using portfolio concepts, Proceedings of IEEE Bucharest Power Tech Conference, pp. 1-7, 2009. DOI: 10.1109/ptc.2009.5281851 [ Links ]
[27] Moreno, R., Rudnick, H. and Barroso, L., First price and second price auction modeling for energy contracts in Latin American electricity markets, Proceedings of 16th Power Systems Computation Conference, pp. 1-7. 2008. [ Links ]
[28] Azevedo, E. and Correia, P., Bidding strategies in Brazilian electricity auctions, International Journal of Electrical Power and Energy Systems, 28 (5), pp. 309-314, 2006. DOI: 10.1016/j.ijepes.2005.12.002 [ Links ]
[29] Garcia-Gonzalez, J., Roma, T., Rivier, J. and Ostos, P., Optimal strategies for selling wind power in mid-term energy auctions, Proceedings of IEEE Power and Energy Society General Meeting, pp. 1-7, 2009. DOI: 10.1109/pes.2009.5276009 [ Links ]
[30] Cramton, P., Dynamic auctions in procurement, in Dimitri, N., Piga, G. and Spagnolo, G. (Eds.), Handbook of Procurement, Cambridge, England: Cambridge University Press, 2006, pp. 220-248. [ Links ]
[31] Cramton, P. and Ausbel, L., Auction many divisible goods, Journal of the European Economic Association, 2, pp. 480-493, 2004. DOI: 10.1162/154247604323068168 [ Links ]
[32] Milgrom, P., Putting auction theory to work, Cambridge: Cambridge University Press, pp. 1-28, 2004. DOI: 10.1017/CBO9780511813825 DOI: 10.1017/CBO9780511813825.004 [ Links ]
[33] Ausubel, L., Cramton, P., Pycia, M., Rostek, M. and Weretka, M., Demand reduction, inefficiency and revenues in Multi-Unit auctions, The Review of Economic Studies, [Online], 2014. [date of reference November 2nd of 2013]. Avaible at: http://www.restud.com/paper/demand-reduction-and-inefficiency-in-multi-unit-auctions/ [ Links ]
[34] Barroso, L., Street, A., Granville, S. and Pereira, M., Offering strategies and simulation of multi item dynamic auctions of energy contracts, IEEE Transactions on Power Systems, 26 (4), pp. 1917-1928, 2011. DOI: 10.1109/TPWRS.2011.2112382 [ Links ]
[35] Taha, H., Operations Research, New Jersey: Pearson Prentice Hall, 2007. [ Links ]
[36] Wolak, F., Measuring unilateral market power in wholesale electricity markets: The California market, 1998-2000, American Economic Association, 93 (2) , pp. 425-430, 2003. DOI: 10.1257/000282803321947461 [ Links ]
[37] Wolak, F., An empirical analysis of the impact of hedge contracts on bidding behavior in a competitive electricity market, International Economic Journal, 14 (2), pp 1-39. 2000. DOI: 10.1080/10168730000080009 DOI: 10.1080/10168730000000017 [ Links ]
H.C. Torres-Valderrama, was born in Bogota, Colombia in 1987, is PhD(s) MSc. He finished his studies in Electric Engineering in the Universidad Nacional de Colombia in 2010. He has been a research assistant in the Research Program of Acquisition and Analysis of Electromagnetic Signals of the Universidad Nacional de Colombia - PAAS-UN Group since 2010. His research interests are power markets, smart grids and energy efficiency.
L.E. Gallego-Vega, was born in Bogota, Colombia, in 1976. He finished his undergraduate, MSc. and PhD. studies in the Department of Electrical Engineering at the Universidad Nacional de Colombia, Bogotá, Colombia. He has been a researcher in the Research Program of Acquisition and Analysis of Electromagnetic Signals of the Universidad Nacional de Colombia - PAAS-UN since 2000, working in research projects mainly related to power quality and lightning protection. He has been involved in teaching activities related to power quality and computational intelligence. His research interests are power markets, power quality analysis and computational intelligence applied to power systems modelling.