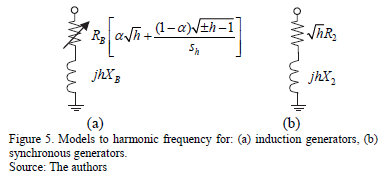Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.192 Medellín July/Aug. 2015
https://doi.org/10.15446/dyna.v82n192.48617
DOI: http://dx.doi.org/10.15446/dyna.v82n192.48617
Time-varying harmonic analysis of electric power systems with wind farms, by employing the possibility theory
Análisis de armónicos variando en el tiempo en sistemas eléctricos de potencia con parques eólicos, a través de la teoría de la posibilidad
Andrés Arturo Romero-Quete, Gastón Orlando Suvire, Humberto Cassiano Zini & Giuseppe Rattá
Instituto de Energía Eléctrica, Universidad Nacional de San Juan - Consejo Nacional de Investigaciones Científicas y Técnicas, San Juan, Argentina, aromero@iee.unsj.edu.ar
Received: April 29th, 2014. Received in revised form: February 10th, 2015. Accepted: July 17th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
This paper focuses on the analysis of the connection of wind farms to the electric power system and their impact on the harmonic load-flow. A possibilistic harmonic load-flow methodology, previously developed by the authors, allows for uncertainties related to linear and nonlinear load variations to be modeled. Moreover, it is well known that some types of wind turbines also produce harmonics, in fact, time-varying harmonics. The purpose of this paper is to present an improvement of the former method, in order to include the uncertainties due to the wind speed variations as an input related with power generated by the turbines. Simulations to test the proposal are performed in the IEEE 14-bus standard test system for harmonic analysis, connecting to the network a wind farm composed by ten Full Power Converter (FPC) type wind turbines. Results obtained show that uncertainty in the wind speed has a considerable effect on the uncertainties associated with the computed harmonic voltage magnitudes.
Keywords: full power converter, harmonic distortion, possibility distribution, power system, uncertainty, wind turbine.
Resumen
En este trabajo se analiza el impacto de la conexión de parques eólicos, en el flujo de cargas armónicas en un sistema de potencia. Algunos generadores eólicos producen armónicos debido a la electrónica de potencia que utilizan para su vinculación con la red. Estos armónicos son variables en el tiempo ya que se relacionan con las variaciones en la velocidad del viento. El propósito de este trabajo es presentar una mejora a la metodología para el cálculo de incertidumbre en el flujo de cargas armónicas, a través de la teoría de la posibilidad, la cual fue previamente desarrollada por los autores. La mejora consiste en incluir la incertidumbre debida a las variaciones de la velocidad del viento. Para probar la metodología, se realizan simulaciones en el sistema de prueba de 14 barras de la IEEE, conectando en una de las barras un parque eólico compuesto por diez turbinas del tipo FPC. Los resultados obtenidos muestran que la incertidumbre en la velocidad del viento tiene un efecto considerable en las incertidumbres asociadas a las magnitudes de las tensiones armónicas calculadas.
Palabras clave: convertidor de potencia AC/DC - DC/AC; distorsión armónica, distribución de posibilidad, sistemas de potencia, incertidumbre, generador eólico.
1. Introduction
Electricity is a product of particular importance for the progress of society. An electric power system allows such a product to be generated, transformed and transmitted and finally supplied to the end customers. All of society's efforts and investments (e.g., in human resources, physical assets, research and development, etc.) in electric power systems have a common aim: "to ensure electricity in sufficient quantity in time and place, with adequate reliability at the lowest cost and controlling that environmental impacts remain within acceptable limits".
To achieve this aim, the scientific and technical community specializing in power engineering has set its expectations on the development of Smart Grids. In this field, there are many issues that have only partially been solved, which deserve special attention and require intensive research and development. One such issue is related to the connection of new electricity sources based on renewable resources, e.g., solar, wind, geothermal, etc., to the power systems.
This paper focuses on the analysis of the connection of wind farms and their impact on power quality. First, the main aspects to be considered when harmonics have to be modeled in the network, including wind farms' generator fleet, are discussed and developed.
Then, the general formulation of a possibilistic harmonic load-flow methodology, previously developed by the authors, that allows for modeling uncertainties related to linear and nonlinear load variations, is presented.
Moreover, as is well known, some types of wind turbines also produce harmonics. Therefore, in this paper, an improvement of the former proposed methodology is developed in order to deal with this specific issue. In fact, with the modifications, the improved possibilistic harmonic load-flow method is able to model the uncertainty due to the wind speed variations as an input related to electric power generated by the turbines. The new proposal is capable of computing the possibility distributions of the harmonic voltage distortion at all buses of a power system.
Finally, the proposed method is tested by performing simulations in the IEEE 14-bus standard test system for harmonic analysis, connecting to the network a wind farm composed by ten wind turbines of the Full Power Converter (FPC) type.
2. Time-varying harmonics in electric power systems
2.1. Fourier series and harmonics
Harmonics in power systems are a steady state perturbation, characterized by a deviation of the voltage (or current) wave shape from the ideal sine form. Since the wave shape remains periodic, this deviation can be precisely described and quantified by decomposing the distorted wave into its Fourier series.
Fourier's theory proves that any periodic function could be represented by the sum of a fundamental and a series of higher order harmonic components at frequencies that are integer multiples of the fundamental component. Such series establish a relationship between the function in time and frequency domains 0.
The Fourier series of a periodic function f(t), with period T and angular frequency w = 2p/T, can be written as:
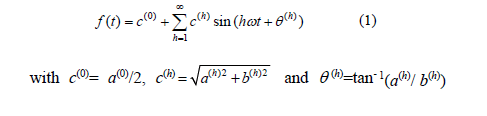
where: h: harmonic component order, c(0): magnitude of the DC component, c(h): peak value of the harmonic component (h) and q (h): phase angle of the harmonic component (h), the Fourier coefficients a(0), a(h) and b(h) are given by:
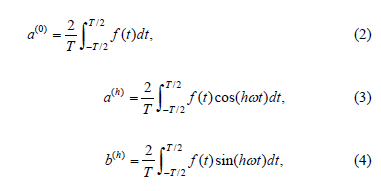
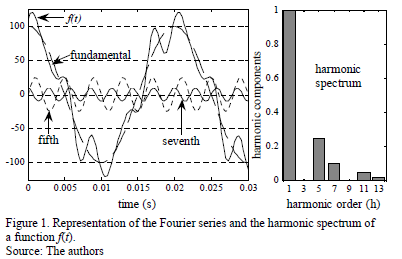
Fig. 1 shows the decomposition of a function f(t) in its harmonic components. The harmonic spectrum is also shown, which is obtained by dividing the peak value of each harmonic component by the peak value of the fundamental component: c(h)/c(1).
2.2. Causes of harmonics in electric power systems
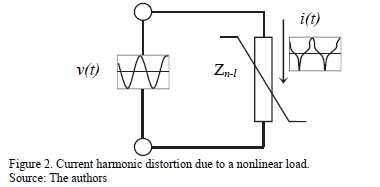
Linear devices satisfy the superposition principle, i.e.: if i(t) is the current flowing through it when a voltage v(t) is applied, then a current a×i(t) will flow if the applied voltage is a×v(t). A non-linear load is a device for which this relationship does not hold. Fig. 2 illustrates this concept.
In an ideal linear power system, both voltage and current waveforms are perfect sine waves. In real power systems, however, there are nonlinear components for which the current is not a sinusoid, even if a perfect sine voltage were applied. This non-sinusoidal current produces voltage drops in other linear or nonlinear impedances and, consequently, the voltage wave is distorted in the whole system.
It is noted that harmonic distortion is a growing problem in power systems due to the increasing use of nonlinear loads.
2.3. Time-varying harmonics
As mentioned above, harmonics are conceptualized as a steady-state phenomenon, that is, the waveform to be analyzed is assumed to be repeated periodically from -∞ to ∞.
In practical situations, however, the voltage and current distortion levels as well as their fundamental components are continually changing in time. This is due to the fact that the network configuration usually changes and its linear and nonlinear loads vary all the time; in addition, even if they were constant their parameters are not usually well-known. All these features make harmonic distortion a phenomenon involving uncertainty.
Therefore, it is inadequate that the harmonic load-flow calculation, in a real power system, be performed on a deterministic basis, i.e., assuming that all the relevant parameters are well known and non-random. In fact, these kinds of studies only provide a static and certain image of a varying and uncertain situation.
Methodologies based on probability theory, with different degrees of sophistication, have been developed to deal with these uncertainties [2]. Practical application of them, however, often has to deal with the lack of information to describe in probabilistic terms the amount and type of medium size and small distributed nonlinear loads (NLs), as well as the composition of linear loads (LLs). This suggests that in many practical cases, the available information for harmonic load flow can be better described through fuzzy measures like possibility distributions.
2.4. Effects of harmonics on the network
There are several problems related to harmonics, such as:
- Overheating of neutral conductors,
- Overheating of transformers,
- Overloading of capacitors for power factor correction,
- Problems with induction motors,
- Control failures in electronic devices that detect the zero crossing of the voltage wave, and others.
3. Modeling the power system components at harmonic frequencies
3.1. Model of Nonlinear Loads
Accurate modeling of nonlinear loads is a difficult issue because of their inherent complexity and because some of them are constantly changing their operational modes. In this section, basic models of nonlinear loads from a deterministic point of view are presented.
In methodologies based on frequency domain analysis, the common practice is to model nonlinear loads through harmonic current sources, whose amplitudes and phases depend on a set of parameters that characterize their harmonic behavior and their operating state.
The simplest model assumes that harmonic currents do not depend on the applied voltage waveform, but only on its power frequency component. For example, for thyristor-controlled rectifiers, expressions like can be used to compute the amplitude and phase of the harmonic components of the injected currents at node j,
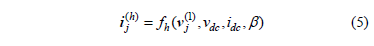
 is the power frequency component of the applied voltage at node j, vdc and idc the voltage and current in the DC side of the rectifier, and b the switching angle of the thyristors.
is the power frequency component of the applied voltage at node j, vdc and idc the voltage and current in the DC side of the rectifier, and b the switching angle of the thyristors.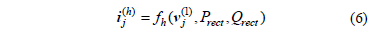
More detailed models have been developed for some of the most important devices based on power electronics; however, such models can be used only when the characteristics of the nonlinear device are well known. This, unfortunately, is not the most common scenario in the case of real electric power systems.
3.2. Behavior and Models of Harmonic Frequencies of the Main Elements of an Electric Power System
Modeling of electric power system elements over a wide range of frequencies is relatively well documented in the bibliography [3,6].
However, due to the importance of this topic, typical harmonic frequency models representing the elements in common power systems, such as transformers, lines and cables, shunt capacitors and loads, are described in what follows.
3.2.1. Transformers
The transformer is usually modeled as a lumped impedance which represents its leakage impedance. Such lumped impedance comprises a series inductance with resistance; this is because the frequency dependent effects are not significant for the harmonic frequencies of common interest. However, other complex models include the nonlinear characteristics of core loss resistance, the winding stray capacitance, the core saturation, the skin effects, etc. Effects of stray capacitance are usually noticeable only for frequencies higher than 4 kHz.
Furthermore, for three-phase transformers the winding connections are important for determining the effect of the transformer on zero-sequence harmonic components, i.e., delta connections isolate these currents from one voltage level to the next. Other connections such as zigzag windings are used to mitigate harmonics.
3.2.1. Overhead lines and underground cables
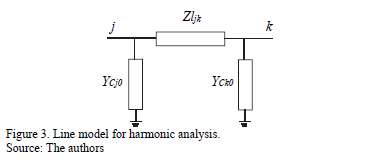
For balanced harmonic analysis, the models of typical lines or cables can be further simplified into a single-phase p-circuit, as shown in Fig. 3, which uses positive and zero sequence data.
In Fig. 3, Zljk comprises a resistance and a series reactance connected between nodes j and k of the network. Moreover, admittances Ycj0 and Yck0 represent two capacitors connected between their respective nodes and earth.
The main issues in modeling lines and cables are the frequency dependence of per-unit length series impedance and the long line effects. As a result, the level of detail of their models depends on the line length and harmonic order.
Thus, as a first approximation, it can be considered that the series resistance is independent of frequency, and that both the series reactance and the capacitive admittances depend linearly on the frequency.
Additionally, more complex models, especially long lines and high frequency harmonics, consider the Skin effect correction in the series resistance and propagation effects by associating several p-circuits in series.
3.2.2. Aggregate load model: shunt capacitors and loads
As in other power system studies, it is only practical to model an aggregate load for which reasonably good estimates of active (MW) and reactive (MVAR) power are usually readily available. However, this information is insufficient to establish an adequate load model at harmonic frequencies. In fact, the system harmonic impedance is sensitive to the model parameters, model topology and the actual load composition.
In agreement with what was previously stated, the important components of the load for harmonic analysis are:
- The resistive component (passive loads),
- The step-down transformer (distribution or service transformers),
- The motor components (motive loads),
- The non-linear loads (exposed at section 3.1), and
- The shunt capacitors and filters (such as power factor compensation capacitors and so on).
Linear passive loads have a significant effect on system frequency response, primarily near resonant frequencies, i.e., the resistive component provides damping when the overall system response is near a parallel resonance (high impedance).
The aggregate load model should include the distribution or service transformer. At power frequencies the effect of distribution transformer impedance is not of concern in the analysis of the high voltage network; however, at harmonic frequencies the impedance of the transformer is practically an inductance in series with the load. Moreover, it is also important to discriminate the motor components from the overall load because the active power absorbed by rotating machines does not exactly correspond to the value of a damping resistance.
Furthermore, it is clear that the nonlinear load components determine the levels of harmonic currents injected to the system.
Finally, the shunt capacitors and the stray inductance of the supply system can resonate at or near one of the harmonic frequencies.
Several models to aggregate loads at harmonic frequencies have been proposed in the bibliography [3,7]. However, load representation for harmonic analysis is still an active research area.
Section 6 of this paper deals with the fact that most of the magnitude and composition parameters, which are necessary to achieve an adequate load model representation, are known with uncertainty for real power systems. In effect, the influence of such uncertain parameters in a general load model is studied in [7].
3.3. Model of a wind turbine at harmonic frequencies
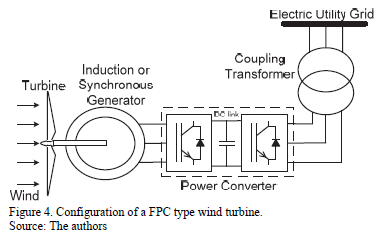
There are several types of wind turbines, among which include: Fixed Speed Induction Generator (FSIG), Doubly Fed Induction Generator (DFIG) and Full Power Converter (FPC). Each type of system has advantages and disadvantages inherent to the technology used, and pursuing the same goal: maximum energy transfer from the wind turbine to the grid, at the lowest cost, and ensuring adequate levels of electromagnetic compatibility. However, this paper will only deal with the modeling of harmonic frequency of the wind turbine FPC type, as they are widely used in wind farms in Latin America, and also have a characteristic harmonic spectrum by multiples of the grid frequency [8]. Despite this, in the future the study may be extended to other turbine models.
The basic configuration of a wind turbine type FPC is presented in Fig. 4. The two main components to be modeled to harmonic frequency are the generator and the converter.
3.3.1. Generator
In synchronous generators, the rotating magnetic field established by a harmonic current in the stator rotates at a speed significantly different from that of the rotor. Therefore, for harmonic frequencies, the impedance is usually taken to be either the negative sequence impedance or the average of the direct and quadrature subtransient impedances [3]:
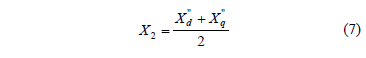
In the case of induction generators, the inductance is represented through the locked rotor reactance.
In both cases, the dependency of the resistance on the frequency may be important due to the skin effect and the eddy current losses; therefore, this dependence may be considered by increasing the resistance value at the fundamental frequency by 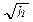 , where h is the harmonic order.
, where h is the harmonic order.
Furthermore, in induction machines the "a" parameter is considered, which relates the rotor resistance R1 with the locked rotor resistance RB, by a = R1/RB, and has a typical value equal to 0.5. Additionally, the slip at harmonic frequency sh is given by ,
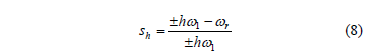
where wr is the rotor speed and the sign + or - depends on the positive or negative sequence of the harmonic order considered.
The models for harmonic frequency for induction and synchronous generators are shown in Fig. 5.
3.3.2. Converter
In an FPC type wind turbine the electric parameters, which vary with the wind speed, are transformed to grid parameters by a converter. The commutation valves used in the converter are Insulated Gate Bipolar Transistors (IGBT) with anti-parallel diodes. On the side of the generator, the convert transforms a three-phase AC voltage of variable amplitude and frequency in a constant DC voltage. On the side of the grid, the converter is responsible for converting this DC voltage into an AC voltage phase, with constant amplitude and frequency (exactly like the power grid where the unit is connected).
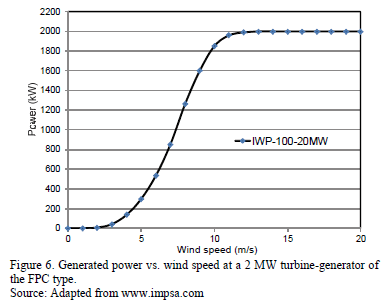
Using digital signal processors, the vector control is performed in the converter (PWM technology). The control algorithms are diverse and depend on the manufacturer, but always look for the optimum use of turbine-generator. In Fig. 6 the characteristic curve of wind speed versus generated power through a commercial generator of 2 MW is shown.
Although a characteristic function of the harmonic behavior of a wind turbine-generator type FPC has not been fully defined (e.g., similar expressions to those defined in and for a converter), there is information, such as that presented in Table 1, which relates the harmonic current, iw(h), injected by the wind generator, as a percentage of the fundamental frequency current, iw(1), (50 or 60 Hz). Note that this type of data is normally provided by the manufacturer and it is obtained from the electric power quality tests.
Thus, using information from Fig. 6 and Table 1, it is possible to model the harmonic current that injects a wind turbine-generator according to the wind speed, in this case a wind generator 2 MVA.
4. Possibilistic harmonic load-flow
4.1. Uncertainty management
Most real-world decisions are made within an environment in which: goals, constraints, possible actions (solution space) and consequences are not precisely known. To deal quantitatively with imprecision, usually techniques and concepts of probability theory are employed. However, it must be considered, that when uncertainty is modeled by using probability density functions, PDFs, it is implicitly accepted that the imprecision of whatever nature can be compared with randomness, an assumption that may be questionable. For example, in many situations, the decision maker cannot measure or express an explicit function for all determinant parameters within a decision process. This is due to various reasons, e.g., incomplete information, insufficient knowledge, lack of or inaccuracy of models, or that the cost involved to acquire the lacking information is high regarding the improvement in results. Therefore, in those situations, it could be advisable to appeal to other types of information, namely: experience, intuition, ideology, beliefs, feelings, etc., i.e., options with a degree of subjectivity, but not of arbitrariness.
Fuzzy sets and possibility theories provide a formal framework to model vague relationships or concepts, such as, size, pollution, economics, satisfaction, adequacy, etc. Definitions for the formal treatment of the fuzzy sets and possibility distributions can be found in [10], and applications to the specific problem of harmonic analysis in [11-14].
4.2. The possibilistic harmonic load-flow
Through references [11-14], a complete formulation for calculating the harmonic load-flow, considering uncertainties in the input parameters, has been presented. Such uncertainties are modeled by possibility distributions. Readers are encouraged to review such references to achieve a better understanding of the methodology described below.
4.2.1. General formulation for the case of possibilistic independence
The simpler case not involving possibilistic dependences will be considered first. For this purpose, consider the general expression of the harmonic bus voltages, i.e.:
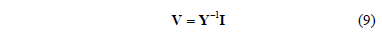
where the harmonic order has not been identified for notational simplicity.
When harmonic interaction is neglected (harmonic penetration approach, [3]) components ik (k = 1 n) of vector I do not depend on the harmonic voltages.
Moreover, the diagonal elements of Y and the injected currents ik, depend on the model of the linear and nonlinear loads, and on a number of parameters describing their magnitudes and compositions. For the sake of generality, in this section no hypotheses will be made regarding these aspects as the development of a specific model is postponed until section 4.3.
However, by assuming that a generic vector 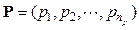 of np parameters completely describes the loads of the system, all the injected currents and the bus admittance matrix in can be determined accordingly, i.e:
of np parameters completely describes the loads of the system, all the injected currents and the bus admittance matrix in can be determined accordingly, i.e:
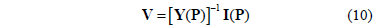
By denoting 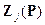 the jth row of
the jth row of 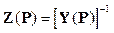 , the amplitude of the harmonic voltage at a generic bus j, can be written as:
, the amplitude of the harmonic voltage at a generic bus j, can be written as:
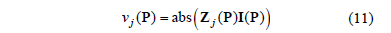
or, using a more general notation:
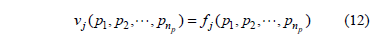
When pk are uncertain parameters described through fuzzy numbers 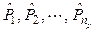 with independent membership functions
with independent membership functions 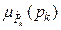 , k = 1
np, the harmonic voltage vjbecomes a possibilistic variable, expressed by a fuzzy number
, k = 1
np, the harmonic voltage vjbecomes a possibilistic variable, expressed by a fuzzy number 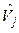 . Thus:
. Thus:
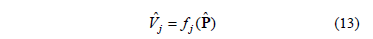
where 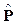 is the fuzzy Cartesian product:
is the fuzzy Cartesian product: 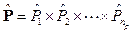 , whose membership function is (see [13]):
, whose membership function is (see [13]):
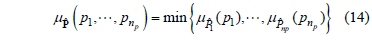
Accordingly, the membership function of 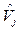 can be written as:
can be written as:
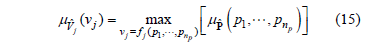
and by replacing in ,
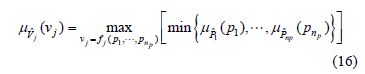
Analogously, the following relationships can be written in terms of the a-cuts (for definition see [10]):
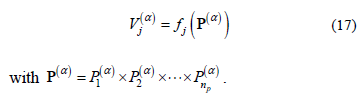
Therefore, each a-cut is the interval:
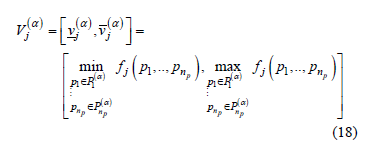
and can be determined solving two optimization problems (minimization and maximization respectively).
4.2.2. General Formulation for the case of possibilistic dependence
A more general situation, whenever the possibilistic dependences to be modeled are of the type due to a well-defined physical connection among fuzzy variables whose possibility distribution functions have been determined independently, is analyzed in what follows.
In this general case the uncertain variables are a set of np parameters 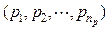 , with possibility distribution functions
, with possibility distribution functions 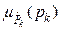 , k = 1
np, such as the total active bus loads; the load due to nonlinear devices, static linear devices and induction motors; the starting current of induction motors; kind and operating point of nonlinear devices, etc.
, k = 1
np, such as the total active bus loads; the load due to nonlinear devices, static linear devices and induction motors; the starting current of induction motors; kind and operating point of nonlinear devices, etc.
In general, among these parameters some deterministic relationships exist (e.g., active load due to linear and nonlinear devices must add up to the total active load) that can be expressed through a system of nd < np equations.
In this way, nd parameters can be expressed in terms of the remaining 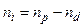 as follows:
as follows:
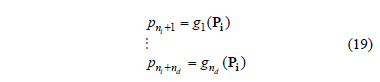
where 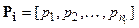 . Here it is assumed, without loss of generality, that the first niparameters are independent, and that are the expressions for the dependent ones.
. Here it is assumed, without loss of generality, that the first niparameters are independent, and that are the expressions for the dependent ones.
Now, if the possibility distribution functions 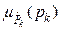 are compatible and all of them are equally reliable, then the standard fuzzy intersection operator, [11], can validly be applied to obtain the joint distribution functions, for each node; i.e.:
are compatible and all of them are equally reliable, then the standard fuzzy intersection operator, [11], can validly be applied to obtain the joint distribution functions, for each node; i.e.:
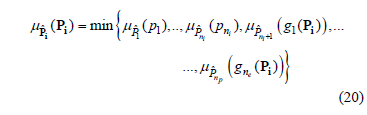
that can also be written as:
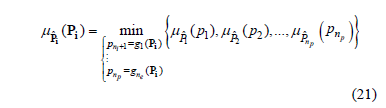
Moreover, from a deterministic viewpoint, the harmonic voltage at bus j is, in general, a function of parameters pk, with k = 1 np.
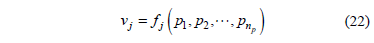
Therefore, according to the extension principle, the possibility distribution function of vj can be written as:
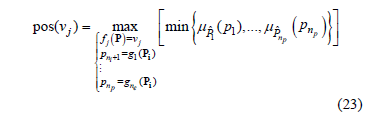
which is a direct generalization of equation above.
Similarly, the a-cuts of 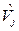 are the intervals:
are the intervals:
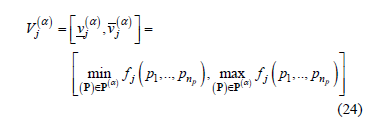
and can be determined solving the following optimization problems:
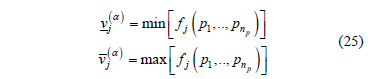
both subject to:
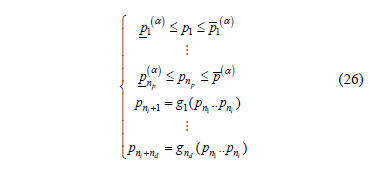
4.2.3. Possibilistic harmonic load-flow algorithm
4.2.4. Fuzzy modeling of linear and non-linear loads
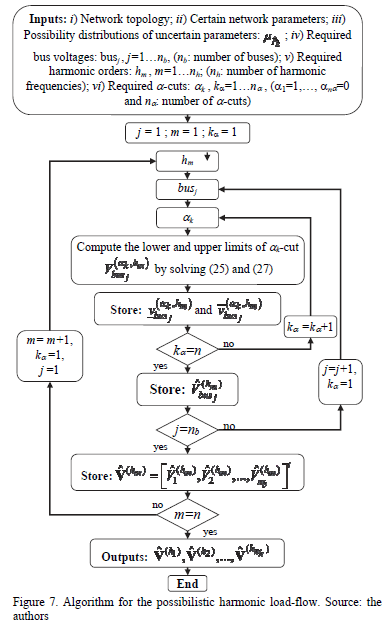
The methodology to calculate the possibilistic harmonic load-flow is summarized in Fig. 7. However, for its suitable implementation, it is important to establish an appropriate set of parameters pk, k=1 np, to describe the information available regarding some features of loads, nonlinear loads and wind generators, thus allowing to compute the admittances from node to ground, and the harmonic currents injected at each node.
The main steps for developing a nodal model are: 1) define the circuit which models the harmonic load behavior, 2) select a set of fuzzy parameters describing the available information with respect to the composition and magnitude of loads and wind generators (these parameters are called model parameters, and differ from the electric circuit parameters identified in the first step), 3) establish the relationships between model and the circuit parameters.
4.2.5. General model of the aggregated load for harmonic analysis
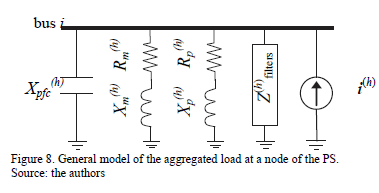
Several studies suggest the electric circuit shown in Fig. 8, [7], as a suitable model for harmonic load-flow calculation, where each branch represents the sum of loads with similar characteristics. This model also allows the inclusion of the wind generator as an RL branch and a harmonic current source.
where 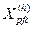 models capacitors for power factor correction.
models capacitors for power factor correction. 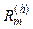 and
and 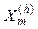 model rotating machinery.
model rotating machinery. 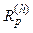 and
and 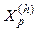 model passive loads and small engines. i(h) models harmonic currents injected by nonlinear devices (rectifiers, inverters, wind turbines etc.); and filters model the RLC circuits installed to filter harmonics.
model passive loads and small engines. i(h) models harmonic currents injected by nonlinear devices (rectifiers, inverters, wind turbines etc.); and filters model the RLC circuits installed to filter harmonics.
4.2.6. Fuzzy parameters
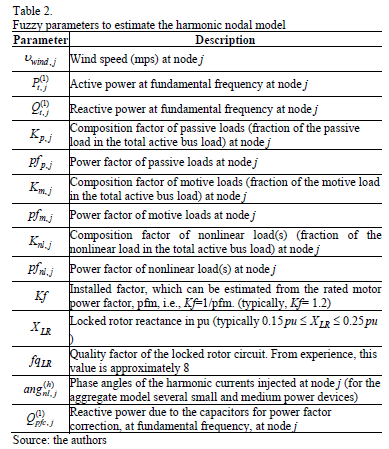
The circuit parameters in the load model of Fig. 8 are uncertain and, in principle, could be described through their possibility functions. In practice, however, the available information usually refers to other characteristics of the load, the wind generator, and the environment, e.g., total active and reactive power, the percentage of it due to nonlinear devices, the wind speed, etc. Table 2 shows the model parameters, which are usually available in practice.
These model parameters, together with the appropriate expressions, allow the parameters of the circuit in Fig. 8 to be computed.
4.2.7. Relationships between the model parameters and the aggregated load parameters
For each harmonic frequency, nonlinear loads are represented by current sources at their respective nodes, and link the model parameters by means of expressions as and . In addition, the model for the harmonic current injected by a wind turbine corresponds to that presented in Section 3.
Regarding linear loads, detailed expressions that relate the model parameters with the elements of the aggregate circuit of Fig. 8, are presented in the Appendix (Section 8) of reference [13].
5. Case study
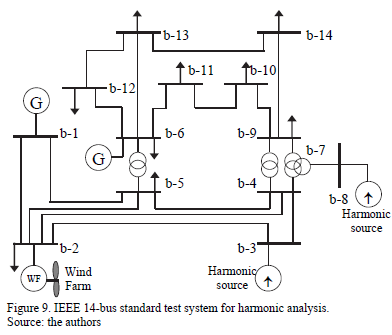
5.1. Description of the electric power system
The test system is presented in Fig. 9. Main parameters of the power system are summarized in [15]. Furthermore, in Fig. 7 of reference [13], the values of the uncertain parameters to model aggregated harmonic loads and sources are presented. For example, these uncertain parameters are modeled through triangular possibility distributions, and the values reported in [11,13] are the same employed for this case study. The only difference is that for a 20 MW wind farm of ten generators, each one of 2 MW, is included at the generation bus 2. Moreover, it is assumed that wind speed is known with uncertainty, and that it can vary between 5 mps and 20 mps. Under other wind speed conditions, the generators are turned off due to security reasons.
5.2. Results
The aim of the simulation is to compare the results obtained in both cases: i) the case in which the generator at bus 2 corresponds to a synchronous machine that does not inject harmonics into the network (this case corresponds with that reported in reference [13]), and ii) the proposed case in this article, in which the generator at bus two is replaced by ten FPC-type wind generators, each one of 2 MW.
5.3. Discussion
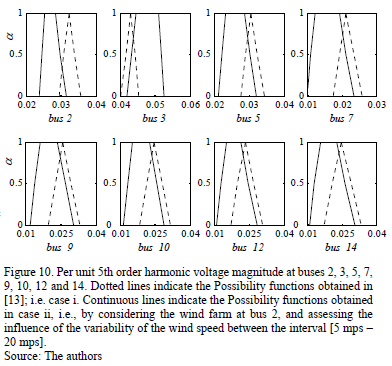
From results presented in Fig. 10, it can be concluded that the wind farm connection has an impact over the 5th harmonic voltage magnitudes at all buses of the power system.
In particular, in most of the buses, there is a decrease in the harmonic distortion, surely due to phasorial cancellation between the harmonic currents flowing through the network. However, this situation is different at bus 3, where the harmonic voltage distortion increases considerably and reaches levels that can be intolerable from the electromagnetic compatibility point of view.
It can also be noted that obtained possibility distributions, in the case ii, are trapezoidal. This is the result of modeling the uncertainty related to the wind speed as an interval, unlike the other uncertain parameters that are modeled with triangular possibility distributions. It is, therefore, concluded that there is uncertainty in the wind speed; i.e., an input parameter, has a considerable effect on the uncertainties associated with the harmonic voltage magnitudes, i.e., the outputs of the possibilistic harmonic load-flow.
6. Conclusions
This work has focused on including the wind-turbine FPC type within the methodology for calculating the possibilistic harmonic load-flow. The methodology is able to consider the uncertainties due to the deficiency of information regarding harmonic sources and the magnitude and composition of linear loads, i.e., wind turbines, nonlinear devices, and conventional loads.
The Possibility Theory has been selected to model uncertainty because it seems to be an interesting alternative for situations where the information is too vague to define reliable probability distributions, a common situation in the context of harmonic studies.
The possibilistic harmonic load-flow has shown flexibility allowing include wind farms as harmonic sources. In fact, the reformulated method has been proven in the IEEE 14-bus standard test system for harmonic analysis.
In order to evaluate the performance of the proposal, a comparison with previously published simulations, in which wind farms were not considered, was performed in this article. Results obtained show that uncertainty in the wind speed has a considerable effect on the uncertainties associated with the computed harmonic voltage magnitudes; therefore, this uncertainty must be considered when harmonic studies must be developed.
It is hoped that the methodology developed contributes to the solution of real problems related with harmonics in electric power systems. For example, problems such as decision making under uncertainty, harmonic filter design, harmonic filters and capacitors location, analysis of the impact of the connection wind farms, among others.
In future work, research efforts must be conducted for the development of harmonic models for other types of wind turbines, e.g., DFIG type wind turbines, and their inclusion in the possibilistic harmonic load-flow method.
References
[1] Fourier, J., Theorie analytique de la chaleur, par M. Fourier. Chez Firmin Didot, père et fils, 1822. [ Links ]
[2] Ribeiro, P.F., Editor. Time-Varying waveform distortions in Power Systems. J. Wiley & Sons Press, 2009. [ Links ]
[3] IEEE, Task force on harmonics modeling and simulation. Tutorial on harmonics modeling and simulation. IEEE Publication TP-125-0, 1998. [ Links ]
[4] IEEE, Std 519-1992. IEEE Recommended practices and requirements for harmonic control in electrical power systems, 1992. [ Links ]
[5] IEEE, Task force on harmonics modeling and simulation. Modeling and simulation of the propagation of harmonics in electric power networks. IEEE Trans. on Power Delivery, 11 (1), pp. 452-465, 1996. [ Links ]
[6] CIGRE, Working Group 36-05. Harmonics, characteristic parameters, methods of study, estimates of existing values in the network. Electra, 77, pp. 35-54, 1981. [ Links ]
[7] Romero, A.-A., Zini, H.-C., Ratta, G. and Dib, R., A novel fuzzy number based method to model aggregate loads for harmonic load-flow calculation, Transmission and Distribution Conference and Exposition: Latin America, 2008 IEEE/PES, pp. 1-8, 13-15, 2008. [ Links ]
[8] Baroudi, J.A., Dinavahi, V. and Knight, A.M., A review of power converter topologies for wind generators. Renewable Energy, Elsevier, 32, (14), pp. 2369-2385, 2007. [ Links ]
[9] Tentzerakis, S.T. and Papathanassiou, S.A., An investigation of the harmonic emissions of wind turbines. Energy Conversion, IEEE Transactions on, 22 (1), pp. 150-158, 2007. [ Links ]
[10] Zimmermann, H.J., Fuzzy set theory and its applications. Kluwer Academic Publishers, Third Edition 1996. [ Links ]
[11] Romero, A.A., Zini, H.C. and Rattá, G.. Modelling input parameter interactions in the possibilistic harmonic load flow. Generation, Transmission & Distribution, IET, 6 (6), pp. 528-538, 2012. [ Links ]
[12] Romero, A.A., Zini, H.C. and Rattá, G., An overview of approaches for modelling uncertainty in harmonic load-flow. Ingeniería e Investigación, 31 (2), pp. 18-26, 2011. [ Links ]
[13] Romero, A.A., Zini, H.C., Rattá, G. and Dib, R., Harmonic load-flow approach based on the possibility theory. Generation, transmission & distribution, IET, 5 (4), pp. 393-404, 2011. [ Links ]
[14] Romero, A.A., Zini, H.C., Rattá, G. and Dib, R., A fuzzy number based methodology for harmonic load-flow calculation, considering uncertainties. Latin American Applied Research, 38, pp. 205-212, 2008. [ Links ]
[15] IEEE, Task force on harmonics modeling and simulation. Test systems for harmonics modeling and simulation. IEEE Transactions on Power Delivery, 14, pp. 579-585, 1999. [ Links ]
A.A. Romero-Quete, was born in Colombia in 1978. He received his BSc. in Electrical Engineering degree in 2002, from the Universidad Nacional de Colombia and his PhD. in 2009 from the Instituto de Energía Eléctrica, Universidad Nacional de San Juan (IEE-UNSJ), Argentina. He worked and researched as a high voltage test technique engineer at the Laboratorio de Ensayos Eléctricos Industiales, Fabio Chaparro, UNC until 2003, when, he was awarded a scholarship from the German Academic Exchange Service (Deutscher Akademischer AustauschDienst - DAAD) to conduct PhD. studies at IEE-UNSJ. Currently. He works as a researcher at the Consejo Nacional de Investigaciones Científicas y Técnicas, CONICET, at the IEE-UNSJ, Argentina. His research interests include asset management, power quality, and high voltage test techniques.
G.O. Suvire, was born in San Juan, Argentina. He graduated in Electric Engineering from the Universidad Nacional de San Juan (UNSJ), Argentina, in 2002 and received his PhD. from the same university in 2009, carrying out part of his doctorate in the COPPE institute, at the Federal University of Rio de Janeiro in Brazil, supported by CAPES. From 2009 to 2011, he worked as a Postdoctoral research fellow for the Argentinean National Council for Science and Technology Research (CONICET) at the Institute of Electrical Energy (IEE), UNSJ, Argentina. He is currently an assistant professor of Electrical Engineering at UNSJ, Argentina. His research interests include simulation methods, power systems dynamics and control, power electronics modeling and design, and the application of wind energy and energy storage in power systems.
H.C. Zini, was born in San Juan, Argentina, on February 4, 1958. He received his BSc. degree in Electrical Engineering in 1985, from the Universidad Nacional de San Juan (UNSJ), Argentina,| and his PhD degree at UNSJ in 2002. Currently, he is a senior researcher and Consulting Engineer with the Instituto de Energía Eléctrica of UNSJ, Argentina. In 1998, he completed a one-year postgraduate stage at CESI, Milan, Italy, working on electromagnetic transient calculation. His research interests are electromagnetic transients and power quality.
G. Rattá, was born in Italy in 1950. He received his BSc. degree Electromechanical Engineering in 1974, from Universidad Nacional de Cuyo-Argentina. Since 1997 he has been director of the IEE-UNSJ, Argentina. Prof. Rattá is currently an assistant professor in the UNSJ, Argentina. He is also member of the Commission of Postgraduate Evaluation. His research interests include transient behavior of power system components and power quality.