DOI: http://dx.doi.org/10.15446/dyna.v82n192.45512

Compressive sensing: A methodological approach to an efficient signal processing

Sensado compresivo: Una aproximación metodológica para un procesamiento de señales eficiente

Evelio Astaiza-Hoyos ^a, Pablo Emilio Jojoa-Gómez ^b & Héctor Fabio Bermúdez-Orozco ^c

^a Facultad de Ingeniería, Grupo GITUQ, Universidad del Quindío, Armenia, Colombia. eastaiza@uniquindio.edu.co
^b Facultad de Ingeniería Electrónica y Telecomunicaciones, Grupo GNTT, Universidad del Cauca, Popayán, Colombia. pjojoa@unicauca.edu.co
^c Facultad de Ingeniería, Grupo GITUQ, Universidad del Quindío, Armenia, Colombia. hfbermudez@uniquidio.edu.co

Received: September 10^th, 2014. Received in revised form: April 14^th, 2015. Accepted: May 19^th, 2015.

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

---

Abstract
Compressive Sensing (CS) is a new paradigm for signal acquisition and processing, which integrates sampling, compression, dimensionality reduction and optimization, which has caught the attention of a many researchers; SC allows the reconstruction of dispersed signals in a given domain from a set of measurements could be described as incomplete, due to that the rate at which the signal is sampled is much smaller than Nyquist's rate. This article presents an approach to address methodological issues in the field of processing signals from the perspective of SC.

Keywords: Compressive Sensing, Sampling, Compression, Optimization, Signal Processing, Methodology

Resumen
Sensado Compresivo (SC) es un nuevo paradigma para la adquisición y procesamiento de señales, el cual integra muestreo, compresión, reducción de dimensionalidad y optimización, lo cual ha captado la atención de una gran cantidad de investigadores; SC permite realizar la reconstrucción de señales dispersas en algún dominio a partir de un conjunto de mediciones que podrían denominarse incompletas debido a que la tasa a la cual la señal es muestreada es mucho menor que la tasa de Nyquist. En este artículo se presenta una aproximación metodológica para abordar problemas en el ámbito del procesamiento de señales desde la perspectiva de SC.

Palabras clave: Sensado Compresivo, Muestreo, Compresión, Optimización, Procesamiento de Señales, Metodología.

---

1. Introducción

La principal motivación en Sensado Compresivo (SC) es que muchas señales del mundo real pueden aproximarse adecuadamente por señales dispersas, es decir, que pueden aproximarse por una combinación lineal de términos de una base vectorial, en la cual solo se tienen algunos términos significativos, razón por la cual, se considera que SC es una tecnología promisoria la cual contribuirá al mejoramiento significativo de la forma en que actualmente se realiza el procesamiento de señales, reduciendo los costos computacionales y con ello optimizando la utilización de otros recursos tales como energía.

Para obtener una representación comprimida se calculan los coeficientes en la base seleccionada (por ejemplo Fourier o una base Wavelet [1,2]) y luego se mantienen sólo los coeficientes más grandes, sólo éstos se almacenarán, mientras que el resto de ellos se hacen cero cuando se recupera la señal comprimida.

La pregunta inmediata ante este escenario es: ¿existe una manera directa de obtener la versión comprimida de la señal?, sin embargo, medir directamente los coeficientes mayores es imposible, ya que normalmente no se sabe a priori, cuáles de ellos son en realidad los más grandes. Sin embargo, SC proporciona una manera de obtener la versión comprimida de una señal usando sólo un pequeño número de mediciones lineales y no adaptativas. Incluso, SC predice que es posible recuperar la señal a partir de mediciones sub-muestreadas de la misma, mediante métodos computacionalmente eficientes, por ejemplo optimización convexa.

Es de anotar que, las medidas lineales arbitrariamente sub-muestreadas, descritas por la denominada matriz de sensado en general, no tendrán éxito en la recuperación de vectores dispersos. Razón por la cual se han formulado algunas condiciones necesarias y suficientes que se deben cumplir por la matriz para permitir recuperar vectores dispersos; estas condiciones son bastante difíciles de comprobar cuando la matriz de sensado es determinista, al menos cuando se apunta a trabajar con la mínima cantidad de mediciones. De hecho, en la actualidad, como se muestra en [1,2] se obtienen grandes avances utilizando matrices aleatorias, en las que las entradas de la matriz son independientes e idénticamente distribuidas de acuerdo a cualquier distribución sub-gausiana, esto hace que la cantidad de mediciones requeridas sea menor que en el caso de matrices deterministas de acuerdo a la caída pronunciada de la función de distribución, lo que implica la concentración de los valores representativos de la señal.

El proceso completo, para abordar un problema desde el paradigma de SC, consta de tres partes fundamentales: 1.) Representación dispersa de la señal. 2.) Toma de medidas y codificación lineal y 3.) Recuperación dispersa o decodificación no lineal; etapas que se tratan en detalle en el resto del artículo.

El principal objetivo del presente artículo es establecer una primera aproximación a un marco de referencia metodológico, mediante el cual, se definan no solamente las etapas en la solución de problemas basados en SC, sino también en los criterios de desarrollo de las mismas, basándose en definiciones, teoremas y técnicas que serán proporcionadas e ilustradas. Igualmente se busca responder a las preguntas típicas en el ámbito del SC tales como: ¿Qué características o condiciones debe cumplir la matriz de sensado para garantizar recuperación de la señal sensada? ¿Cuantas medidas deben tomarse de una señal dispersa para garantizar recuperación? ¿Cómo seleccionar el algoritmo de recuperación más adecuado? La estructura del artículo se presenta de acuerdo a las preguntas formuladas anteriormente.

2. Representación dispersa de la señal

Generalmente, las señales reales pueden representarse con un muy buen nivel de aproximación, mediante una combinación lineal de algunos pocos elementos de una base conocida; cuando esta representación es exacta, se dice que la señal es dispersa, lo cual permite capturar el hecho que en muchos casos, señales que residen en altas dimensiones, contienen relativamente poca información comparada con su ambiente dimensional. Matemáticamente, se dice que una señal x es k-dispersa cuando ésta tiene a los sumo k valores no cero, donde

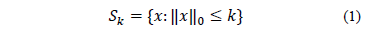
La ec. (1), denota el conjunto de todas las señales 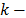dispersas, y el operador 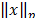denota la norma 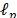del vector 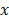, cuando 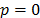la norma definida en la ec. (2) no cumple la desigualdad triangular, por lo tanto por definición se tiene que 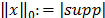y representa la cardinalidad del soporte del vector 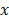; la norma 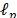se define como se muestra en la ec. (2).

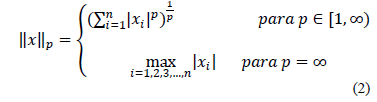
Típicamente en la realidad las señales no son en sí mismas dispersas, pero admiten ser representadas de manera dispersa en alguna base 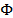, por lo tanto 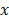puede representarse como se ilustra en la ec. (3).

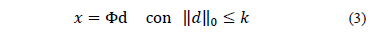
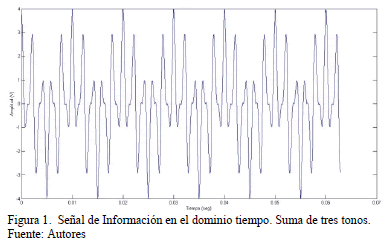
Por ejemplo, en el dominio del tiempo, una señal típica de información en el ámbito de las telecomunicaciones luce como la Fig. 1, donde no es claro que la señal sea dispersa.

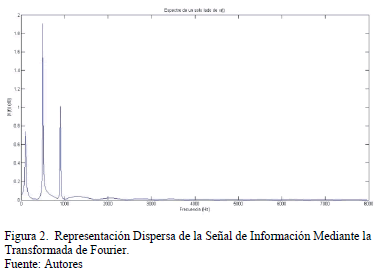
Sin embargo, al obtener su transformada de Fourier, la cual se ilustra en la Fig. 2, puede verse que la mayoría de los coeficientes de la señal son muy pequeños, por lo tanto, puede obtenerse una representación bastante aproximada de la señal haciendo cero los coeficientes muy pequeños mediante un método de umbral, consiguiendo de esta manera, una representación 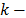dispersa de la señal (en este caso ).

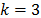Al medir el error de aproximación utilizando una norma 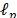, se está realizando un procedimiento que permite obtener la mejor aproximación de 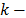términos de la señal original, esta medida de error, es el eje central de la aproximación no lineal [3] no lineal porque la selección de cuales coeficientes se mantienen en la aproximación depende de la señal en sí misma.

Es importante considerar que un modelo disperso es altamente no lineal, siempre que los elementos seleccionados de la base para representar una señal pueden cambiar de señal a señal, lo cual puede apreciarse cuando se realiza una combinación lineal de dos señales 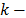dispersas, combinación que en general no será 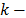dispersa, dado que los soportes de las señales no necesariamente coinciden, aunque si se puede generalizar que si 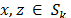luego .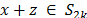

En la práctica, un aspecto de gran importancia es que solo pocas señales reales son verdaderamente dispersas, pero en su gran mayoría pueden aproximarse a señales dispersas [4,5], por lo tanto, puede calcularse el error de aproximar una señal 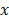por alguna señal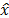 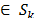como se indica en la ec. (4).

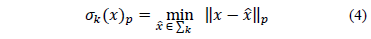
Si 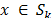es claro que 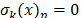para cualquier .

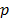3. Diseño de matrices de sensado

Asumiendo que la señal 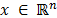es 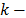dispersa, de la cual se tomarán 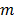medidas lineales mediante un sistema de adquisición; que puede representarse matemáticamente como lo indica la ec. (5).

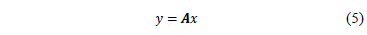
Donde es una matriz de tamaño 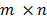y 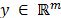. La matriz representa una disminución de la dimensionalidad de la señal 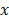dado que la mapea desde su espacio original 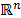, el cual es generalmente grande, a un espacio 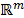, donde 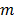es en general mucho más pequeño que 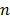. En este caso igualmente se asume que las medidas son no adaptativas, lo cual significa que las filas de la matriz son fijas, y por lo tanto no dependen de las medidas adquiridas.

De acuerdo a lo anterior, se pueden formular las siguientes dos preguntas: ¿Cómo puede realizarse el diseño de la matriz de sensado de tal manera que esta garantice la conservación de la información contenida en la señal 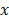? ¿Cómo puede reconstruirse o recuperarse la señal original 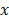a partir de las medidas tomadas 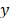?; para dar respuesta a estas preguntas, y dado que el motivo primario del presente artículo es realizar una primera aproximación a un marco de referencia metodológico para la aplicación de SC, no se realiza directamente una propuesta sobre un procedimiento de diseño, sino que se ilustran las propiedades que debería tener la matriz de sensado para permitir la preservación de la información y garantizar la reconstrucción de la señal original de manera única, para ello, se parte de la introducción de algunos conceptos, definiciones y teoremas dados a continuación.

Inicialmente se introduce el concepto de espacio nulo de la matriz denotado como se indica en la ec. (6).

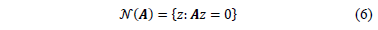
Dado que el interés, es recuperar todas las señales dispersas 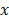a partir de las medidas 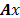, por lo tanto, es claro que para cualquier par de vectores diferentes 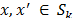, se debe tener que 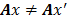, ya que de otra manera es imposible diferenciar 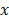de 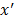basándose solamente en las medidas 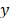, ya que si se presenta que 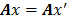, luego 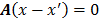con 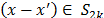, de donde se aprecia que permite representar de manera única a todos los vectores dispersos 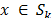si y solamente si 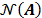no contiene vectores en 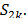En este artículo, para caracterizar esta propiedad se utilizará la definición de la "chispa" (spark) de una matriz [6].

Definición 1: La "chispa" (spark) de una matriz se define como el menor número de columnas de que son linealmente dependientes.

La anterior definición permite plantear el siguiente teorema, el cual garantiza que 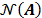no contiene vectores en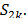

Teorema 1[6]: Para cualquier vector 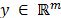, existe al menos una señal 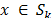, tal que 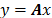si y solamente si

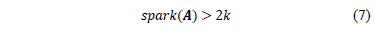
La demostración del Teorema 1 se realiza por contradicción en [6].

Dado que 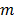es la cantidad de filas de la matriz , en el peor de los casos, el rango de la matriz coincide con el número de filas, y por consiguiente 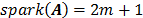, por lo tanto, se infiere que 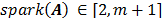y por lo tanto del Teorema 1 de la ec. (7) se tiene que .

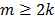Cuando se trabaja con señales exactamente dispersas, la "chispa" de la matriz proporciona una caracterización completa de cuando es posible reconstruir la señal dispersa a partir de las muestras medidas; sin embargo, cuando se trabaja con señales aproximadamente dispersas se deben considerar algunas condiciones más restrictivas sobre el espacio nulo de la matriz [7], donde se debe garantizar, que 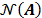no contiene vectores que sean muy compresibles, adicionalmente a vectores que sean dispersos. Por lo anterior, suponiendo que 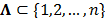es un subconjunto de índices, y sea 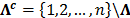. Se representa como 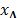al vector de longitud 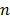obtenido haciendo cero las entradas de 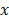indexadas por 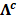; de forma similar, se representa como 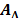a la matriz de tamaño 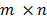obtenida convirtiendo en el vector cero las columnas de indexadas por .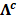

Definición 2: Una matriz satisface la propiedad de espacio nulo de orden 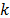, si existe una constante 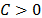tal que

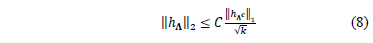
Para todo 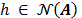y para todo 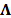tal que 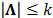. Donde el operador denota cardinalidad.

Por lo tanto, la propiedad de espacio nulo cuantifica el hecho de que los vectores en el espacio nulo de la matriz no deberían ser demasiado concentrados en un pequeño subconjunto de índices. Por ejemplo, si un vector 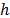es estríctamente 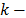disperso, luego existe un 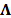tal que 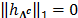y por lo tanto, la (8) implica que 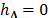. Por lo tanto, si una matriz satisfice la propiedad de espacio nulo, luego el único vector 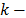disperso en 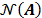es .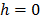

Para describir completamente las implicaciones de la propiedad de espacio nulo en el diseño de la matriz de sensado, y por consiguiente, en el contexto de recuperación dispersa, es necesario introducir algunos conceptos con respecto a cómo se mide el desempeño de los algoritmos de recuperación de señales dispersas cuando se trabaja con señales que en general son no dispersas. Para ello, considerando que 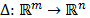representa el método de recuperación de la señal, luego, aplicando la ec. (8) al error de aproximación del método y utilizando la ec. (4) se llega a la expresión en la ec. (9).

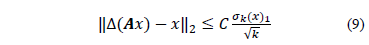
Condición que garantiza recuperación exacta de toda señal 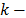dispersa posible, pero también garantiza un grado de robustez en el escenario de trabajar con señales no dispersas, que depende directamente, de que tan bien se realiza la aproximación de dichas señales a vectores 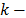dispersos[7].

Teorema 2 [5]: Sea 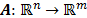describe una matriz de sensado, y sea 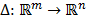describe un algoritmo de recuperación dispersa. Si el par (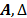) satisface la ec. (9), luego satisface la propiedad de espacio nulo de orden .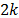

La demostración del teorema se encuentra en [7].

Sin embargo, cuando las medidas de la señal dispersa se encuentran contaminadas por algún tipo de ruido, tal como ruido blanco o ruido de cuantización, se deben considerar condiciones aún más fuertes, dado que la propiedad de espacio nulo no considera el ruido. Es por lo anterior que en [8] se introduce la condición denominada propiedad de isometría restringida aplicada sobre la matriz de sensado.

Definición 3: Una matriz satisface la propiedad de isometría restringida de orden 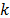, si existe un 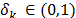tal que

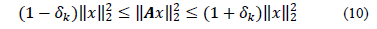
Para todo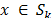

Si una matriz satisface la propiedad de isometría restringida de orden 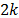, luego, de la ec. (10) se puede interpretar que la matriz conserva la distancia de cualquier par de vectores 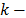dispersos, lo cual tiene implicaciones fundamentales respecto al ruido.

Lema 1[9]: Supóngase que satisface la propiedad de isometría restringida de orden 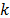con constante 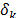. Sea 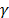un entero positivo. Luego satisface la propiedad de isometría restringida de orden 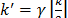con constante .

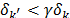El límite inferior de la propiedad de isometría restringida es una condición necesaria para la recuperación de todas las señales 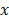a partir de sus medidas 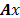, por los mismos motivos que la condición de espacio nulo es necesaria.

Definición 4: Sea 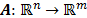describe una matriz de sensado, y sea 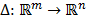describe un algoritmo de recuperación dispersa. Se dice que el par (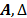) es C-estable si para cualquier 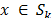y para cualquier 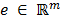se tiene que

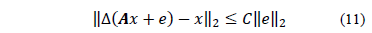
La ec. (11) indica que si se adiciona una pequeña cantidad de ruido a las medidas, el impacto de dicha adición sobre la señal recuperada no debe ser arbitrariamente grande.

Teorema 3 [4]: Si el par (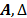) es C-estable luego

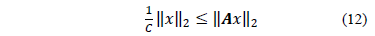
Para todo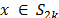

La demostración del teorema 3 se encuentra en [8]. Del teorema 3 (ec. (12)) se puede afirmar que si se desea reducir el impacto del ruido en la señal recuperada, se debe ajustar la matriz de sensado (puede pensarse en escalarla) de tal manera que cumpla la propiedad de isometría restringida, obteniendo de esta manera un ajuste de la ganancia de la señal si la magnitud del ruido es independiente de la selección de , alcanzando de esta manera una alta relación señal a ruido, de tal manera que eventualmente el ruido pueda considerarse despreciable.

Hasta el momento, con respecto a la cantidad de medidas requeridas para garantizar la recuperación de una señal dispersa, se tiene el límite inferior determinado por el teorema 1, el cual indica que debe ser 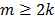para el caso de señales exactamente 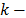dispersas que cumplan con la propiedad de espacio nulo (adicionalmente no se considera el ruido); por lo tanto, la idea ahora, es identificar cual es el mínimo número de medidas requeridas para garantizar la recuperación de una señal 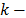dispersa basadas en la propiedad de isometría restringida.

Teorema 4 [4]: Sea una matriz de tamaño 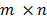que satisfice la propiedad de isometría restringida de orden 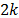con constante 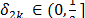. Luego

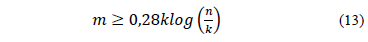
La demostración del teorema 4 se encuentra en [8]. La restricción 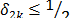se realiza por conveniencia.

La ec. (13), establece un límite inferior para la cantidad de medidas requeridas para la recuperación de la señal dispersa cuando la matriz de sensado satisface la propiedad de isometría restringida de orden .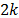

Verificar que una matriz de sensado satisface cualquiera de las propiedades tales como la "chispa", la propiedad de espacio nulo, o la propiedad de isometría restringida requiere típicamente realizar una búsqueda combinatoria sobre todo el espacio de submatrices 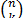, por lo tanto, es preferible utilizar propiedades sobre la matriz que se puedan calcular con mayor facilidad, donde, la propiedad de coherencia de la matriz es una de esas propiedades [10,11].

Definición 5: La coherencia de una matriz , denotada por 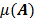, es el mayor valor absoluto del producto interno entre cualquier par de columnas 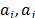de , y definida como se ilustra en la ec. (14).

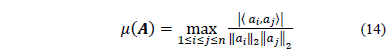
En [12-14] se muestra el límite de Welch, el cual es el límite inferior de la coherencia de una matriz, por lo tanto 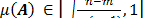, donde puede apreciarse que si 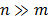el límite inferior es aproximadamente .

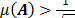Lema 2[11]: Para cualquier matriz ,

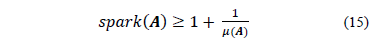
La demostración se realiza en [11].

Por medio de la combinación del teorema 1 (ec. (7)) con el lema 2 (ec. (15)) se puede proponer la siguiente condición sobre la matriz de sensado de tal manera que se garantiza unicidad de la correspondencia de la señal dispersa 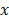con sus medidas .

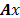Teorema 5[10]:Si

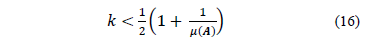
Luego, para cada vector de mediciones 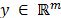existe al menos una señal 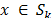tal que .

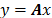El teorema 5 (ec. (16)) junto con el límite de Welch proporcionan un límite superior al nivel de dispersión 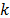que garantiza unicidad utilizando coherencia, el cual se indica en la ec. (17).

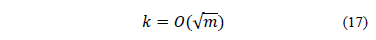
De acuerdo a lo presentado hasta el momento en este artículo, puede indicarse que la construcción de la matriz de sensado es una tarea dispendiosa en la cual es de vital importancia satisfacer las propiedades que garantizan la recuperación de la señal con la menor cantidad posible de mediciones, por ello, en [5,15-17] se han estudiado técnicas de construcción de matrices de sensado determinísticas, las cuales satisfacen las propiedades de recuperación, pero requieren de gran cantidad de medidas, por ejemplo en [16], la técnica de construcción propuesta requiere que 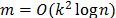, afortunadamente, estas limitaciones pueden ser superadas aleatorizando la construcción de la matriz de sensado. Por ejemplo, si es una matriz aleatoria de tamaño 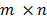cuyas entradas son independientes e idénticamente distribuidas, con distribuciones continuas, luego 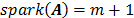con probablidad 1. De manera más significativa, matrices aleatorias satisfacen la propiedad de isometría restringida con alta probabilidad, si las entradas siguen una distribución gausiana, Bernoulli o en general cualquier distribución subgausiana y requieren una cantidad de medidas 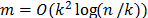[18]. La utilización de matrices aleatorias tiene otros beneficios adicionales tales como que las medidas son democráticas, lo cual significa, que es posible recuperar una señal utilizando cualquier subconjunto suficientemente grande de medidas, otro beneficio es que en la práctica, con frecuencia, se tiene interés de tomar medidas de una señal 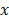que no es dispersa en su base original, pero que es dispersa con respecto a una base 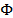, por lo tanto, se requiere que el producto 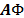cumpla con la propiedad de isometría restringida. Si se utiliza una construcción determinista, sería necesario tener en cuenta la base 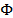en la construcción de , pero cuando se construye de manera aleatoria se puede evitar esta consideración.

4. Algoritmos de recuperación de la señal

Existen cinco clases de técnicas computacionales para resolver problemas de aproximación dispersa:

• Búsqueda Codiciosa: Refina iterativamente una solución dispersa por medio de identificación sucesiva de uno o más componentes que producen la mejor aproximación [19].
• Relajación Convexa: Este tipo de técnica reemplaza el problema combinatorio por un problema de optimización convexa. Resuelve el problema convexo con algoritmos que explotan la estructura del problema [20].
• Métodos Bayesianos: En esta técnica se asume una distribución a priori que favorece la dispersión para los coeficientes desconocidos; se desarrolla un estimador de máximo a posteriori que incorpora la observación; identifica una región de masa posterior significativa [21], o promedia sobre los modelos más probables [22].
• Optimización no Convexa: Convierte el problema 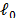en un problema no convexo relacionado y trata de identificar un punto estacionario. [23].
• Fuerza Bruta: Con esta técnica se realiza una búsqueda sobre todo el conjunto de posibles soportes, utilizando métodos de plano cortante para reducir el número de posibilidades [24].

A continuación se realiza una descripción general de los algoritmos basados en Búsqueda Codiciosa y los algoritmos de Relajación Convexa, dado que estos dos métodos son los que presentan como ventaja el ser computacionalmente prácticos y conducen a soluciones demostrablemente correctas bajo condiciones bien definidas [25-28]. Los métodos Bayesianos y basados en optimización no convexa, se basan en principios sólidos, pero en la actualidad no ofrecen garantías sólidas de solución [29,30]; en cuanto a los métodos de Fuerza Bruta, son algorítmicamente correctos, pero solo son eficientes en problemas de pequeña escala[2,31,32].

4.1. Algoritmos basados en búsqueda codiciosa

Los algoritmos basados en búsqueda codiciosa se basan en aproximaciones sucesivas de los coeficientes y del soporte de la señal, identificando de manera iterativa el soporte de la señal hasta alcanzar un criterio de convergencia, o por obtener de manera alternativa una aproximación mejorada de la señal dispersa en cada iteración considerando la falta de correspondencia con los datos medidos.

El algoritmo de Búsqueda de Correspondencia Ortogonal (Orthogonal Matching Pursuit - OMP) [19] es tal vez el más simple al interior de esta categoría, este algoritmo inicia buscando la columna de la matriz de sensado mayormente correlacionada con las medidas, luego se repite este paso, correlacionando las columnas con la señal residual, la cual se obtiene restando las contribuciones de una estimación parcial de la señal del vector de mediciones original.

El algoritmo 1 muestra la estructura formal de OMP, donde 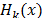denota el operador de umbralización dura sobre 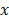, el cual establece en cero todas las entradas de 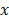excepto aquellas 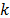entradas de mayor magnitud. El criterio de parada puede consistir de un límite sobre la cantidad de iteraciones donde también se limite el número de entradas no cero del vector 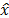, o un criterio que verifique que .

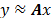Algoritmo 1. Búsqueda de Correspondencia Ortogonal - OMP

Entradas: Matriz de sensado , vector de medidas .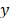
Inicializar: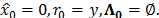
For 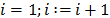hasta que se cumpla el criterio de parada

% Estimación de la señal de forma residual
% Agrega la mayor entrada residual del soporte.
% Actualiza la estimación de la señal.
% Actualiza la medición residual.

Fin For

Retorna: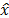

OMP garantiza recuperación de la señal 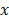en exactamente 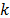iteraciones para señales exactamente 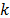- dispersas libres de ruido para matrices que satisfacen la propiedad de isometría restringida [33] y matrices que cumplen la propiedad de coherencia [34]; en los dos casos, los resultados solo aplican cuando .

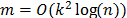4.2. Algoritmos basados en relajación convexa

Los algoritmos basados en relajación convexa son otro enfoque fundamental de aproximación dispersa, los cuales reemplazan la función combinatoria 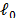con la función convexa 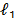, lo cual, convierte el problema combinatorio en un problema de optimización convexa, concretamente [35], la norma 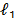es la función convexa más aproximada a la función 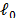. El enfoque natural, desde el cual se aborda el problema de aproximación dispersa es encontrar la solución dispersa de 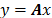, resolviendo

Sin embargo el problema planteado en la ec. (18) es un problema combinatorio el cual en general es NP-Hard [36], y el simple hecho de trabajar con todos los soportes de cardinalidad 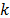se convierte en un problema computacional intratable, al reemplazar la norma 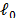por la norma 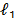el problema se convierte en el planteado en la ec. (19).

Cuando se trata con mediciones imperfectamente dispersas (medidas contaminadas por ruido), se considera el modelo de sensado dado por la ec. (20).

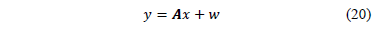
Donde es la matriz de sensado de tamaño 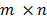, 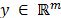es el vector de mediciones y 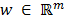es el vector de ruido, por lo tanto, las entradas de 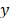son las medidas de 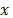contaminadas por ruido, por lo tanto el problema de optimización de la ec. (19) se convierte en

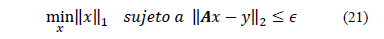
O de manera equivalente

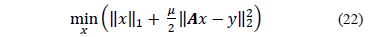
Los dos algoritmos o problemas de minimización son equivalentes en el sentido que la solución de un problema es también la solución del otro siempre que los parámetros 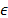y 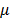se establezcan adecuadamente; sin embargo la correspondencia entre 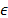y 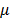no se conoce de manera a priori, dependiendo de la aplicación y la información disponible, uno de los dos puede ser más fácil de obtener, lo que hace que uno de los dos problemas enunciados en las ec. (21) y ec. (22) sea preferido sobre el otro. El seleccionar adecuadamente 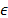o 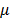es un problema que es muy importante en la práctica, por lo cual, principios generales de selección incluyen 1.) Realizar presunciones estadísticas sobre 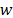y 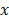e interpretar las ec. (21) o ec. (22) como por ejemplo estimaciones de máximo a posteriori. 2.) Validación cruzada (realizar la reconstrucción a partir de un subconjunto de medidas y validar la recuperación sobre el otro subconjunto de medidas) y 3.) Encontrar los mejores valores de los parámetros sobre un conjunto de datos de prueba y utilizar estos parámetros sobre los datos actuales con ajustes apropiados, para compensar las diferencias en escala, rango dinámico, dispersión y nivel de ruido.

4.3. Búsqueda codiciosa o relajación convexa

Los dos métodos permiten garantizar la recuperación de la señal original siempre que se cumpla con una cantidad adecuada de medidas, sin embargo, dada la naturaleza de la búsqueda codiciosa que construye y corrige progresivamente el soporte de la solución, su desempeño sobre señales que siguen una distribución que decae rápidamente es mejor que los algoritmos basados en relajación convexa, dado que requieren una menor cantidad de mediciones; por otra parte, los algoritmos basados en recuperación convexa tienden a tener un desempeño más consistente por lo cual, la calidad de la solución tiende a afectarse menos por la velocidad de caída de la distribución de la señal.

La búsqueda codiciosa puede extenderse al modelo base de CS, en el cual, las señales no solamente son dispersas, sino que sus soportes se encuentran restringidos a ciertos modelos, como por ejemplo, estructuras en árbol; algunos de estos modelos son difíciles de representar como modelos de optimización convexa; por otra parte, es difícil extender la búsqueda codiciosa a funciones objetivo o a funciones de energía. La optimización dispersa, naturalmente acepta funciones objetivo y restricciones de muchos tipos, especialmente si son convexas; sin embargo, si un problema puede ser resuelto por los dos métodos, se debe examinar la velocidad de caída de la distribución de la señal.

5. Marco de referencia metodológico

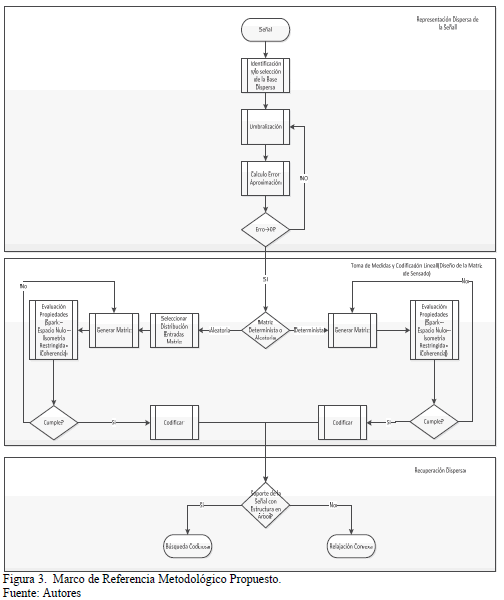
Finalmente, se presenta en resumen el marco de referencia metodológico propuesto para realizar un procesamiento de señales eficiente basado en CS; la Fig. 3 ilustra las etapas y las consideraciones basadas en las secciones anteriores, el marco de referencia metodológico propuesto se valida en [37].

6. Conclusiones

En este artículo se presentan los resultados más importantes para la definición de una metodología y una primera aproximación hacia un marco de referencia metodológico para el procesamiento de señales basada en sensado compresivo, permitiendo de esta manera realizar la representación dispersa de señales reales, realizar el diseño adecuado de matrices de sensado y seleccionar eficientemente el algoritmo de reconstrucción adecuado, dado que la literatura actual es lo suficientemente extensa como para convertir en un gran problema el cómo abordar el procesamiento de señales desde este nuevo paradigma.

Finalmente, se considera que SC es una tecnología promisoria la cual contribuirá al mejoramiento significativo de la forma en que actualmente se realiza el procesamiento de señales, reduciendo los costos computacionales y con ello optimizando la utilización de otros recursos tales como energía; igualmente, se considera que aún es un campo en el cual se pueden generar gran cantidad de aportes en el diseño de matrices de sensado aleatorias y seudoaleatorias que permitan realizar una implementación práctica real de bajos requerimientos computacionales, además de buscar el diseño de algoritmos de recuperación de señal eficientes, que articulados a las matices de sensado, permitan minimizar la cantidad de mediciones requeridas para garantizar estabilidad y exactitud en la recuperación de la señal.

Referencias

[1] Candès, E.J., Tao, J.T. and Romberg, J., Robust. Uncertainty principles: Exact signal reconstruction from highly incomplete frequency information, IEEE Trans. Inform. Theory, 52 (2), pp. 489-509, 2006. DOI: 10.1109/TIT.2005.862083        [ Links ]

[2] Donoho, D.L., Compressed sensing, IEEE Trans. Inform. Theory, 52 (2), pp. 1289-1306, 2006. DOI: 10.1109/TIT.2006.871582        [ Links ]

[3] DeVore, R.A. Nonlinear approximation. Cambridge University Press, 1998.         [ Links ]

[4] Davenport, M., Random observations on random observations: Sparse signal acquisition and processing. PhD Thesis, Rice University, 2010.         [ Links ]

[5] Indyk, P., Explicit constructions for compressed sensing of sparse signals. Proc.ACM-SIAM Symp Discrete Algorithms (SODA), San Franciso, CA, 2008.         [ Links ]

[6] Donoho, D. and Elad, M., Optimally sparse representation in general (nonorthogonal) dictionaries via L1 minimization. Proc Natl Acad Sci, 100 (5), pp. 2197-2202, 2003.         [ Links ]

[7] Cohen, A., Dahmen, W. and DeVore. R., Compressed sensing and best k-term approximation. J. Am. Math. Soc., 22 (1), pp. 211-231, 2009.         [ Links ]

[8] Candès, E. and Tao, T., Decoding by linear programming. IEEE Trans Inform Theory, 51 (12), pp. 4203-4215, 2005. DOI: 10.1109/TIT.2005.858979        [ Links ]

[9] Needell, D. and Tropp, J., CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl Comput Harmon Anal, 26 (3), pp. 301-321, 2009.         [ Links ]

[10] Donoho, D. and Elad, M., Optimally sparse representation in general (nonorthogonal) dictionaries via L1 minimization. Proc Natl Acad Sci, 100 (5), pp. 2197-2202, 2003.         [ Links ]

[11] Tropp, J. and A. Gilbert. Signal recovery from partial information via orthogonal matching pursuit. IEEE Trans Inform. Theory, 53 (12), pp. 4655-4666, 2007. DOI: 10.1109/TIT.2007.909108.         [ Links ]

[12] Rosenfeld, M., In Praise of the Gram Matrix, on The Mathematics of Paul Erdös II, R.L. Graham and J. Nešetřil, Eds. Springer Berlin Heidelberg, pp. 318-323, 1997.         [ Links ]

[13] Strohmer, T. and Heath, R., Grassmanian frames with applications to coding and communication. Appl Comput Harmon Anal, 14 (3), pp. 257-275, 2003.         [ Links ]

[14] Welch, L., Lower bounds on the maximum cross correlation of signals. IEEE Trans Inform Theory, 20 (3), pp. 397-399, 1974. DOI: 10.1109/TIT.1974.1055219        [ Links ]

[15] Bourgain, J., Dilworth, S., Ford, K., Konyagin, S. and Kutzarova, D., Explicit constructions of RIP matrices and related problems. Duke Math J, 159 (1), pp. 145-185, 2011.         [ Links ]

[16] DeVore, R., Deterministic constructions of compressed sensing matrices. J. Complex, 23 (4), pp. 918-925, 2007.         [ Links ]

[17] Haupt, J., Applebaum, L. and Nowak, R., On the restricted isometry of deterministically subsampled fourier matrices. On 44^th Annual Conference on Information Sciences and Systems (CISS), pp. 1-6, 2010. DOI: 10.1109/CISS.2010.5464880        [ Links ]

[18] Achlioptas, D., Database-friendly random projections: Johnson-Lindenstrauss with binary coins, in: Special issue on PODS 2001 (Santa Barbara, CA). J. Comput. Syst. Sci., 66, pp. 671-687, 2003.         [ Links ]

[19] Mallat, S. and Zhang, Z., Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process, 41 (12), pp. 3397-3415, 1993. DOI: 10.1109/78.258082        [ Links ]

[20] Chen, S.S., Donoho, D.L. and Saunders, M.A., Atomic decomposition by basis pursuit, SIAM Rev., 43 (1), pp. 129-159, 2001.         [ Links ]

[21] Wipf, D. and Rao, B., Sparse bayesian learning for basis selection. IEEE Trans. Signal Processing, 52 (8), pp. 2153-2164, 2004.         [ Links ]

[22] Schniter, P., Potter, L.C. and Ziniel, J., Fast bayesian matching pursuit: Model uncertainty and parameter estimation for sparse linear models. On: Information Theory and Applications Workshop, pp. 326-333, 2008.         [ Links ]

[23] Chartrand, R., Exact reconstruction of sparse signals via nonconvex minimization, IEEE Signal Processing Lett., 14 (10), pp. 707-710, 2007. DOI: 10.1109/LSP.2007.898300        [ Links ]

[24] Miller, A., Subset Selection in Regression. CRC Press, 2002.         [ Links ]

[25] Becker, S., Bobin, J. and Candès, E., NESTA: A fast and accurate first-order method for sparse recovery. SIAM J. Imag. Sci., 4 (1), pp. 1-39, 2011. DOI: 10.1137/090756855         [ Links ]

[26] Becker, S., Candès, E. and Grant, M., Templates for convex cone problems with applications to sparse signal recovery. Math Prog Comp, 3 (3), pp.165-218, 2011. DOI: 10.1007/s12532-011-0029-5.         [ Links ]

[27] Ben-Haim, Z., Eldar, Y.C. and Elad, M., Coherence-based performance guarantees for estimating a sparse vector under random noise. IEEE Trans Sig Proc., 58 (10), pp. 5030-5043, 2010. DOI: 10.1109/TSP.2010.2052460        [ Links ]

[28] Donoho, D., Elad, M. and Temlyahov, V., Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Trans. Inform. Theory, 52 (1), pp. 6-18, 2006. DOI: 10.1109/TIT.2005.860430        [ Links ]

[29] Lobato, A., Ruiz, R., Quiróga, J. y Recio, A., Recuperación de señales dispersas utilizando orthogonal matching pursuit (OMP), Revista Ingeniería e Investigación, 29 (2), pp. 112-118, 2009.         [ Links ]

[30] Gilbert, A., Li, Y., Porat, E. and Strauss, M., Approximate sparse recovery: Optimizaing time and measurements. In Proc. ACM Symp. Theory of Comput., Cambridge, MA, USA, 2010.         [ Links ]

[31] Gilbert, A., Strauss, M., Tropp, J. and Vershynin, R., One sketch for all: Fast algorithms for compressed sensing. In Proc. ACM Symp. Theory of Comput., San Diego, CA, USA, 2007. DOI: 10.1145/1250790.1250824        [ Links ]

[32] Candés, E. and Tao, T., Near optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans Information Theory, 52 (12), pp. 5406-5425, 2006. DOI: 10.1109/TIT.2006.885507        [ Links ]

[33] Davenport, M. and Wakin, M., Analysis of orthogonal matching pursuit using the restricted isometry property. IEEE Trans Inform Theory, 56 (9), pp. 4395-4401, 2010. DOI: 10.1109/TIT.2010.2054653        [ Links ]

[34] Tropp, J., Greed is good: Algorithmic results for sparse approximation. IEEE Trans Inform Theory, 50 (10), pp. 2231-2242, 2004. DOI: 10.1109/TIT.2004.834793        [ Links ]

[35] Gribonval, R. and Nielsen, M., Highly sparse representations from dictionaries are unique and independent of the sparseness measure, Aalborg University, Tech. Rep., 2003.         [ Links ]

[36] Natarajan, B.K., Sparse approximate solutions to linear systems, SIAM Journal on Computing, 24, pp. 227-234, 1995.         [ Links ]

[37] Astaiza, E., Jojoa P. and Bermudez, H., Compressive spectrum sensing based on random demodulation for cognitive radio, submitted to IEEE Trans. Prof. Commun.2015.         [ Links ]

E. Astaiza-Hoyos, es Ing. en Electrónica en 1998, de la Universidad del Cauca, Colombia; MSc. en Ingeniería, área de Telecomunicaciones, en 2008, de la Universidad del Cauca, Colombia. Actualmente es candidato a Dr. en ciencias de la Electrónica. Es profesor asociado en programa de Ingeniería Electrónica de la Universidad del Quindío, Colombia. Es investigador del grupo de Investigación en Telecomunicaciones - GITUQ, de la Universidad del Quindío, Colombia. Sus áreas de interés: comunicaciones inalámbricas, sensado de espectro.

P.E. Jojoa-Gómez, es Ing. en Electrónica en 1993, de la Universidad del Cauca, Colombia. MSc. en Ingeniería, área de Sistemas Electrónicos, 1999, Universidad de Sao Paulo, Brasil y Dr, en Ingeniería, Área de Sistemas Electrónicos, en 2003, Universidad de Sao Pablo, Brasil. Es coordinador del grupo de Investigación en Nuevas Tecnologías de Telecomunicaciones. Áreas de interés: Procesamiento digital de señales y filtraje adaptativo.

H.F. Bermúdez-Orozco, es Ing. en Electrónica en 2000, MSc. en Electrónica y Telecomunicaciones, en 2010, de la Universidad del Cauca Colombia. Actualmente es estudiante de Doctorado en Ingeniería Telemática. Es profesor asociado del programa de Ingeniería Electrónica y Coordinador del Grupo de Investigación en Telecomunicaciones - GITUQ, de la Universidad del Quindío, Colombia. Sus áreas de interés: Comunicaciones inalámbricas, sistemas radiantes y propagación, modelado de tráfico de servicios telemáticos.