Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.192 Medellín July/Aug. 2015
https://doi.org/10.15446/dyna.v82n192.42423
DOI: http://dx.doi.org/10.15446/dyna.v82n192.42423
Fortran application to solve systems from NLA using compact storage
Aplicativo en Fortran para resolver sistemas de ALN usando formatos comprimidos
Wilson Rodríguez-Calderón a & Myriam Rocío Pallares-Muñoz b
a Programa de Ingeniería Civil, Universidad Cooperativa de Colombia, Neiva, Colombia. wilson.rodriguez@campusucc.edu.co
b Programa de Ingeniería Civil, Universidad Surcolombiana, Neiva, Colombia. myriam.pallares@usco.edu.co
Received: March 3rd, 2014. Received in revised form: February 22th, 2015. Accepted: May 26th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
Educational software of Numerical Linear Algebra (NLA) friendly was developed, with the last developments in compact storage formats or compressed formats. This software generates the possibility to have own tools, handling for teaching processes in undergraduate, research and advanced formation. Having a tool own computational for the solution of lineal algebra problems generates advantages, since, all the details, hypothesis, restrictions, applications and kindness of the software can be known of first hand, without necessity of requesting expensive support services. The incorporation of storage advanced elements, programming and acceleration of the solution of NLA problems in the software, not allow alone solve academic cases, but also real problems that induce the user to a better understanding of the problems in an efficient and widespread way.
Keywords: Numerical Linear Algebra, NLA, sparse matrix, storage formats, compressed sparse row, compressed sparse column, modified compressed sparse row format, modified compressed sparse column.
Resumen
Se desarrolló un software educativo de Álgebra Lineal Numérica (ALN) amigable y con los más recientes desarrollos en esquemas de almacenamiento compacto o formatos comprimidos. Este software genera la posibilidad de contar con herramientas propias, manipulables e intervenibles para procesos de docencia e investigación. Contar con una herramienta computacional propia para la solución de problemas de álgebra lineal genera ventajas muy importantes, toda vez que se pueden conocer todos los detalles, hipótesis, restricciones, aplicaciones y bondades del software de primera mano, sin la dependencia de costosos servicios de soporte. La incorporación de elementos avanzados de almacenamiento, programación y aceleración de la solución de problemas de ALN en el software, permite no sólo resolver casos académicos, si no también problemas reales que llevan al usuario a comprender mejor la resolución de sistemas de manera eficiente y generalizada.
Palabras clave: Álgebra Lineal Numérica, ALN, matrices dispersas, esquemas de almacenamiento, formato comprimido por filas, formato comprimido por columnas, formato comprimido por filas modificado, formato comprimido por columnas modificado.
1. Introducción
El Álgebra Lineal Numérica (ALN) posee gran cantidad de aplicaciones. Su desarrollo se remonta a la aparición de los computadores ya que con ellos tomó gran importancia la teoría de propagación de error, el concepto de aproximación y se desarrollaron muchos algoritmos de métodos numéricos, entre los que se encuentran los de ALN. Desde la época en que aparecieron los computadores, el tamaño y complejidad de los problemas ha crecido de manera sustantiva y los problemas de ALN no han sido ajenos a esta situación, lo que ha obligado a que se busquen algoritmos, esquemas y estrategias que puedan resolver problemas de gran tamaño con la menor cantidad de almacenamiento a velocidades muy rápidas y de la manera más segura, estable y precisa posible. La labor no ha sido fácil ya que si bien los computadores han evolucionado y poseen mejores características en la actualidad, aún poseen claras dificultades ante la demanda de almacenamiento, rapidez y control de la propagación del error. Buena parte de los problemas de ALN a nivel académico y profesional involucran una gran cantidad de cálculo inalcanzable manualmente. Tal actividad requiere la utilización de software especializado de alto costo cuyas curvas de aprendizaje pueden ser largas sobre todo en temas especializados. Además estos programas comerciales cuentan con un nivel de ayuda e información teórica restringidos para su buen manejo. El desarrollo de herramientas computacionales propias permite evitar equivocaciones graves que normalmente surgen cuando se manipulan cajas negras; esta expresión hace referencia a la poca o nula intervención del usuario en el desarrollo de los programas comerciales. Por lo general, este confía en los algoritmos de los paquetes que usa aunque desconozca de manera total o parcial los detalles de las rutinas que solucionan el problema, no por incapacidad de quien maneja el software, sino porque los programas no dan acceso a la información. Así las cosas, puede ser cuestionable el empleo ciego de estos paquetes, ya que se pierde la rigurosidad, sobre todo a nivel académico en donde los procesos de enseñanza-aprendizaje deben ser sólidos y bien fundamentados. Una alternativa de tratamiento computacional de sistemas lineales medianamente grandes consiste en la utilización de hojas de cálculo diseñadas específicamente para un caso particular, pero, se requeriría un buen tiempo para el simple montaje de las mismas. Por esto, se justifica el desarrollo de un software educativo de ALN amigable y con los últimos desarrollos en esquemas de almacenamiento compacto o formatos comprimidos cuyo objetivo es almacenar matrices dispersas que pueden provenir de la solución numérica de EDP por Elementos Finitos, Diferencias Finitas o de la resolución de Cadenas de Markov. Un software educativo de estas características superaría en gran parte los inconvenientes mencionados, toda vez que genera la posibilidad de contar con herramientas propias, manipulables e intervenibles para procesos de docencia en pregrado, investigación y formación avanzada. Contar con una herramienta computacional propia para la solución de problemas de Álgebra Lineal, genera ventajas competitivas y pedagógicas muy importantes, ya que se pueden conocer todos los detalles, hipótesis, restricciones, aplicaciones y bondades del software de primera mano, sin la dependencia de costosos servicios de soporte. La incorporación de elementos avanzados de almacenamiento, programación y aceleración de la solución de problemas de ALN en el software, permite no sólo resolver casos académicos, sino también problemas reales que llevan al usuario a comprender mejor los problemas de una manera eficiente y generalizada.
2. Métodos
Por restricciones de extensión, no se detallan todos los aspectos de los métodos, pero si los más importantes que justifican la pertinencia de este trabajo, incluyendo las referencias bibliográficas.
Frecuentemente, los métodos numéricos y en especial los que sirven para resolver ecuaciones diferenciales, conducen a problemas de Álgebra Lineal Numérica en los que las matrices tienen alguna estructura y la mayoría de sus elementos son nulos (matrices dispersas). Para estos problemas, el ALN ofrece métodos especiales en los que se está trabajando en la actualidad. De hecho, la resolución de sistemas lineales es seguramente el foco computacional más importante de la mayoría de las aplicaciones de ciencias e ingeniería. Nótese que las matrices que aparecen al discretizar una Ecuación Diferencial Parcial (EDP) por el Método de los Elementos Finitos (MEF) o Diferencias Finitas (DF) son dispersas; los problemas actuales que se resuelven por MEF manejan una cantidad considerable de incógnitas; si se buscara almacenar las matrices mediante una matriz densa se requerirían muchos bytes que vuelven imposible este tipo de almacenamiento, por consiguiente se requiere formatos diferentes para almacenar la matriz. Anteriormente, se utilizaban formatos de Banda y de Skyline, que tenían el defecto de almacenar parte de los ceros de la matriz por lo que se conviriteiron en ineficientes. Los formatos comprimidos superan los problemas de almacenamiento de los ceros de la matriz.
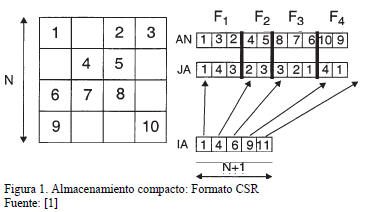
En el formato Comprimido por Filas (CSR) de la Fig. 1, se usan tres vectores unidimensionales AN, JA, IA para almacenar la matriz A. El vector AN almacena los coeficientes no nulos de la matriz por filas, JA almacena los índices de columna para cada uno de los elementos de AN, el vector IA almacena los índices iniciales de cada fila dentro de la estructura AN/JA. La longitud total de AN y JA es el número total de elementos no nulos que contenie la matriz A (NZ) y la longitud del vector IA es el número de filas más una (N+l). Dentro de una fila no existe un orden específico pero es útil colocar como primer elemento de la fila el elemento de la diagonal. Con ello se accede al elemento diagonal de la fila i-ésima con la expresión: AN (IA (i)) [1].
El formato comprimido por columnas (CSC) es análogo a CSR. Se usan los mismos tres vectores unidimensionales para almacenar la matriz A. Ahora el vector AN almacena los coeficientes no nulos ordenados por columnas, JA almacena los índices de fila para cada elemento de AN y el vector IA almacena los índices de inicio de columna dentro de AN/JA.
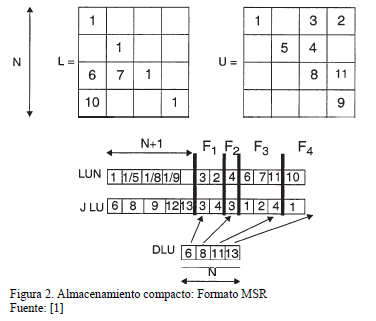
Como toda matriz no singular se puede factorizar de forma A=LU donde L es una matriz triangular inferior con su diagonal llena de unos y U una matriz triangular superior, U es la misma matriz que resulta de la eliminación Gaussiana y L la que resulta de almacenar los pivotes del proceso de factorización. El formato comprimido por filas modificado (MSR) de la Fig. 2, almacena las matrices L y U juntas. La diagonal principal de la matriz L no se almacena y se usan tres vectores unidimensionales LUN, JLU, DLU para almacenar las matrices
L y U. El vector LUN almacena todos los coeficientes no nulos de las matrices, esto es, en las primeras N posiciones se almacenan los elementos diagonales de U invertidos, la posición N+1 no se usa, y a partir de la posición N+2 se almacenan por filas primero los coeficientes de L y después los de U. El vector JLU almacena a partir de la posición N+2 los índices de columna para cada uno de los elementos de LUN. Las primeras N+1 posiciones del vector JLU almacenan los índices donde comienzan las filas dentro de LUN y de JLU. El vector DLU almacena los índices donde comienzan los elementos de U dentro de cada fila [1].
El formato comprimido por columnas modificado (MSC) es análogo al MSR; se emplean los mismos tres vectores unidimensionales para almacenar las matrices L y U. En este caso, el vector LUN almacena por columnas, el vector JLU los índices de fila y el vector DLU almacena los índices dentro de cada columna.
2.1. Métodos directos
Si la matriz A es simétrica, entonces U=DLt donde D es una matriz diagonal. La factorización A=LDLt genera un ahorro en el algoritmo ya que sólo es necesario uno de los triángulos de la matriz para realizar la factorización y hay menos operaciones aritméticas ya que sólo se calcula L y una matriz diagonal; si además la matriz A es definida positiva todos los elementos de D también lo son y A=LD1/2D1/2Lt=(LD1/2)(LD1/2)t=GGt. Esta factorización llamada de Cholesky permite ahorrar operaciones [3].
En los algoritmos de factorización con matriz densa, el algoritmo LU almacena los factores L y U en la misma variable que contiene a la matriz definiéndola como un arreglo bidimensional de tamaño NxN. En el algoritmo LDLt, se reemplaza el triángulo inferior de la matriz A por L y la diagonal por D; los elementos de la diagonal se usan para multiplicar y dividir simultáneamente. Finalizada la factorización, los elementos diagonales sólo se usan para dividir, por ello en la matriz se almacenan estos elementos invertidos. Durante el proceso se tiene un vector auxiliar que almacena los valores sin invertir para evitar excesos de divisiones. En el algoritmo de factorización GGt, la matriz G es triangular inferior y el algoritmo de factorización reemplaza el triángulo inferior de la matriz A por la matriz G.
En los algoritmos de factorización con matriz dispersa, el algoritmo debe adaptarse al formato de almacenamiento de manera que si la matriz está almacenada en CSR se debe usar algoritmos orientados por filas y en CSC algoritmos por columnas. El procedimiento consiste en sacar la fila i-ésima de la matriz A y ponerla en un arreglo sobre el que se hacen los cálculos y almacenar los elementos no nulos del arreglo en el formato correspondiente de las matrices de salida.
Es necesario disponer de un algoritmo que permita conocer el lugar exacto donde estarán los elementos no nulos de las matrices de salida o factorización simbólica, el cual se basa en la observación de la forma en que evoluciona el proceso de eliminación gaussiana sobre el grafo asociado a la matriz. Esta factorización tiene complejidad de orden O(N) [1].
Los métodos directos tienen el problema del llenado adicional que introducen en la matriz lo cual hace inviable su uso en gran parte de las aplicaciones, además poseen un grado de paralelismo bajo que limita su escalabilidad en sistemas paralelos y pueden presentar problemas de exactitud numérica [1]. La propagación de error al emplear un método directo multiplica el error relativo en los datos por el número de condición de la matriz, en otros casos que no requieren demasiada exactitud los métodos directos hacen trabajo inneceario.
2.2. Métodos iterativos
La solución a los problemas de los métodos directos la tienen los métodos iterativos que no modifican la estructura de la matriz de coeficientes ya que su principal operación es el producto matriz por vector. Por esto, no requieren tanta memoria como los métodos directos ni presentan dificultades de paralelización cuando se resuelven problemas de gran tamaño ya que la operación matriz por vector es paralelizable. Aunque la convergencia de un método iterativo puede volverse lenta, siempre es ajustable a la exactitud deseada [1]. Los métodos iterativos pueden ser clásicos y de proyección. Los clásicos: Jacobi, Gauss-Seidel, SOR, SSOR, Chebyshev y los de Proyección que son más eficaces: GMRES, Gradiente, Biconjugado BiCGstab, CGS y Gradiente Conjugado (CG).
La metodología general de los métodos de proyección consiste en que, dado un sistema lineal nxn, Ax=b y el subespacio vectorial K de dimensión m<n, generado por la base Vº[v1...vm] se tome como aproximación de 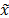 el vector x=Vy, donde y es un vector de dimensión m. El criterio más usado para seleccionar y es forzar al vector residuo, r=b-Ax para que sea ortogonal a otro subespacio L de dimensión m generado por la base Wº[w1...wm], esto es, se impone que: Wt.(b-AVy)= 0. Se tiene entonces que y=(WtAV)-1-Wtb, suponiendo que la matriz WtAV es no singular, es decir, se reduce el problema original a resolver un sistema lineal de mxm. Los métodos de proyección eligen diferentes subespacios K y L para hacer la aproximación y se formulan sobre el sistema del error y no en el sistema original, es decir, dada una primera aproximación a la solución x0, se busca un vector de corrección e que aproxime la solución exacta del sistema A
el vector x=Vy, donde y es un vector de dimensión m. El criterio más usado para seleccionar y es forzar al vector residuo, r=b-Ax para que sea ortogonal a otro subespacio L de dimensión m generado por la base Wº[w1...wm], esto es, se impone que: Wt.(b-AVy)= 0. Se tiene entonces que y=(WtAV)-1-Wtb, suponiendo que la matriz WtAV es no singular, es decir, se reduce el problema original a resolver un sistema lineal de mxm. Los métodos de proyección eligen diferentes subespacios K y L para hacer la aproximación y se formulan sobre el sistema del error y no en el sistema original, es decir, dada una primera aproximación a la solución x0, se busca un vector de corrección e que aproxime la solución exacta del sistema A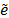 =r0, donde
=r0, donde 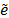 =
=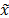 -x0 es el vector error. Entonces la aproximación a la solución se da como x=x0+e. Aunque existen muchas opciones para elegir los subespacios K y L la más usada es que K y L sean subespacios de Krylov de dimensión m asociados a la matriz A y al vector v, generados por la base {v, Av, A2v,...,Am-1v} y denotados por Km(A,v). Los subespacios de Krylov son simples, permiten invertir la matriz WtAV y generar una base ortonormal de Km(A,v) (por el método de Arnoldi). Después de m iteraciones del método de Arnoldi se obtiene la matriz
-x0 es el vector error. Entonces la aproximación a la solución se da como x=x0+e. Aunque existen muchas opciones para elegir los subespacios K y L la más usada es que K y L sean subespacios de Krylov de dimensión m asociados a la matriz A y al vector v, generados por la base {v, Av, A2v,...,Am-1v} y denotados por Km(A,v). Los subespacios de Krylov son simples, permiten invertir la matriz WtAV y generar una base ortonormal de Km(A,v) (por el método de Arnoldi). Después de m iteraciones del método de Arnoldi se obtiene la matriz 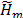 de dimensión (m+1)xm y sus elementos no nulos son los coeficientes hij generados por el algoritmo. La matriz Hm es la matriz
de dimensión (m+1)xm y sus elementos no nulos son los coeficientes hij generados por el algoritmo. La matriz Hm es la matriz 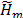 a la que se le ha eliminado la fila (m+1). La matriz Hm es simplemente la proyección de la matriz A sobre el subespacio Km(A,v1) con
a la que se le ha eliminado la fila (m+1). La matriz Hm es simplemente la proyección de la matriz A sobre el subespacio Km(A,v1) con 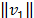 =1. Es decir: Hm=WmtAWm, donde Wm=[w1...wm] y la matriz
=1. Es decir: Hm=WmtAWm, donde Wm=[w1...wm] y la matriz 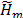 cumple la relación AWm=Wm+1
cumple la relación AWm=Wm+1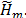 Sintentizando, el algoritmo general del método de proyección es,
Sintentizando, el algoritmo general del método de proyección es,

En el Método del Gradiente Conjugado, para una matriz A simétrica definida positiva, la matriz Hm es tridiagonal en lugar de superior [1]; esto permite una serie de simplificaciones importantes a nivel de cálculo en el método de Arnoldi y el algoritmo resultante (llamado también método simétrico de Lanzcos) calcula una matriz nxn simétrica tridiagonal tal que, T=WtAW, donde W=[w1...wm] es una base ortonormal y T es como la expresión (1).
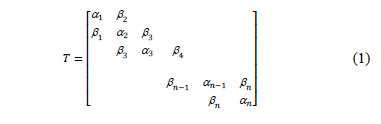
Al reescribir T=WtAW como AW=WT se tiene que Awj=bjwj-1+ajwj+bj+1wj+1 con j=1, 2,...,n, entendiendo que b1=bn+1=0. Multiplicando esta ecuación por wjt se encuentra que aj= wjtAwj y bj+1wj+1=(A-ajI)wj-bjwj-1º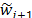 . Si
. Si 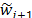 ¹1 y como
¹1 y como 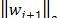 =1 entonces bj+1=
=1 entonces bj+1=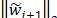 . Estas relaciones conducen a un método iterativo para calcular los coeficientes aj y bj. Lanzcos es un algoritmo para el cálculo de los autovalores de A; se calculan los coeficientes aj y bj hasta m<n y se aproximan los autovalores de A mediante los autovalores de Tm que son triviales dado que Tm es simétrica tridiagonal. El Gradiente Conjugado ó algoritmo simétrico de Lanzco aplicado a la resolución de un sistema de ecuaciones es un proceso de optimización para encontrar el mínimo de la forma cuadrática,
. Estas relaciones conducen a un método iterativo para calcular los coeficientes aj y bj. Lanzcos es un algoritmo para el cálculo de los autovalores de A; se calculan los coeficientes aj y bj hasta m<n y se aproximan los autovalores de A mediante los autovalores de Tm que son triviales dado que Tm es simétrica tridiagonal. El Gradiente Conjugado ó algoritmo simétrico de Lanzco aplicado a la resolución de un sistema de ecuaciones es un proceso de optimización para encontrar el mínimo de la forma cuadrática, 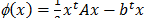 .
.
Este algoritmo optimiza hasta reducir la norma del error respecto a la matriz A en cada paso como se muestra en la ecuación (2).
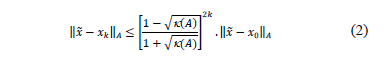
donde k(A) es el número de condición de A. El algoritmo del Gradiente Conjugado es,

La lentitud de la convergencia de los métodos iterativos hace necesario que se agregue precondicionadores en el esquema numérico que los aceleren, los cuales están basados en manipulaciones algebraicas de la matriz para obtener una aproximación de la inversa [5]. Un precondicionador busca una matriz M que sea una buena aproximación de A y más fácil de invertir; entonces, se usa M-1 para corregir las sucesivas aproximaciones del método iterativo. Es decir, si r es el residuo en la iteración m-ésima, se calcula em=M-1 rm que será una aproximación del error en el paso m-ésimo y se corrige la solución como xm=xm+em. Existen numerosas aproximaciones para conseguir precondicionadores. Las tres más importantes son las factorizaciones incompletas, los precondicionadores polinomiales y los de aproximación dispersa de la inversa SPAI.
Los precondicionadores polinomiales se basan en aproximar la inversa de la matriz A mediante un polinomio. Esto es, A-1=Pm(A)=q0I+q1A+
+qmAm. Los coeficientes del polinomio se eligen de forma que se minimice 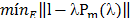 donde E es un intervalo que incluye el espectro de A. El problema de minimización tiene diferentes soluciones en función de que norma se considere. Si se toma la norma infinito para
donde E es un intervalo que incluye el espectro de A. El problema de minimización tiene diferentes soluciones en función de que norma se considere. Si se toma la norma infinito para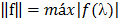 , la solución es según la ecuación (3).
, la solución es según la ecuación (3).
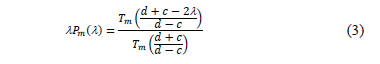
Donde Tm(l) es el polinomio de Chebyshev de primera clase de grado m, y E=[c, d] . El problema que presentan es la necesidad de disponer de un buen intervalo del espectro de A, lo contrario requeriría grados grandes del polinomio para una buena aproximación.
Los precondicionadores SPAI buscan una matriz M tal que AM sea tan cercana a la identidad como sea posible. Esto es, minimizar ||AM-I|| en la norma de Frobenius, 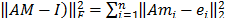 donde ei, es el vector i-ésimo de la base canónica. Cada columna de M se puede calcular en paralelo resolviendo el problema de mínimos cuadrados
donde ei, es el vector i-ésimo de la base canónica. Cada columna de M se puede calcular en paralelo resolviendo el problema de mínimos cuadrados 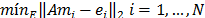 . La inversa de A generalmente es mucho más densa que A, pero los coeficientes significativos de A-1 son muy pocos, esto es, M es una matriz dispersa, por lo tanto, el problema es de dimensión pequeña y puede resolverse eficientemente. Dado que la estructura de M no es conocida a priori, se inicia con una estructura diagonal y se avanza en el llenado hasta que
. La inversa de A generalmente es mucho más densa que A, pero los coeficientes significativos de A-1 son muy pocos, esto es, M es una matriz dispersa, por lo tanto, el problema es de dimensión pequeña y puede resolverse eficientemente. Dado que la estructura de M no es conocida a priori, se inicia con una estructura diagonal y se avanza en el llenado hasta que 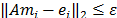 para i=1, ...,N con 0 < e < 1, o cuando se llega a un nivel de llenado permitido [1].
para i=1, ...,N con 0 < e < 1, o cuando se llega a un nivel de llenado permitido [1].
Las factorizaciones incompletas son los únicos precondicionadores que son generales y no requieren la estimación de ningún parámetro. Se trata de factorizar la matriz A (LU, Cholesky, LDLt) sin introducir todo el llenado que se produce en la factorización [3]. Como resultado, el precondicionador puede aplicarse resolviendo dos sistemas triangulares cuya dispersión y complejidad de cálculo dependerá del tipo de factorización incompleta que se haya aplicado. Las formas de factorizaciones incompletas son: sin llenado -ILU(0), ICH(0)-, con llenado usando como criterio la posición dentro de la matriz -ILU(k), ICH(k)- con llenado, usando como criterio umbrales numéricos -ILU(t), ICH(t)- [4,7-11].
Las factorizaciones ILU(0) se usan para resolver EDP, son simples ya que no introducen llenado. La factorización incompleta tiene la misma cantidad de elementos no nulos y en las mismas posiciones que en la matriz A; esto permite reusar para el precondicionador todos los vectores de índices usados para la matriz con el consecuente ahorro de memoria, sin embargo, no son muy potentes.
El parámetro k de una factorización ILU(k) en el contexto de EDP para problemas discretizados mediante diferencias finitas, indica el número de columnas alrededor de la diagonal en las que se permite llenado [1].
Las factorizaciones ILU(t) deciden introducir o no un llenado lij en función de si es superior o inferior a un umbral determinado que se calcula en relación al valor de los elementos de la fila i-ésima de A usando el parámetro t. El cálculo se realiza usando cualquier medida que puede ser el valor medio de los elementos de la fila i-ésima o cualquier norma de la fila i-ésima. Estas factorizaciones son de aplicación general [1].
La factorización incompleta ILUt (fil,t) de aplicación genérica supera la falta de control fino de ILU(t) sobre la cantidad total de llenado que se permite; sigue una doble estrategia en la introducción del llenado, esto es, al factorizar la fila i-ésima se introducen los llenados que superen un umbral numérico relativo a la fila i-ésima (parámetro t) y finalizada la factorización de la fila i-ésima sólo se almacenan en la estructura de datos de salida los elementos que tiene la matriz A en la fila i-ésima más dos veces fil(fil más en la parte L, y fil más en la parte U). Se elige almacenar los elementos con un valor absoluto mayor. t sirve para controlar el umbral numérico de cálculo y el parámetro fil para la cantidad efectiva de llenado.
Para implementar todos los métodos anteriormente descritos, se desarrolló un aplicativo en Fortran para manejar las cuatro estructuras de datos para matrices dispersas. Se muestran dos casos, uno de factorización LU con la matriz de entrada simétrica y dispersa, en formato CSC y las matrices LU en formato MSC, y otro, de gradiente conjugado con precondcionador ILUt(fil,tol) para una matriz de entrada almacenada en formato CSR y las matrices de salida en formato MSR.
Los datos de la Tabla 1, se traducen en la matriz de entrada A para la factorización LU del primer problema.
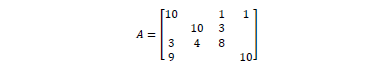
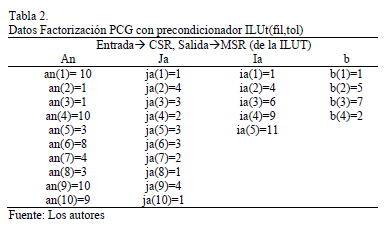
Los datos de la Tabla 2, se traducen en la matriz de entrada A para la factorización PCG con precondidinador ILUt(fil,tol) del segundo problema.
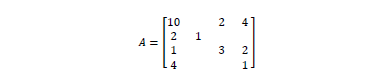
3. Resultados
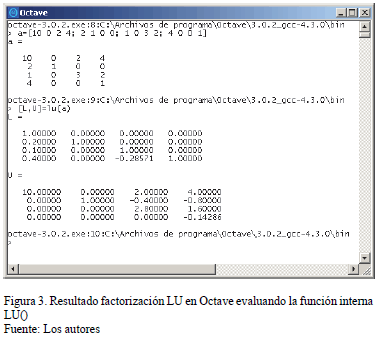
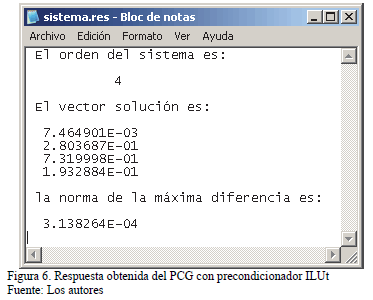
La Fig. 3 muestra los resultados obtenidos de la factorización LU realizada en el CAS OCTAVE (Sistema de Álgebra Computacional libre usado para la validación) y la Fig. 4 presenta la ventana que despliega los resultados de la factorización LU en formato MSC haciendo uso del software desarrollado en Fortran. Por su parte, en la Fig. 5, se muestra la solución del sistema lineal de ecuaciones de prueba en Octave empleando funciones internas propias del CAS.
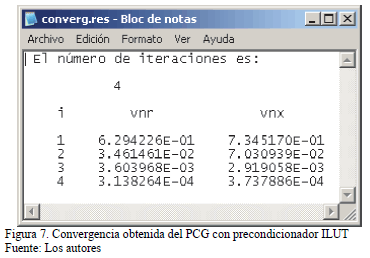
Las Figs. 6, 7 y 8 muestran respectivamente las ventanas que despliegan los resultados haciendo uso del software desarrollado en Fortran de la factorización PCG con precondicionador ILUt; la convergencia obtenida del PCG con precondicionador ILUt y la factorización ILUt en formato MSR. En la notación, vnr es el valor de la norma del residuo, vnx es el valor de la norma de la diferencia entre soluciones consecutivas.
4. Conclusiones
Los resultados conseguidos haciendo uso del CAS OCTAVE aunque no son en formatos comprimidos, permitieron validar numéricamente las salidas del software desarrollado en Fortran para la factorización LU y la solución de un sistema de ecuaciones lineales por el PCG precondicionado con ILUT, teniendo en cuenta que si bien las implementaciones son diferentes, las respuestas son muy similares.
A pesar que los sistemas para realizar las pruebas son pequeños, el verdadero poder de los algoritmos se encuentra en su aplicación a grandes sistemas procedentes de la discretización de EDP o de la resolución de cadenas de Markov. Se espera establecer en futuras pruebas, comparaciones en tiempos CPU (costo computacional) de la solución de sistemas de matrices dispersas grandes que permitan medir las ventajas de los formatos comprimidos, y con ello, muy seguramente se dispondrá mayores argumentos para emplear estos desarrollos en aplicaciones de gran complejidad numérica o en la solución de modelos numéricos de tipo industrial.
Referencias
[1] CIMNE, Introducción al Cálculo Paralelo, 2000. [ Links ]
[2] Fortes, C. et. al., Implementation of direct and iterative methods for a class of Helmholtz wave problems. Computers & Structures [Online]. 82 (17-19), pp. 1569-1579, 2004. Disponible en: http://www.sciencedirect.com/science/article/pii/S0045794904001439. DOI: 10.1016/j.compstruc.2004.03.053 [ Links ]
[3] Lin, Ch. and Moré, J., Incomplete Cholesky factorizations with limited memory. SIAM Journal on Scientific Computing [Online]. 21 (1), pp. 24-45, 2006. [Consultado: 4 de Septiembre de 2014]. Disponible en: http://epubs.siam.org/doi/abs/10.1137/S1064827597327334. DOI: 10.1137/S1064827597327334 [ Links ]
[4] Rodríguez, W. and Pallares, M., Three-dimensional modeling of pavement with dual load using finite element. DYNA 82 (189), pp. 30-38 2015. DOI: 10.15446/dyna.v82n189.41872 [ Links ]
[5] Saad, Y., ILUM: A multi-elimination ILU preconditioner for general sparse matrices. SIAM Journal on Scientific Computing [Online]. 17 (4), pp. 830-847, 2012. [Consultado: 27 de Noviembre de 2014]. Disponible en: http://epubs.siam.org/doi/abs/10.1137/0917054. DOI: 10.1137/0917054 [ Links ]
[6] Saad, Y. and Van der Vorst, H., Iterative solution of linear systems in the 20th century. SIAM Journal on Scientific Computing [Online]. 123 (1-2), pp. 1-33, 2001. [Consultado: 27 de Noviembre de 2014]. Disponible en: http://www.sciencedirect.com/science/article/pii/S037704270000412X DOI: 10.1016/S0377-0427(00)00412-X [ Links ]
[7] Saad, Y. and Zhang, J., BILUM: Block versions of multielimination and multilevel ILU preconditioner for general sparse linear systems. SIAM Journal on Scientific Computing [Online]. 20 (6), pp. 2103-2121, 2006. [Consulta: 1 de Mayo de 2015]. Disponible en: http://epubs.siam.org/doi/abs/10.1137/S106482759732753X. DOI: 10.1137/S106482759732753X [ Links ]
[8] Saad, Y. y Zhang, J., BILUTM: A domain-based multilevel block. ILUT preconditioner for general sparse matrices. SIAM Journal on Matrix Analysis and Applications [Online]. 21 (1), pp. 279-299, 2006. [Consulta 15 de Marzo de 2014]. Disponible en: http://epubs.siam.org/doi/abs/10.1137/S0895479898341268. DOI: 10.1137/S0895479898341268 [ Links ]
[9] Shen, Ch. And Zhang, J., Parallel two level block ILU preconditioning techniques for solving large sparse linear systems. Parallel Computing Journal-Elsevier [Online]. 28 (10), pp. 1451-1475, 2002. [Consulta: Junio de 2010]. Disponible en: http://www.sciencedirect.com/science/article/pii/S0167819102001473. DOI: 10.1016/S0167-8191(02)00147-3 [ Links ]
[10] Young, D., et al., Application of sparse matrix solvers as effective preconditioners. SIAM Journal on Scientific and Statistical Computing [Online]. 10 (6), pp. 1186-1199, 2006. [Consulta: Junio de 2004]. Disponible en: http://epubs.siam.org/doi/abs/10.1137/0910072. DOI: 10.1137/0910072 [ Links ]
[11] Zhang, J., Preconditioned iterative methods and finite difference schemes for convection-diffusion. Applied Mathematics and Computation-Elsevier. [Online]. 109 (1), pp. 11-30, 2000. [Citado Agosto de 2014]. Disponible en: http://www.sciencedirect.com/science/article/pii/S0096300399000132. DOI: 10.1016/S0096-3003(99)00013-2 [ Links ]
W. Rodríguez-Calderón, received the BSc. Eng in Civil Engineering in 1998 from the UIS, the MSc. degree in Numerical Methods in Engineering-UPC in 2002, is Dr. student in UFRGS, Brazil. He has worked as a professor and researcher for over fifteen years. Currently, he is a full professor in the Civil Engineering Program, Engineering Faculty, of the Universidad Cooperativa, Neiva, Colombia. His research interests include: simulation, modeling; statistical and computational intelligence techniques; and optimization using metaheuristics. ORCID: 0000-0001-9016-433X
M.R. Pallares-Muñoz, received the BSc. Eng in Civil Engineering in 1998, from the UIS, the MSc. degree in Numerical Methods in Engineering in 2004, form the UPC. She has worked as a professor and researcher for over ten years. Currently, he is a full professor in the Civil Engineering Program, Engineering Faculty, of the Universidad Surcolombiana, Neiva, Colombia. Here research interests include: simulation and computational modeling. ORCID: 0000-0003-4526-2357