Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.193 Medellín set./out. 2015
https://doi.org/10.15446/dyna.v82n193.45989
DOI: http://dx.doi.org/10.15446/dyna.v82n193.45989
An improvement to the classification based on the measurement of the similarity quality using fuzzy relations
Una mejora a la clasificación basada en la medida calidad de la similaridad utilizando relaciones borrosas
Yumilka B. Fernández-Hernández a, Yaima Filiberto a, Mabel Frias a, Rafael Bello b & Yaile Caballero a
a Facultad de Informática, Universidad de Camagüey, Camagüey, Cuba.{yumilka.fernandez, yaima.filiberto, mabel.frias, yaile.caballero}@reduc.edu.cu
b Centro de Estudios Informáticos, Universidad Central de Las Villas, Santa Clara, Cuba. rbellop@uclv.edu.cu
Received: October 10th, 2014.Received in revised form: May 4rd, 2015.Accepted: June 3rd, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
The learning of classification rules is a classic problem of the automatic learning. The algorithm IRBASIR for the induction of classification rules based on similaridad relations allows to discover knowledge starting from decision systems that contain features with continuous and discrete domains. This algorithm has shown to obtain higher results than other well-known algorithms. In this article, several modifications to this algorithm based on the Fuzzy sets theory are proposed, taking into account the measure quality of similarity. The experimental results show that using the fuzzy sets theory allow to obtain higher results than the original algorithm.
Keywords: classification rules; fuzzy sets; similarity relations.
Resumen
El aprendizaje de reglas de clasificación es un problema clásico del aprendizaje automático. El algoritmo IRBASIR para la inducción de reglas de clasificación basado en relaciones de similaridad permite descubrir conocimiento a partir de sistemas de decisión que contienen rasgos tanto discretos como continuos. El mismo ha mostrado obtener resultados superiores a otros algoritmos conocidos en este tema. En este artículo se proponen varias modificaciones a este algoritmo basadas en la Teoría de los Conjuntos Borrosos, debido a las ventajas que estos poseen, teniendo en cuenta la medida calidad de similaridad. Los resultados experimentales muestran que utilizando la Teoría de los Conjuntos Borrosos se obtienen resultados estadísticamente superiores al algoritmo original.
Palabras clave: reglas de clasificación; conjuntos borrosos; relaciones de similaridad.
1. Introducción
En este artículo se propone el empleo de relaciones borrosas en el algoritmo IRBASIR [1] el cual es un método de inducción de reglas de clasificación cuya principal ventaja es su utilización para sistemas de decisión con rasgos de condición heterogéneos, es decir, pueden existir tanto rasgos discretos como continuo. El mismo se distingue de otros métodos en que no requiere discretizar los dominios continuos, y la parte condicional de la regla no se expresa como una conjunción de condiciones elementales. El algoritmo se basa en el empleo de una relación de similaridad que permite construir las clases de similaridad de los objetos. Este algoritmo busca el conjunto mínimo de reglas siguiendo una estrategia de cubrimiento secuencial, para lo cual construye clases de similaridad de los objetos del sistema de decisión. Teniendo en cuenta estas características se proponen tres modificaciones a este algoritmo basadas en el uso de las relaciones borrosas por las ventajas que estas presentan y que se mencionan a continuación.
El tema de las relaciones borrosas es analizado por L.A. Zadeh en [2], en el cual se propone un marco conceptual unificado para el tratamiento de las relaciones. Las relaciones borrosas proporcionan un mayor grado de libertad para expresar las preferencias humanas y permiten cierta tolerancia [3,4]. Como un elemento importante de la SoftComputing [5], el uso de las relaciones borrosas hace los métodos computacionales más flexibles y tolerantes a la imprecisión, especialmente en el caso de datos mezclados (variables continuas y discretas).
Zadeh amplió la teoría clásica de conjuntos para poder operar con clases definidas por predicados vagos y logró esa ampliación generalizando el concepto de pertenencia a un conjunto A para el que sólo existían, hasta ese momento, dos posibilidades: x pertenece a A o x no pertenece a A, que expresado mediante la función característica o de elección de Boole se representa por mA(x) = 1 o mA(x) = 0, respectivamente. Zadeh introdujo la idea de los conjuntos borrosos Ã, caracterizados por funciones características generalizadas o funciones de pertenencia mÃ, cuyos valores no son sólo los números 0 y 1, sino todos los números entre 0 y 1; la pertenencia dejó de ser abrupta para ser graduada.
En los conjuntos borrosos la pertenencia a un conjunto es cuestión de grados entre el "pertenece" y "no pertenece", entre "verdadero" y "falso", son los grises situados entre el blanco y el negro. Generalizamos entonces la función característica, de modo tal que pueda tomar cualquier valor real del intervalo [0, 1].
Sea E un conjunto continuo o discreto, se llama subconjunto borroso de E (en inglés fuzzy set) a todo conjunto de pares ordenados (1):
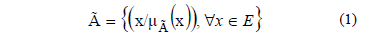
Donde: mà : E → [0 ,1] es la función característica de pertenencia y mÃ(x) es el grado o nivel de pertenencia de x a E.
La teoría de los conjuntos borrosos es ampliamente usada para resolver y analizar problemas en diferentes ramas de las investigaciones [6].
Por su parte los conjuntos aproximados han demostrado ser efectivos para el análisis de datos, siendo el aprendizaje automático una de las áreas de trabajo donde mayor interés ha despertado.
La Teoría de Conjuntos Aproximados (Rough Sets Theory, RST) fue introducida por Z. Pawlak en 1982 [7]. La filosofía de los conjuntos aproximados se basa en aproximar cualquier concepto, un subconjunto duro del dominio como por ejemplo, una clase en un problema de clasificación supervisada, por un par de conjuntos exactos, llamados aproximación inferior y aproximación superior del concepto. Con esta teoría es posible tratar tanto datos cuantitativos como cualitativos, y en particular son útiles para tratar la incertidumbre causada por inconsistencias en la información; la inconsistencia describe una situación en la cual hay dos o más valores en conflicto para ser asignados a una variable [8].
Entre las ventajas de la RST para el análisis de datos está que solo se basa en los datos originales y no necesita cualquier información externa; no es necesaria ninguna suposición acerca de los datos [9].
Se ha utilizado en muchas investigaciones el uso de los conjuntos borrosos unido al uso de los conjuntos aproximados [10], lo cual se denomina Conjuntos Borrosos Aproximados (Fuzzy Rought Set).
Los Conjuntos Borrosos Aproximados han tenido amplia aplicación en la rama del aprendizaje- máquina, pero también ha sido útil para la recuperación de la información mejorada [11] y se han presentado trabajos sobre la aplicación de estos conjuntos en el contexto de los Sistemas de Información de Investigación Actuales (CRISs)( Current Research Information Systems) [12].
Teniendo en cuenta las características de los conjuntos borrosos y los conjuntos aproximados, se le han realizado modificaciones al algoritmo IRBASIR que es utilizado para el descubrimiento de reglas de clasificación.
El mismo está basado en la medida calidad de la similaridad, lo cual conlleva a que su desempeño depende del uso de algunos parámetros, entre ellos dos umbrales que permiten definir la similaridad entre los objetos (expresiones (2) y (3)); la novedad de este trabajo radica en usar los conjuntos borrosos para facilitar el uso de algunos parámetros en el algoritmo IRBASIR.
2. Trabajos relacionados
En la literatura [13] se utilizan diferentes algoritmos para clasificación de reglas, dentro de los más conocidos se encuentran LEM2, EXPLORE y MODLEM. El primero basa su funcionamiento en tratar de encontrar un subconjunto mínimo de reglas que permita realizar la clasificación. LEM2 resuelve la inconsistencia usando la teoría de los conjuntos aproximados.
Por su parte el algoritmo EXPLORE extrae de los datos todas las reglas de decisión que cumplen determinados requisitos. El algoritmo puede manejar ejemplos inconsistentes ya sea mediante el uso de la teoría de los conjuntos aproximados, para definir las aproximaciones de las clases de decisión, o mediante la determinación de umbral apropiado para la confianza de las normas inducidas a ser utilizados en la pre-poda.
El algoritmo MODLEM realiza un cubrimiento secuencial generando un conjunto mínimo de reglas de decisión para cada concepto de decisión (clase de decisión y en caso de ejemplos inconsistentes). Este conjunto mínimo de reglas (también llamado cubrimiento local) intenta cubrir todos los ejemplos positivos del concepto de decisión dado.
En [14] se proponen 3 técnicas para clasificación de reglas en conjuntos que tienen datos de tipo numérico, estas técnicas llevan en su proceso la discretización de los mismos.
En [1] se propone el algoritmo IRBASIR. Este algoritmo permite descubrir conocimiento a partir de sistemas de decisión que contienen tanto rasgos con dominio discreto como continuo, pues la diferencia entre ambos tipos de dominios sólo radica en la función de comparación de rasgos que se utilice; lo cual hace que no requiera realizar ningún proceso de discretización, ni antes del aprendizaje como ID3 o LEM2 ni durante el aprendizaje como C4.5 o MODLEM.
3. Medida calidad de la similaridad basada en conjuntos borrosos
El método de construcción de relaciones de similaridad propuesto en [15] se basa en la medida calidad de la similaridad y esta a su vez en las relaciones R1 y R2 definidas por las expresiones (2) y (3):
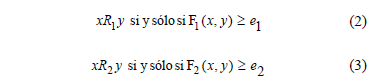
donde la función F1(x,y) se define por la expresión (4):
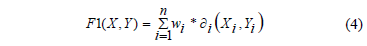
donde: n es la cantidad de rasgos; wi es el peso del rasgo i; Xi, Yi son los valores del rasgo i en los objetos X, Y respectivamente; 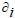 es la función de comparación para el rasgo i. Así de esta forma, el cálculo de la inseparabilidad entre dos objetos depende del conjunto de pesos wi, pues usualmente las funciones de comparación de los rasgos se conocen.
es la función de comparación para el rasgo i. Así de esta forma, el cálculo de la inseparabilidad entre dos objetos depende del conjunto de pesos wi, pues usualmente las funciones de comparación de los rasgos se conocen.
Este enfoque tiene el problema de necesitar los umbrales e1 y e2, los cuales se convierten en parámetros del método, y como es conocido los parámetros pueden introducir grados de dificultad en el desempeño de los algoritmos. Seguidamente se propone un enfoque basado en el empleo de conjuntos borrosos para flexibilizar el papel de los umbrales e1 y e2.
Las relaciones (2) y (3) se sustituyen por las relaciones (5) y (6):
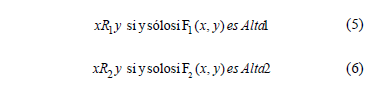
donde Alta1 y Alta2 son conjuntos borrosos definidos por las expresiones (7) y (8) para calificar la similaridad entre los objetos x e y respecto a los rasgos de condición y el rasgo de decisión respectivamente. Los valores utilizados en (7) y (8) se deben a los buenos resultados obtenidos con estos.
Alta 1
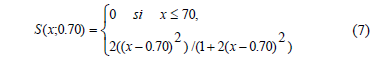
Alta 2
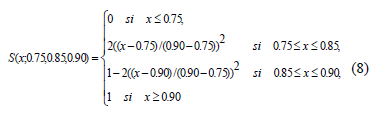
Nótese que definidas de esta forma las relaciones R1 y R2 son relaciones binarias borrosas según [16].
A partir de los conjuntos borrosos Alta1 y Alta2 se pueden construir los conjuntos borrosos N1(x) y N2(x) según las expresiones (9) y (10):
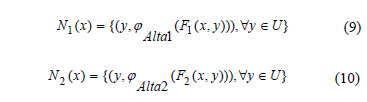
El grado de similaridad entre ambos conjuntos para un objeto x se calcula como la semejanza entre los conjuntos borrosos N1(x) y N2(y) [17] mediante la expresión (11):
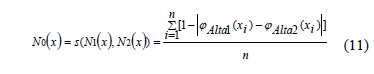
Usando la expresión (11) la medida calidad de la similaridad de un sistema de decisión (Decision System, DS) con un universo de N objetos se define por (12):
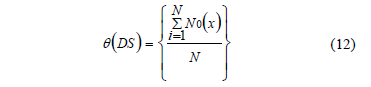
4. Algoritmo IRBASIR y nuevas modificaciones
4.1. Algoritmo IRBASIR (Inducción de Reglas Basado Enrelaciones de Similaridad)
El algoritmo IRBASIR funciona teniendo en cuenta que dado un sistema de decisión DS=(U, AÈ{d}), con m objetos, el conjunto A contiene n rasgos de dominios continuos o discretos.
P1. Definir las medidas de similaridad locales.
Construir las funciones de comparación de rasgos ¶i(x,y) para cada rasgo en A, tales que permiten comparar los valores de ese rasgo; por ejemplo la expresión (13)
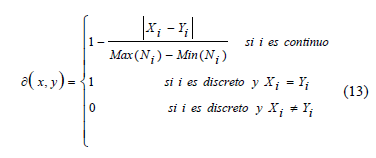
P2. Construir una relación de similaridad R, como la definida por (2) donde F1 puede estar definida como (4).
P3. Construir reglas de clasificación según el procedimiento GenRulesRST basado en R.
Activar GenRulesRST.
Para encontrar los valores wi para (4) se propone usar el método PSO+RST publicado en [18]. El procedimiento GenRulesRST genera reglas de clasificación y sus correspondientes valores de certidumbre.
Procedimiento GenRulesRST
Este es un procedimiento iterativo en el cual se buscan objetos del sistema de decisión no tenidos en cuenta previamente, se construye su clase de similaridad usando una relación de similaridad y se construye una regla de la forma Si Swi*¶i()≥e entonces Q que cubra los objetos que tienen como valor de decisión la clase mayoritaria en la clase de similaridad. Se usa un arreglo de m componentes, denominado Usado [], en el cual Usado[i] tiene un valor 1 si el objeto ya fue usado por el procedimiento GenRulesRST, ó 0 en otro caso.
P1: Inicializar contador de objetos
Usado[j] ← 0, para j=1, ,m
RulSet ← f
i ← 0
P2: Comienza procesamiento del objeto Oi
i ← índice del primer objeto no usado
Si i=0 entonces Fin del proceso de generación de reglas.
Sino Usado[i] ← 1
P3: Construir la clase de similaridad del objeto Oi según R
Calcular [Oi]R [x]R denota la clase de similaridad del objeto x
P4: Generación de una regla de decisión
Si |f([Oi]R)|=1 entonces {/*Construir la regla que describa esta clase de similaridad con consecuente igual al valor de decisión del objeto Oi*/
k ← d(Oi)
C ← [Oi]R}
Sino { /*Construir la regla que describa esta clase de similaridad con consecuente igual al valor de decisión mayoritario en [Oi]R */
k ← valor de decisión mayoritario de los objetos en [Oi]R
C ← objetos de [Oi]R con clase k}
Activar GenRulSim(k, [Oi]R, C; Rul) /* este procedimiento construye una regla de decision*/
RulSet ← RulSet U { Rul }
P5: Marcar como usados a todos los objetos en C cubiertos por la regla Rul y con consecuente k.
P6: Ir a P2
Donde |f([Oi]R)| denota la cantidad de valores de decisión distintos de los objetos en la clase de similaridad [Oi]R.
Procedimiento GenRulSim(k, Cs, C; Rul)
Este procedimiento construye una regla de decisión que se retorna en Rul a partir de los parámetros de entrada k (denota una clase de decisión), Cs (clase de similaridad del objeto que se procesa) y C (subconjunto de Cs conteniendo solo los objetos de clase k).
P1: Construir un vector P con n componentes de referencia (uno para cada rasgo de condición) para el conjunto de objetos en C.
P(i) ← f(Vi), donde Vi es el conjunto de valores del rasgo i en los objetos en C
P2: Generar la regla a partir del vector de referencia P.
Rul ← If w1*¶1(X1,P1)+ + wn*¶n(Xn,Pn) ≥ e then d=k
Donde los pesos wi son tomados de la función F1, expresión (4); e es el umbral usado en la relación de similaridad R; Pi es el valor del rasgo i en el vector de referencia P; y ¶i es la función de comparación para el rasgo i.
P3: Calcular la certidumbre de la regla.
Considerar las medidas de accuracy (Acc) y coverage (Cov):
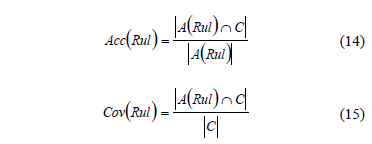
Donde A(Rul) es el conjunto de objetos en Cs para los cuales el antecedente de la regla Rul se cumple.
En el paso P1 de GenRulSim la función f denota un operador de agregación; por ejemplo: Si los valores en Vi son reales se debe usar el promedio, si son discretos, la moda. El propósito es construir un prototipo o centroide para un conjunto de objetos similares. Aquí se ha usado un enfoque parecido a como se hace en el algoritmo k-mean [19].
4.2. Modificaciones al algoritmo IRBASIR.
El uso de relaciones borrosas plantea un problema para usar el algoritmo IRBASIR para descubrir reglas de decisión, ya que este se basa en utilizar la clase de similaridad de un objeto para a partir de ella construir un prototipo de esa clase de similaridad, y usando el prototipo se construye la regla de decisión. Pero ahora la clase de similaridad contiene todos los objetos, lo que con un grado distinto de pertenencia, de modo que no es posible construir el prototipo de cada clase de similaridad. Seguidamente se proponen varias alternativas para construir la clase de similaridad, y a partir de ella poder usar el algoritmo IRBASIR.
Variante 1 (IRBASIRV1-F): Modificación del Paso 2 al Algoritmo IRBASIR[1], utilizando la Reducción al caso duro usando un alfa-corte[20].
Una alternativa para enfrentar el problema es usar una relación dura para construir la clase de similaridad, para lo cual se puede usar un enfoque basado en el concepto de alfa-corte. De modo que la clase de similaridad de un objeto x se define por la expresión (16):
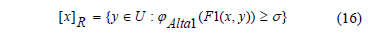
Donde s se utiliza con el valor 0.70, pues con ese valor los resultados obtenidos son mejores. Y se utiliza ese mismo valor de sigma como umbral para construir la condición de la regla de decisión que se genera a partir de esta clase de similaridad.
Variante 2(IRBASIRV2-F): Modificación del Algoritmo IRBASIR[1] en el Paso 2, utilizando cardinalidad media.
En [21] se define el concepto de cardinalidad de un gránulo de información borroso (fuzzy information granule) de la forma siguiente:
Sea un universo de objetos U=
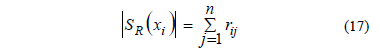
Basándose en esta definición se propone construir la clase de similaridad de un objeto xi como el conjunto de objetos del universo cuyo grado de similaridad con xi sea superior a la cardinalidad media del gránulo SR(xi), y se define por la expresión (18):
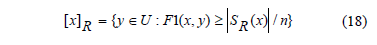
Variante 3 (IRBASIR-V3): Modificación del método de cálculo de peso utilizado por IRBASIR (en el Paso 2[18]) para encontrar el conjunto de pesos, utilizando Alta 1 y Alta 2 (7) y (8).
El peso de los atributos utilizando los conjuntos borrosos se calculó usando las expresiones (7) y (8) para Alta 1 y Alta 2, respectivamente.
5. Resultados experimentales
Con el fin de evaluar la precisión de las modificaciones propuestas se realizó el siguiente estudio. Se compararon las modificaciones con el algoritmo original IRBASIR [1] y con IRBASIR-RED [22] y el que obtuvo mejores resultados se comparó con 4 algoritmos: C4.5 implementado en la herramienta KEEL [23]; LEM2, MODLEM y EXPLORE de la herramienta ROSE2.
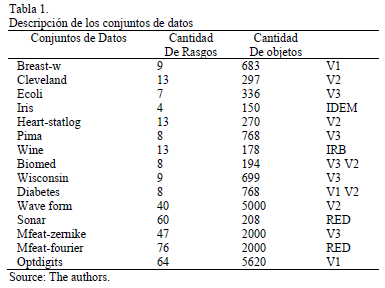
Para realizar los experimentos se seleccionaron 15 conjuntos de datos tomados de University of California, Irvine (UCI) repository [24] que fueron particionados utilizando validación cruzada 10 fcv (tenfold crossvalidation) [25]. En la Tabla 1 se resumen las propiedades de los conjuntos de datos seleccionados.
Experimento 1: Comparar los resultados de precisión de los métodos propuestos para cada uno de los conjuntos de datos, para las diez particiones que se realizaron.
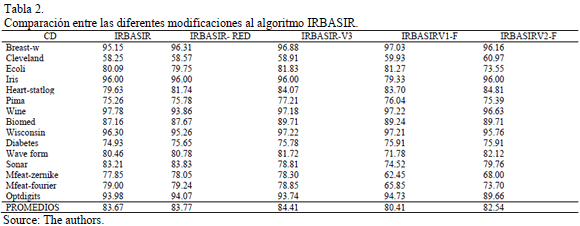
Objetivo: Determinar cuál de los algoritmos propuestos es significativamente superior al resto, en cuanto a la exactitud general de la clasificación. En la Tabla 2 se muestran los resultados experimentales de la comparación entre los algoritmos.
Experimento 2: Comparar la precisión del mejor de los algoritmos propuestos con el resto de los clasificadores para cada uno de los conjuntos de datos, para las diez particiones que se realizaron.
Objetivo: Determinar si este método es significativamente superior o al menos similar, al resto de los algoritmos, en cuanto a la exactitud general de la clasificación.
En la Tabla 2 se muestran los resultados experimentales de la comparación entre los algoritmos. Al final de cada columna está el valor promediado de cada algoritmo. Para comparar los resultados se utilizaron test de comparaciones múltiples con el fin de encontrar el mejor algoritmo.
Según los resultados obtenidos en la Tabla 2 se puede observar que IRBASIRV1-F e IRBASIRV3- obtienen mejores resultados para bases pequeñas con pocos atributos (breast-w, ecoli, diabetes, pima, biomed, wisconsin), para bases pequeñas con una cantidad mayor de atributos IRBASIRV2-F realiza mejor la clasificación. Los resultados para bases grandes demuestran que si son menos atributos (waveform, mfeat-zernike) la clasificación la realiza mejor IRBASIRV2-F e IRBASIRV3-, con más atributos (64) obtiene mejores resultados IRBASIRV1-F; mientras que con 76 atributos(mfear-fourier), el algoritmo IRBASIR-RED, que utiliza selección de atributos es mejor.
En la Tabla 3 se puede observar que el mejor ranking entre los algoritmos propuestos lo tiene IRBASIR-V3. El Test de Iman-Davenport (F-distribution con 2 y 28 grados de libertad) fue empleado con el fin de encontrar diferencias significativas entre los algoritmos propuestos, obteniendo mediante el Test de Friedman valor de p-value: 0.386741. De esta forma en la Tabla 4 se muestran los resultados del procedimiento de Holm para comparar los algoritmos propuestos.
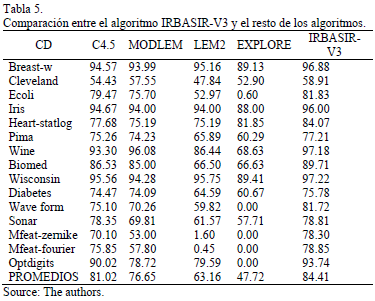
En la Tabla 5 se puede observar como la precisión de la clasificación es mejor para el algoritmo seleccionado (IRBASIR-V3) teniendo en cuenta el promedio general de la misma.
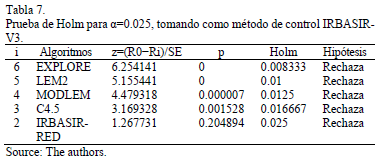
Como se puede observar en las Tablas 6 y 7 el método IRBASIR-V3 es significativamente superior a LEM2, MODLEM, EXPLORE, C4.5, IRBASIR-RED e IRBASIR.
Teniendo en cuenta los resultados de los experimentos 1 y 2 el algoritmo que obtiene mejores resultados de forma general, valorando el promedio general de la clasificación de todas las bases es el algoritmo IRBASIR-V3.
6. Conclusiones
En este artículo se propusieron tres modificaciones al algoritmo IRBASIR (IRBASIR-V3, IRBASIRV1-F, IRBASIRV2-F) utilizando relaciones de similaridad borrosas, y se realizaron estudios que incluyeron la comparación con otros métodos. Teniendo presente que los algoritmos no obtienen el mismo comportamiento para todas las bases, los resultados experimentales muestran que de todos los algoritmos IRBASIR-V3, donde se modifica el método de cálculo de peso en el Paso 2 [23] que utiliza IRBASIR, utilizando conjuntos borrosos, obtiene resultados estadísticamente superiores que los demás.
Referencias
[1] Filiberto, Y. y Bello, R., Algoritmo para el aprendizaje de reglas de clasificación basado en la teoría de los conjuntos aproximados extendida, DYNA 78 (169), pp. 62-70, 2011. [ Links ]
[2] Zadeh, L.A., Similarity relations and fuzzy orderings, Information Sciences 3, pp. 177-200, 1971. [ Links ]
[3] Bodenhofer, U., A similarity-based generalization of fuzzy orderings preserving the classical axioms. International Journal on Uncertainty and Fuzziness Knowledge-Based Systems, 8 (5), pp. 593-610, 2000. DOI: 10.1142/S0218488500000411 [ Links ]
[4] Martín, G., Cornelis, C. and Naessens H., Personalizing information retrieval in CRISs with fuzzy sets and rough sets, Proceedings of the 9th International Conference on Current Research Information Systems (CRIS2008), pp. 51-59, 2008. [ Links ]
[5] Verdegay, J.L., Yager R.R. and Bonissone P.P., On heuristics as a fundamental constituent of soft computing. Fuzzy Sets and Systems 159, pp. 846-855, 2008. DOI: 10.1016/j.fss.2007.08.014. [ Links ]
[6] Mendel, J.M., Uncertain rule-based fuzzy logic systems, Prentice Hall PTR, Upper Saddle River, New Jersey, 2001. [ Links ]
[7] Pawlak, Z., Rough Sets. International Journal of Computer and Information Sciences 11, pp. 341-356, 1982. DOI: 10.1007/BF01001956. [ Links ]
[8] Parsons, S., Current approaches to handling imperfect information in data and knowledges bases. IEEE Trans. On knowledge and data enginnering, 8 (3), 1996. DOI: 10.1109/69.506705. [ Links ]
[9] Tay, F.E. and Shen, L., Economic and financial prediction using rough set model. European Journal of Operational Research 141, pp.641-659, 2002. DOI: 10.1016/S0377-2217(01)00259-4. [ Links ]
[10] Cornelis, C., De Cock, M. and Kerre, E., Intuitionistic fuzzy rough sets: At the crossroads of imperfect knowledge Expert Systems, 20 (5), pp. 260-270, 2003. DOI: 10.1111/1468-0394.00250. [ Links ]
[11] De Cock, M. and Cornelis, C., Fuzzy rough set based web query expansion, Proceedings of Rough Sets and Soft Computing in Intelligent Agent and Web Technology, International Workshop at WIIAT2005, pp. 9-16, 2005. [ Links ]
[12] Magalhães, S.T., Rough Sets, International Journal of Computer and Information Sciences 11 (5), pp. 341-356, 1982. [ Links ]
[13] Charchalis, A. and Pawletko, R., The use of expert system for marine diesel engine diagnosis. Zeszyty Naukowe Akademii marynarki Wojennej Rok LIII NR 1 (188), pp. 49-56, 2012. [ Links ]
[14] Grzymala-Busse, J., Three strategies to rule induction from data with numerical attributes. Transactions on Rough Sets II, LNCS 3135, pp. 54-62, 2004. DOI: 10.1007/978-3-540-27778-1_4 [ Links ]
[15] Filiberto, Y., Caballero, Y., Larrua, R. and Bello, R., A method to build similarity relations into extended rough set theory, In: Proceedings of the 10th International Conference on Intelligent Systems Design and Applications (ISDA 2010), pp. 1314-1319, 2010. DOI: 10.1109/ISDA.2010.5687091. [ Links ]
[16] Hu Q.H., Xie Z.X. and Yu D.R., Hybrid attribute reduction based on a novel fuzzy-rough model and information granulation, Pattern Recognition 40, pp. 3509-3521, 2007. DOI: 10.1016/j.patcog.2007.03.017. [ Links ]
[17] Wang, W., New similarity measures on fuzzy sets and on elements. Fuzzy Sets and Systems 85 (3), pp. 305-309, 1997. DOI: 10.1016/0165-0114(95)00365-7. [ Links ]
[18] Filiberto, Y., et al., Using PSO and RST to predict the resistant capacity of connections in composite structures, In: International Workshop on Nature Inspired Cooperative Strategies for Optimization (NICSO 2010) Springer, pp. 359-370, 2010. DOI: 10.1007/978-3-642-12538-6_30. [ Links ]
[19] Xindong, W., Top 10 algorithms in data mining. Knowledge Information System 14, pp. 1-37, 2008. DOI: 10.1007/s10115-007-0114-2 [ Links ]
[20] Sivanandam, S.N., Sumathi, S. and Deepa, S.N., Introduction to fuzzy logic using MATLAB. Springer-Verlag Berlin Heidelberg, 2007. DOI: 10.1007/978-3-540-35781-0. [ Links ]
[21] Hu, Q.H., Yu, D.R., Xie Z.X. and Liu, J.F., Fuzzy probabilistic approximation spaces and their information measures, IEEE Transactions on Fuzzy Systems, 14 (2), pp. 191-201, 2006., DOI: 10.1109/TFUZZ.2005.864086 [ Links ]
[22] Fernández Y., Bello R., Filiberto Y., F, Frias M., Caballero Y., Effects of using reducts in the performance of the IRBASIR algorithm, DYNA, 80 (182), pp. 182-190, 2013. [ Links ]
[23] Alcalá-Fdez, J., Fernandez, A., Luengo, J., Derrac, J., García, Sánchez, S. and Herrera, L.F. KEEL Data-Mining software tool: Data set repository, integration of algorithms and experimental analysis framework. Journal of Multiple-Valued Logic and Soft Computing 17 (2-3) pp. 255-287, 2011. [ Links ]
[24] Asuncion, A. and Newman D., UCI machine learning repository. A study of the behaviour of several methods for balancing machine learning training data. SIGKDD Explorations 6 (1), pp. 20-29, 2007. [ Links ]
[25] Demsar, J., Statistical comparisons of classifiers over multiple data sets. Journal of Machine Learning Research (7), pp. 1-30, 2006. [ Links ]
Y.B. Fernández-Hernández, recibió su título de Ing. Informática en 2004 en la Universidad de Camagüey (UC), Cuba y MSc. en Teleinformática en 2006 en la Universidad Central de Las Villas (UCLV), Cuba. Su interés científico se encuentra en la disciplina de la inteligencia artificial, en particular el aprendizaje de máquina, softcomputing, y la toma de decisión. Ha participado en congresos internacionales y con alto nivel científico. Es miembro del Grupo de Investigación en Inteligencia Artificial. ORCID: 0000-0002-9569-5348
Y. Filiberto, Recibida en Ing. Informática en 2006 y MSc. en Informática Aplicada en 2008, en la Universidad de Camagüey (UC), Cuba y Dra. en 2012 en la Universidad Central de Las Villas (UCLV), Cuba. Su interés científico se encuentra en la disciplina de la inteligencia artificial, en particular el aprendizaje de máquina, KDD y toma de decisiones. Ha publicado alrededor de 30 trabajos científicos. Actualmente directora de ciencia y técnica en la Universidad de Camagüey, Cuba. ORCID: 0000-0003-2279-2953
M.Frías, recibió su título de Licenciado en Ing. Informática de la Universidad de Camagüey, Cuba, en 2011. MSc. en Ciencia de la Computación en 2015. Es profesor de la Facultad de Informática. Su interés científico se encuentra en la disciplina de la inteligencia artificial, en particular el aprendizaje de la máquina y softcomputing. Es miembro del grupo de Investigación en Inteligencia Artificial. ORCID: 0000-0001-7361-6680
R. Bello, recibió su título de Licenciado en Cibernética y Matemáticas en la Universidad Central de Las Villas (UCLV), Cuba, en 1982, y Dr. en 1987. Su interés científico se encuentra en la disciplina de inteligencia artificial, sobre todo metaheurísticas, softcomputing, aprendizaje de máquina, y la toma de decisiones. Ha publicado alrededor de 200 trabajos científicos. Es miembro de la Academia Cubana de la Ciencia y el Director del Centro de Estudios en Informática de la UCLV. ORCID: 0000-0001-5567-2638
Y. Caballero, recibió su título de Licenciado en Ciencias de la Computación en la Universidad Central de Las Villas (UCLV), Cuba, en 2001, y Dra. en 2007. El interés científico es en la disciplina de inteligencia artificial, en particular metaheurísticas, Softcomputing, aprendizaje de máquina, y la toma de decisión. Ha publicado más de 140 trabajos científicos. Es miembro de la Academia Cubana de la Ciencia. ORCID: 0000-0002-6725-5812